Abstract
Performance on visual working memory tasks decreases as more items need to be remembered. Over the past decade, a debate has unfolded between proponents of slot models and slotless models of this phenomenon. Zhang and Luck (2008) and Anderson, Vogel, and Awh (2011) noticed that as more items need to be remembered, “memory noise” seems to first increase and then reach a “stable plateau.” They argued that three summary statistics characterizing this plateau are consistent with slot models, but not with slotless models. Here, we assess the validity of their methods. We generated synthetic data both from a leading slot model and from a recent slotless model and quantified model evidence using log Bayes factors. We found that the summary statistics provided, at most, 0.15% of the expected model evidence in the raw data. In a model recovery analysis, a total of more than a million trials were required to achieve 99% correct recovery when models were compared on the basis of summary statistics, whereas fewer than 1,000 trials were sufficient when raw data were used. At realistic numbers of trials, plateau-related summary statistics are completely unreliable for model comparison. Applying the same analyses to subject data from Anderson et al. (2011), we found that the evidence in the summary statistics was, at most, 0.12% of the evidence in the raw data and far too weak to warrant any conclusions. These findings call into question claims about working memory that are based on summary statistics.
The English novelist Samuel Butler stated that “life is the art of drawing sufficient conclusions from insufficient premises” (Jones, 1912). Nothing is truer in the empirical sciences, where data are generally noisy and time to collect them is limited. In such a setting, progress critically depends on the application of proper statistical techniques to assess the evidence that data provide for different candidate models. Virtually all reputable model comparison techniques are directly or indirectly based on the probability of the raw data (in psychophysics: individual-trial subject responses) given a hypothesized model and a hypothesized set of model parameters. This probability is called the likelihood of the model and its parameters, and common methods, like Bayes factors (Kass & Raftery, 1995), the Akaike information criterion (Akaike, 1974), the Bayesian information criterion (Schwartz, 1978), and the deviance information criterion (Spiegelhalter, Best, Carlin, & Van der Linde, 2002), are all derived from it.
In recent years, many papers have debated the nature of working memory limitations (including Alvarez & Cavanagh, 2004; Anderson & Awh, 2012; Anderson, Vogel, & Awh, 2011; Bays, Catalao, & Husain, 2009; Bays, Gorgoraptis, Wee, Marshall, & Husain, 2011; Bays & Husain, 2008; Buschman, Siegel, Roy, & Miller, 2011; Donkin, Nosofsky, Gold, & Shiffrin, 2013; Elmore et al., 2011; Fougnie, Suchow, & Alvarez, 2012; Fukuda, Awh, & Vogel, 2010; Heyselaar, Johnston, & Pare, 2011; Keshvari, Van den Berg, & Ma, 2013; Lara & Wallis, 2012; Luck & Vogel, 2013; Rouder, Morey, Cowan, Morey, & Pratte, 2008; Sims, Jacobs, & Knill, 2012; Van den Berg, Awh, & Ma, 2014; Van den Berg, Shin, Chou, George, & Ma, 2012; Wilken & Ma, 2004; Zhang & Luck, 2008). A key aspect of this debate has been whether or not there exists an upper limit to the number of items that can be held in visual working memory. The common metaphor is that visual working memory consists of “slots” that can “hold” items; when the slots are full, extra items are discarded. By contrast, in a “slotless” model, the quality of a memory would gradually decrease as more items have to be remembered but no items are completely discarded (Palmer, 1990; Wilken & Ma, 2004).
To compare slot models with slotless models, many studies have, appropriately, used model likelihoods based on raw data (e.g., Donkin et al., 2013; Fougnie et al., 2012; Keshvari, Van den Berg, & Ma, 2013; Lara & Wallis, 2012; Rouder et al., 2008; Sims et al., 2012; Van den Berg et al., 2014). Among the studies that have not, two stand out because of the strong evidence in favor of slot models they appear to provide: Zhang and Luck (2008), which we will refer to as paper 1, and Anderson et al., 2011, which we will refer to as paper 2. Subsequent papers by Anderson, Vogel, and Awh (Anderson & Awh, 2012; Anderson, Vogel, & Awh, 2013) used very similar methods. These studies have been heralded as strong evidence in favor of slot models (Luck & Vogel, 2013), and therefore, a close examination of their methods is highly relevant to the debate on working memory limitations.
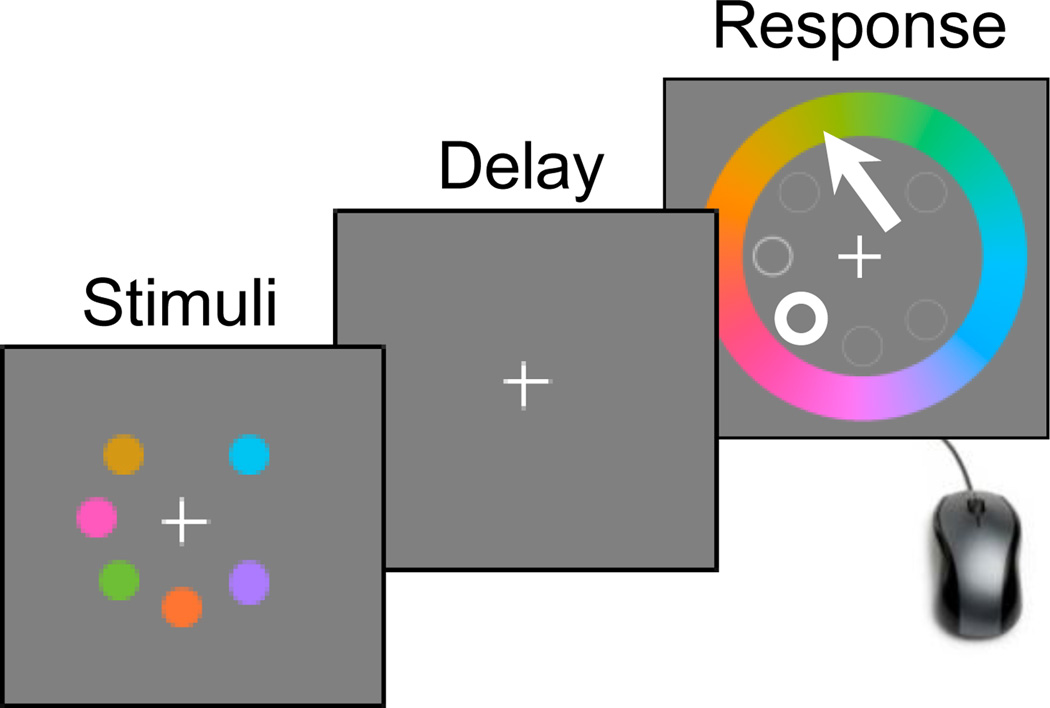
Papers 1 and 2 both use the delayed-estimation task developed by Wilken and Ma (2004). In this task (Fig. 1), observers estimate, on a continuous scale, the remembered feature value of a target item chosen randomly from a set of items in a sample display. For example, color memory was tested by having subjects click on a color wheel to report the color they remembered of an item that was previously present at an indicated position. The data from delayed-estimation experiments are captured by error histograms, one for each set size (number of items to be remembered). Error histograms based on the data from paper 2, made available by its authors, are shown in Fig. 2a.
Fig. 1.
Trial procedure of a typical delayed-estimation experiment (Wilken & Ma, 2004). Subjects view a set of items and, after a delay, report the value of one item—for instance, by clicking on a color wheel
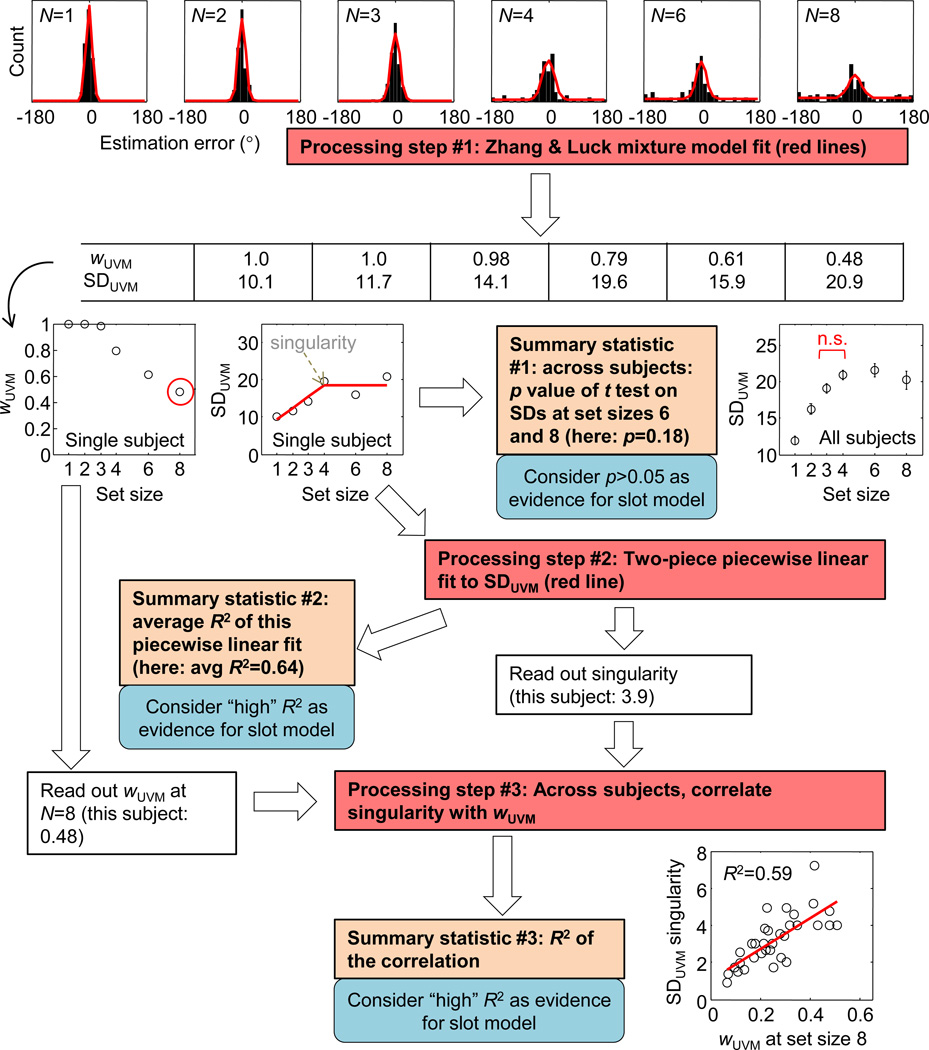
Fig. 2.
Model comparison methods used by Zhang and Luck (2008) and Anderson et al. (2012). Raw data consist of distributions of estimation errors, one for each set size (top row). Both papers fit a mixture of a uniform distribution and a Von Mises distribution to the raw data (red curves). The mixture model has two parameters: the weight of the Von Mises component (wUVM) and its circular standard deviation (SDUVM). Both papers observe a “plateau” in SDUVM at higher set sizes, and proceed to compare slot and slotless models on the basis of the p value of a t test on differences in SDUVM values between two set sizes. Paper 2 applies further data-processing steps to obtain two more summary statistics that are used for model comparison
To summarize the information in such sets of response errors, Paper 1 introduced an analysis method by which a mixture of a uniform distribution and a Von Mises (circular normal) distribution is fitted to the measured errors at a given set size (Fig. 2a, red lines). The uniform distribution is assumed to correspond to random guesses, the Von Mises distribution to estimates of a memorized item. Paper 2 applied the same method. Both papers observed that the width of the Von Mises distribution (which we refer to as SDUVM) increases at small set sizes but then seems to stay constant. They performed a set of t tests between the SDUVM values at different set sizes to confirm the existence of a plateau in SDUVM at larger set sizes. They explained this apparent plateau by postulating that an item either is assigned a slot and receives resource or is not and receives no resource. When set size is smaller than the number of slots, adding items results in less resource per item and a wider Von Mises component in the mixture fit. When there are more items than slots, however, the number of remembered items in a slot model is always equal to the number of slots; hence, adding items will not result in a widening of the Von Mises component in the mixture model.
The width of the Von Mises distribution at a given set size is an example of a summary statistic, a quantity that is derived from the raw data that is intended to capture their essence. Papers 1 and 2 introduced several other summary statistics based on this plateau prediction of the slot model, one of which is the p value of the above-mentioned t test. The main claim of both papers is that the values of the summary statistics computed from subject data provide strong evidence for their slot model and rule out the entire class of slotless models.
Here, we evaluated how well the slot model proposed in papers 1 and 2 can be distinguished from the slotless model of Van den Berg et al. (2012) by either the raw data or one of the plateau-related summary statistics. Using synthetic data sets, we found that the two models could be recovered near-perfectly from the raw data but only poorly from the summary statistics. Moreover, the expected model evidence in the summary statistics was, at most, 0.15% of that in the raw data. Repeating our analysis on subject data from paper 2, we found that the summary statistics provide, at most, 0.12% of the evidence in the raw data. Taken together, our results show that the model comparison methods used in papers 1 and 2 are untrustworthy and, therefore, that the conclusions of those papers are premature. More generally, we conclude that the field must stop using summary statistics for model comparison and, instead, use methods based on model likelihoods obtained from raw data.
Background
Figure 2 and Table 1 illustrate the rather involved processing steps that papers 1 and 2 go through to compute summary statistics.
Table 1.
Description of the raw data and the summary statistics used by Papers 1 and 2
| Type of Data D | Notation | Definition |
| Raw Data | Estimation Errors on Individual Trials | |
| Summary statistic #1 | p value of t test | p value of t test on SDUVM between set sizes 3 and 4 |
| Summary statistic #2 | R2 of piecewise linear | Coefficient of determination of the piecewise linear fit to SDUVM as a function of set size |
| Summary statistic #3 | R2 of singularity | Correlation between the singularity in the piecewise linear fit and wUVM at set size 8 |
Summary statistic #1: p value of t test on SD in set sizes 3 and 4
In the slot model of papers 1 and 2, when set size exceeds working memory capacity K, each remembered item is remembered with the same mnemonic noise, regardless of set size. Hence, the slot model predicts that mnemonic noise is constant for set sizes that exceed K. By contrast, a slotless model would predict that mnemonic noise keeps increasing indefinitely, because all items are remembered and mnemonic precision decreases with set size. On the basis of this presumed difference, papers 1 and 2 reasoned that if a subject shows no significant difference between estimated mnemonic noise at two set sizes that presumably are equal to or greater than K, this would provide strong evidence for the presence of a slot limit.
To examine this quantitatively, paper 1 introduced an analysis method in which a mixture of a uniform and a Von Mises (circular normal) distribution is fitted to a subject’s estimation errors at a particular set size (processing step #1 in Fig. 1):
| (1) |
where y is an estimation error and I0 is the modified Bessel function of the first kind of order zero (here and elsewhere, it is assumed that stimuli, estimates, and estimation errors have the domain [0,2π)). The weight and concentration parameter of the Von Mises component, denoted wUVM and κUVM, respectively, are free parameters, which were fitted using maximum-likelihood estimation. Each estimate of κUVM is converted to a standard deviation (Mardia & Jupp, 1999), where I1 is the modified Bessel function of the first kind of order 1 (this slightly funny function is often used because it reduces to the regular standard deviation in the limit of large κUVM). The top row of Fig. 2 shows wUVM and SDUVM at every set size for a single subject. Paper 1 states that
Experiment 1 (N = 8) tested this model using set sizes of 3 or 6 coloured squares (Fig. 1c). s.d. did not vary significantly across set sizes (F < 1).… This result rules out the entire class of working memory models in which all items are stored but with a resolution or noise level that depends on the number of items in memory.
In a similar vein, paper 2 states the following:
SD values rose monotonically as set size increased until set size 4, after which a stable asymptote was apparent. This impression was confirmed by conducting paired t tests on the SD values obtained from individual subject data (individual fits described below): (set size 1–2, t(40) = 0.63, p < 0.001; set size 2–3, t(40) = 8.04, p < 0.001; set size 3–4, t(40) = 1.95, p = 0.059; set size 4–6, t(40) = 0.167, p = 0.869; set size 6–8, t(40) = 0.724, p = 0.473). Thus, the resolution by set size function derived from the aggregate data was well described by a bilinear function, as predicted by the discrete-resource model,1
and for a second experiment,
SD values … achieved asymptote at larger set sizes (set size 1–2, t(29) = −13.29, p < 0.001; set size 2–3, t(29) = −4.94, p < 0.001; set size 3–4, t(29) = −0.13, p = 0.45; set size 4–5, t(29) = −0.72, p = 0.24; set size 5–6, t(29) = 0.038, p = 0.49).
Similar statements are found in Anderson and Awh (2012; Anderson et al., 2013). Thus, we define summary statistic #1 to be the p value of a t test on SDUVM between two set sizes that are presumably at or above capacity. Following the recommendation of Dr. Edward Awh (personal communication), we decided to use set sizes 3 and 4, but we found similar results when we used set sizes 6 and 8.
Summary statistic #2: Goodness of fit of piecewise linear function
Papers 1 and 2 observe a plateau in the function of SDUVM versus set size, N. Therefore, paper 2 fits, by minimizing the mean squared error, a piecewise linear function2 to the SDUVM estimates as a function of N (processing step #2 in Fig. 1):
This function rises linearly when set size is smaller than or equal to a positive real number γ and is flat thereafter. Paper 2 refers to γ as the “inflection point” of the function, but the correct term is singularity.3 The motivation that the authors give for fitting this function is that slot models would predict that SDUVM exactly follows such a function but slotless models would not.4 Therefore, if SDUVM as function of set size is fitted well by this piecewise linear function, this is considered evidence for slot models and against slotless models:
Thus, discrete-resource models predict that WM resolution (operationalized by the SD parameter in the mixture model) will follow a bilinear function across set sizes, with resolution for the stored items reaching a stable plateau once the item limit has been exceeded. To test this prediction, we examined whether or not the resolution by set size function was well described by a bilinear function at both the group and individual subject level.… The bilinear function provided a strong fit to SD by set size functions for each individual observer (average R2 = 0.55).
Finally, the key finding from experiment 1 was also replicated; … the bilinear function again provided a strong fit to SD by set size functions for each individual observer (average R2 = 0.65).
Similar statements are found in (Anderson & Awh, 2012; Anderson et al., 2013). Thus, we define summary statistic #2 as the goodness of the fit of the piecewise linear function to SDUVM as function of set size, as expressed by the coefficient of determination, R2, averaged across subjects.
Summary statistic #3: Correlation between wUVM and singularity
Finally, Paper 2 computes the correlation between the singularity in the piecewise linear fit (i.e., the value of γ) and the value of wUVM at set size 8 (processing step #1 in Fig. 1). The reasoning here is that slot models presumably predict a strong correlation and slotless models do not. The authors argued that their data show a strong correlation between these two variables and that this supports their slot model:
In addition, the data confirmed the predicted correlation between individual item limits (estimated using Pmem for set size 8) and the set size at which SD reached asymptote (R2 = 0.657; t(40) = 8.76; p < 0.0001). [T]he item limit determined for each observer was strongly predictive of the set size at which the resolution by set size function reached asymptote. This finding confirms a clear prediction of discrete-resource models5, 6
and later,
Finally, the key finding from experiment 1 was also replicated; estimates of the item limit for each observer strongly predicted the set size at which WM resolution reached asymptote for each subject (R2 = 0.525; t(28) = 5.554; p < 0.0001).
Thus, summary statistic #3 is the R2 of the correlation (across subjects) between the singularity in the piecewise linear fit, γ, and the value of wUVM at set size 8.
Method
Models
To evaluate the effectiveness of the three summary statistics when comparing working memory models, we considered two models—one slot model and one slotless model. The slot model is the slots-plus-resources model that was introduced by paper 1 and advocated by paper 2. In this model, the observer has K slots to store items, where K is called the capacity. When the number of items in a display, N, is smaller than K, the available memory precision, J1, is equally divided among the N items, so that the precision per item, denoted J, is equal to J1/N. Precision is inversely related to the width of the error distribution (see the Appendix). When N ≥ K, precision is equally divided among K randomly selected items, so that J = J1/K for each item in memory and J = 0 for the remaining items. This model has two free parameters, J1 and K. Elsewhere, we termed this type of model the equal precision with a fixed number of slots model (EPF; Van den Berg et al., 2014), and we follow that terminology here. The EPF model is very similar to the slots-plus-averaging model favored by paper 1.
In the slotless model that was tested in papers 1 and 2, a fixed amount of memory precision is evenly distributed across all N items; thus, the quality with which items are remembered decreases with N. Here, we used a recently proposed variant of this model, which incorporates variability in precision and was found to provide a better description of working memory data than did the original slotless model (Van den Berg et al., 2012). In this model, all N items are remembered, but the precision per item, J, varies across items and trials. We model J as being drawn independently for each item from a gamma distribution with mean and scale parameter τ. Thus, memory precision is only, on average, equal for each item. This model also has two free parameters, J̄1 and τ. Following Van den Berg et al. (2014), we refer to this model as the variable precision with all items remembered (VPA) model. Mathematical specifications of both models are found in the Appendix.
Our aim was not to examine whether working memory performance is best described by the EPF or the VPA model. Although these particular models have been advocated for in recent papers (EPF, papers 1 and 2; VPA, Fougnie et al., 2012; Van den Berg et al., 2012), it is important to keep in mind that many other possible slot and slotless models are conceivable. In other work, we performed a comprehensive comparison of a large number of slot and slotless models (Van den Berg & Ma, 2013). Our goal here was to examine how informative the proposed summary statistics are for comparing slot and slotless models of working memory. In this context, EPF and VPA merely serve as plausible examples of these classes of models. If the methods used by papers 1 and 2 cannot distinguish these example models, then, by extension, they are not suitable for categorically comparing slot and slotless models.
Synthetic data
To obtain model predictions, we generated synthetic data from both the EPF and the VPA models. We define a synthetic data set as a collection of 45 synthetic subjects, all of which were generated using the same model (either EPF or VPA), but with different parameter combinations. We used set sizes 1, 2, 3, 4, 6, and 8. The set sizes and number of subjects matched those used in Experiment 1 of paper 2. We varied the number of trials per subject across analyses. For a given number of trials per subject, we generated 1,000 synthetic data sets from each model. For each data set, we have four data types: the raw data and three summary statistics.
To make the synthetic data statistically similar to subject data, we drew parameter values (log J1 and K for EPF; log J̄1 and log τ for VPA) for each synthetic subject from a bivariate normal distribution7 (Fig. 1a) with the same mean and covariance as the maximum-likelihood estimates that we obtained from fitting the models to the subject data from Experiment 1 of paper 2. The values drawn for K in the EPF model were rounded the nearest integer. Thus, our simulations are likely relevant to model comparison based on subject data. To verify that the precise form of the parameter distribution does not affect our conclusions, we also tried uniform distributions over all parameters.
Log Bayes factors
We denote the data by D; they could be either the raw data or one of the summary statistics. A principled and, in some sense, optimal way to compare two models is to compute their posterior probabilities given the data (Kass & Raftery, 1995; Lynch, 2007); in our case, these probabilities are denoted p(EPF|D) and p(VPA|D). Evidence for the EPF model, relative to the VPA model, is captured by the log posterior ratio,
Thus, L measures the strength of the evidence in favor of the EPF model. If L is positive, EPF is the best-fitting model; otherwise, VPA. Applying Bayes’s rule and assuming equal prior probabilities over the two models, we can rewrite L as
| (2) |
which is known as the log Bayes factor. Mathematical details of how we computed log Bayes factors can be found in the Appendix. All the results reported below remain qualitatively unchanged when we use AIC, AICc, or BIC, instead of log Bayes factors. Thus, what matters for conclusions about model evidence is what data type is used for D (raw data or summary statistics), not exactly which likelihood-based measure of evidence is used.
Model recovery and model evidence
Recall that we have two generating models (EPF and VPA), 1,000 synthetic 45-subject data sets generated from each model, four data types for each data set (raw data and three summary statistics), and one log Bayes factor based on each data type and each data set; finally, we repeat all of this for several numbers of trials per synthetic subject. The sign of the log Bayes factor indicates whether the selected model is EPF or VPA: Positive Bayes factors indicate evidence for the EPF model, and negative ones for the VPA model. We define model recovery rate as the percentage of correct model selections among the 1,000 data sets, where a correct model selection is defined as the sign of the log Bayes factor being positive when applied to synthetic EPF data and negative when applied to VPA data. We define expected model evidence (for the EPF model relative to the VPA model) as the log Bayes factor averaged across the 1,000 data sets. Thus, we obtain one model recovery rate and one value of expected model evidence for each combination of a generating model, data type, and number of trials.
Results
Model recovery and model evidence from raw data
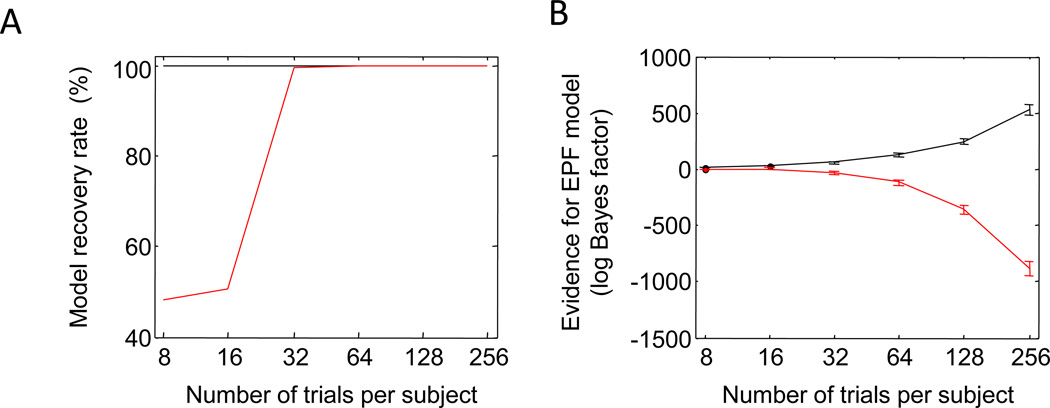
When comparing models, we want to be confident that the winning model is indeed the one that describes reality best. This means that we would like to use a model comparison method that gives a perfect or near-perfect model recovery rate on synthetic data: When synthetic data are generated using Model X, the ideal model comparison method would select Model X 100% of the time. Moreover, model recovery rate and expected model evidence should, on average, increase with the size of the data set.
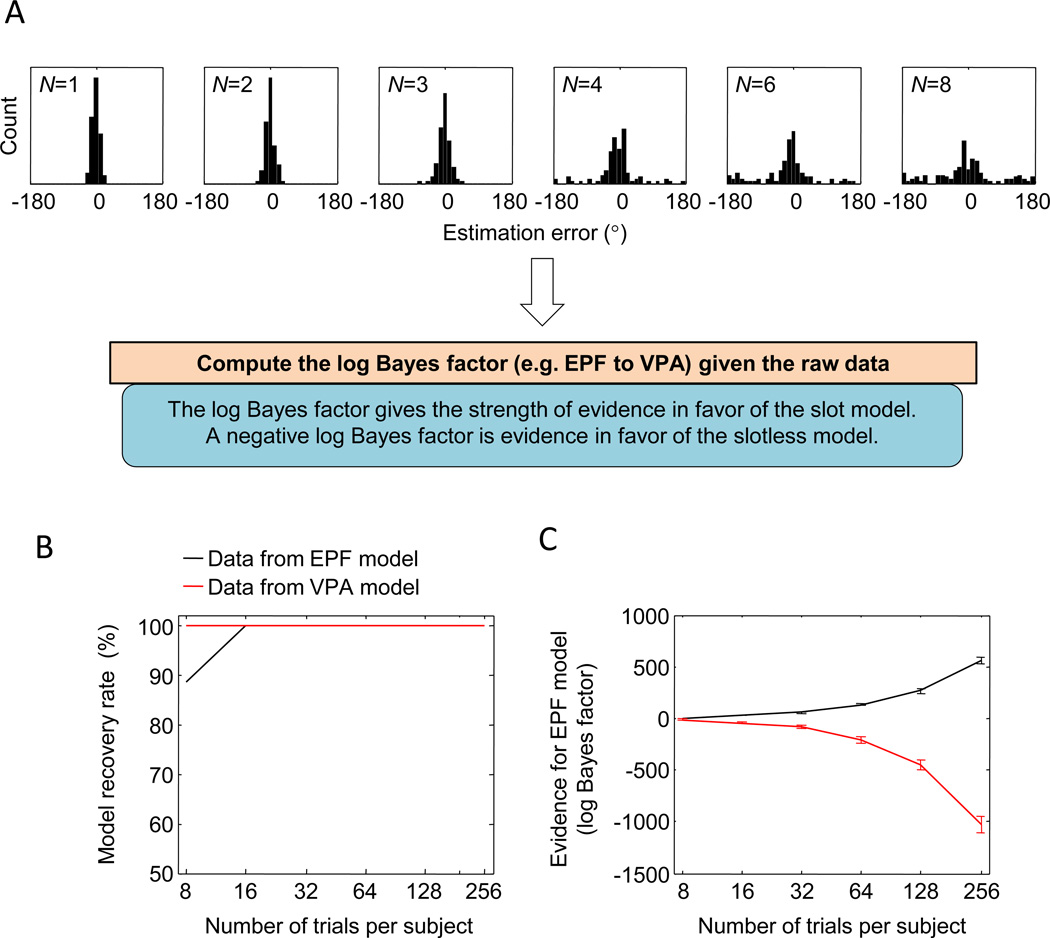
We first evaluated whether these criteria are satisfied if we select a model based on the log Bayes factors based on the raw data (Fig. 3a). We used synthetic data (see the Method section) with 8, 16, 32, 64, 128, and 256 trials per subject to compute the model recovery rate from the raw data (Fig. 3b). On EPF data sets with 8 trials per subject, the VPA model was in 12% of the cases incorrectly selected as the most likely model, but for all synthetic EPF and VPA data sets with 16 or more trials per subject, model recovery rate was 100%. Hence, as few as 16 trials per subject with 45 subjects, for a total of 720 trials, were sufficient to near-perfectly recover these two models when raw data were used.
Fig. 3.
Model comparison using log Bayes factors based on the raw data. a In contrast to the process described in Fig. 2, comparing models using the log Bayes factors based on individual-trial responses is straightforward and does not involve any preprocessing of data. b Using synthetic EPF (black) and VPA (red) data sets consisting of 45 subjects each, the generating models are recovered perfectly even at 16 trials per subject. c The expected log Bayes factor increases monotonically in magnitude with the number of trials per subject. It is consistently positive when the synthetic data are generated from the EPF model (black) and negative when they are generated from the VPA model (red), indicating that the predictions of the models are sufficiently different to allow for an easy distinction. Error bars indicate standard deviations across synthetic data sets
The expected model evidence in raw EPF and VPA data increased monotonically with the number of trials (Fig. 3c). Already at 16 trials per subject, the expected model evidence on EPF and VPA data was 31.4 and −42.6, respectively, both of which are considered decisive evidence (Jeffreys, 1961).8
These results indicate that the EPF and VPA models are easy to distinguish from raw data using a likelihood-based model selection method. Next, we will examine how well the models can be distinguished using summary statistics.
Summary statistic #1: p value of t test on SD in set sizes 3 and 4
The first summary statistic in papers 1 and 2 is the p value of a t test on SDUVM between set sizes 3 and 4. Papers 1 and 2 claimed evidence for slot models based on finding a p value higher than .05. The critical problem is the implicit assumption that slotless models will produce a difference in SDUVM that is significant with a p value smaller than .05. Neither paper 1 nor paper 2 produces any evidence for this statement, and we show here that it is not true.
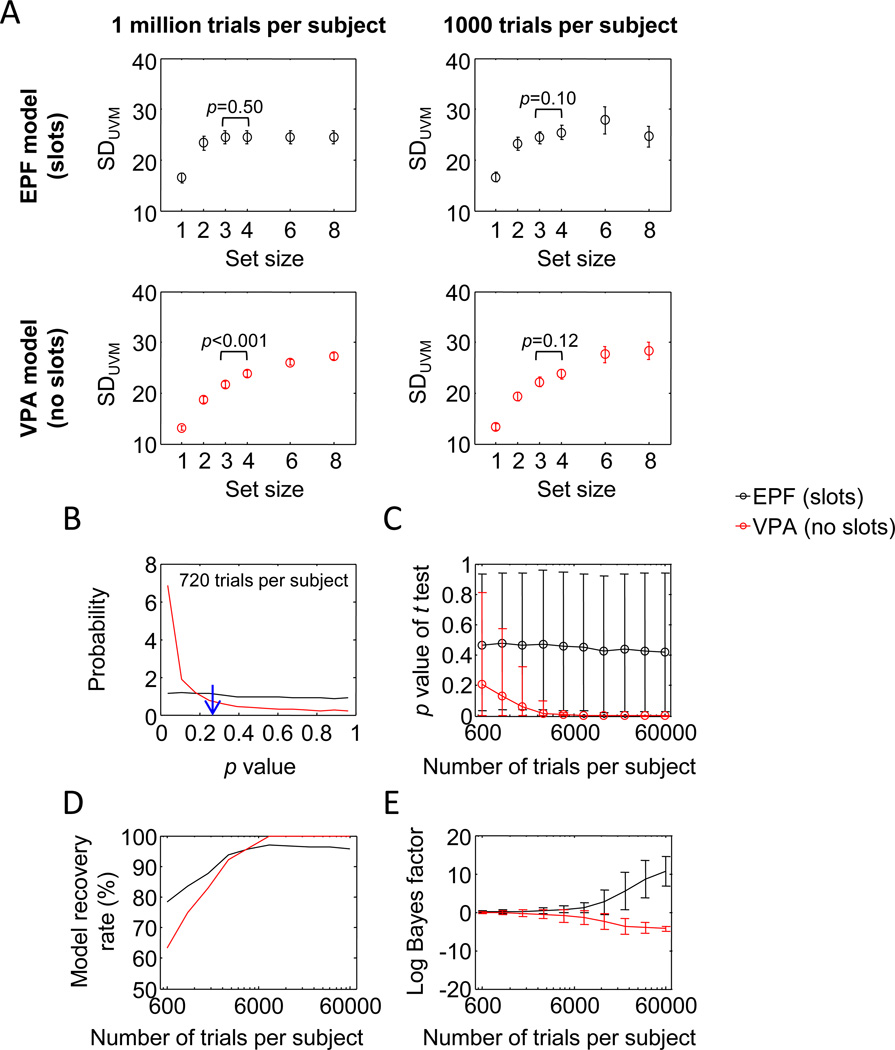
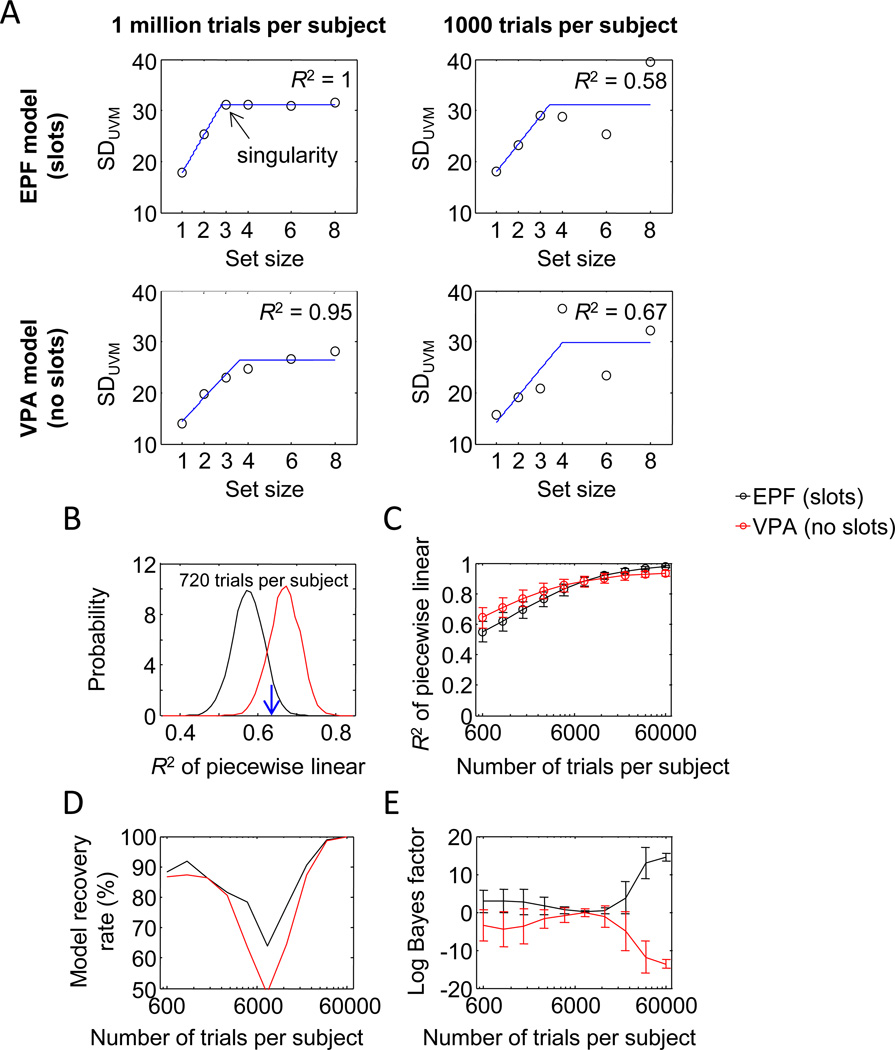
We generated synthetic data (see the Method section) to approximate the predicted distribution of summary statistic #1 under both models. When the number of trials per subject was very large and the estimates of SDUVM thus essentially noiseless, the EPF model showed a clear plateau in SDUVM, and the VPA model a monotonic increase (Fig. 4a, left). Consistent with the reasoning behind the methods in papers 1 and 2, we found that the difference between set sizes 3 and 4 was highly significant in the VPA model (p < .001), but not in the EPF model (p = .54). However, when we reduced the number of trials per subject to a value that is more representative for subject data sets (Fig. 4a, right), the estimates of SDUVM became noisy, and neither model produced a significant difference. Hence, for data sets with a realistic number of trials, p > .05 does not seem to be a sensible criterion to distinguish the models.
Fig. 4.
Is summary statistic #1 (p value of t test on SDUVM between set sizes 3 and 4) suitable for model comparison? a SDUVM as a function of set size for four example synthetic data sets (45 subjects each). When the number of trials per subject is large, the EPF model predicts that SDUVM increases for set sizes below memory capacity and is constant for set sizes above capacity (top left). By contrast, the VPA model predicts that SDUVM increases indefinitely (bottom left). A t test between the SDUVM values at set sizes 3 and 4 is significant on the VPA data, but not on the EPF data. However, when the number of trials is of the same order of magnitude as in the empirical data sets (right), the SDUVM estimates become noisy under both models, and a t test does not produce a significant difference in either of these example cases. b Distributions of the p value at 720 trials per subject (the number of trials used in Experiment 1 of paper 2). The distributions largely overlap, indicating that the p value is of little value in distinguishing EPF from VPA data (the blue arrow indicates the p value from Experiment 1 in paper 2). c Mean and 95% confidence interval of the p value as a function of the number of trials. d Model recovery performance based on log Bayes factors computed from summary statistic #1 as a function of the number of trials. Compare with Fig. 3b. e The amount of evidence for the EPF model (log Bayes factor) as a function of the number of trials (mean and standard deviation across synthetic data sets). Compare with Fig. 3c
In fact, if we use 720 trials per subject as in Experiment 1 of paper 2, it is impossible to impose any criterion on the p value that cleanly separates the models: The distributions are broad and overlap, meaning that any p value could have come from either model (Fig. 4b). The value from the subject data of Experiment 1 in paper 2 (indicated with a blue arrow) is slightly more probable under the VPA model, but the difference is so small that this result is inconclusive (we will quantify this in the Model Evidence in Empirical Data section below). The overlap of the predicted distributions of p values is seen not only at 720 trials per subject, but also at up to thousands of trials per subject, meaning that the models cannot be distinguished well (Fig. 4c). Hence, comparing summary statistic #1 with a criterion is a very poor method for comparing slot and slotless models.
To extract the most information from summary statistic #1, one can compute the log Bayes factor of the two competing models using the value of the summary statistic as “data” (see the Method section and the Appendix). The log Bayes factor takes into account the precise distributions of the p value predicted by the models. We found that log Bayes factors based on summary statistic #1 (Fig. 4d) produced much lower model recovery rates than did log Bayes factors based on the raw data (Fig. 3b). In addition, expected model evidence in summary statistic #1 (Fig. 4e) was very weak, as compared with expected model evidence in raw data (Fig. 3c). These results indicate that even when analyzed in the best possible way, summary statistic #1 cannot distinguish the EPF from the VPA model and, therefore, cannot distinguish between slot and slotless models in general.
Summary statistic #2: Goodness of fit of piecewise linear function
Paper 2 fits a two-piece piecewise linear function to SDUVM as a function of set size (processing step #2 in Fig. 1). Summary statistic #2 is the goodness of the fit of this function, as measured by R2. Relatively high values of this R2 are taken as evidence for the slot model.
The critical problem with this reasoning is the implicit assumption that slotless models would predict a low R2. It is not clear what this assumption is based on, because the authors do not specify what relationship a slotless model would predict for SDUVM versus set size.9 To examine the distributions of summary statistic #2 under both models, we derived model predictions from the synthetic data sets in the same way as we did for summary statistic #1. When the number of trials was very large, the piecewise linear fit was nearly perfect for the EPF model and less good for the VPA model (Fig. 5a, left). However, for data sets of a size that is more representative for subject data, estimates of SDUVM were noisy under both models, and the piecewise linear function did not provide a good fit to either (Fig. 5a, right).
Fig. 5.
Is summary statistic #2 (R2 of piecewise linear fit to SDUVM versus set size) suitable for model comparison? a SDUVM as a function of set size for four example single-subject synthetic data sets. When the number of trials is large, a piecewise linear function perfectly captures the SDUVM trend in the EPF data (top left) and provides a slightly worse fit in the VPA data (bottom left). However, when the number of trials is of the same order of magnitude as in the empirical data sets (right), the SDUVM estimates become noisy under both models, and the R2 of the piecewise linear function does not seem to be informative about the underlying model. b Distributions of the R2 value at 720 trials per subject (the number of trials used in Experiment 1 of paper 2). The distributions partly overlap, indicating that the R2 value cannot reliably distinguish EPF from VPA data (the blue arrow indicates the R2 value from Experiment 1 in paper 2). c Mean and 95% confidence interval of the R2 value as a function of the number of trials. d Model recovery performance based on log Bayes factors computed from summary statistic #2 as a function of the number of trials. Compare with Fig. 3b. e The amount of evidence for the EPF model (log Bayes factor) as a function of the number of trials (mean and standard deviation across synthetic data sets). Compare with Fig. 3c
Figure 5b shows the predictions obtained with 720 trials per subject, as in Experiment 1 of paper 2. Somewhat surprisingly, in this regime of relatively small data sets, the VPA model predicted, on average, a higher R2 than did the EPF model, contrary to the assumption made in paper 2. More important, the distributions strongly overlap, meaning that the R2 values are uninformative about the model that generated the data. The R2 value obtained from the subjects in Experiment 1 of paper 2 (indicated with a blue arrow in Fig. 5b) was, on average, .635 ± .040. Finding this value is slightly more probable under the VPA model than it is under the EPF model, but the difference is so small that the result is inconclusive (we will quantify this in the Model Evidence in Empirical Data section below).
Under both models, the predicted R2 increased as a function of the number of trials in a data set (Fig. 5c). The predictions overlapped strongly between the models, indicating that they are difficult to distinguish on the basis of this summary statistic. The predicted curves crossed around 6,000 trials per subject. As a result, model recovery rates did not monotonically increase with the number of trials per subject (Fig. 5d). The expected model evidence followed the same trend (Fig. 5e). This is an undesirable feature of a model comparison method, since it means that it could be detrimental to collect more data! Overall, the expected model evidence was low, as compared with the raw data.
Summary statistic #3: Correlation between singularity and wUVM
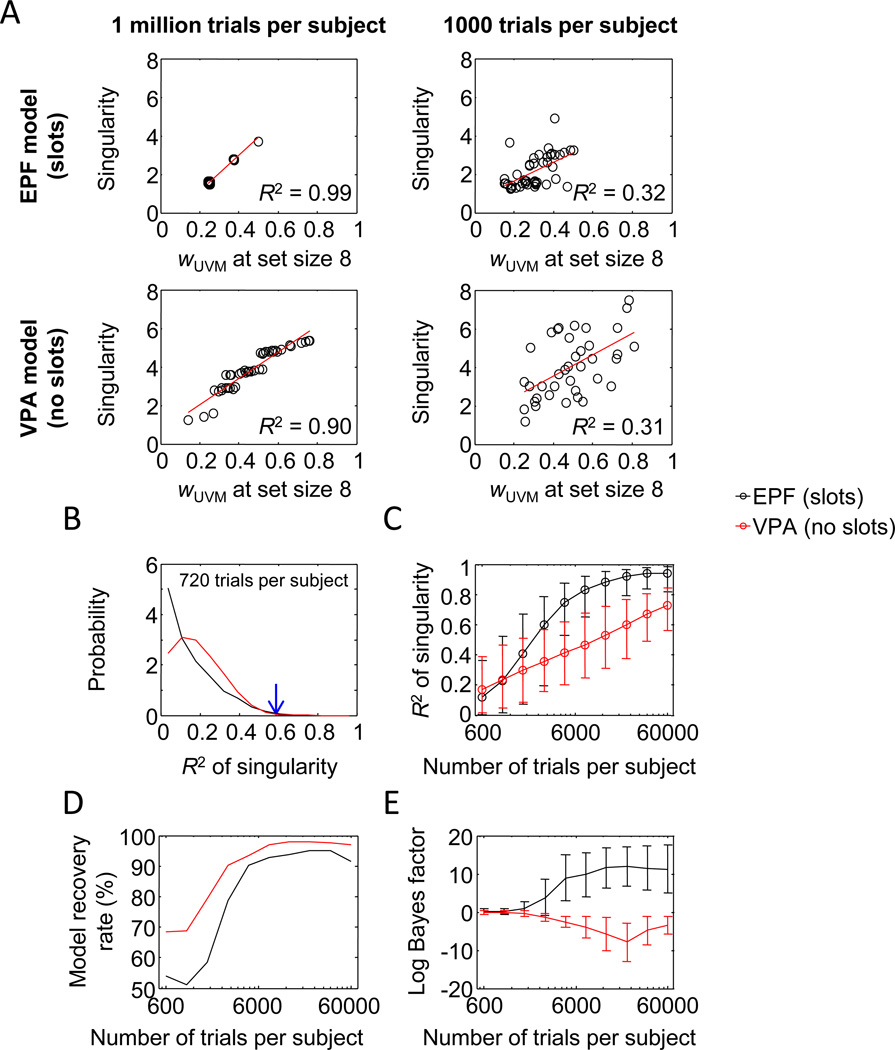
The third summary statistic that was used in paper 2 to argue in favor of slot models is the correlation between the singularity of the piecewise linear fit discussed in the previous section and wUVM at set size 8 (supposed to be proportional to memory capacity). The authors argued that the observed R2 of the correlation between these two variables supports the EPF model. When the number of trials is very large, the EPF model predicts a very high R2 between these two variables. It is unclear, however, what it predicts when the number of trials is similar to that in subject data, and neither is it clear what a slotless model would predict. The authors seem to have assumed that the correlation would be low in slotless models.
The results from our analysis of synthetic data show that the assumption that the correlation is strong in slot models but weak in slotless models is wrong (Fig. 6a). Both models predict a strong correlation when the number of trials per subject is large and a weak correlation when the number of trials is low. Using 720 trials per subject, the predicted distributions of summary statistic #3 strongly overlap between the models (Fig. 6b). Surprisingly, the value found in the empirical data (R2 = .59) is highly unlikely under both models. One possible explanation is that neither model is a good description of the data. However, given that the estimates of wUVM at set size 8 and of the singularity tend to be noisy in small data sets, it seems unlikely under any model to find a strong correlation between these two summary statistics. Therefore, a more plausible explanation may be that the empirical value is a statistical outlier.
Fig. 6.
Is summary statistic #3 (R2 of singularity versus wUVM) suitable for model comparison? a Correlation between wUVM at set size 8 and the singularity (IP) of the piecewise linear fit for four example synthetic data sets (45 subjects each). When the number of trials is large, wUVM and IP are near-perfectly correlated in the EPF data (top left). The correlation is slightly lower in the VPA data (bottom left). However, when the number of trials is of the same order of magnitude as in the empirical data sets (right), estimates of wUVM and IP are more noisy, and the correlations much weaker. b Distributions of the R2 value at 720 trials per subject (the number of trials used in Experiment 1 of paper 2). The distributions highly overlap, indicating that the R2 value cannot reliably distinguish EPF from VPA data (the blue arrow indicates the R2 value from Experiment 1 in paper 2). c Mean and 95% confidence interval of the R2 value as a function of the number of trials. d Model recovery performance based on log Bayes factors computed from summary statistic #2 as a function of the number of trials. Compare with Fig. 3b. e The amount of evidence for the EPF model (log Bayes factor) as a function of the number of trials (mean and standard deviation across synthetic data sets). Compare with Fig. 3C
Both models predict that the correlation will increase with the number of trials per subject, and their predictions strongly overlap, unless a very large number of trials is used (Fig. 6c). Model recovery rate (Fig 6d) and expected model evidence (Fig. 6e) are again low, in comparison with the raw data (Fig. 3). Hence, summary statistic #3 also is uninformative, as compared with raw data analysis.
Model evidence in synthetic data: Summary
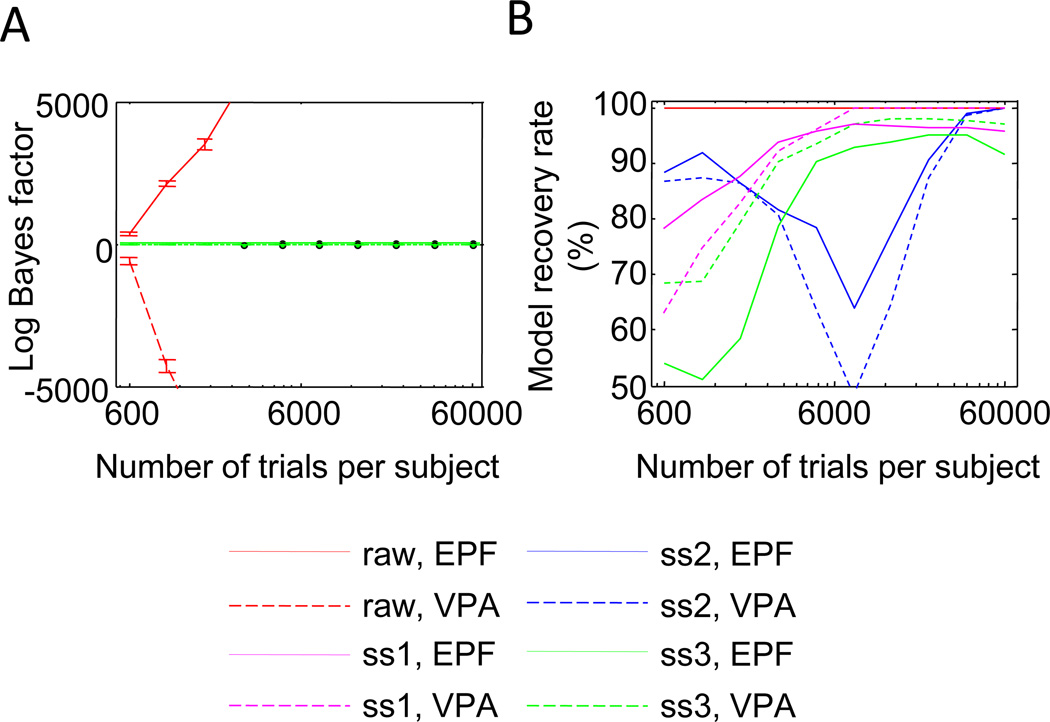
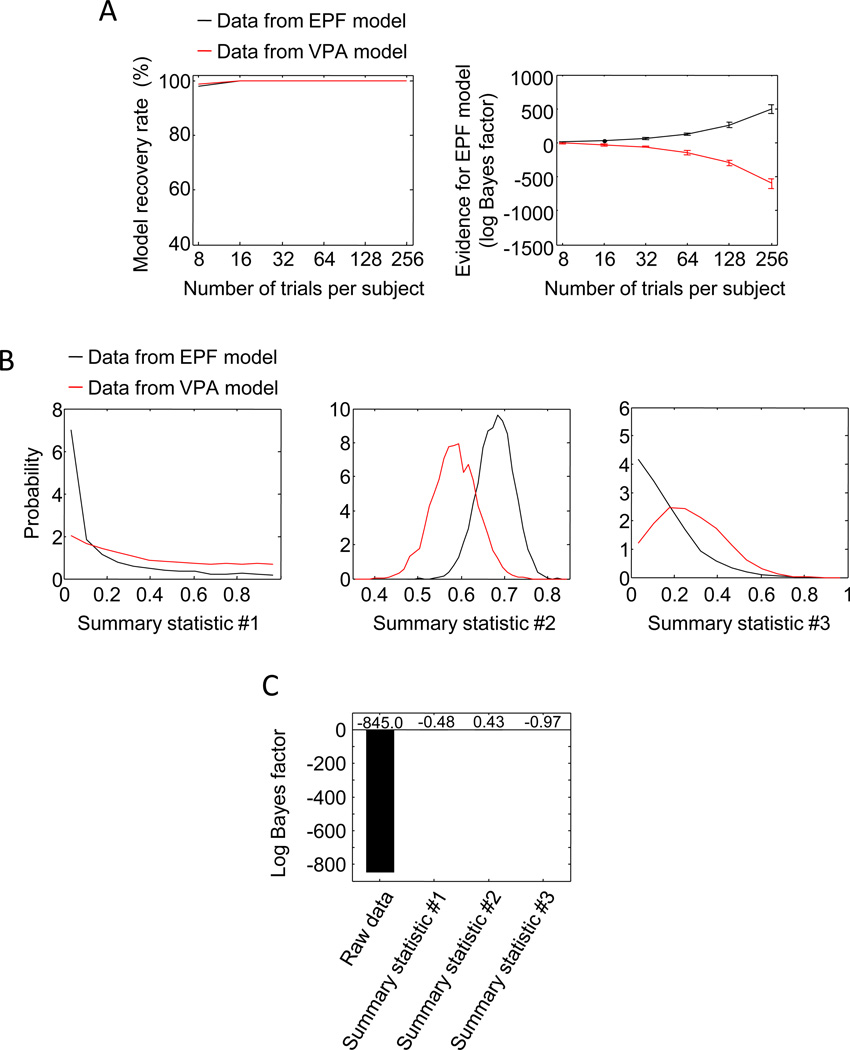
We draw two important conclusions from the results thus far (Fig. 7). First, expected model evidence in summary statistics is negligible, as compared with the evidence in raw data (Fig. 7a). At 720 trials per subject, the expected model evidence in synthetic EPF data was 0.59, 3.04, and 0.13 for the three summary statistics and 1,504 for the raw data. The values obtained from the synthetic VPA data were −0.79, −3.04, and −0.11 for the three summary statistics and −3,112 for the raw data. Hence, summary statistic #2 was the most informative of the three but still provided only 0.15% of the expected model evidence contained in the raw data.
Fig. 7.
Comparison of model evidence and model recovery performance in the raw data and the three summary statistics (ss1, ss2, ss3). a The amount of EPF model evidence (log Bayes factor) in the summary statistics is negligible, as compared with the amount of evidence in the raw data. Detailed plots for each of the summary statistics can be found in Figs. 4c, 5c, and 6c. b Model recovery rate based on summary statistics is low, as compared with that based on raw data
Our second conclusion, so far, is that model recovery rate based on summary statistics is poor, as compared with model recovery rate based on raw data (Fig. 7b). Again, summary statistic #2 was the most informative summary statistic, reaching 99% model recovery at about 43,660 trials per subject, for a total of 1.96 million trials in the data set. The other two summary statistics did not reach 99% in the range that we tested. When performing model selection based on raw data, however, only 15 trials per subject (675 in total) were needed to reach the same level of accuracy (see Fig. 3b).
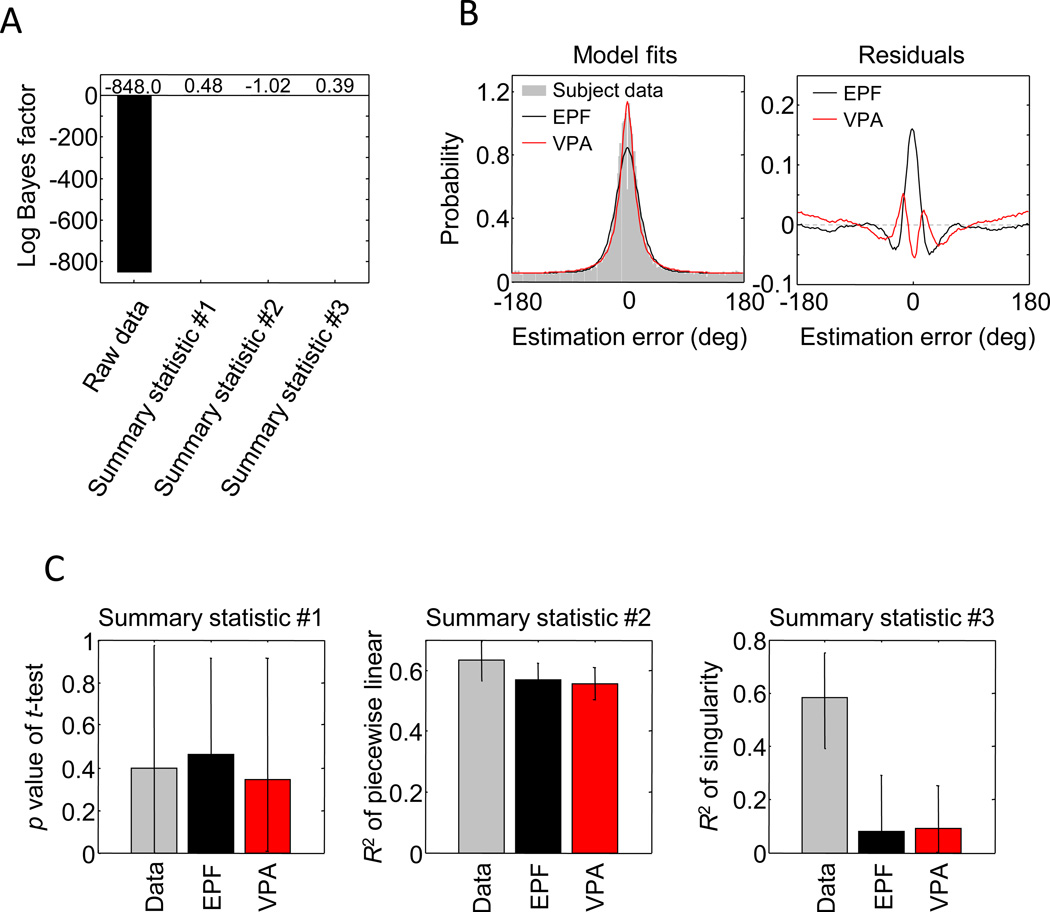
Model evidence in empirical data
The simulation results suggest that model evidence from summary statistics tends to be only a small fraction of the evidence contained in the raw data. We next examined whether the same is true for the subject data from Experiment 1 of paper 2. The expected model evidence in the summary statistics was 0.48, −1.02, and 0.39, respectively (Fig. 8a), which are all inconclusive (Jeffreys, 1961). By contrast, the expected model evidence in the raw data was −848.0, providing overwhelmingly strong evidence in favor of the VPA model (it means that the VPA model is e848 times more likely to have generated the subject data than the EPF model). Thus, on subject data, the most informative summary statistic (#2) provided only 0.12% of the expected model evidence in the raw data.
Fig. 8.
Model evidence and fits to subject data from Experiment 1 of paper 2. a Model evidence computed from the subject data of Experiment 1 in paper 2. Model evidence derived from the summary statistic is negligible, as compared with the evidence provided by the raw data. b Left: Maximum-likelihood fits to error histograms (“raw data”). Model predictions were obtained by simulating 50,000 trials per set size per subject, with parameter values set to the subject’s maximum-likelihood estimates. Subject data and model predictions are collapsed across set sizes and subjects. Right: Model residuals (data minus fit) averaged across subjects and set sizes (180 bins, smoothed using a sliding window with a width of 4 bins). The EPF model shows a clear peak at the center, indicating that the empirical distribution of the estimation error is narrower than the fitted distribution. The residual of the VPA model is smaller, consistent with the finding shown in panel a that this model provides a better fit to the raw data than does the EPF model. c Maximum-likelihood fits to summary statistics. The EPF and VPA models fit all three summary statistics approximately equally well. Error bars indicate 95% confidence intervals
These results suggest that the models make very different predictions at the level of raw data, but not at the level of the summary statistics. This is confirmed in Fig. 8b, c, which show the maximum-likelihood fits of the models to both the raw data and the three summary statistics. A clear difference is observed in the goodness of fit to the raw error histograms, but the fitted values of the summary statistics are very similar between the models.10 As was suggested by Fig. 6b, neither of the models accounts well for the observed value of summary statistic #3, possibly because it is an outlier.
Making strong claims about slot versus slotless models would require a more extensive model comparison, which we do elsewhere (Van den Berg et al., 2014). The main message of the present article is methodological: Conclusions about working memory models based on plateau-related summary statistics are unwarranted, because these statistics are virtually devoid of evidence. However, we can state that between the EPF and VPA models, the VPA model is a much better description of the subject data in paper 2 than is the EPF model, which is consistent with findings in earlier work (Keshvari et al., 2013; Van den Berg et al., 2012).
Model comparison based on Kolmogorov–Smirnov tests
Paper 2 performs one more analysis on its behavioral data—namely a Kolmogorov–Smirnov (KS) test to examine whether the empirical error distributions are compatible with the distributions predicted by the models. This analysis also has problems. First, the authors apply the KS test to pooled subject data. This is problematic because the mixture of many uniform-plus-Von-Mises distributions is not uniform-plus-Von-Mises. Hence, even if the EPF model were a perfect model for single-subject data, it would not be a good model for pooled data. Rather than expecting that the KS test rejects the VPA model but not the EPF model, by applying the test to pooled data, the authors should have expected it to reject both models. Second, while the KS test works best on raw data, the authors used histograms (15 bins) of the data as input to the test (personal communication with the authors). We applied the KS test to the raw data from paper 2 and found results that are inconsistent with those reported in paper 2: The null hypothesis that the data follow the distribution predicted by the EPF model is rejected at four out of six set sizes.
Robustness under varying the parameter distribution
All simulation results presented thus far were based on synthetic data generated using parameter values drawn from a distribution with the same mean and covariance as the maximum-likelihood estimates obtained from the subject data of paper 2 (see the Method section). The motivation for using this prior distribution was that we wanted to make the synthetic data statistically similar to empirical data; after all, there would be little relevance in showing that the models can or cannot be distinguished on data sets that are statistically very different from subject data. Nevertheless, our conclusions would ideally not depend strongly on the choice of parameter distribution. To examine this, we performed two additional analyses.
First, we examined to what extent our results changed if we replaced the “empirical” prior distributions by uniform distributions. In this analysis, we independently drew the values of all four parameters (log J1, and K in EPF models; log J̄1 and log τ in VPA models) from a uniform distribution on [1,5], both when generating the synthetic data and when marginalizing over parameters in the computation of log Bayes factors (Equation 4). We found that the model recovery rate (Fig. 9a) and log Bayes factors (Fig. 9b) obtained from raw data were hardly affected by this change of prior distribution (cf. Fig. 3b, c): Only very few trials were required to distinguish the models near-perfectly. Furthermore, we found that the predicted distributions of the summary statistics depended quite strongly on the choice of prior distribution over parameters (Fig. 9b; cf. Figs. 4b, 5b, 6b). However, there was no noticeable difference in the model evidence obtained from subject data (Fig. 9c). Hence, our findings did not noticeably change when replacing the empirical prior distribution by a uniform one.
Fig. 9.
Effect of the prior distribution over parameters on model comparison using raw data. When computing expected log Bayes factors, a prior distribution over parameter values is used at two places: when generating synthetic data and when marginalizing over parameters to compute the log Bayes factor for a single synthetic subject. a Same as Figs. 3b and 3c, except that both the generating and marginalization prior distribution were uniform distributions instead of a bivariate Gaussian derived from empirical values. b Predicted distributions of the summary statistics under the uniform prior distributions (cf. Figs. 4b, 5b, 6b). c Model evidence obtained from subject data under the uniform prior distributions (cf. Fig. 8a)
Second, experimenters often have little knowledge of the true distribution over parameters. Therefore, we examined how strongly the success of model comparison using raw data depends on using the “correct” prior in the marginalization step. To this end, we replaced in that step the empirical prior distributions, p(θEPF,i|EPF) and p(θVPA,i|VPA) in Equation 4, by the uniform distributions that we also used in the previous analysis. However, we did not replace the prior in the generative part of the analyses (which is used when computing the expected value of the log Bayes factor), with the consequence that the marginalization prior does not match the generative prior. We found that the model recovery rate drops to chance when 8 or 16 trials are used per subject (Fig. 10a; cf. Fig. 3b) but is near-perfect when 32 or more trials are used per subject. Similarly, while the magnitudes of the expected log Bayes factors under this uninformative marginalization prior are lower than under the informative one, 32 trials per subject are sufficient to reliably distinguish the models (Fig. 10b; cf. Fig. 3c). Hence, even when using an “incorrect” prior in the marginalization step, model recovery based on raw data is still orders of magnitude better than model recovery based on summary statistics using the “correct” prior in the marginalization.
Fig. 10.
Effect of the using the “wrong” prior distribution in the marginalization step when computing log Bayes factors from raw data. a Same as Fig. 3b, except that the prior distribution used in the marginalization step was a uniform distribution instead of the bivariate Gaussian derived from empirical values. b Same as Fig. 3c, except that the prior distribution used in the marginalization step was a uniform distribution, instead of the bivariate Gaussian derived from empirical values
Discussion
The appearance of a plateau in estimates of mnemonic noise has been repeatedly cited as strong evidence in favor of slot models and against slotless models of working memory (Anderson & Awh, 2012; Anderson et al., 2011, 2013; Fukuda et al., 2010; Luck & Vogel, 2013; Zhang & Luck, 2008). Here, we have shown that the reasoning in those papers is incorrect: At realistic numbers of trials, values of plateau-related summary statistics are very similar, at least, between one slot model and one slotless model and, thus, cannot be used to reliably distinguish the two classes of models. This means that model claims based on plateau-related summary statistics should, in general, not be trusted, and especially not if no validation of the methods is provided.
The mere definition of the plateau on which the summary statistics are based (or the complexity of Fig. 1) indicates how far removed it is from the raw data: It is a plateau in the dependence on set size of the circular standard deviation of the Von Mises component in a fit of a mixture of a Von Mises distribution and a uniform distribution to the estimation errors. To illustrate that valuable information is thrown out by processing the data, consider processing step #1, in which is the raw responses are summarized in the mixture model parameters, wUVM and SDUVM. The information that is discarded is captured by the residual, the difference between the raw data and the mixture model fit. In earlier work, we showed that the residual can be highly informative about the model that underlies the data: The EPF model predicts a flat residual, while the VPA predicts a residual that peaks at zero error and has negative side lobes (Van den Berg et al., 2012). Hence, summarizing a data set by wUVM and SDUVM amounts to throwing out informative aspects of the data.
Would other summary statistics fare better than the ones used by papers 1 and 2? For example, the EPF model predicts that when the number of trials is very high, the estimate of K obtained from wUVM is identical to that obtained from the singularity in the piecewise linear function. Thus, one could suggest the regression slope rather than the correlation of those two quantities as a summary statistic. As another example, the EPF model predicts that subjects will tend to have a singularity in SDUVM, whereas slotless models do not. Therefore, the number of subjects with a singularity smaller than the largest set size could be another summary statistic. A third example would be the presence of a significant difference in wUVM between the lowest and highest set size. A fourth example would be p values returned by the KS tests on the error distributions. The list can go on, but the ones we have tried suffer from the same flaw as the summary statistics examined above: On synthetic data, at realistic numbers of trials, they cannot convincingly distinguish between the EPF and VPA models.
However, even if a summary statistic could be found that does not suffer from this flaw when analyzed in the best possible way (i.e., using likelihoods), there are strong general reasons to avoid summary statistics. First, no data processing can ever increase the expected model evidence, a theorem proven by Kullback (1997) and known as the data processing inequality. In practice, most data processing will decrease the amount of evidence. Thus, it is always best to use the raw data. Second, the choice of which summary statistics to use to compare models is, at best, arbitrary and, at worst, biased. Third, one may need to invent novel summary statistics each time when a model is added to the comparison. For example, even if a plateau-related summary statistic could distinguish between slot and slotless models, it might not be able to distinguish a slot model with equal precision from one with variable precision. Analyzing raw data avoids all these problems.
Given the drawbacks of comparing models based on summary statistics, why is the practice still common in the working memory field? Part of the reason might be that analyzing summary statistics seems generally easier, less time-consuming, and not as computationally demanding as using likelihood-based methods on the raw data. However, as we experienced in performing the analyses presented here, properly validating a summary statistic using synthetic data is, in fact, more work than computing model likelihoods from the raw data! Another reason may be “the curse of plots,” researchers’ tendency to summarize results in graphs (such as SDUVM vs. set size), which could encourage a search for qualitative, visible differences, instead of a formal analysis of individual-trial data. Plotted quantities are usually summary statistics and rarely a complete representation of the raw data. If a difference between models is not readily visible in a plot, that does not mean the models are indistinguishable; it simply means that we have not thought of the right projection of the data into a low-dimensional subspace. Although visualizing selected features of data is critical for the purpose of scientific communication, analyzing those features should always be secondary to analyzing individual-trial data for the purpose of model comparison.
Paper 2 goes beyond the behavioral analyses examined here and also reports neural data. They show that contralateral delay activity in ERP data (Vogel & Machizawa, 2004) is fitted well by a piecewise linear function and that its magnitude correlates with individual differences in estimated memory capacity (K in the EPF model). They argue that both findings are consistent with slot models, but not with slotless models. However, slotless models were not explicitly considered. Fair consideration of slotless models would include a search for markers in the neural signal that correlate with quantities in the slotless model, such as ones that rise or fall monotonically with set size. More generally, as compared with the behavioral models we discussed here, there is an extra unknown when analyzing ERP data—namely, how a behavioral quantity maps to a neural quantity. There are currently no first-principle (e.g., biophysical) models for this mapping, which necessitates arbitrary assumptions and complicates model comparison. For these reasons, we do not believe that, as of now, ERP data can contribute to formal comparison of slot and slotless models.
In the debate about the nature of working memory limitations, we sometimes hear the lament that models are becoming practically impossible to distinguish as they are refined. This concern can, in many cases, be addressed by using raw data instead of summary statistics for model comparison. Whereas model comparisons based on the three summary statistics were inconclusive for the data of paper 2, Bayes factors based on the raw data pointed out a clear and unambiguous winning model. While ultimately, some models might be hard to distinguish even on the basis of raw data, the study of working memory limitations would benefit greatly from avoiding summary statistics for model comparison.
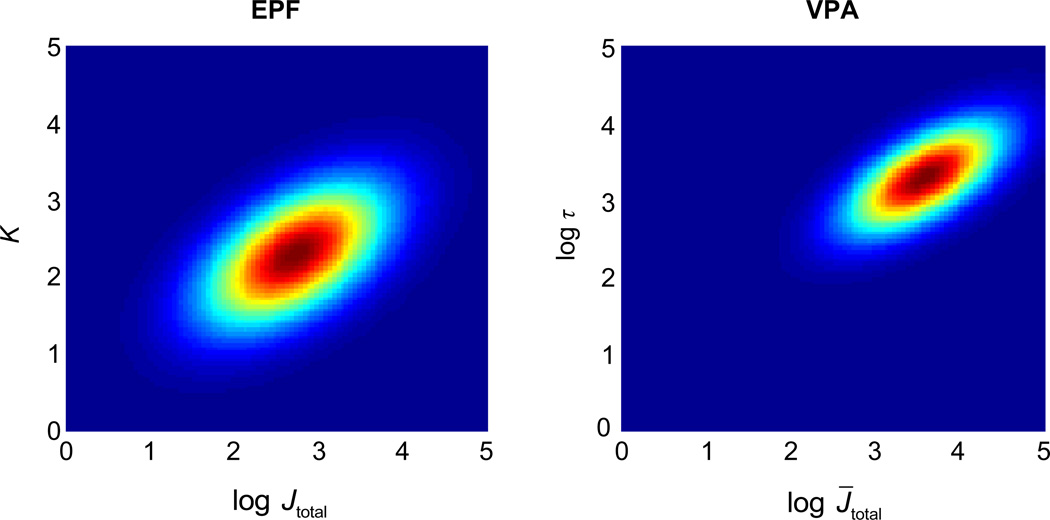
Figure A1. Prior distributions on parameter values in the EPF (left) and VPA (right) models.
Both distributions are bivariate normal distributions. To ensure that synthetic data had approximately the same statistics as subject data, we set the mean and covariance of these distributions equal to the mean and covariance of the maximum-likelihood estimates of the subject data of Experiment 1 in Paper 2. Samples of parameter K in the EPF model were rounded to the nearest integer value. These prior distributions were used in two places: (1) to draw parameter values when generating synthetic data and (2) to sample parameter values when approximating marginal model likelihoods.
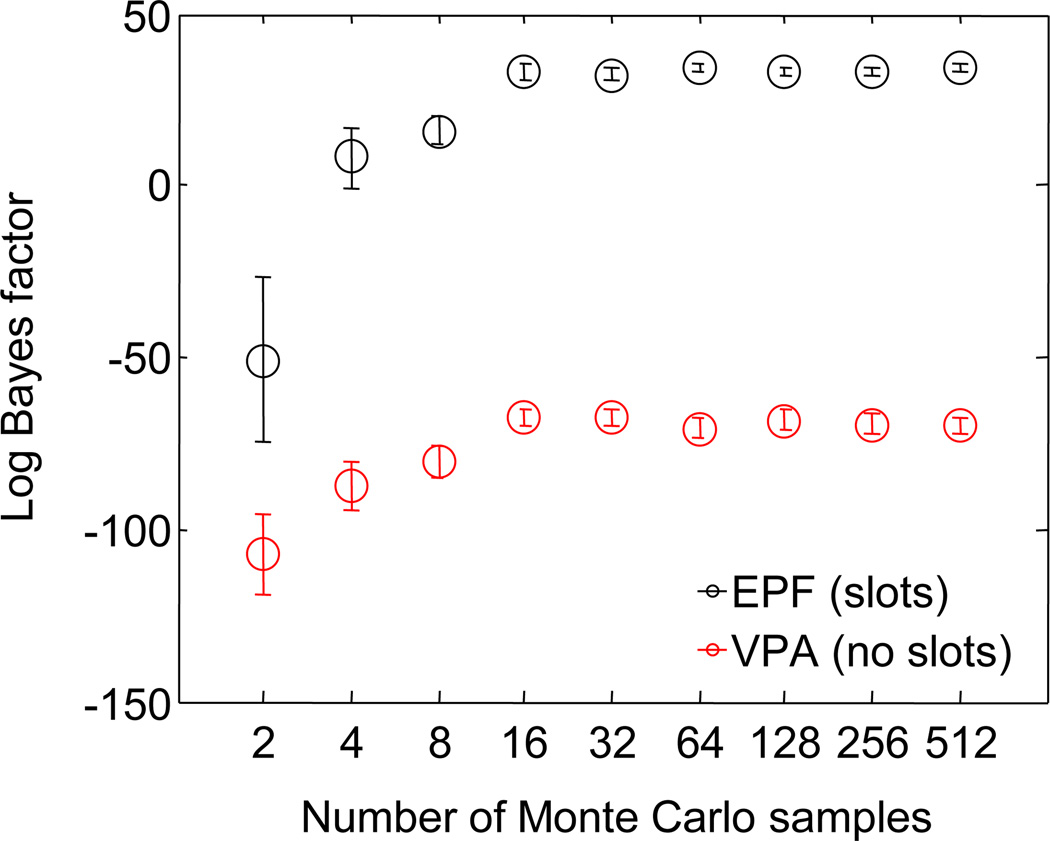
Figure A3. Effect of number of samples drawn from the prior distribution over parameters when computing expected log Bayes factors.
Computation of expected log Bayes factors involves an integration over the parameter prior. In the main analyses, we performed this integration numerically by drawing 500 Monte Carlo samples from the prior distribution over parameters. To check whether 500 is sufficient to obtain stable and unbiased estimates, we computed the log Bayes factor as a function of the number of samples (averages and standard errors over 100 runs with 1 synthetic subject with 720 trials distributed across set sizes 1,2,3,4,6, and 8). When the number of samples is small, the log Bayes factor is unstable (large error bars) and biased (systematically lower than the asymptote). However, it converges at around 16 samples, which indicates that 500 was sufficient to obtain stable and unbiased results.
Appendix
Relation between memory precision and noise
Before specifying the EPF and VPA models, we need to define memory precision. All models of working memory to date have assumed that memories of circular variables (such as color and orientation) are corrupted by Von Mises-distributed noise. In a delayed-estimation task, the stimulus estimate is equal to the memory. This means that if the stimulus is s and the estimate is ŝ, then the distribution of ŝ given s for a given value of mnemonic precision J is
where I0 is the modified Bessel function of the first kind of order 0. The width of this memory distribution is quantified by the concentration parameter κ: the higher κ, the less noise. If p ŝ | s, J had been Gaussian, one would naturally define precision J as the inverse of the variance of this Gaussian (Palmer, 1990; Shaw, 1980). A general way to define precision is as Fisher information, which sets an upper limit on the performance of a stimulus estimator (Keshvari et al., 2012, 2013; Van den Berg et al., 2014; Van den Berg et al., 2012). For a Gaussian distribution, Fisher information is indeed equal to inverse variance, while for a Von Mises distribution, J is related to the concentration parameter through (Van den Berg et al., 2012), where I1 is the modified Bessel function of the first kind of order 1. This relationship is close to linear, with the biggest deviations occurring at small κ.
Response probabilities predicted by the models
In the EPF (slots-plus-resources) model (Zhang & Luck, 2008), the observer remembers all items when set size, N, is smaller than capacity, K, and K items otherwise. When N ≥ K, all items are remembered, each with precision . (A more general form, in which precision was J1Nα, was considered in Van den Berg et al. [2014] and Van den Berg [2012].) The concentration parameter κ is then defined by the relation . When N > K, on each trial, K randomly selected items are remembered with precision , whereas the other N − K items are not remembered at all. If a nonremembered item is probed, the observer guesses randomly. Then, the distribution of the observer’s estimate ŝ is
where κ is now defined by . The free parameters of the EPF model are K and J1; K can take on any positive integer value, and J1 any positive real value. In the VPA model (Van den Berg et al., 2012), the observer remembers all N items. Mnemonic precision J is drawn, independently for each item, from a gamma distribution with mean and scale parameter τ:
(note that in many texts, the shape parameter instead of the mean is specified). A more general form, in which mean precision was J̄1Nα, was considered in (Van den Berg et al., 2014; Van den Berg et al., 2012). The distribution of the observer’s estimate is then
We evaluated this integral numerically through Monte Carlo simulation by drawing 1,000 samples of J. The free parameters of the VPA model are J̄1 and τ; both parameters can take on any positive real value. In both models, at each value of N, we evaluated p ŝ | s for 180 equally spaced values of ŝ −s.
Log Bayes factors
Raw data
Using conditional independence of the raw data across subjects, the log Bayes factor of the EPF and VPA models equals
| (3) |
where D denotes the complete set of all data and Di the data from the ith subject. The model likelihoods in the numerator and denominator are computed by averaging over all possible parameter values, an operation known as marginalization:
| (4) |
where θEPF,i and θVPA,i denote the (two-dimensional) EPF and VPA parameter vectors for the ith subject, respectively. We define the prior distributions over these parameters, p(θEPF,i|EPF) and p(θVPA,i|VPA), respectively, as bivariate normal distributions. To make the synthetic data statistically similar to subject data, we set the means and covariances of these distributions to the means and covariances of the maximum-likelihood estimates under the respective models obtained from the subject data of Experiment 1 in paper 1.
Since Di consists of the ith subject’s individual-trial responses, we can directly evaluate the likelihoods p(Di|EPF,θEPF,i) and p(Di|VPA,θVPA,i) using the equations in the Response Probabilities Predicted by the Models section. The integrals were evaluated numerically by drawing 500 parameter vectors from the prior distributions and averaging the corresponding likelihoods. To examine whether 500 was sufficient to obtain stable and unbiased estimates, we performed a separate analysis in which we computed the log expected Bayes factor as a function to the number of samples (Fig. 3a). We found that convergence starts at around 16 samples, meaning that 500 is more than sufficient to obtain stable and unbiased estimates.
Summary statistics
When D is a summary statistic, we cannot use the second part of Equation 3, because each summary statistic is computed from the data of all subjects, not the data of an individual subject. Instead, we have
where θ now denotes the vector parameters across all subjects. In our simulations, for both models, θ is a 90-dimensional vector, since we have 45 subjects per data set, with two free parameters each. The priors are factorizable, but the likelihoods are not, and therefore,
| (5) |
We approximated numerator and denominator by simulating, per model, 1,000 data sets of 45 subjects each, whose parameters we drew from the prior distributions described above. For each set, we evaluated the summary statistic D. In this way, we built two empirical distributions over D, one for the EPF model and one for the VPA model, each with 50 equally spaced bins on [0,1]. If a bin had no counts, we set the value of the distribution equal to 10−4 (one order of magnitude below 1 divided by the number of simulations). This produced the distributions shown in Figs. 4b, 5b, and 6b. These distributions were used to compute L at every value of D in Equation 5.
Model recovery rate and expected model evidence
The model recovery rate was the percentage of synthetic data sets for which the generating model was selected as the most likely model (i.e., the percentage of EPF data sets for which L was positive and the percentage of VPA data sets for which L was negative). The expected model evidence was the average of L over the synthetic data sets generated from each model. Incidentally, the two expected Bayes factors thus obtained (one for data generated from the EPF model and one for data generated from the VPA model) are mathematically identical to the Kullback–Leibler divergences between the data distributions under both models (Cover & Thomas, 1991). These information-theoretic quantities measure the separation between the data distributions. Large expected model evidence means that the data distributions are far separated.
Note that these quantities were computed in a way that was extremely favorable to the summary statistics. To compute the log Bayes factor for a given summary statistic, one requires an estimate of the “theoretical” distribution of that summary statistic under both models. We obtained these estimated distributions from the same synthetic data as those used to estimate the expected log Bayes factors. This constitutes overfitting, and, therefore, the model recovery rates and expected model evidence values we report are upper bounds on the true values. Our results show that even these upper bounds are inferior to using the raw data for D. This problem does not appear when estimating log Bayes factors based on raw data, because the “theoretical” distribution of the raw data is given by the models and, therefore, does not need to be estimated through simulation.
To compute the model evidence for the subject data, we looked up the value of L for the empirical value of the summary statistic D.
Model fits to summary statistics (Fig. 8c)
To compute model fits to the summary statistics, we generated 100 synthetic data sets with 45 subjects each, with parameter values set to the maximum-likelihood estimates of the subjects. For each synthetic data set, we computed the summary statistic. Figure 8c shows the means and confidence intervals from those 100 runs. Confidence intervals for the subject data were obtained by using a bootstrap method: We computed each summary statistic 100 times by randomly drawing with replacement 45 subjects from the subject pool.
Footnotes
SD is the notation used by papers 1 and 2 for SDUVM.
Paper 2 refers to this function as a “bilinear function.” However, a bilinear function is a function of two variables that is linear in both.
An inflection point is a point where the second derivative changes sign. In a piecewise linear function, all pieces have a second derivative of zero. However, the point γ is special because the first derivative is discontinuous; this is an example of a singularity.
A problem with this analysis is that the authors incorrectly assumed that SDUVM rises linearly at set sizes below capacity. However, no model, slot or slotless, has proposed such a relationship between (circular) standard deviation and set size; instead, the (circular) variance is typically assumed to rise linearly with set size. In practice, these are hard to distinguish when the rising part of the curve is small.
Pmem is the notation paper 2 uses for wUVM. We changed notation because Pmem is associated with the interpretation that an item is either memorized with a fixed precision (with probability Pmem) or completely discarded. We do not subscribe to this interpretation (Van den Berg et al., 2014; Van den Berg et al., 2012) and therefore opted for a more neutral notation. For the same reason, we do not refer to SDUVM as memory noise, precision, or resolution.
Our correlation plot in Fig. 1 is not identical to that in Fig. 4B in paper 2, and the R2 we find is lower. The reason is that the singularity estimates reported in paper 2 were inaccurate, due to a mistake in their analysis: Due to poor initialization of the optimization method used for fitting the mixture model, it often returned SDUVM estimates corresponding to a local maximum, instead of the global maximum of the likelihood function. After correcting this mistake, Anderson and colleagues find a different plot and an R2 of about .55 instead of .65 (personal communication with the authors).
The log transformations on J1, J̄1, and τ were performed because a normal distribution to the logarithms of the parameter estimates fitted much better than a normal distribution to the original values (the differences in maximum log likelihood were larger by 122, 158, and 152, respectively).
The results in Fig. 3c are asymmetric: The evidence for the EPF model tested on EPF data is systematically lower than the evidence for the VPA model tested on VPA data. This indicates that the VPA model is better at "mimicking" EPF data (specifically, a uniform component in the estimate distribution) than the EPF model is at mimicking VPA data (specifically, a mixture of precisions in the estimate distribution). This asymmetry is a property of the models, not a shortcoming of the model comparison method. The validity of the model comparison method follows from the 100% model recovery rate.
In a subsequent paper (Anderson & Awh, 2012), the same authors asserted that slotless models would predict a logarithmic function. However, this assertion is unfounded. Some slotless models in the literature postulate a power law function between precision and set size (Bays & Husain, 2008; Van den Berg et al., 2012), but this does not correspond to a logarithmic relationship between SDUVM and set size.
The reason why the EPF fit to the raw data is worse than the fits shown in Fig. 2 of paper 2 is that the latter does not show the fit of the EPF model, but of the mixture model in Equation 1, which is fitted separately at each set size and thus has a total of 12 parameters.
References
- Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19(6):716–723. [Google Scholar]
- Alvarez GA, Cavanagh P. The capacity of visual short-term memory is set both by visual information load and by number of objects. Psych Science. 2004;15:106–111. doi: 10.1111/j.0963-7214.2004.01502006.x. [DOI] [PubMed] [Google Scholar]
- Anderson DE, Awh E. The plateau in mnemonic resolution across large set sizes indicates discrete resource limits in visual working memory. Atten Percept Psychophys. 2012;74(5):891–910. doi: 10.3758/s13414-012-0292-1. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Anderson DE, Vogel EK, Awh E. Precision in visual working memory reaches a stable plateau when individual item limits are exceeded. J Neurosci. 2011;31(3):1128–1138. doi: 10.1523/JNEUROSCI.4125-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Anderson DE, Vogel EK, Awh E. Selection and storage of perceptual groups is constrained by a discrete resource in working memory. J Exp Psych Hum Percept Perform. 2013;39(3):824–835. doi: 10.1037/a0030094. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Bays PM, Catalao RFG, Husain M. The precision of visual working memory is set by allocation of a shared resource. J Vision. 2009;9(10):1–11. doi: 10.1167/9.10.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays PM, Gorgoraptis N, Wee N, Marshall L, Husain M. Temporal dynamics of encoding, storage, and reallocation of visual working memory. J Vis. 2011;11(10) doi: 10.1167/11.10.6. 10.1167/11.10.6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays PM, Husain M. Dynamic shifts of limited working memory resources in human vision. Science. 2008;321(5890):851–854. doi: 10.1126/science.1158023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buschman TJ, Siegel M, Roy RE, Miller EK. Neural substrates of cognitive capacity limitations. Proc Natl Acad Sci. 2011;108(27):11252–11255. doi: 10.1073/pnas.1104666108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cover TM, Thomas JA. Elements of information theory. New York: John Wiley & Sons; 1991. [Google Scholar]
- Donkin C, Nosofsky RM, Gold JM, Shiffrin RM. Discrete-slots models of visual working-memory response times. Psych Rev. 2013 doi: 10.1037/a0034247. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elmore LC, Ma WJ, Magnotti JF, Leising KJ, Passaro AD, Katz JS. Visual short-term memory compared in rhesus monkeys and humans. Curr Biol. 2011;21(11):975–979. doi: 10.1016/j.cub.2011.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fougnie D, Suchow JW, Alvarez GA. Variability in the quality of visual working memory. Nat Commun. 2012;3:1229. doi: 10.1038/ncomms2237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, Awh E, Vogel EK. Discrete capacity limits in visual working memory. Curr Opin Neurobiol. 2010;20(2):177–182. doi: 10.1016/j.conb.2010.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyselaar E, Johnston K, Pare M. A change detection approach to study visual working memory of the macaque monkey. J Vision. 2011;11(3):11–10. doi: 10.1167/11.3.11. 11. [DOI] [PubMed] [Google Scholar]
- Jeffreys H. The theory of probability. 3rd ed. Oxford University Press; 1961. [Google Scholar]
- Jones HF, editor. The notebooks of Samuel Butler. A.C. Fifield; 1912. [Google Scholar]
- Kass RE, Raftery AE. Bayes factors. Journal of the American Statistical Association. 1995;90(430):773–795. [Google Scholar]
- Keshvari S, Van den Berg R, Ma WJ. Probabilistic computation in human perception under variability in encoding precision. PLoS ONE. 2012;7(6):e40216. doi: 10.1371/journal.pone.0040216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keshvari S, Van den Berg R, Ma WJ. No evidence for an item limit in change detection. PLoS Comp Biol. 2013;9(2):e1002927. doi: 10.1371/journal.pcbi.1002927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kullback S. Information theory and statistics. Courier Dover Publications; 1997. [Google Scholar]
- Lara AH, Wallis JD. Capacity and precision in an animal model of short-term memory. J Vision. 2012;12(3):1–12. doi: 10.1167/12.3.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luck SJ, Vogel EK. Visual working memory capacity: from psychophysics and neurobiology to individual differences. Trends Cogn Sci. 2013;17(8):391–400. doi: 10.1016/j.tics.2013.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch SM. Introduction to Applied Bayesian Statistics and Estimation for Social Scientists. Springer; 2007. [Google Scholar]
- Mardia KV, Jupp PE. Directional statistics. John Wiley and Sons; 1999. [Google Scholar]
- Palmer J. Attentional limits on the perception and memory of visual information. J Exp Psychol Hum Percept Perform. 1990;16(2):332–350. doi: 10.1037//0096-1523.16.2.332. [DOI] [PubMed] [Google Scholar]
- Rouder J, Morey R, Cowan N, Morey C, Pratte M. An assessment of fixed-capacity models of visual working memory. Proc Natl Acad Sci U S A. 2008;105(16):5975–5979. doi: 10.1073/pnas.0711295105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz GE. Estimating the dimension of a model. Annals of Statistics. 1978;6(2):461–464. [Google Scholar]
- Shaw ML. Identifying attentional and decision-making components in information processing. In: Nickerson RS, editor. Attention and Performance. VIII. Hillsdale, NJ: Erlbaum; 1980. pp. 277–296. [Google Scholar]
- Sims CR, Jacobs RA, Knill DC. An ideal-observer analysis of visual working memory. Psychological Review. 2012;119(4):807–830. doi: 10.1037/a0029856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, Van der Linde A. Bayesian measures of model complexity and fit (with discussion) Journal of the Royal Statistical Society, Series B. 2002;64(4):583–639. [Google Scholar]
- Van den Berg R, Awh E, Ma WJ. Factorial comparison of working memory models. Psych Rev. 2014 doi: 10.1037/a0035234. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van den Berg R, Ma W. A plateau, so what? The uninformativeness of summary statistics in working memory studies. Atten Percept Psychophys. 2013 doi: 10.3758/s13414-013-0618-7. under review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van den Berg R, Shin H, Chou W-C, George R, Ma WJ. Variability in encoding precision accounts for visual short-term memory limitations. Proc Natl Acad Sci U S A. 2012;109(22):8780–8785. doi: 10.1073/pnas.1117465109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogel EK, Machizawa MG. Neural activity predicts individual differences in visual working memory capacity. Nature. 2004;428(6984):748–751. doi: 10.1038/nature02447. [DOI] [PubMed] [Google Scholar]
- Wilken P, Ma WJ. A detection theory account of change detection. J Vision. 2004;4(12):1120–1135. doi: 10.1167/4.12.11. [DOI] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. Discrete fixed-resolution representations in visual working memory. Nature. 2008;453(7192):233–235. doi: 10.1038/nature06860. [DOI] [PMC free article] [PubMed] [Google Scholar]