Evaluating Random Forests for Survival Analysis using Prediction Error Curves

Abstract

Prediction error curves are increasingly used to assess and compare predictions in survival analysis. This article surveys the R package pec which provides a set of functions for efficient computation of prediction error curves. The software implements inverse probability of censoring weights to deal with right censored data and several variants of cross-validation to deal with the apparent error problem. In principle, all kinds of prediction models can be assessed, and the package readily supports most traditional regression modeling strategies, like Cox regression or additive hazard regression, as well as state of the art machine learning methods such as random forests, a nonparametric method which provides promising alternatives to traditional strategies in low and high-dimensional settings. We show how the functionality of pec can be extended to yet unsupported prediction models. As an example, we implement support for random forest prediction models based on the R-packages randomSurvivalForest and party. Using data of the Copenhagen Stroke Study we use pec to compare random forests to a Cox regression model derived from stepwise variable selection. Reproducible results on the user level are given for publicly available data from the German breast cancer study group.

1. Introduction

In survival analysis many different regression modeling strategies can be applied to predict the risk of future events. Often, however, the default choice of analysis relies on Cox regression modeling due to its convenience. Extensions of the random forest approach (Breiman 2001) to survival analysis provide an alternative way to build a risk prediction model. This bypasses the need to impose parametric or semi-parametric constraints on the underlying distributions and provides a way to automatically deal with high-level interactions and higher-order terms in variables and allows for accurate prediction (Ishwaran, Kogalur, Blackstone, and Lauer 2008). In certain applications it is of interest to compare the predictive accuracies of Cox regression to random forest or other strategies for building a risk prediction model. Several measures can be used to assess the resulting probabilistic risk predictions. Most popular are the Brier and logarithmic scoring rules (Gneiting and Raftery 2007) and rank statistics like the concordance index which equals the area under the ROC curve (AUC) for binary responses (Harrell, Lee, and Mark 1996). For event time outcome in survival analysis these measures can be estimated pointwise over time, where pioneering work was done by Graf, Schmoor, Sauerbrei, and Schumacher (1999) for the time-dependent Brier score and by Heagerty, Lumley, and Pepe (2000) for time-dependent ROC analysis. Performance curves are obtained by combining time pointwise measures.

In this article we concentrate on prediction error curves that are time dependent estimates of the population average Brier score. However, similar results are usually obtained with the time-dependent AUC. At a given time point t, the Brier score for a single subject is defined as the squared difference between observed survival status (e.g., 1=alive at time t and 0=dead at time t) and a model based prediction of surviving time t. Typically the survival status at time t will be right censored for some data. Thus, inverse probability of censoring weights (IPCW) were proposed (Graf et al. 1999; Gerds and Schumacher 2006) to avoid bias in the population average.

An important issue in prediction is correct prediction error estimation. If a risk prediction model fits well over the training data used to build the model, and has good prediction accuracy (assessed using the training data), we would like to know if it continues to predict well over independent validation data and what that prediction accuracy is. Various data splitting algorithms have been proposed, based on cross-validation and bootstrap, to correctly estimate the prediction accuracy of a model in the typical situation where a single data set has to be used to build the prediction models and again to estimate the prediction performance (Efron and Tibshirani 1997; Gerds and Schumacher 2007; Adler and Lausen 2009).

We present the R (R Development Core Team 2009) package pec, short for prediction error curves , that is available from the Comprehensive R Archive Network at http://CRAN. R-project.org/package=pec. The package provides functions for IPCW estimation of the time-dependent Brier score and has an option for selecting between ordinary cross-validation, leave-one-out bootstrap, and the .632+ bootstrap for estimating risk prediction performance. It is also possible to compute prediction error curves with independent test data. An important feature of pec is that the entire model building process can be taken into account in the evaluation of prediction error, including data dependent steps such as variable selection, shrinkage, or tuning parameter estimation. By using repeated data splitting (either cross-validation or bootstrap), this yields estimates of the prediction error that are a composite of the prediction accuracy and the underlying variability of the prediction models due to whatever data dependent steps were used for their construction over the training splits of the data (Gerds and van de Wiel 2011).

To illustrate the usage of pec we have extended the package to work with prediction models obtained using the R-packages randomSurvivalForest (Ishwaran and Kogalur 2007; Ishwaran et al. 2008) and party (Hothorn, Bühlmann, Dudoit, Molinaro, and van der Laan 2006) which implement extensions of the random forest method for survival data. The new functions are illustrated in a worked out example where we analyse the data of the Copenhagen stroke study (COST) (Jørgensen, Nakayama, Raaschou, Gam, and Olsen 1994). Earlier analyses of COST were based on a Cox regression model where the model was obtained by backward stepwise selection (Andersen, Andersen, Kammersgaard, and Olsen 2005). We compare the Cox prediction model obtained in this fashion to random forest prediction models.

2. Predicting survival

2.1. Data structure

A survival prediction model uses data on the life history of subjects (the response) and their characteristics (the predictor variables). The response is (T̃_iΔ_i), where T̃_i is the minimum of the survival time T_i and the right censoring time C_i and ${\Delta }_i=\mathcal{I}\{T_i\le C_i\}$ is the status (censoring) value indicating a patient died (Δ_i = 1) or was right-censored (Δ_i = 1). The predictor variables $X_i=(X_i^1,\dots ,X_i^K)$ for subject i usually consists of both continuous scale variables, like age or blood pressure, or qualitative variables, like gender or genotype.

Example. We reconsider the data of the Copenhagen stroke study (COST) (Jørgensen et al. 1994). In the COST study 993 patients were enrolled after being admitted to a hospital with a stroke and were followed for 10 years. Recorded for each patient was the length of time from admission to death, for those who died, otherwise the length of time from admission to the maximal time where the patient was known to be alive was recorded (i.e., right censored). Table 1 provides summary information for the 13 variables collected in the study.

Table 1.

Shown are the count (percentage) of COST patients with factor level “yes” and the minimum and maximum values for continuous predictor variables stratied by gender.

Predictor variables			Sex
	Coding/Range	Variable name	Female (n=555)	Male (n=438)	Total (n=993)	Missing (n=475)
Factors:
Hyper tension	yes/no	hypTen	172(33.73%)	134(31.83%)	306(32.87%)	62(6.24%)
Myocardial infarction	yes/no	myoInf	102(20.28%)	87(21.01%)	189(20.61%)	76(7.65%)
Previous stroke	yes/no	prevStroke	101 (19.46%)	94(22.17%)	195(20.68%)	50(5.04%)
Other disabling disease	yes/no	othDisease	130(24.76%)	75(17.56%)	205(21.53%)	41(4.13%)
Alcohol intake	yes/no	alcohol	74(16.55%)	187(48.83%)	261(31.45%)	163(16.41%)
Diabetes	yes/no	diabetes	72(13.95%)	76(17.8%)	148(15.69%)	50(5.04%)
Smoking status	yes/no	smoke	161(36.51%)	203(53.7%)	364(44.44%)	174(17.52%)
Atrial fibrillation	yes/no	atrialFib	109(19.96%)	53(12.16%)	162(16.5%)	11(1.11%)
Hemorrhage	yes/no	hemor	42(9.5%)	19(5.23%)	61(7.58%)	188(18.93%)
Continuous:
Age	min/max	age	25/98	28/93	25/98	0(0%)
Scandinavian stroke score	min/max	strokeScore	0/58	0/58	0/58	7(0.7%)
Cholesterol	min/max	cholest	1.7/11.6	1.5/10.5	1.5/11.6	233(23.46%)

For the purpose of illustration we construct three hypothetical new patients with values in the range of the predictor space defined by the COST patients and store them in a data frame called newData. These new “patients” have different ages, but do not differ otherwise: All are females, have a strokeScore of 38, a mean value of 6 for cholest, and the remaining predictor variables set to the value ”no”.

2.2. Stepwise variable selection in Cox regression

A Cox regression model specifies the conditional cumulative hazard function dependent on the vector of predictor variables $X_i=(X_i^1,\dots ,X_i^K)$:

$$\Lambda (t\mid X_i)={\Lambda }_0\left(t\right)\exp \left({\beta }^{\frac{T}{}}{X}_i\right).$$

Here Λ₀ is an unspecified increasing function, referred to as the cumulative baseline hazard and $\beta =({\beta }_1,\dots ,B_K)\in {\mathbb{R}}^K$ is an unknown vector of regression coefficients.

Many different variable selection strategies can be applied within the context of Cox regression. Our approach will be to use backward stepwise variable selection (implemented using the function fastbw of the rms package, Harrell Jr 2009) using the Akaike information criteria (AIC). We then fit a Cox model using only those variables selected in the stepwise procedure (we use cph from the rms package for the Cox regression analysis). In total, our approach is:

Step 1. Run fastbw using AIC.

Step 2. Fit a Cox regression model using the predictors selected in Step 1.

Step 3. Using the estimates of β and Λ₀ obtained in Step 2, calculate for a subject with predictor values x:

$${\widehat{S}}^{\mathrm{cox}}(t\mid \mathbf{x})=\exp \left(-{\widehat{\Lambda }}_0\left(t\right)\exp \left[{\widehat{\beta }}^{\mathsf{T}}\mathbf{x}]\right]\right).$$

Note that the AIC criterion is likelihood based and closely related to the logarithmic scoring rule, which is strictly proper (Gneiting and Raftery 2007), and hence should be adequate for identifying a prediction model. However, as with any automated model selection procedure the result can be quite unstable (Austin and Tu 2004).

2.3. Random forests

A random forest is a nonparametric machine learning strategy that can be used for building a risk prediction model in survival analysis. In survival settings, the predictor is an ensemble formed by combining the results of many survival trees. The general strategy is as follows:

Step 1. Draw B bootstrap samples.

Step 2. Grow a survival tree based on the data of each of the bootstrap samples b = 1, . . . , B:

(a) At each tree node select a subset of the predictor variables.

(b) Among all binary splits defined by the predictor variables selected in (a), find the best split into two subsets (the daughter nodes) according to a suitable criterion for right censored data, like the log-rank test.

(c) Repeat (a)-(b) recursively on each daughter node until a stopping criterion is met.

Step 3. Aggregate information from the terminal nodes (nodes with no further split) from the B survival trees to obtain a risk prediction ensemble.

In what follows we consider two different implementations of random forests from the two R packages: randomSurvivalForest (Ishwaran et al. 2008) and party (Hothorn et al. 2006). To describe the risk predictions for the forest ensembles, let ${\mathcal{T}}_b$ denote the bth survival tree and let ${\mathcal{T}}_b\left(\mathbf{x}\right)$ denote the terminal node of subjects in the bth bootstrap sample with predictor x (each x will sit inside a unique terminal node due to the recursive construction of the tree). Note that when bootstrap samples are drawn with replacement then subjects from the original data set may occur multiple times. Let c_ib be the number of times subject i occurs in the bth bootstrap sample. Note that c_ib = 0 if the ith subject is not included in the bth bootstrap sample. Using the counting process notation (Andersen, Borgan, Gill, and Keiding 1993)

$${\tilde{N}}_i\left(s\right)=\mathcal{I}({\tilde{T}}_i\le s,{\Delta }_i=1);{\tilde{Y}}_i\left(s\right)=\mathcal{I}({\tilde{T}}_i>s),$$

we have

$${\tilde{N}}_b^{\ast }(s,\mathbf{x})=\sum _{i=1}^N{c}_{ib}\mathcal{I}(X_i\in {\mathcal{T}}_b\left(\mathbf{x}\right)){\tilde{N}}_i\left(s\right);{\tilde{Y}}_b^{\ast }(s,\mathbf{x})=\sum _{i=1}^N{c}_{ib}\mathcal{I}(X_i\in {\mathcal{T}}_b\left(\mathbf{x}\right)){\tilde{Y}}_i\left(s\right).$$

Thus, in the terminal node corresponding to covariate value x,Ñ_b*(s, x) counts the uncensored events until time s and Ỹ_b*(s, x) is the number at risk at time s.

Random survival forests (randomSurvivalForest)

In random survival forests (Ishwaran et al. 2008), the ensemble is constructed by aggregating tree-based Nelson-Aalen estimators. Specifically, in each terminal node of a tree, the conditional cumulative hazard function is estimated using the Nelson-Aalen using the “in-bag” data (i.e., subjects in the bootstrap sample):

$${\widehat{H}}_b(t\mid \mathbf{x})={\int }_0^t\frac{{\tilde{N}}_b^{\ast }(\mathrm{d}s,\mathbf{x})}{{\tilde{Y}}_b^{\ast }(s,\mathbf{x})}.$$

The ensemble survival function from random survival forest is

$${\widehat{S}}^{\mathrm{rsf}}(t\mid \mathbf{x})=\exp \left(-\frac{1}{B}\sum _{b=1}^B{\widehat{H}}_b(t\mid \mathbf{x})\right).$$ (1)

Conditional inference forests (party)

The conditional inference forest for survival analysis (Hothorn, Lausen, Benner, and Radespiel-Tröger 2004) utilizes a weighted Kaplan-Meier estimate based on all subjects from the training data at x for prediction. Its ensemble survival function is

$${\widehat{S}}^{\mathrm{cforest}}(t\mid \mathbf{x})=\prod _{s\le t}\left(1-\frac{{\sum }_{b=1}^B{\tilde{N}}_b^{\ast }(\mathrm{d}s,\mathbf{x})}{\sum _{b=1}^B{\tilde{Y}}_b^{\ast }(s,\mathbf{x})}\right).$$ (2)

If the underlying survival function is continuous, then this is asymptotically equivalent to

$$\exp \left(-{\int }_0^t\frac{{\sum }_{b=1}^B{\tilde{N}}_b^{\ast }(\mathrm{d}s,\mathbf{x})}{\sum _{b=1}^B{\tilde{Y}}_b^{\ast }(s,\mathbf{x})}\right).$$

Comparison to equation (1) shows that the way trees are aggregated in conditional inference forests is different from the random survival forest approach. Conditional inference forests put more weight on terminal nodes where there is a large number of subjects at risk:

$$\frac{{\sum }_{b=1}^B{\tilde{N}}_b^{\ast }(\mathrm{d}s,\mathbf{x})}{\sum _{b=1}^B{\tilde{Y}}_b^{\ast }(s,\mathbf{x})}=\frac{1}{B}\sum _{b=1}^B\left[\frac{{\tilde{Y}}_b^{\ast }(s,\mathbf{x})}{\frac{1}{B}{\sum }_{b=1}^B{\tilde{Y}}_b^{\ast }(s,\mathbf{x})}\right]\frac{{\tilde{N}}_b^{\ast }(\mathrm{d}s,\mathbf{x})}{{\tilde{Y}}_b^{\ast }(s,\mathbf{x})}.$$

In contrast, random survival forests uses equal weights on all terminal nodes. It is diffcult to say which formula may be better in general, however.

3. Extracting predicted survival probabilities

The S3-methods predictSurvProb.x extract survival probabilities from R objects of class x. Implemented are methods for the following classes (package): matrix (base), aalen (timereg), cox.aalen (timereg), mfp (mfp), coxph (survival), survnnet (survnnet), rpart (rpart), cph (rms), survfit (survfit), prodlim (prodlim). Note however that the package survnnet is currently not available from CRAN.

We now explain how we have extended the package pec to work with R objects of classes fastbw (rms), rsf (randomSurvivalForest), and cforest (party). Section 3.4 then shows some details for writing new extensions.

3.1. Selected Cox regression

The following function selectCox evaluates Step 1 and Step 2 the stepwise variable selection strategy for the Cox regression model described in Section 2.2.

selectCox <- function(formula,data,rule=“aic”){ require(rms) require(prodlim) fit <- cph(formula,data,surv=TRUE) bwfit <- fastbw(fit,rule=rule) if (length(bwfit$names.kept)==0){ newform <- reformulate(“1”,formula[[2]]) newfit <- prodlim(newform, data=data)} else{ newform <- reformulate(bwfit$names.kept, formula[[2]]) newfit <- cph(newform,data,surv=TRUE) } out <- list(fit=newfit,In=bwfit$names.kept) out$call <- match.call() class(out) <- “selectCox” out }

The function cph from rms is used to fit a Cox regression model using the selected predictor variables, with one exception: If the set of selected predictor variables in Step 1 is empty, then the Kaplan-Meier method is applied to predict survival via the function prodlim (prodlim). The resulting R object is assigned to the S3-class selectCox.

Step 3 of Section 2.2 is implemented using the function predictSurvProb. This passes its arguments to predictSurvProb.cph or predictSurvProb.prodlim, depending on whether or not the selected set of predictor variables was empty.

predictSurvProb.selectCox <- function(object,newdata,times,...){ predictSurvProb(object[[1]],newdata=newdata,times=times,...)}

3.2. Random survival forest package: rsf

A random survival forest model is fitted with the function rsf (randomSurvivalForest) which results in an object of S3-class rsf. Using the built-in predict.rsf method we extract the averaged cumulative hazard function for each line in newdata at the event times of the original data set (see Section 2.3). The survival probabilities are then computed via formula (1) and with the help of the function sindex (prodlim) these are evaluated at the requested times.

predictSurvProb.rsf <- function (object, newdata, times, ...) { N <- NROW(newdata) class(object) <- c(“rsf”, “grow”) S <- exp(-predict.rsf(object, test=newdata)$ensemble) if (N==1) S <- matrix(S,nrow=1) Time <- object$timeInterest p <- cbind(1,S)[,1+sindex(Time, times),drop=FALSE] if (NROW(p) != NROW(newdata) || NCOL(p) != length(times)) stop(“Prediction failed”) p }

3.3. Party package: cforest

A conditional inference forest model (Section 2.3) is fitted with the function cforest (party) and results in an S4-class object. We get around the class problem by creating a wrapper function pecCforest. The fitted cforest S4-class object is stored in a list which is supplied with the call. The output is assigned to the S3-class pecCforest.

pecCforest <- function(formula,data,...){ require(party) out <- list(forest=cforest(formula,data,...)) class(out) <- “pecCforest” out$call <- match.call() out}

The treeresponse method (party) can be applied to the list element pecCforest$forest of the S3-class object in order to extract survival probabilities for newdata at times (see formula (2)). The resulting object is a list which contains for each line in newdata the Kaplan-Meier curve in form of a survfit object (survival). We then apply predictSurvProb.survfit to the elements of the list.

predictSurvProb.pecCforest <- function (object, newdata, times, ...) { survObj <- treeresponse(object$forest,newdata=newdata) p <- do.call(“rbind”,lapply(survObj,function(x){ predictSurvProb(x,newdata=newdata[1,,drop=FALSE],times=times)})) if (NROW(p) != NROW(newdata) || NCOL(p) != length(times)) stop(“Prediction failed”) p }

Example (continued). We use the complete case data of the COST study that contains data from 518 patients with no missing values in any of the 13 predictor variables.

R> library(“pec”)

R> library(“survival”)

R> library(“rms”)

R> library(“randomSurvivalForest”)

R> library(“party”)

R> cost <- na.omit(cost)

We fit a random survival forest model based on 1000 trees under default settings of the package (Ishwaran and Kogalur 2007). We also fit a conditional inference forest model via pecCforest based on 1000 trees, otherwise using the default options. Finally a selected Cox regression model is fitted via selectCox as described above.

R> fitform <- Surv(time,status)~age+sex+hypTen+myoInf+prevStroke+othDisease + alcohol+diabetes+smoke+atrialFib+hemor+strokeScore+cholest

R> fitcox <- selectCox(fitform, data=cost, rule=“aic”)

R> set.seed(13)

R> fitrsf <- rsf(fitform,data=cost,forest=TRUE,ntree=1000)

R> set.seed(13)

R> fitcforest <- pecCforest(fitform, data=cost, controls=cforest_classical(ntree=1000))

To illustrate the results we predict the 10 year survival probabilities for the hypothetical new patients stored in the R object newData (see Section 2.1).

R> pcox <- predictSurvProb(fitcox,newdata=newData,times=10*365.25)

R> prsf <- predictSurvProb(fitrsf,newdata=newData,times=10*365.25)

R> extends <- function(...)TRUE

R> pcf <- predictSurvProb(fitcforest,newdata=newData,times=10*365.25)

The function extends is required to ensure that cforest yields a survival probability. This is not necessary if only functions in party are used.

Table 2 shows the results.

Table 2.

Predicted survival (in %) for newData at 10 years based on the selected Cox regression model (selectCox) and two random forest models: Random survival forest (rsf) and conditional inference forest (cforest) both based on 1000 trees.

Patient Id	Age	selectCox	rsf	cforest
newData 1	28	86.05	54.2	47.73
newData 2	74	24.17	34.31	20.66
newData 3	95	1.91	13.56	9.74

Compared to Cox regression both random survival forest approaches yield less extreme predictions on the boundary of the age range (rows 1 and 3) at 10 year survival. This may be explained by the fact that a random forest is a “nearest neighbor type” method whereas a Cox regression model extrapolates the trend found in the center of the age range. Interestingly, for all newData the conditional inference forest model predicts a lower 10 year survival chance than the random survival forest model.

We use the function plotPredictSurvProb to plot the predicted survival curves for new subjects for a given modeling strategy. It applies the predictSurvProb method to predict at all event times but other time points can be selected. The following code produces the curves in Figure 1.

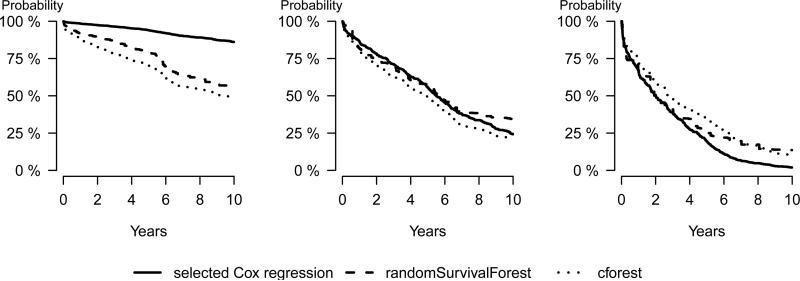
Figure 1.

Predicted survival curves for newData[1,] left panel, newData[2,] middle panel, and newData[3,] right panel. Both random forest approaches used 1000 trees.

R> par(mfrow=c(1,3))

R> lapply(1:3, function(x){ + plotPredictSurvProb(fitcox,newdata=newData[x,],lty=1) + plotPredictSurvProb(fitrsf, newdata=newData[x,],add=TRUE,lty=2) + plotPredictSurvProb(fitcforest, newdata=newData[x,], add=TRUE, lty=3) + })

Figure 1 displays the survival curves for the hypothetical new patients for each of the three different methods. The three models yield similar prediction at the median age but differ for the young and old patients. For these patients, Cox regression is more extreme. This is consistent with what we saw in Table 2.

3.4. Writing new extensions

A predictSurvProb method has three required arguments:

• object: The fitted R object.

• newdata: A data frame with the predictor variables.

• times: A vector of time points.

To extend the functionality of pec a function predictSurvProb.x can be written which extracts survival probabilities from an object of class x and returns them in a matrix with as many columns as there are times and as many rows as there are lines in newdata. It is possible to pass further arguments to the predictSurvProb method via the argument model.args of the function pec. For example the function predictSurvProb.rpart uses an optional argument train.data. Note that a requirement for repeated data splitting (cross-validation) is that the R object contains its call which has to be a list in which the argument data can be modified. Note also that presently only S3-objects are supported by the functionality of pec, but that it is relatively easy to wrap S4-objects into the required form, as shown earlier for cforest.

4. Prediction error curves

The function pec compares the predictive performances of rival survival modeling strategies over time. As outlined in the introduction, several measures are available for assessing a model in survival analysis. Here we restrict attention to prediction error defined as the time-dependent expected Brier score:

$$\mathrm{BS}(t,\widehat{S})=\mathsf{E}{(Y_i\left(t\right)-\widehat{S}(t\mid X_i))}^2.$$

Here the expectation is taken with respect to the data of a subject i which does not belong to the training set, and $Y_i\left(t\right)=\mathcal{I}(T_i\ge t)$ is the true status of subject i and Ŝ(t|X_i) is the predicted survival probability at time t for subject i with predictor variables X_i. Useful benchmark values for the Brier score are 33%, which corresponds to predicting the risk by a random number drawn from U[0, 1], and 25% which corresponds to predicting 50% risk for everyone. The most important benchmark is the expected Brier score of a prediction model which ignores all predictor variables. In survival analysis the Kaplan-Meier estimate of survival calculated with all training samples yields such a null model.

4.1. Estimation from right censored data

The function pec provides several estimates of the expected Brier score. For the estimation of this prediction error the true status is replaced by the observed status defined as ${\tilde{Y}}_i\left(t\right)=\mathcal{I}({\tilde{T}}_i>t)$ and the squared residuals are weighted using inverse probability of censoring weights (IPCW) (Gerds and Schumacher 2006), given by

$${\widehat{W}}_i\left(t\right)=\frac{(1-{\tilde{Y}}_i\left(t\right)){\Delta }_i}{\widehat{G}({\tilde{T}}_i-\mid X_i)}+\frac{{\tilde{Y}}_i\left(t\right)}{\widehat{G}(t\mid X_i)}$$ (3)

whereĜ(t|x) ≈ P(C_i > t|X_i = x) is an estimate of the conditional survival function of the censoring times. If an independent test data set D̃_M is available, the expected Brier score is estimated by

$$\widehat{\mathrm{BS}}(t,\widehat{S})=\frac{1}{M}\sum _{i\in {\tilde{D}}_M}{\widehat{W}}_i\left(t\right){\{{\tilde{Y}}_i\left(t\right)-\widehat{S}(t\mid X_i)\}}^2,$$

where M is the number of subjects in D̃_M andŜ is based on a training data.

The weights (3) can be optionally estimated using the function ipcw by making use of the marginal Kaplan-Meier estimator (ignoring the predictor variables), a Cox regression model, or an additive Aalen regression model. Furthermore, in the case of only discrete covariates the stratified Kaplan-Meier for the censoring times can be used and in case of a single continuous covariate a nonparametric kernel type estimator. See Section 6 for more discussion on how to choose the appropriate method in practice.

4.2. Cross-validation

Several methods are implemented to deal with over-fitting in situations where only one data set is available for building the prediction models and for the estimation of prediction performance (Gerds and Schumacher 2007). Optionally the function computes one or all of the following estimates:

• AppErr: Apparent or re-substitution estimate.

• BootCvErr: Bootstrap cross-validation estimate (bootstrap with or without replacement).

• crossvalErr: k-fold cross-validation estimate.

• loocvErr: Leave-one-out cross-validation estimate.

• NoInfErr : No information estimate.

• Boot632Err: Efron's .632 estimate.

• Boot632plusErr: Efron & Tibshirani's .632+ estimate.

Since this terminology which is used in the package pec can be confusing and since also the literature is not always consistent, we provide explicit formulae for all estimates below. Note that the term “bootstrap cross-validation” has been used for example in Fu, Carroll, andWang (2005) for an estimate which is currently not implemented in pec, where models are trained in bootstrap samples and validated in the full data. Note further that the estimate termed “leave-one-out bootstrap” (see below) was defined in Efron and Tibshirani (1997) and is also not implemented in the current version of pec. The subsampling version of the bootstrap .632+ estimate was proposed in Binder and Schumacher (2008).

• The apparent estimate of the prediction error re-substitutes the data of the N subjects, D_N, that were used to build the models as follows:

$$\mathrm{AppErr}(t,\widehat{S})=\frac{1}{N}\sum _{i\in D_N}{\widehat{W}}_i\left(t\right){\{{\tilde{Y}}_i\left(t\right)-\widehat{S}(t\mid X_i)\}}^2.$$

• The bootstrap cross-validation approach splits the data D_N into many bootstrap training samples D_b and corresponding test samples D_N \ D_b (b = 1, . . . , B). Here bootstrap samples can either be drawn with or without replacement from the original data. Then, models Ŝ_b are trained with the bootstrap training data D_b, corresponding test samples are predicted and residuals are computed. Finally the bootstrap cross-validation estimate of the prediction error is calculated by averaging over the test data sets:

$$\mathrm{BootCvErr}(t,\widehat{S})=\frac{1}{B}\sum _{b=1}^B\frac{1}{M_b}\sum _{i\in D_N{D}_b}{\widehat{W}}_i\left(t\right){\{{\tilde{Y}}_i\left(t\right)-{\widehat{S}}_b(t\mid X_i)\}}^2.$$

For bootstrap without replacement (subsampling) M_b is a fixed user defined number smaller than N and the same for each b, and is the size of the bootstrap samples for resampling without replacement. For bootstrap with replacement M_b is the number of subjects not drawn in the bootstrap sample D_b. We note that the bootstrap cross-validation estimate (with replacement) is closely related to the leave-one-out bootstrap estimate, which is given by reversing the order of summation:

$$\frac{1}{N}\sum _{i=1}^N\frac{1}{K_i}\sum _{b:i\in D_N{D}_b}{\widehat{W}}_i\left(t\right){\{{\tilde{Y}}_i\left(t\right)-{\widehat{S}}_b(t\mid X_i)\}}^2$$

where K_i is the number of bootstrap samples where the ith subject is left-out. As noted above the leave-one-out bootstrap estimate is currently not implemented in pec.

• k-fold cross-validation is similar to bootstrap cross-validation and differs only in the way in which training and test sets are constructed. The number of training sets is fixed by k in k-fold cross-validation. The data D_N are split into k subsets D_j (j = 1, . . . , k) and models Ŝ_j are trained with the data D_N \ D_j where the jth subset is removed. The data in the jth D_j are used as test set. The cross-validation estimate is then obtained by averaging:

$$\mathrm{crossvalErr}(t,\widehat{S})=\frac{1}{k}\sum _{j=1}^k\sum _{j\in D_j}{\widehat{W}}_i\left(t\right){\{{\tilde{Y}}_i\left(t\right)-{\widehat{S}}_j(t\mid X_i)\}}^2.$$

Typical choices for k are 5 and 10. Since the resulting estimate may depend on how the data are split into k pieces, the function pec allows to repeat k-fold cross-validation B times. For example, when the user specifies splitMethod=cv10 and B=20 then 10-fold cross-validation is repeated 20 times and the average of the 20 cross-validation estimates returned.

• Leave-one-out cross-validation is the same as N-fold cross-validation. Models S_i are trained on the data D⁻ⁱ_N = D_N \ {(Y_i, X_i)} and validated on {(Y_i, X_i)}:

$$\mathrm{loocvErr}(t,\widehat{S})=\frac{1}{N}\sum _{i\in D_N}{\widehat{W}}_i\left(t\right){\{{\tilde{Y}}_i\left(t\right)-{\widehat{S}}_i(t\mid X_i)\}}^2.$$

Note that the leave-one-out cross-validation estimate is not random.

• The bootstrap .632 estimate of the prediction error is a weighted linear combination of the apparent estimate and the bootstrap cross-validation estimate:

$$\mathrm{Boot}632\mathrm{Err}(t,\widehat{S})=(1-0.632)\cdot \mathrm{AppErr}(t,\widehat{S})+0.632\cdot \mathrm{BootCvErr}(t,\widehat{S})$$

The constant 0.632 is independent of the sample size and corresponds to the probability to draw with replacement subject i into the bootstrap sample: P ( (Y_i, X_i) ∈ D_b) = 1–(1–1/N)^N ≈ (1–e⁻¹) ≈ 0.632.

• The bootstrap .632+ estimate of the prediction error is a weighted combination of the apparent estimate, the bootstrap cross-validation estimate and the no information estimate given below (Efron and Tibshirani 1997; Gerds and Schumacher 2007). The bootstrap .632+ estimate of the prediction error is given by

$$\begin{array}{cc}\hfill \mathrm{Boot}632\mathrm{Err}(t,\widehat{S})=& (1-\frac{0.632}{(1-0.368\cdot \omega )}\cdot \mathrm{AppErr}(t,\widehat{S})+\frac{0.632}{(1-0.368\cdot \omega )}\cdot \mathrm{BootCvErr}(t,\widehat{S})\hfill \\ \hfill \omega =& \frac{\min (\mathrm{BootCvErr}(t,\widehat{S}),\mathrm{NoInfErr}(t,\widehat{S}))-\mathrm{AppErr}(t,\widehat{S})}{\mathrm{NoInfErr}(t,\widehat{S})-\mathrm{AppErr}(t,\widehat{S})},\hfill \end{array}$$

where one defines ω = 0.632 in the special case where BootCvErr(t, Ŝ) < AppErr(t,Ŝ).

• The no information estimate is needed to construct the bootstrap .632+ estimate and obtained by permuting the status indicator of the subjects:

$$\mathrm{NoInfErr}(t,\widehat{S})=\frac{1}{N^2}\sum _{j\in D_N}\sum _{i\in D_N}{\widehat{W}}_i\left(t\right){\{{\tilde{Y}}_j\left(t\right)-\widehat{S}(t\mid X_i)\}}^2.$$

See section 6 for more discussion of the different cross-validation estimates and further references.

4.3. Integrated Brier score

The prediction error curves can be summarized with the integrated Brier score defined as

$$\mathrm{IBS}(\mathrm{predErr},\tau )=\frac{1}{\tau }{\int }_0^{\tau }\mathrm{predErr}(u,\widehat{S})du,$$

where predErr refers to any method for estimating the predictive performance, and τ > 0 can be set to any value smaller than the minimum of the maximum times for which estimated prediction errors can be evaluated in each bootstrap sample.

5. Illustration

5.1. COST study

Example (continued). We fit a pec object with the three rival prediction models fitcox, fitrsf, and fitcforest described in Section 3. The models are passed to pec as a list. We choose splitMethod=Boot632plus and base our analysis on the complete data of the COST study with N=518 patients. We set B=1000 and use bootstrap without replacement (sub-sampling) to find training sets of size M=350, and correspondingly test sets of size N-M=168. Note that with this option, pec computes in addition to the .632+ estimate, the apparent estimate, the bootstrap cross-validation estimate, and the no information estimate of the prediction error curves.

The estimation of the IPCW weights (3) depends on two arguments in pec: The argument cens.model specifying the model class, and the predictor variables specified on the right hand side of the formula used to describe the censoring model. In our example there are few censored observations, and we use the Kaplan-Meier estimator for the censoring distribution. The default option is cens.model=“cox” which reverts to Kaplan-Meier when no predictor variables are specified. The left hand side of the argument of formula (either a Surv object or a Hist object) is used to identify the survival response.

The argument keep.index=TRUE controls whether or not to keep the indices of the bootstrap samples and keep.matrix=TRUE controls whether or not to keep for each model all estimates of the prediction error curves obtained in the B cross-validation steps.

R> extends <- function(...)TRUE

R> set.seed(13)

R> fitpec <- pec(list(“selectcox”=fitcox,“rsf”=fitrsf,“cforest”=fitcforest), + data=cost, + formula=Surv(time,status)~1, + splitMethod=“Boot632plus”, + B=1000, + M=350, + keep.index=TRUE, + keep.matrix=TRUE)

Prediction error curves

Prediction models

1 KaplanMeier

2 selectcox

3 rsf

4 cforest

IPCW: marginal model

Method for estimating the prediction error:

Bootstrap cross-validation

Type: subsampling

350 out of 518

No. bootstrap samples: 1000

Sample size: 518

------------------------------------------------------------

Cumulative prediction error, aka Integrated Brier score (IBS) aka Cumulative rank probability score

Range of integration: 0 and 4213 :

IBS[0;4213]

KaplanMeier 0.201

selectcox 0.169

rsf 0.160

cforest 0.171

The print function shows information of the three modeling strategies and of the Kaplan-Meier model, a null model added by default.

The integrated Brier scores between 0 and 4213 days for the bootstrap .632+ estimates of the prediction error are lowest for random survival forest. The selected Cox regression model and the conditional inference forest have approximately the same value. All three models perform substantially better than Kaplan-Meier.

The following command plots prediction error curves estimated with the bootstrap .632+ method for all four models in one graph (Figure 2):

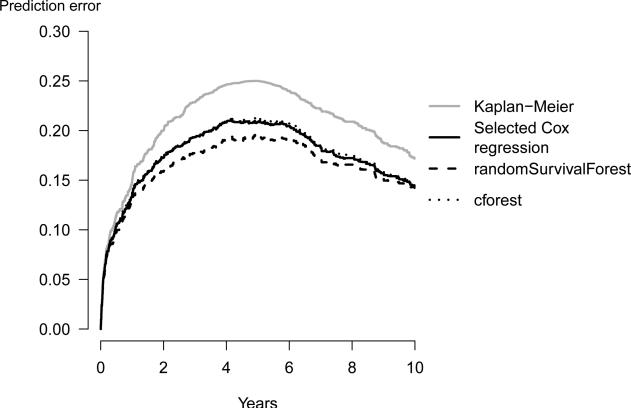
Figure 2.

The bootstrap .632+ estimates of the prediction error based on 1000 bootstrap samples. Both random forest approaches are based on 1000 trees per bootstrap sample.

R> plot(fitpec, predErr=“Boot632plusErr”,xlim=c(0,10*365.25), + axis1.at=seq(0,10*365.25, 2*365.25), axis1.label=seq(0,10,2))

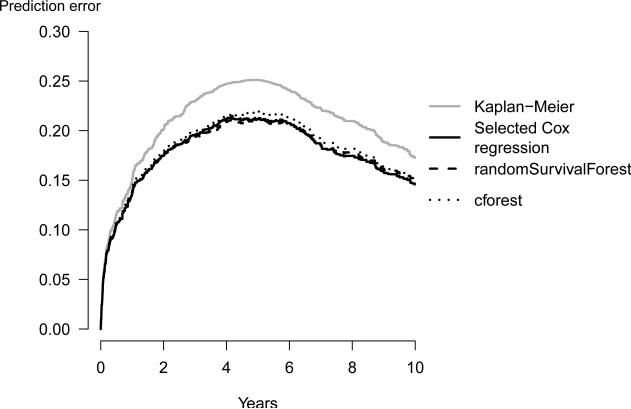
All curves start at time 0 where all subjects are alive and all predictions equal to 1. The prediction error curve of the benchmark Kaplan-Meier model reaches its maximum value, at the median survival time of 4.9 years. This value is 0.25 for prediction errors estimated with the apparent method. For the bootstrap .632+ estimator, random survival forest clearly outperforms the other strategies. However, the bootstrap cross-validation estimates of the prediction error curves of all three strategies are close to each other (Figure 3) showing that at a sample size of M=350 there is no indication that random survival forest outperforms the other strategies. Figure 3 was produced using the following code:

Figure 3.

The bootstrap cross-validation estimates of the prediction error based on 1000 bootstrap samples. Both random forest approaches are based on 1000 trees per bootstrap sample.

R> plot(fitpec,predErr=“BootCvErr”,xlim=c(0,10*365.25), + axis1.at=seq(0,10*365.25, 2*365.25), axis1.label=seq(0,10,2))

The bootstrap .632+ estimate is a combination of the apparent estimate, the bootstrap cross-validation estimate, and the no information estimate, so the difference in the prediction error curves for the bootstrap .632+ estimates compared to the bootstrap cross-validation estimates rely on one of the other estimates. To observe how the different estimates behave for each of the three modeling strategies we plot in Figure 4 the apparent-, the bootstrap-, and the no information estimates of the prediction error together with the bootstrap .632+ estimate and 100 prediction error curves obtained during the cross-validation procedure bootstrap. These latter curves were extracted via the argument keep.matrix=TRUE in pec. The following code produces these figures:

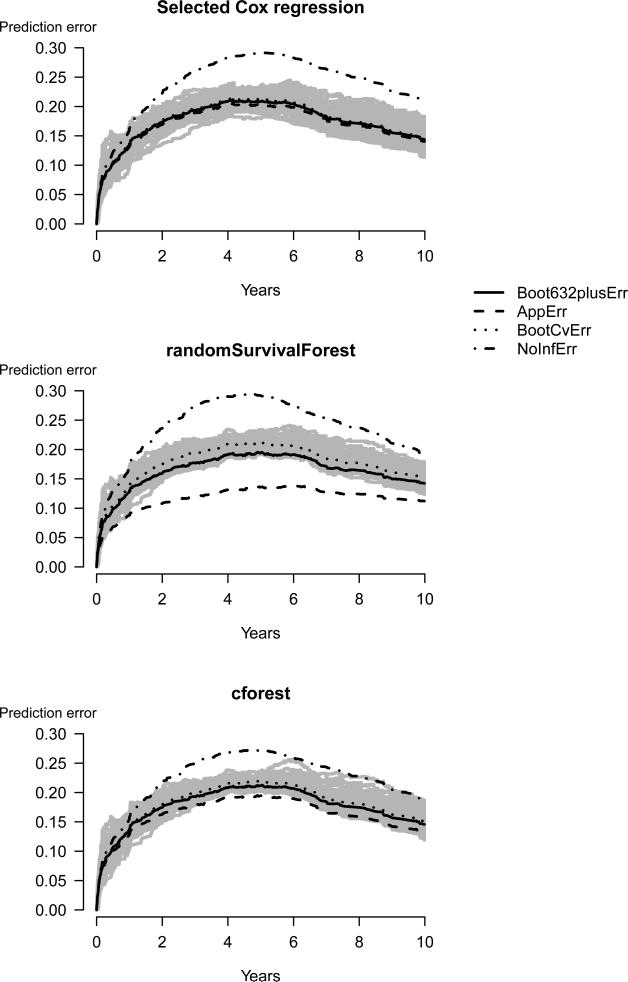
Figure 4.

Each of the three panels shows four different estimates of the prediction error together with a cloud of 100 bootstrap cross-validation curves (grey lines). Both random forest approaches are based on 1000 trees per bootstrap sample.

R> par(mfrow=c(3,1))

R> lapply(2:4,function(x){ + plot(fitpec, + predErr=“Boot632plusErr”, + models=x, + xlim=c(0,10*365.25), + axis1.at=seq(0,10*365.25, 2*365.25), + axis1.label=seq(0,10,2), + special=TRUE, + special.maxboot=100, + special.addprederr=c(“AppErr”, “BootCvErr”,“NoInfErr”)) + })

For both random forest approaches the apparent estimate of the prediction error curves are much lower than the bootstrap cross-validation estimate of the curves.

5.2. Reproducible results: GBSG-2 study

Unfortunately the data from the COST study are not publicly available. Therefore we also present results that are reproducible on the user level based on data provided by the German Breast Cancer Study Group (GBSG2). The GBSG2 study contains data from 686 patients and has complete records of all the predictor variables. As in the worked example of Gerds and Schumacher (2007) we consider the predictor variables age, tumor size, tumor grade, number of positive lymph nodes, and estrogen and progesterone receptors. The data are loaded and prepared as follows:

R> library(“pec”)

R> library(“rms”)

R> library(“randomSurvivalForest”)

R> library(“party”)

R> data(GBSG2)

R> GBSG2$status <- GBSG2$cens

R> GBSG2 <- GBSG2[order(GBSG2$time,-GBSG2$status),]

R> GBSG2$grade.bin <- as.factor(as.numeric(GBSG2$tgrade!=“I”))

R> levels(GBSG2$grade.bin) <- c(“I”,“II/III”)

We compare a random survival forest model, a conditional inference forest model, and a fixed form Cox regression, that is without automatic variable selection: We fit the modeling strategies

R> fitformGBSG <- Surv(time,status)~age+tsize+pnodes+progrec+estrec+grade.bin

R> fitcox <- cph(fitformGBSG,data=GBSG2,surv=TRUE,se.fit=FALSE)

R> set.seed(17)

R> fitrsf <- rsf(fitformGBSG,data=GBSG2,forest=TRUE,ntree=100)

R> set.seed(17)

R> fitcforest <- pecCforest(fitformGBSG, data=GBSG2, controls=cforest_classical(ntree=100))

To achieve user-friendly run times we fitted the forest approaches with only 100 trees each, and consider only 5 splits of the data into training and test sets. Data splitting is based on bootstrap with replacement and we evaluate the bootstrap .632+ estimate of the prediction error. To estimate the weights for IPCW approach use a Cox regression model for the censoring distribution with the same linear predictor as the Cox regression model for the survival times; this is specified by the arguments formula and cens.model. The prediction errors are estimated within the first 2000 days; this is controlled by the argument maxtime.

R> extends <- function(...)TRUE

R> set.seed(2006)

R> fitpec <- pec(list(“Cox”=fitcox,“rsf”=fitrsf,“cforest”=fitcforest), formula=Surv(time,cens)~age+tsize+grade.bin+pnodes+progrec+estrec, data=GBSG2, cens.model=“cox”, splitMethod=“Boot632plus”, maxtime=2000, B=5, keep.index=TRUE, keep.matrix=TRUE)

The function crps (short for continuous rank probability score) computes the integrated Brier scores in pec by integrating e.g. between 0 and 2000:

R> crps.t2000 <- crps(fitpec,times=2000)

R> crps.t2000

	IBS[0;4213]
KaplanMeier	0.201
selectcox	0.169
rsf	0.160
cforest	0.171

These numbers should be reproducible.

6. Discussion

The pec package offers a highly extensible methodology for prediction error curve estimation under almost any type of prediction model. In a sequence of worked out detailed examples, we showed how to incorporate random survival forests, conditional inference forest, and a specific type of backward selection algorithm for Cox regression modeling within the pec framework. We used data from the COST study for illustration, which is a data scenario involving a low-dimensional predictor space, and is a common scenario seen in the field of medical applications. We compared prediction performance of the three modeling strategies and found that the bootstrap cross-validation estimate of the prediction error was comparable across all methods. Interestingly, the .632+ bootstrap estimate showed that random survival forest was best. Also, despite the similarity of the overall bootstrap cross-validation performance, we found that the three strategies yielded different predictions when evaluated at synthetically made predictor values.

6.1. Choosing between cross-validation estimates

Efron and Tibshirani (1997) proposed the .632+ estimate as an improvement on cross-validation for the misclassification rate. The .632+ was studied for other loss functions including the Brier score (Molinaro, Simon, and Pfei er 2005; Jiang and Simon 2007; Wehberg and Schumacher 2004; Gerds and Schumacher 2007). Hence the .632+ estimate is an attractive choice. For high-dimensional settings, Binder and Schumacher (2008) recommended a bootstrap subsampling version of the .632+ estimate where the size of the training sets is set at 63.2% times the full sample size. In any case, for models like the ones obtained with random forests, which can reduce the apparent error to almost zero, the usefulness of the .632+ estimate has not yet been resolved. The main results obtained for the COST study in the present article were therefore based on the bootstrap cross-validation estimate.

6.2. Estimation of weights

The question of which model to use when estimating the weights in the IPCW approach may be hard to answer in general. However, some advice can be given. If there are good reasons to believe that the censoring times C_i are mutually independent of the event times T_i and the covariates X_i, then marginal Kaplan-Meier weights yield consistent estimates of the Brier score (Graf et al. 1999). The result may not be asymptotically efficient (van der Laan and Robins 2003; Gerds and Schumacher 2006) but the advantage is that no further modeling is needed. However, if the censoring times are only conditionally independent of the event times given the covariates then marginal Kaplan-Meier weights will introduce a bias. Instead a so-called working model could be used for the weights, i.e. as obtained by a Cox proportional hazard or an additive Aalen regression model. However, a differet bias will be introduced if the working model is mispecified. This dilemma needs to be resolved in the specific application at hand.

For the comparison of prediction models it is most important that the same IPCW weights are used for all models; this is a feature of the function pec. Also, if we compare differet models that are based on differet subsets of predictor variables, then the working model for the censoring distribution should include and combine all the predictor variables. This is controlled by the argument formula of the function pec.

By default, the weights are estimated using all subjects when bootstrapping or cross-validation is used. However, a new release of pec has an option that allows the weights to be estimated separately in each test sample. In our (short) experience there were no great differences between the two options.

6.3. Model variability

For data-adaptive modeling strategies one would expect models selected from differet training samples to be differet. For example, the algorithm described in Section 2.2 could select a Cox regression model containing two predictor variables in one training sample and a model with three predictor variables in another training sample. Similarly for the random forest approaches the trees will differ across bootstrap samples. This model uncertainty is well known (see e.g. Austin and Tu 2004) and should be considered as a substantial part of the prediction error (Gerds and van de Wiel 2011).

6.4. Other packages

There are several other R-packages for comparing prediction models in survival analysis with the Brier score as an accuracy measure. The package peperr is an early branch of pec featuring parallel computing and separate control of complexity parameters which is of interest for high-dimensional settings. However, presently there are more predictSurvProb methods implemented in pec, and notably peperr only supports Kaplan-Meier weights for the IPCW estimate.

The package ipred provides functionality for estimating the model performance in classification, regression, and survival settings. In the survival context the expected Brier score can be estimated using cross-validation, and bootstrap 632+. But the IPCW weights can only be obtained from the marginal Kaplan-Meier estimate of the censoring survival distribution. As well, only one model is assessed in one call to the function. The pec function allows one to compute the performance of a list of differet modeling strategies simultaneously, which guarantees that exactly the same bootstrap samples are used for the training of all models.

6.5. Alternative assessment measures

As noted in the introduction, ROC curves are another popular method for assessing prediction performance, which can be extended to survival analysis. The package survivalROC offers functions to estimate time-dependent ROC curve the area under the ROC curve (AUC). The package Hmisc provides a popular estimate of the closely related C-index which assesses the frequency of concordant pairs of subjects, where the model predicted the lower risk for the subject with the higher survival time, among all usuable pairs. An IPCW estimate of the C-index which works similar as the function pec is implemented in pec, see Gerds, Kattan, Schumacher, and Yu (2010).

The package survcomp (Haibe-Kains, Sotiriou, and Bontempi 2009) can be used to compute the Brier score, ROC curves, and the C-index. However, there are no cross-validation estimates implemented, and the package can only be used to assess the predictive performances of Cox regression models and Kaplan-Meier risk.

6.6. Further extensions

Extensions of the pec package are in the works. One planned extension is the van de Wiel test (Van de Wiel, Berkhof, and van Wieringen 2009) for pairwise testing of the difference of the prediction error curves from rival modeling strategies at selected time points. Another is an extension to compare modeling strategies in competing risks settings.

We also plan to implement other measures of prediction performance like the time-dependent AUC and the logarithmic score in pec. Note that estimates of the concordance index are readily implemented in pec (Gerds et al. 2010).

Full support for S4 methods is planned for future versions of the package pec.