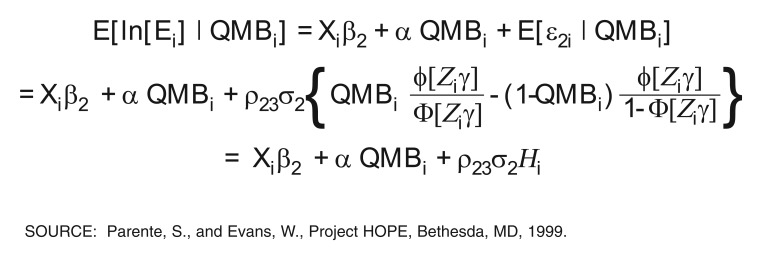Effect of Low-Income Elderly Insurance Copayment Subsidies

Abstract

The authors use a two-part model of demand to model the impact of qualified Medicare beneficiary (QMB) enrollment on medical care use. Assuming QMB enrollment to be exogenous, they find Medicare Part B utilization to be 12 percent higher and Part B expenditures 44 percent greater among QMBs than among eligible non-enrollees. There is no difference between these two groups in overall Part A expenditures. Modeling the possibility that QMB enrollment is endogenous, the authors find qualitatively similar results, but the estimates are not precisely estimated.

Introduction

The Medicare program's cost-sharing provisions—its premiums, deductibles, and copayments—can present a substantial financial hardship for low-income beneficiaries. To alleviate some of this burden, Congress enacted the QMB program. Under this program, implemented in 1990, State Medicaid programs are required to pay Medicare premiums, deductibles, and copayments for beneficiaries with incomes at or below the Federal poverty level¹ (FPL) and assets not exceeding twice the resource limits for Supplemental Security Income (SSI).² Since the program began, policymakers and advocates for the elderly have been concerned about low program participation.

Background

Despite attempts by a variety of public and private organizations to inform eligible seniors about the benefits, many eligible individuals are not participating in the program. A recent study by Families USA (1998) reported that approximately 1.9 million of the 2.4 million low-income elderly and disabled persons who are eligible do not participate in the QMB program. Reports by the U.S. General Accounting Office (1994) and Neumann et al. (1994) confirmed the general accuracy of this estimate.

Neumann et al. (1994) analyzed the barriers to entry into the QMB program. The authors reached three general conclusions: First, the program is not serving many individuals for whom it was intended. Well over 2 million eligible elderly beneficiaries are not participating, and participation remains low even among truly needy individuals. More than 50 percent of those reporting incomes under $1,000 and more than 50 percent of those with at least one hospital visit over the previous 1.5 years do not participate. The data also suggest that a number of persons eligible for the QMB program, both enrolled and not enrolled, are purchasing supplemental insurance coverage, despite the fact that the QMB program was designed to cover most of their out-of-pocket health costs.

Second, beneficiaries who are enrolled as QMBs tend to be those most in need of the program. Beneficiaries enrolled in other government assistance programs, for example, are very likely to participate in the QMB program. Among those eligible for the QMB program, the two subgroups most vulnerable to Medicare out-of-pocket costs—lower income beneficiaries and those with poorer health status—are more likely to enroll in QMB than are higher income seniors and those in good or excellent health. Participation is also higher among black persons and Hispanic persons, those with less education, and those reporting few social contacts (e.g., those reporting no contacts with friends or family members during the previous 2 weeks; widowed, divorced, or never-married individuals; and geographically isolated beneficiaries). Those residing in rural areas and those living far from their usual source of care have higher participation (Neumann et al., 1994).

The third finding to emerge from Neumann et al.'s 1994 study was that most eligible beneficiaries are ill-informed about the QMB program. Only 7 percent of those eligible had ever heard of the program; of the 91 percent who had not heard of the program, almost 40 percent were actually enrolled. Among eligible non-enrollees, the most frequently provided reasons for not enrolling were that they do not believe they need the program (33 percent), they do not think they qualify (27 percent), or they are not aware of it (16 percent).

This study's purpose is to compare the health expenditures of the QMB-enrolled population with those elderly Medicare beneficiaries who are eligible for but not enrolled in the program. Specifically, the study addressed three research questions:

• Is the health care utilization of QMB enrollees significantly different from that of eligible non-enrollees? If so, are differences specific to Medicare Part A or Part B services?

• Is there evidence of adverse selection with respect to enrollment in the QMB program?

• What is the impact of QMB enrollment on Medicare expenditures?

To answer these questions, we analyzed data from the Medicare Current Beneficiary Survey (MCBS) and the MCBS National Claims History File (NCHF). To determine the impact of QMB enrollment on health care utilization, we used a two-part model of demand (Manning et al., 1987) representing the decision to use medical care as well as the intensity of service utilization. In addition, we developed a multi-equation system to account for possible adverse selection in the QMB program.

In our models where QMB enrollment is assumed to be exogenous, we find the probability of any Medicare Part B utilization (i.e., physician and medical supplier services) and expenditures are higher among individuals enrolled in QMB than among eligible non-enrollees. The probability of having any Medicare Part A (i.e., hospital) expenses is also higher among QMBs than among eligible non-enrollees. When we model the possibility that QMB enrollment is endogenous, we find similar results, but the estimates are not precisely estimated.

Data

To complete this analysis, we analyzed data from the MCBS. This survey, sponsored by the HCFA, examines the current status of the Medicare population (Stone, 1993). The MCBS consists of a series of interviews conducted three times a year with a stratified random sample of approximately 12,000 elderly and non-elderly Medicare beneficiaries, focusing on their health care utilization and expenditures, health status, family support, living arrangements, and financial resources.

We analyzed three components of the MCBS, as follows:

• The 1992 Income and Assets (I&A) supplement: The I&A supplement collects detailed information about beneficiaries' financial resources, including sources of income and assets. We identified respondents as eligible for the QMB program if their incomes did not exceed 100 percent of the FPL and their assets did not exceed twice the amount established for SSI eligibility.³

• The QMB supplement: In the spring of 1993, this questionnaire was administered to the sample of MCBS respondents identified as being eligible for the QMB program. The questionnaire was designed to examine beneficiaries' knowledge of the QMB program, their sources of information, and, for non-enrollees, their reasons for not participating.

• The NCHF: The NCHF contains inpatient and outpatient utilization and financial data on all MCBS respondents, including provider charges and Medicare reimbursement, as well as the deductibles and copayments associated with a specific service.

From these MCBS data bases, we created a set of analytic files. First, we used the MCBS to identify a sample of elderly, non-institutionalized beneficiaries who met the eligibility criteria for the QMB program. Next, we merged data from the QMB supplement with two other data bases containing information on our sample of persons eligible for the QMB program: one incorporating data from the MCBS core survey on characteristics of the eligible population and the other containing information from HCFA's 1993 Medicare buy-in file, which was used to determine whether eligible beneficiaries were actually enrolled in the program.⁴

These comprehensive QMB population data bases were then merged with NCHF-derived health care use and expenditure summary files. This portion of the analysis required pre-processing the institutional (e.g., hospital inpatient and outpatient) and non-institutional (e.g., physician and medical suppliers) claims files available as part of the MCBS database. We analyzed claims for services provided during calendar year 1993 (e.g., for dates of service 1/1/93 through 12/31/93). During the preprocessing steps, we removed any transaction or adjudication records that did not record an actual health service use. This preprocessing procedure closely followed the NCHF analytic file creation strategy outlined by Parente et al. (1995). Using only the data elements necessary for the analysis, we generated a resource-use analytic file that summarized each beneficiary's Part A and Part B service use and expenditures, as well as the copayment and deductible amounts paid. This resource-use profile summarized the utilization history of all beneficiaries in the MCBS study population, regardless of QMB participation or eligibility.

Characteristics of the Study Population

Descriptive statistics for the important variables in our sample are presented in Table 1. We report means and standard deviations for the entire sample, as well as for those samples of QMB-eligible persons enrolled and not enrolled in the program.⁵ As indicated in Table 1, the vast majority of QMB-eligible seniors are female, and the average age of respondents is 77. The average respondent has only 8 years of education, and average self-reported income is slightly over $1,000 per year.

Table 1. Variable Definitions and Sample Characteristics.

Variable Name	Definition	Full Sample		Enrolled in QMB		Not Enrolled in QMB
		Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation
QMB Enrollment*	1 if Enrolled in QMB, 0 Otherwise	0.43	0.50	1.00	0.00	0.00	0.00
Female*	1 if Respondent Is Female, 0 Otherwise	0.74	0.44	0.78	0.42	0.71	0.45
Male*	1 if Respondent is Male, 0 Otherwise	0.26	0.44	0.22	0.42	0.29	0.45
Black*	1 if Respondent is Black, 0 Otherwise	0.24	0.43	0.32	0.47	0.19	0.40
Hispanic*	1 if Respondent is Hispanic, 0 Otherwise	0.10	0.30	0.12	0.33	0.09	0.28
White*	1 if Respondent is White, Not Hispanic, 0 Otherwise	0.66	0.47	0.56	0.50	0.73	0.45
Income	Yearly Family Income	$1,269	$1,730	$1,177	$1,721	$1,339	$1,735
Age	Age in Years	77.5	7.81	77.6	7.89	77.4	7.77
Education	Years of Education	8.25	3.70	7.34	3.57	8.94	3.75
Own Home*	1 if Respondent Owns Home, 0 Otherwise	0.43	0.50	0.27	0.44	0.55	0.50
Rent Home*	1 if Respondent Rents Home, 0 Otherwise	0.32	0.47	0.44	0.50	0.23	0.42
Live With Others*	1 if Respondent Lives in Someone Else's Home, 0 Otherwise	0.25	0.43	0.29	0.45	0.22	0.42
Excellent/Very Good Health*	1 if Respondent Is in Excellent or Very Good Health, 0 Otherwise	0.30	0.46	0.23	0.42	0.37	0.48
Good Health*	1 if Respondent Is in Good Health, 0 Otherwise	0.27	0.44	0.25	0.44	0.27	0.45
Fair/Poor Health*	1 if Respondent Is in Fair or Poor Health, 0 Otherwise	0.43	0.50	0.51	0.50	0.37	0.48
ADLs	Number of Reported Restrictions in ADLs	0.42	1.07	0.60	1.24	0.29	0.90
Any Part B MD Charges*	1 if Respondent Had Any Part B Charges for Doctor Services, 0 Otherwise	0.78	0.42	0.85	0.36	0.72	0.45
Any Part B Charges*	1 if Respondent Had Any Part B Charges, 0 Otherwise	0.78	0.41	0.86	0.35	0.72	0.45
Any Part A Charges*	1 if Respondent Had Any Part A Charges, 0 Otherwise	0.20	0.40	0.24	0.43	0.16	0.37
Part B MD Charges	Total Part B Charges for Doctor Services, Given Positive Charges	$2,964	$5,713	$3,378	$4,882	$2,592	$6,347
Part B Charges	Total Part B Charges, Given Positive Charges	$3,967	$7,229	$ 4,549	$6,559	$3,444	$7,752
Part A Charges	Total Part A Charges, Given Positive Charges	$16,065	$21,476	$16,023	$16,483	$16,101	$29,065
Number of Observations	—	1,400	—	605	—	795	—

^*Indicator variable.

NOTES: QMB is qualified Medicare beneficiary. MD is medical doctor. ADLs is activities of daily living.

SOURCE: Parente, S., and Evans, W., Project HOPE, Bethesda, MD, 1999.

In this sample, only 43 percent of eligible adults are enrolled in the QMB program. This estimate is extremely close to the weighted mean of 44 percent reported in Neumann et al. (1994). We also report in this table sample characteristics by QMB enrollment; these findings are consistent with the conclusions of Neumann et al. Eligible beneficiaries enrolled in QMB have lower incomes, lower rates of home ownership, and higher reported activity of daily living (ADL) deficiencies than those not enrolled. In addition QMBs are less likely to report excellent or very good health and more likely to report fair or poor health than are eligible non-enrollees. The only demographic variables that do not demonstrate statistically significant differences between the enrolled and non-enrolled populations are Hispanic ethnicity, income, age, and good health.

In this table, we report six measures of health care utilization. First, we present the proportion of respondents with any Medicare Part B charges for doctor visits; any Part B charges (e.g., outpatient hospital encounters); and any Part A charges. Next, we report mean expenditures for beneficiaries who used any type of health service. These results indicate that both the probability and intensity of use are significantly higher for QMBs than for Medicare beneficiaries who are eligible for but not enrolled in the QMB program. To provide some indication of the magnitude of these differences, in Table 2, we report simple differences in means for all three probability and intensity-of-use measures. For this table, we calculated the mean of log expenditures, because this difference is equivalent to a percentage difference in use.

Table 2. Measures of Health Care Use, by Those Enrolled and Not Enrolled in the QMB Program, and Differences.

Variable	Enrolled in QMB		Not Enrolled in QMB		Difference
	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation
Access-to-Care Measures
Any Physician Charges	0.848	0.015	0.721	0.016	0.127	0.022
Any Part B Charges	0.856	0.014	0.725	0.016	0.131	0.021
Any Part A Charges	0.243	0.017	0.162	0.013	0.081	0.022
Intensity-of-Use Measures
In Physician Charges	7.243	0.063	6.746	0.065	0.497	0.091
In Part B Charges	7.523	0.064	7.012	0.068	0.511	0.093
In Part A Charges	9.228	0.079	9.126	0.090	0.102	0.120

NOTE: QMB is qualified Medicare beneficiary.

SOURCE: Parente, S., and Evans, W., Project HOPE, Bethesda, MD, 1999.

The results reported in Table 2 indicate that among persons eligible for the QMB program, the probability of having any Part B charges is 13.1 percent higher for those enrolled in the program than for those not enrolled, and the probability of having any Part A charges is 8.1 percentage points higher for QMBs than for eligible non-enrollees. Similarly, among persons eligible for the QMB program with positive expenditures in a particular service category, the Part B expenses of QMB enrollees are 51.1 percent higher than those of eligible beneficiaries not participating in the program, and Part A expenses of QMBs are 10.2 percent higher than those of eligible non-enrollees. All differences except the differences in Part A expenses are precisely estimated, and we can easily reject the null hypothesis that the differences are zero.

In the following section, we provide a more detailed analysis of the impact of QMB enrollment on health care utilization. Because QMB enrollees have very different demographic and health characteristics than those not enrolled in the program, we first estimate a multivariate model that controls for differences between seniors. Next we consider whether the QMB program's estimated impact on utilization is a causal relationship or whether this relationship is simple correlation. As noted in Table 1, those in the poorest health—who thus can be expected to have higher rates of health care utilization—are also more likely to enroll in the QMB program. If people who anticipate having large medical expenses are the most likely to enroll in the QMB program, the differences in use between enrolled and non-enrolled seniors reported in Table 2 would overstate the causal impact of enrollment on use. We outline a simple multi-equation system designed to eliminate the potential bias generated by this type of adverse selection.

Methods and Results

We use a two-part model of demand (Manning et al., 1987) to measure the impact of QMB enrollment on medical use from the two-part model; the decision to use medical services and the intensity-of-service utilization are modeled separately. We have modeled the probability-of-use equation as a simple probit and estimated the log-of-positive-expenditures equation by ordinary least squares (OLS). Our two-part model is substantially more complex than previous applications because we suspect that the covariate of interest, QMB enrollment, may be endogenous. Our rationale for treating QMB enrollment as endogenous reflects the possibility that beneficiaries, or family and social workers acting on their behalf, will enroll with the intent of using medical services for significant health conditions. This assumption is substantiated by Neumann et al.'s (1994) finding that the enrolled QMB population had worse health status than the non-enrolled eligible population.

In the next section, we present a standard two-part model of medical care use assuming all covariates in the model are exogenous. We then discuss the results from this exercise. In the final section, we outline in detail a multi-equation system designed to provide unbiased estimates of QMB enrollment, accounting for the potential adverse selection previously described. Estimating these systems appropriately requires the identification of a factor correlated with QMB enrollment but uncorrelated with the probability or intensity of medical care use.

Standard Two-Part Model of Demand

As previously noted, we used the Medicare claims history files to generate three primary measures of health care use for the QMB-eligible population: use of Part B physician services; use of any Part B services; and use of Part A services. All three variables have similar sample characteristics in that a proportion of the population does not use the services, and the distribution of positive expenses is highly skewed. For this class of variables, the standard econometric model is the two-part model of demand. The first equation in the system models factors determining whether a senior has any medical care use, and the second equation models determinants of intensity of use when any use has been observed.

To model the probability of receiving a particular type of care (Part A or Part B covered services), we use a simple probit model. In the model for Part B expenditures, let indicator variable Y_i = 1 if individual i has any Part B charges, and let Y_i = 0 otherwise. The choice problem is described by the latent variable model,

$$Y_i\ast =X_i{\beta }_1+{\mathit{\text{QMB}}}_i\delta +{\varepsilon }_{1i}$$ (1)

where Y_i is the net benefit an individual receives from having positive Part B expenses; X_i is a vector of individual characteristics; QMB_i is an indicator variable that equals 1 if the respondent is enrolled in the QMB program and 0 otherwise; and ε_1i is a normally distributed random error with zero mean and unit variance. Individuals will only use medical services if the expected net benefits are positive; thus the probability of observing Part B expenses is defined as

$$\text{Prob}[Y_i=1]=\text{Prob}[X_i{\beta }_1+{\mathit{\text{QMB}}}_i\delta +{\varepsilon }_{1i}>0]=\Phi [X_i{\beta }_1+{\mathit{\text{QMB}}}_i\delta ]$$ (2)

where -Φ( ) is the evaluation of the standard normal cumulative density function.

Because the probability of use is a nonlinear function of the parameters β₁ and δ, we cannot directly measure the impact of QMB enrollment on use by the magnitude of the parameter. With coefficients from the probit model, we calculate two additional variables to measure the qualitative importance of QMB enrollment on the probability of use. The first variable is defined as the “marginal effect,” and it measures the change in probability of use given QMB enrollment. Mathematically, the marginal effect is defined as ∂ Prob(Y_i = 1)/∂ QMB_i = δ ϕ(X_iβ₁), where ϕ( ) is the evaluation of the standard normal probability density function. The value of the marginal effect will be determined in part by the assumed probability of use without QMB. In this instance, we calculate the marginal effect for a person with an average probability of use, where if μ is the sample mean of the dependent variable (0.78 in the case of Part B charges), the marginal effect can be calculated as δϕ(z) where z = Φ^-1 (μ). The second variable that measures the impact of QMB enrollment on use is defined as the “average treatment effect,” which is the average difference between the probability that a senior would have Part B expenses if he/she were enrolled in QMB. If n is the sample size and β̂₁ and δ̂ are the maximum likelihood estimates of the parameters in equation (2), the average treatment effect equals (1/n)Σ_i[Φ(X_iβ̂₁+δ̂) - Φ(X_iβ̂₁)]. In most applications, the marginal effect and average treatment effect give very similar results. We use the “delta” method to calculate the variance of the marginal and average treatment effects.⁶

In the second part of the two-part demand model, we control for the skewness in medical demand by estimating with OLS the determinants of log expenditures. Using the notation already established, the equation we estimate is of the form

$$\text{In}(E_i)=X_i{\beta }_2+{\mathit{\text{QMB}}}_i\alpha +{\varepsilon }_{2i}\mathit{\text{for}}{E}_i>0$$ (3)

where X is the same set of covariates used in the probit model previously described, and ε_2i is a zero mean random error with Var(ε_1i)=σ²₂. Because log expenditures are linear in QMB enrollment, the primary parameter of interest, α measures the percent increase in medical expenses (given that any have occurred) attributable to QMB enrollment.

If we interpret the coefficients for the QMB variables from the two-part model as the “causal” impact of enrollment on utilization, we can perform a simple simulation to estimate the average per person change in use attributable to QMB enrollment. This simulation is conducted as follows: Let the variables δ̂, β̂₁, α̂, and β̂₂ represent parameter estimates from the two-part demand model for a particular expenditure category. For any individual, the predicted probability of use is defined as Φ(X_iβ̂₂ + QMB_i δ̂), and following Manning et al. (1987), predicted intensity of expenditures is γ̂ exp (X_iβ̂₂ + QMB_i α̂). The variable γ̂ is the “smearing” estimate of Duan (1983), making it possible to transform predictions from a model with logged dependent variables back into a linear scale. To calculate this value, we note that predicted residuals from the log expenditures equation are ε̂_2i = ln(E_i∣E_i>0) - X_iβ̂₂ - QMB_i α̂, and therefore γ̂= (1/n₁)Σ_iexp(ε̂_2i), where n₁ is the number of observations in the data set with positive expenses. Using these values, the predicted expenses for individual i are simply Φ(X_iβ̂₁ + QMB_i δ̂)γ̂ exp(X_iβ̂₂ + QMB_i α̂). To estimate the average impact of QMB on utilization, we use a measure similar to the average treatment effect already discussed. First, we calculate predicted use for all people assuming they were enrolled in the program. This value is by definition Φ(X_iβ̂₁ + δ̂)γ̂ exp (X_iβ̂₂ + α̂) Next, we calculate predicted use assuming no QMB program; this is defined as Φ(X_iβ̂₁) γ̂ exp (X_iβ̂₂)]. The average difference between these two quantities, Δ = (1/n)Σ_i [Φ(X_iβ̂₁ + δ̂)γ̂ exp(X_iβ̂₂ + α̂) - Φ(X_iβ̂₂)γ̂ exp(X_iβ̂₂)]], is the average change in expenditures attributable to QMB enrollment.

Two-part demand estimates for the QMB enrollment indicator variable are reported in Table 3. In all of these models, we use the following covariates: age and age squared, log income, measures of self-reported health status, counts of ADLs, and indicator variables for gender, race, education, home ownership status, region of the country, and urban status. To shorten the exposition, the coefficients for these additional variables are not reported here. The particular variables were chosen based on two criteria. First, we selected variables that have been shown by others to reasonably predict differences across seniors in medical care use. Second, the values of these variables should not be altered by QMB enrollment.

Table 3. Two-Part Model Estimates, Impact of QMB Enrollment on Health Care Use Parameter Estimates and Standard Errors.

Variable	Part B Physician Charges				Part B Charges				Part A Charges
	Probit Model, Any Use		OLS Model, Log Use		Probit Model, Any Use		OLS Model, Log Use		Probit Model, Any Use		OLS Model, Log Use
	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation
QMB Enrollment	0.474	0.092	0.474	0.103	0.455	0.091	0.441	0.106	0.292	0.09	0.025	0.132
Marginal Effect of QMB Enrollment	0.142	0.027	—	—	0.146	0.027	—	—	0.083	0.025	—	—
Average Treatment Effect QMB Enrollment	0.125	0.023	—	—	0.123	0.024	—	—	0.079	0.025	—	—
Mean of Dependent Variable	0.776	—	6.981	—	0.781	—	7.254	—	0.197	—	9.180	—
Number of Observations	1,400	—	1,086	—	1,400	—	1,093	—	1,400	—	276	—
R2	—	—	0.081	—	—	—	0.081	—	—	—	0.141	—
-2 Log Likelihood	1,378.3	—	—	—	1,350.6	—	—	—	1,328.6	—	—	—

NOTES: The marginal effects, ∂ Prob/∂ X, represents the change in the probability of use given QMB enrollment. If β_qmb is the probit coefficient for the QMB variable, and μ is the sample mean of the dependent variable, the marginal effect is calculated as ϕ(z)β_qmb where z = Φ^-1(μ). The average treatment effects represent the average change in the probability of use generated by QMB enrollment. All models include the following list of covariates: age, age squared, log income, and counts of ADLs, plus indicators for whether the respondent is black, Hispanic, female, married, widowed respondents, in excellent health, in good health, owns their home, rents their home, has less than 7 years of education, has 7-8 years of school, has 9-11 years of school, has 12 years of school, has 1-2 living children, has 3-5 living children, has 6 or more living children, whether the respondent lives in the south, west, or midwest, and whether the respondent lives in a metropolitan area. QMB is qualified Medicare beneficiary. ADLs is activities of daily living. OLS is ordinary least squares.

SOURCE: Parente, S., and Evans, W., Project HOPE, Bethesda, MD, 1999.

As the R² values in Table 3 indicate, these controls explain little of the sample variation in the intensity of use. Only the self-reported measures of health status and counts of ADLs are uniformly statistically significant across models. The fact that the demographic characteristics explain little of the sample variation in use is not surprising in light of the highly selective nature of the sample. The QMB-eligible population is, on average, very poor and very old and has a low level of educational attainment. Although these demographic variables typically can explain some of the cross-sectional variability in probability and intensity of use, once the sample has been selected to include only persons eligible for the QMB program, these three variables have little explanatory power.

The probit equations indicate that on average, the probability of having any Part B charges is 12.5 percentage points higher among QMBs than among Medicare beneficiaries eligible for but not enrolled in the QMB program. The probability of having any Part A charges is 7.9 percentage points higher for beneficiaries enrolled in the QMB program than for eligible non-enrollees. Similarly, among beneficiaries with any Part B expenses, the Part B expenditures of QMB enrollees are 44.1 percent higher than those of eligible seniors not participating in the program. Interestingly, the coefficients of the QMB indicator variable from the multivariate, two-part demand model are nearly identical to the simple difference in mean calculations reported in Table 2. This is surprising because the statistics in Table 1 suggest that the observed characteristics of QMB enrollees are very different from non-enrollees.

Combining the results from the probability-of-use and intensity-of-use equations, we can simulate the impact of QMB enrollment on use using the procedure previously outlined. Results from this simulation are reported in Table 4. On average, QMB enrollment increases per person Part B expenditures by $1,918 and Part A charges by $1,326. Approximately 20 percent of the predicted increase in expenditures is attributable to the higher probability of use for QMB enrollees, and 80 percent of the increase is attributable to the change in intensity of use. Nearly all of the increase in Part A expenses can be attributed to the increased probability of use.

Table 4. Predicted Change in per Person Expenditures Attributable to QMB Enrollment.

Item	Part B Physician Charges	All Part B Charges	All Part A Charges
Predicted Change	$1,490	$1,918	$1,326

NOTE: QMB is qualified Medicare beneficiary.

SOURCE: Parente, S., and Evans, W., Project HOPE, Bethesda, MD, 1999.

Controlling for Adverse Selection

The two-part model previously outlined provides unbiased estimates of the impact of QMB enrollment on medical care use if QMB enrollment is not correlated with a person's unobserved propensity to use medical care. Stated differently, the estimates will be unbiased if beneficiaries' enrollment in QMB is unrelated to their expected medical care use. If, however, those who anticipate having large medical expenses or those who have the most contact with health providers are the most likely to enroll in QMB, the two-part estimates already described will greatly overstate the impact of the QMB program. Is this a likely scenario? As results in Table 1 indicate, beneficiaries with the poorest self-reported health status and those with the higher reported ADL deficiencies are the most likely to enroll in the program. The average ADL deficiency for QMBs is 0.6 but only 0.29 for those not enrolled. Similarly, the proportion of the QMB population reporting excellent or very good health is only 0.23, whereas the corresponding proportion for eligible non-enrollees is 0.37. Both of these differences are statistically significant. In general those who could be expected to have higher medical expenses are indeed the most likely to enroll in the QMB program. These results suggest that QMB enrollment may not be random but rather that it is subject to adverse selection.

To correct the two-part estimates for bias introduced by the potential non-random assignment of seniors into the QMB program, we must first model the decision to enroll in the QMB program. Suppose we can monetize the benefits of QMB enrollment, and assume we can write the net benefits of enrolling (QMB) as a function of observed and unobserved characteristics

$${{\text{QMB}}_i}^{\ast }=Z_i\gamma +{\varepsilon }_{2i}$$ (4)

where Z_i is a vector of observables and ε_3i is a zero mean, unit variance, normally distributed random error. An individual will enroll in QMB if the net benefits are positive, i.e., if QMB_i*> 0. To allow for possible adverse selection into the program, we assume that the decision to enroll is correlated with both the decision to use services and the intensity of use. Statistically, this can be accomplished by assuming the unobserved components in the three equations are correlated. Specifically, we assume ε _1i, ε _2i, and ε _3i are distributed as a multivariate normal, where all three variables have zero expected values, but cov[ε_1i, ε_3i] = ρ₁₃ and cov[ε_2i, ε_3i] = ρ₂₃σ₂

Because the decision to enroll and the decision to use medical services are now assumed to be correlated, we must estimate these equations jointly. In our analysis we estimate two separate systems. First, we estimate the enrollment and use equations, and next we jointly estimate the enrollment and intensity-of-use equations. We could estimate a three-equation (use, intensity-of-use, and enrollment-equation) system, but this would require modeling the covariance between the probability-of-use and intensity-of-use equations. This covariance can only be estimated if we can identify a variable that affects the intensity of use but not the probability of use. Given the difficulty in identifying a variable that could be used for this purpose, we follow previous applications of the two-part model (Duan et al., 1982; Manning et al., 1987; Evans and Farrelly, 1998) and assume that the two errors are uncorrelated.

Because both the decision to use services and the decision to enroll in the QMB program are dichotomous, there are four possible states (Y_i = 0, QMB_i =0; Y_i= 0, QMB_i = 1; Y_i = 1, QMB_i = 0; and Y_i = 1, QMB_i = 1). Modeling either the use or the enrollment equation separately can be accomplished through simple probit models. Given the assumed correlation between these two decisions, however, the likelihood function corresponding to this set of events is a bivariate probit. In this system of equations, we estimate the probability of an elderly beneficiary being in one of the four categories already listed.

In light of the potential correlation between the intensity of use and QMB enrollment decisions, single-equation estimates of equation (3) will capture not only the impact of QMB enrollment on use, but also the fact that people with higher anticipated expenses are more likely to enroll in the program. Because the potentially endogenous covariate is discrete (QMB enrollment), controlling for adverse selection cannot be accomplished with a standard model such as two-stage least square. Instead, we draw from the large literature on bias introduced by sample selection to produce a model that controls for non-random selection into the treatment group. Specifically, because we assume that QMB enrollment and intensity of use are correlated, the expected value of the error term in the use equation ε_2i is now correlated with QMB enrollment, thereby violating the primary assumption of OLS models.⁷ In this instance, it is not difficult to show that expected log use is as shown in Figure 1, where ϕ and Φ are evaluations of the standard normal probability density function and cumulative density function respectively and by definition, Φ [Z_iγ] is the probability that a senior will enroll in the QMB program. The variable H is the sample-selection correction term representing the size of bias associated with adverse selection into the QMB program. As the equation in Figure 1 indicates, if ρ₂₃ = 0, then OLS estimates of equation (3) will provide an unbiased estimate of the effect of QMB on use. However, if ρ₂₃ > 0 (ρ₂₃ < 0), then OLS estimates of (3) will over- (under-) estimate α.

Figure 1. Expected Log Use.

The sample selection correction term H is a simple omitted variable that introduces a bias into an OLS equation. To eliminate the bias, we use a two-step procedure outlined in Barnow, Goldberger, and Cain (1981) and LaLonde (1986). The two-step procedure first produces an estimate of the omitted factor H; then the log use equation is re-estimated with the omitted factor replaced. First, we estimate a reduced-form probit model of program enrollment to obtain estimates of γ. Using these values, we construct an estimate of sample-selection term H and include this as an independent variable in the expenditure equation. The second-stage model is then of the form

$$\mathit{\text{In}}[E_i]=X_i{\beta }_2+\alpha {\mathit{\text{QMB}}}_i+\theta {\widehat{H}}_i+{\mu }_i$$ (5)

where μ_i is a random error and the coefficient θ is an estimate of the product ρ₂₃σ₂. Because μ_i is heteroskedastic and we utilize estimates of the sample-selection correction term H rather than actual values, OLS estimates of standard errors are inconsistent. Accordingly, we estimate corrected standard errors using procedures suggested by Heckman (1978, 1979) and Greene (1981).

In practice the vector Z in the QMB enrollment equation will include all variables in X—the covariates in the probability-of-use equation. The bivariate probit model previously outlined can be estimated if there is at least one variable determining QMB enrollment that is uncorrected with an individual's propensity to use services. In the best of all possible worlds, these variables, called instruments, will mimic a random-selection device, giving people different probabilities of enrollment that are uncorrelated with their probability of use. We have identified two potential instruments that we believe fit this definition. The first is the percent of a State's Medicaid population that is elderly. The second is the number of outreach programs States have used to inform seniors about the QMB program.

Elderly Medicare beneficiaries must apply for the QMB program at State Medicaid offices. Seniors represent a small proportion of the Medicaid population, accounting for about 12 percent of all recipients nationwide in 1992. There is, however, tremendous variation among States in the proportion of Medicaid recipients who are elderly. Because some State Medicaid offices may have more experience serving the elderly population, we suspect that seniors are more likely to enroll in QMB if they comprise a larger portion of a State's Medicaid population. Similarly, a large elderly Medicaid population may signal a State's commitment to providing care for the elderly.

Similarly, we suspect that seniors in States with more aggressive QMB outreach programs will have a higher probability of enrollment. As noted earlier, most elderly Medicare beneficiaries eligible for QMB have not enrolled in the program. Since the beginning of the QMB program, many public and private organizations have conducted outreach programs to inform seniors about QMB and facilitate the enrollment process. In a review of these programs, the American Public Welfare Association (1994) identified seven types of outreach programs based on the channel of communication used. These included mass mailings; public service announcements; press releases; brochures; outstationing (providing opportunities to apply for the program in community settings, outside the Medicaid office); working with aging networks; and working with community organizations. Neumann et al. (1994) demonstrated that although QMB enrollment was not correlated with any particular program, enrollment probabilities were higher in States that adopted several outreach strategies. Therefore, we use a count of the number of different outreach programs (0-7) used by a State to inform seniors about the QMB program as an instrument for enrollment. Although QMB enrollment is correlated with the number of State outreach programs and the proportion of a State's Medicaid population that is elderly, we do not expect these variables to be correlated with either probability or intensity of use.

In Table 5 we report coefficients for the two instruments generated from probit models predicting the probability of QMB enrollment. The other covariates in the model include those used in the two-part demand equations. In these models, elderly Medicare beneficiaries living in States that have implemented a number of outreach programs or States with a larger proportion of Medicaid recipients age 65 and over are more likely to enroll in the program. For example, if the proportion of elderly Medicaid recipients increases by 1 percentage point, the probability of enrollment increases by 2.8 percentage points. In the final model, the probit estimates suggest that the addition of one more outreach program increases the probability of enrollment by 3 percentage points. The estimated coefficients reported in Table 5 are all statistically significant.

Table 5. Probit Estimates of QMB Enrollment Equation Parameter Estimates and Standard Errors.

Independent Variable	Model 1				Model 2				Model 3
	Probit Estimates		Marginal Effects		Probit Estimates		Marginal Effects		Probit Estimates		Marginal Effects
	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation
Percent of Medicaid Population That Is Elderly	0.071	0.014	0.028	0.004	0.345	0.057	0.137	0.022	0.066	0.014	0.026	0.005
Percent of Medicaid Population That Is Elderly, Squared	—	—	—	—	-1.319	0.250	0.519	0.098	—	—	—	—
Number of State-Run QMB Outreach Programs	—	—	—	—	—	—	—	—	0.077	0.024	0.030	0.009

NOTES: QMB is qualified Medicare beneficiary. Other exogenous variables include those listed in Table 3.

SOURCE: Parente, S., and Evans, W., Project HOPE, Bethesda, MD, 1999.

In Table 6 we report results from the bivariate probit models where we jointly estimate the decision to use medical care and to enroll in QMB. We estimate models for both Part B and Part A expenses. For each expenditure type, we report four models. First, we report estimates from Table 3 that assumed QMB enrollment was not a function of anticipated medical care use. The final three models use the proportion of Medicaid recipients who are elderly; the square of this number; and the number of State outreach programs as instruments for QMB enrollment. We include the quadratic term in the fraction of the Medicaid recipients who are elderly, because our preliminary work with the data set found distinct non-linearities in the effect of this variable on QMB enrollment. In the bivariate probit models, we report the coefficient of the QMB enrollment variable and the implied average treatment effect.

Table 6. Bivariate Probit Estimates Probability-of-Use Equations from Two-Part Model Parameter Estimates and Standard Errors.

Instrument	Bivariate Probit Estimates				Two-Stage Least Squares Estimates
	Coefficient of QMB Enrollment		Average Treatment Effect		Coefficient of QMB Enrollment		Specification Test Statistic
	Standard Mean	Deviation	Standard Mean	Deviation	Standard Mean	Standard Deviation	Mean	Deviation
Any Part B Charges (Estimates from Table 3)1	0.474	0.092	0.125	0.023	—	—	—	—
Percent of Medicaid Population That Is Elderly	0.492	0.545	0.129	0.139	0.268	0.175	—	—
Percent of Medicaid Population That Is Elderly, and Its Square	0.516	0.391	0.135	0.100	0.196	0.128	0.37	—
Percent of Medicaid Population That Is Elderly and Number of QMB Outreach Programs 0-7	0.579	0.484	0.152	0.123	0.257	0.151	0.02	—
Any Part A Charges (Estimates from Table 3)1	0.292	0.090	0.079	0.025	—	—	—	—
Percent of Medicaid Population That Is Elderly	-0.113	0.518	-0.030	0.138	-0.059	0.172	—	—
Percent of Medicaid Population That Is Elderly, and Its Square	0.034	0.407	0.010	0.109	0.056	0.126	1.02	—
Percent of Medicaid Population That Is Elderly and Number of QMB Outreach Programs 0-7	0.106	0.488	0.029	0.131	0.080	0.147	2.68	—

¹Estimates in Table 3 are the single-equation probit estimates that assume that QMB enrollment is not a function of anticipated medical care use.

NOTES: Other exogenous variables include those listed in Table 3. QMB is qualified Medicare beneficiary.

SOURCE: Parente, S., and Evans, W., Project HOPE, Bethesda, MD, 1999.

In the bivariate probit equations modeling Part B usage, the parameter estimates are similar in magnitude to results from the single-equation probit models. Unfortunately the bivariate probit system estimates are imprecisely estimated. There are two possible reasons for this lack of precision: a lack of explanatory power in the first-stage equation that predicts QMB enrollment or an absence of QMB enrollment impact on Medicare Part B use. In light of the similarity between the system and single-equation estimates, we suspect that the former reason is the more plausible explanation, although we have no way to verify this assertion. In a formal statistical test, we cannot reject the hypothesis that the estimate of the QMB effect on Part B expenditures in the bivariate probit is the same as the estimate in the single-equation estimate. Therefore we cannot reject the hypothesis that the single-equation results reported in Table 3 are the appropriate estimates.

In contrast to the results for Part B use, the bivariate probit estimates for Part A use show no impact of QMB on the probability of use once adverse selection is accounted for. The results in Table 6 consistently show a small and imprecise effect of QMB on hospital use.

In Table 7 we present estimates of the sample-selection model outlined in equation (5). We only report estimates for the log of Part B expenditures, because the QMB enrollment variable was not statistically significant in the single-equation estimates for Part A. For this table we used the same instrument sets employed in Table 6. In the first two columns, we reproduce the single-equation estimates from Table 3. For each model, we report the system estimate of the QMB enrollment variable and the coefficient of the sample-selection correction term H. Much like the results from the bivariate probit model, the two-step sample-selection correction estimates are similar to the single-equation estimates, but the estimate of the QMB enrollment variable is imprecisely estimated.

Table 7. Two-Step Estimates of Intensity-of-Use Equation Part B Expenditures, Parameter Estimates, and Standard Errors.

Variable	Model 1		Model 2		Model 3		Model 4
	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation
QMB enrollment	0.431	0.106	0.360	0.553	0.501	0.357	0.721	0.567
H	—	—	0.241	0.333	-0.043	0.217	-0.170	-0.343
Instrument Set	—	—	Percent of Medicaid population that is elderly		Percent of Medicaid population that is elderly, and its square		Percent of Medicaid population that is elderly, and number of QMB outreach programs (0-7)

NOTES: Other exogenous variables include those listed in Table 3. Standard errors are calculated by the procedure suggested by Greene (1981). The results for model 1 are the single-equation estimates reported in Table 3. QMB is qualified Medicare beneficiary.

SOURCE: Parente, S., and Evans, W., Project HOPE, Bethesda, MD, 1999.

The results from Tables 6 and 7 provide some evidence that, for Part B expenditures, the single-equation estimates reported in Table 3 are not subject to bias due to adverse selection. For Part A expenditures, we find no evidence that QMB enrollment increases the intensity of use, and in the bivariate probit results, we find little evidence that QMB alters the probability of Part A use. However, the results for both Part A and Part B expenditures are plagued by large variances in the parameters of interest.

Conclusions and Implications

Payment of Medicare deductibles and copayments can be a serious economic hardship for seniors eligible for the QMB program. Without this program many seniors may find it too costly to obtain some health services and therefore will not seek medical care when needed.

The major findings in this study are as follows:

• Among QMB-eligible seniors, the probability and intensity of Part B Medicare use are significantly higher among those enrolled in QMB than among those not enrolled. The probability of having any Medicare Part B utilization is 12 percentage points higher among individuals enrolled in QMB than among eligible non-enrollees. Among elderly Medicare beneficiaries that have any Part B use, Part B expenditures are 44 percent higher for those enrolled in QMB than for individuals who are not enrolled.

• Although we find coefficient estimates representing the impact of QMB enrollment in the two-part equations to be statistically insignificant, the parameter estimates are very similar to results from our single-equation approach, where QMB enrollment was treated as exogenous.

• The probability of having any Medicare Part A expenses is 8 percentage points higher among QMBs than among eligible non-enrollees. However, there is no difference between these two groups in overall Part A expenditures.

• In contrast to our results for Part B expenditures, the results from Part A appear to be driven by adverse selection.

• On average QMB enrollees spend $1,900 more per year on health services covered by Medicare Part B and $1,300 more per year on Medicare Part A services than do eligible non-enrollees. Again we stress that the results for Part A appear to be driven by adverse selection, and the Part B results appear to be the result of lowered price for medical care among the QMB population resulting from subsidized copayments and deductibles.

In addition, our findings indicate that the higher utilization levels of QMBs are associated with significant increases in Medicare program expenditures. Based on a simulation of the impact of QMB enrollment on Medicare costs, an assumed national enrollment rate of 45 percent in 1993 would cost Medicare $6.69 billion; nearly 60 percent of this amount is attributed to Part B expenses. Our estimated enrollment of 43 percent would likely mirror these programmatic costs.

Our analysis can also be interpreted in light of the Clinton Administration's recent focus on the QMB population based on the results of a 1998 Families USA study on QMB and SLMB participation. Based on this study, the Clinton Administration asserted that Medicare beneficiaries who are eligible and not enrolled in QMB are “overpaying” for medical care by paying Medicare premiums and cost-sharing expenses out of pocket. Our results suggest that those who are eligible and not enrolled but using Medicare services have better health status than those whom the government has assisted. Although it is true that Medicare beneficiaries are losing approximately $2 billion a year (Families USA, 1998) in missed Medicare subsidies from the QMB and SLMB programs combined, our results tend to show that those with poorer health status are more likely to be enrolled. In an era of fiscal prudence, our results imply that the most vulnerable of the persons eligible for the QMB program are likely to be receiving intended subsidies before those with less urgent medical conditions. However, our findings also suggest that the assistance from the QMB program does provide a financial incentive for beneficiaries to use more Part B services because of reduction in the price of medical care.

Typically the presence of adverse selection in an insurance market is considered a misallocation of a risk-based premium. However, in the case of the QMB program, the presence of adverse selection may be seen by some policy analysts as a desired outcome, given that the intent of the program was to help vulnerable populations near the poverty line obtain necessary medical care. Our results do suggest that some of the differences in Part A cost are due to adverse selection. The interpretation of the results is at the discretion of the priorities of the policymaker. If the “current” goal of the QMB program is to increase health care access to every Medicare beneficiary near the poverty level, then our results would indicate that those enrolled, regardless of health status, are receiving medical care. If the goal of the program is to help those most in need, it is not clear that those with worse health status are getting more care, as identified by presence of adverse selection when we treat QMB enrollment as endogenous.

If we consider the presence of adverse selection in a government-subsidized program as a positive outcome of the QMB initiative, our results suggest that Part A recipients are the greatest benefactors. Those beneficiaries enrolled in the QMB program, or their agents in the form of a family member or social worker, are likely to be considering the expected medical use associated with a serious illness that requires hospitalization.

The QMB program appears to have provided a financial incentive for increased Part B use by lowering the price of receiving the first unit of medical care in an ambulatory setting. Although adding to Medicare program expenditures in the short term, increased access to physician and outpatient services may provide a long-term benefit that can reduce medical expenditures and improve health status, particularly for those beneficiaries with chronic conditions such as diabetes, where medical management is likely to yield health benefits in an elderly population (Weiner et al., 1995).

Our findings suggest several areas for future research. To provide a more precise estimate of the true costs of the QMB program, it would be useful to conduct a longitudinal analysis of the costs of treating a cohort of QMB-eligible beneficiaries over time. Access to Part B services through the QMB program may prevent catastrophic health events that would have been expensive to treat, or it may only forestall them temporarily. In addition, access to Part B services could help to minimize the deleterious effects of ongoing health problems that beneficiaries previously lacked the resources to treat. If these situations are prevalent, the financial impact we have reported overestimates the true cost of the QMB program. More recent findings from Moon, Brennan, and Segal (1998) report the QMB program cost to be only 15 percent greater than our simulation results with a 1997 enrollment rate of 73 percent. Either we have overestimated the financial impact of the program with a 45-percent participation rate, or per capita expenditures of the program decrease over time as enrollment increases and relatively healthier QMB eligibles are enrolled. Only a cohort study could provide a definitive answer as to whether the QMB program saves health expenditures over time.

In summary, our analysis demonstrates that the QMB program has succeeded in meeting its goal of increasing access to medical services for elderly low-income Medicare beneficiaries. Overall, the health status of beneficiaries enrolled in the program was worse than that of eligible non-enrollees. We found significant differences in health care use and expenditures between Medicare beneficiaries enrolled in the QMB program and eligible beneficiaries who are not enrolled. Our results revealed that poorer health status was associated with increased health care use and expenditures. It is clear that QMB-eligible beneficiaries who are enrolled in the program are utilizing its benefits.