Abstract
The Diagnostic Cost Group Hierarchical Condition Category (DCG/HCC) payment models summarize the health care problems and predict the future health care costs of populations. These models use the diagnoses generated during patient encounters with the medical delivery system to infer which medical problems are present. Patient demographics and diagnostic profiles are, in turn, used to predict costs. We describe the logic, structure, coefficients and performance of DCG/HCC models, as developed and validated on three important data bases (privately insured, Medicaid, and Medicare) with more than 1 million people each.
Introduction
Role of Health-Based Payment Models
Since 1985, HCFA has made capitated payments to managed care organizations that enroll Medicare beneficiaries. HCFA, using a demographic risk adjuster to calculate payments equal to 95 percent of what health maintenance organization (HMO) enrollees “would have cost” had they remained in the traditional fee-for-service Medicare program, paid less-than-average dollars for the group who originally transferred into these programs. However, HCFA still appears (on average) to have overpaid, because the early switchers into Medicare managed care were healthier than comparably aged non-switchers (Brown et al., 1993). Anticipating and responding to this problem, HCFA has sponsored much research, including development of the Diagnostic Cost Group (DCG) models, with the goal of being able to better match HMO payments to the health care needs of enrollees. Since 1984, when researchers at Boston University and Brandeis initiated this work for HCFA, DCGs have evolved into a family of methods for using administrative data collected during patient encounters to calculate health-based “expected costs” for populations (Ash et al., 1986, 1989, 1998; Ellis and Ash, 1995; Ellis et al., 1996a, 1996b; Pope et al., 1998, 1999, 2000).
DCG models use age, sex, and diagnoses generated from patient encounters with the medical delivery system to infer which medical problems are present for each individual and their likely effect on health care costs for a population. Some versions of the DCG models focus on diagnoses that form the principal reason for an inpatient admission, now called “PIP diagnoses” (Ash et al., 1989; Ellis and Ash, 1995; Pope et al., 2000). Other versions, such as the DCG/HCC models of this article, utilize the full range of diagnoses generated during all face-to-face encounters with clinicians (Ellis et al., 1996a, 1996b; Ash et al., 1998; Pope et al., 1998). Whereas previous publications using DCGs have calibrated models solely for Medicare samples, in this study, we contrast the ability of DCG/HCC models to predict resources in three different samples: privately insured, Medicaid, and Medicare.
Payment methods establish incentives. For example, when payments follow a “piecework” model, as in traditional fee-for-service medicine, providers are rewarded for doing more—whether the additional utilization is valuable or not. Conversely, capitated payments encourage doing less—whether through efficiency or stinting. Further, flat-rate capitated payments introduce a new perverse incentive: to enroll healthy people and to do the very little required to keep them enrolled. Models that pay each person's expected cost eliminate the incentive to “select on risk” and make efficiency the main way for a plan to achieve a competitive advantage (Van de Ven and Ellis, 2000).
Although risk-adjusted payment solves the problem of perverse patient-selection incentives, linking payments to a risk-adjustment model may lead plans to invest unproductive effort in making their enrollees “look needier” according to that model. For example, models that pay more for health care “users” encourage both appropriate and unnecessary utilization; those that identify illness only through hospitalizations encourage admissions, and those that pay more for people with more coded illnesses encourage “diagnostic discovery.” This last incentive can be good to the extent that it rewards plans that keep better track of their members' chronic illnesses (Greenwald et al., 1998). The degree of imperfection in incentive-setting is one criterion in choosing among payment models. Furthermore, how much imperfection is acceptable depends upon the nature and level of problems associated with available alternatives.
Predicting Costs in a Range of Populations
The original DCG models are prospective, that is, they use baseline, or year 1, data to infer the level of need for health care in year 2 and were developed to predict costs for Medicare beneficiaries. Medical conditions (diagnoses) detected in year 1 are used to organize people into groups with similar levels of future health care need. The distribution of all members by levels of future need characterizes an enrolled group and is used to determine a health-based payment. More recently, we have developed DCG models to calculate expected concurrent expenses, that is, expenses that occur in the same year as the diagnoses used to characterize the population (Pope et al., 1998, 1999, 2000). We have also adapted both prospective and concurrent modeling frameworks for use in Medicaid and commercially insured (private) populations under the age of 65 (Ash et al., 1998).
Concurrent models may be particularly useful for provider profiling and monitoring, because knowing all the medical problems being treated during a period of time is particularly relevant for estimating the level of resources used to treat them. However, prospective models, which predict future costs, are more appropriate for creating payments to managed care organizations that assume financial risk, because they focus on the presence of illnesses, such as cancer and heart disease, that predictably make people more expensive to treat.
In this article, we describe prospective models only, as they apply to three separate populations: a national sample of commercially insured enrollees under age 65, enrollees in Michigan's Medicaid program, and a national sample of Medicare beneficiaries. We refer to these three populations and the models that pertain to them as private, Medicaid, and Medicare. Continuing the tradition in which DCG models were originally developed, these models reflect concern for appropriate incentives in payments to health care plans and providers. All DCG/HCC models (regardless of the population or whether they are concurrent or prospective) rely on a common classification structure, which we describe later. Diversity across populations is handled by using different coefficients, different exclusions of potential predictors from payment models, and different constraints on coefficients across age or eligibility groups.
Model Criteria: Accuracy, Feasibility, and Incentives
The DCG models strive for accurate predictions in the face of limitations on the available data and concerns about incentives. The goal is to effectively predict costs from data that should be present in any health care delivery system, while limiting the rewards for undesirable behavior with respect to either treatment or reporting.
Although our descriptive system does classify all recorded diagnoses in order to create a comprehensive picture of problems seen, concerns about incentives cause us to not model some information. For example, we do not use the number of hospitalizations to predict cost, so as to avoid disadvantaging medical care organizations that are good at treating sick people with fewer hospitalizations. Nor do we count how often a diagnosis appears. Conceptually, DCG models are designed to predict higher costs when they detect additional conditions associated with elevated costs. Based on clinical judgment and concerns about incentives, we exclude some condition categories (CCs) from contributing to predictions entirely. For example, the presence of chemotherapy is noted in the diagnostic codes, and, therefore we classify it into a CC (number 115); however, our prospective models do not pay more for it. Higher payments are based on the presence of a particular type of cancer, rather than a choice of therapy.
Methods
Populations and Data
We describe payment models for three populations whose types of health coverage span the major ways in which health care is provided in the United States today. Specifically, we use:
A nationally dispersed, privately insured (indemnity-covered) population of 1.4 million people in 1992 and 1993 (the private data).
One million individuals covered by Michigan's Medicaid program in 1991-1992 (Medicaid).
Medicare's 5-percent research sample from 1991 and 1992.
The outcome variable, total program costs in year 2, is defined as total covered expenses—an amount that includes copayments, deductibles, and third-party payments—in each data set. Costs for people with less than a full year of entitlement in year 2 are annualized, based on their observed cost per month; in analyses, we treat their data as “fractional observations” (Ellis and Ash, 1995). The three populations differ substantially with respect to age and sex distributions, health care costs, and hospital experience (Table 1). In each population, most of the data are used (in a development sample) to establish the model structure and to fit coefficients, while the rest of the data (the validation sample) are used for measuring model performance. Finally, regressions based upon all the data are used to produce the model coefficients in this article.
Table 1. Age, Sex, Hospital Experience, and Total Health Care Costs in Three Populations1.
| Characteristic or Statistic | Private | Medicaid | Medicare |
|---|---|---|---|
| Number | 1,379,970 | 1,103,367 | 1,360,626 |
| Prediction Year | 1993 | 1992 | 1992 |
| Percent by Age | |||
| 0-17 Years | 26.7 | 51.4 | 0.0 |
| 18-44 Years | 44.9 | 40.0 | 3.2 |
| 45-64 Years | 28.4 | 8.7 | 5.8 |
| 65 Years or Over | 0.0 | 0.0 | 91.0 |
| Percent Female by Age | |||
| 0-17 Years | 51.3 | 50.9 | 0.0 |
| 18-44 Years | 44.9 | 29.4 | 36.1 |
| 45-64 Years | 46.6 | 40.0 | 39.4 |
| 65 Years or Over | — | — | 60.7 |
| Total Prediction-Year Costs | |||
| Mean | $1,592 | $1,430 | $3,778 |
| Standard Deviation | 8,236 | 5,407 | 10,523 |
| Coefficient of Variation | 517 | 378 | 279 |
| Median | 85 | 121 | 516 |
| 99th Percentile | 25,472 | 23,208 | 57,423 |
| Maximum | 2,412,707 | 1,253,880 | 1,533,060 |
| Percent with Zero Prediction-Year Costs | 42.9 | 32.3 | 16.1 |
| Percent Hospitalized in the Prediction Year | 4.8 | 8.4 | 21.2 |
For people with at least 1 month of eligibility in each of the baseline and prediction years.
SOURCE: (Ash et al., 1998; Pope et al., 1998.)
A fourth data set, consisting of 191,877 people under age 65 in a State employee benefit program (State data), is used to further validate the private model's ability to discriminate costs within important subsets of a new population, as described later.
DCG/HCC Models
The letters DCG/HCC are used to distinguish the multicondition Hierarchical Condition Category (HCC) models from the single-condition PIP-DCG model that HCFA is using to calculate payments to Medicare HMOs in the year 2000 (Ingber, 1998; Iezzoni et al., 1998; Health Care Financing Administration, 1999).
Each DCG model is designed to use the diagnostic codes from the International Classification of Diseases, 9th Revision, Clinical Modification (ICD-9-CM) (Public Health Service and Health Care Financing Administration, 1980) on the claims that hospitals and physicians submit to payers. (For a discussion of diagnostic coding issues, refer to Iezzoni, 1997.) Each DCG/HCC model uses the same CCs for prediction, all of which are based on diagnostic codes, rather than procedures. DCG models summarize a person's health from his or her CCs and estimate expected costs based on these profiles. Although DCG models reward medical-problem identification, not all CCs are or should be used to modify payments to plans. In designing DCG models, we have anticipated “DCG creep” (changes in diagnostic coding for the purpose of increasing DCG-based payments) by making the models less sensitive to expected changes. In particular, our models exclude some CCs and impose hierarchies to reduce the sensitivity of predicted costs to three things: (1) variations in coding practice; (2) intentional coding proliferation with the aim of improving provider reimbursement (gaming); and (3) inconsistent coding of less serious or vague conditions.
Diagnostic Groups (DxGROUPs)
With more than 15,000 codes, the distinctions created by ICD-9-CM are too fine to be used directly as a payment classification system. Therefore, we group ICD-9-CM codes into 543 categories, called “DxGROUPs,” which are the building blocks of DCG/HCC models. Each DxGROUP has a two-level numerical label and a short, clinically informative text name. All DxGROUPs with the same “whole number” stem are clinically related. For example, the “4.xy” series refers to infectious diseases, with 4.01 being bacterial enteritis, 4.02 viral enteritis, 4.03 other intestinal infections, 4.04 tuberculosis, and so on.
Each recognized ICD-9-CM code maps to a unique DxGROUP; each DxGROUP encompasses diagnostic codes that describe very similar medical problems. We place in the same DxGROUP alternative codes that can be used for the medical conditions that clinicians generally think of together (such as congestive heart failure and cardiomyopathy or deep vein thrombosis and deep vein thrombosis in pregnancy) or codes for medical conditions that are not easily distinguished (such as chronic bronchitis and emphysema).
Condition Categories
DxGROUPs are clustered in a CC when they contain medically related problems with similar expected costs. We created the 118 diagnosis-based CCs used for modeling in each population using a mix of clinical judgment and empirical cost data. The core physician panel making these judgments consisted of four internists experienced in health services research. Specialist consultants assisted in several areas including pediatrics, HIV/AIDS (human immunodeficiency virus/acquired immunodeficiency syndrome), pediatric surgery, obstetrics, and neonatology. Although we sought to create CCs with at least 500 cases in our private sample of around 1 million people, that goal is subordinated to the objective of clinical homogeneity. For a few conditions (such as mental retardation, quadriplegia, and underweight neonates), we accept significantly smaller numbers.
We eliminate logical inconsistencies in diagnostic coding that can be identified by comparing with age and sex. For example, we drop a diagnosis of uterine disorder in a male. However, we do not drop neonatal codes found in the records of non-infant females. When an infant dies shortly after birth, insurance companies sometimes do not create a separate eligibility record but rather assign the neonatal codes to the mother. Currently, two CCs are used to classify neonatal codes assigned to mothers.
The CCs are organized in broad system groups (such as four CCs for infections, eight for neoplasms, and three each for diabetes and metabolic disorders). Short names (such as Infection1, Diabetes3) denote such CC groups; numbering within a short-name series generally indicates decreasing expected costs (e.g., Neoplasm1 contains metastatic cancers, Neoplasm2 contains high-cost site-specific cancers, Neoplasm3 has moderate-cost cancers, on down to Neoplasm8, benign neoplasms).
Table A in the Technical Note shows for each CC, its number, long name, short name and the CCs that it donimates in the model hierarchy explained in the following section. A complete list of the individual DxGROUPs indicating their organization into CCs is available at www.dxcg.com under the heading “DCG Clinical Classification System in Detail.” (This information can also be obtained by contacting the lead author.)
Table A. Condition Category (CC) Numbers, Long Names, Short Names, and Hierarchies.
| CC Number | CC Long Name | CC Short Name | Dominated CCs |
|---|---|---|---|
| 1 | HIV/AIDS | Infection1 | None |
| 2 | Septicemia (Blood Poisoning)/Shock | Infection2 | None |
| 3 | Central Nervous System Infections | Infection3 | None |
| 4 | Other Infectious Disease | Infection4 | None |
| 5 | Metastatic Cancer | Neoplasm1 | 6, 7, 8, 9, 10, 11, 12 |
| 6 | High-Cost Cancer | Neoplasm2 | 7, 8, 9, 10, 11, 12 |
| 7 | Moderate-Cost Cancer | Neoplasm3 | 8, 9, 10, 11, 12 |
| 8 | Lower Cost Cancers/Tumors | Neoplasm4 | 9, 10, 11, 12 |
| 9 | Carcinoma in Situ | Neoplasm5 | 10, 11, 12 |
| 10 | Uncertain Neoplasm | Neoplasm6 | 11, 12 |
| 11 | Skin Cancer, Except Melanoma | Neoplasm7 | 12 |
| 12 | Benign Neoplasm | Neoplasm8 | None |
| 13 | Diabetes with Chronic Complications | Diabetes1 | 14, 15 |
| 14 | Diabetes with Acute Complications/Non-Proliferative Retinopathy | Diabetes2 | 15 |
| 15 | Diabetes with No or Unspecified Complications | Diabetes3 | None |
| 16 | Protein-Calorie Malnutrition | Metabolic1 | None |
| 17 | Moderate-Cost Endocrine/Metabolic/Fluid-Electrolyte Disorders | Metabolic2 | None |
| 18 | Other Endocrine, Metabolic, Nutritional Disorders | Metabolic3 | None |
| 19 | Liver Disease | Liver | None |
| 20 | High-Cost Chronic Gastrointestinal Disorders | GI1 | 22, 23 |
| 21 | High-Cost Acute Gastrointestinal Disorders | GI2 | 22, 23 |
| 22 | Moderate-Cost Gastrointestinal Disorders | GI3 | 23 |
| 23 | Lower Cost Gastrointestinal Disorders | GI4 | None |
| 24 | Bone/Joint Infections/Necrosis | MSK1 | None |
| 25 | Rheumatoid Arthritis and Connective Tissue Disease | MSK2 | 26 |
| 26 | Other Musculoskeletal and Connective Tissue Disorders | MSK3 | None |
| 27 | Aplastic and Acquired Hemolytic Anemias | Blood1 | 28, 29 |
| 28 | Blood/Immune Disorders | Blood2 | 29 |
| 29 | Iron Deficiency and Other/Unspecified Anemias | Blood3 | None |
| 30 | Dementia | Dementia | None |
| 31 | Drug/Alcohol Dependence/Psychoses | Mental1 | 32, 33, 34, 35 |
| 32 | Psychosis and Other Higher Cost Mental Disorders | Mental2 | 33, 34, 35 |
| 33 | Depression and Other Moderate-Cost Mental Disorders | Mental3 | 34, 35 |
| 34 | Anxiety Disorders | Mental4 | 35 |
| 35 | Lower Cost Mental Disorders/Substance Misuse | Mental5 | None |
| 36 | Profound Mental Retardation | MR1 | 37, 38, 39 |
| 37 | Severe Mental Retardation | MR2 | 38, 39 |
| 38 | Moderate Mental Retardation | MR3 | 39 |
| 39 | Mild/Unspecified Mental Retardation | MR4 | None |
| 40 | Quadriplegia | Neuro1 | 41, 42, 43, 44 |
| 41 | Paraplegia | Neuro2 | 42, 43, 44 |
| 42 | Higher Cost Neurological Disorders | Neuro3 | 43, 44 |
| 43 | Moderate-Cost Neurological Disorders | Neuro4 | 44 |
| 44 | Lower Cost Neurological Disorders | Neuro5 | None |
| 45 | Respirator Dependence/Tracheostomy Status | Arrest1 | 46, 47 |
| 46 | Respiratory Arrest | Arrest2 | 47 |
| 47 | Cardio-Respiratory Failure and Shock | Arrest3 | None |
| 48 | Congestive Heart Failure | Hrt_CHF | 55, 56, 57 |
| 49 | Heart Arrhythmia | Hrt_ARR | 55, 56, 57 |
| 50 | Acute Myocardial Infarction | Hrt_AMI | 51, 52, 55, 56, 57 |
| 51 | Other Acute Ischemic Heart Disease | Hrt_CAD1 | 52, 55, 56, 57 |
| 52 | Chronic Ischemic Heart Disease | Hrt_CAD2 | 55, 56, 57 |
| 53 | Valvular and Rheumatic Heart Disease | Hrt_VHD | 55, 56, 57 |
| 54 | Hypertensive Heart Disease | Hrt_HTN | 55, 56, 57 |
| 55 | Other Heart Diagnoses | Hrt_Misc | 56 |
| 56 | Heart Rhythm and Conduction Disorders | Hrt_Rhythm | None |
| 57 | Hypertension (High Blood Pressure) | HTN | None |
| 58 | Higher Cost Cerebrovascular Disease | Stroke1 | 59 |
| 59 | Lower Cost Cerebrovascular Disease | Stroke2 | None |
| 60 | High-Cost Vascular Disease | Vascular1 | 62, 63 |
| 61 | Thromboembolic Vascular Disease | Vascular2 | 62, 63 |
| 62 | Atherosclerosis/Unspecified | Vascular3 | None |
| 63 | Other Circulatory Disease | Vascular4 | None |
| 64 | Chronic Obstructive Pulmonary Disease | Lung1 | 70, 71 |
| 65 | Higher Cost Pneumonia | Lung2 | 66, 67, 69, 71 |
| 66 | Moderate-Cost Pneumonia | Lung3 | 67, 69, 71 |
| 67 | Lower Cost Pneumonia | Lung4 | 71 |
| 68 | Pulmonary Fibrosis and Other Chronic Lung Disorders | Lung5 | 70, 71 |
| 69 | Pleural Effusion/Pneumothorax | Lung6 | 71 |
| 70 | Asthma | Lung7 | 71 |
| 71 | Other Lung Disease | Lung8 | None |
| 72 | Higher Cost Eye Disorders | Eye1 | 73 |
| 73 | Lower Cost Eye Disorders | Eye2 | None |
| 74 | Higher Cost Ear, Nose, and Throat Disorders | ENT1 | 75 |
| 75 | Lower Cost Ear, Nose, and Throat Disorders | ENT2 | None |
| 76 | Dialysis Status | Urinary1 | 77, 78, 79, 80 |
| 77 | Kidney Transplant Status | Urinary2 | 78, 79, 80 |
| 78 | Renal Failure | Urinary3 | 79, 80 |
| 79 | Nephritis | Urinary4 | 80 |
| 80 | Other Urinary System Disorders | Urinary5 | None |
| 81 | Female Infertility | Genital1 | 82, 83 |
| 82 | Moderate-Cost Genital Disorders | Genital2 | 83 |
| 83 | Low-Cost Genital Disorders | Genital3 | None |
| 84 | Ectopic Pregnancy | Preg1 | 85, 89, 90 |
| 85 | Miscarriage/Abortion | Preg2 | 89, 90 |
| 86 | Completed Pregnancy with Major Complications | Preg3 | 87, 88, 89, 90 |
| 87 | Completed Pregnancy with Complications | Preg4 | 88, 89, 90 |
| 88 | Completed Pregnancy Without Complications (Normal Delivery) | Preg5 | 89, 90 |
| 89 | Uncompleted Pregnancy with Complications | Preg6 | 90 |
| 90 | Uncompleted Pregnancy with No or Minor Complications | Preg7 | None |
| 91 | Chronic Ulcer of Skin | Skin1 | 92 |
| 92 | Other Dermatological Disorders | Skin2 | None |
| 93 | Vertebral Fractures and Spinal Cord Injuries | Injury1 | 97 |
| 94 | Hip Fracture/Dislocation | Injury2 | 97 |
| 95 | Head Injuries | Injury3 | 97 |
| 96 | Drug Poisonings, Internal Injuries, Traumatic Amputations, Burns | Injury4 | 97 |
| 97 | Other Injuries and Poisonings | Injury5 | None |
| 98 | Complications of Care | Complic | None |
| 99 | Major Symptoms | Symptom1 | None |
| 100 | Minor Symptoms, Signs, Findings | Symptom2 | None |
| 101 | Very-High-Cost Pediatric Disorders | Peds | 20, 22, 23, 28, 29, 43, 44, 68, 70, 71 |
| 102 | Higher Cost Congenital/Pediatric Disorders | Cong1 | 104 |
| 103 | Moderate-Cost Congenital Disorder | Cong2 | 104 |
| 104 | Lower Cost Congenital Disorder | Cong3 | None |
| 105 | Extremely-Low-Birthweight Neonates | Baby1 | 106, 107, 108, 109 |
| 106 | Very-Low-Birthweight Neonates | Baby2 | 107, 108, 109 |
| 107 | Serious Perinatal Problem Affecting Newborn | Baby3 | 109 |
| 108 | Other Perinatal Problems Affecting Newborn | Baby4 | 109 |
| 109 | Normal, Single Birth | Baby5 | None |
| 110 | Heart, Lung, Liver Transplant Status | Transplant1 | None |
| 111 | Other Organ Transplant/Replacement | Transplant2 | None |
| 112 | Artificial Opening Status/Attention | Openings | None |
| 113 | Elective/Aftercare | Surgery | None |
| 114 | Radiation Therapy | Radiation | None |
| 115 | Chemotherapy | Chemo | None |
| 116 | Rehabilitation | Rehab | None |
| 117 | Screening/Observation/Special Exams | Screening | None |
| 118 | History of Disease | History | None |
NOTES: HIV is human immunodeficiency virus. AIDS is acquired immunodeficiency syndrome.
SOURCE: (Ash et al., 1998.)
CC Hierarchies
A payment model should not be sensitive to every diagnostic code recorded because this will result in poorly specified coefficients and unstable estimates of the relative risk of populations. For example, a female who has metastatic cancer (CC 5) could also be coded with cancer in two or more specific body sites, such as the liver (CC 6) or connective and soft tissue (CC 7). She may also have been tested for other “uncertain” (CC 10) or “benign” cellular changes (CC 12). A regression model that separately assigns credit for each of these diagnoses will have confounded parameter estimates, because the costs of people with only the simpler problems get averaged in, or confounded, with costs for people with both simple and more consequential conditions. Also, such models reward most the plans that capture as many codes as can be legitimately defended in an audit—a behavior with little social value. To dampen these incentives, we use hierarchies to constrain CC assignment as follows: a person classified into a CC is not also classified into a lower ranked CC in the same hierarchy. An important feature of an HCC model is that the hierarchies are not imposed across unrelated medical problems. For example, for a female with both cancer and diabetes, hierarchies are used to retain only the “worst” evidence of each disease, but both cancer and diabetes CCs are used in predicting her costs next year.
Hierarchies are identified for each CC in the rightmost column of Table A by indicating which CCs are dominated; dominated CCs are zeroed out for a person when a dominating CC is present.
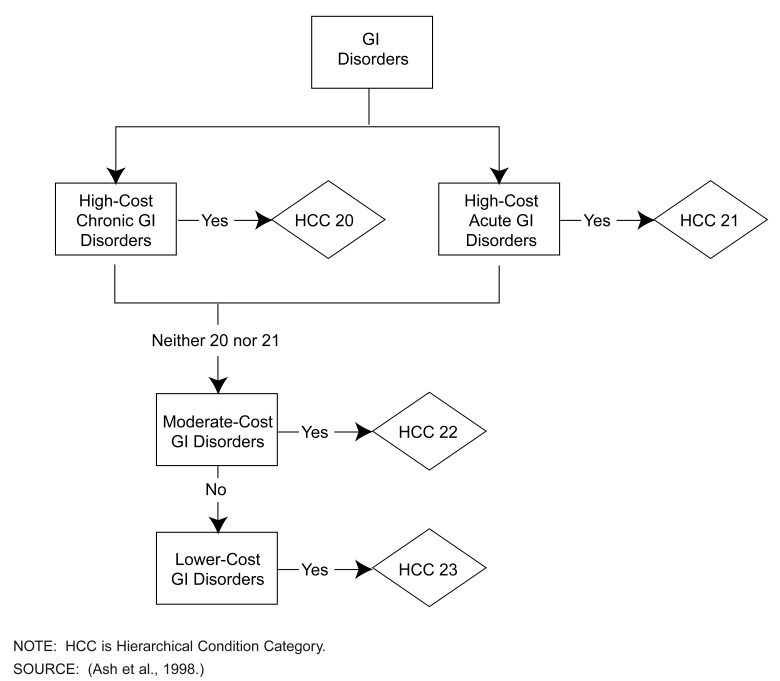
The CC hierarchies capture both chronic and serious acute manifestations of particular disease processes, as well as their seriousness in terms of expected costs. Some hierarchies, such as neoplasm, are simple; CC 5 dominates CC 6, which dominates CC 7, all the way down to CC 12. Other hierarchies, such as gastrointestinal, are more complex, as illustrated in Figure 1. A person may be classified with either, or both, acute and chronic high-cost gastrointestinal problems; however, if either of these is coded, information about moderate or lower cost GI disorders is ignored.
Figure 1. Sample of a Condition Category Hierarchy: Gastrointestinal (GI) Disorders.
Clinically, hierarchies reduce the sensitivity of predicted payments to the coding of less serious manifestations of the same condition; statistically, they make explanatory variables more nearly orthogonal, increasing statistical precision. Imposing hierarchies typically increases the estimated coefficients and t-ratios of serious condition categories.
Excluded Condition Categories
We also exclude some CCs from the models entirely, by constraining their coefficients to be zero; the result is that the presence of that condition for an individual will not increase his or her predicted cost. Money that “disappears” from the prediction when a positive coefficient is constrained to zero is redistributed—generally reappearing as slight increments to demographic variables. Each model still accounts for the costs of treating all conditions.
The most common reason for exclusion is the a priori medical judgment that a current problem triggering this CC this year should have little effect on next-year costs. Examples are (non-melanoma) skin cancers; benign cancers; lower cost ear, nose, and throat disorders; minor injuries; and screening (for example, presence of a routine checkup).
A second reason for exclusion is that a CC does not add to expected costs (either its coefficient in our modeling sample is actually negative or it is not statistically significantly positive). Reassuringly, these are generally the same CCs clinically thought to have little effect on future costs. Excluding CCs that would subtract from the payment preserves the monotonic character of the model. To ensure that adding a code does not reduce predicted costs, each CC with a non-positive coefficient is excluded or constrained, even if it might seem that the CC should be in the model.
A final reason for exclusion is concern over “gaming,” that is, a perverse health plan response to the incentives created by the model. Thus, the models do not pay for the often vague or discretionary conditions included in CCs such as moderate and other endocrine disorders (CCs 17 and 18), and lower cost mental disorders (CC 35). Such exclusions improve the models' attractiveness for setting payments, at the cost of some loss in accuracy.
Coefficient Constraints
Especially for conditions that are rare (such as mental retardation, ranging from mild to profound, in an employed population), unconstrained models can lead to higher payments for less serious conditions. Thus, in a few cases, we impose restrictions across sets of CCs, forcing predictions for conditions that are higher in a hierarchy to be at least as large as predictions for conditions that they dominate (as “profound mental retardation” dominates “mild mental retardation”). These restrictions avoid plans receiving higher payments for “downcoding.” We also do not modify some surprisingly low-cost coefficients that appear to be real artifacts of the coverage or delivery systems to which they apply, in the sense that they capture all costs covered by the program that collected the data but do not reflect expenditures from other sources. An example of this is the relatively low cost for people with renal failure in Medicaid because Medicare is likely to be the primary payer for most of the very high treatment costs for these people.
Clinical Refinements, Including Interactions with Age
The DCG classification system, originally focused on chronic conditions of the elderly, now handles distinctions for a full age and population spectrum. There are 21 DxGROUPs organized into 5 CCs for neonates (ages 0 to 1). Additional new CCs include four for the mentally retarded (common only in Medicaid), five for mental health and substance abuse, five for accidents and injuries, seven for pregnancy, and four for congenital and/or distinctly pediatric problems.
Ultimately, a single comprehensive classification system, with 543 DxGROUPs organized into 118 CCs and a common set of imposed hierarchies, is used to profile the medical problems present for any person, regardless of age, sex, or type of insurance. However, the cost consequences of a given diagnostic profile can be affected by demographics. For example, some CCs are separately priced for pediatric populations (age under 18), in the private or Medicaid populations, when clinical judgment and empirical evidence find substantial differences in utilization by age (e.g., CC 70, asthma, adds $1,513 for adults and only $825 for children in the private data.) The Medicare model also recognizes age/medical interactions for a few conditions (such as HIV and aplastic anemia). For people with such conditions, certain costs are associated with it in elderly persons (those age 65 or over), but additional dollars are associated with costs of care among the disabled (younger persons whose Medicare entitlement derives from disability).
Demographic Variables
In a given year, healthy people, whether they are age 8 or 80, incur few medical expenses. However, average health care costs differ dramatically by age and somewhat by sex. Much of this is driven by differences in disease prevalence because, for example, most children 8 years of age are fully healthy, while most persons age 80 have one or more chronic conditions requiring medical attention. Some of the cost difference is attributable to differences in the nature of certain diseases (or how they are treated) in children, young adults, or seniors. Additionally, however, even among those with no medical problems this year, demographically defined subgroups, such as females of childbearing age, or the oldest old, have different average costs next year. In a prospective model, even after accounting for the medical problems present, the additional effects of age and sex on expected costs remain important.
The three models (private, Medicaid, and Medicare) recognize three key age groups: 0-17 years, 18-64 years, 65 years or over, either by allowing some distinct CC coefficients for those under as opposed to over age 18 in the younger populations or by using distinct Medicare coefficients for those 65 or over.
The private and Medicaid models contain 16 indicators that place people within same-sex, similar-age groups (ages 0-5, 6-12, 13-17, 18-24, 25-34, 35-44, 45-54, and 55-64). The Medicare model constrains coefficients among its disabled enrollees under age 65 to distinguish only ages 0-34 and 35-64; it then makes 5-year breaks between 65 and 94 years of age; the highest age category is 95 or over.
Eligibility Categories
In addition to age and sex categories, the Medicaid model incorporates nine additional variables that distinguish among five distinct groups of enrollees: (1) the blind and disabled (11 percent); (2) those eligible because of other medical problems (8 percent); (3) pregnant women (2 percent); (4) those with poverty-related entitlement (71 percent); and (5) others (9 percent). We assign each person to one of the categories based on reason for entitlement during his or her earliest month of enrollment in year 1. Observed annual expenditures per person in year 2 averaged $1,430 and differed substantially by category. The blind and disabled are by far the most expensive, at $5,585 annually in year 2. Pregnant women cost about twice the average ($2,708); the “other medical” and “other” groups are about average ($1,281 and $1,500, respectively) and the non-medical, poverty-related group, consisting mainly of children enrolled under Aid to Families with Dependent Children, cost about one-half the average ($731).
Four of the new variables are indicators (yes-no variables) that distinguish Medicaid's other subpopulations from the least expensive, poverty-related subgroup. The remaining five additional demographic variables in the model are interactions of eligibility category and duration of (year 1) Medicaid enrollment. These variables allow the model to reflect the fact that recent entrants to the Medicaid program cost more than longer term “stayers,” and that the “premium” for recent entry varies not only by duration of enrollment but by eligibility type. These five variables each have the form:
How all this works is best illustrated with examples, as shown in the following section.
Sample Calculations of Expected Costs
Each HCC model prediction is the sum of a demographic part and a health-status part. We illustrate this in Figure 2 for two privately insured females 58 years of age. The numbers here are private-model coefficients, shown in the first column of Table 2. Both patients' estimated costs begin with a demographic component of $1,730, which is the final prediction for any fully healthy, privately insured female between the ages of 55 and 64. Each of these patients, however, also has medical conditions with expected consequences for future health care costs.
Figure 2. Sample Information Used to Predict Next Year's Expenses for Privately Insured Patients.
Table 2. Statistics for Private, Medicaid, and Medicare Prospective Payment Models.
| Statistic or Variable | Private | Medicaid | Medicare | |||||
|---|---|---|---|---|---|---|---|---|
| Number of Observations | 1,379,023 | 1,103,367 | 1,360,626 | |||||
| Prediction Year Mean Total Costs | 1,593 | 1,430 | 3,778 | |||||
| Number of Model Parameters | 102 | 136 | 96 | |||||
| R2 × 100 | 9.4 | 21.1 | 8.8 | |||||
| Validated R2 × 100 | 9.1 | 23.1 | 8.5 | |||||
| Standard Error | 7,843 | 4,802 | 9,963 | |||||
| Age/Sex Groups | Model Coefficients | |||||||
| Female | ||||||||
| 0-5 Years | 295 | -6 |
|
1,324 | ||||
| 6-12 Years | 241 | 0 | 1,324 | |||||
| 13-17 Years | 479 | 270 | 1,324 | |||||
| 18-24 Years | 613 | 560 | 1,324 | |||||
| 25-34 Years | 1,187 | 337 | 1,324 | |||||
| 35-44 Years | 1,120 | 345 | 1,155 | |||||
| 45-54 Years | 1,401 | 446 | 1,202 | |||||
| 55-64 Years | 1,730 | 537 | 1,698 | |||||
| 65-69 Years | ‡ | ‡ | 1,042 | |||||
| 70-74 Years | ‡ | ‡ | 1,318 | |||||
| 75-79 Years | ‡ | ‡ | 1,675 | |||||
| 80-84 Years | ‡ | ‡ | 1,962 | |||||
| 85-89 Years | ‡ | ‡ | 2,161 | |||||
| 90-94 Years | ‡ | ‡ | 2,258 | |||||
| 95 Years or Over | ‡ | ‡ | 1,897 | |||||
| Male | ||||||||
| 0-5 Years | 312 | 87 |
|
955 | ||||
| 6-12 Years | 271 | 113 | 955 | |||||
| 13-17 Years | 473 | 334 | 955 | |||||
| 18-24 Years | 370 | 86 | 955 | |||||
| 25-34 Years | 574 | 132 | 955 | |||||
| 35-44 Years | 778 | 392 | 904 | |||||
| 45-54 Years | 1,218 | 571 | 887 | |||||
| 55-64 Years | 2,126 | 526 | 1,403 | |||||
| 65-69 Years | ‡ | ‡ | 1,428 | |||||
| 70-74 Years | ‡ | ‡ | 1,743 | |||||
| 75-79 Years | ‡ | ‡ | 2,215 | |||||
| 80-84 Years | ‡ | ‡ | 2,426 | |||||
| 85-89 Years | ‡ | ‡ | 2,725 | |||||
| 90-94 Years | ‡ | ‡ | 3,027 | |||||
| 95 Years or Over | ‡ | ‡ | 2,980 | |||||
| Medicaid Eligibility Categories | ||||||||
| Blind/Disabled | ‡ | 1,449 | ‡ | |||||
| Other Medical | ‡ | 429 | ‡ | |||||
| Poverty-Related | ‡ | 476 | ‡ | |||||
| Pregnant Women | ‡ | 96 | ‡ | |||||
| Other | ‡ | -263 | ‡ | |||||
| Medicaid Amount Added per Missing Base Year Month for | ||||||||
| Blind/Disabled | ‡ | 179 | ‡ | |||||
| Other Medical | ‡ | 71 | ‡ | |||||
| Poverty-Related | ‡ | 56 | ‡ | |||||
| Pregnant Women | ‡ | 296 | ‡ | |||||
| Other | ‡ | 100 | ‡ | |||||
| Condition Categories2 | ||||||||
| 1 | Infection1 | HIV/AIDS | 22,580 | 5,284 | 1,076 | |||
| 2 | Infection2 | Septicemia (Blood Poisoning)/Shock | 8,677 | 3,663 | 3,253 | |||
| 3 | Infection3 | Central Nervous System Infections | 4,658 | † | 760 | |||
| 5 | Neoplasm1 | Metastatic Cancer | 21,884 | 6,331 | 6,185 | |||
| 6 | Neoplasm2 | High-Cost Cancer | 11,967 | 3,278 | 3,905 | |||
| 7 | Neoplasm3 | Moderate-Cost Cancer | 5,863 | 1,288 | 2,128 | |||
| 8 | Neoplasm4 | Lower Cost Cancers/Tumors | 2,372 | 550 | 873 | |||
| 13 | Diabetes1 | Diabetes with Chronic Complications | 7,726 | 3,686 | 3,582 | |||
| 14 | Diabetes2 | Diabetes with Acute Complications/Non-Proliferative Retinopathy | 3,806 | 2,392 | 2,396 | |||
| 15 | Diabetes3 | Diabetes with No or Unspecified Complications | 1,961 | 369 | 1,147 | |||
| 16 | Metabolic1 | Protein-Calorie Malnutrition | 13,639 | 5,012 | 3,594 | |||
| 19 | Liver | Liver Disease | 5,700 | 4,007 | 3,028 | |||
| 20 | GI1 | High-Cost Chronic Gastrointestinal Disorders | 4,312 | 2,944 | 1,336 | |||
| 21 | GI2 | High-Cost Acute Gastrointestinal Disorders | 2,087 | 1,213 | 1,329 | |||
| 22 | GI3 | Moderate-Cost Gastrointestinal Disorders | 1,432 | 748 | 730 | |||
| 24 | MSK1 | Bone/Joint Infections/Necrosis | 3,653 | 3,563 | 2,070 | |||
| 25 | MSK2 | Rheumatoid Arthritis and Connective Tissue Disease | 2,380 | 870 | 1,218 | |||
| 27 | Blood1 | Aplastic and Acquired Hemolytic Anemias | 9,801 | 6,562 | 4,035 | |||
| 28 | Blood2 | Blood/Immune Disorders | 4,248 | 3,637 | 709 | |||
| 30 | Dementia | Dementia | 4,822 | 1,324 | 438 | |||
| 31 | Mental1 | Drug/Alcohol Dependence/Psychoses | 3,568 | 2,223 | 1,122 | |||
| 32 | Mental2 | Psychosis and Other Higher Cost Mental Disorders | 3,092 | 3,599 | 1,288 | |||
| 33 | Mental3 | Depression and Other Moderate-Cost Mental Disorders | 2,171 | 834 | 540 | |||
| 34 | Mental4 | Anxiety Disorders | 1,788 | 771 | 511 | |||
| 36 | MR1 | Profound Mental Retardation |
|
2,544 | 22,370 | † | ||
| 37 | MR2 | Severe Mental Retardation | 2,544 | 16,064 | † | |||
| 38 | MR3 | Moderate Mental Retardation | 2,544 | 11,677 | † | |||
| 39 | MR4 | Mild/Unspecified Mental Retardation | 2,544 | 5,508 | † | |||
| 40 | Neuro1 | Quadriplegia |
|
12,506 | 5,632 | 5,686 | ||
| 41 | Neuro2 | Paraplegia | 12,506 | 3,467 | 5,788 | |||
| 42 | Neuro3 | Higher Cost Neurological Disorders | 3,939 | 1,452 | 1,851 | |||
| 43 | Neuro4 | Moderate-Cost Neurological Disorders | 1,936 | 1,037 | 1,261 | |||
| 45 | Arrest1 | Respirator Dependence/Tracheostomy Status | 41,465 | 24,247 | 9,117 | |||
| 46 | Arrest2 | Respiratory Arrest | 13,396 | 3,538 | 8,087 | |||
| 47 | Arrest3 | Cardio-Respiratory Failure and Shock | 3,416 | 2,673 | 2,809 | |||
| 48 | Hrt_CHF | Congestive Heart Failure | 5,114 | 2,714 | 2,069 | |||
| 49 | Hrt_ARR | Heart Arrhythmia | 1,872 | 928 | 670 | |||
| 50 | Hrt_AMI | Acute Myocardial Infarction | 4,723 | 3,792 | 1,778 | |||
| 51 | Hrt_CAD1 | Other Acute Ischemic Heart Disease | 3,442 | 1,639 | 1,807 | |||
| 52 | Hrt_CAD2 | Chronic Ischemic Heart Disease | 2,871 | 511 | 883 | |||
| 53 | Hrt_VHD | Valvular and Rheumatic Heart Disease | 1,128 | 741 | 938 | |||
| 54 | Hrt_HTN | Hypertensive Heart Disease | 1,346 | 436 | 347 | |||
| 57 | HTN | Hypertension (High Blood Pressure) | 915 | 312 | 216 | |||
| 58 | Stroke1 | Higher Cost Cerebrovascular Disease | 3,902 | 1,523 | 1,919 | |||
| 59 | Stroke2 | Lower Cost Cerebrovascular Disease | 1,795 | 645 | 835 | |||
| 60 | Vascular1 | High-Cost Vascular Disease | 2,486 | 1,420 | 1,268 | |||
| 61 | Vascular2 | Thromboembolic Vascular Disease | 2,505 | 2,316 | 1,429 | |||
| 64 | Lung1 | Chronic Obstructive Pulmonary Disease | 2,633 | 1,034 | 1,669 | |||
| 65 | Lung2 | Higher Cost Pneumonia | 8,092 | 3,455 | 4,037 | |||
| 66 | Lung3 | Moderate-Cost Pneumonia | 3,411 | 492 | 1,229 | |||
| 68 | Lung5 | Pulmonary Fibrosis and Other Chronic Lung Disorders | 3,254 | 936 | 829 | |||
| 69 | Lung6 | Pleural Effusion/Pneumothorax | 2,239 | 2,506 | 1,456 | |||
| 70 | Lung7 | Asthma | 1,513 | 409 | 624 | |||
| 72 | Eye1 | Higher Cost Eye Disorders | 783 | 1,110 | 242 | |||
| 74 | ENT1 | Higher Cost Ear, Nose, and Throat Disorders | 685 | 620 | 147 | |||
| 76 | Urinary1 | Dialysis Status | 37,287 | 3,693 | 6,821 | |||
| 77 | Urinary2 | Kidney Transplant Status | 10,333 | 215 | 6,468 | |||
| 78 | Urinary3 | Renal Failure | 17,834 | 5,742 | 3,107 | |||
| 79 | Urinary4 | Nephritis | 1,050 | 1,026 | 1,627 | |||
| 81 | Genital1 | Female Infertility | 2,242 | 455 | † | |||
| 82 | Genital2 | Moderate-Cost Genital Disorders | 889 | 345 | 89 | |||
| 84 | Preg1 | Ectopic Pregnancy | 1,957 | 951 | † | |||
| 85 | Preg2 | Miscarriage/Abortion | 1,892 | 1,064 | † | |||
| 86 | Preg3 | High-Cost Completed Pregnancy |
|
572 |
|
262 | † | |
| 87 | Preg4 | Moderate-Cost Completed Pregnancy | 572 | 262 | † | |||
| 88 | Preg5 | Normal Delivery | 572 | 262 | † | |||
| 89 | Preg6 | Higher Cost Pregnancy without Completion |
|
4,060 |
|
1,674 |
|
1,634 |
| 90 | Preg7 | Lower Cost Pregnancy without Completion | 4,060 | 1,674 | 1,634 | |||
| 91 | Skin1 | Chronic Ulcer of Skin | 3,756 | 2,468 | 2,473 | |||
| 93 | Injury1 | Vertebral Fractures and Spinal Cord Injuries | 2,992 | 546 | 1,289 | |||
| 94 | Injury2 | Hip Fracture/Dislocation | 1,280 | 463 | 993 | |||
| 95 | Injury3 | Head Injuries | 763 | 95 | 428 | |||
| 96 | Injury4 | Drug Poisoning, Internal Injury, Traumatic Amputation, Burn | 1,588 | 932 | 1,256 | |||
| 98 | Complic | Complications of Care | 2,369 | 1,380 | 798 | |||
| 101 | Peds | Very-High-Cost Pediatric Disorders | 5,901 | 2,067 | † | |||
| 102 | Cong1 | Higher Cost Congenital/Pediatric Disorders | 4,948 | 710 | 2,081 | |||
| 103 | Cong2 | Moderate-Cost Congenital Disorder | 1,603 | 355 | 532 | |||
| 104 | Cong3 | Lower Cost Congenital Disorder | 829 | 334 | 348 | |||
| 105 | Baby1 | Extremely-Low-Birthweight Neonates |
|
13,238 | 1,852 | † | ||
| 106 | Baby2 | Very-Low-Birthweight Neonates | 13,238 | 1,163 | † | |||
| 107 | Baby3 | Serious Perinatal Problem Affecting Newborn | 1,010 | 323 | † | |||
| 108 | Baby4 | Other Perinatal Problem Affecting Newborn | 145 |
|
78 | † | ||
| 109 | Baby5 | Normal, Single Birth | 332 | 78 | † | |||
| 110 | Transplant1 | Heart, Lung, Liver Transplant Status | 26,576 | 5,312 | 3,552 | |||
| 112 | Openings | Artificial Opening Status/Attention | 5,588 | 4,317 | 2,696 | |||
| Age-Interacted Condition Category3 | ||||||||
| AI-1 | Infection1 | HIV/AIDS | † | † | 8,735 | |||
| AI-2 | Infection2 | Septicemia (Blood Poisoning)/Shock | † | -2,615 | † | |||
| AI-15 | Diabetes3 | Diabetes with No or Unspecified Complications | † | -157 | † | |||
| AI-20 | GI1 | High-Cost Chronic Gastrointestional Disorders | † | -924 | 4,241 | |||
| AI-21 | GI2 | High-Cost Acute Gastrointestional Disorders | 1,406 | -313 | † | |||
| AI-22 | GI3 | Moderate-Cost Gastrointestinal Disorders | -1,044 | -460 | † | |||
| AI-24 | MSK1 | Bone/Joint Infections/Necrosis | † | -3,047 | † | |||
| AI-25 | MSK2 | Rheumatoid Arthritis and Connective Tissue Disease | † | -812 | † | |||
| AI-27 | Blood1 | Aplastic and Acquired Hemolytic Anemias | † | -4,872 | 3,365 | |||
| AI-28 | Blood2 | Blood/Immune Disorders | † | -2,108 | 2,019 | |||
| AI-30 | Dementia | Dementia | † | 373 | † | |||
| AI-31 | Mental1 | Drug/Alcohol Dependence/Psychoses | † | -1,135 | 3,315 | |||
| AI-32 | Mental2 | Psychosis and Other Higher Cost Mental Disorders | 346 | 3,842 | 1,204 | |||
| AI-33 | Mental3 | Depression and Other Moderate Cost Mental Disorders | † | 1,876 | † | |||
| AI-36 | MR1 | Profound Mental Retardation | † | -4,752 | † | |||
| AI-37 | MR2 | Severe Mental Retardation | † | -6,924 | † | |||
| AI-38 | MR3 | Moderate Mental Retardation | † | -5,056 | † | |||
| AI-39 | MR4 | Mild/Unspecified Mental Retardation | † | -1,717 | † | |||
| AI-42 | Neuro3 | Higher Cost Neurological Disorders | † | 1,377 | † | |||
| AI-43 | Neuro4 | Moderate-Cost Neurological Disorders | -929 | -224 | † | |||
| AI-58 | Stroke1 | Higher Cost Cerebrovascular Disease | † | -1,450 | † | |||
| AI-59 | Stroke2 | Lower Cost Cerebrovascular Disease | † | 1,417 | † | |||
| AI-64 | Lung1 | Chronic Obstructive Pulmony Disease | -1,904 | -734 | † | |||
| AI-65 | Lung2 | Higher Cost Pneumonia | † | 365 | † | |||
| AI-70 | Lung7 | Asthma | -688 | † | † | |||
| AI-82 | Genital2 | Moderate-Cost Genital Disorders | 348 | 364 | † | |||
| AI-88 | Preg5 | Normal Delivery | † | 395 | † | |||
| AI-90 | Preg7 | Lower Cost Pregnancy without Completion | † | 472 | † | |||
| AI-94 | Injury2 | Hip Fracture/Dislocation | † | 245 | † | |||
| AI-96 | Injury4 | Drug Poisoning, Internal Injury, Traumatic Amputation, Burn | -1,336 | -554 | † | |||
| AI-98 | Complic | Complications of Care | † | -710 | † | |||
| AI-102 | Cong1 | Higher Cost Congenital/Pediatric Disorders | † | 2,757 | † | |||
| AI-103 | Cong2 | Moderate-Cost Congenital Disorder | 1,383 | 911 | † | |||
Indicates a coefficient constrained to zero.
Indicates a variable that is not relevant for a particular model.
The Medicare model combines age/sex categories 0-34 years for each of females and males.
Lines for CCs that are zeroed out in all three prospective models are not listed in this table.
Values are increments or decrements for younger persons in this CC (under 18 for private and Medicaid; under 65 for Medicare) after receiving the basic CC payment coefficient listed in this table.
NOTES: Coefficients joined by a brace are constrained to be the same. CC is condition category. HIV is human immunodeficiency virus. AIDS is acquired immunodeficiency syndrome.
SOURCE: (Ash et al., 1998; Pope et al., 1998.)
Figure 2 shows how the model organizes each patient's ICD-9-CM data into a clinical profile that leads to the health-status part of her prediction. For patient 1, her breast cancer diagnosis adds $2,372; her hypertension, a distinct medical problem, adds another $915, for a total of $5,017. Patient 2 has breast cancer, too, but her cancer has metastasized and is coded at multiple sites (lung, liver, and bone). Note the different ways that additional information about cancer is reflected in the classification: in one, distinct but related diagnoses are classified into the same DxGROUP; in another, related DxGROUPs are classified into the same CC; in a third, one CC is ranked higher than another. In the end, only a single payment amount ($21,884) is calculated for metastatic cancer; any additional codes pertaining to benign or malignant neoplasms are ignored.
Another example clarifies how the Medicaid demographic/eligibility variables work. This time the numbers are drawn from the Medicaid column of Table 2. We compute the predicted cost for a female age 20 with no medical problems and a full year 1 of poverty-related Medicaid by adding $560 (the “female, age 18-24” base amount) to $476 (poverty-related eligibility) for a total of $1,036. If the female had been present for only 10 months in year 1, we add another $112, that is, $56 for each of the two missing year-1 months, for a total of $1,148. If she were present for only 2 months in year 1, we would add 10×56 to $1,036, for a total of $1,596. In contrast, consider a female of the same age and present for 10 months in year 1 but who is eligible for Medicaid because of disability rather than poverty. We add three numbers to arrive at the demographic part of this female's prediction: $560 for age and sex, $1,449 for disability entitlement, and $179×2 for her two missing year-1 months as a disability-entitled person. The demographic part of this female's expected cost next year is then $2,367; in computing her total expected costs, dollars for the future cost implications of her year-1 medical conditions are added to $2,367.
We include one final example to illustrate how health-status information can interact with age. Consider the payment for a Medicare-entitled male 66 years of age, under treatment for drug dependence (CC 31) but with no other recorded illness. His predicted cost is $2,540, computed as the sum of $1,428 for the demographic part (the same for all males between ages 65 and 69) and a $1,122 contribution for CC 31. Consider, however, a second male, also drug-dependent, but only 30 years of age and entitled to Medicare through disability. Here, there is a $5,392 total prediction, the sum of a $955 demographic part (the same for any male under age 35) and $4,437 for drug dependence. The latter number is computed by adding a $3,315 age-interaction for a Medicare enrollee under age 65 in CC 31 to the $1,122 basic payment for any Medicare enrollee in CC 31. The number $3,315 is in the last column of Table 2 in the row labeled AI-31; drug problems cost, on average, $3,315 more to treat in younger (disabled) Medicare enrollees than in the elderly.
Models
Table 2 shows the complete detail (summary statistics and all coefficients for all variables) for the three DCG/HCC models. The models are distinguished in several ways by: (1) which CCs are excluded, (2) which coefficients are constrained, (3) which demographic variables and demographic-medical interactions are included, and (4) what the model coefficients are. We discuss each of these in turn.
Exclusions, which result in coefficients being set to zero, were made for reasons previously described. The lines for the 33 CCs that are excluded from all three models are omitted from Table 2. Exclusions used in specific models appear in Table 2 as omitted coefficients (†). The private model has no model-specific exclusions, Medicaid has one (CC3 central nervous system infections) and Medicare has 16, most of them related to maternity, neonatal and pediatric conditions that are extremely rare in Medicare's predominantly elderly population.
We indicate coefficients that are constrained to be equal by connecting them with a brace. For example, because only 165 people were classified in the 4 mental retardation categories (CCs 36 through 39) in the private model, these 4 coefficients are constrained to a common value of $2,544. The three models differ in the number of constraints imposed across sets of CC coefficients, with the private model employing the most (five) and the Medicare model, the least (one).
A third difference is in the variables included in addition to the age/sex and CC predictors that characterize prospective DCG/HCC models. The Medicaid model has the most: including eligibility categories, missing-months variables, and 31 coefficients for selected age-medical interactions (labeled as AI-2, AI-15, and so on, where the AI number indicates an associated condition category). The private model includes 9 AI variables and the Medicare model, 6. The AI coefficients shown at the end of Table 2 are the increments (decrements, for negative numbers) to the basic CC payments for a younger person with those particular medical problems. “Younger” means under age 65 in Medicare and under age 18 in the other two populations.
Finally, the models differ in the values of their coefficients. A striking feature of Table 2 is the similarity between the CC coefficients in Medicare and Medicaid, estimated to within 20-30 percent for about one-half of the categories; also, for any particular CC, the larger coefficient is about equally likely to be found in either model. Thus, even though average costs are much higher in Medicare than in Medicaid, the incremental costs of treating particular conditions do not differ systematically. Although one source of higher expected costs next year in Medicare is larger age/sex coefficients, the more important explanation is greater disease prevalence. For example, 1.3 percent of the Medicare population has metastatic cancer (CC 5) but only 0.2 percent of the Medicaid population; for chronic complications of diabetes (CC 13), the rates are 1.6 percent versus 0.2 percent; for congestive heart failure (CC 48), 9.8 percent versus 1.1 percent; for acute myocardial infarction (CC 50), 4.2 percent versus only 8 in 10,000.
Medicaid and Medicare coefficients, although similar to each other, are almost always much smaller than coefficients in the private model. Typically, they are not even one-half as large as the private model coefficients. For only a handful of CCs, the Medicaid coefficient exceeds the private model coefficient: CC 32—depression and other moderate-cost mental illness; the four mental retardation CCs—36 through 39; CC 69—pleural effusion/pneumothorax; and CC 72—high-cost eye disorders. In only one instance, CC 79—nephritis, is the Medicare coefficient greater than the private one. We have no explanation for this unusual finding. It is encouraging that the private and Medicaid models are similar in terms of the age-interacted coefficients estimated for the pediatric conditions. Of the eight AI parameters present in both models, seven are of the same sign. Most of the pediatric coefficients, which were identified in the development samples, remain highly significant in these full-data re-estimated models.
In considering the plausibility of particular model coefficients, we note that each coefficient for a CC reflects the increment to expected costs that is independently associated with having the condition. An HIV-positive male's prediction, for example, is the sum of the CC 1 coefficient, all coefficients associated with his other medical problems, and any relevant demographic coefficients. If this male has multiple medical problems, his predicted total costs will be much larger than the coefficient for CC 1 alone. This feature is an important strength of the DCG/HCC multiple-condition model structure (in contrast to single-condition models, such as PIP-DCG), because, in fact, people who are HIV-positive differ widely in the range of medical problems they experience and how expensive they are to treat. This model does not simply pay more for HIV but rather establishes appropriately different payment amounts within the community of people living with HIV by recognizing comorbid conditions.
Measuring Model Performance
Because implementing a risk-adjustment model has serious consequences, we must understand how well the models work. The one universally reported, single-number summary performance measure for risk-adjustment payment models is the R2, or the proportion of variance in costs that the model explains. For reference, demographic payment models in private and Medicare populations have R2 values of less than 2 percent, and the R2 for a demographic/eligibility model in our Medicaid data is 7 percent (Greenwald et al., 1998; Ash et al., 1998; Pope et al., 1998).
Our Medicaid model has the highest explanatory power, with a validated R2 of more than 20 percent, compared with 8 to 9 percent in the other two populations (refer to the fifth row of Table 2). The better fit in Medicaid is attributable to several factors. For one, the distribution of the outcome variable, cost, has a less extreme upper tail (virtually no million-dollar cases) in Medicaid. Additionally, many people with Medicaid coverage are eligible for medical reasons (such as pregnancy or disability), and expenditures within medically defined groups are more predictable than among populations with many non-users (Kronick et al., 1996). Medicaid eligibility categories also distinguish groups (such as children in poor families) that have predictably lower medical costs because they are basically healthy. Finally, the “months out” variables capture the higher expected costs of recent entrants, an important factor in a system with sporadic entitlement.
All three prospective DCG/HCC models rely upon age and sex in addition to diagnostic information, and costs in these populations do differ substantially by age. For example, in the Medicaid and private samples, annual costs are each about $3,500 more for males age 60 than for females age 5; in Medicare, there is a similar difference in annual costs for males age 90 versus females age 65. However, after accounting for differences in the prevalence of medical problems, the demographic coefficients in our models differentiate less. (The disease-adjusted differences are about $1,400 for males age 60 than for females age 5 among the privately insured, about $500 for a similar demographic difference in Medicaid, and $2,000 for males age 90 versus females age 65 in Medicare.) Although age and sex coefficients remain highly statistically significant in each model, information about the presence of serious, chronic disease groups, such as diabetes and renal insufficiency, is far more useful for predicting costs.
Average Costs for Important Subgroups
Although R2 values are always reported, other ways of examining model performance may be more useful in assessing the value of a payment model (Ash and Byrne-Logan, 1998). We use some of these to examine the private DCG/HCC model's performance in a fourth, entirely new data set (a State employee health insurance plan). The methodology is to compare predicted versus actual year-2 average costs within significant subgroups. A predictive ratio (PR) for a model applied to a subgroup of people is formed by dividing the model-predicted costs for the group by their actual costs. Thus, for example, when an age/sex model is used to predict costs for a group of sick people, the PR is likely to be much less than 1.00. Alternatively, when people are identified retrospectively as a group whose costs turned out to be very low, PRs for any prospective model will be much larger than 1.00. Prospective models should never predict zero costs, because no one has zero expected future health care costs.
Figure 3 shows PRs for several clinically defined groups of people in the State data, as predicted by the private DCG/HCC model and by an age/sex model. The medical condition groups were defined by an outside panel convened by HCFA, and membership in each group is contingent upon the presence (during year 1) of at least one panel-specified ICD-9-CM code. Although the age/sex prediction is never more than one-half the actual costs for any of these groups (all PRs are 0.50 or less), the DCG prediction is commonly between 0.95 and 1.05. The DCG model underpredicts most seriously in arthritis, where nearly 4,000 people predicted to cost around $4,300 actually cost nearly $5,800 (PR = 0.74). This is because the panel-identified arthritis subgroup includes anyone with any arthritis code regardless of its specificity, but the DCG model identifies only a smaller, sicker subgroup. The model does pay $2,357 for the presence of a well-defined, systemic rheumatoid disease, such as rheumatoid arthritis (ICD-9-CM 714); however, it does not add dollars for vague codes, such as ICD-9-CM 713 (other arthropathy, joint disorders, derangements, joint pain/stiffness). When a model excludes payment for vague codes associated with real costs, it becomes less accurate; in particular, this model underpays for people with low-level or non-specific joint disorders, even though these disorders can result in significant disability.
Figure 3. Predictive Ratios for the Private Validation Sample, by Presence of Medical Condition.
In another illustration of the predictive value of DCG/HCC models, we divide the private validation sample into 18 groups based on predicted cost levels specified by the DCG/HCC model. The healthiest group, with predicted costs between $250 and $500, contains 21,650 people, or 11.3 percent of the population. (The model does not predict costs of less than $250 for anyone.) The next group, with predicted costs of at least $500 but less than $750, contains another 21.6 percent of people. At the other end of the spectrum, the model predicts costs of $5,000 or more for 5.6 percent of people; among these, just 74 (4/100 of 1 percent) fall into our highest cost prediction group ($40,000 and over). Within each group, we calculate mean actual costs, as well as the means for DCG/HCC-predicted costs and age/sex predicted costs. At the high end, for those with predicted costs over $5,000, the DCG/HCC-predicted amounts track actual costs quite well (meaning that PRs within these groups are not far from 1.00), while the age/sex predicted costs plateau at about $3,300. Figure 4, in which average actual costs, age-sex predicted costs, and DCG-predicted costs are plotted for people in each of these 18 prediction groups, illustrates these points. The data for Figure 4 are in Table 3.
Figure 4. Means of Actual and Predicted Costs for the Private Validation Sample, by DCG-Prediction Group.
Table 3. Means of Actual and Predicted Cost for the Private Validation Sample, by DCG-Prediction Group.
| Predicted Cost Group1 | Actual Costs | DCG-Predicted Costs | Age/Sex Predicted Costs | Counts |
|---|---|---|---|---|
| Less than $250 | — | — | — | 0 |
| 250 | $510 | $417 | $570 | 21,650 |
| 500 | 672 | 620 | 855 | 41,384 |
| 750 | 931 | 867 | 1,262 | 22,649 |
| 1,000 | 1,391 | 1,347 | 1,915 | 28,782 |
| 1,500 | 1,707 | 1,714 | 2,335 | 30,786 |
| 2,000 | 2,295 | 2,242 | 3,140 | 16,100 |
| 2,500 | 2,510 | 2,779 | 3,195 | 5,828 |
| 3,000 | 3,373 | 3,406 | 3,332 | 9,086 |
| 4,000 | 3,993 | 4,451 | 2,695 | 4,944 |
| 5,000 | 4,734 | 5,485 | 2,859 | 3,474 |
| 6,000 | 6,478 | 6,624 | 2,951 | 2,747 |
| 7,500 | 8,025 | 8,557 | 3,012 | 1,980 |
| 10,000 | 11,415 | 11,939 | 3,006 | 1,314 |
| 15,000 | 15,741 | 17,042 | 3,217 | 441 |
| 20,000 | 20,426 | 22,377 | 2,853 | 257 |
| 25,000 | 31,804 | 27,181 | 2,929 | 227 |
| 30,000 | 40,559 | 34,087 | 3,010 | 154 |
| 40,000 | 61,380 | 52,026 | 2,926 | 74 |
Each predicted cost group contains all people whose DCG-predicted dollar cost are at least this great but less than the next higher number.
NOTES: DCG is Diagnostic Cost Group. n = 191,877.
SOURCE: (Ash and Byrne-Logan, 1998.)
In summary, the private model, which was built on a large national data set, predicts costs well within a new population of State employees. It not only distinguishes groups of high- and low-cost individuals but also even identifies a high-cost tail, with small numbers of very expensive people.
The Medicaid and Medicare DCG/HCC models work similarly well (and demographic-only models, similarly poorly) in analogous comparisons of actual and predicted costs in out-of-sample validation data sets (Ash et al., 1998; Pope et al., 1998).
Conclusion
We have extracted disease profiles of individual patients and groups of patients from the kinds of administrative records that many providers have been supplying to health care payers for years. Until now, few plans have used these data to construct a solid “information backbone” for managing care. The unified, multiple-condition DCG modeling framework characterizes individual health status and the disease burden of populations, as well as predicting future levels of resource need. When comparing physicians' practices, patient profiles can be aggregated to describe the various mixes of medical problems that providers handle, at the same time that the model's predictions can help establish fair (risk-adjusted) resource allocations.
Although the original purpose of these models was to enable health care purchasers, such as HCFA, to identify an efficient capitation price, the models actually provide detailed information on the prevalence of disease. Such information helps explain why some providers and plans use more-than-average resources. The DCG/HCC health profiles and the model predictions can be used together to routinely identify patients who are likely to be very costly and to find the particular medical problems that contribute to this expectation. Such information is invaluable for identifying opportunities for selecting, implementing, and evaluating the effectiveness of disease management programs.
Footnotes
Arlene S. Ash and Wei Yu are with Boston Medical Center. Randall P. Ellis is with Boston University. Gregory C. Pope is with Health Economics Research, Inc. John Z. Ayanian is with Brigham and Women's Hospital and is a paid consultant to Health Economics Research, Inc., and DxCG, Inc. David W. Bates, Helen Burstin, and Lisa I. Iezzoni are with Harvard Medical School. Elizabeth MacKay is with the University of Calgary. This research was funded by the Health Care Financing Administration (HCFA) through Contract Numbers 18-C-90462/1-02 and 500-95-048. The views expressed in this article are those of the authors and do not necessarily reflect the views of Boston Medical Center, Boston University, Health Economics Research, Inc., DxCG, Inc., Brigham and Women's Hospital, Harvard Medical School, the University of Calgary, or HCFA.
Reprint requests: Arlene Ash, 720 Harrison Avenue, Suite 1108, Boston, MA 02118. E-mail: aash@bu.edu
References
- Ash A, Porell F, Gruenberg L, et al. An Analysis of Alternative AAPCC Models Using Data from the Continuous Medicare History Sample. Final Report to the Health Care Financing Administration; Health Policy Research Consortium; Boston: Brandeis/Boston Universities; Sep, 1986. [Google Scholar]
- Ash A, Porell F, Gruenberg L, et al. Adjusting Medicare Capitation Payments Using Prior Hospitalization. Health Care Financing Review. 1989;10(4):17–29. [PMC free article] [PubMed] [Google Scholar]
- Ash A, Ellis RP, Yu W, et al. Final Report to the Health Care Financing Administration under Contract Number 18-C-90462/1-02. Boston University; Boston: Jun, 1998. Risk Adjusted Payment Models for the Non-Elderly. [Google Scholar]
- Ash A, Byrne-Logan S. How Well Do Models Work? Predicting Health Care Costs; Proceedings of the Section on Statistics in Epidemiology of the American Statistical Association; Dallas. 1998. [Google Scholar]
- Brown R, Clement DC, Hill JW, et al. Do Health Maintenance Organizations Work for Medicare? Health Care Financing Review. 1993;15(1):7–23. [PMC free article] [PubMed] [Google Scholar]
- Ellis RP, Ash A. Refinements to the Diagnostic Cost Group Model. Inquiry. 1995 Winter;32(4):1–12. [PubMed] [Google Scholar]
- Ellis RP, Pope GC, Iezzoni LI, et al. Final Report to the Health Care Financing Administration. Baltimore, MD.: Apr, 1996a. Diagnostic Cost Group (DCG) and Hierarchical Coexisting Conditions and Procedures (HCCP) Models for Medicare Risk Adjustment. [Google Scholar]
- Ellis RP, Pope GC, Iezzoni LI, et al. Diagnosis-Based Risk Adjustment for Medicare Capitation Payments. Health Care Financing Review. 1996b Spring;17(3):101–128. [PMC free article] [PubMed] [Google Scholar]
- Greenwald LM, Esposito A, Ingber MJ, Levy JM. Risk Adjustment for the Medicare Program: Lessons Learned from Research and Demonstrations. Inquiry. 1998;35(2):193–209. [PubMed] [Google Scholar]
- Health Care Financing Administration, Office of Strategic Planning. Report to Congress: Proposed Method of Incorporating Health Status Risk Adjusters into Medicare+Choice Payments. Baltimore, MD.: Mar, 1999. [Google Scholar]
- Iezzoni LI, editor. Risk Adjustment for Measuring Health Care Outcomes. Health Administration Press; Ann Arbor, Michigan: 1997. [Google Scholar]
- Iezzoni LI, Ayanian JZ, Bates DW, Burstin HR. Paying More Fairly for Medicare Capitated Care. New England Journal of Medicine. 1998 Dec 24;339(26):1933–1938. doi: 10.1056/NEJM199812243392613. [DOI] [PubMed] [Google Scholar]
- Ingber MJ. The Current State of Risk Adjustment Technology for Capitation. Journal of Ambulatory Care Management. 1998;21(4):1–28. doi: 10.1097/00004479-199810000-00002. [DOI] [PubMed] [Google Scholar]
- Kronick R, Dreyfus T, Lee L, Zhou Z. Diagnostic Risk Adjustment for Medicaid: The Disability Payment System. Health Care Financing Review. 1996;17(3):7–33. [PMC free article] [PubMed] [Google Scholar]
- Pope GC, Ellis RP, Liu CF, et al. Final Report to the Health Care Financing Administration under Contract Number 500-95-048. Waltham, MA.: Health Economics Research, Inc.; Feb, 1998. Revised Diagnostic Cost Group (DCG)/Hierarchical Coexisting Conditions (HCC) Models for Medicare Risk Adjustment. [Google Scholar]
- Pope GC, Liu CF, Ellis RP, et al. Final Report to the Health Care Financing Administration. Waltham, MA.: Health Economics Research, Inc.; Feb, 1999. Principal Inpatient Diagnostic Cost Group Models for Medicare Risk Adjustment. [PMC free article] [PubMed] [Google Scholar]
- Pope GC, Ellis RP, Ash AS, et al. Principal Inpatient Diagnostic Cost Group Models for Medicare Risk Adjustment. Health Care Financing Review. 2000 Spring;21(3):93–118. [PMC free article] [PubMed] [Google Scholar]
- Public Health Service and Health Care Financing Administration. International Classification of Diseases, 9th Revision, Clinical Modification. U.S. Government Printing Office; Washington, DC.: Sep, 1980. U.S. Department of Health and Human Services. [Google Scholar]
- Van de Ven WPMM, Ellis RR. Risk Adjustment in Competitive Health Plan Markets. In: Culyer AJ, Newhouse JP, editors. Handbook in Health Economics. North Holland: 2000. [Google Scholar]