Risk Selection and Benefits in the Medicare+Choice Program

Abstract

We estimate the relation between enhanced benefits offered by the Medicare+Choice (M+C) plan in 1999 and a measure of risk selection based on inpatient encounter data. Higher risks are attracted to plans that offer outpatient drug coverage. The risk score increases by 2.2 percent for drug coverage with an annual limit less than $800 and by 3.6 percent for coverage with a limit more than $800. However, some benefits such as dental coverage were related to favorable risk selection. If M+C plans competed on the basis of benefits and premiums, as they would if they could give untaxed premium rebates, benefits that attract high risks would be underprovided.

Introduction

M+C health plans accept the risk of providing a defined set of insurance benefits to an enrolled population in return for a prospective monthly payment from the Federal Government. In addition to the Federal Government payment, M+C plans may collect out-of-pocket premiums from enrollees. In 2001, 83 percent of all risk-plan enrollees were in plans that charged a premium (Pizer, Frakt, and Doksum, 2001). M+C plans also may offer enhanced benefits (e.g., coverage of eyeglasses and prescription drugs, or reduced cost sharing for covered services) that exceed the Medicare entitlement. Despite recent declines, almost all plans offer some enhanced benefits. For example, 87 percent of risk-plan enrollees had access to prescription drug coverage in 2000. Thus, competition for enrollees in the M+C program takes two forms: plans compete to keep their out-of-pocket premiums low and to offer benefits that enhance the Medicare entitlement.

The managed care industry has emphasized that coverage of benefits not available under traditional Medicare is an advantage of their product (American Association of Health Plans, 1999) and has argued against constraints on payment rates that might lead to reductions in benefits. Economists and policymakers normally would agree with the view that competition to provide low premiums and more benefits is good for consumers. Furthermore, if competition drives premiums down to the point where plans just make a normal profit, and if the enhanced benefits just cost what enrollees are willing to pay on the margin, economists would say that the M+C market is efficient. In an efficient market, no one could be made better off without making someone else worse off (Stiglitz, 2000).

But the M+C market does not work like a normal market. By law, M+C health plans can charge only one premium to all enrollees. In other words, for any given benefit package they offer, plans cannot separate their enrollees into classes and charge different premiums to each class according to any characteristic of the enrollees. This restriction has been imposed despite the very strong likelihood that some characteristics related to an enrollee's willingness to pay for benefits are also related to the cost of covered services. For example, an individual who expects to spend $500 per month on medications for high blood pressure will be more likely to buy insurance that covers prescription drugs at a given premium than another individual who has no routine drug expenses. The association between demand and cost is called adverse selection (Cutler and Zeckhauser, 1998), and it has consequences for the efficiency of health insurance markets when plans can charge only one premium. In the following section of the article we explain how adverse selection may lead to inefficiently low levels (possibly zero) of benefits that attract high risks.

Next, we estimate the relation between M+C plan benefits in 1999 and a measure of risk selection based on inpatient encounter data. We find that some benefits, outpatient drug coverage in particular, attract high risks. The implication is that M+C plans will offer too few of these benefits in an unsubsidized market. Public subsidies might be justified for plans to provide more of the benefits that attract high risks. But other benefits (e.g., dental coverage) are associated with favorable selection. Therefore, potential subsidies must be targeted to avoid these benefits. The policy of simply raising M+C payments to encourage provision of all benefits would not be efficient.

M+C Plan Benefits and Risk Selection

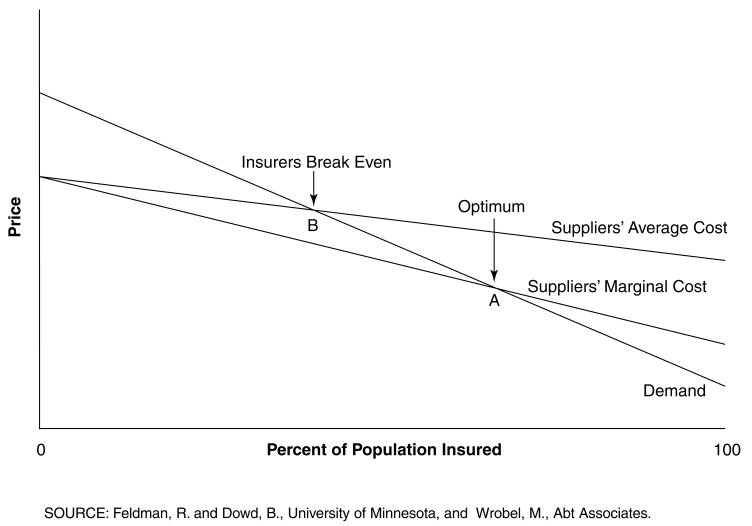
The relation between M+C plan benefits and risk selection can be illustrated by the example of outpatient prescription drugs, which are not covered by traditional Medicare. M+C plans may add this coverage as an enhanced benefit. Figure 1 shows a graph of the market for M+C drug coverage (measured by percent of the population insured).

Figure 1. Market for Drug Insurance with Adverse Selection and One Premium.

Suppose that sicker M+C enrollees have a stronger preference for prescription drug coverage. Then the average cost of drug coverage in Figure 1 will decline as a larger percentage of the population purchases drug coverage, because sicker enrollees will enroll before their less costly peers. Because plans cannot charge separate premiums for each risk class, they must sell drug coverage at a single premium (if they sell it at all). In order for the plan to break even—as would be the case in a competitive market—the single premium must be equal to the plan's average cost. But average cost is greater than the marginal cost of the next enrollee due to the previous enrollment of high-risk beneficiaries. This means that the next enrollee's willingness to pay is greater than marginal cost. It would be efficient for the next enrollee to buy drug coverage because his personal marginal benefit measured by his willingness to pay is greater than personal marginal cost. But he declines the coverage because his marginal benefit is less than the average cost (i.e., the premium that he must pay). This analysis shows that too few people will purchase drug coverage when there is adverse selection and the plan can charge only one premium.

In Figure 1, the marginal cost of drug coverage is less than average cost because of adverse selection. Plans break even at point B where demand equals average cost, but optimal coverage occurs at point A where demand equals marginal cost. Because B lies to the left of A, an inefficiently low percent of the population will purchase drug insurance in a competitive market.

If the plan could charge a separate premium for each risk class (e.g., higher premiums for those who use $500 of drugs per month), enrollees would purchase coverage if the marginal benefit were greater than their personal premium which, in a competitive market, would equal their marginal cost. This method of setting premiums is efficient but is not permitted by Medicare.

In the extreme case, the average cost of offering the benefit could exceed every enrollee's willingness to pay. The M+C plan would have to cancel the benefit entirely, even though some enrollees might be willing to pay more than their marginal cost. Thus, adverse selection leads to inefficiency in two ways: the percent of the market purchasing coverage is too small; and too little coverage—possibly none—is offered.

Public policies to reduce inefficiency in markets for voluntary benefits include onetime enrollment opportunities, subsidies for purchasing the coverage, risk-rated premiums, and making the drug benefit a mandated part of Medicare. Requiring onetime enrollment reduces the incentive for beneficiaries to wait until they become high risk before enrolling. Risk-rated premiums do not seem to be an option for Medicare. Consideration of mandated benefits is warranted when the efficient level of coverage is 100 percent, but less than 100 percent of the market signs up for voluntary coverage. If a universal benefit is mandated, it could be accompanied by subsidies for groups deemed to deserve public assistance in paying the premium (e.g., low-income beneficiaries).

The cost of subsidies in a prescription drug program for Medicare could be very large. The Congressional Budget Office (2002) estimates that the cost of a low-income subsidy under H.R. 4680 (passed by the House of Representatives in September 2000, but not considered by the Senate) would be $141 billion over the period from 2005 to 2012. Other recent proposals for Medicare prescription drug coverage also have large subsidy costs. However, President Bush has said that covering prescription drugs for the elderly will be among the legislative initiatives for his administration, and Republican control of both Houses of the 108th Congress makes passage of a prescription drug benefit for Medicare more likely. Thus, adverse selection related to drug coverage, and the cost of policies to overcome that problem, represent topics of great significance to Medicare policymakers.

Prior Research

A number of studies have examined the issue of adverse or favorable selection in Medicare health maintenance organizations (HMOs) (Brown and Hill, 1994; Virnig et al., 1998; Call et al., 1999; Maciejewski et al., 2001). However, very little research has examined the role of competition over the provision of enhanced benefits. Do the enhanced benefits offered by M+C plans attract more enrollees, and if so, are some benefits more appealing to healthier or to less healthy beneficiaries?

We know of only two studies of adverse selection into M+C plans that offer better benefits. These studies illustrate the two possible approaches—structural and reduced form—that can be used to detect adverse selection.

The structural approach is illustrated by Atherly's (2001) study of the demand for M+C plan enrollment. Atherly postulates that each enrollee has a utility function for plan benefits and premiums. If we index enrollees by the letter “i” and plans by “j,” then enrollee i's utility in plan j can be written as:

$${\mathrm{U}}_{\text{ij}}=\mathrm{\alpha }{\mathrm{P}}_{\mathrm{j}}+\mathrm{\beta }{\mathrm{X}}_{\mathrm{j}}+\mathrm{\gamma }{\mathrm{X}}_{\mathrm{j}}{\mathrm{R}}_{\mathrm{i}}+{\mathrm{u}}_{\text{ij}}$$ (1)

P_j is the premium for plan j, X_j indexes the benefits in plan j, R_i is the enrollee's health risk, α, β, and γ are coefficients to be estimated, and u_ij is a random error that represents the enrollee's unobserved and idiosyncratic valuation of the plan. If these errors are independently and identically distributed across plans with an extreme value distribution, then the parameters of the enrollee's utility function can be estimated by conditional logit analysis. The dependent variable, shown in equation (2), would be the probability that enrollee i joins plan j, or (Pi,j):

$$\mathrm{P}(\mathrm{i},\mathrm{j})=\frac{{\mathrm{e}}^{\alpha P_j+\beta X_j+\gamma X_j{R}_i}}{{\sum }_K{\mathrm{e}}^{\alpha P_k+\beta X_k+\gamma X_k{R}_i}}$$ (2)

The coefficients in (2) are estimates of the marginal utility of premiums and benefits. Hence, this model estimates the structure of the enrollee's utility function.

Economic theory suggests that the marginal utility of premiums, α, should be negative and the marginal utility of benefits, β, should be positive. The sign of γ provides a test for adverse selection related to benefits. If higher-risk enrollees have more utility from benefits, as they would if they more often use the benefits, then γ will be positive.

Atherly estimated the effect of individual enrollee's health status on the likelihood of choosing a plan with a prescription drug benefit. Using data from the Medicare Current Beneficiary Survey (MCBS), he interacted the enrollee's age (a proxy for poor health) with dummy variables indicating whether the plan had any prescription drug coverage and whether it had drug coverage with a total benefit more than $1,000 per year. The coefficient of (age × higher drug benefits) was significant and positive, indicating that older and presumably sicker enrollees prefer plans with generous prescription drug coverage. Atherly also found that diabetics were more likely to join plans that offer vision benefits. These results suggest that there will be too little enrollment in M+C plans with generous drug coverage and vision benefits. It is also likely that M+C plans will offer less than the optimal amounts of such benefits.

The second study to analyze adverse selection over benefits is by Buntin (2000). In contrast to Atherly's structural approach, Buntin estimates a reduced form model that looks for the consequences of adverse selection. If adverse selection exists, then plans that offer more generous benefits than their competitors should exhibit worse average risk. Buntin uses the average plan in the same county as the reference competitor for plan j (we will say more about the reference plan later). Buntin's model can be written as:

$${\mathrm{R}}_{\mathrm{j}}-{\mathrm{R}}_{\mathrm{a}}=\mathrm{\alpha }+\mathrm{\beta }({\mathrm{X}}_{\mathrm{j}}-{\mathrm{X}}_{\mathrm{a}})+{\mathrm{\varepsilon }}_{\mathrm{j}}$$ (3)

R_j is the risk in plan j, R_a is the risk of the average plan in the same county, and ε_j is a random error. The benefit variables on the right-hand side of (3) are measured as differences between plan j and the average plan. The coefficients α and β do not have the same structural interpretation as in Atherly's model—instead, they represent observed effects of benefits on risk in plan j.

Buntin did not have a direct measure of risk in M+C plans, so she used an indirect approach to estimate risk. First, she estimated a cost-prediction model for fee-for-service (FFS) Medicare beneficiaries in the MCBS. The dependent variable was the ratio of the beneficiary's actual Medicare reimbursement to their adjusted average per capita cost rate cell cost, and the independent variables were measures of beneficiary risk. Next, she matched the MCBS risk measures to questions on the Consumer Assessment of Health Plans Survey (CAHPS^®) that most closely matched them. CAHPS^® is administered to 600 enrollees in every M+C plan. Predicted cost ratios for CAHPS^® respondents were averaged to create a measure of risk for each M+C plan. This method relies on assumptions that the cost coefficients from FFS Medicare can be applied to Medicare M+C enrollees, and that a sample of 600 enrollees is sufficiently large to predict plan risk.

Buntin found little evidence that enhanced coverage of services (including a drug benefit) attracts unfavorable risks. However, she did find that risk was positively related to perceived plan quality and the size of the plan's specialist physician network, while it was negatively related to the copayment for specialists' visits and the size of the plan's primary care physician network.

Methods

We used both structural and reduced form approaches to estimate the effects of benefits on M+C plan risk, although only the latter approach was successful. Our sample is all M+C plans that operated in counties with more than one plan in 1999. By equating P(i,j) to the proportion of enrollees with risk status i in the county who chose plan j, we can estimate a grouped version of Atherly's structural model. The set of competing plans varies across counties, but we can designate any one of those plans (denoted by k) as a reference plan and calculate P(i,j)/P(i,k) or the proportion of enrollees with risk status i choosing plan j relative to plan k. Taking the natural logarithm of this ratio, we arrive at an equation that expresses the independent variables as differences between plan j's premium and benefits and those of the reference plan:

$$\text{ln}\left[\mathrm{P}(\mathrm{i},\mathrm{j})/\mathrm{P}(\mathrm{i},\mathrm{k})\right]=\mathrm{\alpha }({\mathrm{P}}_{\mathrm{j}}-{\mathrm{P}}_{\mathrm{k}})+\mathrm{\beta }({\mathrm{X}}_{\mathrm{j}}-{\mathrm{X}}_{\mathrm{k}})+{\mathrm{\gamma }\mathrm{R}}_{\mathrm{i}}({\mathrm{X}}_{\mathrm{j}}-{\mathrm{X}}_{\mathrm{k}})+({\mathrm{u}}_{\text{ij}}-{\mathrm{i}}_{\text{ik}})$$ (4)

Finally, if we assume that the coefficients in (4) do not differ across risk classes, we can estimate the relative proportion of all enrollees choosing plan j as:

$$\text{ln}\left[\mathrm{P}(\mathrm{j})/\mathrm{P}(\mathrm{k})\right]=\mathrm{\alpha }({\mathrm{P}}_{\mathrm{j}}-{\mathrm{P}}_{\mathrm{k}})+\mathrm{\beta }({\mathrm{X}}_{\mathrm{j}}-{\mathrm{X}}_{\mathrm{k}})+\mathrm{\gamma }\mathrm{R}({\mathrm{X}}_{\mathrm{j}}-{\mathrm{X}}_{\mathrm{k}})+({\mathrm{u}}_{\mathrm{j}}-{\mathrm{u}}_{\mathrm{k}})$$ (5)

R is a measure of the average risk in the plan's market area. Equation (5) is the structural model that we estimate in this article.

Although any plan could be chosen as the reference plan in equation (5), we followed the precedent of our previous work (Dowd and Feldman, 1994; Dowd, Feldman, and Coulam, 2003) by using the plan with the lowest out-of-pocket premium in the county as the reference plan. The low-cost plan has particular significance in competitive pricing proposals that peg the Federal Government's premium contribution to the lowest bid submitted by any plan in the county (Dowd, Coulam, and Feldman, 2000). In those proposals, the relative premium for a higher-cost plan is equal to its premium P_j, and thus the coefficient a in equation (5) can be interpreted as the change in ln[P(j)/P(k)] as the higher-cost plan raises its bid by one dollar. When the lowest premium was shared by two or more plans (usually tied at zero), we selected one of the lowest-premium plans at random as the reference plan. Randomly selecting different low-cost reference plans did not change the results of our models.

Equation (5) has a property known as “independence of irrelevant alternatives,” or IIA (McFadden, 1973), which means that the proportion of enrollees choosing plan j relative to the reference plan depends only on the benefits and premiums of those two plans.¹ IIA lets us ignore the premiums and benefits in all other plans when we estimate (5). However, IIA does not hold for the reduced-form model in equation (3), despite the fact that (3) can be derived from the structural demand function (2) (derivation of equation [3] is available on request from the authors).

The significance for our work (and Buntin's) is that selection of a single reference plan in equation (3) is an approximation for the benefits and premiums of all the competing plans. We relied on this approximation for two reasons. First, the number of competing plans differs across counties, so it would be difficult to construct the vector of competitors' benefits and premiums. Second, the number of premium and benefit variables in the extended model is very large, so the model would be extremely difficult to estimate. However, we tested the sensitivity of our approximation to differences in the characteristics of the omitted competitors. In these tests, we created several hypothetical choice models with three plans: plan j, the reference plan, and an omitted competitor. Then we varied the benefits in the omitted plan, making them more or less like those in plan j. As the benefits in the omitted plan improved, risk in plan j and the reference plan both fell, but the difference in risk between plan j and the reference plan was almost constant. These tests suggest that the advantages of using one reference plan in equation (3) outweigh the disadvantages of not considering the benefits and premiums in all competing plans.²

Data

We used the county as the geographic market area because M+C choices for each beneficiary are defined at the county level. Data on benefits and premiums were obtained from the 1999 Medicare Health Plan Compare. (Refer to CMS' Web site at medicare.gov/MPHCompare). Quarterly enrollment data for March 1999 came from the Medicare Managed Care Market Penetration for All Medicare Plan Contractors - Quarterly State/County/Plan Data Files. (Refer to CMS' Web site at cms.gov/healthplans/statistics). The benefit data were coded into meaningful categories (e.g., covered at all or amount of coverage). Binary (0, 1) indicator variables were created for observations with missing variable values. Mammography coverage, pap smear coverage, and hepatitis vaccine coverage were highly correlated, so we created an additive index in which each type of coverage was scored 1 for 100 percent coverage, and 0 for less than 100 percent coverage. (Details of other benefit coding algorithms are available on request from the authors.) Some benefits were dropped because they did not have adequate variance to study their effects on enrollment.

We used the M+C plan's lowest-priced benefit package to characterize its products in each county. This variable has a potential shortcoming in that plans that offer multiple benefit packages, including packages with enhanced high-option benefits, may experience differential selection that may bias our results. To control for possible bias, we included a variable in the risk model for the number of separate benefits packages that the M+C plan offers in each county. If offering more packages is associated with a greater likelihood that one of those packages has high-option benefits, we predict that the coefficient of number of packages will be positive.

We used several variables to measure outpatient prescription drug coverage, because this benefit has particular significance for both risk selection and for proposals to modernize the Medicare Program by adding a prescription drug benefit. The 1997 Balanced Budget Act mandated a demonstration (as yet not implemented) of competitive pricing for M+C plans with a minimum annual outpatient prescription drug benefit of $500. Local demonstration areas could set the limits at the market norm in their area.

We included two indicator variables for drug coverage with an annual cap of less than $800 in benefits (low drug coverage), and drug coverage with a cap more than $800 (high drug coverage), compared with no drug coverage. The median limit was approximately $800 for drug coverage over all M+C plans in 1999 (i.e., the national market norm). For plans with any drug coverage, we included the copayment for brand-name drugs, the copayment for generic drugs, and an indicator if the generic copayment was given as a percentage of the price.

We defined two indicators for staff and group-model HMOs (compared with the omitted category of independent practice associations) and another indicator for whether the plan offered a point-of-service (POS) product. Enrollees in POS products may obtain covered services from providers not in the plan's network, if they are willing to pay more out-of-pocket cost sharing.

In 1999, most M+C plans covered the Medicare Part A hospital copayment.³ However, because this practice was not universal, we included a variable in the model for the hospital copayment in plan j, relative to the low-priced plan in the county.

The dependent variable in the reduced form analysis was constructed from the plan's average risk, as measured by its principal inpatient diagnostic cost group(PIP-DCG) score.⁴ This method uses inpatient encounter data to place each enrollee into one of approximately 12 diagnosis-based payment groups, each corresponding to a range of expected health expenditures (Greenwald et al., 1998). The method also uses age, sex, prior disability status, and entitlement to State payments for Medicare to derive a predicted payment. This measure of M+C plan risk was made available to the authors under a CMS research contract to support the agency in its work on competitive pricing. Its significance here is that it has not been available for previous studies of adverse selection.

Equation (3) suggests that the dependent variable should be calculated as the difference between risk in plan j and risk in the reference plan. Buntin (2000) used the arithmetic difference, but we believe the logarithmic difference in risk is more appropriate. The reason is that the PIP-DCG risk-adjustment factor was designed to multiply the plan's baseline payment rate. CMS's January 15, 1999, notice of M+C risk factors published the incremental PIP-DCG factors in dollar amounts, using a baseline payment per enrollee of $5,100, which is the mean predicted expenditure for FFS beneficiaries during the 1996 calibration year. The incremental factors were later changed to multiplier coefficients (e.g., $5,610 became a coefficient of 1.10). Refer to CMS' Web site at cms.gov/healthplans/rates/2000 for more details. We refer to the dependent variable, measured as a logarithmic difference, as “Plan Risk.”

An anonymous referee noted that the average value of plan risk was 0.0093, suggesting that the average risk score of the plan under consideration is less than 1 percent different from the average risk of the reference plan. While the mean is close to zero, plan risk ranges from −0.174 to +0.275, and the distribution of plan risk is approximately normal, thus facilitating significance tests of the estimated coefficients in our model.

In our structural model, average risk was measured by the enrollment-weighted average PIP-DCG score for all M+C enrollees in the county. Risk is measured at the population level because we want to know whether people who had high-cost hospitalizations in 1998 are more likely to join plans with generous benefits in 1999. The enrollment data used to calculate average risk were from March 1999. The plans' premiums and benefits were determined in September 1998. Thus, there is some overlap with the risk-assessment period. Ideally, we would not want any overlap between the risk assessment period and the enrollment period. However, it is widely believed that the inpatient discharge data submitted by M+C plans in the first year of data collection (July 1997 to June 1998) were inaccurate. CMS undertook attempts to validate and improve the data in the second year (Harlow, 2000). In order to obtain the most accurate data on PIP-DCG scores, we used the second risk assessment period from July 1998 to June 1999.

Results

Table 1 shows the variables used in the analysis and their definitions. All independent variables are measured as differences between the value for plan j and the value for the reference plan.

Table 1. Variable Definitions.

Variable	Definition
Market Share	Natural Log (market share for the jth M+C plan/market share of the lowest-priced plan in the county)
Plan Risk	Natural Log (PIP-DCG score for the jth M+C plan/PIP-DCG for the lowest-priced plan in the county)
Premium	Monthly out-of-pocket premium
Chiropractor	Indicator = 1 if chiropractic services are covered beyond basic Medicare benefit and = 0 if chiropractic services are not covered beyond basic Medicare benefit
Dental	Indicator = 1 if some type of preventive dental exam coverage is provided and = 0 if no coverage, you pay 100 percent
Eyeglasses	Indicator = 1 if there is some type of coverage for eyeglasses/contact lenses and = 0 if there is no coverage, you pay 100 percent
Preventive	Sum of mammography coverage, pap smear coverage, and hepatitis vaccine coverage, where each = 1 if 100 percent covered and = 0 if not 100 percent covered
Laboratory	Indicator = 1 if laboratory services are 100 percent covered and = 0 if laboratory services are not 100 percent covered
Laboratory Missing	Indicator = 1 if laboratory is missing and = 0 if laboratory is not missing
Outpatient Visits	Indicator = 1 if outpatient hospital visits are 100 percent covered and = 0 if outpatient hospital visits are not 100 percent covered
Outpatient Missing	Indicator = 1 if outpatient visits is missing and = 0 if outpatient visits is not missing
Occupational/Physical Therapy	Indicator = 1 if occupational/physical therapy visits are 100 percent covered and = 0 if occupational/physical therapy visits are not 100 percent covered
Rehabilitation Visits	Indicator = 1 outpatient rehabilitation visits are 100 percent covered and = 0 if outpatient rehabilitation visits are not 100 percent covered
Services Outside U.S.	Indicator = 1 if services outside of the U.S. may be covered and = 0 if services outside of the U.S. are not covered
Rx Brand Name Copay	Copayment in dollars for brand-name prescription drugs
Rx Brand Name Copay Missing	Indicator = 1 if Rx brand name copay is missing and = 0 if Rx brand name copay is not missing
Rx Generic Copay	Copayment in dollars for generic prescription drugs
Low Drug Coverage	Indicator = 1 if prescription drugs are covered with an annual limit less than $800 and = 0 otherwise
Rx Copay Percentage	Indicator = 1 if Rx generic copay is a percentage and = 0 otherwise
High Drug Coverage	Indicator = 1 if prescription drugs are covered with an annual limit over $800 and = 0 otherwise
Physical Exam Copay	Copay in dollars for physical examination
Podiatry	Indicator = 1 if podiatry services are covered beyond basic Medicare benefit and = 0 otherwise
Physician Visit Copay	Copayment in dollars for a visit to your personal physician
Skilled Nursing	Indicator = 1 if you do not need to be in the hospital for 3 consecutive days before going to skilled nursing care and = 0 otherwise
X-Rays	Indicator = 1 if X-rays are 100 percent covered and = 0 if X-rays are not 100 percent covered
Point of Service	Indicator = 1 if the M+C plan offers a point-of-service option and = 0 otherwise
Staff Model	Indicator = 1 if the M+C plan is a staff model HMO and = 0 otherwise
Group Model	Indicator = 1 if the M+C plan is a group model HMO and = 0 otherwise
Number of Packages	Number of separate benefit packages offered by the M+C plan in the county
Hospital Inpatient Copay	Hospital inpatient copy in dollars

NOTES: M+C is Medicare+Choice. PIP-DGG is principal inpatient diagnostic cost group. HMO is health maintenance organization.

SOURCE: Feldman, R. and Dowd, B., University of Minnesota, and Wrobel, M., Abt Associates Inc.

Our first analysis estimated the structural demand equation (5). We found that the model including interactions between county risk and plan benefits was highly unstable with coefficient estimates strongly dependent on which benefit variables were included or excluded. Some of the interaction terms had little variance, so we excluded them and focused on a smaller set that kept most of the important variables (e.g., drug coverage). The results were still unstable. Therefore, it appears that the structural model of adverse selection cannot be estimated with our plan-level data, although Atherly (2001) had more success in estimating the model with individual data from the MCBS.

The next analysis used plan risk (the logarithmic difference of risk in plan j compared with risk in the lowest-price plan) as the dependent variable. We estimated the model three times, for three different random draws of the lowest-price plan when there were ties. The results for individual coefficients were very similar, so in Table 2 we present the model that explains the most variance in plan risk.

Table 2. M+C Plan Risk Equation.

Variable	Coefficient	Standard Error	Z-Statistic	Significance Level
Constant	0.8402E-03	0.2159E-02	0.389	0.6972
Premium	0.4118E-03	0.1020E-03	4.039	0.0001
Chiropractor	0.1467E-01	0.3674E-02	3.994	0.0001
Dental	-0.1506E-01	0.3013E-02	-4.998	0.0000
Eyeglasses	0.1719E-01	0.3909E-02	4.397	0.0000
Preventive	0.6595E-02	0.1853E-02	3.559	0.0004
Laboratory	-0.1614E-02	0.8627E-02	-0.187	0.8516
Laboratory Missing	-0.4328E-01	0.2340E-01	-1.849	0.0644
Outpatient Visits	0.6770E-02	0.3812E-02	1.776	0.0757
Outpatient Missing	0.6587E-01	0.2219E-01	2.968	0.0030
Occupational/Physical Therapy	0.1962E-01	0.4066E-02	4.825	0.0000
Rehabilitation Visits	0.3771E-02	0.3296E-02	1.144	0.2525
Services Outside US	0.8727E-02	0.2481E-02	3.518	0.0004
Rx Brand Name Copay	0.1286E-03	0.3124E-03	0.412	0.6806
Rx Brand Copay Missing	0.3692E-01	0.8465E-02	4.362	0.0000
Rx Generic Copay	-0.5207E-02	0.6920E-03	-7.524	0.0000
Rx Copay Percentage	-0.3868E-02	0.1196E-01	-0.323	0.7464
High Drug Coverage	0.3506E-01	0.8563E-02	4.094	0.0000
Low Drug Coverage	0.2157E-01	0.7730E-02	2.791	0.0053
Physical Exam Copay	0.2276E-02	0.5095E-03	4.466	0.0000
Podiatry	-0.1295E-01	0.3222E-02	-4.018	0.0001
Physician Visit Copay	0.5407E-03	0.6349E-03	0.852	0.3944
Skilled Nursing	-0.1691E-01	0.5027E-02	-3.364	0.0008
X-Rays	-0.4335E-01	0.8841E-02	-4.904	0.0000
Point of Service	0.1041E-01	0.4389E-02	2.373	0.0176
Staff Model	0.2834E-01	0.5199E-02	5.450	0.0000
Group Model	0.4647E-03	0.3216E-02	0.144	0.8851
Number of Packages	0.3781E-02	0.1966E-02	1.923	0.0544
Hospital Inpatient Copay	0.2369E-04	0.2887E-04	0.820	0.4120

NOTES: E-nn means multiply the estimated coefficient by 10 to the −nn power. For example, E-02 = 0.01 Number of observations = 1,251 Adjusted R-square = 0.2032.

SOURCE: Feldman, R. and Dowd, B., University of Minnesota, and Wrobel, M., Abt Associates Inc.

We found that better levels of the following benefits attract higher-risk enrollees: coverage of chiropractic services, eyeglasses, preventive care, occupational/physical therapy, coverage of care outside the U.S., and both low and high drug coverage. Coverage of outpatient visits was significant at the 0.0757 level of confidence. Higher generic drug copayment (worse coverage) attracted lower risks, so better levels of this benefit are also considered to attract higher risks.

The importance of adverse selection can be illustrated by focusing on the coefficients of outpatient drug coverage (b = 0.02157 for low coverage and b = 0.03506 for high coverage). This means that a plan with the same baseline risk as the reference plan would become approximately 2.2 percent riskier than the reference plan if it introduced low drug coverage and 3.6 percent riskier if it introduced high drug coverage. At a baseline risk ratio of 1.0, the effect of low drug coverage is approximately e^.02157 = 1.0218; the effect of high drug coverage is e^.03506 = 1.0357. These effects do not change at the third decimal place if we use Kennedy's (1981) correction for the interpretation of dummy variables in semilogarithmic equations. Because the PIP-DCG payments are determined by a multiplier to the baseline payment of $5,100, this implies that the plan's annual payment per enrollee in a fully implemented risk-adjustment system would increase by $111 for low drug coverage and by $182 for high drug coverage. A PIP-DCG score of 1.0218, as in low drug coverage, implies a payment increase of 0.0218 × $5,100 = $111. A score of 1.0357 implies an increase of 0.0357 × $5,100 = $182.

The following coefficients show that in some cases better benefits attract lower risks: dental coverage, podiatrist coverage, skilled nursing coverage, and X-ray coverage. Higher physical examination copayment is also placed into the category of benefits that lead to favorable selection. Some of the coefficients indicate that favorable selection related to benefits may be large. For example, the size of the favorable selection effect for X-ray coverage appears to be larger than the adverse effect of offering drug coverage.

Offering a POS product is associated with adverse risk selection. This is not surprising, because higher-risk enrollees should place more value on being able to see non-network providers. However, staff-model HMOs (e.g., Kaiser) have worse risks than independent practice associations, which offer enrollees greater freedom of choice and therefore, should be more attractive to higher risks. It may be the case that enrollees in staff-model HMOs are more loyal to their providers, or they may have aged into the same M+C plan that covered them when they were employed. The indicator for group-model HMOs was not significant.

Some of the benefit variables did not have significant effects on risk selection. Among these were coverage for laboratory services and outpatient rehabilitation visits, and copayments for brand-name drugs, physician office visits, and hospital inpatient care. The last finding is somewhat surprising—it suggests plans that offer good hospital benefits do not attract high-cost enrollees.

The number of benefit packages offered by an M+C plan had a positive (at P = 0.0544), but small impact on risk selection. This finding suggests that the additional benefit packages are likely to have high-option benefits and, thus are likely to attract higher risks.

Plans with higher premiums attract higher risks, other things held equal. One explanation for this finding is that plans with higher premiums have better benefits that attract higher risks, and we have not included all relevant benefits in the model. An example of an omitted benefit may be the size and quality of the plan's physician network.

Another explanation for the positive premium coefficient may be the method we used to construct the variables, with the lowest-premium plan as the reference plan. It is likely that high-premium plans have better benefits than the reference plan, and if better benefits attract high risks, they also will have higher risks than the reference plan.⁵ Should a high-premium plan raise its premium, it will lose disproportionately more low-risk enrollees who are less attracted to benefits, leaving the high-premium plan with a worse risk score. This conclusion (which is demonstrated formally in an appendix available on request from the authors) would hold even if all risk types had the same utility for premiums and all relevant benefits were included in the model.

To determine if the second explanation for a positive premium coefficient was plausible, we reversed the order of the reference plans and selected the highest-priced plan as the reference plan. Despite this change, we continued to find evidence that plans with higher premiums have worse risks. The signs and significance levels of other variables (including prescription drug benefits) generally were unaffected by this change. Thus, we think that the more likely explanation for the positive premium coefficient is omitted plan quality variables. This explanation would be consistent with Buntin's (2000) findings.

Discussion

We followed Buntin's (2000) approach by estimating a reduced form model of M+C plans' risk as a function of the plans' benefits and premiums. In contrast to Buntin's results, we found significant adverse risk selection related to several benefits. Drug coverage and drug coverage with a limit more than $800 both were more attractive to higher risks, as were several other benefits. The findings with respect to drug coverage are consistent with Atherly's (2001) analysis of individual risk selection. However, other benefits, including dental coverage and skilled nursing care beyond the standard Medicare benefit, were related to favorable risk selection. It is difficult to draw conclusions from our findings.

It is also difficult to determine from our findings whether too many or too few enhanced benefits are provided in the current M+C marketplace. If all M+C plans competed on the basis of benefits and premiums, we could say the benefits that attract high risks (e.g., drug coverage) would be underprovided, and benefits that attract low risks would be overprovided. However, even with recent payment cutbacks, some M+C plans do not compete on the basis of premiums. Zero-premium plans exclusively use benefits to attract enrollees, so it could be the case that these plans overprovide all types of enhanced benefits (Pizer, Frakt, and Feldman, 2003).

If M+C payment policy continues to push more plans toward charging premiums, our results will have significance for Medicare policymakers. The findings imply that subsidies for enhanced coverage should be targeted toward benefits that attract high risks. On this basis, a subsidy for enhanced drug coverage would be warranted. A subsidy could be implemented in two ways: by adjusting the Federal Government payment to the plan, as is currently done in the M+C program; or by using an administrative mechanism similar to those that would provide subsidies for low-income enrollees in H.R. 4680 and other proposals (Congressional Budget Office, 2002). Such proposals involve determining who would be eligible, how much the Federal Government would pay, and how the subsidy would be shared between the Federal and State governments.

If payments to M+C health plans were fully and accurately adjusted for enrollee risk, additional subsidies would not be needed. However, at this time only 10 percent of plans' payments are risk adjusted (this percentage is scheduled to increase to 30 percent on January 1, 2004). Our findings will be relevant at least for the near term. Conversely, the findings suggest that plans should be discouraged from offering benefits that attract favorable risks, possibly by reducing payments to plans that offer such benefits.

Our work is subject to several significant methodological qualifications. First, all types of benefits and the plans' premiums are likely to be endogenous. It was not possible to eliminate this bias, given the large number of potentially endogenous variables and the limited number of exogenous instruments available to this study. Second, the benefit measures were derived from data on CMS' Web site (Centers for Medicare & Medicaid Services, 2003). We cannot verify the accuracy of the plans' reported benefits. Furthermore, our coding scheme may have introduced measurement error into some of the variables, and some benefits did not have enough variation to study their effects. Thus, our results depend on the current M+C market environment and may not generalize if some plans withdraw benefits in the future.

From a policy perspective, the results are dependent on a particular measure of risk that is limited to the future cost implications of certain episodes of inpatient hospital care. It may not be sensitive to benefits that primarily affect outpatient spending. CMS is currently designing a risk adjuster that will be neutral to diagnoses identified in inpatient or outpatient settings. CMS is required by statute to adjust payments for M+C organizations based on the health status of Medicare beneficiaries. As of January 1, 2004, a new risk adjustment model will be introduced that is based on approximately 61 disease groups that are statistically and clinically significant for the Medicare population. The model is designed to be site neutral because it does not pay differentially for diagnoses identified in inpatient or outpatient settings. Refer to CMS' Web site at cms.hhs.gov/healthplans/riskadj/FactSheet.asp for more details. Another important point is that our measure of risk does not include the differential spending by high-risk enrollees on the prescription drugs themselves. Therefore, our findings only show that prescription drug coverage attracts enrollees with high non-drug expenses, as measured by the plan's PIP-DCG score.

Despite these qualifications, we believe that there is evidence of both favorable and unfavorable risk selection related to M+C plan benefits. The patterns of selection have implications for M+C plans and for public policy to subsidize the provision of outpatient prescription drug benefits in a competitive market environment for M+C health plans.