Prospective Payment for Medicare Inpatient Psychiatric Care: Assessing the Alternatives

Abstract

This article reports the findings of an empirical analysis of per case and per diem models of prospective payment for Medicare inpatient psychiatric care. Quantitative measures are presented that show the improvement of a per diem model over a per case model. The research supports the viability of per diem prospective payment and identifies directions for future research that would refine current per diem models.

Introduction

When the Medicare inpatient hospital prospective payment system (PPS) was implemented in 1983, psychiatric care provided in specialty psychiatric hospitals and certified psychiatric units (CPUs) of general hospitals was exempted because of concerns that the diagnosis-related groups (DRGs) were not adequate for psychiatric cases. The research subsequently undertaken did not support per case (per discharge) prospective payment because it failed to develop a patient classification system sufficiently successful in explaining variation in the cost of psychiatric cases. Twenty years later, Medicare still pays for psychiatric care in the DRG-exempt facilities under the largely cost-based system created in the 1982 Tax Equity and Fiscal Responsibility Act (TEFRA).

A recent article by Lave (2000) cites 2 key reasons for the limited success of the research that has attempted to identify patient characteristics that explain psychiatric cost differences. First, most systems have relied on diagnosis as the primary classification variable because it is available in administrative data, and diagnosis has less to do with the cost of psychiatric care than factors unavailable in administrative data. Second, it is difficult to measure treatment costs of individual patients because routine cost (largely nursing and other common services furnished on a hospital unit) is a large proportion of total psychiatric costs. Under Medicare cost reporting conventions, all patients within the same facility are assigned the same routine per day cost. As a result, patient characteristics will only explain cost variation to the extent that facilities with different cost levels treat different proportions of patients with identifiable characteristics, such as age and sex.

Although difficulties have been encountered in developing an inpatient psychiatric PPS based on patient characteristics, there are valid reasons for emphasizing patient characteristics. A basic principle of Medicare prospective payment has been that payment incentives should not influence the setting in which care is provided. Hence patient, rather than facility, cost differences should be the basis for differentiating payments. Paying higher rates to CPUs within general hospitals, whose costs are generally higher than those of freestanding psychiatric hospitals, would violate this principle. Other facility characteristics are inappropriate payment variables because they would inhibit incentives for efficient care delivery. For example, adjusting per diem payments for differences in the occupancy rate would mean paying higher rates to facilities with lower occupancy.

As early as 1986, it was proposed to deal with the limitations of per case PPS by paying prospectively determined per diem rates (rather than per case rates) that decline across blocks of higher lengths of stay (LOS) (Frank and Lave, 1986). The most recent mandate to develop a PPS for inpatient psychiatric care in the 1999 Balanced Budget Refinement Act (BBRA) effectively acknowledges the lack of success of the prior research efforts to develop a per case system and adopt a per diem approach. In principle, it should be easier to account for case level variation in resource use with a per diem system. Whereas a per case system must account for differences in both LOS and per diem resource intensity, a per diem system automatically adjusts for differences in LOS and only needs to account for variation in per diem resource intensity.

Renewed research on payment for inpatient psychiatric care is particularly timely for several reasons. Most evident is the need to develop a per diem system to respond to the BBRA mandate. However, it is also useful to re-examine the feasibility of a per case system, because many changes have occurred in the delivery of this care because most of the research on per case systems was conducted in the 1980s. The introduction of new medications, which dramatically expanded the use of medications, have facilitated community placement for persons with serious and persistent mental illness. LOS in inpatient psychiatric care has declined substantially in all types of psychiatric facilities. During the 1990s, managed care accelerated these trends resulting in the closure of many psychiatric hospitals. Managed care directly affected patients covered by private insurance and Medicaid. Managed care's impact on Medicare beneficiaries occurred primarily by inducing changes in practice patterns.

The BBRA mandate was the stimulus for three recent studies: CMS contracted with RTI International, to develop measures of patient-specific per diem cost that improve on previously available cost measures using a patient sample from 40 psychiatric facilities (Cromwell et al., 2003). RTI also collected individual patient characteristics information beyond what is available in current administrative records. Under a second study funded by CMS, Fries developed a survey instrument that CMS could use to collect supplemental patient data (Federal Register, 2003). The American Psychiatric Association engaged The Health Economics and Outcomes Research Institute (THEORI) of the Greater New York Hospital Association to test the feasibility of using available administrative information to develop a per diem payment system (Heller and Vaz, 2001).

This article complements other recent research by comparing alternative per diem prospective payment models with per case payment. We assess empirically how well the per diem approach, by automatically adjusting for LOS differences, addresses the problem that thwarted prior attempts to pursue a per case PPS. Unlike the RTI study, we are constrained by the same data limitations that have affected most of the research over the past 20 years because we use currently available Medicare administrative data. However, our results are not limited to a sample of psychiatric facilities, but include all Medicare certified hospitals and units. Our analysis of per diem cost variation is similar to that of THEORI, but by explicitly comparing per case and per diem systems, we elucidate the differences between the two approaches. Perhaps most importantly, our results have implications for future research on refinements of psychiatric PPS.

The next section of this article provides background data on per case and per diem costs for the major types of facilities that provide inpatient psychiatric care to Medicare beneficiaries. We also estimate the relative contributions of variation in LOS and per diem cost to variation of cost per case and discuss the types of factors responsible for variation in the duration versus the daily intensity of resource use. The remainder of the article reports our analysis of payment alternatives—the data, our modeling of costs and payments, and the estimated impacts of simulated payment systems.

To briefly summarize our findings, variation in resource use at the case level remains large and difficult to explain despite the large declines in inpatient LOS that have occurred since the late 1980s. As a result, even a simple per diem system with only a wage adjustment achieves substantial improvement in matching payments and costs at the case level. The simple per diem system can be improved by the addition of a limited number of variables commonly found in Medicare PPS, together with a modest outlier policy. However, the most powerful explanatory variables (facility size and occupancy rates) are not desirable choices for inclusion in a per diem payment system because of their potentially perverse incentive effects.

Background

Per case and per diem costs vary widely among inpatient psychiatric facilities. Table 1 shows these cost measures for the three types of freestanding psychiatric hospitals and certified (distinct part) units of general hospitals subject to the TEFRA payment system for the services they provide to Medicare beneficiaries. In 2002, there were 1,436 certified units and 493 freestanding hospitals (Centers for Medicare & Medicaid Services, 2003). Approximately one-half of the freestanding hospitals are private for-profit institutions.

Table 1. Medicare Admissions, Length of Stay, and Costs, by Type of Inpatient Psychiatric Facility.

Measure	Psychiatric Hospitals			Certified Psychiatric Units
	Non-Profit	For-Profit	Public
Admissions	75,899	27,753	23,343	340,377
Length of Stay (Days)
Mean	11.8	12.3	21.9	11.6
Standard Deviation	9.6	12.0	24.0	10.3
Median	9	9	13	9
Cost Per Case
Mean	$5,305	$6,525	$8,428	$7,136
Standard Deviation	4,549	6,670	9,311	6,481
Median	4,062	4,547	4,955	5,364
Cost Per Day
Mean	456	537	410	638
Standard Deviation	131	162	140	192
Median	428	516	362	600

SOURCE: Cotterill, P.G. and Thomas, F.G.: Data from the 1999 MedPAR 100 percent file of exempt hospital psychiatric discharges.

Since cost per case is the product of cost per day multiplied by LOS, LOS information is also included in Table 1. In 1999, mean per case costs ranged from a high of $8,428 for public psychiatric hospitals to a low of $5,305 in for-profit hospitals. Most of this difference is due to the much higher mean (Medicare covered) LOS in public hospitals (21.9 days versus 11.8 days). The longer LOS of public hospitals is noteworthy because there is relatively little difference in LOS among the other three types of facilities. Excluding the public hospitals, per case and per diem costs follow the same rank order: the certified units are most costly, the for-profit hospitals are least expensive, and the non-profits are inbetween.

There are important differences between the factors that produce variation in LOS—duration of resource use—and the factors responsible for variation in the cost per day—intensity of resource use. The LOS depends on how fast a patient responds to a course of treatment and other factors that influence the time required to stabilize the crisis that triggered the inpatient admission. In addition, the perceived ability of a patient to cope outside the facility may influence the duration of the inpatient stay, which also may be influenced by the availability of necessary community supports.

By comparison, daily resource intensity depends on the intensity of the service delivered and the composition of staff required to treat a patient. Patient characteristics such as the inability to perform activities of daily living and the need for one-to-one observation are among the factors that influence these staffing needs. Ancillary services also vary in daily intensity depending on both the psychiatric and medical needs of the patient. Average daily ancillary intensity is likely to be greater for shorter LOS as many laboratory and other diagnostic services occur early in the stay. Daily resource intensity also depends on facility factors that determine the amount of fixed cost allocated to each day of care, such as the size or scale of the facility (which determines whether the facility is able to take advantage of economies of scale) and the occupancy rate (which determines how efficiently the facility uses its existing resources). Especially relevant for CPUs are the accounting statistics that determine the amount of overhead costs from the entire hospital that are allocated to the CPU. Although we think that the effect of size on cost per day is largely economic, a correlation between size and a variety of patient characteristics could also play a role.

Method of Analysis

The challenge in designing a PPS is to find direct or indirect measures that capture sources of cost variation that facilitate access to needed care; induce appropriate patterns of patient care; promote the efficient delivery of care; provide a level playing field among types of facilities; and are not easily gamed to generate higher payment levels unaccompanied by any benefits in care provided.

Regression analysis was used to identify patient and facility characteristics that explain variation in per case and per diem costs. Using the results of the regression analysis, we developed and simulated several hypothetical payment systems:

• Model 1—A per case payment system using regression coefficients for selected variables from our per case cost regression.

• Model 2—A simple single rate per diem payment system that automatically pays for LOS differences, but contains no adjustments to the per diem rate other than the hospital wage index.

• Model 3—A per diem system with additional rate adjustments drawn from our cost per day regression.

• Model 3a—Model 3 with the addition of outlier payments.

• Model 4—Another per diem system with facility adjustments that do not meet the criteria cited earlier for inclusion in a PPS.

We evaluated the payment systems using two sets of measures. First, we regressed per case costs on per case payments to determine the degree of correspondence between per case payments and costs. Comparing Model 1 to Model 2 indicates the improvement associated with automatically adjusting for LOS differences (Frank and Lave, 1986). Comparing Model 2 to Model 3 shows the additional refinement associated with the addition of generally accepted payment variables to the per diem system. This comparison provides a measure of the benefits of a per diem system that can be achieved with currently available data. Finally, Models 3, 3a, and 4 tell us the relative improvements in matching payments and costs attributable to outlier payments, compared with the addition of generally unacceptable facility type payment variables such as size and occupancy. This comparison provides a barometer of the prognosis for future payoffs from attempts to further refine a per diem system.

As a second evaluation tool, we present payment to cost ratios for various groups of facilities under the different payment systems. This analysis complements the regression results by showing the types of facilities that face different degrees of correspondence between their payments and costs under the alternative systems.

Cost Data

We computed per case and per diem costs for each Medicare inpatient psychiatric admission, inclusive of routine operating, ancillary, and capital components using information from a 20-percent sample of 1999 MedPAR claims and matching 1999 Medicare cost reports. The method used is a standard accepted method commonly used to construct a Medicare cost per discharge for inpatient acute care (Newhouse, Cretin, and Witsberger, 1989). For each MedPAR inpatient psychiatric stay, routine costs were estimated by multiplying routine cost per day from the facility's Medicare cost report by the number of Medicare covered days on the MedPAR stay record. Ancillary costs were estimated by multiplying each departmental cost to charge ratio by the corresponding ancillary charges on the MedPAR stay record. Total cost per case was calculated by summing routine and ancillary costs for the stay. Total cost per day was calculated by dividing the total cost per case by the number of Medicare covered days in the stay. As noted earlier, the data are potentially limited for the purpose of determining the extent to which differences in patient characteristics influence per diem cost of inpatient psychiatric care.

The limitation results from Medicare cost accounting practice, under which routine per diem costs do not vary among patients within a facility.¹ That is, a patient requiring intensive staff attention is assigned the same routine cost as a patient requiring little staff attention. Although this limitation applies to routine costs for all types of Medicare inpatient care, it assumes heightened importance for psychiatric care because routine costs represent approximately 90 percent of total costs. As a result, our cost measure may fail to capture a major source of variation in routine cost attributable to differences in patient characteristics.

This limitation does not apply to ancillary costs because they can be measured at the patient level using Medicare claims as reported in MedPAR. However, there are differences in charging practices between freestanding psychiatric hospitals and CPUs that affect our measurement of ancillary costs. For example, there are approximately 169 hospitals in our data that do not bill separately for ancillary charges; the majority of these all-inclusive rate providers are State psychiatric hospitals. Also, emergency room (ER) charges for a patient admitted to a CPU via the ER of a general hospital appear on the claim filed for the psychiatric unit. However, inpatient claims from a freestanding psychiatric hospital would contain no ER charges because these hospitals do not generally operate ERs.

Cost Regressions

Cost regressions were run using a 20-percent sample of approximately 90,000 discharges from inpatient psychiatric facilities in 1999. Our dependent variables were the natural logarithms of per case and per diem costs. The cost variables were transformed to logarithms to correct for the right skewness of the cost distributions. This section gives a brief summary of the independent variables that were included in the regressions from which our hypothetical payment systems were constructed. As noted previously, our analysis is limited to variables available in Medicare administrative data. The complete regression results can be found in Table 2.

Table 2. Case-Level Inpatient Psychiatric Cost Regressions, Based on 1999 Data.

Independent Variable	Dependent Variable
	ln (Cost/Case)		ln (Cost/Day)		ln (Cost/Day)
	Coefficient	t	Coefficient	t	Coefficient	t
Wage Index: Ln 1999 Wage Index	0.849	44.99	0.664	108.790	0.670	124.33
Rural Location Indicator	0.175	20.24	0.149	53.120	0.023	9.03
Size: Ln ADC	NA	NA	NA	NA	-0.172	-164.58
Occupancy: Ln Occupancy Rate	0.018	1.88	-0.279	-88.520	-0.126	-42.95
Teaching: Ln (1+ Residents to ADC)	0.402	12.53	0.523	50.340	0.598	65.17
Age Over 65 indicator	0.398	64.48	0.126	62.090	0.076	42.09
Length of Stay Indicators
1 Day	NA	NA	0.227	50.070	0.204	50.91
2-4 Days	NA	NA	0.116	46.300	0.092	41.45
5-8 Days	NA	NA	0.049	23.210	0.032	17.26
Comorbidity Indicators
HIV	-0.056	-1.38	0.081	6.200	0.077	6.66
Hemophilia	0.045	0.26	0.122	2.160	0.137	2.74
Tracheostomy	-0.197	-1.48	0.105	2.440	0.064	1.70
Psychiatric	0.148	3.80	0.032	2.500	0.025	2.24
Infectious Disease	0.099	4.22	0.068	8.990	0.050	7.48
ESRD Renal Failure Acute	0.021	0.36	0.090	4.780	0.071	4.28
ESRD Renal Failure Chronic	0.065	2.28	0.109	11.840	0.078	9.54
Malignant Neoplasms	0.033	1.07	0.089	9.030	0.065	7.48
Diabetes	0.199	3.61	0.105	5.870	0.069	4.36
Severe Malnutrition	0.216	2.20	0.114	3.610	0.101	3.62
Chemical Dependency	-0.067	-2.81	0.015	1.990	0.018	2.60
Heart and Rheumatic Fever	0.154	1.57	0.150	4.730	0.129	4.62
Atherosclerosis with Gangrene	0.381	1.68	0.182	2.480	0.171	2.63
Chronic Respiratory Failure	0.106	3.36	0.107	10.490	0.079	8.78
Colostomy	0.172	3.56	0.108	6.910	0.070	5.06
Osteomelitis Gangrene	0.074	1.51	0.114	7.210	0.082	5.90
Poison	-0.292	-6.97	0.136	9.990	0.096	8.04
Diagnosis Related Group (DRG) Indicators
424 Procedure Principal Group Indicator	0.690	14.42	0.206	13.280	0.173	12.62
425 Acute Adjustment Reaction	-0.260	-10.75	0.092	11.730	0.064	9.20
426 Depressive Neurosis	-0.455	-32.62	-0.003	-0.700	-0.008	-1.92
427 Neurosis, Except Depressive	-0.462	-19.28	0.005	0.690	0.006	0.89
428 Disorders of Personality	-0.219	-7.21	0.029	2.900	0.027	3.13
429 Organic Disturbances	0.029	2.93	0.021	6.450	0.015	5.19
431 Childhood Disorders	-0.131	-2.86	-0.002	-0.160	-0.015	-1.14
432 Other Mental Disorders	-0.184	-1.89	-0.070	-2.220	-0.024	-0.87
433 Alchohol/Drug Use, LAMA	-1.072	-24.09	-0.120	-8.330	-0.081	-6.34
521 Alcohhol/Drug Use, W/CC	-0.322	-13.93	0.027	3.630	0.031	4.76
522 Alchohol/Drug Use, W/O Rehab	-0.152	-4.20	-0.022	-1.900	-0.018	-1.72
523 Alchohol/Drug Use, W/O Rehab	-0.419	-29.80	-0.111	-24.230	-0.054	-13.28
012 Degenerative Nervous System Discord	0.066	4.45	0.061	12.700	0.014	3.30
023 Non-Traumatic Stupor & Coma	-0.371	-4.74	0.087	3.440	0.098	4.39
Additional Control Variables
Ancillary Indicator	0.062	5.00	-0.265	-65.580	-0.093	-25.07
Year Indicator	0.039	3.56	0.026	7.200	-0.008	-2.69
Indicator for Occupancy Under 30%	0.117	8.19	-0.038	-8.180	-0.019	-4.70
Indicator for Occupancy Over 105%	0.478	7.06	0.100	4.570	0.079	4.10
Number of Observations	93,263	—	93,263	—	93,263	—
Degrees of Freedom	40	—	43	—	44	—
R2	0.1157	—	0.3149	—	0.467	—

NOTES: NA is not applicable. All LOS coefficients are relative to stays of more than 8 days. All DRG coefficients are relative to DRG 430 (Psychoses). The additional control variables were not used in any of the payment simulations. The ancillary indicator identified facilities that do not charge separately for ancillary services. The year indicator identified cases were 1998 Medicare cost reports were used to backfill for missing 1999 reports in constructing the dependent variable. The two occupancy indicators identified facilities with extremely high and low values.

SOURCE: Cotterill, P.G. and Thomas, F.G., Centers for Medicare & Medicaid Services, 2004.

Patient Characteristics

Age is an important variable in both the per case and per diem regressions. Age was treated as a dichotomous variable—split at age 65, which primarily separates Medicare's disabled and elderly populations. Mental illness is the qualifying disabling condition for a large proportion of disabled Medicare beneficiaries treated in psychiatric facilities. There are differences in the distribution of principal diagnoses between these two groups. For example, dementia is more common among the elderly, whereas schizophrenia and alcohol/drug abuse are more common among the disabled. There are also differences in the types of facilities used. The elderly are more frequently treated in CPUs, possibly because they are more likely to have both medical and psychiatric conditions. The fact that the age coefficient is approximately three times greater in the per case than in the per diem regression clearly implies that age is an important factor in explaining LOS differences, as well as daily intensity differences.

A large number of diagnosis and comorbidity variables were included in the cost regressions. The principal diagnosis code listed on the claim was used to assign each case to 1 of 15 mental health DRGs. The largest positive payment adjustment is for DRG 424 (Surgical Procedure with Principal Diagnosis of Mental Illness) whose cases would be paid approximately 70 percent more than DRG 430 on a per case basis and 21 percent more than DRG 430 on a per day basis.² In general, the DRG regression coefficients tend to be larger in absolute value in the per case than in the per diem regressions. Most commonly, they identify DRGs with a shorter LOS than DRG 430.

Seventeen groups of secondary diagnoses were included in the cost regressions as comorbid conditions (secondary diagnoses). In the per diem regressions, all 17 comorbid conditions are more costly than a case with none of the 17 comorbid conditions. Comparing the per case and per diem coefficients reveals no clear patterns, but overall the differences between the coefficients are smaller than the analogous differences in the DRG coefficients.

In general, the same patient characteristic variables were used as independent variables in both per case and per diem cost regressions. The exception was the LOS, which was only included in the per diem regressions. We used four LOS categories (for stays of 1 day, 2-4 days, 5-8 days, and 9 or more days). The regressions indicate that per diem cost declines as LOS increases. This statistically significant finding is consistent with the fact that ancillary and certain administrative costs occur disproportionately in the early days of a stay. In 1999, the median LOS for Medicare patients was 9 days. Relative to a stay of 9 or more days, per diem costs are approximately 23 percent more for a 1-day stay, 12 percent more for a 2-4 day stay, and approximately 5 percent more for a 5-8 day stay.

Facility Characteristics

All cost regressions—per case and per diem—contained the following facility characteristics, which are familiar variables that have been included in other Medicare PPSs: the hospital wage index (in logarithms), a teaching variable (the logarithm of one plus the ratio of psychiatric residents to the average daily census), and a rural location indicator. All these variables are positively correlated with cost and are statistically significant. The coefficients differ in magnitude between the per case and per diem regressions, but not dramatically.

We used the same form of the teaching variable (adding one to the ratio) as used in the indirect medical education adjustment of the inpatient hospital PPS for operating costs and for the low-income patient adjustment in the inpatient rehabilitation facility PPS (Federal Register, 2001). The advantages of using average daily census rather than number of beds as the denominator of the ratio were discussed in the final rule for putting inpatient hospital capital payments under prospective payment (Federal Register, 1991). For CPUs, the teaching variable reflects the number of interns and residents assigned to the CPU. Interns and residents assigned elsewhere in the hospital are excluded.

We also analyzed, but subsequently excluded from the regressions, another facility variable familiar from other Medicare payment systems. The disproportionate share proportion (DSH) is the sum of the proportion of Medicare days of care provided to recipients of supplemental security income and the proportion of total days of care provided to Medicaid beneficiaries. For CPUs, both ratios were computed specifically for the psychiatric units and not the entire hospital.

The DSH variable was highly significant in the per diem cost regressions; however, its sign was negative, indicating that per diem costs are lower in facilities with higher disproportionate share ratios. THEORI's previously cited study (Heller and Vaz, 2001) also found a negative relationship using a similar variable.

We tried a variety of supplemental analyses in an attempt to better understand the observed relationship, but never found a positive relationship between per diem cost and the DSH ratio. These analyses did yield an interesting result. Among freestanding psychiatric hospitals, there was no evidence of a statistically significant relationship, positive or negative. The negative relationship is confined to the psychiatric units of general acute care hospitals.

Three facility characteristics traditionally considered inappropriate payment variables for the reasons cited earlier were evaluated in the regressions. These variables were size (measured by the average daily census, or occupied beds), the occupancy rate, and a CPU indicator variable. These variables are much more powerful as explanatory variables in the per diem than in the per case regressions. It is possible that some interacted combinations of patient and community variables could be found that would capture some of these facility effects, but such an approach was beyond the scope of our study.

We hypothesized that per diem costs are strongly related to facility size and occupancy. These variables are measures of the level of a facility's efficiency. Size measures whether the facility's service volume is large enough to capture economies of scale. Occupancy (as measured by the ratio of actual days to available days) measures the extent to which the facility is efficiently utilizing its capacity. These variables play different roles in different payment models. In the cost regression used to develop Model 3, the occupancy rate was included as a control variable to improve the estimates of the effects of other factors that may more appropriately be used to adjust payments. Then in developing the hypothetical payment Model 4, which contains expanded facility characteristics, the regression coefficients of both the size and occupancy variables are transformed into payment adjustors.

On average, CPUs have much higher per diem costs than freestanding psychiatric hospitals. Table 1 shows that, in 1999, the average per diem cost of the CPUs was $639, compared with $466 for freestanding psychiatric hospitals. Some of the patient characteristics and other facility variables that we include in our cost regressions explain part, but not all, of the cost difference between freestanding hospitals and CPUs.

Controlling for facility size, occupancy, and comorbidities reduced the magnitude of the estimated hospital-CPU cost difference from 37 to approximately 19 percent. Several factors may play a role in the remaining difference: a large proportion of psychiatric admissions to these units enter the hospital through the ER; many of these admissions have medical conditions that could not be treated in a freestanding psychiatric hospital; psychiatric hospitals and units may utilize different patterns of care and staffing; and some units may absorb high overhead costs from other parts of the hospital.

We do not know precisely what characteristics of rural facilities are responsible for their higher per diem costs. However, the vast majority of rural facilities are small units within small general acute care hospitals. Consequently, the magnitude of the rural regression coefficient is highly sensitive to whether size is included in the cost regression (Table 2).

Payment Simulations

The payment models were developed using the results of the cost regressions. Regression coefficients were converted to payment adjustment factors for categorical variables (the patient's DRG, comorbidities, age, and LOS) by treating each coefficient as an exponent of the base e (the base for natural logarithms). The resulting payment factors represent the proportional effect of each variable relative to a reference variable (omitted category). Non-categorical variables (the wage index, teaching intensity, facility size, and occupancy) were converted to payment variables by taking the antilog of the product of the regression coefficient and the value of the variable. This calculation is equivalent to raising the unlogged value of the variable to the exponential power represented by the regression coefficient.

For all payment models, aggregate payments were equated to aggregate costs, commonly referred to as making total payments “budget neutral” to aggregate costs. This approach differs from the statutory requirement in the BBRA, which would set estimated first year aggregate PPS payments equal to estimated aggregate TEFRA payments (in the absence of PPS). Our approach is more appropriate for the analysis presented in this article, whose objective is to assess the degree to which alternative payment models correspond to costs at the case and facility levels. It should also be noted that to strengthen our test of the alternative payment models, we used a different 20 percent sample of MedPAR claims for payment simulations and evaluation (the validation phase of the study) than was used for the cost regressions (the development phase).

Evaluation of Payment Models

As noted earlier, we used two methods to evaluate how well a payment system matches payments to costs (which we call the accuracy of the system). First, we ran linear regressions of cost per case on payments per case (Carter et al., 2000). As described in greater detail following, the slope coefficient and the R² from these regressions provide information about the relative accuracy of the payment models. These results are shown in Table 3. Second, we calculated payment to cost ratios for selected groups of facilities to determine whether particular types of facilities would likely be advantaged or disadvantaged under the various payment models. These results are shown in Table 4.

Table 3. Facility-Level Regressions of Costs on Payments for Alternative Payment Models.

Payment Model	Unit of Payment	Model Description	Cost Per Case Regressed on Payments Per Case
			Slope Coefficient1	R2
1	Case	Payments adjusted for wage index, rural location, teaching, age, DRG, and comorbidity.	1.34 (18.7)	0.15
2	Day	Simple—Payments adjusted for wage index only.	0.63 (52.7)	0.59
3	Day	Refined—Payments adjusted for wage index, rural location, teaching, age, DRG, comorbidity, and length of stay.	0.70 (58.9)	0.64
3a	Day	Refined with Outlier Policy—Same basic adjustments as Model 3, plus outlier payments 2% of total payments.	0.75 (76.4)	0.75
4	Day	Expanded—Payments adjusted for same factors as Model 3 plus facility adjustments for size and occupancy.	0.99 (88.6)	0.80

¹t statistics are shown in parentheses.

NOTE: DRG is diagnosis-related group.

SOURCE: Cotterill, P.G.. and Thomas, F.G., Centers for Medicare & Medicaid Services, 2004.

Table 4. Payment-to-Cost Ratios for Alternative Payment Models, by Type of Inpatient Psychiatric Facility.

Group of Interest	Model
	Number of Facilities	1	2	3	3a	4
		Per Case	Per Diem Simple	Per Diem Refined	Per Diem Plus Outliers	Per Diem Expanded
Hospitals
Non-Profit	80	1.03	1.09	1.08	1.07	0.99
For-Profit	234	1.13	1.24	1.16	1.15	1.14
Public	162	0.72	1.44	1.38	1.35	1.03
Certified Psychiatric Units	1,417	1.00	0.92	0.94	0.94	0.98
Total	1,893
Rural	438	1.03	0.83	0.94	0.96	0.99
Urban	1,455	1.00	1.03	1.01	1.01	1.00
Total	1,893
Psychiatric Unit ADC
< 12	707	0.97	0.76	0.81	0.83	0.97
12-25	440	1.07	0.93	0.94	0.94	1.00
26-50	199	1.05	1.02	1.03	1.02	0.98
51-75	44	0.95	1.11	1.09	1.07	0.95
>76	27	0.81	1.15	1.16	1.15	0.88
Total	1,417
Hospital ADC
< 12	53	1.00	0.87	0.86	0.88	1.05
12-25	73	1.06	1.08	1.03	1.03	1.12
26-50	151	1.19	1.22	1.15	1.13	1.15
51-75	53	1.03	1.25	1.18	1.17	1.07
>76	146	0.83	1.41	1.35	1.32	1.01
Total	476

NOTE: ADC is average daily census.

SOURCE: Cotterill, P. and Thomas, F., Centers for Medicare & Medicaid Services, 2004.

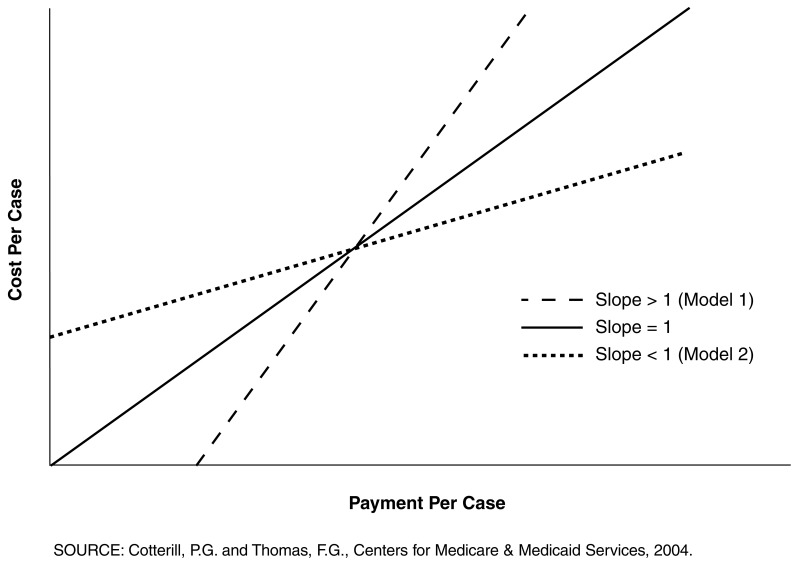
Since we have equated aggregate payments and aggregate costs for each system, the slope coefficient of the cost-payment regressions measures the relationship between the levels of per case costs and payments. Hence, for each payment model, the slope indicates whether there is a systematic bias toward over or under payment relative to cost. A slope greater than 1.0 indicates that for low levels of per case payment, payment tends to be less than cost, and for high levels of per case payment, payment tends to exceed cost. The converse is true for a slope less than 1.0: at low per case payment levels, payment tends to exceed cost, and at high per case payment levels, payment tends to be less than cost (Figure 1). As the slope coefficient pivots from either greater or less than 1.0 toward 1.0, the areas of systematic differences between cost and payment decrease. For systems where aggregate costs and payments are equal, the regression lines for alternative systems rotate through a common point of intersection, which represents the coordinates of the mean values of the cost and payment variables. More precisely, there will be a single point of intersection when the analysis is conducted at the case level.³

Figure 1. Payment System Bias.

The R² indicates the goodness of fit of the payment system, or the degree of variation in costs among cases or facilities receiving a given level of payment. The R² can be interpreted as a measure of the degree of precision of the payment system. The R² of the per case cost-payment regression is a better measure for evaluating payment models than the R² of the cost regression reported in Table 2 for two reasons. First, the cost-payment R² reflects relationships measured in dollars (the real unit of interest) rather than logarithms. Second, because it reflects only the effects of payment variables, the cost-payment R² provides a more consistent measure of the explanatory power of the payment variables. The cost regression R² sometimes includes the effects of additional variables that are not used for payment.

The per case cost-payment regression can be run with either the case or the facility as the unit of observation. In general, both levels of analysis are relevant for assessing payment accuracy. The accuracy of case level pricing is important because we do not want to create incentives for facilities to discriminate among different types of patients. Facility level accuracy is important for the financial stability of facilities. Also, facility level accuracy acknowledges the limits to pricing accuracy at the case level and the need for facilities to average their payments across their high- and low-cost patients. In our case, a strong reason for focusing on the facility level measures is the fact that our routine per diem cost variable does not vary among patients in the same facility, which in turn means that our case level R² would be overstated. As a result, we report only facility level results.

Alternative facility weighting schemes are likely to produce somewhat different facility level results depending on the distribution of cases by size of facility. We present the results where facilities are equally weighted because we think equal weighting best reflects the concept of fairness or equity among providers. The case-weighted facility results do not differ dramatically from the results shown in Table 3. Both sets of facility results yield the same qualitative comparisons among the alternative payment models.

The results of the per case cost-payment regression reflect payment-cost relationships among individual facilities. The payment-to-cost ratios supplement the regression results by showing how differences in payment accuracy relate to specific facility characteristics. In Table 4, we display payment-to-cost ratios for the four types of psychiatric facilities discussed previously. In addition, facilities have been classified by rural-urban location, and hospitals and CPUs have been categorized by size.

Model 1 Versus Model 2

We first compare the per case payment model (Model 1) to the simple per diem model (Model 2), in which the per diem rate is adjusted only for area wage differences. From the slope coefficients shown in Table 3, we see that both models display systematic bias, but in opposite directions. The slope coefficient of the per case model (1.34) is substantially greater than 1.0, whereas the slope coefficient for the simple per diem model (0.63) is well below 1.0. The per case cost regression did not yield strong payment variables by which payments per case could be adjusted to variations in cost per case. Therefore, under Model 1, per case payments tend to be fairly tightly clustered around the mean, and per case costs vary greatly. As a result, the per case cost-payment regression for Model 1 has a steep slope (1.34) and a low R² (0.15). By automatically adjusting for LOS variation, the primary factor that produces variation in payments per case, Model 2 spreads per case payments much more widely around their mean and produces a better fit (R²=0.59) of the per case cost-payment regression line. Because relatively low cost cases tend to have relatively short LOS, their per case payments tend to decrease. Conversely, because relatively high per case cost cases tend to have relatively long LOS, their per case payment tend to increase. These relationships combine to produce a flatter slope for Model 2's per case cost-payment regression line compared with that of Model 1. The fact that Model 2's slope (0.63) is substantially less than 1.0 results from the fact that Model 2 does not account for much of the variation in per diem cost. Hence cases with relatively short LOS, but relatively high per diem cost are underpaid, and cases with relatively long LOS, but relatively low per diem cost are overpaid.

These relationships are evident in Table 4. Under Model 1, public hospitals have per case payments that average only 72 percent of their average per case cost. This result is consistent with the relatively high per case cost and long LOS of public hospitals shown in Table 1. Similarly, the largest CPUs and hospitals tend to be underpaid relative to cost with ratios of 0.81 and 0.83, respectively. For Model 2, the results are dramatically reversed. Public hospitals (relatively low per diem cost) have average per case payments that exceed their average per case cost by 44 percent. However, the per diem cost of public hospitals could be understated due to their frequently limited cost accounting systems and intergovernmental transfers. Also, large facilities (both hospitals and CPUs) have payment to cost ratios substantially greater than 1.0. Conversely, it is the relatively high per diem cost very small facilities and rural facilities whose average payments are less than average cost.

Model 2 Versus Model 3

The comparison of Models 2 and 3 shows the effects of additional per diem rate adjustors for a patient's age, DRG, comorbidities, LOS, and the level of a facility's teaching activity and rural/urban location. These variables increase the slope coefficient from 0.63 to 0.70, which can be interpreted as a 10-percent reduction in the systematic bias of Model 2. That is, under Model 3, there are reductions in the overpayment of low per case payment facilities and underpayment of high per case payment facilities. The payment to cost ratios tell a similar story. The Model 2 ratios that are well above 1.0 are reduced in Model 3, and the Model 2 ratios that are below 1.0 increase in Model 3. The effect of the specific adjustment for rural facilities in Model 3 raises their payment to cost ratio from 0.83 to 0.94. Also, Model 3 raises the payment to cost ratio for the smallest group of CPUs (0.76 in Model 2 and 0.81 in Model 3).

The precision of the per diem model increases, as the R² rises from 0.59 to 0.64, a 9-percent increase. Although these gains are not trivial, clearly there remains room for further improvement.

Model 3 Versus Model 4

Model 3 reflects the use of most variables available in current administrative data that were found to be statistically important in explaining per diem cost variation and that generally have been judged acceptable for use in PPS. Model 4 contains payment adjustors for the size (as measured by average daily census) and the occupancy rate of the psychiatric facility—adjustments with potentially negative effects on efficiency. For example, smaller facilities that may be unable to take advantage of economies of scale would receive higher per diem payments than larger facilities, and low occupancy facilities that use their available resources less efficiently would receive higher per diem payments than high occupancy facilities. Nevertheless, Table 3 shows that Model 4 substantially improves both the bias and precision of the per diem payment system. The slope coefficient rises to 0.99, a 32-percent improvement over Model 3. The R² increases to 0.80, compared with Model 3's R² of 0.64. The payment-to-cost ratios of Model 4 generally improve compared with those of Model 3. However, there are a few cases where the changes overcompensate. For example, in Table 4, the Model 3 ratio for the largest group of CPUs is 1.16, and under Model 4, it falls to 0.88.

Model 3a

Given the strong performance of Model 4, but our belief that size and occupancy are undesirable payment variables, we are left with the question whether other alternative payment adjustments might approach the level of Model 4's performance. One option is to add outlier payments to Model 3. Model 3a is the same as Model 3, but with the addition of outlier payments for expensive cases totaling 2 percent of total payments. Cases become eligible for outlier payments once their estimated cost exceeds a threshold that is a fixed amount greater than the PPS payment for the case. Outlier payments were calculated as 80 percent of estimated costs above the qualifying threshold for the first 8 days of the stay and 60 percent for the 9th day and beyond. Under the 2-percent constraint, 8.7 percent of all cases qualify for outlier payments.

Table 3 shows that outlier payments substantially improve the performance of Model 3. The slope coefficient rises to 0.75 from 0.70, and the R² rises to 0.75 from Model 3's R² of 0.64. Also shown in Table 3 is a modest improvement in the payment-to-cost ratios in Model 3a compared with Model 3. Although Model 3a falls short of Model 4's performance, outlier payments are shown to be an effective means of improving system accuracy without using undesirable payment variables.

However, the limited ability of outlier payments to reduce systematic bias must be recognized. For example, expanding outlier payments to almost 5 percent of total payments (not shown in Table 3) only increases the slope coefficient from 0.75 (Model 3a) to 0.79, still well below Model 4's slope of 0.99. Further, the percent of cases qualifying for outlier payments rises from 8.7 to 24.0 percent, which indicates that relatively small outlier payments are being spread among a large number of cases. This means that, at 5 percent, outlier payments have already targeted the extremely costly cases and are being spread much more widely among cases experiencing payment shortfalls. In fact, one could say that once they become this frequent, outlier payments are no longer functioning according to the primary objective of outlier policy, which is to reduce unsystematic risk that facilities may experience due to the random acquisition of very unusual patients.

By covering so many cases, a 5-percent outlier policy is attempting to compensate for systematic risk. The substantially higher slope in Model 4 strongly suggests that the systematic bias of Models 2 and 3 results from structural economic factors (size and occupancy) rather than patient characteristics. With 5 percent outlier payments, Model 3a matches the level of precision of Model 4 (R² = 0.80), which demonstrates that a model can be biased, but relatively precise. (It should be noted, however, that the two measures are not entirely independent. Generally, we expect a reduction in bias to be accompanied by a gain in precision, as is the case in comparing Models 2, 3, and 4.)

Discussion

On November 28, 2003, CMS issued a proposed rule to implement a PPS for inpatient psychiatric facilities that is very similar to Model 3a (Federal Register, 2003). Our analysis supports the view that Model 3a is a viable payment system for inpatient psychiatric care provided to Medicare beneficiaries. Model 3a's R² of 0.75 compares favorably with other Medicare PPSs. For example, facility level R² for the inpatient rehabilitation facility PPS range from 0.43 to 0.66, depending on the level of outlier payments (Carter et al., 2000). Also, the hospital level R² for the original inpatient hospital PPS based on a log-linear cost regression was 0.72 (Pettengill and Vertrees, 1982). This R² is probably somewhat higher than would be the R² based on a regression directly comparable to Model 3a's linear per case cost-payment regression because the cost regression included at least one major variable (bed size) that was not included in the payment model. In addition, R² of logarithmic regressions are frequently higher than those of comparable linear regressions.

Comparisons of Model 3a to other PPSs are not available in terms of the facility level slope coefficient that we have termed a measure of bias. More commonly, similar information has been conveyed using payment-to-cost ratios for various groups of facilities. We also supplemented our analysis with payment-to-cost ratios and demonstrated that the bias of Model 3a manifests itself primarily among public hospitals (high payment-to-cost ratios) and very small facilities (low payment to cost ratios).

Nevertheless, there are advantages to the single summary measure of bias presented by the slope coefficient, which are illustrated by the slope comparisons we made among Models 3, 3a, and 4. Through these comparisons, we identified the source of the bias and determined that outlier payments could reduce, but not eliminate, it. Specifically, we traced the bias to the effects of facility size and occupancy differences on per diem cost.

Our findings have implications for future research. First, to refine Medicare payment for inpatient psychiatric services, it will be necessary to focus on the differences between large and small facilities. Patient characteristics may explain some of these differences. For example, large public hospitals are characterized as treating chronic, long-term patients, whereas CPUs more commonly treat persons facing short-term crises. However, economic factors strongly influence size and occupancy, and it seems unlikely that refined patient characteristics can successfully address the bias issue.

Second, it will not be easy to collect detailed patient information from small facilities. A survey of all facilities, such as the instrument on which CMS is requesting comment in the proposed rule (Federal Register, 2003), is a possibility. However, collecting data on small facilities in studies like the CMS-funded RTI project would be very expensive and inefficient from a sampling perspective.

Our findings do not answer the policy question of whether the bias of the system should be reduced through direct adjustments for size and occupancy, especially adjustments that would benefit certain small facilities. This question raises additional questions about the role of small CPUs that require further research: On the one hand, it can be argued that many small CPUs warrant special treatment under a psychiatric PPS because they are a critical source of access to inpatient psychiatric services (as in isolated rural areas). Even where access is not a concern, there may be a need to separate certain psychiatric patients from other inpatients within the hospital that may justify supporting standby capacity for what would otherwise be an inefficient use of resources. On the other hand, many small CPUs may merely be a creation of Medicare payment policy whose reason for being is to gain exemption from the original DRG-based hospital PPS. We also need a better understanding of the type of care being provided in small geropsychiatric units, almost all of whose patients are elderly Medicare beneficiaries.

A related issue concerns small rural hospitals with CPUs that want to become critical access hospitals (CAH) and have had to give up their CPUs in order to meet the CAH size and LOS requirements. The Medicare Prescription Drug, Improvement, and Modernization Act of 2003 allows CAHs to establish psychiatric and rehabilitation distinct-part units of no more than 10 beds. Under this provision, CPUs in CAHs eventually will be paid under the inpatient psychiatric PPS, but does it make sense to apply a separate psychiatric PPS to small CPUs in small CAHs that are being paid on the basis of cost for most of the services they provide? Alternatively, would it be better to revise the qualifying criteria for CAHs to include psychiatric care and pay for it the same as for other CAH inpatient and outpatient services?