Financial Gains and Risks in Pay-for-Performance Bonus Algorithms

Abstract

Considerable attention has been given to evidence-based process indicators associated with quality of care, while much less attention has been given to the structure and key parameters of the various pay-for-performance (P4P) bonus and penalty arrangements using such measures. In this article we develop a general model of quality payment arrangements and discuss the advantages and disadvantages of the key parameters. We then conduct simulation analyses of four general P4P payment algorithms by varying seven parameters, including indicator weights, indicator intercorrelation, degree of uncertainty regarding intervention effectiveness, and initial baseline rates. Bonuses averaged over several indicators appear insensitive to weighting, correlation, and the number of indicators. The bonuses are sensitive to disease manager perceptions of intervention effectiveness, facing challenging targets, and the use of actual-to-target quality levels versus rates of improvement over baseline.

Introduction

The burgeoning research on the sizable geographic variation in surgery rates (Wennberg et al., 1999; Weinstein et al., 2004; 2006), the prevalence of medical errors, and the generally unacceptable quality of care in a variety of settings (Chassin et al., 1998; Institute of Medicine, 2001) has motivated both public and private health insurers to incorporate financial incentives for improving quality into their payment arrangements with care organizations. Both risk and reward (i.e., carrot and stick) approaches are being used (Bokhour et al., 2006; Epstein, 2006; Trude, Au, and Christianson, 2006; Williams, 2006; Fisher, 2006; Rosenthal and Dudley, 2007; Center for Health Care Strategies, 2007). Payors may simply provide an add-on or allow higher updates to a provider's fees or they may pay an extra amount whenever a desired service is performed (e.g., a $10 payment for a mammogram). These are part of a reward (carrot) strategy. Alternatively, payors may reduce payments or constrain fee updates for unacceptable quality performance—the risk (stick) strategy. A hybrid of the two approaches involves self-financing quality bonuses. Under a self-financing scheme, as with Michigan Medicaid's Health Plan Bonus/Withhold system (Center for Health Care Strategies, 2007), payors pay for quality improvements out of demonstrated savings generated by providers or managed care organizations.

P4P arrangements use financial incentives to engender changes in patient care processes that, in turn, are expected to lead to improved health outcomes. Evidence-based patient care studies have produced a list of care processes that lead to better outcomes (National Committee for Quality Assurance, 2006; Agency for Healthcare Research and Quality, 2006; National Quality Forum, 2006; Institute of Medicine, 2006). Much less attention has been given to the payout algorithms themselves. Yet, how the incentives are structured may be as or more important than the quality indicators (QIs) in encouraging quality improvements.

In this article, we first present several possible P4P payment models and their key parameters. As part of this exercise, we highlight the effects of the number of indicators on bonus levels, how they are weighted, and how targets are set. We then simulate actual quality performance against a pre-set target and test the sensitivity of a plan's expected bonus and degree of financial risk to different bonus algorithms and key parameters. Finally, we conclude by suggesting steps that payors should follow in designing P4P incentive programs.

P4P Payment Model

Many private and State Medicaid P4P programs use a simple payment scheme that pays a fixed amount for providing a quality-enhancing service (e.g., mammograms, a primary care visit). Service-specific P4P payment is narrow, however, and is not adequate to encourage higher quality in managing the chronically ill. One likely risk model underlying an insurer's expected bonus payout across several P4P indicators is based on an organization's actual performance relative to a target rate. (In some P4P models, organizations must pay back up front case management fees if quality targets are not met. The modeling and results are easily recast in a penalty framework.) In most cases, a target rate, t, is determined as an improvement over the local baseline rate, λ_base, i.e.,

$${\mathrm{t}}_{\text{ip}}={\mathrm{\lambda }}_{\text{base},\text{ip}}(1+{\mathrm{\alpha }}_{\text{ip}})$$ (1)

where α_ip = the required rate of improvement over baseline for the i-th indicator in the p-th plan. Using a local population baseline rate serves as a control for varying risk factors. The rate of improvement might be set unilaterally by the payor or negotiated with the plan. The patient care organization or disease management plan is assumed to have formed its own expected level of performance, E[λ_ip], based on a likely rate of quality improvement, E[ρ_ip], due to its intervention:

$$\mathrm{\text{E}}[{\mathrm{\lambda }}_{\text{ip}}]={\mathrm{\lambda }}_{\text{base},\text{ip}}(1+\mathrm{\text{E}}[{\mathrm{\rho }}_{\text{ip}}]).$$ (2)

A physician group or managed care organization's expectation of success or failure, therefore, depends on managers' opinions regarding the effectiveness of their intervention to improve quality, e.g., increasing use of beta blockers. Their expected improvement depends on expected intervention effectiveness, μ, over baseline, conditional on the level of investment that managers make in trying to meet the target. Actual improvement in any year, y, also depends on a truly random element, ε_ipy, that would occur in any single year due to other factors (e.g., shift in patient case mix, flu epidemic). An organization's level of investment is under its control and likely a function of the risk and rewards to achieving the target. However, we do not model the feedback investment effect; rather, we assume that it is at some reasonable level—possibly to assure that the organization has at least a 50-percent chance of achieving or exceeding the target rate.

Uncertainty exists surrounding the effectiveness of an organization's strategy to improve quality on any particular indicator, as reflected in its variance, σ_iμ². Random variation in a single year's performance out of many different years, σ_ie², adds to the uncertainty. The panel of patients can vary in terms of their level of illness or care-seeking with a particular organization. The pure random error component is likely to be trivial when yearly quality performance is based on large samples of patients. It seems reasonable to assume that managers' own uncertainty regarding systematic intervention effectiveness dominates most estimates of random temporal risk, again for a reasonable investment. Random risk could dominate at already high baseline levels, however, as discussed later in the article.

A care group's expected total percentage bonus, E[TB],¹ in meeting a set of prespecified quality and satisfaction targets can be expressed as the maximum percent of outlays (fees) eligible for bonuses, MG, multiplied by a weighted average (ω) of the bonus percentages that an organization might expect to achieve on each indicator, E[B_i].

P4P quality payouts to a group depend on the payout algorithm used. For a single indicator, E[B_i] could take one of four forms: (1) all or nothing, (2) a continuous unconstrained proportion between zero and 100 percent; (3) a continuous proportion constrained by a lower and upper bound, or corridor; or (4) a composite score allowing above-target gains to offset failures across several indicators in the p-th plan. The four are:

1. All or Nothing

   $$\begin{array}{c}\mathrm{E}[{\mathrm{B}}_{\mathrm{i}}]=0:\mathrm{\text{E}}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{\text{t}}}_{\text{ip}}<1.0\\ =1:\mathrm{\text{E}}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{\text{t}}}_{\text{ip}}>=1.0.\end{array}$$

2. Continuous Unconstrained

   $$\mathrm{\text{E}}[{\mathrm{\text{B}}}_{\mathrm{\text{i}}}]=\mathrm{\text{E}}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{\text{t}}}_{\text{ip}}:0<=\mathrm{E}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{t}}_{\text{ip}}<=1.0$$

3. Continuous Constrained

   $$\begin{array}{l}\mathrm{E}[{\mathrm{B}}_{\mathrm{i}}]=0:\mathrm{E}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{t}}_{\text{ip}}<\text{LL}(\text{lower limit})\\ =\mathrm{\theta }•\mathrm{E}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{t}}_{\text{ip}}:\text{LL}<=\mathrm{E}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{t}}_{\text{ip}}<\\ =\text{UL}(\text{upper limit});0<\mathrm{\theta }<1.0=\text{UL}\\ :\mathrm{E}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{t}}_{\text{ip}}>\text{UL}\end{array}$$

4. Composite

   $$\begin{array}{l}\mathrm{E}[\mathrm{B}]={\sum }_{\mathrm{i}}\mathrm{E}[{\mathrm{B}}_{\mathrm{i}}]={\sum }_{\mathrm{i}}{\mathrm{\omega }}_{\mathrm{i}}\mathrm{E}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{t}}_{\text{ip}}:\\ 0<=\mathrm{E}[{\mathrm{\lambda }}_{\text{ip}}]/{\mathrm{t}}_{\text{ip}}<=\infty .\end{array}$$

The organization's ultimate interest is in the overall E[B] fraction of the potential bonus dollars it receives when summed across all N indicators. In the first three bonus scenarios, each indicator's performance and payout is evaluated separately, then indicator payout percents are averaged to arrive at the overall total bonus fraction. Indicator-specific fractions can either be equally or differentially weighted. The fourth, composite, bonus algorithm does not evaluate each indicator separately. Rather, relative actual-to-target performance is measured completely unconstrained for each indicator, and the final bonus is determined only after averaging the unconstrained performance ratios. Because individual indicator ratios could be greater than 1.0, over-achievement on some indicators can offset under-achievement on others. The payor would likely constrain the total bonus percentage not to exceed 1.0.

Instead of basing the bonus percent on the ratio of actual-to-target levels within a period, as in the previous four scenarios, a payor could scale payments to the ratio of actual-to-expected rates of improvement in the baseline rate. The conversion formula between levels and rates is:

$$\begin{array}{c}\mathrm{\lambda }/\mathrm{t}={\mathrm{\lambda }}_{\text{base}}(1+\mathrm{\rho })/{\mathrm{\lambda }}_{\text{base}}(1+\mathrm{\alpha })\\ =[1/(1+\mathrm{\alpha })]+[\mathrm{\alpha }/(1+\mathrm{\alpha })]•(\mathrm{\rho }/\mathrm{\alpha }).\end{array}$$ (3)

Actual-to-target levels depend not only on relative rates of improvement, ρ/α, but on the absolute target improvement rate (α) as well, a subtle distinction that can produce large differences in expected payouts. Depending on the particular payment algorithm, using relative performance levels gives organizations credit for simply achieving the baseline rate (1/(1+ α)). For example, at zero improvement over baseline (ρ = 0) and targeted improvement of α = 25%, λ/t = 0.80. The all-or-nothing arrangement is insensitive to the use of relative levels or growth rates over baseline as any success below target would produce a zero bonus. The other three arrangements potentially allow for positive bonus payments even if the plan achieves zero or negative performance compared with the initial baseline rate. Consequently, using ρ/α in place of λ/t can produce very different bonus percentages as shown in the simulation analysis.

Summarizing quality improvement incentives across the four P4P models, the overall expected gain in fees due to quality bonuses can be written as a function of several predetermined or pre-existing parameters and a plan's expectation of intervention effectiveness: MG,N, ω, t[λ_base, α], E[λ∣ μ, ε]. MG percentages of at least 10 percent are generally considered necessary to motivate behavioral change in physicians (Center for Health Care Strategies, 2007). Even still, bonuses that an organization realistically can expect to receive can be a minor fraction of the overall percentage of fees (MG) offered by payors for quality improvements.

We now turn to a brief discussion of three of the six factors that most directly affect expected bonuses; namely, N, ω, t. (Determination of MG is considered outside any P4P negotiations between payors and care organizations.)

Number of QIs

Because physicians see a variety of patients every day, several QIs are required to measure quality for even a modest share of their caseload. Risk diversification across more indicators, by contrast, does reduce the variance of the expected gain.² Assuming disease managers are risk averse, more indicators reduce their risk of no bonus or having to pay back a portion of their up front fees from low quality. Because indicator interdependence also raises bonus variance, we simulate the risk effects of both the number and varying degrees of indicator correlation.

QI weights

Payers usually provide financial incentives to improve quality for several different illnesses. Uncertainty surrounds not only intervention success in improving care processes, but in how much these processes improve the quality of life (Landon, Hicks, O'Malley, 2007; Siu et al., 2006; Werner and Bradlow, 2006). Whether higher payor weights for outcome-effective indicators substantially raise the level and risk associated with bonus payouts is explored using simulation methods.

Setting targets

One can think of a target as a mean rate with a frequency distribution of performance likelihoods around the local base line that is shifted upwards by the intervention. To challenge providers, a payor could set a target rate of improvement, a, over baseline that an organization would be expected to have a 50-50 percent chance of achieving.

Another strategy assumes that an ideal performance level, λ_ideal, exists applicable to all regions and groups, and group performance is measured against this goal. The ideal level could be clinically based on perfect practice, or on local best practice among high-performing groups, or on national averages across all provider groups. A flexible approach would base an indicator's target on the difference between the baseline and ideal rates:

$${\mathrm{t}}_{\mathrm{i}}={\mathrm{\lambda }}_{\text{base}}+\mathrm{\psi }[{\mathrm{\lambda }}_{\text{ideal}}-{\mathrm{\lambda }}_{\text{base}}]=(1-\mathrm{\psi }){\mathrm{\lambda }}_{\text{base}}+\mathrm{\psi }{\mathrm{\lambda }}_{\text{ideal}}$$ (4)

where ψ <= 1.0 is the required fraction of the difference between the ideal and base rate of performance that must be closed in any period. The ψ parameter functions as an ideal standard weight. When ψ = 1.0, eq. (4) reduces to t = λ_ideal. Any 50-50 percent actuarially fair σ rate of improvement has a ψ analog for a given λ_ideal/λ_base ratio:

$$\mathrm{\psi }=\mathrm{\alpha }/({\mathrm{\lambda }}_{\text{ideal}}/{\mathrm{\lambda }}_{\text{base}}-1).$$ (5)

Payors should be aware of the implications of setting a in terms of the percentage shortfall (ψ) from ideal that they expect to be closed.

Still another targeting approach would require only that actual performance be statistically higher than the baseline rate. Adjusting only for random variation above baseline implicitly assumes (near-) zero intervention effectiveness. It is reasonable for payors to expect a sizable, positive, intervention effect on quality over-and-above random annual variation; an effect that should dominate sampling effects at most baseline levels below 50 percent.

Simulation Methods

We simulated the impacts of the four payout algorithms on the level and variability in gains (paybacks) by varying seven key elements in the structure of final payouts:

• Uncertainty About Achieving Target Growth Rate (α)—Low, medium, high.

  A low level of uncertainty about intervention effectiveness is based on a (hypothetical) vector of symmetric probabilities around α =0.25 with an effect size standard deviation (S.D.) of 0.051 and a coefficient of variation (CV) of 20 percent (Research & Education Association, 1978).

  Medium Level of Uncertainty—A medium probability-of-success distribution is associated with a S.D. of 0.125 (around 0.25).

  High Uncertainty—Associated with a S.D. of 0.165 and a 40 percent chance of achieving less than three-fifths or more than seven-fifths of the targeted rate of improvement.

For simplicity, we assumed that any difference in bonus percentages is due to the intervention.

• Number of Indicators—Five versus 10 (all equally weighted).

• Indicator Weights—Five equally weighted or 1-in-5 weighted 50 percent with 4-in-5 weighted 12.5 percent.

• Degree of Indicator Correlation—None; 1 pair-in-5; 2 pairs-in-5 correlated 50 or 90 percent.

• Target Rate of Improvement over Baseline—150 percent (2.5 times), 25 percent (baseline model), 7.2 percent, 5.8 percent. The 5.8 percent target improvement is based on 1.96 S.D. above a baseline level 53.3 percent assuming a 1,000 beneficiaries, λ_ideal = 0.80, and ψ = 0.50.

• Expected Intervention Effect—An unbiased, fair (50-50 percent) target versus a payor's biased target that is 20, 33, or 50 percent above an intervention's expected achievement. Pay outs are evaluated on relative actual-to-target levels.

• Relative Growth Rates—An unbiased plan expectation of meeting or exceeding the target growth rate, a, versus an expected improvement rate only 80, 67, or 50 percent of the target rate. Payouts are evaluated on relative improvement over baseline.

To determine the variation in indicator-specific bonus fractions, we simulated performance from 500 random draws, r_ipd, or trials,³ from a normal distribution of plan actual improvement rates with a prespecified low, medium, or high variance (i.e., we simulated ρ_ipd = E[ρ_ip] + r_ipdσ_ρ). In the baseline simulation, E[ρ] = α = 0.25 and σ_ρ = 0.125. Thus, if a random normal draw had r_ipd = 1.96 S.D., then our simulated ρ = 0.25+1.96(.125) = 0.495. Note that simulating an improvement of 20 percent translates into a relative performance ratio λ/t = 96 percent according to eq. (3). The resulting relative performance ratios are then converted to indicator payout percentages using the bonus algorithms previously described in algorithms 1-4. A final overall bonus percentage is determined by aggregating across indicators using equal or variable weights. Simulation results are compared with the baseline set of parameters: α = 0.25, N = 5, σ_ρ = 0.125, along with equal indicator weights and no correlation among indicators.

Results

Table 1 presents mean and first quartile threshold bonus percentages from varying the values for seven key parameters across 19 simulations. The four payout algorithms are all-or-nothing, continuous, constrained (LL = 0.90; UL = 1.0; 50 percent bonus between limits), and composite. All of the simulations base final bonus percentages on relative actual-to-target quality levels except the last panel of results based on relative growth rates that do not include any baseline target bias. First, we compare algorithm results for the standard baseline model. We then discuss the sensitivity of the results to variation in the seven parameters.

Table 1. Simulated Pay-for-Performance Bonus Fractions and 25th Percentile Thresholds, by Bonus Algorithm.

Parameter		Bonus Algorithm1
		All-or-Nothing		Continuous		Constrained2		Composite
		Mean	25th Percentile	Mean	25th Percentile	Mean	25th Percentile	Mean	25th Percentile
		Bonus Fraction
1.	Baseline Simulation3	0.50	0.40	0.96	0.95	0.67	0.60	1.00	0.97
Uncertainty
2.	σ(ρ) = 0.051	0.50	0.40	0.98	0.98	0.75	0.70	1.00	0.99
3.	σ(ρ) =0.165	0.50	0.40	0.95	0.93	0.64	0.50	1.00	0.96
Number of Indicators
4.	10 Indicators	0.51	0.40	1.00	0.95	0.68	0.60	1.00	0.98
Weights
5.	1 Indicator @ 50%; 4@12.5%	0.48	0.25	0.96	0.94	0.66	0.50	1.00	0.96
Indicator Correlation
6.	1 pair @ 0.50 correlation	0.50	0.40	0.96	0.95	0.83	0.77	1.00	0.97
7.	2 pairs @ 0.50 correlation	0.50	0.40	0.96	0.95	0.67	0.60	1.00	0.97
Target Improvement Over Base (λ/t)
8.	50%/20%{α=E[ρ]}	0.50	0.40	0.98	0.97	0.74	0.70	1.00	0.98
8a.	50%/20%{α=1.5E[ρ]}	0.00	0.00	0.70	0.68	0.00	0.00	0.70	0.68
9.	75%/70% {α=E[ρ]}	0.50	0.40	0.95	0.94	0.65	0.50	1.00	0.96
10.	56.4%/53.3%{α=1.96σε}	0.50	0.40	0.95	0.94	0.65	0.50	1.00	0.96
10a.	56.4/53.3%{E[ρ]=1.5(1.96σε)}	0.59	0.40	0.97	0.95	0.73	0.60	1.00	0.96
Expected Intervention Effect(λ/t)
11.	α = 1.2E[ρ]	0.34	0.20	0.94	0.92	0.54	0.40	0.96	0.93
12.	α = 1.33E[ρ]	0.24	0.00	0.92	0.89	0.44	0.30	0.93	0.90
13.	α = 1.5E[ρ]	0.15	0.00	0.89	0.86	0.33	0.20	0.90	0.87
Relative Growth Rates (ρ/α)
14.	α = E[ρ]	0.50	0.40	0.81	0.73	0.54	0.40	0.99	0.84
15.	α = 1.2E[ρ]	0.34	0.20	0.70	0.60	0.37	0.20	0.79	0.64
16.	α = 1.33E[ρ]	0.24	0.00	0.61	0.51	0.28	0.20	0.66	0.51
17.	α = 1.5E[ρ]	0.15	0.00	0.50	0.39	0.18	0.00	0.49	0.34

¹Statistics for 19 simulations of bonus payments are based on 500 random normal trials with specified target growth rate for 5-10 quality indicators. A full explanation of each simulation may be found in the Results section of this article.

²Statistics based on 50 percent bonus for 0.90<λ/t<1.0, and 0 or 1.0 at lower/upper limit.

³Based on 5 equally weighted, uncorrelated, indicators, α=0.25 target improvement rate, σ(ρ) =0.125, from baseline rate = 53.3 percent.

NOTES: E[ρ], σ(ρ) = the mean and standard deviation of a plan's own expected intervention effectiveness over baseline; 1.96σ_ε = 1.96 standard deviations (95 percent confidence level) above baseline level assuming a 53-percent baseline rate and 1,000 patients.

SOURCE: Statistics based on simulations conducted by Cromwell, J., Drozd, E., Smith, K., and Trisolini, M., RTI International.

The all-or-nothing algorithm has an expected mean baseline bonus of 50 percent and a first quarter threshold of 40 percent when performance is aggregated across all five indicators. While an organization has a 50 percent chance of no bonus on any particular indicator, it has a 75-percent chance of receiving 40 percent or more of the entire bonus when failures on some indicators are offset by success on others. Out of 500 trials of 5 indicators, only 15 resulted in no overall bonus payout compared with roughly 250 “failed” trials with no bonus on each indicator separately.

Organizations paid on a continuous algorithm could expect to receive 96 percent of their overall bonus percentage. Such a high percentage is the result of making minimum bonus payments of 80 percent or more even when the organization simply achieves the baseline rate.

When bonuses are constrained to just 50 percent for actual-to-target ratios between 0.90 and 1.0 and nothing below 0.90, the expected bonus percentage falls from 96 to 67 percent. The first quartile threshold of 60 percent suggests a low likelihood of a very small bonus even with a constrained bonus structure.

Under a composite payment algorithm, an organization given an (unbiased) 50-50 percent target could expect to receive 100 percent of its overall bonus. This expectation is slightly higher than under a 0-100 percent continuous algorithm because the composite algorithm allows indicator-specific bonus rates in excess of 100 percent.

The degree of disease manager uncertainty, the number of indicators, how indicators are weighted, or the correlation among indicators has little effect on average expected bonuses. As long as an organization believes it has a 50-50 percent chance of achieving the target growth rate and could exceed or fall short of the rate with equal likelihood, the type of payment arrangement determines mean bonuses.

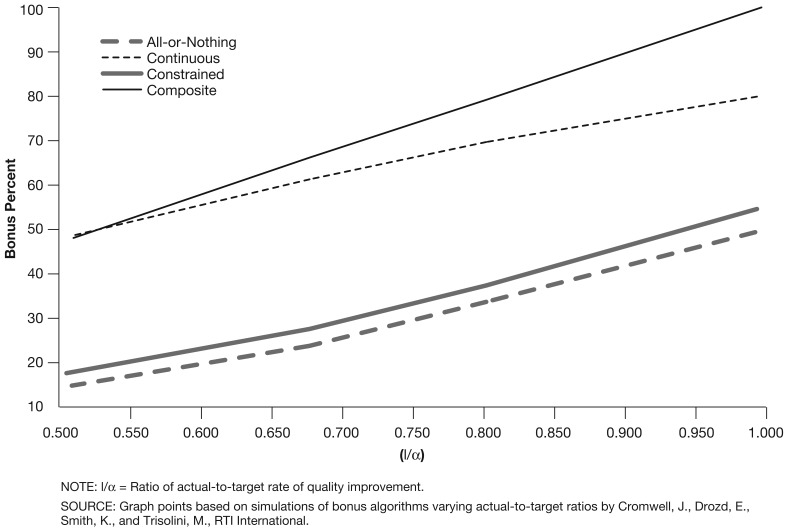
By contrast, all four payment algorithms are somewhat or very sensitive to the use of relative growth rates and overly optimistic target improvements over baseline (Table 1 and Figure 1). Expected intervention effect simulations show expected bonuses using relative actual-to-target levels. If bonuses were based on a target growth rate that was 50 percent above what a plan expected to achieve with its intervention (sim #13), then the expected bonus percentage under an all-or-nothing algorithm falls from 50 percent (baseline simulation) to 15 percent. Similarly, a constrained algorithm with no bonus below 90 percent of the target produces an expected bonus of only 33 percent. Continuous and composite payment algorithms based on target levels are much less sensitive to overly optimistic target growth rates. This is because quality improvements falling between the actual and target levels are generating substantial bonuses that do not occur at all in an all-or-nothing scenario or only in a limited fashion in a constrained scenario.

Figure 1. Actual-to-Target Rates of Quality Improvement and Bonus Percentages, by Four Payment Algorithms.

It may be unrealistic to assume that an organization expected to raise the baseline rate from 20 to 50 percent has the same fair chance as another required to improve only 5 percentage points (sim #8, 8a). If an organization faced with a 30-percentage point increase felt that it could only achieve one-half the improvement over baseline (sim #8a) then expected all-or-nothing and constrained bonuses fall to zero due to the relatively narrow (assumed) range of uncertainty surrounding the organization's low expected improvement over its target. Continuous and composite bonuses decline from nearly 100 to 70 percent for organizations required to raise scores 30 percentage points but who expect to achieve only one-half as much.

Conversely, a payor may be too conservative when setting the target to only 1.96σ_ε above the baseline target for large patient populations with very small mean standard errors. All-of-nothing expected bonuses increase from 50 to 59 percent (sim #10, 10a) if the organization believed its intervention's effectiveness would be 1.5 times greater than 1.96σ_ε. Constrained bonuses increase from 65 to 73 percent. Continuous and composite bonuses remain at nearly 100 percent because of the high baseline floor and an overall ceiling on the full bonus.

Bonuses based on relative growth rates (ρ/α) without any baseline bias are somewhat less under the continuous and constrained payment algorithms. Even when target growth over baseline equals plan expected improvement, bonuses decline from 96 and 67 percent (sim #1) to 81 and 54 percent (sim #14), respectively, in the continuous and constrained models. This is because growth rates, unlike levels, do not reward plans if they achieve zero improvement. Neither the all-or-nothing or composite algorithm is affected by a switch in payment focus to growth rates because the former never turns actual-below-targeted improvement rates into bonuses while composite payment arrangements treat rates and levels of improvement the same under equal growth expectations. Because relative growth rates factor out the baseline bias, average expected bonuses generally fall to their lowest levels if targeted growth over baseline is 50 percent or more of what a plan expects to accomplish.

Discussion

Payors naturally seek the most cost-effective way to reward managed care plans and provider groups when they improve quality. This requires quality bonuses to be neither too easy nor too difficult to achieve. Based on our simulation results, their strategy should be to

• Select QIs that are more closely linked to patient outcomes.

• Set challenging target rates of improvement over baseline per formance levels.

• Tie bonus (or penalty) percentages to true improvements over baseline levels.

All bonus incentive arrangements appear to be relatively insensitive to how much weight a payor puts on outcome-oriented indicators. To encourage better outcomes, payors should avoid giving weight to less critical process measures.

Challenging targets can be thought of a weighted average of the baseline and ideal performance level. Setting the ideal target weight too high will produce unreachable targets that can discourage any serious investment in quality improvement. All-or-nothing or tightly constrained payment methods are particularly punitive if targets are not actuarially fair. On the other extreme, simply requiring organizations to achieve a target statistically different from the baseline rate implicitly assumes very little (no) material intervention effect— especially for large patient populations.

Our findings also indicate that any method with fair targets that rewards near-target performance or that allows offsets through over-target performance will guarantee organizations a very high percentage of their total bonus (or very little payback of management fees) regardless of their intervention's effectiveness. Even without near-target or above-target offsets, an averaging process still occurs across multiple indicators that substantially reduces an organization's risk of receiving small or zero bonuses, overall.

Limitations

We assumed a normal distribution of uncertainty around simulated target rates of improvement over baseline. If organizations are risk averse, the likelihood function should be right skewed and more weight given to below-target performance. We adjusted for risk aversion by simulating expected performance below target which should give similar results to a log-normal or other skewed uncertainty distribution.

We assumed no feedback loop of bonus payments on an organization's investment in improving quality. This should produce a downward bias in expected bonus payments. We had no way of estimating the disease management production function to quantify the extent of the bias, but it is reasonable to assume that organizations faced with low expected bonuses would invest more to raise their bonuses—at least up to a point.

Finally, an important unknown is the marginal effectiveness of quality improvement interventions at very low or very high baseline levels. We simulated expected bonus impacts at low and high baselines that show considerable sensitivity to organizational confidence in meeting the target. This issue remains unanswered and may best be resolved through P4P trial and error initiatives.