Abstract
Gecko and many insects have adopted nanoscale fibrillar structures on their feet as adhesion devices. Here, we consider adhesion between a single fiber and a substrate by van der Waals or electrostatic interactions. For a given contact area A, the theoretical pull-off force of the fiber is σthA where σth is the theoretical strength of adhesion. We show that it is possible to design an optimal shape of the tip of the fiber to achieve the theoretical pull-off force. However, such design tends to be unreliable at the macroscopic scale because the pull-off force is sensitive to small variations in the tip shape. We find that a robust design of shape-insensitive optimal adhesion becomes possible only when the diameter of the fiber is reduced to length scales on the order of 100 nm. In general, optimal adhesion could be achieved by a combination of size reduction and shape optimization. The smaller the size, the less important the shape. At large contact sizes, optimal adhesion could still be achieved if the shape can be manufactured to a sufficiently high precision. The robust design of optimal adhesion at nanoscale provides a plausible explanation for the convergent evolution of hairy attachment systems in biology.
Gecko and many insects (Fig. 1) have evolved fibrillar structures on their feet to achieve extraordinary adhesion on vertical walls and ceilings. These “hairy” biological attachment systems consist of finely structured protruding hairs with size ranging from a few hundred nanometers to a few micrometers, depending on the animal species. The density of surface hairs increases with the body weight of the animal, and gecko has the highest density among all animal species that have been studied (1). Different mechanisms (2, 3) have been proposed in the past for biological attachment structures, but only until recently has strong evidence been presented (4, 5) that molecular adhesion by van der Waals interaction plays a dominant role in the attachment by fibrillar structures in biology. This discovery may appear somewhat surprising because it takes a much greater force to pull a gecko away from a ceiling than removing a human hand from a table, even though the same van der Waals force is expected to exist in both situations. A question thus arises: What determines the adhesion strength of a fiber in adhesive contact with a substrate? The chemical nature of materials cannot explain why the same van der Waals force results in strong adhesion in geckos but not in humans. Apparently, nature has evolved mechanisms to use weak van der Waals forces in animal species for which adhesion is crucial for survival.
Fig. 1.
The nanoscale fibrillar structures in animals with hairy attachment pads. The density of surface hairs increases with the body weight of animal, and gecko has the highest density among all animal species. (Photograph courtesy of S. Gorb, Max Planck Institute for Metals Research. Adapted from ref. 14.)
Dry adhesion between solid objects has been an active topic of research in contact mechanics. The Johnson–Kendal–Robert (JKR) (6) and Derjaguin–Muller–Toporov models (7) are particularly useful in modeling adhesive contact at two opposite extremes of a dimensionless parameter representing the ratio between the elastic deformation of the contacting surfaces and the effective range of surface interaction forces. The transition between JKR and Derjaguin–Muller–Toporov theories is described by the Maugis–Dugdale model (8) based on a cohesive description of the surface forces. More recent studies have expanded these theories to coupled normal and shear loading (9, 10) and to viscoelastic materials (11).
Various mechanical models have been developed to model specific fiber-array structures (12, 13), and significant progress has been made in using the JKR model to show that the hairy attachment systems, in which a macroscopic contact area is split into many smaller contact patches, could greatly enhance the adhesive strength (5, 14). However, little is known about why the characteristic size of the fibrillar ultrastructure of bioattachment systems falls in a narrow range between a few hundred nanometers and a few micrometers. In addition, no effort has been made to address the optimal conditions under which the theoretical pull-off force σthA, where σth is the theoretical strength of molecular interaction and A is the cross-sectional area of the fiber, can be achieved. A thorough understanding of these issues could also be of value to structural engineering and artificial materials design (15).
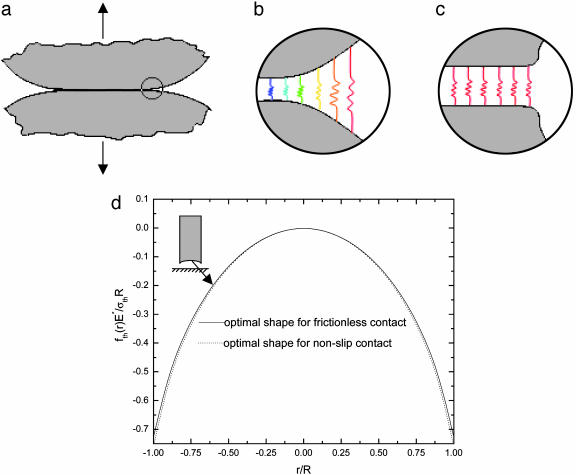
In conventional engineering, if two elastic bodies (Fig. 2a) are joined together by adhesion and then subject to an externally applied load, stress concentration is expected to occur near the edge of the joint (Fig. 2b). As the load increases, the intensity of stress concentration ultimately reaches a critical level to drive a crack to propagate and break the joint. Under this circumstance, the material in the joint is not being used most efficiently because only a small fraction of material is highly stressed at any instant of time, and failure occurs by incremental crack propagation. On the other hand, it is theoretically always possible to design the shape of the contact bodies so that at the instant of pull-off, the stress is uniformly distributed† over the contact region with magnitude equal to the theoretical adhesion strength σth (Fig. 2c).
Fig. 2.
Shape sensitivity of the pull-off force. (a) Two structures are bonded together and subject to an external load. (b) Stress concentration occurs at the edge and could initiate a crack to propagate and break the joint. The springs represent the molecular interaction forces between the contacting surfaces. (c) The optimum distribution of stress at pull-off is a uniform tensile stress equal to the theoretical strength of adhesion σth. (d) The optimal shape profiles of a rigid fiber in frictionless or nonslip contact with an elastic substrate. The solid line curve is the optimal shape profile for frictionless contact, and the dotted line curve is the optimal shape profile for the nonslip contact. Here the Poisson ratio is taken to be ν = 0.3.
Assuming that the molecular adhesion force between two contacting bodies is determined by the separation between them, a uniform stress field at pull-off requires a uniform separation of the two contacting bodies over the entire contact region. In other words, the optimal adhesion occurs if the contacting surfaces perfectly conform to each other at the critical moment of pull-off. The tip geometry of the fiber, which gives rise to a uniform stress field at pull-off from a substrate, can thus be calculated by the theory of elasticity (see Appendix). Why hasn't such an optimal shape been evolved in nature or used in engineering? One problem is that the optimal shape described here is sensitive to small variations in the shape of the tip of the fiber. In fact, only a small variation in geometry is needed to alter the tip shape to induce a singular stress field like that near a crack. Here, in contrast to the optimal shape, we also introduce a definition for the “singular shape” such that the stress distribution is equivalent to the singular stress distribution associated with a crack external to the connecting area A at pull-off. The difference between the optimal shape and the singular shape is often very small. This can be illustrated by considering the case of a rigid fiber in contact with an elastic substrate. If friction is neglected, the singular shape is just a flat-ended fiber that can be described by the shape function
 |
[1] |
In contrast, the optimal shape giving rise to the theoretical pull-off force is (see Appendix)
 |
[2] |
where E(·) is the complete elliptic integral of the second kind, R is the radius of the fiber, and E* is defined as E* = E/(1 – ν2), E being Young's modulus and ν Poisson's ratio of the substrate. Normally, the ratio σth/E* is quite small (1–2%) and so is the difference between fcrack(r) and fth(r). If friction is included with no slip along the interface between the fiber and substrate, the optimal shape of Eq. 2 would be modified by an additional term of
 |
A derivation of these solutions is given in Appendix. The optimal shape for the case of nonslip contact differs only slightly from that for the frictionless case, as plotted in Fig. 2d. More general friction cases are found to lie in between these two limits. These results show that the effect of shear plays only a minor role in the optimal shape problem.
The pull-off force associated with the singular shape can be calculated according to the Griffith condition for crack initiation (16) as
 |
[3] |
and that associated with the optimal shape is
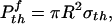 |
[4] |
where Δγ is the work of adhesion. For van der Waals interaction, Δγ usually ranges between 10 and 50 mJ/m2. We shall assume Δγ = 10 mJ/m2 in this article. Taking the effective interaction range of van der Waals force to be 0.5 nm, we estimate σth to be ≈20 MPa.
In general, it is difficult to determine the singular and optimal shapes in closed form solutions, although they can be calculated by numerical methods such as the finite element method. In the case of an elastic fiber in contact with a rigid substrate (a more realistic model of bioattachment systems), the flat-ended fiber becomes the optimal shape. In this case, the singular shape cannot be determined in closed form.
Fortunately, detailed solutions of the singular and optimal shapes are not necessary to calculate the associated pull-off forces. In fact, it can be shown that the same results in Eqs. 3 and 4 apply to an elastic fiber on a rigid substrate when E* is interpreted as the modulus of the fiber. More generally, for an elastic fiber with Young's modulus Ef and Poisson's ratio νf in contact with an elastic substrate with Young's modulus Es and Poisson's ratio νs, the pull-off force associated with the singular shape would still be given by Eq. 3 if E* is properly generalized according to
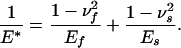 |
[5] |
The pull-off force associated with the optimal shape is always defined by Eq. 4.
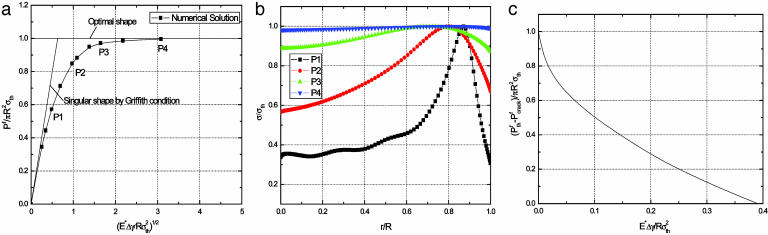
Fig. 3a plots the normalized adhesive strength Pf/(πR2σth) as a function of the nondimensional parameter 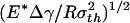 . The predictions from Eqs. 3 and 4 are plotted as two straight solid lines. We have also developed a numerical method to determine the pull-off force associated with the singular shape of a rigid fiber on an elastic substrate with molecular interaction characterized by the Lennard–Jones potential (17)
. The predictions from Eqs. 3 and 4 are plotted as two straight solid lines. We have also developed a numerical method to determine the pull-off force associated with the singular shape of a rigid fiber on an elastic substrate with molecular interaction characterized by the Lennard–Jones potential (17)
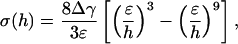 |
[6] |
where ε is the equilibrium distance at zero interaction and h is the separation between two interactive surfaces.
Fig. 3.
Saturation of adhesion strength for the singular shape of a fiber. (a) The variation of the normalized pull-off force with the nondimensional parameter  . (b) The distribution of the adhesive stress along the contact radius for different fiber radii. (c) The shape sensitivity of adhesion strength. As
. (b) The distribution of the adhesive stress along the contact radius for different fiber radii. (c) The shape sensitivity of adhesion strength. As  increases, or the fiber radius decreases, the difference between the adhesive strength of the singular shape and that of the optimal shape decreases, eventually vanishing at a critical length on the order of 100 nm.
increases, or the fiber radius decreases, the difference between the adhesive strength of the singular shape and that of the optimal shape decreases, eventually vanishing at a critical length on the order of 100 nm.
The numerically calculated values of the pull-off force for the singular shape, shown as filled squares in Fig. 3a, agree with the prediction of Eq. 3 based on Griffith condition for large fiber sizes but asymptotically approach the theoretical adhesion strength as the fiber size decreases. This trend occurs because the theoretical strength is the upper limit of adhesion. The Griffith condition assumes that failure always occurs by crack propagation, i.e., a crack is assumed to nucleate at the edge of the contact and propagates to break the joint. This assumption breaks down for very small fibers. The results of Fig. 3a show that the theoretical adhesion strength can be achieved in two ways; the first is by accurately adopting the optimal shape of the tip of the fiber, and the second is by reducing the diameter of the fiber. If theoretical strength is achieved, failure occurs no longer by crack propagation but rather by a uniform detachment over the entire contact region. For very small sizes, the condition for crack propagation cannot be satisfied before the theoretical strength is reached. The calculated pull-off force associated with the singular shape based on the Lennard–Jones potential shows a smooth transition between two failure modes, crack propagation at large sizes and uniform detachment at small sizes. Fig. 3b shows the distribution of adhesive traction at pull-off for the singular shape with different fiber sizes. Note that the adhesive traction becomes more and more uniform as the fiber size decreases, eventually becoming uniform at a critical size.
At macroscopic sizes, a small variation in the tip shape of the fiber results in large changes in pull-off force. For example, taking Δγ = 10 mJ/m2, σth = 20 MPa, and E* = 1 GPa (the case of a keratinous fiber in contact with a rigid substrate) and fiber radius equal to 1 mm, the pull-off force for the optimal shape is estimated to be 62.8 N and that for the singular shape is only 0.5 N. In other words, small variations in geometry result in large changes in pull-off force. The design of optimal shape, although theoretically feasible, is unrealizable in practice at the macroscopic scale. Fig. 3c shows that the difference between the adhesive strength of the optimal shape and that of the singular shape decreases as the size of the fiber is reduced. At the critical size
 |
[7] |
the strength of the singular shape predicted by Eq. 3 becomes equal to that of the optimal shape predicted by Eq. 4. Taking Δγ = 10 mJ/m2, σth = 20 MPa, and E* = 1 GPa, we estimate Rcr ≈ 64 nm. From these results we can conclude that the sensitivity of adhesion strength to tip geometry of the fiber decreases as the fiber diameter is reduced, and a robust design of optimal adhesion becomes possible around a critical size at which the pull-off force is no longer sensitive to variations in tip geometry. This length scale is ≈100 nm and indicates that the nanometer size of the fibrillar ultrastructure (spatula) of gecko and many insects may be the result of optimization for reliable and optimal adhesion. It has recently been shown (18, 19) that the nanometer size of mineral particles in bone-like biological materials may have been selected to ensure optimum fracture strength and maximum tolerance of crack-like flaws. The present study shows that the nanoscale dimension may play a crucial role in achieving reliable adhesion in a fibrillar structure.
The optimal adhesion strength described here can be compared with the JKR solution for a fiber having radius of curvature R at the tip in contact with a flat surface. The ratio of the optimal solution to that of JKR is
 |
[8] |
For Δγ ≈ 10 mJ/m2, σth ≈ 20 MPa, this ratio is calculated to be as large as 106 for a fiber with a radius of ≈1 mm and 103 for that ≈1 μm. Therefore, a huge magnification of pull-off force can be achieved by modification of the tip shape (shape optimization). Depending on animal species and convenience, optimal adhesion could be achieved by a combination of size reduction and shape optimization. The smaller the size, the less important the shape. At large sizes, the optimal adhesion could still be achieved if the shape could be manufactured to sufficiently high precision.
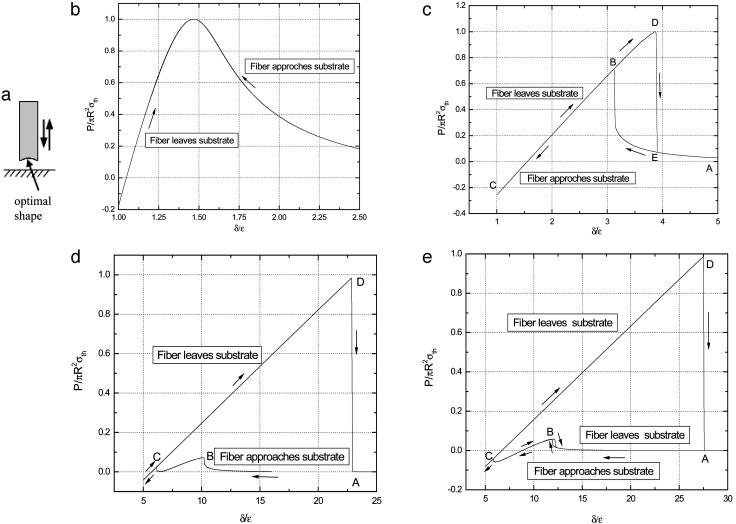
The discussion so far has been focused on how to achieve the theoretical pull-off force by size reduction or shape optimization. It is also interesting to investigate the variation in adhesive force as a fiber approaches or withdraws from a substrate. For this purpose, we have calculated the quasi-static process of an optimally shaped (Eq. 2) rigid fiber approaches an elastic substrate (Fig. 4a). Of special interest is how the interaction force changes as the fiber size decreases toward the critical size for shape insensitivity.
Fig. 4.
Variation of adhesive force as the optimally shaped rigid fiber approaches and withdraws from an elastic substrate. (a) Schematic illustration of the problem. (b–e) Different behaviors of fibers with radius equal to 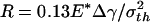 (b),
(b), 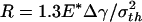 (c),
(c), 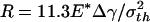 (d), and
(d), and 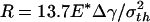 (e). δ is the separation between the substrate and the center of the tip surface of the fiber, and ε is the equilibrium distance at zero interaction.
(e). δ is the separation between the substrate and the center of the tip surface of the fiber, and ε is the equilibrium distance at zero interaction.
Figs. 4 b–e display the variation of the normalized adhesive force P/πR2σth asafunctionof δ/ε, where δ is the separation between the substrate and the center of the tip surface of the fiber. Fibers of different sizes approaching and withdrawing from a substrate are considered. Fig. 4b shows the behavior of a fiber with radius 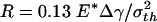 (3.2 nm for Δγ = 10 mJ/m2, σth = 20 MPa and E* = 1 GPa). For this fiber, the approach and withdrawal follow the same path with no hysteresis. As the fiber approaches the substrate, the adhesive force is always attractive and the fiber is drawn to the substrate until an equilibrium contact position is reached with zero interactive force. As the fiber is withdrawn from the equilibrium position, a maximum adhesive force exists equal to the theoretical pull-off force, confirming that the tip shape is indeed optimized.
(3.2 nm for Δγ = 10 mJ/m2, σth = 20 MPa and E* = 1 GPa). For this fiber, the approach and withdrawal follow the same path with no hysteresis. As the fiber approaches the substrate, the adhesive force is always attractive and the fiber is drawn to the substrate until an equilibrium contact position is reached with zero interactive force. As the fiber is withdrawn from the equilibrium position, a maximum adhesive force exists equal to the theoretical pull-off force, confirming that the tip shape is indeed optimized.
Fig. 4c shows the behavior of a larger fiber with 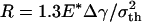 (32.5 nm for Δγ = 10 mJ/m2, σth = 20 MPa, and E* = 1 GPa). Now the approach and withdrawal follow different paths, giving rise to a hysteresis. During approaching, the adhesive force is always positive and the fiber is drawn toward the substrate until equilibrium. The approaching process is unstable. At a critical distance from substrate, there is a sudden increase in adhesive force and the fiber jerks toward the substrate. During withdrawal, the adhesive force increases until reaching the theoretical pull-off force and then abruptly drops to a small value.
(32.5 nm for Δγ = 10 mJ/m2, σth = 20 MPa, and E* = 1 GPa). Now the approach and withdrawal follow different paths, giving rise to a hysteresis. During approaching, the adhesive force is always positive and the fiber is drawn toward the substrate until equilibrium. The approaching process is unstable. At a critical distance from substrate, there is a sudden increase in adhesive force and the fiber jerks toward the substrate. During withdrawal, the adhesive force increases until reaching the theoretical pull-off force and then abruptly drops to a small value.
For a even larger fiber with 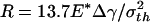 (342.5 nm for Δγ = 10 mJ/m2, σth = 20 MPa, and E* = 1 GPa) shown in Fig. 4e, the theoretical adhesive strength cannot be achieved spontaneously. As the fiber approaches the substrate, the adhesive force vanishes at two equilibrium positions. Only after the second equilibrium position can the fiber achieve the theoretical pull-off force on withdrawal. If the fiber is pulled back near the first equilibrium position, full contact between the fiber and substrate has not been achieved and the withdrawal goes back along the approaching path BA with a tiny hysteresis and small pull-off force. Between the two equilibrium positions, the adhesive force is actually negative, implying that an externally applied pressure is needed to reach full contact. In this case, the theoretical pull-off force cannot be achieved unless full contact is achieved by pressing the fiber hard enough against the substrate before withdrawal.
(342.5 nm for Δγ = 10 mJ/m2, σth = 20 MPa, and E* = 1 GPa) shown in Fig. 4e, the theoretical adhesive strength cannot be achieved spontaneously. As the fiber approaches the substrate, the adhesive force vanishes at two equilibrium positions. Only after the second equilibrium position can the fiber achieve the theoretical pull-off force on withdrawal. If the fiber is pulled back near the first equilibrium position, full contact between the fiber and substrate has not been achieved and the withdrawal goes back along the approaching path BA with a tiny hysteresis and small pull-off force. Between the two equilibrium positions, the adhesive force is actually negative, implying that an externally applied pressure is needed to reach full contact. In this case, the theoretical pull-off force cannot be achieved unless full contact is achieved by pressing the fiber hard enough against the substrate before withdrawal.
The preceding analysis indicates that a threshold radius exists for the spontaneous approaching of substrate, which is calculated to be 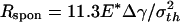 for a rigid fiber interacting with an elastic substrate. The behavior of such a fiber at threshold radius is shown in Fig. 4d. Taking Δγ ≈ 10 mJ/m2, E* ≈ 1 GPa, and σth ≈ 20 MPa, Rspon is estimated to be ≈282.5 nm. Fibers with radius smaller than Rspon can spontaneously achieve full contact without externally applied pressure and attain the theoretical pull-off force. The same concept is expected to hold for the more general case of an optimally shaped elastic fiber approaching an elastic substrate.
for a rigid fiber interacting with an elastic substrate. The behavior of such a fiber at threshold radius is shown in Fig. 4d. Taking Δγ ≈ 10 mJ/m2, E* ≈ 1 GPa, and σth ≈ 20 MPa, Rspon is estimated to be ≈282.5 nm. Fibers with radius smaller than Rspon can spontaneously achieve full contact without externally applied pressure and attain the theoretical pull-off force. The same concept is expected to hold for the more general case of an optimally shaped elastic fiber approaching an elastic substrate.
The concepts described in this article are not just limited to adhesion of fibrillar structures. The concept of a critical length for robust optimal adhesion can be generalized to a pair of arbitrary contacting bodies through the following definitions and theorems.
Definition 1. The optimal shape of two objects in adhesive contact over a surface area A is defined as such that the stress distribution is uniform and equal to the theoretical strength σth of adhesion at pull-off. The optimal shape can be calculated from the configuration at pull-off by elasticity. If desired, the optimal shape can be determined by numerical methods such as the fine element method.
Definition 2. The singular shape of two contacting objects over a surface area A is defined as such that the stress distribution is equivalent to the singular stress distribution associated with a crack external to the connecting area A at pull-off. The singular shape can be calculated from the configuration at pull-off by elasticity.
Theorem 1. As the size of the contact area decreases, the adhesive strength associated with the singular shape increases until it reaches the theoretical strength of adhesion near the critical size defined by Eq. 7. At the critical size, the strength of adhesion is no longer sensitive to the local geometry of the contacting objects. The optimal shape and the singular shape give rise to the same pull-off force.
Theorem 2. Optimal adhesion at theoretical strength could be achieved by a combination of size reduction and shape optimization. The smaller the size, the less important the shape optimization becomes. At large contact sizes, optimal adhesion could still be achieved if the shape can be manufactured to a sufficiently high precision.
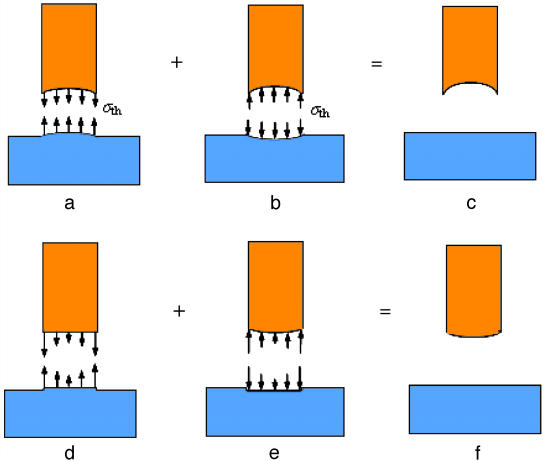
Because these concepts are based on the classical subjects of elasticity and linear elastic fracture mechanics, for which the basic existence and uniqueness theorems have long been proven (20), we do not find it necessary to go beyond setting up the boundary value problems for the singular and optimal shapes. Fig. 5 a–c shows schematically the linear elastic boundary value problems for the optimal shape and Fig. 5 d–f shows those for the singular shape. The conclusions of this article are generally applicable as long as the elastic boundary problems depicted in Fig. 5 can be solved to obtain the optimal and singular shapes. Further discussions are made in Appendix, where we also show how to obtain the analytical solution for the optimal shape in the special case of a rigid fiber in contact with an elastic substrate.
Fig. 5.
Methodology for determining the optimal and singular shapes for dry adhesion between two solid objects. (a) Deformed configuration of the optimal shape at pull-off. At this state, a uniform stress equal to the theoretical adhesion strength σth is distributed over the contact region. (b) Reverse of the pull-off configuration by superposition of a uniform pressure equal to σth over the contact region, which results in the undeformed configuration of the optimal shape depicted in c. (d) Deformed configuration of the singular shape at pull-off. At this state, a singular stress equivalent to that associated with a crack external to the contact region is assumed to be distributed over the contact interface. (e) Reverse of the pull-off configuration by superposition of a singular pressure distribution over the contact region, giving the undeformed configuration of the singular shape depicted in f.
The concepts developed in this article should be of general value in the understanding of biological attachment systems and the design of engineering systems. In the present study, we have implicitly assumed that the fibrillar structure is soft enough to achieve conformal contact with a rough surface. The effect of surface roughness should be more systematically investigated in the future. Also, we have not considered many important aspects of optimal design for dry adhesion. Open questions still exist that should be subjected to further investigation. For example, the more general cases involving coupled tension, shear, and bending loads on a fibrillar structure can be investigated under similar questions with respect to optimized adhesion or friction. It will be especially interesting to consider these issues in conjunction with the effects of the aspect ratio, distribution, and collective behaviors of a fibrillar structure.
Acknowledgments
This work has been supported by the Max Planck Society, the National Science Foundation of China, and the Chang Jiang Scholar program through Tsinghua University.
Appendix
Fig. 5a shows that the optimal shape of a fiber is defined as such that a uniform distribution of normal stress equal to the theoretical adhesion strength σth is achieved at pull-off. Fig. 5c shows that the substrate is assumed to be flat in its undeformed configuration. We can use these conditions to calculate the undeformed configuration of the optimal shape of the fiber.
To determine the optimal shape, a uniform pressure with magnitude equal to σth is separately applied over the contact region of the two objects which will deform as depicted in Fig. 5b. Superposing Fig. 5a and Fig. 5b should yield the optimal shape of the fiber and the undisturbed flat surface of the substrate (Fig. 5c). Here, in Fig. 5, one of the contacting objects (substrate) has been assumed to be a flat surface, and we focus on finding the optimal shape of the fiber. This limitation can be easily removed by generalizing the methodology to two arbitrary contacting objects. We can always use two conforming surfaces with a uniform distribution of theoretical adhesion strength σth to determine the undeformed configurations of the two objects by reverse elasticity. The solution is unique only when the deformed configuration of the contact interface is prescribed or known. If the deformed configuration of the conforming interface is not known, we can in principle find an infinite number of solutions for the optimally shaped contacting surfaces which give rise to the theoretical pull-off force. In the problem depicted in Fig. 5, the deformed configuration of the substrate is assumed to be a flat surface and this condition should lead to a unique solution for the deformed configuration of the conforming contact interface and the optimal shape of the fiber.
Figs. 5 d–f describes similar relationships that can be used to determine the singular shapes for the contacting objects. We emphasize again that the pull-off forces associated with the optimal and singular shapes given by Eqs. 3–5 do not require solutions to these shapes.
A critical step in the methodology to determine the optimal and singular shapes for general adhesive joints is the boundary value problem defined in Fig. 5 b and e which involves compressive loading on the two objects. Assuming the deformation of the objects is small (linear elastic) at pull-off, the existence and uniqueness theorems of elasticity (20) guarantee that the solution can be uniquely determined. For very compliant structures, the condition of small deformation at pull-off may be violated and the methodology may breakdown. In those cases, the two theorems given in the article may cease to be valid.
As illustration, in the following text, we show how the optimal shape of a rigid cylindrical fiber in contact with an elastic half-space is determined. In the case of frictionless contact, the normal surface displacement caused by a uniform normal traction σth applied over a circular region of an initially perfectly flat half-space is given by (21)
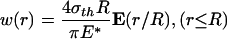 |
[A1] |
where E(·) is the complete elliptic integral of the second kind, E* is defined as E* = E/(1 – ν2), E being Young's modulus and ν being Poisson's ratio of the half-space. According to Fig. 5a, the optimal adhesion occurs if the contacting surfaces should perfectly conform to each other at the critical moment of pull-off. Therefore, the optimal shape for the rigid fiber tip is simply given by
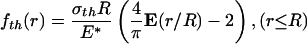 |
[A2] |
where a constant has been added such that fth (0) = 0.
Similarly, the optimal shape of a rigid cylindrical fiber in nonslip contact with an elastic half-space can be determined. In this case, the relative tangential displacements along the contact interface are fully constrained and the effects of radial shear tractions over the contact region must be taken into account. The normal surface displacement caused by a uniform normal traction σth with fully constrained tangential displacement over a circular region of an initially perfectly flat half-space is given by
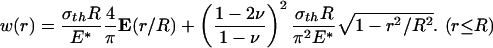 |
[A3] |
Letting the tip shape of the rigid fiber conform to this function yields the optimal shape
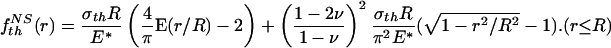 |
[A4] |
where a constant has been added to make f NSth (0) = 0. Here, NS stands for “no slip.”
Eqs. A2–A4 also apply to the case of an elastic cylindrical fiber within the approximation of linear elasticity.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviation: JKR, Johnson–Kendal–Robert.
Footnotes
Stress concentration can still exist near the edge of the contact region before pull-off occurs.
References
- 1.Scherge, M. & Gorb, S. (2001) Biological Micro and Nano-Tribology (Springer, New York).
- 2.Gillett, J. D. & Wigglesworth, V. B. (1932) Proc. R. Soc. London Ser. B 111, 364–376. [Google Scholar]
- 3.Stork, N. E. (1980) J. Exp. Biol. 88, 91–107. [Google Scholar]
- 4.Autumn, K., Liang Y. A., Hsieh, S. T., Zesch, W., Wai, P. C., Kenny, T. W., Fearing, R. & Full, R. J. (2000) Nature 405, 681–685. [DOI] [PubMed] [Google Scholar]
- 5.Autumn, K., Sitti, M., Liang, Y. C. A., Peattie, A. M., Hansen, W. R., Sponberg, S., Kenny, T. W., Fearing, R., Israelachvili, J. N. & Full, R. J. (2002) Proc. Natl. Acad. Sci. USA 99, 12252–12256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Johnson, K. L., Kendall, K. & Roberts, A. D. (1971) Proc. R. Soc. London Ser. A 324, 301–313. [Google Scholar]
- 7.Derjaguin, B. V., Muller V. M. & Toporov, Y. P. (1975) J. Colloid Interface Sci. 53, 314–326. [Google Scholar]
- 8.Maugis, D. (1992) J. Colloid Interface Sci. 150, 243–269. [Google Scholar]
- 9.Johnson, K. L. (1997) Proc. R. Soc. London Ser. A 453, 163–179. [Google Scholar]
- 10.Kim, K. S., McMeeking, R. M. & Johnson, K. L. (1998) J. Mech. Phys. Solids 46, 243–266. [Google Scholar]
- 11.Haiat, G., Huy, M. C. P. & Barthel, E. (2002) J. Mech. Phys. Solids 51, 69–99. [Google Scholar]
- 12.Persson, B. N. J. (2003) J. Chem. Phys. 118, 7614–7621. [Google Scholar]
- 13.Hui, C. Y., Jagota, A., Lin, Y. Y. & Kramer, E. J. (2002) Langmuir 18, 1394–1407. [Google Scholar]
- 14.Arzt, E., Gorb, S. & Spolenak, R. (2003) Proc. Natl. Acad. Sci. USA 100, 10603–10606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Geim, A. K., Dubonos, S. V., Grigorieva, I. V., Novoselov, K. S., Zhukov, A. A. & Shapoval, S. Yu. (2003) Nat. Mater. 2, 461–463. [DOI] [PubMed] [Google Scholar]
- 16.Griffith, A. A. (1921) Philos. Trans. R. Soc. London A 221, 163–198. [Google Scholar]
- 17.Greenwood, J. A. (1997) Proc. R. Soc. London Ser. A 453, 1277–1297. [Google Scholar]
- 18.Gao, H., Ji, B., Jäger, I. L., Arzt, E. & Fratzl, P. (2003) Proc. Natl. Acad. Sci. USA 100, 5597–5600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gao, H.& Ji, B. (2003) Eng. Fract. Mech. 70, 1777–1791. [Google Scholar]
- 20.Timoshenko, S. P. & Goodier, J. N. (1985) Theory of Elasticity (McGraw–Hill, Auckland).
- 21.Johnson, K. L. (1985) Contact Mechanics (Cambridge Univ. Press, Cambridge, U.K.).