Photochemical Tyrosine Oxidation in the Structurally Well-Defined α₃Y Protein: Proton-Coupled Electron Transfer and a Long-Lived Tyrosine Radical

Abstract

Tyrosine oxidation–reduction involves proton-coupled electron transfer (PCET) and a reactive radical state. These properties are effectively controlled in enzymes that use tyrosine as a high-potential, one-electron redox cofactor. The α₃Y model protein contains Y32, which can be reversibly oxidized and reduced in voltammetry measurements. Structural and kinetic properties of α₃Y are presented. A solution NMR structural analysis reveals that Y32 is the most deeply buried residue in α₃Y. Time-resolved spectroscopy using a soluble flash-quench generated [Ru(2,2′-bipyridine)₃]³⁺ oxidant provides high-quality Y32–O• absorption spectra. The rate constant of Y32 oxidation (k_PCET) is pH dependent: 1.4 × 10⁴ M^–1 s^–1 (pH 5.5), 1.8 × 10⁵ M^–1 s^–1 (pH 8.5), 5.4 × 10³ M^–1 s^–1 (pD 5.5), and 4.0 × 10⁴ M^–1 s^–1 (pD 8.5). k^H/k^D of Y32 oxidation is 2.5 ± 0.5 and 4.5 ± 0.9 at pH(D) 5.5 and 8.5, respectively. These pH and isotope characteristics suggest a concerted or stepwise, proton-first Y32 oxidation mechanism. The photochemical yield of Y32–O• is 28–58% versus the concentration of [Ru(2,2′-bipyridine)₃]³⁺. Y32–O• decays slowly, t_1/2 in the range of 2–10 s, at both pH 5.5 and 8.5, via radical–radical dimerization as shown by second-order kinetics and fluorescence data. The high stability of Y32–O• is discussed relative to the structural properties of the Y32 site. Finally, the static α₃Y NMR structure cannot explain (i) how the phenolic proton released upon oxidation is removed or (ii) how two Y32–O• come together to form dityrosine. These observations suggest that the dynamic properties of the protein ensemble may play an essential role in controlling the PCET and radical decay characteristics of α₃Y.

Introduction

Tyrosine serves as a one-electron redox cofactor in biocatalytic and multistep electron-transfer (ET) processes.¹⁻⁶ A combination of three fundamental properties makes redox reactions involving tyrosine radicals interesting from biochemical and biotechnical perspectives. First, tyrosine is a high-potential redox cofactor. Nature uses a range of organic molecules and inorganic complexes in ET but few of these redox-active species can participate in reactions occurring in the +1.0 V versus normal hydrogen electrode (NHE) range.⁷⁻⁹ Tyrosine radical cofactors thus fulfill an important role in biology by operating at the upper oxidizing edge of the functional redox scale.

Second, tyrosine oxidation–reduction involves proton-coupled electron transfer (PCET).^2,6,9−14 This is a consequence of the acid dissociation constants associated with the oxidized (pK_OX < 0) and reduced (pK_RED ∼ 10) states of tyrosine relative to the limited pH range of structurally stable and catalytically active proteins. Mechanistically, the e^–/H⁺ loss or gain may occur as a single coupled event (concerted electron–proton transfer, CEPT) or follow a stepwise pathway with ET followed by proton transfer, or vice versa. The electron and proton acceptor/donor can be the same molecule, e.g., hydrogen-atom abstraction by the Y–O• radical from a C–H bond, or separate molecules, often denoted a bidirectional, or multisite reaction. In the latter case the process may in turn involve proton transfers local to the radical site, such as protonation and deprotonation of an amino acid next to a transiently oxidized tyrosine in a multistep ET chain,^5,6 or more extended proton transfers involving multiple protein residues and/or interior water molecules.^2,15−17 The characteristics of the protonic reactions coupled to the tyrosine redox cycle are critical in determining the biochemical function of the redox-active residue. This notion has triggered a number of studies on small-molecule tyrosine/phenol model systems^9−14,18 with the long-term goal of forming an experimental and theoretical framework for PCET processes in chemistry and in biology. This work aims to complement and significantly extend these model studies by characterizing tyrosine-based PCET reactions occurring in the low-dielectric environment of a well-structured protein.

Third and finally, phenol-based species such as tyrosine are inherently reactive in their oxidized form.¹⁹ When tyrosine radicals are generated in solution by, e.g., radiolysis or UV photolysis, rapid radical–radical dimerization (∼5 × 10⁸ M^–1 s^–1) occurs with bityrosine (C_ortho–C_ortho) and isobityrosine (C_ortho–O) as the major products.²⁰⁻²³ The high reactivity of tyrosine radicals has been effectively harnessed in some biotechnology applications as it forms the basis for the tyramide signal amplification technique in immunohistochemistry. Here tyramide (tyrosine labeled with a reporter molecule) is enzymatically oxidized to the radical state in situ and then allowed to cross-link with surface residues of a target protein in cell or tissue preparations. A similar approach was recently used for mapping the location of mitochondrial proteins in the living cell.²⁴ In these applications, the reactivity of the radical is an important factor controlling the labeling radius. The protein matrix can modulate the tyrosine radical half-life (t_1/2) by many orders of magnitude and, in some cases, extend it into the hours time scale.^6,17 A detailed description of these protein induced radical-stabilization effects is currently not available.

Protein-based tyrosine oxidation–reduction involves high-potential PCET reactions and a reactive oxidized state. To gain a detailed mechanistic understanding of this important protein redox species involves delineating: (i) the thermodynamics involved, i.e., to measure the formal reduction potential (E°′) of the protein Y–O•/Y–OH redox couple and investigate how the solution pH and the protein environment influence this value; (ii) the PCET reactions associated with Y–O• formation at a buried protein site; and (iii) the structural and dynamic basis for the large difference in stability observed between tyrosine radicals formed in aqueous and in proteinous media. Thus far, it has not been possible to systematically investigate and map these characteristics for naturally occurring tyrosine radicals. Direct electrochemical measurements have not been feasible due to the high-positive potentials involved. Mechanistic PCET studies have predominantly been conducted on small-molecule models. It is not straightforward to translate the understanding gained from small molecules in solution to reactions occurring in proteins. Uncontrolled radical reactions and migration are known to occur in proteins that use tyrosine for functional redox chemistry and in response to oxidative stress. These are overall fairly poorly understood events. The α₃X protein model system was specifically developed to study the influence of the protein matrix on the thermodynamic and kinetic properties of aromatic amino-acid radicals.^25,26 The α₃X proteins are based on a de novo three-helix bundle scaffold designed to contain a single buried radical site. This redox site (position 32) is occupied by a tyrosine (in the α₃Y protein),²⁵ an unnatural 3,5-difluorotyrosine residue (in α₃(3,5)F₂Y),²⁷ a tryptophan (in α₃W),²⁵ or a covalently attached phenol (in the mercaptophenol-α₃C proteins).²⁸ The α₃X model proteins display structural characteristics typical of well-folded natural proteins.^25,29−31 The aromatic natural or unnatural residue located in position 32 is redox active,^25,27,28,30 while the α₃ scaffold itself is redox inert.^28,30,31 Thus far, square-wave voltammetry (SWV) studies have shown that residue 32 can be reversibly oxidized and reduced in α₃Y,³² 2-mercaptophenol-α₃C,³¹ and α₃(3,5)F₂Y.²⁷ These proteins thus provide E°′(Y–O•/Y–OH) or E°′(phenol–O•/phenol–OH) values that are uncompromised by the typical irreversibility of phenol-based systems.

In this report we extend the characterization of the α₃Y system to include structural and kinetic analyses. The solution structure of α₃Y was obtained by heteronuclear multidimensional NMR spectroscopy.³³ Time-resolved spectroscopy with flash-quench generated Ru(bpy)₃³⁺ oxidant³⁴ was used to investigate the kinetic properties of Y32–O• formation and decay. Absorption spectra collected on the transient Y32–O• species reflect a long-lived radical generated at significant yield at both pH 5.5 and 8.5. The pH-dependence and k^H/k^D kinetic isotope effects associated with Y32–O• formation suggest a concerted PCET process or a proton-first oxidation mechanism. The decay of Y32–O• was found to be remarkably slow with a t_1/2 in the 2–10 s range at both pH 5.5 and 8.5. Second-order kinetics and fluorescence data provide evidence that radical–radical dimerization is the dominating mechanism by which Y32–O• decays. Correlating the observed Y32–O• formation, stabilization and decay characteristics with the α₃Y structure suggests that the properties of the protein ensemble³⁵ may play a significant role in modulating the redox properties of the buried Y32 residue.

Materials and Methods

Construction of α₃F by Site-Directed Mutagenesis

A Phe codon (TTC) was introduced at position 32 of α₃Y using a modified pET32b-α₃Y plasmid³⁰ as template and forward primer 5′-C GGC CGT ATT GAA GAA CTG AAA AAA AAA TTC GAA GAA CTG AAA AAA AAA ATT GAA GAA C-3′ and reverse primer 3′-G TTC TTC AAT TTT TTT TTT CAG TTC TTC GAA TTT TTT TTT CAG TTC TTC AAT ACG GCC G-5′. The mutation was performed using the Stratagene QuikChange kit and confirmed by sequencing (Integrated DNA Technologies).

Expression and Purification of α₃X Proteins

α₃Y and α₃F were expressed as thioredoxin fusions using a modified pET32b vector (Novagen) transformed into BL21-CodonPlus(DE3)-RIL cells (Stratagene). Protein expression was induced with 1 mM IPTG (final concentration) for 3–4 h at 37 °C in LB medium or for 24 h at 30 °C in minimal media. The minimal media cultures contained ¹⁵NH₄Cl (1 g/L) and uniformly labeled ¹³C glucose (2 g/L; Cambridge Isotope Laboratories). Protein used for the prochiral methyl assignments³⁶ was expressed in minimal media containing ¹⁵NH₄Cl (1 g/L), uniformly labeled ¹³C glucose (0.2 g/L) and unlabeled glucose (1.8 g/L). Cells from 2 to 4 L cultures were harvested by centrifugation (5000 × g, 15 min, 4 °C), resuspended (5 mL/g cell paste) in buffer A (20 mM Tris-HCl, 500 mM NaCl, 5 mM imidazole, pH 7.9), treated with lysozyme (300 μg/mL, 30 min, 30 °C), and lysed by sonication. The lysate was clarified by centrifugation (12000 × g, 20 min, 4 °C), passed over a nickel column (10 mL His·bind resin, EMD Millipore) equilibrated with buffer A, and the thioredoxin fusions eluted with a linear 0–40% buffer B (20 mM Tris-HCl, 500 mM NaCl, 1 M imidazole, pH 7.9) gradient over 40 min (flow rate 1.5 mL/min). Fractions containing the thioredoxin fusions were identified by SDS-PAGE. Thrombin (T6634; Sigma-Aldrich) was added to the pooled fusion-protein fractions (thrombin/protein ratio 1:2000 (w/w)), and the resulting mixture dialyzed against 20 mM Tris-HCl, 500 mM NaCl, 2.5 mM CaCl₂, pH 8.0 at RT for >16 h. The digestion/dialysis mixture was passed over a nickel column (10 mL His·bind resin equilibrated with buffer A) to remove the His-tagged thioredoxin and any remaining undigested fusion products. α₃Y or α₃F (sample injection volume 5–10 mL) was isolated by reversed-phase HPLC (218TP C18 column, particle size 10 μm, column size 10 × 250 mm; Grace/VYDAC) using a linear water/acetonitrile/0.1% (w/v) trifluoroacetic acid gradient (30–60% acetonitrile over 45 min, flow rate 5 mL/min), and stored as lyophilized powder. The protein purification steps were monitored by SDS-PAGE. Purity was evaluated by reversed-phase HPLC (218TP C18 column, particle size 5 μm, column size 4.6 × 250 mm; Grace/VYDAC) using a linear water/acetonitrile/0.1% (w/v) trifluoroacetic acid gradient (20–70% acetonitrile over 50 min, flow rate 1 mL/min).

Circular Dichroism (CD) Spectroscopy

CD data were collected at 25 °C using an Aviv 202 CD spectrometer equipped with an automated titration system. Protein stability measurements were conducted by dissolving lyophilized α₃Y in 20 mM sodium acetate, 20 mM potassium phosphate (for pH 4.5 and 8.5 samples) or 20 mM potassium phosphate, 20 mM sodium borate (pH 9.9) to an 230 nm ellipticity around −250 mdegrees (1 mm path length). Protein stock solutions were added to 20 mM buffer containing 0 and 9.5 M urea, respectively. The final pH was 4.5, 8.5, or 9.9 in the protein/buffer and protein/buffer/urea solutions. The protein dilution step generated a final 222 nm ellipticity in the −170 to −210 mdegrees range (10 mm path length) at zero molar denaturant. The urea denaturation experiments were performed by automated equal-volume (2.0 mL) titration controlled from the Aviv software. Global stability values were determined by fitting the denaturation curves as described in ref (37).

Size-Exclusion Chromatography

Gel filtration was performed at room temperature using an analytical Superdex 75 10/300 GL column (GE Healthcare) equilibrated with 20 mM potassium phosphate, 20 mM sodium borate, 40 mM KCl, pH 7.0. Samples were prepared in the same buffer and the α₃Y loading concentration 300 μM, the sample injection volume 100 μL, the detection path length 10 mm, and the flow rate 0.5 mL/min.

NMR Spectroscopy

Standard multidimensional NMR experiments³³ were collected at 30 °C on 500 and 750 MHz Bruker Avance III spectrometers equipped with cryoprobes. The (H)CCH₃-TOCSY data set was collected on the 500 MHz spectrometer, while all other data sets were collected at 750 MHz. Sample conditions were as follows: (i) 950 μM ¹³C(10%),¹⁵N(100%)-labeled α₃Y in 30 mM deuterated sodium acetate, 30 mM NaCl, 0.02% (w/v) sodium azide, 250 μM 4,4-dimethyl-4-silapentane-1-sulfonic acid (DSS), 99.99% D₂O, pH* 5.6 (glass electrode pH reading uncorrected for deuterium isotope effects) (for prochiral methyl assignments); (ii) 950 μM ¹³C,¹⁵N-labeled α₃Y in 30 mM deuterated sodium acetate, 30 mM NaCl, 0.02% (w/v) sodium azide, 250 μM DSS, 99.99% D₂O, pH* 5.6 (for HCCH-TOCSY, (H)CCH₃-TOCSY, 2D ¹H-¹H NOESY, 3D NOESY-¹³C,¹H-HSQC, and 4D ¹³C,¹H-HMQC-NOESY-¹³C,¹H-HMQC data sets); (iii) 950 μM ¹³C,¹⁵N-labeled α₃Y in 30 mM deuterated sodium acetate, 30 mM NaCl, 0.02% (w/v) sodium azide, 250 μM DSS, 8.0% D₂O, pH* 5.6 (all other data). Backbone N, H, C, CA and side chain CB resonance assignments were derived from analyses of triple resonance 3D HNCO, HN(CA)CO, HNCACB, and CBCA(CO)NH experiments.³³ Side chain resonance assignments were obtained from 3D CC(CO)NH-TOCSY, H(CC)(CO)NH-TOCSY, HCCH-TOCSY, and (H)CCH₃-TOCSY data.³³ Resonance assignments of backbone (99%) and side chain (97%) atoms were essentially complete.³⁸ Prochiral methyl assignments (100% completeness) were performed using the trace glucose labeling strategy.³⁶ Backbone ϕ and ψ torsion angle restraints were obtained from backbone N, C, CA, HA and side chain CB chemical shifts using the TALOS+ Web server.³⁹ NOE distance restraints were derived from 3D NOESY-¹⁵N,¹H-HSQC, 4D ¹⁵N,¹H-HSQC-NOESY-¹³C,¹H-HSQC, and 4D ¹³C,¹H-HMQC-NOESY-¹³C,¹H-HMQC spectra.³³ NOEs between protons associated with the aromatic ring of Y32 and aliphatic protons were obtained from 2D ¹H-¹H NOESY and 3D NOESY-¹³C,¹H-HSQC data.³³ The mixing time was 140 ms for all NOESY experiments. Proton chemical shifts were referenced to DSS directly and ¹³C and ¹⁵N chemical shifts indirectly. NMR data were processed using Felix95 (Accelrys Inc., San Diego, CA) and analyzed with SPARKY.⁴⁰

Structure Calculations

Structures were generated from experimental NMR restraints by simulated annealing molecular dynamics using the Crystallography and NMR System (CNS) software.⁴¹ NOE-derived proton–proton distance restraints were grouped in distance ranges of 1.7–3.0, 1.7–4.0, and 1.7–5.0 Å corresponding to strong, medium and weak NOE cross-peak intensities, respectively. When one or two methyl groups were involved, the upper boundary was increased by 0.5 and 1.0 Å, respectively. Backbone torsion angle and hydrogen-bond restraints were derived from the secondary structure predictions made by the TALOS+ analysis. One thousand trial structures were generated and further evaluated using the CNS accept.inp script (cutoff set to zero for NOE and backbone dihedral angle violations above 0.1 Å and 2°, respectively) to obtain a final collection of refined structures. The 32 lowest-energy structures from this collection form the deposited structural ensemble. Solvent accessible surface area (SASA) analyses were performed using MOLMOL.⁴² Residue depth analysis and cavity detection were performed using the DEPTH Web server.⁴³ Structural depictions were generated using PyMOL (Schrödinger, LLC).

Data Deposition

NMR chemical shifts have been deposited in the BMRB Biological Magnetic Resonance databank (www.bmrb.wisc.edu; accession number 19668). Coordinates of the 32 lowest energy structures have been deposited in the RCSB Protein Data Bank (www.rcsb.org; structure ID 2MI7).

Sample Preparation for Flash Photolysis Measurements

The buffer solvents used for the transient absorption (TA) measurements were 20 mM K₂HPO₄, 20 mM sodium borate decahydrate (PB buffer), 40 mM KCl in high-purity water (17 MΩ), or D₂O (Aldrich, 99.96% minimum isotopic purity). Sodium borate was dehydrated for solutions prepared in D₂O by pulling vacuum on a sample heated above 150 °C for 1 h. For TA measurements two solutions were prepared separately; the first solution contained [Ru(bpy)₃]Cl₂ and α₃Y, and the second solution contained [Co(NH₃)₅Cl]Cl₂ (Aldrich 99.995% or Alfa Aesar). Immediately prior to a photolysis measurement, the two solutions were mixed under dark conditions to avoid unnecessary light contamination. Final concentrations were 35–50 μM for [Ru(bpy)₃]Cl₂ and 1–8 mM for [Co(NH₃)₅Cl]Cl₂. The α₃Y concentration was varied between 70 μM and 940 μM as determined spectroscopically using the extinction coefficient of Y32 (ε₂₇₇ 1490 M^–1 cm^–1).²⁵ The α₃F concentration was 300 μM as determined by the Bradford assay (Bio-Rad). Solution pH was adjusted to pH 5.5 or 8.5 by adding 1 M HCl (aq) or 1 M NaOH (aq) for experiments in water or by titrating DCl in D₂O (Aldrich, 99% atomic purity) or NaOD in D₂O (Aldrich, 99% atomic purity) for experiments performed in D₂O. The pH of each fresh and photolyzed solution was measured with a Metrohm pH meter fitted with a microelectrode that had been calibrated at the start of each day of experimentation. Samples were deoxygenated by gently bubbling the solutions for 20 min with high-purity N₂ and then maintained by a constant flow of nitrogen in the headspace of the cuvette during each measurement.

Transient Absorption Measurements

All optical measurements were performed at 23 ± 1 °C. Three types of TA measurements were performed in the present study to collect transient spectra and TA kinetics traces at a chosen wavelength on long (>120 s) and short (<1 s) time scales. Samples were contained in low-volume cuvettes of dimensions 2 × 10 or 4 × 10 mm. To generate transient spectra samples were excited with a 447.5 nm LED (Luxeon Star, Rebel premounted LED fitted with carlco 29.8/10 mm lens) that was controlled by an HP 8116A 50 MHz pulse/function generator to supply reproducible pulse lengths of 500, 250, or 100 ms. Changes in absorption as a function of time were detected in a right angle configuration by an Agilent 8453 diode array UV–vis spectrometer set to collect a spectrum every 2.5 s. To monitor absorption differences at a specific wavelength on very long time scales, samples were excited by the same LED set up. Monochromatic light was sent through the sample and detected at a right angle in a Cary 5000 UV–vis NIR spectrometer with time resolution of 33 ms. To follow faster TA kinetics, sample excitation was provided by a frequency doubled Nd:YAG laser (Quantel, BrilliantB) that delivered 10 ns pulses at 532 or 460 nm at ca. 30 or 13 mJ/pulse, respectively. Analyzing light was provided by an unpulsed 150 W Xe lamp in a flash photolysis spectrometer (Applied Photophysics LKS.60). To minimize sample excitation by the probe light, we employed a double monochromator setup where light was passed through a monochromator (bandwidth 4.65 nm) set to the desired detection wavelength prior to reaching the sample, and light that passed through the sample was directed through a second monochromator (bandwidth 4.65 nm) prior to reaching the P928 five stage photomultiplier tube (PMT). The PMT signal was digitized using an Agilent Technologies Infiniium digital oscilloscope (600 MHz). TA traces were generated within the Applied Photophysics LKS software package. Flash photolysis measurements were performed at four different sample conditions: pH 5.5 and 8.5 and pD 5.5 and 8.5. Two independent experiments with different α₃Y protein concentrations were conducted per sample condition using freshly prepared protein stock solutions. For each experiment, 4 individual samples were prepared for measurement. Controls with α₃F were performed in identical fashion to experiments with α₃Y where two experiments using freshly prepared samples were performed in H₂O at pH 5.5 and 8.5. Due to sacrificial quenching conditions and the presence of an impurity that led to competitive quenching of [Ru(bpy)₃]³⁺ (vide infra), care was taken to consider only the kinetics traces that were reproducible from shot to shot. For α₃Y kinetics, data from the first 1–10 up to 1–50 laser shots were not considered due to varying influence of the competing reaction. Subsequent shots generated highly reproducible traces (<10% deviation in k_obs) and allowed for data averaging. For l-tyrosine kinetics, data from the first 10–20 laser shots were used. Reported kinetics are taken from an average of 10 to 20 shots at each time window of interest. Curve fitting and data analysis was performed with Igor Pro or Matlab. All reported concentrations of α₃Y have an estimated uncertainty of 10%.⁴⁴ The Y32–O• yields are reported with a 10% standard deviation and derived using an ε₄₁₀ of 3000 ± 300 M^–1 cm^–1.^45,46 Rate constants and k^H/k^D kinetic isotope effect (KIE) values (Table 2) are reported to one standard deviation.

Table 2. Photochemical Oxidation of α₃Y and l-Tyrosine^a.

pH(D)	[α3Y] (μM)	kobs (s–1)	yield Y32–O•	kPCET (M–1 s–1)	KIE	[X] × kCOMP (s–1)	kY–O• (M–1 s–1)
pH 5.5	70	1.6 ± 0.1	0.58	(1.1 ± 0.2) × 104	2.5 ± 0.5	0.86 ± 0.04	(1.7 ± 0.7) × 104
	170	5.4 ± 0.1	0.55	(1.6 ± 0.2) × 104		2.7 ± 0.04
pD 5.5	410	4.9 ± 0.1	0.46	(5.4 ± 0.7) × 103		2.7 ± 0.05	–
	150	1.4 ± 0.1	0.58	(5.4 ± 0.9) × 103		0.79 ± 0.04
pH 8.5	580	210 ± 3	0.47	(1.7 ± 0.2) × 105	4.5 ± 0.9	110 ± 2	(1.1 ± 0.3) × 104
	890	420 ± 10	0.36	(1.9 ± 0.3) × 105		250 ± 6
pD 8.5	480	56 ± 1	0.28	(3.3 ± 0.5) × 104		40 ± 1	–
	940	130 ± 4	0.38	(4.8 ± 0.7) × 104		85 ± 2

	[Y] (μM)	kobs (s–1)	Yield Y–O•	kPCET (M–1 s–1)			kY–O• (M–1 s–1)
pH 5.5	260	420 ± 50	1.0	(2.5 ± 0.3) × 106		–	(1.9 ± 0.2) × 108
pH 8.5	260	(5.4 ± 0.1) × 104	1.0	(2.1 ± 0.2) × 108		–	(6.8 ± 0.9) × 108

^aRate constants and k^H/k^D KIEs are reported to one standard deviation.

Results and Discussion

The α₃X Protein Model System

α₃Y is a member of the α₃X family of de novo proteins specifically designed to study the redox chemistry of amino-acids radicals.^25,26 Nature uses four amino-acid types as “in house” one-electron redox cofactors: cysteine, glycine, tryptophan, and tyrosine.¹ Redox-active cysteine and glycine residues are typically found near or at the active site and are directly involved in the catalytic reactions.^1,47 Redox-active tryptophan and tyrosine residues can be found either at the active site or in intermediate positions along ET pathways spanning tens of Å. The high-potential ET/PCET characteristics of aromatic amino-acid radicals have excited considerable experimental and theoretical interest. For example, the PCET reactions of the catalytically essential Y_Z residue in photosystem II⁴⁸ and the tryptophan- and/or tyrosine-containing multistep ET/PCET chains in E. coli ribonucleotide reductase,⁶ DNA photolyase,⁴⁹ and MauG^50,51 represent systems of long-standing interest. Gray and co-workers have applied protein engineering and “hopping map” analyses to gain insights to ET involving aromatic residues.^5,52−54 Over the past 15 years a number of studies on small-molecule systems have provided insights to the PCET characteristics of phenol and tyrosine compounds in solution.^9−14,18,48 Theoretical work is starting to lay the foundation for PCET processes in general.⁵⁵

An important goal for the α₃X system is to provide a bridging link between the natural systems, whose complexity often obscures detailed analyses of the redox chemistry, with the small-molecule phenol/tyrosine systems. The latter are in general more easily characterized, but their biomimetic capability is limited. The α₃X model system was thus made to study tryptophan and tyrosine redox reactions occurring inside a structured protein. The α₃X proteins are based on a 65-residue three-helix bundle scaffold with a dedicated redox site as position 32 (see Figure 1 legend). Recently, the development of the α₃X system reached a milestone when it was demonstrated by SWV that residue 32 can be reversibly oxidized and reduced in several α₃X proteins.^27,31,32 The SWV studies provided E°′ values for the Y–O•/Y–OH (or phenol–O•/phenol–OH) redox couple in α₃Y, 2-mercaptophenol-α₃C (2MP-α₃C), and α₃(3,5)F₂Y at various pH conditions. Thus, solid thermodynamic data can be obtained thereby proving an important piece of information for mechanistic PCET studies of the α₃X system. This provides an advantage over many other tyrosine/phenol-based PCET model systems in which electrochemical quasi/irreversibility introduces an uncertainty. Additionally, the SWV studies showed that the tyrosine and phenol radicals formed in α₃Y, 2MP-α₃C and α₃(3,5)F₂Y are surprisingly long-lived with a lower limit of their radical t_1/2 on the tens to hundreds of ms time scale.^27,31,32 In this study we describe the solution NMR structure of α₃Y to place the observed redox reversibility and radical stabilizing properties within a structural context. In addition, the protein radical species, Y32–O•, was optically characterized, and kinetic studies were performed to obtain a more detailed description of Y32–O• formation and decay.

Figure 1.

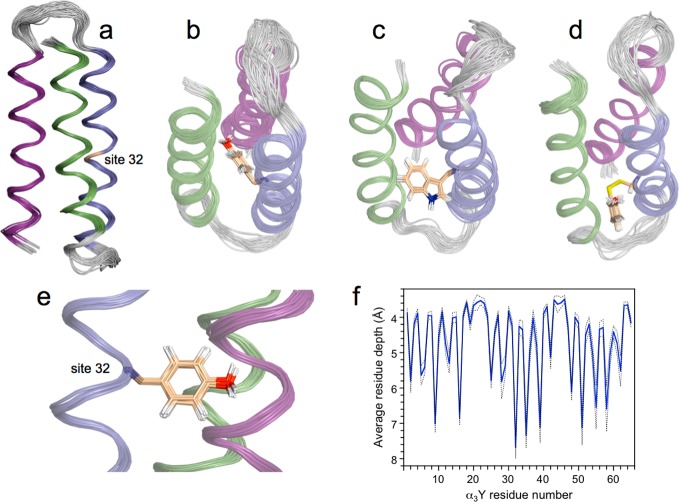
The a₃X family of designed radical proteins is based on (a) a three-helix bundle scaffold containing the following residues: GSR(1)-VKALEEKVKALEEKVKA-LGGGGR-IEELKKKX(32)EELKKKIEE-LGGGGE-VKKVEEEVKKLEEEIKK-L(65). The radical site (residue 32, labeled X) is placed in an internal position in the middle of the central helix and occupied by (b and e) Y32 in α₃Y (PDB ID 2MI7), (c) W32 in α₃W (PDB ID 1LQ7),²⁹ and (d) 2-mercaptophenol (2MP) in 2MP-α₃C (PDB ID 2LXY).³¹ The helical segments of α₃Y, α₃W, and 2MP-α₃C are color coded with helices 1, 2, and 3 shown in green, blue, and purple, respectively. Unstructured loop regions are shown in gray. The quality of the α₃Y solution NMR structure with (b and e) and without (a) the side chain of the redox-active Y32 residue is illustrated by ribbon diagrams of the deposited 32-membered structural ensemble. NMR experimental restraints and statistics for the structural ensemble are given in Table 1. (f) The average depth⁴³ of all residues in α₃Y.

Structural Analysis of α₃Y

The solution structure of α₃Y was obtained by heteronuclear multidimensional NMR spectroscopy.³³ Sample conditions and experiments used for obtaining resonance assignments and experimental restraints are described in Materials and Methods. The resonance assignments of α₃Y were essentially complete (99% and 97% of backbone and side chain atoms, respectively; 100% of isopropyl groups) and have been deposited at the BMRB (accession number 19668). NOE-based distance, backbone dihedral angle and hydrogen-bond restraints used for the structure calculations are summarized in Table 1. The CNS program was used to calculate trial structures by simulated annealing molecular dynamics.⁴¹ The calculations were based on an average of 14.4 experimental restraints per residue of which 2.5 represent interhelical distances (Table 1). The final collection of trial structures was evaluated and refined using the CNS accept.inp script to generate the 32-membered structural ensemble deposited at the RCSB Protein Data Bank (PDB code 2MI7).

Table 1. Experimental Restraints and Structural Statistics for the α₃Y Solution NMR Structure.

Experimental Restraints
NOE – intraresidue	221
NOE – sequential (|i–j| = 1)	184
NOE – medium range (1 < |i–j| < 5)	214
NOE – long-range (|i–j| ≥ 5)	165
NOE restraints – all	784
backbone dihedral angles	106
hydrogen bonds	43
experimental restraints – all	933
restraints per residue	14.4
long-range restraints per residue	2.5
Residual Restraints Violations
NOE distance > 0.1 Å	0
backbone dihedral angle > 2°	0
number of structures in ensemble	32
RMSD from Experimental Restraints
NOE distance deviation (Å)	0.0068 ± 0.0005
maximum NOE distance deviation (Å)	0.10
backbone angle deviation (deg)	0.262 ± 0.024
maximum backbone angle deviation (deg)	1.0
RMSD from Idealized Covalent Geometry
bonds (Å)	0.0014 ± 0.0001
angles (deg)	0.357 ± 0.003
impropers (deg)	0.252 ± 0.007
Ramachandran Plot Statistics
most favored regions (%)	99.0
additionally allowed regions (%)	0.9
generously allowed regions (%)	0.1
disallowed regions (%)	0
RMSD to Average Coordinates
backbone atoms (Å) (residues 1–65)	0.413
all heavy atoms (Å) (residues 1–65)	0.898
backbone atoms (Å) (residues 2–18, 24–41, 48–64)	0.261
all heavy atoms (Å) (residues 2–18, 24–41, 48–64)	0.886
all heavy atoms (Å) (18 core residues)	0.467

Figure 1 shows side (panels a and e) and top (panel b) views of the α₃Y structure displayed as a ribbon diagram superposed by a least-square fit to the first structure in the ensemble. The α₃Y structure is shown with (panels b and e) and without (panel a) the side chain of the redox-active Y32 residue. As a comparison, the solution NMR structures of α₃W (panel c)²⁹ and 2MP-α₃C (panel d)³¹ are also shown in Figure 1. The α₃Y structure displays minimal deviations from experimental restraints and idealized covalent geometries, as shown in Table 1. The RMSD to the mean coordinates is 0.41 Å for backbone atoms and 0.90 Å when included all heavy atoms. For the α-helical regions, the RMSD is 0.26 Å for backbone atoms and 0.89 Å for all heavy atoms. The main interior of α₃Y is composed of six interhelical layers: (V2, L42, V48), (L5, I39, V51), (V9, L35, V55), (L12, Y32, L58), (V16, L28, I62), and (L19, I25, L65) that are stacked on top of each other. The average RMSD to the mean coordinates is 0.47 Å for the heavy atoms in these 18 residues. Thus, the positions of residues that form the hydrophobic core of α₃Y are well-defined.

To serve as a useful model system for protein-based PCET studies it is important that the α₃Y scaffold is overall structurally pH insensitive. PCET reactions are strongly influenced by short-range interactions, and pH-induced large-scale structural changes could complicate detailed analyses of the redox chemistry. α₃Y contains three α-helices, and they are colored green (residue V2–A18), blue (R24–E41), and purple (V48–K64) in Figure 1. The α₃Y structure shows that the protein is 80% α-helical (52 of 65 residues) at pH 5.6. An α-helical content of 51 ± 1 residue is typical for the α₃X proteins as determined by CD and NMR spectroscopic studies.^27,29,31 There is no significant change in the α-helical content of α₃Y between pH 5 and 10.^25,30

The global stability of α₃Y is equally insensitive to the pH in this range [ΔG(pH 4.5) −3.3 ± 0.1 kcal mol^–1; ΔG(pH 5.0) −3.7 ± 0.1 kcal mol^–1; ΔG(pH 5.5) −3.9 ± 0.1 kcal mol^–1; ΔG(pH 8.2) −3.7 ± 0.1 kcal mol^–1; ΔG(pH 8.5) −3.8 ± 0.1 kcal mol^–1; ΔG(pH 9.9) −3.5 ± 0.1 kcal mol^–1; Figure S1].^27,30 Additionally, 2D NMR ¹⁵N-HSQC spectra obtained at pH 5.5, 7.0, and 8.5 show that there are no major changes in the tertiary structure of the α₃Y scaffold.³⁰ We conclude that thermodynamic and kinetic studies conducted in the pH 5–10 range reflects a structured protein for which no large-scale global changes have been induced.

α₃Y was specifically designed to study protein-based tyrosine oxidation–reduction.²⁵ The tyrosine targeted for redox chemistry was thus placed in a predicted core position with the aim to completely shield this residue from the bulk solvent. A SASA analysis⁴² of the α₃Y structure (Table S1) reveals the same basic pattern of exterior and interior residues as observed earlier for the NMR structures of α₃W²⁹ and 2MP-α₃C.³¹ Y32 is centrally placed between helices 1, 2, and 3 (Figure 1b,e) and has effectively no SASA (0.2 ± 0.2% across the NMR structural ensemble with a maximal value of 0.8%). The SASA description of α₃Y was complemented with a residue depth analysis (Figure 1f).⁴³ These analyses differ in that the former describes the average solvent accessibility of a specific residue or atom, while the latter describes the closest distance between a specific residue or atom to bulk solvent. The Y32 residue displays an average depth of 7.7 ± 0.3 Å and is the most deeply buried amino acid of all residues in the entire protein. The atoms associated with the side chain of Y32 have an average depth of 8.1 ± 0.4 Å, and the phenol oxygen atom has an average depth of 6.3 ± 0.4 Å. These results confirm a key design goal for α₃Y, i.e., to bury the redox-active tyrosine. They are also relevant in order to understand the interactions between the protein and a soluble photosensitizer system and the photochemically induced redox kinetics of Y32. These topics are discussed in more detail below.

Photogeneration of Y32–O•

The flash-quench methodology^34,56 was employed to generate the radical state of α₃Y. Previous voltammetry investigations of α₃Y have identified Y32 as the sole redox-active residue in this protein³⁰ and showed that E°′(Y32–O•/Y32-OH) is 1.070 and 0.910 V versus NHE at pH 5.5 and 8.5, respectively.³² In this potential range [Ru(bpy)₃]³⁺ is a good choice of oxidant, with an E°′[Ru(bpy)₃]^3+/2+ of +1.26 V versus NHE. [Ru(bpy)₃]³⁺ can be generated with a laser flash in situ when in the presence of an oxidative quencher. In the present study aqueous buffered analyzing solutions of pH 5.5 or 8.5 contained the sensitizer [Ru(bpy)₃]Cl₂, the irreversible oxidative quencher [Co(NH₃)]Cl₂, and the α₃Y protein.

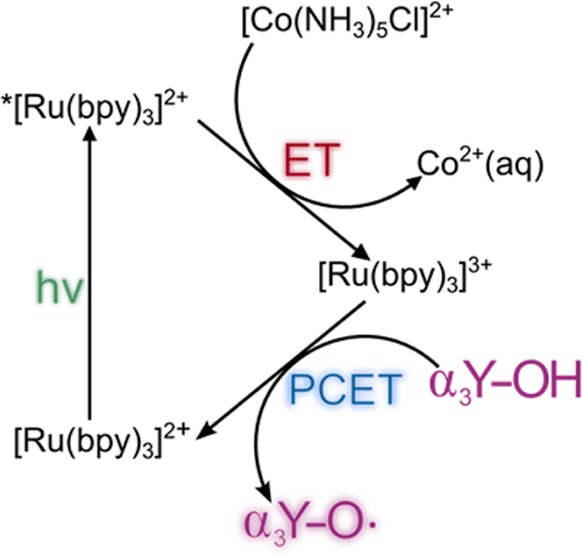
Scheme 1 summarizes the chemical reactions that lead to the formation of Y32–O•. Briefly, a flash of light excites [Ru(bpy)₃]²⁺ which is then quenched by [Co(NH₃)₅Cl]Cl₂ with a rate constant of 9 × 10⁸ M^–1 s^–1. These reactions generate [Ru(bpy)₃]³⁺ as well as the decomposition products Co²⁺(aq), NH₄⁺(aq) and Cl^–(aq).^57,58 Y32 is oxidized via a PCET process, which forms Y32–O• and restores the [Ru(bpy)₃]²⁺ species.

Scheme 1. Generation of Y32–O• by Flash-Quench Photolysis.

The spectra shown in Figure 2 represent the difference between an absorbance spectrum recorded prior to a short pulse of excitation light and an absorbance spectrum collected at some time after the pulse. Each set of spectra was generated from a freshly prepared sample that was exposed to a 447.5 nm flash of light to initiate the photochemical reaction. A well-resolved spectrum is observed 2.5 s after the light pulse at both pH 5.5 and pH 8.5. The spectral line shape is pH insensitive and displays a set of peaks at 410 and 390 nm as well as a broad absorption centered around 600 nm. The displayed spectra are in excellent agreement with previously reported spectra of phenol-based radicals, though with significantly improved resolution.^46,59,60 α₃Y contains only a single tyrosine (Figure 1), and the transient spectra shown in Figure 2 can thus unambiguously be assigned to Y32–O•.

Figure 2.

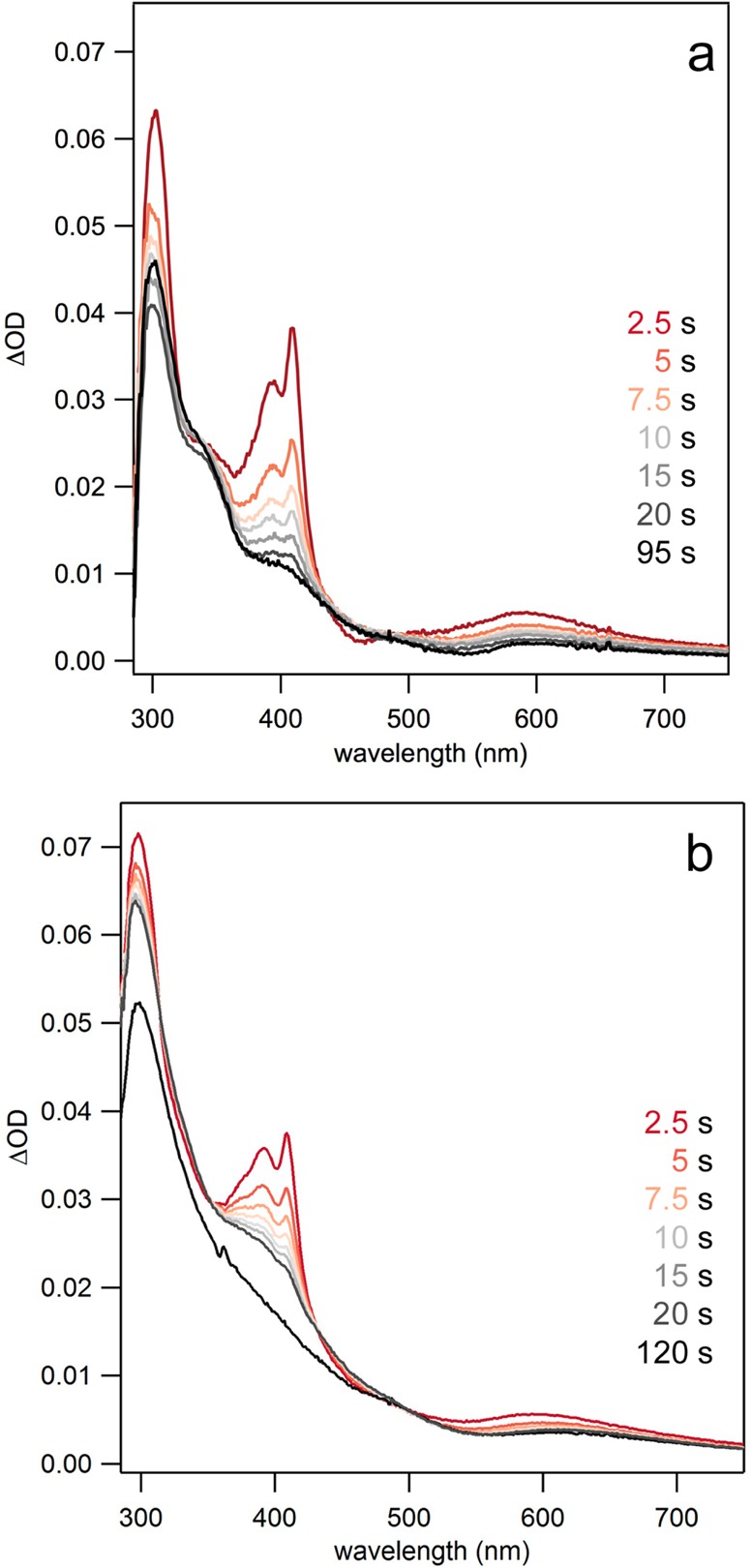
Flash-quench TA spectra showing distinct absorption features associated with the Y32–O• species in α₃Y at (a) pH 5.5 from 2.5 to 95 s and (b) pH 8.5 from 2.5 to 120 s after a 500 ms pulse of 447.5 nm light. Conditions: 35–50 μM [Ru(bpy)₃]Cl₂, 1–8 mM [Co(NH₃)₅]Cl₂, 300 μM α₃Y in 20 mM PB buffer, 40 mM KCl.

Inspection of Figure 2 reveals that the Y32–O• spectra have quite intense features after 2.5 s has elapsed. The transient spectra provide direct evidence for a very long-lived radical state, on the time scale of several seconds, at both pH 5.5 and 8.5. From SWV studies of α₃Y the radical t_1/2 was estimated to be >0.030 s,³² and the displayed 2.5 s Y32–O• spectra are consistent with that finding. After 10 s has elapsed the peaks at 390, 410, and 600 nm exhibit greatly diminished intensities pointing to a loss in the Y32–O• concentration. At very long time scales the spectra in Figure 2 show a single broad absorption, wherein the sharp features representing Y32–O• are no longer present. The remaining absorption (or light scattering) features are due to the presence of cobalt phosphate/oxide precipitates that form at very long time scales. Cobalt phosphate/oxides are well-known to form in solutions containing Co²⁺, phosphate, and an oxidant (i.e., [Ru(bpy)₃]³⁺).^61,62 Further discussion and characterization of these products are given in the Supporting Information. In the next two sections we describe the kinetics associated with the generation and decay of Y32–O•.

Kinetics and Yield of Y32–O• Generation

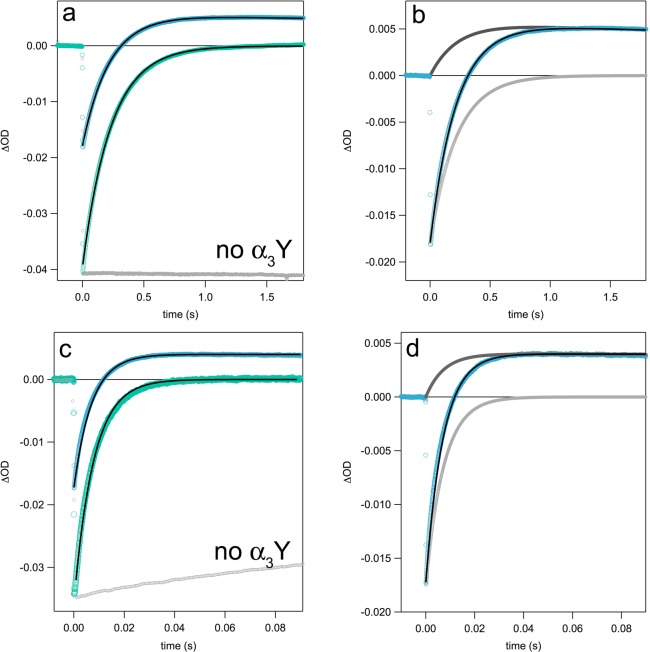
The formation of Y32–O• could be followed by ns laser flash photolysis on solutions prepared in an identical fashion to the samples used to generate the spectra shown in Figure 2. The initial [Ru(bpy)₃]²⁺ bleach maximum that occurs at ca. 450 nm recovers as the [Ru(bpy)₃]³⁺ species oxidizes Y32-OH (Figure 3). Under the present experimental conditions, 3–9 μM [Ru(bpy)₃]³⁺ is generated per laser flash (estimated from ε₄₅₀(Ru³⁺) – ε₄₅₀(Ru²⁺) = 10000 M^–1 cm^–1),⁶³ while the concentration of α₃Y varied from 70 μM to 940 μM. Thus, the TA traces corresponding to detection at 450 nm were fit to a single-exponential recovery function (pseudo-first-order kinetics). Figure 3a,c shows 450 nm TA traces with corresponding fit for α₃Y at pD 5.5 and 8.5, respectively.

Figure 3.

TA kinetic traces collected at 450 (green) and 410 nm (blue) after ns laser excitation. 450 nm traces were fit to a single exponential (pseudo-first-order), while 410 nm traces were fit using a model for concurrent pseudo-first-order growth and second-order decay. (a) TA traces for a solution of 410 μM α₃Y in D₂O at pD 5.5. A 450 nm trace from control experiments with no α₃Y is shown in light gray. (b) The 410 nm trace from panel (a) is shown with fit (black) and contributions from Y32–O• (dark gray) and [Ru(bpy)₃]²⁺ recovery (light gray) to the observed signal. (c) TA traces for a solution of 940 μM α₃Y in D₂O at pD 8.5. The 450 nm trace from a control experiment with no α₃Y (light gray) shows a slow recovery to baseline as a result of the formation of cobalt phosphate/oxides. (d) The 410 nm trace from panel (c) is shown with fit (black) and contributions from Y32–O• (dark gray) and [Ru(bpy)₃]²⁺ recovery (light gray) to the observed signal. TA kinetic traces for all pH(D) conditions and protein concentrations can be found in the Supporting Information in Figure S5.

In order to extract the rate constant for PCET (k_PCET) from k_obs, the yield of Y32–O• was determined. The initial [Ru(bpy)₃]²⁺ bleach can be observed at 450 nm and at 410 nm. However, at the latter wavelength the initially negative TA signal evolves over time into the positive absorption of Y32–O• (cf. Figure 2) that remains for the duration of the experimental time scale, up to 4.5 s. The initial bleach in the 410 or 450 nm traces, immediately after the flash-quench reactions, can be used to quantify the amount of [Ru(bpy)₃]³⁺ generated (ε₄₁₀(Ru³⁺) – ε₄₁₀(Ru²⁺) = 4500 M^–1 cm^–1).^56,64 The amplitude of the positive TA signal at 410 nm can be used to quantify the amount of Y32–O• generated per flash using an ε₄₁₀ of 3000 M^–1 cm^–1 for Y–O•.^45,46

For the l-tyrosine control studied at pH 8.5 (Figure 4b) the concentration of Y–O• generated matched the initial concentration of [Ru(bpy)₃]³⁺, giving a Y–O• yield of 100%. For l-tyrosine at pH 5.5, the apparent Y–O• yield obtained from the positive signal maximum at 410 nm is lower. At this pH, however, radical formation is slower and partly occurs simultaneously with Y–O• decay via radical–radical dimerization (vide infra). Consequently, a model of pseudo-first-order growth followed by a second-order decay was incorporated into the fitting routine (Figures S4 and S5, see Supporting Information for details). This fit model was able to reproduce the 410 nm TA signal for l-tyrosine at pH 5.5, using a Y–O• yield of 100% (Figure 4a). Applying this fitting model to the 410 nm TA signals for α₃Y showed that, based on the initial concentration of [Ru(bpy)₃]³⁺ after a laser flash, the α₃Y–O• yield is <100%. This observation points to a competing reaction that reduces [Ru(bpy)₃]³⁺ on a comparable time scale to the Y32 PCET reaction. The kinetics of the growing TA signal at 410 or 450 nm therefore represent the sum of two processes such that k_obs = [α₃Y] × k_PCET + [X] × k_COMP, where [X] is the concentration of the competitive reactant. Control experiments (Figure 3a,c, gray traces) show that [Ru(bpy)₃]³⁺ reduction (estimated from the 450 nm bleach recovery) in the absence of α₃Y is negligible on the time scale of the Y32 PCET reaction. Additional control experiments suggest that the competing reaction is oxidation of trace amounts of impurity in trifluoroacetic acid (TFA; vide infra) that remains after the final reversed-phase HPLC step in the purification of α₃Y.

Figure 4.

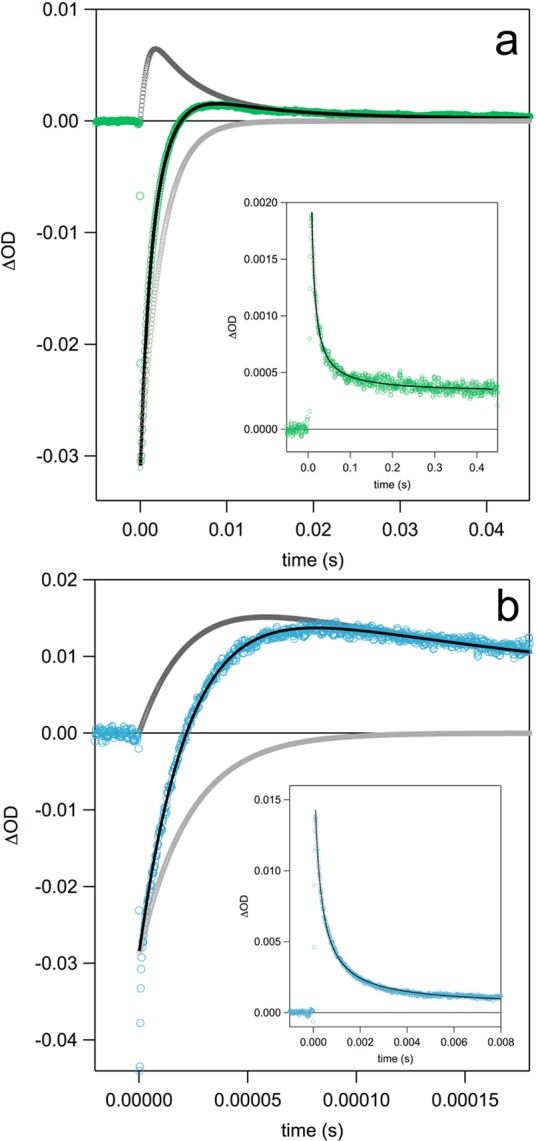
TA traces corresponding to l-tyrosine collected at 410 nm after laser excitation. The traces follow the growth and decay of the l-tyrosine radical at (a) pH 5.5 and (b) pH 8.5 with separate fits (black) to a model for concurrent pseudo-first-order growth and second-order decay. Contributions to the 410 nm signal from Y–O• and [Ru(bpy)₃]²⁺ recovery are shown in dark gray and light gray, respectively. Insets show the decay of the l-tyrosine radical with fits to second-order decay (black). Conditions were the same as in Figure 3 except that the experiments were carried out in H₂O. α₃Y was replaced with 260 μM l-tyrosine.

Figure 3 shows TA signals recorded at 450 and 410 nm at pD 5.5 and 8.5 with 410 μM and 940 μM α₃Y, respectively. The fits at 450 and 410 nm gave the same value for k_obs within experimental uncertainty. TA traces and corresponding fits for all other pH(D) and [α₃Y] conditions are given in the Supporting Information. Figure 4 shows TA traces and fits collected at 410 nm for l-tyrosine. Rate constants for PCET and radical yields for [α₃Y] and l-tyrosine are summarized in Table 2. Rate constants for PCET were obtained from the relationships: k_obs = [α₃Y] × k_PCET + [X] × k_COMP and Yield(Y32–O•) = [α₃Y] × k_PCET/k_obs.

Control experiments using a Y32F variant of α₃Y, α₃F, were carried out to test for possible photochemical reactivity of the protein scaffold. α₃F is predicted to be redox inert as the reduction potential of phenylalanine ≫ E°′[Ru(bpy)₃]^3+/2+. α₃F control experiments were conducted at pH 5.5 and 8.5 under identical conditions to the photochemical α₃Y studies (Figure S6). At both pH 5.5 and 8.5, α₃F showed behavior identical to what was observed for solutions containing only [Co(NH₃)₅Cl]²⁺ and [Ru(bpy)₃]²⁺ after 4–5 laser shots were supplied to the sample. This shows that α₃F does not react with [Ru(bpy)₃]³⁺ on the time scale examined. The first few shots to α₃F samples showed a kinetic response that diminished with each subsequent shot (Figure S6). This kinetic response is attributed to a trace amount (ca. 10 μM) of impurity in TFA that is quickly consumed within a few laser shots. Both α₃F and α₃Y are isolated by reversed-phase HPLC using a standard water/acetonitrile/TFA(0.1% w/v) solvent system and then freeze-dried. Most of the TFA is expected to evaporate during the lyophilization step, but some fraction will remain in the dried protein powder. One additional flash photolysis control experiment was carried out with [Ru(bpy)₃]²⁺, [Co(NH₃)₅Cl]²⁺ and ∼10 mM TFA (Figure S7). The TFA experiment showed a nearly identical kinetic response to that of the α₃F control (Figure S6). Based on the observation that the photochemically active impurity is consumed after only a few laser shots, it is clear that neither the α₃F protein nor TFA is oxidized by [Ru(bpy)₃]³⁺. We conclude that a small impurity in TFA is oxidized to regenerate [Ru(bpy)₃]²⁺ under the experimental conditions used in this study (see Supporting Information for further details).

Importantly, the α₃F control experiments demonstrate that there is no competitive reactivity with [Ru(bpy)₃]³⁺ from the α₃ protein scaffold itself. This conclusion is consistent with earlier voltammetry studies showing that there is no Faradaic current from the protein scaffold at pH 5.5, 7.0, and 8.5 up to at least 1.4 V versus NHE.^28,30,31

We found that α₃Y PCET rate constants were strongly pH dependent with k_PCET equal to 1.8 × 10⁵ and 1.4 × 10⁴ M^–1 s^–1 at pH 8.5 and 5.5, respectively. α₃Y samples were prepared in D₂O buffer to exchange the phenolic proton on the Y32 side chain. In D₂O slower and strongly pH-dependent rate constants were observed with k^D_PCET equal to 4.0 × 10⁴ M^–1 s^–1 and 5.4 × 10³ M^–1 s^–1 at pD of 8.5 and 5.5, respectively. The KIE (= k^H/k^D) was found to be ∼4.5 for pH 8.5 and ∼2.5 for pH 5.5. Samples of α₃Y prepared in D₂O were incubated for 2–10 h prior to measurement to allow for isotopic exchange. The samples gave the same kinetic behavior irrespective of the exchange time suggesting that the H/D exchange was complete in <2 h. The pH-dependence of the PCET rates and the significant KIE is not consistent with a stepwise ETPT (electron-transfer followed by proton-transfer) reaction. Deprotonation of Y32–OH•+ would be ultrafast (pK_OX < 0) and the overall reaction therefore rate limited by the initial pH-independent ET step. The significant KIE indicates involvement of proton transfer in the rate-determining step suggesting that Y32 oxidation occurs via a concerted PCET reaction (CEPT) or a proton-first mechanism (PTET). Possible primary and secondary proton acceptors include protein residues near the Y32 oxygen, protein water, bulk water, and buffer molecules, e.g., HPO₄^2–.^65,66

Kinetics of Y32–O• Decay

In principle, Y32–O• may decay via three different mechanisms: intermolecular radical–radical dimerization where two Y32–O• species couple to form a bityrosine or isobityrosine product, intermolecular radical–protein reaction where Y32–O• reacts with a α₃Y molecule in its nonradical reduced state, and/or intramolecular radical–protein reaction where Y32–O• reacts with a nearby residue. TA kinetic traces were recorded on a long time scale in order to characterize the Y32–O• decay reaction. Figure 5 shows 410 nm decay traces collected from four freshly prepared samples each containing the same starting concentration of α₃Y. Each sample was exposed to a 500 ms long, 447.5 nm LED excitation pulse. Neutral density filters were used to vary the concentration of the light-induced [Ru(bpy)₃]³⁺ oxidant and, consequently, the initial concentration of Y32–O•.

Figure 5.

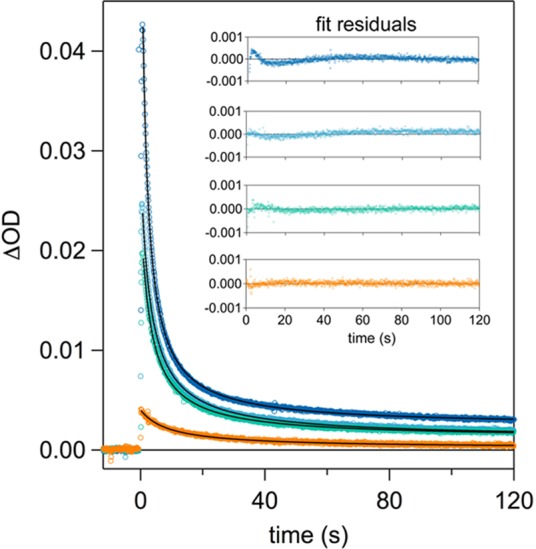
TA kinetic traces recorded at 410 nm for α₃Y at pH 5.5. All excitation pulses at 447.5 nm were 500 ms in duration, where neutral density filters of varying strengths were used to modulate the amount of light supplied to the sample. This gave a wide range of initial Y32–O• concentrations, specifically: 34 μM (dark blue), 21 μM (light blue), 16 μM (green), and 3 μM (orange). The inset of the plot shows residuals to a second-order fit for each trace.

Monoexponential fits (corresponding to a unimolecular or pseudo-first-order process) did not satisfactorily reproduce the kinetic traces in Figure 5. Instead, the kinetics traces were very well fit with a second-order decay fit function that assumed a mechanism of two radical species forming one product (i.e., 2Y32–O• → P). In all four traces, the 410 nm signal does not quite return to baseline. As with the transient difference spectra shown in Figure 2, this can be attributed to the formation of cobalt phosphate/oxide precipitates that scatter UV and visible wavelengths of light (see Supporting Information). The observed t_1/2 (defined as t_1/2 = 1/[Y32–O•]₀ × k₂) is 2, 3, 4, and 10 s for initial Y32–O• concentrations of 34, 21, 16 and 3 μM, respectively.

The notion of a process that is second-order in [Y32–O•] is supported by the following evidence: the second-order fit is satisfactory for all traces in Figure 5 and those given in the Supporting Information (Figure S8) for an observation time that is more than 20 times greater than t_1/2. That is, the observation window is sufficiently long that significant deviations from second-order kinetics would be obvious. Although the initial concentration of Y32–O• varied by a factor of 10 in the series of experimental traces shown in Figure 5, the second-order rate constant varied by no more than a factor of 2.5. Specifically for initial Y32–O• concentrations of 34, 21, 16, and 3 μM the second-order rate constant was 1.4 × 10⁴, 1.5 × 10⁴, 1.7 × 10⁴, and 3.4 × 10⁴ M^–1 s^–1, respectively. The trace with the lowest initial Y32–O• concentration (3 μM) was the outlier of the series. The deviation of this sample from the others in this series (and the traces displayed in Figure S8) can be explained by interference from scattered light by cobalt phosphate/oxides. This interference will be more pronounced for TA traces with smaller amplitudes. Despite the deviation in rate, the TA trace recorded on the 3 μM α₃Y sample was best fit to a second-order model. This series of flash photolysis measurements demonstrates that the second-order rate constant of decay has, at most, a small dependence on the initial Y32–O• concentrations, while the radical t_1/2 value decreases with increasing initial concentration. The kinetics is thus consistent with an intermolecular dimerization mechanism where two radicals react to form one product. The second-order dependence on Y32–O• concentration is not consistent with an intermolecular radical–protein mechanism where the Y32–O• radical reacts with a reduced α₃Y molecule. This would manifest as a pseudo-first-order process on the basis that [reduced α₃Y] ≫ [oxidized α₃Y] and give a monoexponential decay. Nor are the observed decay characteristics consistent with an intramolecular radical-protein reaction, which would also show monoexponential decay consistent with a unimolecular process.

Spectroscopic analysis of the protein products following photolysis provides the second piece of evidence for a decay process that is second-order in [Y32–O•]. Dityrosine is a well-known marker for radiolytically induced tyrosine radical–radical dimerization.^{20−22,67,68} These dimer species exhibit a characteristic emission whose maximum appears around 410 nm. To investigate whether photochemically treated α₃Y exhibited this characteristic emission spectrum, reacted protein solutions were dialyzed to remove sensitizer and quencher molecules. Once isolated, the emission spectrum of the protein products was recorded at an excitation wavelength of 325 nm and gave a spectrum with a maximum centered at 402 nm. Further, a fluorescence excitation spectrum of the protein products was recorded and was consistent with reported excitation spectra for dityrosine. To confirm that the emission spectrum was unique to the photolyzed protein reaction products, an emission spectrum of non-photolyzed α₃Y was recorded at an excitation wavelength of 310 nm. The sample of unreacted α₃Y was nonemissive under these conditions, indicating that the emission in photolyzed samples is due to photochemically produced protein products. The emission spectrum of l-tyrosine flash photolysis products was also recorded and showed a strikingly similar spectrum (centered at 404 nm) to that of α₃Y photoproducts (see Figure S9), which provided further evidence for dimer formation as the pathway for Y32–O• decay. Absorption spectra, emission spectra, and further details are provided in the Supporting Information.

The l-tyrosine data shown in Figure 4 provide a clear contrast to the observed Y32–O• decay kinetics. The lifetime of the l-tyrosine radical is much shorter, and second-order fits gave a rate constant of k_Y–O• = 2–7 × 10⁸ M^–1 s^–1, which is in agreement with previously reported rate constants for Y–O• dimerization.^22,69 The rate of dimerization in l-tyrosine is more than 4 orders of magnitude larger than for α₃Y, demonstrating the remarkable stabilization effect of the protein.

CD spectroscopy and gel-filtration control measurements were conducted to check for perturbing interactions between the protein and the photochemical system. Figure S10A displays CD spectra that confirm that the helical content of α₃Y remains the same in the absence and presence of 40 μM [Ru(bpy)₃]Cl₂. Equivalent CD spectra could not be obtained on samples containing [Co(NH₃)₅Cl]Cl₂ due to total light absorption/scattering at relevant concentrations of the quencher, even when using a short path length cuvette. Gel-filtration chromatograms were obtained from α₃Y samples containing the sensitizer or the quencher. α₃Y remains monomeric, and there is no indication of dimerization in the presence of either 40 μM [Ru(bpy)₃]Cl₂ or 4 mM [Co(NH₃)₅Cl]Cl₂ (Figure S10B–D). Thus, the photochemical system does not pre-induce dimer formation prior to light absorption and radical generation. These results are consistent with the electrostatic considerations since the species involved are all cationic at the conditions used for the flash-quench measurements. α₃Y has a calculated isoelectric point of 9.4⁷⁰ and is thus predicted to carry a net positive charge at both pH 5.5 and 8.5.

General Discussion and Concluding Remarks

Y32 is buried inside the hydrophobic core of α₃Y (Figure 1b,e), and the residue exhibits effectively no SASA (Table S1). The atoms associated with the Y32 side chain and the phenol oxygen have an average depth of 8.1 ± 0.4 and 6.3 ± 0.4 Å, respectively. Aliphatic CH, CH₂, and CH₃ groups dominate the protein pocket in which the Y32 side chain resides. There are no hydrophilic groups close to the phenol oxygen and, consequently, no obvious primary proton acceptor/donor. Yet, voltammetry studies show that Y32 can be reversibly oxidized and reduced and that the protein stays overall charge neutral on the time scale of the electrochemical measurements.³² That is, redox-driven proton release and uptake occur on the sub-ms time scale. In this study we provide evidence that photochemical oxidation of Y32 occurs via a PCET process yielding a significant amount of Y32–O• (up to 58%) that slowly decays (t_1/2 2–10 s) via an intermolecular radical–radical dimerization reaction (Tables 2 and S2). In the following section we discuss these observations and propose that Y32–O• formation and decay are to some extent conformationally controlled events.

We directly observe photogeneration of Y32–O• via an oxidant in solution, on a ms to s time scale, providing evidence for a PCET reaction. There is no discernible intermediate between the recovery of [Ru(bpy)₃]²⁺ and the formation of Y32–O• (Figure 3). Should PCET proceed via a stepwise, PTET mechanism, the intermediate Y32–O^– species would be short-lived and not accumulate. The lack of an observable intermediate does therefore not prove that the reaction is concerted, although the strongly pH-dependent rates and the significant KIE are consistent with a CPET reaction. Until further pH-dependent kinetic data have been obtained, we cannot rule out the possibility of a stepwise PTET mechanism. However, we can rule out that the oxidation reaction occurs via an equilibrium fraction of solvent-exposed Y32–O^–. For l-tyrosine and phenol (pK_red values ∼10) the deprotonated tyrosinate/phenolate species is very reactive and therefore gives a major contribution to the observed k_PCET even at pH 8.5.⁷¹ The pK_red of Y32 is higher (11.3),^25,30 and at pH 5.5 the small fraction of Y32–O^– (on the order of 1 × 10^–6) cannot account for the observed value of k_PCET = 1.3 × 10⁴ M^–1 s^–1, not even with a diffusion controlled rate. At pH 8.5 the reaction via Y32–O^– is, at most, of minor importance. This can be understood by comparing the rate increase from pH 5.5 (where the tyrosine form dominates the reaction for both α₃Y and l-tyrosine) to pH 8.5, which is much weaker for α₃Y than for l-tyrosine (Table 2). Specifically, k_PCET from pH 5.5 to 8.5 increases 10- and 100-fold for α₃Y and l-tyrosine, respectively (Table 2).

It is also important to point out that Y32 oxidation cannot occur only via the globally unfolded state of α₃Y. The fraction of unfolded protein is <0.3% at both pH 5.5 and 8.5 (Figure S1). This is not consistent with the relative values of k_PCET for α₃Y and l-tyrosine above. If globally unfolded α₃Y would be the only photochemically active species, the difference in k_obs between Y32 and l-tyrosine should be considerably larger than the experimentally observed numbers. Further, if protein unfolding/folding is much slower than the PCET reaction, the concentration of globally unfolded α₃Y in the sample (<1 μM) is too small to account for the complete consumption of flash-generated [Ru(bpy)₃]³⁺ (3–9 μM/flash) with the pseudo-first-order kinetics that we observe. Instead, we can be confident that PCET occurs through bimolecular encounter of [Ru(bpy)₃]²⁺ with folded α₃Y and electron tunneling through the protein matrix. The lower k_PCET of Y32 relative to the k_PCET of l-tyrosine can be explained by the longer electron-tunneling distance (Figure 1f) and the smaller translational diffusion coefficient of the α₃Y macromolecule (1.47 ± 0.01 × 10^–6 cm² M^–1)³² relative to the l-tyrosine molecule. Another likely contribution could be a less facile deprotonation of Y32 and/or a longer proton-tunneling distance. We will return to this issue below.

The radical stabilization effect of the protein is dramatic, leading to a t_1/2 range of 2–10 s under the present experimental conditions. The good agreement with second-order kinetics suggests predominantly decay by intermolecular radical–radical coupling (Figures 5 and S8, Table S2). This conclusion is supported by the detection of an emission spectrum consistent with dityrosine from photochemically treated α₃Y samples (Figure S9). The kinetics also suggests that an intramolecular reaction of Y32–O•, by, e.g., hydrogen-atom abstraction or coupling to neighboring residues, is negligible during its lifetime. The protein matrix thus provides excellent protection for the radical, while allowing Y32 to undergo reversible PCET reactions in voltammetry experiments.

Examination of the Y32 site provides an explanation for the high stability of Y32–O•. The distribution of the unpaired electron in Y–O• radicals follows an odd-alternate pattern with high spin densities at the para (CG) and ortho (CE1 and 2) ring carbons and at the phenol oxygen.⁷² In tyrosine the para position is sterically protected, and reactions occur mainly at the ortho carbons and the phenol oxygen. Four aliphatic residues, V9, L12, V55, and L58, are found near the Y32 side chain (Figure 6). Fifteen methyl hydrogens reside within 3 Å of the Y32 ortho carbons and phenol oxygen. Five additional aliphatic hydrogens are within 4 Å of these ring positions. In contrast, the closest carboxyl (from E13 and E59) and amine (from K8 and K15) hydrogens are on an average between 5 and 10 Å from the predicted reactive positions of the Y32 aromatic ring. Likewise, the closest backbone amide hydrogens (from L12, E13 and K56) are at a distance of about 5–6 Å. Small-molecule studies have shown that phenol radicals are 4–5 orders of magnitude less reactive in abstracting hydrogen atoms from C–H bonds relative to O–H bonds.^12,15,73,74 It is likely that the high stability of Y32–O• arises from a situation in which only C–H bonds are in the direct vicinity of Y32–O•.

Figure 6.

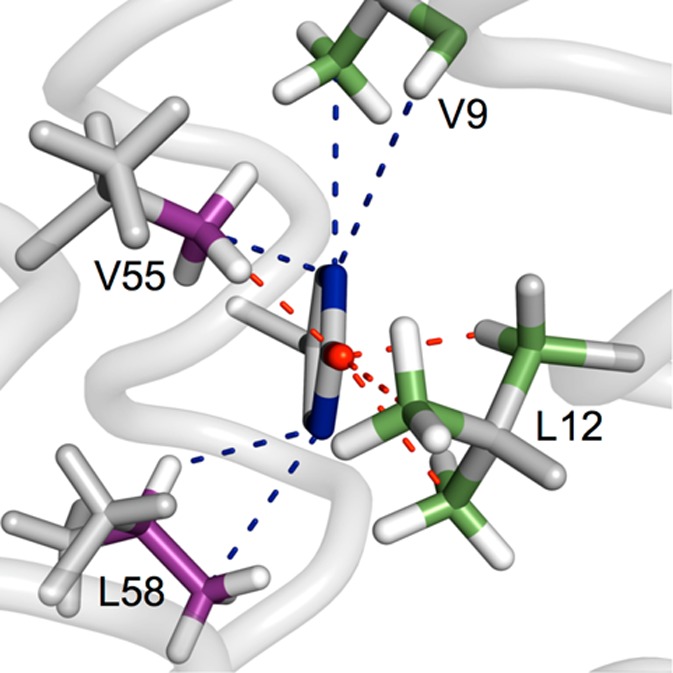
Atoms found close to the ortho ring positions (Y32 CE carbons, blue) and the phenol oxygen (Y32 O, red) of Y32. The radical spin density is high at these ring positions, which makes them particularly reactive toward the surrounding environment. The average atom–atom distances found in the α₃Y NMR structure are Y32CE/V9CG3 3.27 ± 0.05 Å; Y32CE/V9HA 3.90 ± 0.14 Å; Y32O/L12HB3 2.19 ± 0.04 Å; Y32O/L12CD3 2.74 ± 0.11 Å; Y32CE/L12CD2 2.80 ± 0.13 Å; Y32CE/L58CD3 3.52 ± 0.17 Å; Y32CE/L58HG 2.85 ± 0.15 Å; Y32O/V55CG2 2.78 ± 0.07 Å; and Y32CE/V55CG2 3.09 ± 0.12 Å.

As described above, Y32 is completely buried (Figure 1), and it is unclear (i) how the phenolic proton released upon oxidation is removed and (ii) how two Y32–O• species are able to combine to form dityrosine. A search for protein cavities⁴³ predicted a pocket ∼4 Å from the Y32 phenol oxygen in only 14 of the 32 structures that form the NMR ensemble. Even if a pocket is present, it may not be occupied by water.⁷⁵ Thus, the native structure does not provide a clear candidate for the primary proton acceptor, and it seems that a partially unfolded state is required. It is important to emphasize that proteins constantly interconvert between the native fully folded structure and minor populations of partially unfolded states. This occurs with all proteins and is often an important part of their function.³⁵ These structural fluctuations can broadly be divided into local (e.g., movement of a single side chain), subglobal (e.g., transient unfolding/folding of a secondary structure such as an α-helix), and global (transient unfolding/folding of the entire protein) events. For α₃Y, local and/or subglobal unfolding may be involved in radical formation by proving an essential proton-tunneling configuration in the oxidation process. This could, e.g., occur by transient water or buffer access to the Y32 site. Local, subglobal, and/or global unfolding must be involved in radical decay by allowing two Y32–O• species to come in close contact. Importantly, this predicts that the free energies between the native state and partly unfolded states are key parameters controlling the stability of protein tyrosine radicals. In order to fully understand the radical chemistry it appears important to investigate the nature of the ensemble of states that α₃Y occupies. Studies are in progress to address this issue.

In conclusion, structural fluctuations in the protein matrix appear to be involved in both the oxidation process and in the decay of the radical. Radical formation following a CEPT or PTET mechanism from the fully folded native state of α₃Y is unlikely since there is no proton acceptor near the Y32 side chain. Oxidation solely from the globally unfolded state can also be excluded, for reasons described in detail above. Thus, local (e.g., movement of a single side chain allowing transient access of water into the Y32 site) and/or subglobal (e.g., transient unfolding of a helical segment increasing the exposure of Y32) events must be involved in the generation of the Y32–O• state. Since tunneling of protons is much more sensitive to distance than that of the electrons, due to the larger mass of the former, we tentatively suggest that protein dynamics mainly influence the proton component of the CEPT/PTET process. Electron tunneling from the Y32 side chain to the soluble [Ru(bpy)₃]³⁺ oxidant should less sensitive. We further conclude that locally, subglobally, and/or globally unfolded states could partly or all be involved in radical–radical dimerization. Future work will aim to resolve what structural fluctuations (states) control Y32–O• formation (by controlling the coupled protonic reactions) and its decay (by controlling radical–radical contact). These results highlight that studies of protein model systems, rather than small-molecule or peptide systems, not only allow for a higher level of design of the PCET reaction environment but also offer the possibility to gain insight into PCET in biology and illuminate possible mechanisms for protein radical formation, stabilization, and decay.

Supporting Information Available

SASA analysis; urea denaturation plots; cobalt phosphate/oxide characterization; description of fitting routines; kinetic fits and simulations for α₃Y; TA kinetics traces of α₃F and TFA control experiments; additional TA kinetic traces of Y32–O• decay; steady-state absorbance/fluorescence spectra for α₃Y and l-tyrosine. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States