Folding Simulations for Proteins with Diverse Topologies Are Accessible in Days with a Physics-Based Force Field and Implicit Solvent

Abstract

The millisecond time scale needed for molecular dynamics simulations to approach the quantitative study of protein folding is not yet routine. One approach to extend the simulation time scale is to perform long simulations on specialized and expensive supercomputers such as Anton. Ideally, however, folding simulations would be more economical while retaining reasonable accuracy, and provide feedback on structure, stability and function rapidly enough if partnered directly with experiment. Approaches to this problem typically involve varied compromises between accuracy, precision, and cost; the goal here is to address whether simple implicit solvent models have become sufficiently accurate for their weaknesses to be offset by their ability to rapidly provide much more precise conformational data as compared to explicit solvent. We demonstrate that our recently developed physics-based model performs well on this challenge, enabling accurate all-atom simulated folding for 16 of 17 proteins with a variety of sizes, secondary structure, and topologies. The simulations were carried out using the Amber software on inexpensive GPUs, providing ∼1 μs/day per GPU, and >2.5 ms data presented here. We also show that native conformations are preferred over misfolded structures for 14 of the 17 proteins. For the other 3, misfolded structures are thermodynamically preferred, suggesting opportunities for further improvement.

Proteins typically function properly only after folding into a specific three-dimensional structure. Experimental techniques can very accurately determine folded structures, as evidenced by greater than 90 000 structures available in the protein data bank.¹ However, this remains a small subset of the number of known sequences.² Moreover, folding is a dynamic process, involving transitions among many unfolded states.^3,4 Insight to the factors controlling the folding landscape is crucial to designing proteins with new or enhanced functionality, determining the structures of proteins not yet characterized experimentally, or understanding detrimental effects of protein misfolding and aggregation.

Atomistic simulation models could potentially elucidate folding with full spatial, temporal and energetic resolution, but millisecond-scale simulation is far from routine.⁵ One way around the time scale problem is approaches like Rosetta, where a combination of empirical and physical rules aids in the prediction of the final native coordinates.⁶ Limited experimental data can also be used to focus the search.^7,8 The structural optimization approach, however, does not provide physical details about the folding process, and may be less useful for misfolded, disordered, or dynamic proteins where physics-based approaches may be more successful. Folding@Home uses distributed computing to harvest numerous but relatively short simulations, which can be assembled into models describing folding.⁹ Recently, Shaw and colleagues used the specialized Anton supercomputer¹⁰ to fold 12 proteins.¹¹ This brute-force calculation spanning ∼8 ms remains state of the art.

Is there a way to simulate protein folding dynamics in atomic resolution using inexpensive computer hardware that would make these protocols more widely accessible? Implicit solvent models can dramatically accelerate folding due to lower viscosity that facilitates chain diffusion.¹² Pairwise variants of the generalized Born (GB) model¹³ perform particularly well on inexpensive GPUs,¹⁴ leveraging a vast consumer video game market to make folding simulations more widely accessible. However, many fast GB models are inaccurate,¹⁵ often with incorrect secondary structures preferences and ion pair strength, thus succeeding in anecdotal cases but lacking broad transferability. GBMV2¹⁶ is arguably the most accurate GB model, but at a cost of reduced speed. The best performing combination of implicit solvent and protein force field can result from fortuitous cancellation of error in models that have significant but sometimes compensating weaknesses.¹⁷

Recently, we reported development of a new fast pairwise GB model that was trained to reproduce more accurate Poisson–Boltzmann solvation across a broad range of peptide and protein systems.¹⁸ Here, we combine it with our widely used ff99SB protein force field,¹⁹ along with our recently updated protein side chain parameters.²⁰ The solvent and protein energetics were trained for independent accuracy, in an attempt to avoid cancellation of error and improve transferability. In this report, we demonstrate that this new physics-based combined model is an attractive trade-off, enabling accurate folding for all but 1 of a set of 17 proteins ranging from 10 to 92 amino acids.

We address two key issues in detail: the sampling problem (whether simulations can fold to the correct structure) and the accuracy problem (whether the preferred structure in the simulated ensemble is native-like). An additional aspect of simulated folding is whether the overall nature of the energy landscape is accurately modeled (e.g., can the model reproduce experimental measurements of protein stability or folding cooperativity). While desirable, such studies are beyond the focus of this report.

Peptides and proteins studied. A total of 17 systems were simulated (Supporting Information, Table S1), including 12 studied by Shaw and colleagues:¹¹ CLN025, Trp-cage, BBA, villin HP36, WW domain GTT, NTL9₃₉, BBL, protein B, homeodomain 2P6J, the NuG2 variant of protein G, α3D, and λ-repressor. We added a second WW domain (Fip35), and several larger systems: NTL9₅₂, cold shock protein A (CspA), hypothetical protein 1WHZ, and Top7. Unless otherwise noted, RMSD values are for Cα atoms in regions well-defined in structures based on experiments, as are fraction of native contacts (Q).

Simulation details. All MD simulations used the GPU implementation¹⁴ of pmemd in AMBER14²¹ with the combination of GB-Neck2,¹⁸ mbondi3 intrinsic radii,¹⁸ and ff14SBonlysc, which includes ff99SB¹⁹ with new side chain dihedral parameters from ff14SB.²⁰ We did not use the backbone dihedral modifications from ff14SB, since they are empirical adjustments aimed at improving agreement between experiment and simulations in explicit water. The protocol delivered 0.6 to 1.4 μs/day (Table S2). Additional details are provided as Supporting Information.

Our goal in this study is to investigate feasibility of simulating all-atom folding for a variety of proteins with a single force field and solvent model combination, using widely available computer hardware and software. Systems range from short peptides to proteins of nearly 100 amino acids, with topologies including all α-helix, all β-sheet, and combinations. Experimental folding times vary from microseconds to seconds (Table S2).

We first performed a baseline study on native state dynamics of 2 proteins, CspA and lysozyme, and compared backbone order parameters from the resulting simulations to those obtained from experiment as well as from simulation with explicit water (Figure S1). We obtained excellent quantitative agreement (0.05 and 0.02 RMSD to experimental and TIP3P S² for CspA, and 0.02 RMSD to both experimental and TIP3P S² for lysozyme), suggesting that more challenging tests were warranted.

We separate our analysis of protein folding below along two general goals. First, we address sampling: despite the limitations of the implicit solvent model, can standard MD simulations properly fold to the correct experimentally determined structure when starting from a fully extended conformation? Second, we address accuracy: is the experimental structure also the most favorable in our model? The latter goal is significantly more challenging; the physics must be accurate enough to reproduce the correct global free energy minimum for a variety of topologies and secondary structure combinations, and the populations of the minima must be well converged in order to make precise predictions. For several of the larger systems studied here, convergence was not readily achieved in standard MD, and thus we used replica exchange (REMD²²). The ability to use REMD supports our premise that in some cases disadvantages of implicit solvent can be offset by significant advantages; although ∼1 μs REMD in explicit water for proteins up to ∼40 amino acids has been reported (for example, see ref (23)), it currently remains computationally intractable for proteins of the size studied here, especially with solvent box sizes large enough to enclose unfolded conformations.²⁴

Can simulations fold to native conformations? Simulations starting in extended conformations were able to locate structures in excellent agreement with experiment for 16 of the 17 systems (Table S2). All of the proteins smaller than 50 amino acids fold well in standard MD on this time scale, reaching Cα RMSD values below 2 Å, except BBL which reaches 3.2 Å (all time series data are in the Supporting Information). This includes systems with β-sheet (the hairpin CLN025 and the 3-stranded sheets Fip35 and GTT), α-helix (tc5b, HP36, and protein B) and mixed α/β (BBA and NTL9₃₉). In REMD, these systems all fold to <2.1 Å Cα RMSD and contact fractions Q > 0.9, with minimum RMSD values often below 1 Å. While it is beyond the scope of this work to fully analyze side chain packing accuracy, the heavy atom RMSD of the Fip35 conformation with the lowest Cα RMSD is 1.8 Å, while that of NTL9₃₉ is 1.0 Å, suggesting that highly accurate folding is achievable with our protocol.

The larger proteins (50–92 amino acids) tend to become kinetically trapped in standard MD on the microsecond time scale, with only the entirely α-helical proteins homeodomain (1.9 Å), α3D (2.5 Å), and λ-repressor (4.4 Å) finding native-like conformations. The enhanced sampling in REMD provides notable benefit, with 16 of the 17 proteins now folding to structures with RMSD under 3 Å (Figure 1). Only the NuG2 variant was unable to sample the correct conformation; the minimum RMSD is 4.8 Å and the maximum Q is ∼0.6 (Figures S51–S54). Here, folding successfully occurs for the region including the first hairpin and helix, but the second hairpin has not yet formed. NuG2 simulations initiated from the experimental structure underwent unfolding to ∼10 Å RMSD, followed by refolding to an accurate native state (<1.0 Å RMSD, Figure S51).

Figure 1.

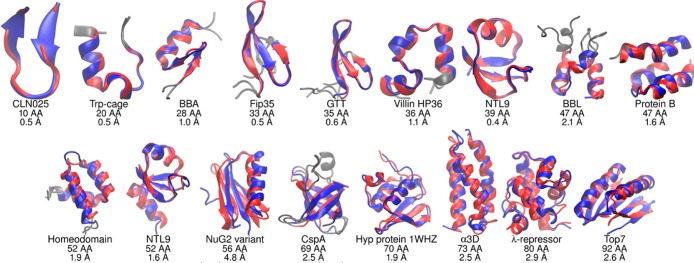
Comparison of structures based (red) on experiment and (blue) lowest RMSD in simulations started from extended conformations. Under each structure is shown the protein name, chain length, and Cα RMSD value (gray regions were poorly defined by experiment and are excluded, see text for details).

One advantage of simulating folding is that it is possible to analyze folding pathway(s). Direct comparison to kinetics experiments is precluded by our use of low viscosity to enhance sampling. Instead, we consider the relative flux through folding pathways, presenting one example since a comprehensive analysis is beyond the scope of the present manuscript. We analyzed which of the 2 hairpins in Fip35 folded first in 12 folding events seen in MD from the extended structure (Figure S20). The 4:1 ratio for hairpin 1 folding first is in excellent agreement with the 4:1 ratio reported for explicit solvent simulations of the same system.²⁵

Does the model show the correct structure preferences? Next, we address the more challenging issue of accuracy, and whether our model could predict a qualitatively reasonable structure if it were not already known, by comparing the experimental structure to the most populated simulation cluster. For 10 of 17 systems, multiple (>3) folding and unfolding events were observed in the standard MD runs; however, the larger proteins remained poorly converged even on the microsecond time scale. We therefore use the REMD ensembles to obtain qualitative estimates of the preferred conformations for each protein. The cluster with the largest population was in good agreement with conformations based on experiment for roughly half (8 of 17) of the proteins studied (RMSD values are provided in Table S2, with structures shown in Figure S2). Once again, performance tended to be better for proteins under 50 amino acids, with CLN025, Trp-cage, Fip35, GTT, HP36, and NTL9₃₉ all preferring the correct structure, with representative structure RMSD values of 0.6–2.3 Å. For protein B, the representative structure has an RMSD value of 4.2 Å: properly folded but with a slight rotation of the middle helix relative to the core. In the case of BBA, the native zinc finger fold is present in the ensemble, but with lower population than the preferred alternate structure with RMSD of 4.6 Å, in which the hairpin and helix are both still present, but with somewhat longer hairpin and shorter helix. Although NTL9₅₂ folds properly in the simulations, the 6.0 Å RMSD for the most populated cluster reflects an otherwise properly folded structure with an alternate conformation of the loop connecting β-strands 1 and 2. Neglecting this loop, the RMSD of the largest cluster becomes a more reasonable 4.2 Å (Figure S46). The only protein under 50 amino acids that prefers an incorrect fold is BBL, which locates the correct fold from extended structures, but favors a conformation with 8.3 Å RMSD in which the region connecting the N- and C-terminal helices becomes disordered. However, the second and third most populated clusters have more reasonable RMSD values of 4.3 and 4.8 Å. Lindorff-Larsen et al.¹¹ estimated a very low melting temperature in BBL simulations (270 ± 10 K), suggesting that BBL also challenges MD with explicit water. For the other seven proteins >50 amino acids, only homeodomain and α3D have most populated clusters (23% and 33%, respectively) that are close to the experimental fold (3.2 and 4.0 Å, respectively). The second most populated cluster of homeodomain (8%) is even closer to experiment (2.3 Å). For both systems, differences are predominantly in the surface loops; RMSDs for the 3 helices are 2.5 Å for homeodomain and 2.1 Å for α3D.

As discussed above, the NuG2 variant was the only system that never sampled the native conformation, thus the cluster populations cannot report on whether the correct structure would be preferred if folding had occurred. To explore this further, we carried out an additional ∼40 ns “seeded” REMD simulation continuing from the end of the previous one, but adding two equilibrated native structures at two new temperatures in the middle of the previous temperature ladder (see Supporting Information). Our expectation was that the REMD exchanges would sort the more favorable structures at the lower temperatures. The simulations showed a strong preference for the native fold over the other structures, moving both low RMSD structures to low temperatures (Figure S55). We next competed six native and six misfolded structures from the initial REMD run. The native structures were again strongly preferred at low temperature (Figure S56), suggesting that our model correctly identifies the NuG2 native fold, and misfolding represents a sampling failure.

The other four systems for which the largest cluster in REMD was non-native (RMSDs of 10–12 Å) were CspA, 1WHZ, λ-repressor, and Top7. In each case, examination of RMSD history for each of the replicas in REMD showed that only a few replicas properly folded, and likewise, only a few misfolded. The data suggest that even though the structures are reproducibly sampled, REMD remains unreliable for distinguishing the relative stability of these alternate conformations. We again turned to a seeded REMD approach for gaining additional insight into the conformational preferences of our model. In each case, native-like structures were alternated in the temperature ladder with representative structures from misfolded clusters with large populations (Figures S61, S68, S77, S86). The results suggest that, among the four proteins with unconverged ensembles, our model can accurately identify the native conformation for CspA and Top7. For CspA, only two replicas misfolded in REMD, and two others located a near-native fold, suggesting poor population convergence even after ∼30 μs of REMD, which is perhaps not surprising given the experimental folding rate of ∼5 ms.²⁶ REMD seeded with native, near-native, and misfolded structures showed a strong preference for the native structure at the lowest temperatures. Top7 showed similar behavior, with the highest population misfolded structure only being sampled by 1 REMD replica. Seeded REMD combining the misfolded and correctly folded structures showed a strong preference for the correct fold, moving all misfolded structures to higher temperatures. Interestingly, two of the Top7 replicas that were initially misfolded underwent spontaneous refolding to the correct structure during this run. The results provide additional evidence that that our model prefers the native fold and that the variety of kinetic traps that the Top7 simulations encountered was a result of the noncooperative, seconds-time scale folding experimentally observed for this system.²⁷

In contrast to the other systems, the seeded REMD results suggest that the model fails to accurately recognize the native conformation of λ-repressor and 1WHZ, preferring misfolded over native structures at low temperature. λ-repressor shows transient folding to the native structure in REMD, but prefers a misfolded structure with the 5 α-helices largely present, but packed against the first helix in a clockwise fashion, rather than counterclockwise as seen in the native fold (SI Figure S87). 1WHZ also folds to the correct structure with a 3-stranded β-sheet and 3 helices, but the preferred structure replaces the first β-strand with a helix and the last two helices with two β-strands. Otherwise, the RMSDs of the first helix and N-terminus (residues 1 to 18) and the second and third β-strands (residues 28 to 44) are both 1.8 Å.

To summarize the analysis of our second goal (conformational preferences), all 11 proteins smaller than 55 amino acids were reasonably converged and all except BBL preferred the native fold, with some differences in loop regions. For the six larger proteins, only α3D appears well converged in the REMD runs, with the others all sampling multiple clusters and having populations that indicated the model favors non-native folds. We used a seeded REMD approach to evaluate the relative populations of native vs non-native folds, and found that NuG2, CspA, and Top7 prefer native conformations, while the model prefers misfolded structures for λ-repressor and 1WHZ. Overall, the data suggest correct preference for the native fold in 14 of the 17 proteins that we studied (Figure S2).

We presented ab initio folding for a set of 17 proteins, ranging from 10 to 92 amino acids, with different topologies and secondary structure content. We used an efficient implicit solvent model¹⁸ combined with an accurate protein force field, using the Amber software running on GPUs. This largely solves the sampling aspect of folding proteins of this size; we demonstrated that folding to the correct structure is achievable for all but 1 of the systems that we studied, within run times of several days to weeks. For the larger proteins where convergence was inadequate, we used REMD to evaluate the extent to which our model could correctly predict preference of native over misfolded structures; such analysis remains highly challenging in explicit water. Despite being able to fold to correct structures, some of the systems showed stronger preference for alternate, non-native structures, ranging from misfolded loops to incorrect topologies. In many of the systems, overall thermal stability also seems too weak in our model, which could be improved with more accurate treatment of nonpolar solvation contributions. Future detailed analysis of possible trends in misfolding, quantitative relative stabilities of the alternate basins, along with application to a larger range of systems, could provide crucial insight into the limitations in accuracy of our models and possible routes for further improvement.

Supporting Information Available

Detailed methods, tables with system details, additional figures, RMSD values, REMD temperatures, cluster populations, plots of RMSD vs time, Q vs time, RMSD histograms, seeded REMD details, structural analysis, and Fip35 folding paths. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

^# H.N. and J.M. contributed equally.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States