Abstract
We present a simple physical model that demonstrates that the native-state folds of proteins can emerge on the basis of considerations of geometry and symmetry. We show that the inherent anisotropy of a chain molecule, the geometrical and energetic constraints placed by the hydrogen bonds and sterics, and hydrophobicity are sufficient to yield a free-energy landscape with broad minima even for a homopolymer. These minima correspond to marginally compact structures comprising the menu of folds that proteins choose from to house their native states in. Our results provide a general framework for understanding the common characteristics of globular proteins.
Protein folding (1–5) is complex because of the sheer size of protein molecules, the twenty types of constituent amino acids with distinct side chains, and the essential role played by the environment. Nevertheless, proteins fold into a limited number (6, 7) of evolutionarily conserved structures (8, 9). It is a familiar, yet remarkable, consequence of symmetry and geometry that ordinary matter crystallizes in a limited number of distinct forms. Indeed, crystalline structures transcend the specifics of the various entities housed in them. Here, we ask the analogous question (10): is the menu of protein folds also determined by geometry and symmetry?
We show that a simple model that encapsulates a few general attributes common to all polypeptide chains, such as steric constraints (11–13), hydrogen bonding (14–16), and hydrophobicity (17), gives rise to the emergent free-energy landscape of globular proteins. The relatively few minima in the resulting landscape correspond to putative marginally compact nativestate structures of proteins, which are assemblies of helices, hairpins, and planar sheets. A superior fit (18, 19) of a given protein or sequence of amino acids to one of these predetermined folds dictates the choice of the topology of its native-state structure. Instead of each sequence shaping its own free energy landscape, we find that the overarching principles of geometry and symmetry determine the menu of possible folds that the sequence can choose from.
Following Bernal (20), the protein problem can be divided into two distinct steps: first, analogous to the elucidation of crystal structures, one must identify the essential features that account for the common characteristics of all proteins; second, one must understand what makes one protein different from another. Guided by recent work (21, 22) that has shown that a faithful description of a chain molecule is a tube and using information from known protein native-state structures, our focus, in this paper, is on the first step: we demonstrate that the native-state folds of proteins emerge from considerations of symmetry and geometry within the context of a simple model.
We model a protein as a chain of identical amino acids, represented by their Cα atoms, lying along the axis of a self-avoiding flexible tube. The preferential parallel placement of nearby tube segments approximately mimics the effects of the anisotropic interaction of hydrogen bonds whereas the space needed for the clash-free packing of side chains is approximately captured by the non-zero tube thickness (21, 22). Here, we carefully incorporate these key geometrical features by means of an extensive statistical analysis of experimentally determined native-state structures in the Protein Data Bank (PDB).
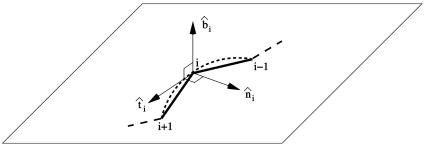
A tube description places constraints on the radii of circles drawn through both local and nonlocal triplets of Cα positions of a protein native structure (22, 23). Furthermore, when one deals with a chain molecule, the tube picture underscores the crucial importance of knowing the context that an amino acid is in within the chain. The standard coarse-grained approach considers the locations of interacting amino acid pairs. Here, instead, we incorporate the strongly directional hydrogen bonding between a pair of amino acids, through an analysis of the PDB to determine the constraints on the mutual orientation of the local coordinate systems defined from a knowledge of the locations of the Cα atoms (see Methods and Fig. 1). The geometrical constraints associated with the tube and hydrogen bonds that we consider here are representative of the typical aspecific behavior of the interacting amino acids.
Fig. 1.
Sketch of the local coordinate system. For each Cα atom i (except the first and the last one), the axes of a right-handed local coordinate system are defined as follows. The tangent vector t̂i is parallel to the segment joining i – 1 with i + i. The normal vector n̂i joins i to the center of the circle passing through i – 1, i, and i + 1, and it is perpendicular to t̂i. t̂iand n̂i along with the three contiguous Cα atoms lie in a plane shown in the figure. The binormal vector b̂i is perpendicular to this plane. The vectors t̂i, n̂i, and b̂i are normalized to unit length.
There are two other ingredients in the model: a local bending penalty, which is related to the steric hindrance of the amino acid side chains, and a pair-wise interaction of the standard type mediated by the water (17). Even though these two properties clearly depend on the specific amino acids involved in the interaction, here, we choose to study the phase diagram of a homo-peptide chain by varying its overall hydrophobicity and local bending penalty, while keeping them constant along the chain. This is the simplest and most general way to assess their relevance in shaping the free-energy landscape.
Methods
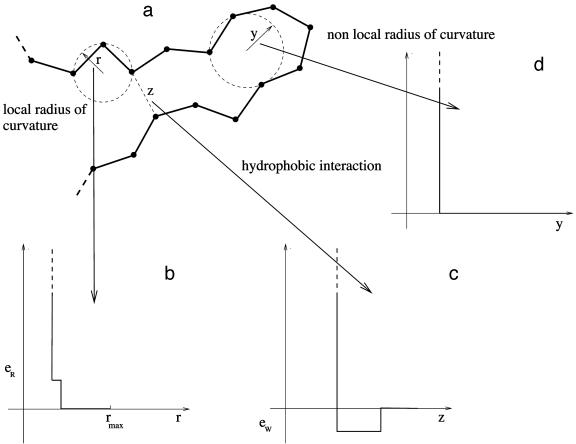
Tube Geometry. The protein backbone is modeled as a chain of Cα atoms (Fig. 2a) with a fixed distance of 3.8 Å between successive atoms along the chain, an excellent assumption for all but non-cis proline amino acids (24). The geometry imposed by chemistry dictates that the bond angle associated with three consecutive Cα atoms is between 82° and 148°.
Fig. 2.
Sketch of a portion of a protein chain. (a) The black spheres represent the Cα atoms of the amino acids. The local radius of curvature r is defined as the radius of the circle passing through three consecutive atoms and is constrained to lie between 2.5 Å and 7.9 Å (rmax). A penalty eR is imposed when 2.5 ≤ r ≤ 3.2 (see b). The hydrophobic interaction, eW, is operative when two atoms separated by more than two along the sequence are within 7.5 Å of each other (see c). Note that two nonadjacent atoms cannot be closer than 4 Å. A flexible tube is characterized by the constraint that none of the three-body radii is less than the tube thickness, chosen here to be 2.5 Å (see b and d).
Self-avoiding conformations of the tube whose axis is the protein backbone are identified by considering all triplets of Cα atoms and drawing circles through them and ensuring that none of their radii is smaller than the tube radius (25) (Fig. 2a). At the local level, the three-body constraint ensures that a flexible tube cannot have a radius of curvature any smaller than the tube thickness, to prevent sharp corners, whereas, at the nonlocal level, it does not permit any self-intersections. There is an inherent local anisotropy due to the special direction singled out by consecutive atoms along the chain, which enforces a preference for parallel alignment of neighboring tube segments in a compact conformation.
The backbone of Cα atoms is treated as a flexible tube of radius 2.5 Å, a constraint imposed on all (local and nonlocal) three-body radii, an assumption validated for protein native structures (23). It is interesting to note that recent observations of residual dipolar couplings in short peptides (26) in the denatured state have demonstrated their stiffness and their anisotropic deformability; the building blocks of proteins are relatively stiff segments with strong directional preferences.
Sterics. Steric constraints require that no two nonadjacent Cα atoms are allowed to be at a distance closer than 4 Å. Ramachandran and Sasisekharan (11) showed that steric considerations based on a hard sphere model lead to clustering of the backbone dihedral angles in two distinct α and β regions for non-glycyl and non-prolyl residues. The two backbone geometries that allow for systematic and extensive hydrogen bonding (14–16) are the α-helix and the β-sheet, obtained by a repetition of the backbone dihedral angles from the two regions, respectively (13). Short chains rich in alanine residues, which are a good approximation to a stretch of the backbone, can adopt a helical conformation in water (see refs. 27–32 for a detailed discussion of experimental conditions that would lead to a helical conformation). However, when one has more heterogeneous side chains, the helix backbone could sterically clash with some side chain conformers, resulting in a loss of conformational entropy (33). When the price in side chain entropy is too large, an extended backbone conformation results, pushing the segment toward a β-strand structure (13). These steric constraints are approximately imposed through an energy penalty (denoted by eR) when the local radius of curvature is between 2.5 Å and 3.2 Å. (The magnitude of the penalty does not depend on the specific value of the radius of curvature, provided it is between these values.) There is no cost when the local radius exceeds 3.2 Å. Note that the tube constraint does not permit any local radius of curvature to take on a value less than the tube radius, 2.5 Å.
Hydrogen Bonds. We do not allow more than two hydrogen bonds to form at a given Cα location. In our representation of the protein backbone, local hydrogen bonds form between Cα atoms separated by two residues along the sequence with an energy defined to be –1 unit whereas nonlocal hydrogen bonds are those that form between Cα atoms separated by more than three residues along the sequence with an energy of –0.7. This energy difference is based on experimental findings that the local bonds provide more stability to a protein than do the nonlocal hydrogen bonds (34). Cooperativity effects (35, 36) are taken into account by adding an energy of –0.3 units when consecutive hydrogen bonds along the sequence are formed. There is some latitude in the choice of the values of these energy parameters. The results that we present are robust to changes (at least of the order of 20%) in these parameters.
Geometrical Constraints Due to Hydrogen Bonding. Three noncollinear consecutive atoms (i – 1, i, and i + 1) of the chain define a plane. At atom i (special care is needed to adapt these rules to atoms at the C and N termini), one may define a tangent vector (along the direction joining the i – 1 and i + 1 atoms) and a normal vector (along the direction joining the ith atom and the center of the circle passing through the three atoms), which together define a plane. One then defines a binormal vector 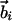 perpendicular to the plane with the tangent, normal, and binormal forming a right-handed local coordinate system (Fig. 1). This coordinate system defines the context of an amino acid within a chain, a feature that plays a crucial role in the tube picture. For hydrogen bond formation between atom i and j, the distance between these atoms ought to be between 4.7 Å and 5.6 Å (4.1 Å and 5.3 Å) for the local (nonlocal) case. A study of protein native state structures reveals an overall nearly parallel alignment of the axes defined by three vectors: the binormal vectors at i and j and the vector
perpendicular to the plane with the tangent, normal, and binormal forming a right-handed local coordinate system (Fig. 1). This coordinate system defines the context of an amino acid within a chain, a feature that plays a crucial role in the tube picture. For hydrogen bond formation between atom i and j, the distance between these atoms ought to be between 4.7 Å and 5.6 Å (4.1 Å and 5.3 Å) for the local (nonlocal) case. A study of protein native state structures reveals an overall nearly parallel alignment of the axes defined by three vectors: the binormal vectors at i and j and the vector 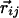 joining the i and j atoms. A hydrogen bond is allowed to form only when the binormal axes are constrained to be within 37° of each other whereas the angle between the binormal axes and that defined by
joining the i and j atoms. A hydrogen bond is allowed to form only when the binormal axes are constrained to be within 37° of each other whereas the angle between the binormal axes and that defined by 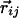 ought to be <20°. Additionally, for the cooperative formation of nonlocal hydrogen bonds, one requires that the corresponding binormal vectors of successive Cα atoms make an angle >90°. The first and the last residues of the chain are special cases because their binormal vectors are not defined. In order for such residues to form a hydrogen bond (with each other or with other internal residues in the chain), it is required that the angle between the associated ending peptide link and the connecting vector to the other residue participating in the hydrogen bond is between 70° and 110°. As in real protein structures, when helices are formed, they are constrained to be right-handed. This constraint is enforced by requiring that the backbone chirality associated with each local hydrogen bond is positive. The chirality is defined as the sign of
ought to be <20°. Additionally, for the cooperative formation of nonlocal hydrogen bonds, one requires that the corresponding binormal vectors of successive Cα atoms make an angle >90°. The first and the last residues of the chain are special cases because their binormal vectors are not defined. In order for such residues to form a hydrogen bond (with each other or with other internal residues in the chain), it is required that the angle between the associated ending peptide link and the connecting vector to the other residue participating in the hydrogen bond is between 70° and 110°. As in real protein structures, when helices are formed, they are constrained to be right-handed. This constraint is enforced by requiring that the backbone chirality associated with each local hydrogen bond is positive. The chirality is defined as the sign of 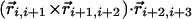 ..
..
Our approach for the derivation of the geometrical constraints imposed by hydrogen bonds is similar to that carried out at the level of an all-atom description of the protein chain (37). For the simpler Cα atom-based description, hydrogen bond energy functions have been introduced previously (38, 39) but without any input from a statistical analysis of protein structures.
Hydrophobic Interactions. The hydrophobic (hydrophilic) effects mediated by the water are captured through a relatively weak interaction eW (either attractive or repulsive) between Cα atoms that are within 7.5 Å of each other (Fig. 2c). Note that hydrogen bonds can easily be formed between the amino acid residues in an extended conformation and the water molecules. Within our model, the intra-chain hydrogen bond interaction introduces an effective attraction, because water molecules are not explicitly present. The hydrophobicity scale is thus renormalized (e.g., even when eW is weakly positive, there could be an effective attraction resulting in structured conformations such as a single helix or a planar sheet). A negative eW is, in any case, crucial for promoting the assembly of secondary motifs in native tertiary arrangements. The properties of the model are summarized in Table 1.
Table 1. Summary of all geometrical and energetical parameters involved in the model definition.
| Parameter | Constraint |
|---|---|
| Tube approximation* | Rijk ≥ 2.5Å, ∀i < j < k |
| Local radius of curvature | 2.5Å ≤ Ri-1,i,i+1 ≤ 7.9Å, ∀1 < i < N† |
| Self-avoidance | rij ≥ 4Å, ∀i < j - 1 |
| Amino acid specific? | No |
| Local hydrogen bond‡ | j = i + 3 |
| Cα-Cα distance | 4.7Å ≤ rij ≤ 5.6Å |
| Binormal-binormal correlation§ | 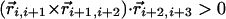 |
| Binormal-connecting vector§¶∥ | 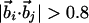 |
| Chirality | 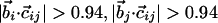 |
| Energy | -1 |
| Amino acid specific? | No |
| Nonlocal hydrogen bond‡ | j > i + 4 |
| Cα-Cα distance | 4.1Å ≤ rij ≤ 5.3Å |
| Binormal-binormal correlation§ | 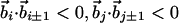 |
| Binormal-connecting vector§¶ | 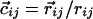 |
| Energy | -0.7 |
| Amino acid specific? | No |
| Cooperative hydrogen bonds | between (i, j) and (i ± 1, j ± 1) |
| β-sheet zig-zag pattern§** | 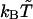 |
| Energy per pair | -0.3 |
| Amino acid specific? | No |
| Bending rigidity | Ri-1,i,i+1 ≤ 3.2Å |
| Energy | eR |
| Amino acid specific? | Yes (for a heteropolymer) |
| Hydrophobic contact | j > i + 2 |
| Cα-Cα distance | rij ≤ 7.5Å |
| Energy | ew |
| Amino acid specific? | Yes (for a heteropolymer) |
All geometrical properties have been derived by means of a thorough analysis of PDB native structures.
Rijk is the radius of a circle drawn through the Cα positions of i, j, and k.
N is the number of residues.
Each residue is constrained to form no more than two hydrogen bonds (except the residues located at the chain termini, which form at most one hydrogen bond).
Applied only when the corresponding binormal vectors exist.
For i = 1 and/or j = N, this is replaced by the constraint that the connecting vector is making an angle between 70° and 110° with the extremal peptide links.
The connecting vector, 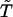 is a unit vector joining i and j.
is a unit vector joining i and j.
Applied when at least one of the two cooperative hydrogen bonds is nonlocal.
Results and Discussion
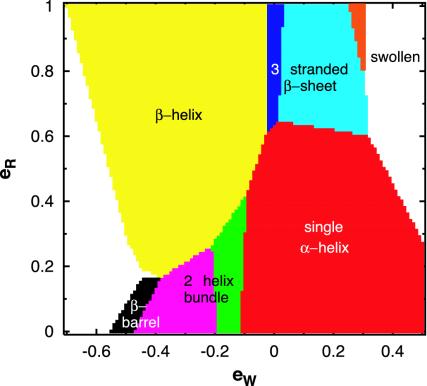
Fig. 3 shows the ground state phase diagram obtained from Monte-Carlo computer simulations using the simulated annealing technique (40). [The solvent-mediated energy, eW, and the local radius of curvature energy penalty, eR, (see Methods for a description of the energy parameters) are measured in units of the local hydrogen bond energy.] When eW is sufficiently repulsive (hydrophilic) (and eR > 0.3 in the phase diagram), one obtains a swollen phase with very few contacts between the Cα atoms. When eW is sufficiently attractive, one finds a very compact, globular phase with featureless ground states with a high number of contacts.
Fig. 3.
Phase diagram of ground state conformations. The ground state conformations were obtained by using Monte-Carlo simulations of chains of 24 Cα atoms. eR and eW denote the local radius of curvature energy penalty and the solvent-mediated interaction energy, respectively. Over 600 distinct local minima were obtained in different parts of parameter space, starting from a random conformation and successively distorting the chain with pivot and crankshaft moves commonly used in stochastic chain dynamics (43). A Metropolis Monte-Carlo procedure is used with a thermal weight exp(–E/T), where E is the energy of the conformation and the temperature T is set initially at a high value and then decreased gradually to zero. In the orange phase, the ground state is a two-stranded β-hairpin. Two distinct topologies of a three-stranded β-sheet (dark and light blue phases) are found corresponding to conformations shown in conformations i and j in Fig. 4, respectively. The helix bundle shown in conformation b in Fig. 4 is the ground state in the green phase whereas the ground state conformation in the magenta phase has a slightly different arrangement of helices. The white region in the left of the phase diagram has large attractive values of eW, and the ground state conformations are compact globular structures with a crystalline order induced by hard sphere packing considerations (44) and not by hydrogen bonding (conformation l in Fig. 4).
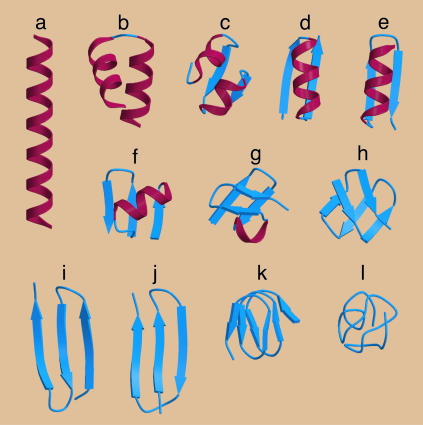
Between these two phases (and in the vicinity of the swollen phase), a marginally compact phase emerges (the interactions barely stabilize the ordered phase) with distinct structures including a single helix, a bundle of two helices, a helix formed by β-strands, a β-hairpin, three-stranded β-sheets with two distinct topologies, and a β-barrel-like conformation. Strikingly, these structures are the stable ground states in different parts of the phase diagram. Furthermore, other conformations, closely resembling distinct supersecondary arrangements observed in proteins (6), such as the β-α-β motif, are found to be competitive local minima whose stability can be enhanced by sequence design (for example, nonuniform values of curvature energy penalties for single amino acids and hydrophobic interactions for amino acid pairs). Fig. 4 shows a compendium of various structures obtained in our studies, including for comparison a generic compact conformation of a conventional polymer chain (with no tube geometry or hydrogen bonds), which neither is made up of helices or sheets nor possesses the significant advantages of protein structures. Although there is a remarkable similarity between the structures that we obtain and protein folds, our simplified coarse-grained model is not as accurate as an all-atom representation of the polypeptide chain in capturing features such as the packing of amino acid side chains.
Fig. 4.
molscript representation of the most common structures obtained in our simulations. Helices and strands are assigned when local or nonlocal hydrogen bonds are formed according to the described rules. Conformations a, b, h, i, j, and k are the stable ground states in different parts of the parameter space shown in Fig. 3. Conformations c, d, e, f, and g are competitive local minima. Conformation l is that of a generic compact polymer chain, obtained by switching off hydrogen bonds, the tube constraint, and curvature energy penalty, and is obtained on maximizing the total number of hydrophobic contacts.
The fact that different putative native structures are found to be competing minima for the same homopolymeric chain clearly establishes that the free-energy landscape of proteins is pres-culpted by means of the few ingredients used in our model. At the same time, relatively small changes in the parameters eW and eR lead to significant differences in the emergent ground state structure, underscoring the sensitive role played by chemical heterogeneity in selecting from the menu of native state folds.
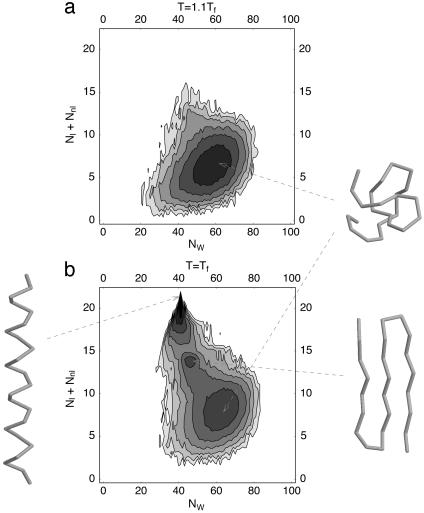
Fig. 5a is a contour plot of the free energy at a temperature higher than the folding transition temperature (identified by the specific heat peak) for the parameter values eW = –0.08 and eR = 0.3 for which the ground state is an α-helix (Fig. 3). The free energy landscape has just one minimum corresponding to the denatured phase whose typical conformations are somewhat compact but featureless. The contour plot at the folding transition temperature (Fig. 5b) has three local minima corresponding to an α-helix, a three-stranded β-sheet, and the denatured state. At lower temperatures, the α-helix is increasingly favored and the β-sheet is never the global free-energy minimum. Many protein-folding experiments show that, for small globular proteins at the transition temperature, only two states (folded and unfolded) are populated. The appearance in the present framework of multiple states for a homopolymer chain suggests that two-state folders might have been evolutionarily selected by sequence design favoring the native-state conformation over competing folds in the presculpted landscape.
Fig. 5.
Contour plots of the effective free energy at high temperature (T = 0.22) and at the folding transition temperature Tf = 0.2. The effective free energy, defined as F(Nl + Nnl,NW) =–lnP(Nl + Nnl,NW), is obtained as a function of the total number of hydrogen bonds Nl + Nnl and the total number of hydrophobic contacts NW from the histogram P(Nl + Nnl,NW) collected in equilibrium Monte-Carlo simulations at constant temperature. The spacing between consecutive levels in each contour plot is 1 and corresponds to a free energy difference of 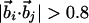 , where
, where 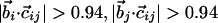 is the temperature in physical units. The darker the color, the lower the free-energy value. There is just one free-energy minimum corresponding to the denatured state at a temperature higher than the folding transition temperature (a) whereas one can discern the existence of three distinct minima at the folding transition temperature (b). Typical conformations from each of the minima are shown in the figure.
is the temperature in physical units. The darker the color, the lower the free-energy value. There is just one free-energy minimum corresponding to the denatured state at a temperature higher than the folding transition temperature (a) whereas one can discern the existence of three distinct minima at the folding transition temperature (b). Typical conformations from each of the minima are shown in the figure.
Such a design is indeed straightforward within our model. For example, the α-β-α motif shown in Fig. 4d (which is a local energy minimum for a homopolymer) can be stabilized into a global energy minimum for the sequence HPHHHPPPPHHPPHHPPPPHHHPP, with eW = –0.4 for HH contacts and eW = 0 for other contacts, and eR = 0.3 for all residues.
It is interesting to note that lattice models of compact homopolymers yield large amounts of secondary structure (41); local radius of curvature constraints are built into lattice models. However, an all-atom study of polyalanine has shown that compactness alone is insufficient to obtain secondary structures (42). Even a simple tube subject to an attractive self-interaction favoring compaction has a tendency to form helices, hairpins and sheets when the ratio of the tube thickness to the range of attractive interaction is tuned properly (22). Our work here underscores the importance of hydrogen bonds in stabilizing both helices and sheets simultaneously (without any need for adjustment of the tube thickness), allowing the formation of tertiary arrangements of secondary motifs. Indeed, the fine tuning of the hydrogen bond and the hydrophobic interaction is of paramount importance in the selection of the marginally compact region of the phase diagram in which protein native folds are found. It is also important to note that proteins are relatively short chain molecules compared with conventional polymers. These are special features of proteins, which distinguishes them from generic compact polymers.
A free-energy landscape with 1,000 or so minima (7) with correspondingly large basins of attraction leads to stability and diversity, the dual characteristics needed for evolution to be successful. Proteins are those sequences that fit well (18) into one of these minima and are relatively stable. Yet, the fact that the marginally compact phase lies in the vicinity of a phase transition to the swollen phase allows for an exquisite sensitivity of protein structures to the right types of perturbations. Thus, a change in the external environment (e.g., an ATP molecule binding to the protein) could reshape the free-energy landscape, allowing for a different, stable, and easily foldable conformation.
In summary, within a simple, yet realistic, framework, we have shown that protein native-state structures can arise from considerations of symmetry and geometry associated with the polypeptide chain. The sculpting of the free-energy landscape with relatively few broad minima is consistent with the fact that proteins can be designed to enable rapid folding to their native states. The limited number of folds arises from the geometrical constraints imposed by sterics and hydrogen bonds. In the marginally compact phase, not only does one have a space-filling conformation (the nearby backbone segments have to be placed near each other to avail of the attractive potential), which is effective in expelling water from the hydrophobic core, but also these segments need to have the right orientation with respect to each other to respect the geometrical constraints imposed by the hydrogen bonds.
Acknowledgments
We thank Buzz Baldwin, Hue-Sun Chan, Morrel Cohen, Russ Doolittle, Davide Marenduzzo, George Rose, and Harold Scheraga for their invaluable comments. This work was supported by Progetti Di Rilevante Interesse Nazionale 2003, Fondo Integrativo Speciale Ricerca 2001, the National Aeronautics and Space Administration, National Science Foundation (NSF) Integrative Graduate Education and Research Traineeship Grant DGE-9987589, NSF Materials Research Science and Engineering Centers, and the award of a postdoctoral fellowship at the Abdus Salam International Center for Theoretical Physics (to T.X.H.).
References
- 1.Wolynes, P. G., Onuchic, J. N. & Thirumalai, D. (1995) Science 267, 1619–1620. [DOI] [PubMed] [Google Scholar]
- 2.Dill, K. A. & Chan, H. S. (1997) Nat. Struct. Biol. 4, 10–19. [DOI] [PubMed] [Google Scholar]
- 3.Dobson, C. M., Sali, A. & Karplus, M. (1998) Angew. Chem. Int. Ed. Engl. 37, 868–893. [DOI] [PubMed] [Google Scholar]
- 4.Fersht, A. R. (1998) Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding (Freeman, New York).
- 5.Baker, D. (2002) Nature 405, 39–42. [DOI] [PubMed] [Google Scholar]
- 6.Chothia, C. & Finkelstein, A. V. (1990) Annu. Rev. Biochem. 59, 1007–1039. [DOI] [PubMed] [Google Scholar]
- 7.Chothia, C. (1992) Nature 357, 543–544. [DOI] [PubMed] [Google Scholar]
- 8.Denton, M. & Marshall, C. (2001) Nature 410, 417–417. [DOI] [PubMed] [Google Scholar]
- 9.Chothia, C., Gough, J., Vogel, C. & Teichmann, S. A. (2003) Science 300, 1701–1703. [DOI] [PubMed] [Google Scholar]
- 10.Wolynes, P. G. (1996) Proc. Natl. Acad. Sci. USA 93, 14249–14255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ramachandran, G. N. & Sasisekharan, V. Adv. Protein Chem. 23, 283–438. [DOI] [PubMed]
- 12.Pappu, R. V., Srinivasan, R. & Rose, G. D. (2000) Proc. Natl. Acad. Sci. USA 97, 12565–12570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Baldwin, R. L. & Rose, G. D. (1999) Trends Biochem. Sci. 24, 26–33. [DOI] [PubMed] [Google Scholar]
- 14.Pauling, L., Corey, R. B. & Branson, H. R. (1951) Proc. Natl. Acad. Sci. USA 37, 205–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pauling, L. & Corey, R. B. (1951) Proc. Natl. Acad. Sci. USA 37, 729–740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Eisenberg, D. (2003) Proc. Natl. Acad. Sci. USA 100, 11207–11210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kauzmann, W. (1959) Adv. Protein Chem. 14, 1–63. [DOI] [PubMed] [Google Scholar]
- 18.Bryngelson, J. D. & Wolynes, P. G. (1987) Proc. Natl. Acad. Sci. USA 84, 7524–7528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Benner, S. A. (2001) Nature 409, 459. [DOI] [PubMed] [Google Scholar]
- 20.Bernal, J. D. (1939) Nature 143, 663–667. [Google Scholar]
- 21.Maritan, A., Micheletti, C., Trovato, A. & Banavar, J. R. (2000) Nature 406, 287–290. [DOI] [PubMed] [Google Scholar]
- 22.Banavar, J. R. & Maritan, A. (2003) Rev. Mod. Phys. 75, 23–34. [Google Scholar]
- 23.Banavar, J. R., Maritan, A., Micheletti, C. & Trovato, A. (2002) Proteins 47, 315–322. [DOI] [PubMed] [Google Scholar]
- 24.Creighton, T. E. (1993) Proteins: Structures and Molecular Properties (Freeman, New York).
- 25.Banavar, J. R., Gonzalez, O., Maddocks, J. H. & Maritan, A. (2003) J. Stat. Phys. 110, 35–50. [Google Scholar]
- 26.Ohnishi, S. & Shortle, D. (2003) Proteins 50, 546–551. [DOI] [PubMed] [Google Scholar]
- 27.Ingwall, R. T., Scheraga, H. A., Lotan, N., Berger, A. & Katchalski, E. (1968) Biopolymers 6, 331–368. [DOI] [PubMed] [Google Scholar]
- 28.Marqusee, S., Robbins, V. H. & Baldwin, R. L. (1989) Proc. Natl. Acad. Sci. USA 86, 5286–5290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Scholtz, J. M., York, E. J., Stewart, J. M. & Baldwin, R. L. (1991) J. Am. Chem. Soc. 113, 5102–5104. [Google Scholar]
- 30.Spek, E. J., Olson, C. A., Shi, Z. & Kallenbach, N. R. (1999) J. Am. Chem. Soc. 121, 5571–5572. [Google Scholar]
- 31.Vila, J. A., Ripoll, D. R. & Scheraga, H. A. (2000) Proc. Natl. Acad. Sci. USA 97, 13075–13079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vila, J. A., Ripoll, D. R. & Scheraga, H. A. (2001) Biopolymers 58, 235–246. [DOI] [PubMed] [Google Scholar]
- 33.Creamer, T. P. & Rose, G. D. (1992) Proc. Natl. Acad. Sci. USA 89, 5937–5941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shi, Z., Krantz, B. A., Kallenbach, N. & Sosnick, T. R. (2002) Biochemistry 41, 2120–2129. [DOI] [PubMed] [Google Scholar]
- 35.Liwo, A., Kazmierkiewicz, R., Czaplewski, C., Groth, M., Oldziej, S., Rackovski, R. J., Pincus, M. R. & Scheraga, H. A. (1998) J. Comput. Chem. 19, 259–276. [Google Scholar]
- 36.Fain, B. & Levitt, M. (2003) Proc. Natl. Acad. Sci. USA 100, 10700–10705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hunt, N. G., Gregoret, L. M. & Cohen, F. E. (1994) J. Mol. Biol. 241, 214–225. [DOI] [PubMed] [Google Scholar]
- 38.Kemp, J. P. & Chen, Z. Y. (1998) Phys. Rev. Lett. 81, 3880–3883. [Google Scholar]
- 39.Trovato, A., Ferkinghoff-Borg, J. & Jensen, M. H. (2003) Phys. Rev. E 67, 028105. [DOI] [PubMed] [Google Scholar]
- 40.Kirkpatrick, S., Gelatt, C. D., Jr., & Vecchi, M. P. (1983) Science 220, 671–680. [DOI] [PubMed] [Google Scholar]
- 41.Chan, H. S. & Dill, K. A. (1990) Proc. Natl. Acad. Sci. USA 87, 6388–6392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Yee, D. P., Chan, H. S., Havel, T. F. & Dill, K. A. (1994) J. Mol. Biol. 241, 557–573. [DOI] [PubMed] [Google Scholar]
- 43.Sokal, A. D. (1996) Nucl. Phys. B Proc. 47, Suppl., 172–179. [Google Scholar]
- 44.Zhou, Y., Hall, C. K. & Karplus, M. (1996) Phys. Rev. Lett. 77, 2822–2825. [DOI] [PubMed] [Google Scholar]