Numerical simulation of drifting snow sublimation in the saltation layer

Abstract

Snow sublimation is an important hydrological process and one of the main causes of the temporal and spatial variation of snow distribution. Compared with surface sublimation, drifting snow sublimation is more effective due to the greater surface exposure area of snow particles in the air. Previous studies of drifting snow sublimation have focused on suspended snow, and few have considered saltating snow, which is the main form of drifting snow. In this study, a numerical model is established to simulate the process of drifting snow sublimation in the saltation layer. The simulated results show 1) the average sublimation rate of drifting snow particles increases linearly with the friction velocity; 2) the sublimation rate gradient with the friction velocity increases with increases in the environmental temperature and the undersaturation of air; 3) when the friction velocity is less than 0.525 m/s, the snowdrift sublimation of saltating particles is greater than that of suspended particles; and 4) the snowdrift sublimation in the saltation layer is less than that of the suspended particles only when the friction velocity is greater than 0.625 m/s. Therefore, the drifting snow sublimation in the saltation layer constitutes a significant portion of the total snow sublimation.

Drifting snow is a common phenomenon¹ and may lead to phase change of snow particles due to moisture in the unsaturated atmosphere, i.e., drifting snow sublimation (DSS). DSS not only causes changes in mass and crystal shapes of snow particles² but also affects the occurrence, accumulation, and distribution of snowdrifts and even induces disasters, particularly avalanches³. Thus, studies of DSS are of glaciological and hydrological importance⁴.

Snow sublimation occurs in primarily two ways, surface and drifting snow sublimation. The former is based on water vapour transfer between the snowpack and the atmospheric boundary layer and has more uniform distribution and frequent occurrence than DSS, including occurring when wind speeds are less than the threshold level for snow transport. DSS is potentially more effective than surface sublimation because it has a relatively greater exposed surface area⁵. Many studies have demonstrated that snow sublimation, especially DSS, has significant effects on snow surface mass balance. Déry and Yau⁶ showed that the combined processes of surface and drifting snow sublimation depleted 29 mm yr⁻¹ snow water equivalent (SWE) over Antarctica, approximately 17–20% of its annual precipitation, and more than 100 mm yr⁻¹ SWE in the northern hemisphere. Strasser et al.⁷ estimated snow sublimation for the Berchtesgarden National Park and found that DSS was highly spatially variable and depleted more than 1000 mm SWE on crests and ridges in one winter, roughly 70% of the local winter snowfall. MacDonald et al.⁸ evaluated the contribution of sublimation to snow mass balance in the Canadian Rocky Mountains and found that snow mass losses caused by surface and drifting snow sublimation were 20–32% of the cumulative snowfall, of which DSS loss accounted for 17–19%.

Thorpe and Mason⁹ studied the sublimation rate of a single ice sphere through wind tunnel measurements and proposed an expression for it, closely related to the size of the snow particles and the relative velocity between the airflow and the particles. Since then, this expression has been widely used to estimate the sublimation rate of drifting snow¹⁰,¹¹,¹². Wever et al.¹³ demonstrated that the number density of snow particles was the most important controlling factor in the total DSS rate and found that the accurate particle number density played a key role in calculating DSS events. Thus, in the study of DSS, it is essential to precisely describe the motion state of the snow, e.g., the vertical concentration distribution of the snow particles and the relative velocity between the airflow and the snow particles, to evaluate the sublimation rate of the drifting snow. Unfortunately, in many current studies, such as Déry et al.¹⁴ and Bintanja¹⁵, empirical formulas and assumptions were used to describe the motion state of the snow particles. Moreover, the height of the lower boundary of the drifting snow defined by some researchers or used for calculations in empirical formulas¹⁶ was generally assumed to be approximately 0.1 m. Apparently, such treatments cannot fully describe the effect of DSS in the saltation layer, in which most saltating particles generally move at heights less than 0.1 m. Recently, Groot Zwaaftink et al.¹⁷ studied snow sublimation in complex terrain, obtaining the concentration distribution of snow particles using Alpine3D, and combining it with the formula for the sublimation rate given by Thorpe and Mason⁹ to estimate DSS. However, in their study, the sublimation of snow particles in the saltation layer was again not considered.

Saltation in the range of several to tens of centimeters¹⁸,¹⁹,²⁰ is the primary mode of motion of drifting snow, accounting for 3/4 of the total snow transport mass. However, as discussed above, previous studies of DSS have primarily focused on suspended snow, and few have addressed saltating snow. In this study, we begin preliminary research on DSS in the saltation layer. First, a saltation model for the coupling effect between wind and snow particles is established to simulate the saltating process of snow particles, and then sublimation of snow particles in the saltation layer is evaluated based on the sublimation rate expression of a single ice sphere derived by Thorpe and Mason⁹. The results indicate that under the same environmental conditions, the snowdrift sublimation rate increases linearly with the friction velocity; as the temperature and undersaturation of air increase, the gradient of the sublimation rate increases with the friction velocity; under certain initial friction velocities, the snowdrift sublimation of the saltating particles is greater than that of suspended particles, indicating that DSS in the saltation layer is of considerable importance and cannot be neglected.

Results

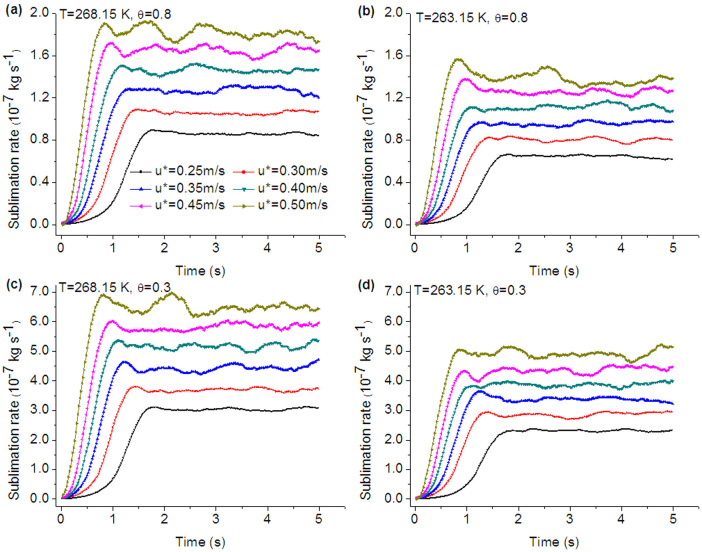
In wind-blown snow, snow particles are entrained and transported by the wind, while the wind field is simultaneously influenced by the snow particles, indicating a self-regulating feedback mechanism between the saltating particles and the wind field. In this mechanism, the drag force associated with particle acceleration reduces the wind velocity in the saltation layer, thus limiting the entrainment of further particles²¹. At a given wind speed, the number of snow particles in the saltation layer initially increases rapidly with time and then decreases gradually until it reaches a steady state, i.e., the number of particles in the layer will not increase further. The time for the wind-blown snow to reach steady state decreases as the friction velocity increases²¹,²². Figure 1 shows the temporal evolution of DSS with different friction velocity (ranging from 0.25 m/s to 0.5 m/s) under different environmental conditions, with a temperature of 263.15 K or 268.15 K and humidity of 0.3 or 0.8. As shown in Figure 1, as time advances, the snowdrift sublimation rate first increases rapidly, then decays slightly, and finally approaches a dynamic steady state, consistent with the development processes of snow saltation. As the friction velocity increases, the time for snowdrift sublimation rate to reach the dynamic steady state decreases. For example, the time to steady state for the sublimation rate is approximately 2 s at a friction velocity of 0.25 m/s, whereas it is less than 1 s at a friction velocity of 0.5 m/s (Fig. 1a). Figure 1 also shows that with temperature and relative humidity held constant, the sublimation rate increases with friction velocity. A comparison of Figure 1a, 1b, 1c, and 1d clearly shows that the sublimation rate increases with increasing temperature with the relative humidity and friction velocity held constant. Similarly, the sublimation rate increases with decreasing humidity with the temperature and friction velocity held constant. The effects of environment conditions on the sublimation rate in our simulations are consistent with previous studies, i.e., DSS easily occurs at warmer temperatures and greater wind speeds²³.

Figure 1. Changes in the sublimation rate of drifting snow with time and friction velocity (u*ranges from 0.25 m/s to 0.5 m/s) under varying environmental conditions (Temperature of 263.15 K or 268.15 K and relative humidity of 0.3 or 0.8).

At the sublimation rate steady state, Figure 2 shows the relationship of the average sublimation rate of the drifting snow to the initial friction velocity under several environmental conditions. In wet and cold environmental conditions (T = 263.15 K, θ = 0.8), shown as a red dot in Figure 2, and at the lowest friction velocity of 0.25 m/s, the sublimation rate is 0.644 × 10⁻⁷ kg/s in our study, indicating that it will deplete 0.6 mm d⁻¹ SWE. As the environment becomes warmer and drier and the friction velocity increases, the sublimation rate increases until reaching the optimum environmental conditions (T = 268.15 K, θ = 0.3) in our simulations, shown as green triangles in Figure 2. When the friction velocity is 0.5 m/s, the sublimation rate reaches 6.51 × 10⁻⁷ kg/s, corresponding to 5.6 mm d⁻¹ SWE.

Figure 2. Relationship between the average sublimation rate of drifting snow and the initial friction velocity with the sublimation rate at steady state under varying environmental conditions.

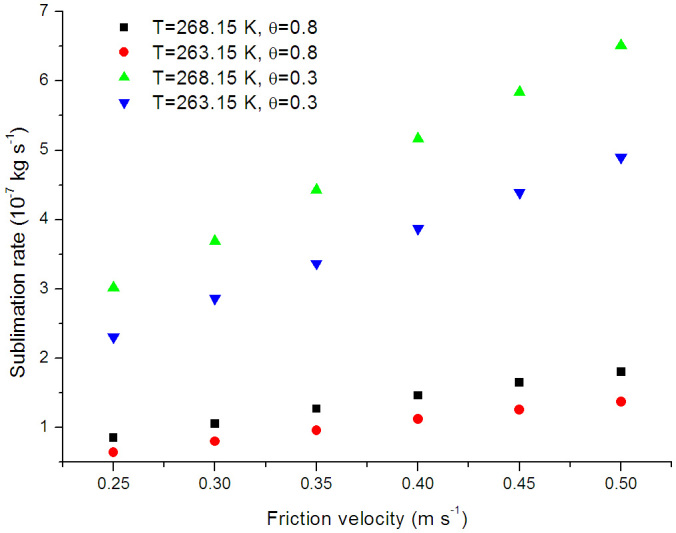
Neumann et al.²⁴ experimentally determined the sublimation rate by controlling a series of experimental parameters, including sample temperature (−5, −9, −13, −19 and −23°C), relative humidity, snow microstructure, and the airflow rate (between 1 and 10 LPM), and found that the snowdrift sublimation rate linearly increased with the airflow rate at the same temperature. As shown in Figure 2, under the same environmental conditions, the snowdrift sublimation rate linearly increases with increasing friction velocity. Therefore, our simulation results are qualitatively in agreement with the experimental results of Neumann et al.²⁴. Moreover, Figure 2 also shows that as the temperature and the undersaturation of air increase, the gradient of the sublimation rate with the friction velocity increases. This phenomenon is especially obvious when air temperature is 268.15 K and the relative humidity is 30%.

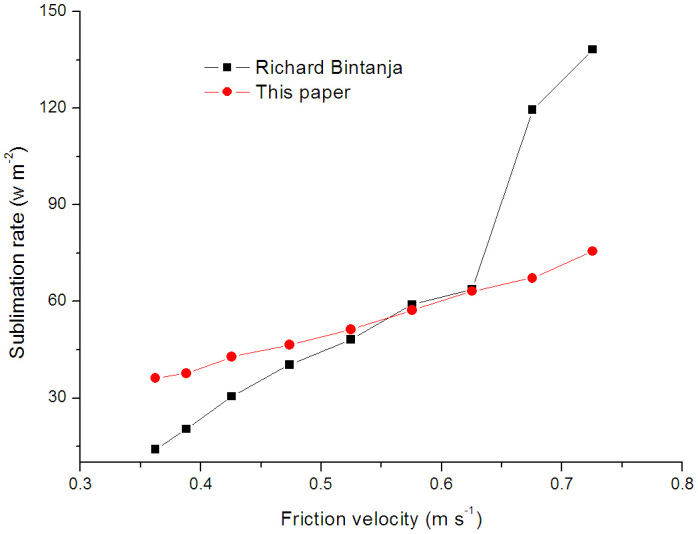
Bintanja²⁵ studied the relationship between the surface and snowdrift sublimation in the katabatic wind region of the Antarctic ice sheet. He assumed that the vertical distribution of the suspended-particle density obeys the standard power-law relation²⁶ and calculated the snowdrift sublimation rate of suspended snow particles. In this study, the motion equations of wind blowing snow are established to obtain the particle velocity and the vertical distribution of particle number density in the saltation layer. Then, the sublimation rate is calculated using the expression of Thorpe and Mason⁹ under the same values of model variables associated with particles as used by Bintanja²⁵. For comparison purposes, the results of Bintanja are shown with our results in Figure 3. The snowdrift sublimation of Bintanja is obviously less than ours when the friction velocity is less than 0.525 m/s. In other words, the DSS of saltating particles is greater than that of suspended particles, and the difference between them gradually increases as the friction velocity decreases. When the friction velocity is greater than 0.362 m/s but less than 0.525 m/s, the sublimation rate of saltating particles ranges from 36.3 W m⁻² to 51.3 W m⁻², i.e. 1.1 mm d⁻¹ SWE to 1.6 mm d⁻¹ SWE, indicating that the snowdrift sublimation rate in the saltation layer is so considerable that it should be considered. The snowdrift sublimation rate of saltating particles is less than that of the suspended particles only with a very high friction velocity (great than 0.625 m/s). Therefore, DSS in the saltation layer is of significance and should not be neglected in the prediction of DSS. Figure 3 also shows that the snowdrift sublimation rate in the saltation layer increases linearly with the friction velocity, reaching 75.6 W m⁻² at a friction velocity of 0.726 m/s.

Figure 3. A comparison between the sublimation rates of saltating particles and suspended particles of snow.

Discussion

In this study, we used a saltation model that includes the coupling effect between wind and snow particles in combination with the sublimation rate expression for a single ice sphere to evaluate the sublimation of snow particles in the saltation layer. We showed the development process of DSS in the saltation layer, i.e., the snowdrift sublimation rate first increases rapidly, then decays slightly, and finally approaches a dynamic steady state consistent with snow saltation. At the steady state, the average sublimation rate of saltating snow particles increases linearly as the friction velocity increases, and as the temperature and the undersaturation of air increase, the sublimation rate gradient with the friction velocity increases. When the initial friction velocity is less than 0.525 m/s, the snowdrift sublimation of the saltating particles is greater than that of the suspended particles; the snowdrift sublimation in the saltation layer is less than that of the suspended particles only when the friction velocity is greater than 0.625 m/s.

Saltation is the main mode of motion of drifting snow. The particle number density of the saltation layer is greater than that of the suspension layer. However, previous studies of DSS have concentrated primarily on the suspended snow particles by using many assumptions and empirical formulas and neglecting the snowdrift sublimation in the saltation layer. Thus, very little is known regarding DSS in the saltation layer or its contribution to the total DSS. This study focuses on the snowdrift sublimation of saltating particles by simulating the saltation process of wind drifting snow to derive the relative velocity between the airflow and the snow particles and the vertical distribution of particle number density in the saltation layer, which are very important in the calculations of DSS⁹,¹³. We showed the development processes and some properties of DSS in the saltation layer, which had not previously been stated in the literature. In addition, we demonstrated the significance of DSS in the saltation layer. When the wind speed is relatively low and fewer snow particles are suspended, the snowdrift sublimation rate in the saltation layer may be more than twice that in the suspension layer. Even as the wind speed increases to suspend more snow particles, snowdrift sublimation in the saltation layer remains significant and cannot be neglected. In general, the DSS in the saltation layer has significant impact on the prediction of DSS and deserves additional studies. Because DSS plays an important role in snow surface mass balance as well as the distribution of snow cover, the results of this paper are of glaciological and hydrological importance.

Methods

The simulation of DSS includes simulating the snow saltation process and numerically calculating the sublimation of saltating particles. Snow particle saltation can be divided into four sub-processes including the aerodynamic entrainment, particle trajectories, particle-bed collisions, and wind modification²¹.

Basic equations for snow particle trajectory. Assuming that the drifting snow grain is spherical and subject to gravity, buoyancy force and drag force in the air, its motion equations are²¹

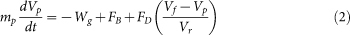where m_p and W_g are the mass and weight of the snow particle, respectively; U_f, V_f, U_p, and V_p are the horizontal and vertical velocities of the airflow and the snow particle, respectively; is the relative velocity between the airflow and the snow particle; x_p and y_p are the horizontal position and vertical height of the snow particle, respectively; 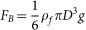and 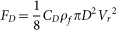are the buoyancy force and the drag force applied on the snow particle, respectively; ρ_f is the air density; D is the diameter of snow particle; g is the acceleration of gravity; and C_D is the drag coefficient.

Basic equation of the flow. Within the atmospheric surface layer, the mean horizontal wind velocity u satisfies the Navier-Stokes equation²⁷

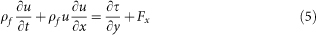where x is the coordinate aligned with the mean wind direction, y is the vertical direction, τ is the fluid shear stress, and the force per unit volume that the snow particles exert on the fluid in the stream-wise direction, F_x, is

where n is the number of particles per unit volume of fluid at height y, and a_iis the horizontal acceleration of particle i.

According to Prandtl's mixing length theory, for steady flow that is fully developed over an infinite plane bed, Equation (5) can be simplified as²¹

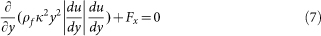where κ is the von Karman constant.

Aerodynamic entrainment. When the wind velocity increases over a snow surface, snow particles begin lifting off the surface and into the air. The number of aerodynamically entrained snow particles can be described by the excess shear stress rule originally proposed by Anderson and Haff²⁸,²⁹. To determine the best value of the dimensional constant in the rule, the following relationship based on the conservation of momentum derived by Shao and Li³⁰ is used:

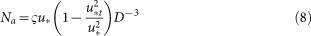where N_a is the number of snow particles entrained by wind per unit area and unit time, ς is a dimensionless coefficient of 1 × 10⁻³ in our simulations, u_* is the friction velocity, and u_*t is the threshold friction velocity. Following the previous saltation models³¹, the vertical speed of all aerodynamically entrained particles is set as .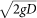

Splash process. In the saltation layer, snow particles alternately impact the surface and bounce forward into the air. They may rebound successively or even eject other particles from the surface. This process is called the splash process. The following three splash functions for drifting snow, proposed by Sugiura and Maeno³² based on experiments, are used to determine the number and motion state of the splashed particles:

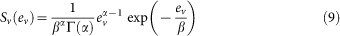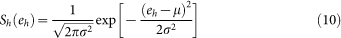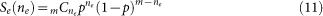In Equation (9), S_v is the probability distribution of the vertical restitution coefficient e_v, Γ(α) is the gamma function, and α and βare the shape and scale parameters for the gamma distribution function, respectively. In Equation (10), S_his the probability distribution of the horizontal restitution coefficient e_h, and μ and σ are the mean and variance, respectively. In Equation (11), S_e is the probability distribution function of the number of ejected particles n_e, a binomial distribution function with mean mp and variance mp(1 − p). The parameters α, β, μ, σ, m and p were measured at −15°C as a function of the impact velocity and angle for a drifting snow particle on a bed of compacted snow particles³².

Drifting snow sublimation rate. The total DSS rate, Q_S(kg/s), of the saltation layer within the computational domain is obtained by summing the mass loss of all saltating particles of the domain:

where 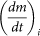is the mass loss rate corresponding to the i-th particle. At air temperature T and undersaturation δ( = θ − 1), the rate of change in mass of a single particle of radius r due to sublimation, as given by Thorpe and Mason⁹, is

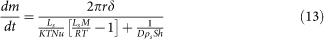where θ is the relative humidity of air, L_sis the latent heat of sublimation (2.834 × 10⁶ J kg⁻¹), M is the molecular weight of water (0.018 kg mol⁻¹), R is the universal gas constant (8.31 J mol⁻¹ K⁻¹), K is the molecular thermal conductivity of the atmosphere (0.024 J m⁻¹ s⁻¹ K⁻¹), D is the molecular diffusivity of water vapour in the atmosphere, ρ_s is water vapour density at saturation, and Nu and Sh are the Nusselt number and the Sherwood number, respectively, both dimensionless and variable with wind velocity and particle size. According to Thorpe and Mason⁹ and Lee³³,

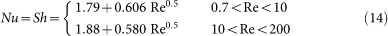where Re = DV_r/υ is the Reynolds number, and υ is the kinematic viscosity of air.

Calculation procedures. The length, width, and height of the computational domain sampled from the saltation layer above the surface are 1.0 m, 0.01 m, and 1.0 m, respectively. Along the wind direction, the incident and outgoing boundaries of the snow particles are periodic, and the upper boundary is the rebound boundary. The threshold friction velocity of the snow sample is 0.21 m s⁻¹, and the snow bed roughness is 3.0 × 10⁻⁵ m³⁴. As mentioned above, snow particles are considered to be spheres with diameter of 200 μm and density of 910 kg m⁻³.

The time step length used to calculate the trajectories and velocities of saltating snow particles is 0.00001 s. In each step, the new location and velocity of each drifting snow particle are calculated. Then the location is used to determine whether the snow particle falls on the snow bed or not. And the velocity is plugged into equations (13) and (14) to determine the rate of change in mass of the particle. The initial wind field is logarithmic and then modified every 0.001 s.

As the snow particles fall on the snow bed, where they impart their energy to and splash or eject other snow particles, the velocity and angle of the ejected particles satisfy the splash functions based on the motion state of the incident particles and the actual situation of the wind field at that time. If the bed shear stress is greater than the initial shear stress of the critical fluid, some particles are entrained from their random positions on the snow surface of the domain. The vertical speed is 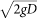, and the number of aerodynamically entrained snow particles is recalculated every 0.01 s.

Based on the results derived from the above operation, the sublimation rate of drifting snow under with relative humidity of 0.3 and 0.8, temperature of 268.15 K and 263.15 K, and initial friction velocity between 0.25 m/s and 0.5 m/s is recorded every 0.02 s according to Equation (12). The calculation is conducted continuously until both the vertical profile of the horizontal mass flux and the sublimation rate of the drifting snow are practically in steady state. This process takes 5 s.

Author Contributions

X.D. provided the results of the numerical simulation and wrote the main manuscript text. N.H. provided the theoretical model and participated in analyzing the results and writing the manuscript. All authors reviewed the manuscript.