Frequency of gaps observed in a structurally aligned protein pair database suggests a simple gap penalty function

Abstract

Gap penalty is an important component of the scoring scheme that is needed when searching for homologous proteins and for accurate alignment of protein sequences. Most homology search and sequence alignment algorithms employ a heuristic ‘affine gap penalty’ scheme q + r × n, in which q is the penalty for opening a gap, r the penalty for extending it and n the gap length. In order to devise a more rational scoring scheme, we examined the pattern of gaps that occur in a database of structurally aligned protein domain pairs. We find that the logarithm of the frequency of gaps varies linearly with the length of the gap, but with a break at a gap of length 3, and is well approximated by two linear regression lines with R² values of 1.0 and 0.99. The bilinear behavior is retained when gaps are categorized by secondary structures of the two residues flanking the gap. Similar results were obtained when another, totally independent, structurally aligned protein pair database was used. These results suggest a modification of the affine gap penalty function.

INTRODUCTION

The Human Genome Project and other sequencing projects have produced a vast number of protein sequences about which nothing is known but the sequence. In order to begin to understand the biological role of these proteins, they have to be classified and related to other already known proteins. The first step in this function annotation process is usually a search for homologous proteins in the protein sequence databases.

Homology search tools generally (1–5) use a score function that assigns a score for each aligned residue pair and a penalty for each gap in the alignment. The score for aligned residue pairs is obtained from examining large numbers of aligned protein sequences, and there is a firm theoretical basis that provides guidance on how to select the score function that will yield an optimal alignment (6).

The gap penalty is also important for the sensitivity (ability to find remotely related sequences) of the search tool and the accuracy of the alignment. Most sequence homology detection algorithms employ the ‘affine gap penalty’ scheme of the form (q + r × n), where n is the length of the gap and q and r are empirically chosen parameters representing the cost of opening and extending a gap, respectively. The affine gap penalty scheme recognizes that it costs to open a gap as well as to extend an existing one and has proved to be superior to length proportional gap costs, which often produce a large number of short insertions or deletions (7). However, no firm theoretical or experimental support has been presented for such a gap penalty scheme. It has also been criticized for over-penalizing long gaps (8). Several methods for improving this gap penalty function have been proposed (7–10).

There have been several attempts to deduce a gap penalty function by examining patterns of insertions–deletions (indels) in aligned sequences (11–13). The assumption used in these studies is that a linear relationship exists between the gap penalty and the logarithm of the probability of gap lengths. Under such an assumption, an exponential distribution of gap lengths will give rise to an affine gap penalty scheme. Benner et al. (11) examined a database of aligned protein sequence pairs that they constructed and concluded that the frequency distribution of gap lengths observed in this database was best described by a power law. However, they aligned protein sequences using dynamic programming methods with explicit gap penalty functions, thus introducing a certain circularity to the analysis. More recently, Qian and Goldstein (13) examined gaps that occur in structurally aligned proteins. Using the FSSP database (14), they fitted the probability distribution of gap lengths to a complex quadruple exponential function. There have been several other efforts to derive gap penalty functions by examining insertions and deletions that occur in human gene–pseudogene pairs (12,15). However, it is likely that the constraints placed on the formation of gaps in functional proteins are different from neutral pseudogenes, and thus gap penalty functions derived from the latter may not be applicable for detecting homologous proteins.

Here, we report the results of an examination of the pattern of gaps that occur in a database of structurally aligned protein domain pairs constructed from an all-against-all pairwise structural alignment of 3992 SCOP (16) protein domains of low sequence homology. We find that the distributions of the logarithm of the probability of gaps, as a function of gap length, exhibit a bilinear behavior with a break at a gap of length 3. The slope of the regression line at long gap lengths (>3) is much smaller than that for the short gap lengths (≤3). The statistical support for the bilinear regression is very strong, with R² values of 1.0 and 0.99 for the first and the second linear segments, respectively. Assuming a linear relation between the gap penalty function and the logarithm of the probability of observing a gap of given length, these results suggest a modification of the affine gap penalty scheme.

MATERIALS AND METHODS

Generation of a structurally homologous protein domain pair (SHoPP) database

Pairwise structural superposition of protein domains. A non-redundant set of 3992 protein domains with <40% sequence identity to each other, which excluded structures determined by NMR, were selected from the ASTRAL SCOP v1.59 database (17). These domains were subjected to an all-against-all pairwise structural superposition using the structure comparison program SHEBA (18) in order to generate a structurally superposed domain pair set. The computations were performed on the NIH Biowulf cluster (a Beowulf parallel processing system), and a total of 7 966 036 domain pairs were structurally superposed by this method.

Selection of structurally homologous domain pairs. Members of the structurally homologous protein domain pair database (SHoPP) were selected from the superposed domain pair set using the following criteria: (i) m ≥ 40; (ii) m ≥ 0.6 × number of residues in the larger domain of the domain pair; (iii) the root-mean-square deviation of superposed residues ≤2.0 Å. These criteria are based on the number of superposed residue pairs m. Residue pairs were considered to be superposed if the distance between the respective alpha carbons was <3.5 Å after superposition of the domains by SHEBA. These criteria were developed, in part, by manual examination of a sample of superposed domain pairs.

The structurally homologous protein domain pair database (SHoPP) consists of 9806 domain pairs that satisfied the above criteria. Domain pairs selected in this manner also had z scores >3 with respect to each domain, when the z score was defined as

where m_f is m divided by the number of residues in the larger domain, <m_f> is the mean of m_f over all pairs involving the given domain and σ is the standard deviation of m_f over all pairs involving the given domain.

Classification of gaps

The structural alignment of two protein domains also yields a concomitant sequence alignment containing regions of aligned residues separated by gaps. The gaps that occurred in the SHoPP database were classified in terms of the secondary structure of the residues flanking the gap as follows.

Definitions of secondary structure. Secondary structure assignments were made using the program DSSP (19). H, I and G were classified as helical (H), B and E as strand (S) and S and T as coil (C).

Classification of gaps by secondary structure. Gaps were classified in terms of the secondary structure of the amino acids immediately before (g_init) and immediately after (g_end) the gap. Using the simplified three-state classification of secondary structure, gaps were divided into five types: (i) gaps occurring within a helix (g_init = g_end = H); (ii) gaps occurring within a strand (g_init = g_end = S); (iii) gaps occurring in a coil region (g_init = g_end = C); (iv) gaps at the edge of a helix (g_init = H, g_end = C or g_init = C, g_end = H); (v) gaps at the edge of a strand (g_init = S, g_end = C or g_init = C, g_end = S).

Gaps that occur at the junction of a helix and a strand (g_init = H, g_end = S or g_init = S, g_end = H) were ignored because there were too few cases where a helix and a sheet were directly adjacent to each other.

Probability of a gap

All gaps were classified in terms of gap type (as described above) and the length of the gap. The probabilities were computed by converting raw frequencies into normalized frequencies. For example, the probability of a gap of length n occurring within a helix (where the secondary structure of the residues at positions g_init = H and g_end = H) was computed as follows:

where

refers to the number of gaps of length n between residues of secondary structure type H and H in the SHoPP database. Probabilities for other types of gaps were computed in an analogous manner.

RESULTS

Structurally homologous protein domain pair database (SHoPP)

The ASTRAL SCOP v1.59 (17) database contained 3992 protein domains with <40% sequence identity among them. An all-against-all structure comparison of these protein domains, using the structure comparison program SHEBA (18), resulted in 9806 domain pairs that were judged to be structurally highly homologous to each other according to the criteria detailed in Materials and Methods. The SHoPP database consists of these protein domain pairs.

Analysis of probability distribution curves

The numbers of gaps observed in the SHoPP database, categorized by length and the secondary structure of the residues flanking the gap, are given in Table 1. The total numbers of residue pairs in the coil, helix and strand regions were roughly the same (last row of Table 1). However, as expected, more gaps occurred between coil residues than between residues of any other secondary structural types. For gaps of length >2, the frequency of gaps within a coil region is ≥10 times that of gaps of similar length within a helical or strand region. This result is consistent with the expectation that the relatively unstructured coil regions are more likely to tolerate insertions than regions of regular secondary structure such as helices and strands.

Table 1. Frequency of gaps found in SHoPP database by length and by gap type.

Gap lengtha	Gap type
	Within coil	Within strand	Within helix	Edge of strand	Edge of helix
0b	493 602	576 334	499 274	189 739	96 990
1	25 587	7978	4396	6500	4529
2	9093	1166	1515	1250	1292
3	3224	314	332	451	335
4	2290	162	191	175	136
5	1721	70	109	196	106
6	976	54	72	112	46
7	617	33	47	67	40
8	417	34	54	38	46
9	394	14	32	34	23
10	255	8	31	30	19
Total	538 176	586 167	506 053	198 592	103 562

^aGaps of length >10 were not considered for analysis, as they were judged to be too few in number for some gap types.

^bThis is the number of residue pairs without a gap, for each gap type.

The probability of a gap of given length occurring in a given secondary structural region was obtained by dividing the number of gaps of that length and secondary structural type by the total number of residue pairs of the same secondary structural type (equation 1). The negative logarithms of these probabilities, plotted as a function of the gap length for each of the five secondary structural types, are given in Figure 1. Interestingly, each type exhibits a similar trend: a rapid linear increase for gaps of length ≤3, followed by another linear, but more gradual, increase. Each plot is well approximated by two linear regression lines given by

Figure 1.

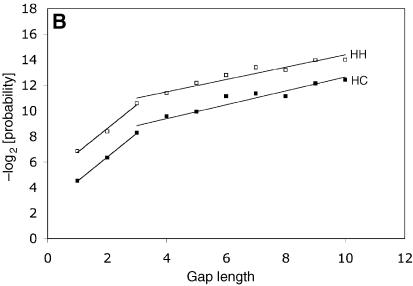
Probability distribution of gaps, by length, for data from the SHoPP database. Gaps have been categorized by the secondary structure of the residues flanking the gap (see Materials and Methods). (A) CC, gaps within a coil; SC, gaps at the edge of a strand; SS, gaps within a strand. (B) HH, gaps within a helix; HC, gaps at the edge of a helix.

g(n) = q₁ + r₁ × n (n ≤ 3)

= q₂ + r₂ × n (n > 3)    2

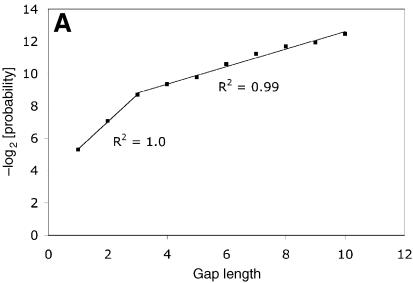
where g(n) is the negative of the logarithm to base 2 of the probability of a gap of length n. The best-fitting values for the parameters q and r are given in Table 2. The values for the square of the correlation coefficient (R²) are given in Table 3. For all types, the gradient r₁ of the first regression line is larger the gradient r₂ of the second regression line by a factor of 3–4 (Table 3). The combined data (Fig. 2A) exhibited similar behavior, and could also be well approximated by two linear regression lines with R² values of 1.0 and 0.99, indicating almost perfect linear regression.

Table 2. Linear regression line coefficients^a,b.

Gap type	Line 1 (gap length 1–3)		Line 2 (gap length 3–10)
	q1	r1	q2	r2
Within coil	2.902	1.495	5.789	0.537
Within strand	4.013	2.334	9.073	0.697
Within helix	4.875	1.864	9.547	0.482
Edge of strand	3.158	1.925	7.458	0.560
Edge of helix	2.616	1.879	7.213	0.543
Combinedc	3.631	1.698	7.189	0.543

^aFor plots in Figures 1 and 2A.

^bThe regression line is represented as y = q + r × n, where y = –log₂[probability] and n is the gap length.

^cPooled data in which categorization of gaps by secondary structure is ignored.

Table 3. Correlation coefficients for the first (R₁, gap lengths 1–3) and the second (R₂, gap lengths ≥3) regression lines and the ratio of slopes (r₁/r₂) of the two regression lines for the logarithm of the probability versus length for gaps found in SHoPP and DAPS databases.

Gap type	SHoPPa			DAPSb
	R12	R22	r1/r2	R12	R22	r1/r2
Within coil	1.0	0.98	2.79	0.99	0.99	2.40
Within strand	0.99	0.97	3.36	0.96	0.92	4.00
Within helix	0.99	0.93	3.87	0.99	0.97	3.30
Edge of strand	1.0	0.92	3.45	1.0	0.99	3.75
Edge of helix	0.98	0.95	3.44	0.98	0.98	3.07
Combinedc	1.0	0.99d	3.14	1.0	0.99d	2.90

^aFor the regression lines in Figures 1 and 2A.

^bCorresponding regression lines are not shown except for the combined category, which is shown in Figure 2B.

^cPooled data in which categorization of gaps by secondary structure is ignored.

^dWhen gaps of length ≤15 were considered, the R₂² values (gaps of length 3–15) for the combined data were 0.98 and 0.99 for the SHoPP and DAPS databases, respectively.

Figure 2.

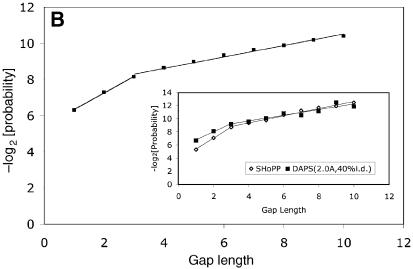
Probability distribution of gaps, by length, for the combined data (irrespective of secondary structure type), in (A) the SHoPP database and (B) the DAPS database (20). The inset shows an analogous plot for a subset of DAPS, created by selecting protein domain pairs that satisfy the dual criteria of pairwise sequence identity ≤40% and RMSD ≤2.0 Å. For comparison with data from SHoPP, the plot from (A) has been included in the inset.

The shape of the probability distribution curve for gaps is independent of structural database

In order to verify that the observations made above are not a property of the particular database used, we computed the gap probability distributions using another database, DAPS, which was constructed independently by Mallick et al. (20). The SHoPP and DAPS databases differed from each other in the definition of protein domains (17,21), computer programs used for the structural alignment of domains (18,22) and criteria used for selection of domain pairs to the database (see Materials and Methods). SHoPP, with 9806 domain pairs, was considerably smaller than DAPS, which had 34 778 pairs. All SHoPP entries had a sequence identity ≤40% and a root-mean-square deviation (RMSD) ≤2.0 Å. By contrast, DAPS had 1592 entries with a sequence identity of 100%, and 1717 domain pairs with RMSD >5 Å. Nevertheless, the probability distribution curves obtained for the two databases are very similar (Fig. 2); each exhibits a strong bilinear character, with a break at a gap of length 3 and a ratio of 3–4 between the gradients of the first and second regression lines. For a subset of DAPS satisfying some of the selection criteria adopted in the construction of SHoPP (sequence identity ≤40%, RMSD ≤2.0 Å), the differences in the values of the coefficients for the two regression lines in Figure 2 were significantly reduced such that the two curves were nearly superimposed (inset to Fig. 2B).

DISCUSSION

We have found that the distribution of the negative logarithm of the probability of gaps, by length, observed in the SHoPP database could be well represented by a bilinear function with the breakpoint at the gap of length 3 (equation 2 and Fig. 2). The values of the parameters of equation 2 are given in Table 2. The bilinear equation is an excellent representation of the data as can be seen from the values of the square of the correlation coefficient, R², which are 1.0 and 0.99, respectively, for the first and second regression lines (Table 3). Remarkably, similar bilinear behavior, with a break at a gap of length 3, is observed for each gap type when gaps are categorized by the secondary structural environment (within coil, within helix, within strand etc.) (Fig. 1).

It is not clear why the gap-length distribution is bilinear with a break at 3. This is not a property of the SHoPP database alone, since the same basic behavior is observed in the DAPS and apparently also in the FSSP (see below) databases, which are all entirely independent of each other. Since the bilinear behavior is observed for all secondary structural environments, the mechanism that produces this behavior is operating outside the constraints of the secondary structure of the protein. There are many mechanisms that will cause an insertion and/or a deletion in a protein sequence (23,24). A linear regression with gap length is expected if each gap (of unit length) is introduced independently (12). However, the reason for the break in the regression line at length 3 is unclear at present.

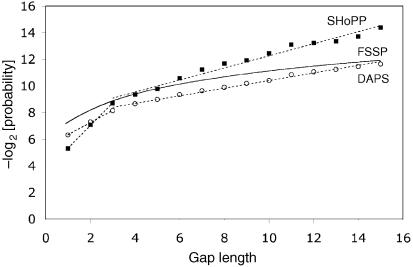
The gap-length distribution in aligned protein sequence databases has been studied before (11,13). Benner et al. (11) used protein pairs that were aligned by sequence homology using dynamic programming and a gap penalty function. They concluded that the gap-length distribution followed a power law rather than the exponential behavior that we observe. The difference may arise from the different methods used to obtain the alignments. Qian and Goldstein (13) studied gaps that occur in the FSSP database, which consists of proteins that were structurally aligned like the SHoPP and DAPS databases. They fitted their data to a multi-exponential function that includes four terms. The logarithm of this function looks rather different from the bilinear form that we observe, but the function was designed to fit gaps of lengths up to 200 residues or longer. In the range of gap lengths between zero and 15, the negative logarithm of this function gives a curve that is similar to those obtained using the SHoPP or DAPS databases in this study (Fig. 3). This is quite remarkable since the three databases are quite independent of each other in that they were made using three different sets of protein domains and three different structure alignment algorithms.

Figure 3.

A fitted curve (13) depicting the probability distribution of gaps for the FSSP database, for gaps up to 15 in length. Analogous data for the SHoPP and DAPS databases have also been included for comparison.

It has been shown that an amino acid substitution matrix made of log odds ratios will tend to reproduce target frequencies in properly designed sequence alignment algorithms (6). Similarly, it does not seem unreasonable to expect that a gap penalty function that is set equal to the logarithm of the odds of observing gaps in aligned sequence databases will reproduce the observed frequency of gaps in well-designed sequence alignment procedures that allow gaps. This assumption is implicit in a number of previous works on gap penalty (11–13). We acknowledge, however, that this is an assumption for which there is no proof at present (7,9).

The function g(n) of equation 2 does not give the gap penalty function even under this assumption, since the log odds ratio includes another term, beside those given by equation 2, which corresponds to the log probability of gaps expected in random alignments. This latter term has yet to be determined. However, we expect this term to take a simple form and that the full gap penalty function will take the basic form of equation 2.

The bilinear gap penalty is a piecewise linear gap penalty function (10,25) which is different from other suggested forms (11,12,15). The slope of the regression line for long gaps is always smaller than that for shorter gaps (Fig. 2 and Table 3). Therefore the gap penalty function based on equation 2 will assign relatively smaller gap penalties for long gaps than the affine gap penalty does. This would be an advantage, since the latter tends to over-penalize long gaps (8).

Although the logarithm of the probability distribution of gap lengths for all gap types exhibits the same bilinear behavior as noted above, the parameters describing the regression lines are clearly a function of the secondary structure of residues flanking the gap (Table 2). Thus division of gaps into just two categories, based on the presence/absence of a coil residue flanking the gap (26), is an oversimplification when modeling gap penalty functions where the structure of the query sequence is known (or predicted). Such secondary structure-dependent gap penalty functions could be useful in cases wherein protein sequences are aligned to a known protein structure.

When considering a non-affine gap penalty scheme, computational cost can be an issue (8). The affine gap penalty, as well as the bilinear gap penalty described in this work, belong to the class of convex (also called concave) gap penalties, where g(k+1) – g(k) ≤ g(k) – g(k –1) and k is the gap length. Waterman and Beyer (27) showed that the computational complexity for aligning two sequences of lengths m and n using a convex gap penalty was, at most, O[mn(m + n)]. This was later improved to O{mn[log(m)]} by Miller and Myers (25), who also showed that, for a piecewise linear convex gap penalty made from K straight lines, the computational complexity is reduced to O[mnlog(K)]. Since the bilinear gap penalty presented here is a special case for K = 2, the computational complexity is O(mn), the same as for the affine gap penalty. This is a major advantage of the bilinear form of the gap penalty, which is not shared by a multi-exponential form like that suggested by the studies of Qian and Goldstein (13).