Effect Size, Statistical Power and Sample Size Requirements for the Bootstrap Likelihood Ratio Test in Latent Class Analysis

Abstract

Selecting the number of different classes which will be assumed to exist in the population is an important step in latent class analysis (LCA). The bootstrap likelihood ratio test (BLRT) provides a data-driven way to evaluate the relative adequacy of a (K −1)-class model compared to a K-class model. However, very little is known about how to predict the power or the required sample size for the BLRT in LCA. Based on extensive Monte Carlo simulations, we provide practical effect size measures and power curves which can be used to predict power for the BLRT in LCA given a proposed sample size and a set of hypothesized population parameters. Estimated power curves and tables provide guidance for researchers wishing to size a study to have sufficient power to detect hypothesized underlying latent classes.

In recent years, latent class analysis (LCA) has proven to be an important and widely used statistical tool in the social, behavioral, and health sciences. This technique, a form of finite mixture modeling (see McLachlan & Peel, 2000), can be used to identify underlying subgroups in a population. LCA can identify subgroups characterized by the intersection of particular behaviors, risk factors, or symptoms (e.g., Bucholz, Hesselbrock, Heath, Kramer, & Schuckit, 2000; Keel et al., 2004; Lanza et al., 2011; Rindskopf & Rindskopf, 1986; Uebersax & Grove, 1990), such as symptoms of psychosis (e.g., Shevlin, Murphy, Dorahy, & Adamson, 2007), nicotine withdrawal symptoms (e.g., Xian et al., 2005), or adolescent risk behaviors (e.g., Collins & Lanza, 2010). Despite the benefits of the measurement model provided by LCA, several difficulties in applications of this method remain. One critical issue is that of model selection, especially selection of the number of classes, sometimes called “extraction” of classes (e.g., Nylund, Asparouhov, & Muthén, 2007). The interpretation of all model parameters depends on the assumed number of classes. Simulations done to examine the performance of model selection tools in class extraction (e.g., Dziak, Coffman, Lanza, & Li, 2012; Nylund et al., 2007; Wu, 2009; Yang, 2006) have shown that having too small a sample often leads to choosing too few classes to adequately describe the data-generating model. However, to the best of our knowledge there is no information in the literature about how to predict specifically how large a sample size N is actually needed to avoid such underextraction in practice.

In LCA, the failure to identify a substantively important, but perhaps not highly prevalent, latent class may lead to a violation of the local (conditional) independence assumption of LCA (i.e., the latent class variable is no longer adequate to fully describe the population covariance between the items; see Collins & Lanza, 2010). It may also cause a loss of important scientific information. For example, in the Shevlin et al. (2007) study, wrongly collapsing the “hallucination” (hallucinations only) and “psychosis” (multiple severe symptoms) classes together might give a misleadingly simplistic picture of the distribution of psychotic symptoms. Thus, statistical power for detecting latent classes can be as important to the LCA user as statistical power for detecting significant effects is to the user of regression models. Although statistical power has been studied in the context of ANOVA and regression (e.g., Cohen, 1988) and in some covariance structure models (e.g., MacCallum, Browne, & Sugawara, 1996; MacCallum, Lee, & Browne, 2010; MacCallum, Widaman, Zhang, & Hong, 1999; Preacher & MacCallum, 2002; Satorra & Saris, 1985; Yuan & Hayashi, 2003), little is known about statistical power for detecting classes in LCA.

In this study we attempt to address this gap. First, we briefly review the bootstrap likelihood ratio test (BLRT), a very helpful procedure for testing hypotheses about the number of classes for LCA (see Nylund et al., 2007). Second, we briefly review how simulations can be used to construct power estimates for the BLRT given assumptions about the true population structure. Third, we propose effect size formulas based on the Cohen’s w and Kullback-Leibler discrepancy measures. These formulas can be used in generalizing the results of our power simulations to new scenarios. Next, we provide extensive simulation results that show the usefulness of these effect size formulas. Finally, we provide tables and formulas for predicting required N for the BLRT in LCA and demonstrate their usefulness with additional simulations based on published latent class models. This work may help researchers decide how large a sample should be in order to have sufficient statistical power in tests for LCA class extraction. To our knowledge, power resources of this kind for the LCA BLRT were not previously available.

Choosing the Number of Classes in LCA

The LCA model for categorical observed items can be defined as follows. Let y_j represent element j of a response pattern y. Let I(y_j = r_j) equal 1 when the response to item j is r_j, and 0 otherwise. Then

$$P(\mathbf{Y}=\mathbf{y})=\sum _{c=1}^K{\gamma }_c\prod _{j=1}^J\prod _{r_j=1}^{R_j}{\rho }_{j,r_j\mid c}^{I(y_j=r_j)},$$ (1)

where γ_c is the probability of membership in latent class c and ρ_j,rj|c is the probability of response r_j to item j, conditional on membership in latent class c (see Lanza, Collins, Lemmon, & Schafer, 2007). The γ parameters represent the latent class membership probabilities. The ρ parameters represent item response probabilities conditional on latent class membership. The γ and ρ parameters can be estimated by maximum likelihood using the EM algorithm (Dempster, Laird, & Rubin, 1977).

The parameters of Model (1) cannot be estimated or interpreted without specifying a value of K. Sometimes theoretical reasons for choosing a particular K are available, but more often researchers wish to use the data to guide their choice. They wish to avoid both underextraction (choosing a K that is too small) and overextraction (choosing a K that is too large). One approach is to compare models with 1, 2, 3, … latent classes, comparing the fit of each model to that of its predecessor using either a significance test or some relative fit criterion. If a K-class model fits significantly better than a (K −1)-class model, then the true population is assumed to have at least K classes.

The (K −1)- and K-class models can be compared by their best fitted log likelihoods. A naïve approach involves comparing the likelihood ratio test (LRT) statistic 2ℓ_H1 −2ℓ_H0, where ℓ denotes the fitted log likelihood, to a χ² distribution with degrees of freedom df = d_H1 − d_H0, where d denotes the number of parameters in the model. However, p-values from this test are not valid because the usual asymptotic theory for the likelihood ratio statistic does not apply for comparing mixture models with different numbers of components. The parameter spaces of these models are not nested in the usual way,¹ and, as a result, p-values from this naïve test are not accurate (see Lin & Dayton, 1997; Lindsay, 1995; McLachlan & Peel, 2000). A more valid test can be obtained by the parametric bootstrap likelihood ratio test (BLRT), as further described by Feng and McCulloch (1996) and McLachlan and Peel (2000) and advocated by Nylund, Asparouhov, and Muthén (2007). The BLRT uses the same test statistic as the naïve test, but it does not make the problematic assumption that the statistic has a χ² distribution under the null hypothesis. Instead, it uses an empirical estimate of the null hypothesis distribution.

The LCA BLRT can be performed as follows. First, fit the null ((K −1)-class) and alternative (K-class) models to the observed dataset, and calculate the test statistic for each. Model identification must be examined for each latent class model being compared. In practice this requires multiple starting values. Next, using the parameter estimates from the null model, generate B separate random datasets. Simulation evidence in McLachlan (1987) suggests that B should be at least 99 to obtain optimal power; we use B = 100 in this paper.² Now fit the null and alternative models to each generated dataset and calculate the log likelihood for each null and alternative model. Calculate the test statistic 2ℓ_H1 − 2ℓ_H0. In order to improve the chances of finding the global maximum likelihood solution for each model, multiple starting values should be used for each model here also.³ The empirical distribution of the B test statistics derived from the generated datasets can now serve as a reference distribution from which to calculate a critical value or a p-value for the test statistic obtained from the observed dataset.

In particular, let b be the number of generated datasets having calculated test statistics larger than the observed test statistic for the real dataset. Then the bootstrap p-value is calculated as b/B or (b + 1)/(B + 1) (see Boos, 2003). The intuition is that if H₀ is true, then the observed dataset will closely resemble the artificial datasets simulated under H₀; otherwise, it will be significantly different. Unlike the naïve test, this test generally is approximately valid; that is, it empirically provides a true Type I error rate of approximately the specified nominal α or below when the null hypothesis is correct. Depending on the situation and the implementation of the test, it is possible for even a bootstrap test to have true Type I error rates slightly higher than nominal in some situations (e.g., see simulation results in McLachlan & Peel, 2000, p. 199) but it still does much better than than a naïve test would do (see Nylund et al., 2007, p. 554). There have been two main barriers to greater use of the BLRT. First, until recently, few software packages have provided it. However, it is implemented in Mplus (Muthén & Muthén, 2007), and a SAS macro for performing the BLRT in simple models using PROC LCA (Dziak, Lanza, & Xu, 2011; Lanza et al., 2007) is also available at http://methodology.psu.edu/downloads/sasbootstrap. Second, the BLRT can be computationally intensive. The LCA model must be fit multiple times (for different starting values) to each of B separate datasets, which may take minutes or even hours. Nonetheless, the BLRT is of special interest as the only widely used test for class extraction to provide a valid, known α level, so in this paper we focus on the power of the BLRT.

The valid α level suggests that the risk of erroneously extracting too many classes can be controlled: that is, if the true number of classes is K and Model (1) holds, then size K will only be rejected 5% of the time or less in an α = .05 test of size K versus size K + 1. However, even when a test is valid (i.e., controls Type One error), it may still have low power (fail to control Type Two error). In the context of LCA, this means that although the BLRT is usually not very likely to extract too many classes (since its Type One error probability for a given comparison is very close to, or below, 5% for an α = .05 test; see Nylund et al., 2007, p. 554) it is still likely that it may extract too few classes if the sample size is insufficient (see p. 555). In the context of a test, underextraction of classes can be viewed as a lack of statistical power.

Consider the comparison of two models: a (K −1)-class model and a K-class model. By analogy to classic techniques, one could call the (K −1)-class model the null hypothesis and the K-class model the alternative hypothesis:

$$\begin{array}{l}{H}_0:\text{The}\text{population}\text{consists}\text{of}K-1\text{latent}\text{classes}.\\ H_1:\text{The}\text{population}\text{consists}\text{of}K\text{latent}\text{classes}.\end{array}$$ (2)

The latent classes are assumed to be defined as in Model (1). Thus we are considering Type I error here to denote choosing the K-class model when the (K −1)-class model is true, and Type II error to mean choosing the (K −1)-class model when the K-class model is true. Also by analogy to classic tests, the “α level” can be operationally defined as the probability of choosing the K-class model given a true (K −1)-class model, and “power” as the probability of choosing the K-class model given a true K-class model (i.e., one minus the Type II error probability). In an exploratory context, a comparison of a smaller to a larger model is likely to be done several times in sequence (1 vs. 2, 2 vs. 3, etc.) but for convenience we focus on a single step in this process.

An Example of Simulated Power for the BLRT

As in classical settings (Cohen, 1988), power depends on N, as well as on the assumed parameters under both H₀ and H₁. However, no theoretical formula, such as Cohen (1988) had for predicting the power of simpler tests, is available for predicting the power of the BLRT in LCA. Therefore, determining power here requires simulation. Consider the following example. Suppose that five forms of drug use (e.g., perhaps alcohol, tobacco, inhalants, cocaine, and prescription drug abuse) are being considered in a study of a particular population of at-risk youth, and participants are to be asked whether or not they had used each substance during the past year. These five questions corresponds to five dichotomous items in a LCA. Suppose furthermore that in truth there are three classes. Members of the first class (“low use,” 60% of the population) have an independent 10% chance of endorsing each item. The second (“selective use,” 30%) has a 90% chance of endorsing the first three items, but only 10% of endorsing the last two. The third class (“high use,” 10%) has a 90% chance for each item. A researcher gathers a sample of size N from this population, without knowing the true class structure, and tests the (false) null hypothesis that there are two classes in the population versus the (true) alternative hypothesis that there are three. What would the power be for this test given N, or what N is required to obtain adequate power to select the true 3-class model?

Power curves can be estimated by simulating data for a range of Ns and comparing the results. For each sample size in N = 50, 100, 150, we simulated 1000 datasets. In each, we fit the 2-class and 3-class models and compared them using a bootstrap test with B = 100 and α = .05. For comparison, we also show the proportion selecting the three class model as better than the two-class model if each of four other approaches are used: BLRT at a different α level, Akaike’s Information Criterion (AIC; Akaike, 1973), Schwarz’s Bayesian Information Criterion (BIC; Schwarz, 1978), or adjusted BIC (see Sclove, 1987). The proportion selecting the three-class model under each condition is shown in Table 1, which suggests that for the BLRT at a standard α = .05, a power of about 80% would be achieved when N is slightly over 100. As expected, a higher or lower α is also associated with higher or lower power for the BLRT, respectively. The rejection probability for the two-class model using AIC is comparable to that of the α = .05 bootstrap test in this case, and the rejection probability for the BIC is much lower. However, the rejection probabilities of the IC’s cannot really be interpreted as “power” here, because the ICs are not intended as null hypothesis tests.

Table 1.

Simulated power for a three-class hypothetical model for different sample sizes

N	Proportion Correctly Selecting 3-Class over 2-Class Model
	Using BLRT			Using Information Criteria
	α = .01	α = .05	α = .10	AIC	BIC	Adj. BIC
50	0.24	0.44	0.55	0.37	0.04	0.94
100	0.49	0.72	0.81	0.77	0.11	0.91
150	0.73	0.90	0.94	0.93	0.21	0.95

Note. BLRT=bootstrap likelihood ratio test, AIC=Akaike information criterion (Akaike, 1973), BIC=Bayesian information criterion (Schwarz, 1978), Adj. BIC = Adjusted BIC (see Sclove, 1987).

Of course, it is wise to consider multiple possible scenarios when planning a study. Thus, suppose we still assume a true H₁ with K = 3, but we are not sure about the class probabilities or the class-specific item response probabilities. Thus, we consider that the class memberships may be either approximately equal (34%, 33%, 33%) or unequal (60%, 30%, 10%). We also allow the class-specific responses to be .90 for high and .10 for low (a condition which we think of as strong measurement, or strong class separation), .80 and .20 (medium measurement), or .70 and .30 (weak measurement). This leads to six scenarios arranged in a factorial design as shown in Table 2. The simulated power for each, with N = 100, shown in Table 3, suggests that measurement strength and relative class size both have drastic effects on power (Dziak, Min, & Lanza, 2009). Unequal class sizes and poor measurement led to a power of only 4% for the α = .05 BLRT at N = 100, while the same test had a power of 99% under strong measurement and equal class sizes.

Table 2.

Four hypothetical three-class models

	Model 1			Model 2			Model 3			Model 4			Model 5			Model 6
Class label:	No/Low	Med	High	No/Low	Med	High	No/Low	Med	High	No/Low	Med	High	No/Low	Med	High	No/Low	Med	High
Prob. of membership:	.60	.30	.10	.34	.33	.33	.60	.30	.10	.34	.33	.33	.60	.30	.10	.34	.33	.33
Prob. of Yes response:
Item 1	0.30	0.70	0.70	0.30	0.70	0.70	0.20	0.80	0.80	0.20	0.80	0.80	0.10	0.90	0.90	0.10	0.90	0.90
Item 2	0.30	0.70	0.70	0.30	0.70	0.70	0.20	0.80	0.80	0.20	0.80	0.80	0.10	0.90	0.90	0.10	0.90	0.90
Item 3	0.30	0.70	0.70	0.30	0.70	0.70	0.20	0.80	0.80	0.20	0.80	0.80	0.10	0.90	0.90	0.10	0.90	0.90
Item 4	0.30	0.30	0.70	0.30	0.30	0.70	0.20	0.20	0.80	0.20	0.20	0.80	0.10	0.10	0.90	0.10	0.10	0.90
Item 5	0.30	0.30	0.70	0.30	0.30	0.70	0.20	0.20	0.80	0.20	0.20	0.80	0.10	0.10	0.90	0.10	0.10	0.90

Table 3.

Statistical power for several hypothetical models having three latent classes, five items, and N = 100

Model	Measurement Strength	Class Sizes	Proportion Correctly Selecting 3- over 2-Class Model
			BLRT			Information Criteria
			α = .01	α = .05	α = .10	AIC	BIC	Adj. BIC
1	Low	Unequal	0.01	0.04	0.08	0.08	0.00	0.29
2		Equal	0.01	0.05	0.11	0.10	0.00	0.35
3	Medium	Unequal	0.03	0.15	0.24	0.25	0.00	0.55
4		Equal	0.17	0.40	0.53	0.57	0.02	0.79
5	High	Unequal	0.49	0.72	0.81	0.77	0.11	0.91
6		Equal	0.94	0.99	1.00	1.00	0.73	1.00

Note. The model number in this table corresponds to the model number in Table 2. BLRT=bootstrap likelihood ratio test, AIC=Akaike information criterion (Akaike, 1973), BIC=Bayesian information criterion (Schwarz, 1978), Adj. BIC = Adjusted BIC (see Sclove, 1987). Low, medium and high “measurement strength” mean that ρ values are either .70 and .30, .80 and .20, or .90 and .10 for items typically endorsed or not endorsed, respectively, by members of each class, as presented in Table 2. Unequal and equal “class sizes” mean that the population class proportions are either different (10%, 30%, 60%) or approximately the same (34%, 33%, 33%) for members of each class.

Effect Size Formulas

The findings in Table 3, as well as prior simulation work (e.g. Collins, Fidler, Wugalter, & Long, 1993; Lin & Dayton, 1997; Nylund et al., 2007; Wu, 2009), show that sample size requirements in LCA depend on several factors, such as relative class size and measurement strength. However, it is not clear how to use these ideas to generate a recommended minimum N for a particular situation. In general, estimation of power requires some assumptions about the true characteristics of the population or process being studied. For some simple tests, this is classically expressed in terms of an effect size measure (as in Cohen, 1988). An effect size measure can be useful both for prospective power analysis and perhaps also for quantifying the practical significance of obtained results. This simple idea may generalize to more complicated models.

For example, in the context of structural equation modeling (SEM) with multivariate normal data, it is known that for a given null hypothesis about the population covariance matrix, there can often be infinitely many sets of parameter values for H₁ offering exactly the same power against a given H₀ (MacCallum et al., 2010). This is a result of the higher dimensionality of the space in which the alternative hypothesis is defined (see MacCallum et al., 2010). However, although the situation appears more complicated than the hypotheses about single parameters considered by Cohen (1988), one can nevertheless still estimate power using a discrepancy measure based on the population difference in likelihood functions for the two population models. Such a population discrepancy measure is analogous to an effect size for a classic test, in that it can be used to solve for the power of the likelihood ratio test once df, N, and α are specified (MacCallum et al., 1996; MacCallum et al., 2010; Satorra and Saris, 1985). The term “effect size” as we use it here is not intended to be interpreted as meaning the “effect” of an exogenous variable; we simply mean that it is a single number which can act as a working definition of how far the null hypothesis is from the alternative hypothesis, for the sake of describing results or predicting power. We now seek such an effect size for the LCA BLRT as well, despite the lack of multivariate normality and the presence of a mixture structure in LCA.

Cohen’s w

We first propose that w, an effect size measure that Cohen (1988) proposed for classic Pearson χ² tests of hypotheses about contingency tables with m cells, may be used in a modified way for LCA as well. For a contingency table, let

$$w=\sqrt{\sum _{i=1}^{n_{\text{cells}}}\frac{{(P_{1i}-P_{0i})}^2}{P_{0i}}},$$ (3)

where P_0i represents the probability of the ith cell, calculated under H₀, and P_1i represents the probability of the ith cell, calculated under H₁. Then w² has a form like a Pearson χ² test statistic, except that it uses assumed population proportions instead of sample proportions, and it does not directly depend on N. For an LCA model, the set of possible response profiles can be viewed as cells in a contingency table. For example, if there are 6 dichotomous items y₁, …, y₆, then there are 2⁶ possible response profiles y = y₁,…, y₆, and the probability of each of these profiles can be calculated using Model (1) for H₀ and H₁ separately. Thus, w can be calculated given the hypothetical γ and ρ parameter values for the models corresponding to H₀ and H₁.

For a classic χ² test of fit or of independence, without latent variables, Cohen’s w is directly a function of the χ² noncentrality parameter and thus of power for a given df. Thus, in that specific context, if one knows N, df, the α level of the test, and the value of w, and if the asymptotic assumptions for the χ² test are met, power can be computed directly with no additional information required. For LCA applications, in which classic χ² tests are not necessarily applicable, some information may be lost by condensing all of the many γ and ρ parameters for H₁ and H₀ into the single value w, but as we later show, w is a fairly good predictor of approximate power.

The Kullback-Leibler Discrepancy

Similarly, we also propose the Kullback-Leibler (KL; Kullback & Leibler, 1951) discrepancy between H₀ and H₁ as another useful effect size measure for the LCA BLRT. KL is a nonparametric measure of how different two fitted probability models are fromeach other. Denoting the models as M_a and M_b, the KL discrepancy can be written as

$$KL(M_a,M_b)={\mathrm{E}}_{M_a}\left(log\left(\frac{L_{M_a}(\mathbf{y})}{L_{M_b}(\mathbf{y})}\right)\right),$$ (4)

where L is the fitted likelihood and E_Ma denotes the expectation computed under M_a. For many kinds of models, KL can be used to express how well a likelihood ratio test will be able to detect the difference between the models, since it is the expected value of the log likelihood ratio (see Ferguson, 1996; van der Vaart, 1998). Using H₁ for M_a and H₀ for M_b, Expression (4) becomes

$$KL(H_1,H_0)=\sum _{i=1}^{n_{\text{cells}}}{P}_{1i}\left(log\left(\frac{P_{1i}}{P_{0i}}\right)\right).$$ (5)

In calculating w or KL, we add a small constant such as 10⁻³⁰ to each P₀ and P₁ to avoid dividing by 0 or taking a logarithm of 0 in the case of sparse data, although if the data is very sparse there may still be some numerical instability. Expression (5) cannot be re-expressed as a function of Expression (3), or vice versa; therefore, power predictions based on the two different effect size measures cannot be expected to match exactly. However, each measure is based on the degree of difference between the P₀ values and the P₁ values, and a value of zero for one effect size measure implies a value of zero for the other. w and KL are related to two classical ways of measuring the discrepancy between two probability models (the Pearson and Kullback-Leibler discrepancies, respectively, are further described in Zucchini, 2000), and they also closely resemble the Pearson χ² and likelihood or deviance G² LCA fit statistics (see Collins et al., 1993; Dayton, 1998), respectively. A brief outline of a convenient approach to calculating the w and KL effect size measures, requiring only a proposed set of γ and ρ parameters under H₁, is given in Appendix 1. We implement this approach in a SAS macro available at http://methodology.psu.edu/LcaEffectSizes.

Two Simpler Effect Size Formulas

Both the w and the KL measures described above include an expected cell proportion P₀ in the denominator for each possible cell. When there are J items, there are at least 2^J cells, so some expected cell proportions, and hence some denominators, will be extremely small. This raises questions about numerical stability and accuracy. Thus we next consider a measure based on the “index of dissimilarity” goodness-of-fit measure mentioned by Dayton (1998, p. 20). Revised somewhat for comparing two proposed population models rather than one proposed population model and a sample, it would be

$$I_D(H_1,H_0)=\frac{1}{2}\sum _{i=1}^{n_{\text{cells}}}\mid P_{1i}-P_{0i}\mid .$$ (6)

All three criteria considered so far involve P_0i and P_1i, the fitted probabilities for each cell of the contingency table under each hypothesized model. This is reasonable because these probabilities are the values that LCA models are intended to predict, in the same way that factor analysis models seek to predict covariance matrix entries (see Collins et al., 1993). However, it is inconvenient in that there are many such probabilities (up to 2^J if each item is dichotomous, and more otherwise), some of which may be at or near zero. In a different context, sparse contingency tables are known to pose difficulty in interpreting X² and G² fit statistics, which similarly involve a sum of ratios of tiny quantities over many cells (Collins et al., 1993; Muthén, 2008; Wu, 2009). Thus, one might wish for an effect size measure that would not directly involve the P_0is and P_1is.

From Wu (2009) and from Table 3, we know that having one or more extremely small classes (low γ values) and/or having one or more pairs of classes with similar response probabilities (similar ρ values), reduces power. Thus, among different possible parameter sets for a given model size (i.e., within a given combination of the number of items J and the number of H₁ classes K), $\underset{k=1,\dots ,K}{min}({\gamma }_k)$ and $\underset{k,k^{\prime }=1,\dots ,K}{min}\left({\sum }_{j=1}^J{({\rho }_k-{\rho }_{k^{\prime }})}^2\right)$ should each be positively related to power. Presumably, if one or more of the two similar classes was also a rare class, then there might be an even stronger tendency to lump the rare class into its more common neighbor. Thus, perhaps an ad-hoc measure of class separability such as

$$\mathit{SEP}=\underset{k,k^{\prime }=1,\dots ,K}{min}\left({\gamma }_k{\gamma }_{k^{\prime }}\left(\sum _{j=1}^J{({\rho }_k-{\rho }_{k^{\prime }})}^2\right)\right)$$

might be well correlated with power. This would be easier to calculate since it does not require P₀ or P₁ values. However, as we show later in our simulations, neither I_D nor SEP works as well for predicting power as w or KL.

Simulation Experiment 1: Performance of the Effect Size Formulas

For the proposed effect size measures to be useful, they must first be shown to be predictive of power. Therefore, we did a simulation experiment as follows. For each of the 3 ×2 = 6 combinations of J = 5, 9, or 13 dichotomous items and of K=3 or 5 classes, we created 10 random sets of γ and ρ parameters, each defining a possible joint population distribution of J dichotomous LCA items with no covariates. The probability ρ of a yes response on each item was generated as an independent uniform random variable for each class. Random γ parameters were generated such that for k = 1, …, K, ${\gamma }_k=e_k/\left({\sum }_{j=1}^K{e}_j\right)$ where the e_j are independent from an exponential distribution with mean 1. For the simple case of K = 2, this method would let γ₁ be uniformly distributed between 0 and 1 (Casella & Berger, 1990; Jambunathan, 1954), and so γ₂ would be uniformly distributed as well because γ₂ = 1 − γ₁. Also, random ρ parameters for the yes response were randomly drawn from a uniform distribution from 0 to 1. After this, to prevent extreme scenarios, parameter draws having any γ or ρ values less than .05 or ρ values greater than .95 were replaced with new random draws.

Within each of these 3 ×2 ×10 random sets of parameters, we generated 100 datasets with N = 500 each and 100 datasets with N = 1000 each, with the exception that in conditions with J = 13 and N = 1000 only 50 datasets per parameter set were generated in order to save computation time. We also generated an extra 10 random sets of γ and ρ parameters for the J = 5, K = 3 condition, the J = 9, K = 3 condition, and the J = 9, K = 5 condition to obtain additional information; for each of these additional parameter sets we generated 50 datasets with N = 500 and 50 datasets with N = 1000 per parameter set. These three conditions were of special interest because they were neither near-saturated like the J = 5, K = 5 condition, nor computationally burdensome like the J = 13 conditions. The total number of parameter sets was 200, and counting all of the 50 or 100 datasets per parameter set, the total number of datasets was 15000. For each of these datasets, we performed a BLRT to compare the (false) H₀ that there were K −1 classes to the (true) H₁ that there were K classes. Since each BLRT involved the original dataset plus 100 bootstrap samples, and for each bootstrap sample the null and alternative model were fitted with 50 random starts each, the process required 15000 ×(100 + 1) ×(50 + 50), or over 150 million LCA models to be fitted. The total computational cost was about 278 days distributed over several Linux processors.

The upper four panels of Figure A1, in the online appendix, show scatterplots of the relationships of the four effect size measures considered (w, KL, I_D and SEP) with power in the J = 5, K = 3 case. Both w and KL seem to be strongly related to power. The other two measures are much poorer predictors of the power of the BLRT and are therefore not considered further. Figure A1 also shows scatterplots of power against the Ramaswamy rescaled entropy statistic (Muthén, 2004; Ramaswamy, DeSarbo, Reibstein, & Robinson, 1993) for H₀ and H₁.⁴ The entropy statistic measures how clearly or confidently a model classifies the subjects in terms of posterior probabilities, but from the figure it is clear that neither H₀ entropy nor H₁ entropy by itself is a good effect size measure for a test; these plots appear to be mostly noise, with little or no systematic relationship with power.

Within each combination of J and K, the w and KL measures were strongly but not perfectly correlated (r > .95), except for the J = 13, K = 3 condition in which r = .78 due to an outlier. The outlier may have been due to a poorly calculated w caused by a near-zero denominator for one of the responses in one parameter draw. The range of values of w and KL which were observed differed by J and K. Because of the independent random ρ values, each item provided at least some evidence against H₀ (i.e., there were no items with exactly the same ρ value for two or more classes), so higher J was associated with higher w and KL and thus higher power. Also, roughly speaking, the larger K was, the more closely a (K −1)-class model could approximate a K-class model, so the effect size was lower.

It would be possible to interpolate the points for N = 500 or for N = 1000 in order to get a point estimate of power for any value of the effect size measure (within the observed range) assuming the given value of N. However, it would be impractical to have to simulate separate power curves for each possible value of N. It would be more useful if the N = 500 and N = 1000 curves could be combined with a single x-axis and a single fit curve, allowing for interpolation and some extrapolation to new values of N. It seems plausible to assume additivity (e.g., that 500 independent observations from an H₁ with a discrepancy of KL = 0.02 from the H₀ would provide the same amount of evidence against H₀ as would 1000 independent observations from an H₁ with KL = 0.01 from the H₀). Thus, perhaps N × KL can replace KL on the x-axis of the plots and separate curves are not needed. The same approach may work with w, although it is necessary to square w before multiplying by N, because of the square root over the sum in Model (3). Figures 1 and 2 show that additivity seems to apply, just as it would in a classic LRT.

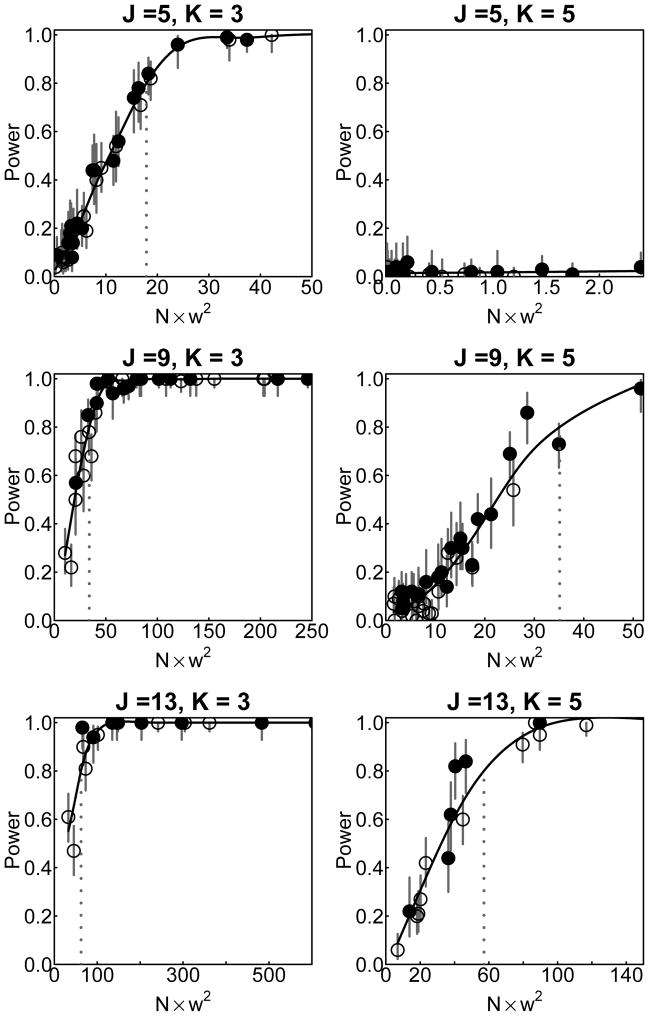
Figure 1.

Scatterplot of N × w² and simulated power for each simulated combination of number of items J and number of classes K. Empty circles represent N = 500 scenarios and solid circles represent N = 1000 scenarios. The fit curves are obtained from a smoothing spline with roughness penalty coefficient chosen subjectively. A vertical dotted line marks the estimate of $m_{80}^{(w^2)}$, which we denote as the value of N × w² for which power exceeds .80.

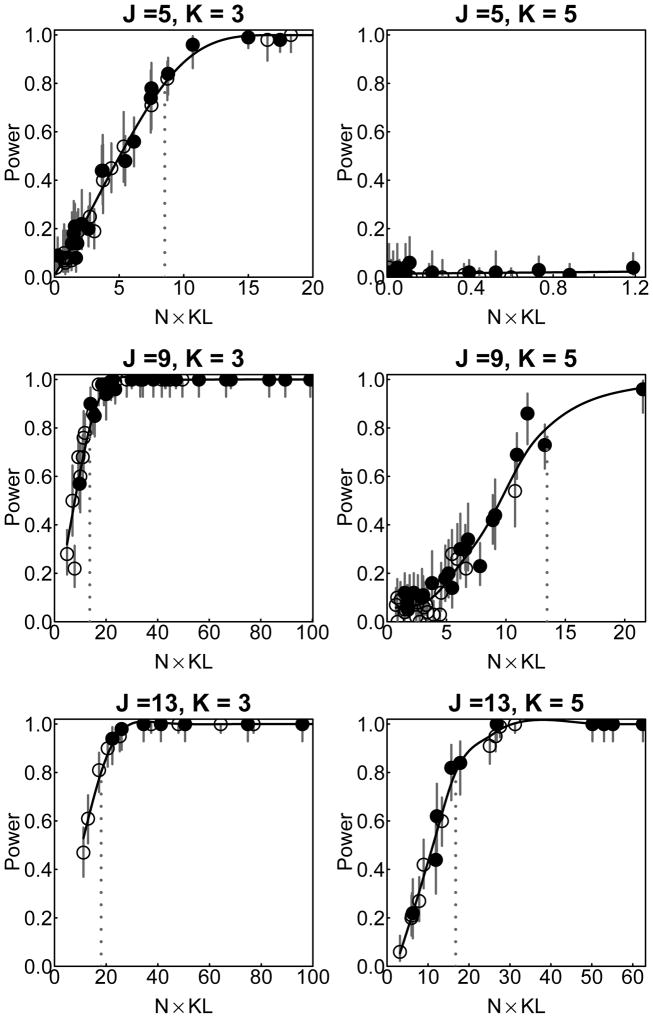
Figure 2.

Scatterplot of N × KL and simulated power for each simulated combination of number of items J and number of classes K. Empty circles represent N = 500 scenarios and solid circles represent N = 1000 scenarios. The fit curve is obtained in a similar way to that of Figure 1. A vertical dotted line marks the estimate of $m_{80}^{(KL)}$, which we denote as the value of N × KL for which power exceeds .80.

An appealing feature of Figures 1 and 2 is that it is possible to characterize what kind of parameter set for H₁ is likely to be associated with a BLRT power of a given value (e.g., .80) at a given α for testing H₀ against H₁. In the J = 5, K = 3 scenario, for example, it appears from Figure 1 that power of .80 would be obtained by parameter sets for which N × w² > 18. Denoting this minimum N × w² value as $m_{80}^{(w^2)}$, the researcher could choose

$$N=m_{80}^{(w^2)}/(w^2)$$ (7)

as being likely to detect a given true discrepancy of w. Equivalently, a true discrepancy of at least about $w=\sqrt{m_{80}^{(w^2)}/N}$ is needed to have 80% power to reject H₀ with a sample size of N. $m_{80}^{(w^2)}=18$ translates to a requirement for N = 1800, N = 200, and N = 72, for w = .1, .3, and .5, respectively, the “small,” “medium” and “large” benchmark values used (in a different context) by Cohen (1988). A minimum N × w² to obtain 90% power, although not specifically marked on the plot, could be obtained similarly and denoted $m_{90}^{(w^2)}$. Similarly, minimum N × KL benchmarks, denoted $m_{80}^{(KL)}$ and $m_{90}^{(KL)}$, can be estimated from Figure 2, and at least

$$N=m_{80}^{(KL)}/KL$$ (8)

is needed to obtain a power of at least .80 with a true discrepancy of KL of H₁ from H₀. These estimates are shown in Table 4. However, w and KL were always near zero in the J = 5, K = 5 condition, because the H₁ models were almost saturated (29 parameters for a 2⁵ = 32-cell contingency table) and perhaps poorly identified, and so the values of $m_{80}^{(w^2)},m_{80}^{(KL)}$, etc., could not be estimated for that condition.

Table 4.

Estimated constants m based on bootstrap simulation experiments

Number of Items	Number of Classes	Estimated $m_{80}^{(w^2)}$	Estimated $m_{90}^{(w^2)}$	Estimated $m_{80}^{(KL)}$	Estimated $m_{90}^{(KL)}$
Empirical Estimates from Experiment 1
5	3	17.9	21.4	8.5	10.3
9	3	34.0	40.8	13.7	16.6
9	5	35.1	43.3	13.5	16.5
13	3	62.3	79.0	18.1	21.6
13	5	57.1	70.9	16.7	20.7
Smoothed Empirical Estimates from Experiment 2
4	any	14.8	18.0	7.2	8.7
5	any	16.2	19.9	7.1	8.6
6	any	18.5	22.8	7.9	9.5
7	any	22.0	27.1	9.1	11.0
8	any	26.4	32.4	10.6	12.6
9	any	30.8	38.0	11.7	14.1
10	any	35.5	43.8	12.7	15.4
11	any	40.4	49.6	13.6	16.3
12	any	46.7	57.3	14.8	17.7
13	any	54.6	67.3	16.2	19.2
14	any	64.1	79.5	17.3	20.6
15	any	74.3	92.7	18.3	21.7

Note. $m_{80}^{(w^2)}$ represents the constant in Expression (7) for predicting from w the required N to obtain a target power of .80, and $m_{90}^{(w^2)}$ represents the equivalent for a target power of .90. $m_{80}^{(KL)}$ represents the constant in Expression (8) for predicting from KL the required N to obtain a power of .80, and $m_{90}^{(KL)}$ represents the equivalent for a target power of .90. “any” denotes a combined estimate for 2 through 6 classes.

It is clear from Table 4 that $m_{80}^{(w^2)}$ depends on J and possibly also on K. The dependence of power curves on model dimensionality is not surprising. The same holds for power in other covariance structure models (see, e.g., MacCallum et al., 2010; Saris & Satorra, 1993). Even in the simple case of a χ² test of fit or of independence on a contingency table (i.e., without latent variables, and with the assumption that N is adequate per cell for the appropriate χ² asymptotics to hold), Cohen (1988) still had to provide separate power tables depending on the df of the model. The underlying formula for the noncentrality parameter upon which the power calculations were based was the same, but the reference noncentral χ² distribution depended on the df of the test.

For the LCA BLRT there is no reference χ² distribution. However, we can define an ad-hoc df for the test, as the number of distinct, freely estimated parameters in H₁ minus the number of distinct, freely estimated parameters in H₀. The number of free parameters in Model (1) with dichotomous items is K −1 of γ parameters plus J × K of ρ parameters. Thus, for comparing a H₁ of K classes to a H₀ of (K −1) classes, the difference is df = J + 1, i.e., 1 more γ parameter and J more ρ parameters. Recall that in a classic χ² test with high N and no latent variables, power can be computed using only N, w, and df (see Cohen, 1988). Therefore, we next conducted further simulations to test whether, in the LCA case, power could be adequately approximated using only N × w² or N × KL and df (or equivalently J) and tabulated simulation results.

Simulation Experiment 2: Constructing a Table of Benchmark Sample Size Requirements

A thorough examination of the dependence of quantities such as $m_{80}^{(w^2)}$ on the number of items J and number of classes K requires additional simulations with more different values of J and K. Therefore, we performed new simulations on each combination of J = 4, 5, 6, 7, 8, 9, 10, 11, 13, 15 and K = 2, 3, 4, 5, 6. It was hypothesized that the shape of the power curves (i.e., the m values) would depend mainly on J and not K, although K might influence a point’s position on the x-axis (i.e., the effect size). If this conjecture is true, it would simplify the task of predicting power, since a useful reference table could be constructed by merely tabulating m values for every J in a range of interest, and not for every combination of J and K.

For each combination of J and K, we generated 10 random draws of parameters as described earlier. For each of these sets of random parameters, we simulated 200 datasets each with N = 750. For the easier scenarios (J > 2K), in which power might be high for every draw at N = 750, we additionally generated 200 more datasets having only N = 250 for each draw. In order to make this large number of simulations feasible, we employed a computational shortcut instead of doing the full BLRT each time. Resulting computational time was 554 days.⁵ Table 5 shows the median w and KL for the sets of parameters drawn under each combination of J and K. Figures 3 and 4 show how w and KL, respectively, are related to power within different values of J.

Table 5.

Median effect size estimates for testing K-class models constructed using randomly generated parameter draws, versus (K − 1)-class models, in Experiment 2

Number of Items	Median w					Median KL
	Number of Classes					Number of Classes
	2	3	4	5	6	2	3	4	5	6
4	0.153	0.050				0.011	0.001
5	0.283	0.107	0.035			0.027	0.005	0.001
6	0.438	0.114	0.057	0.039		0.057	0.006	0.002	0.001
7	0.631	0.201	0.102	0.063	0.039	0.116	0.018	0.005	0.002	0.001
8	0.478	0.234	0.102	0.122	0.055	0.067	0.023	0.005	0.007	0.002
9	0.759	0.326	0.159	0.132	0.080	0.172	0.041	0.011	0.008	0.003
10	0.881	0.394	0.202	0.167	0.108	0.149	0.059	0.016	0.012	0.005
11	1.047	0.459	0.261	0.164	0.138	0.201	0.064	0.024	0.010	0.008
13	1.094	0.616	0.376	0.315	0.199	0.271	0.097	0.050	0.034	0.016
15	2.295	0.835	0.539	0.401	0.297	0.384	0.183	0.091	0.048	0.026

Note. Medians rather than means are reported due to right skew.

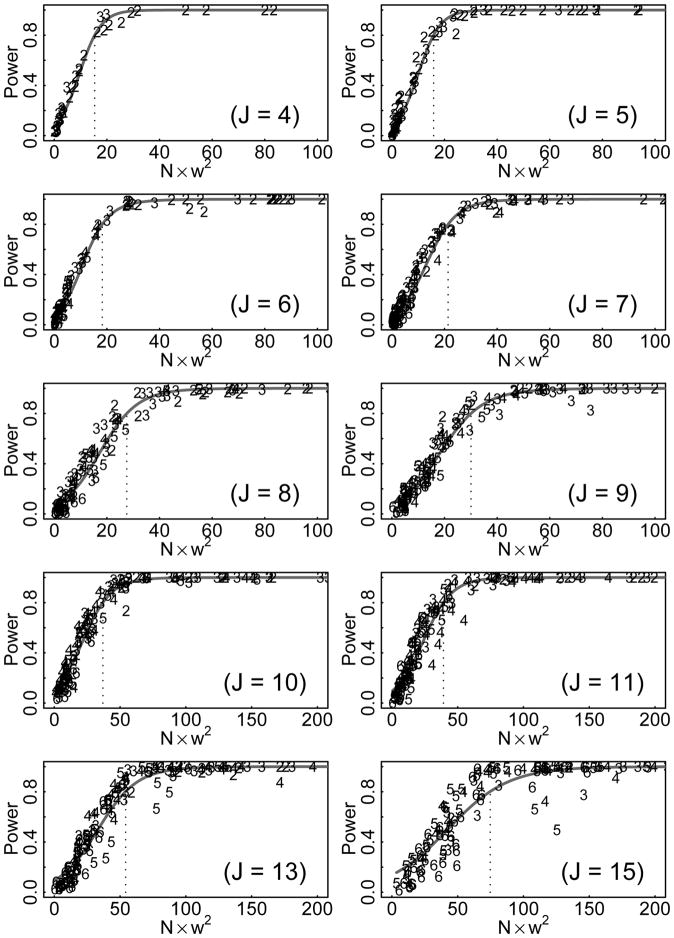
Figure 3.

Scatterplot of N × w² and simulated power for models based on different random parameter draws in Experiment 2. The plot symbols for each simulated model are numerals representing the number of classes for that model. The fit curves are obtained from a smoothing spline with roughness penalty coefficient chosen subjectively. A vertical dotted line marks the $m_{80}^{(w^2)}$ estimate.

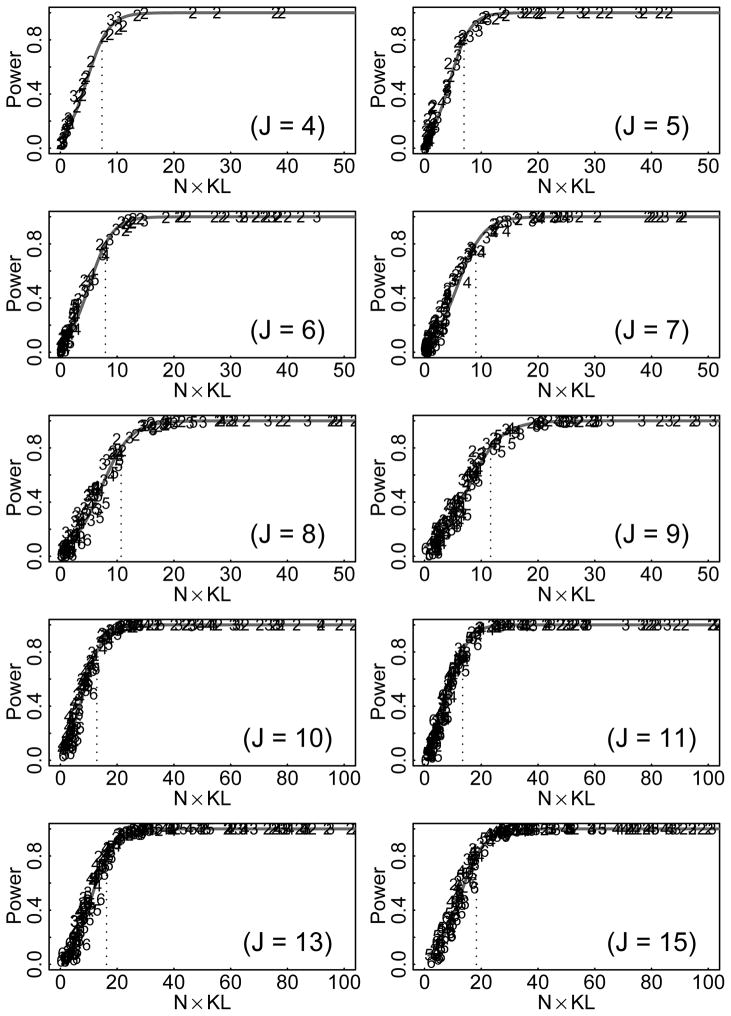
Figure 4.

Scatterplot of N × KL and simulated power for models based on different random parameter draws in Experiment 2. The plot symbols for each simulated model are numerals representing the number of classes for that model. The fit curves are obtained from a smoothing spline with roughness penalty coefficient chosen subjectively. A vertical dotted line marks the $m_{80}^{(KL)}$ estimate.

Fit curves were applied to Figures 3 and 4 using nonparametric smoothing. Estimates for the m constants described earlier were obtained for each plot by simply recording where these curves crossed .80 or .90. These estimates, considered as a function of J, were then smoothed in an attempt to reduce random error and allow interpolation to the J = 12 and J = 14 cases, which had been omitted to save computer time.⁶ The resulting estimates are shown in the second part of Table 4.

Especially for KL, a single curve for each J did fairly well in summarizing the relationship of effect size to power regardless of K. Although this does not prove that K does not affect the power curve, it does suggest that a table of $m_{80}^{(KL)}$ constants indexed only by J may be useful. The curve (i.e., the power for a given effect size) did not depend noticeably on K, although the position of points on the curve (i.e., the effect size actually obtained) did depend heavily on K. Table 5 shows that the effect sizes obtained depend jointly on J and K, with highest effect sizes observed when J is large and K is small.

Simulation Experiment 3: Validating Estimated Sample Size Requirements Using Empirical Models

The plots from Experiment 2 provide sufficient information to make power predictions for a wide range of LCA scenarios. However, there are still some reasons to be uncertain about the performance of these predictions. First, they are based on a computational shortcut. The m estimates for a given J (e.g., J = 9) in Table 4 seem to be slightly lower on average for comparable conditions in Experiment 2 (with the shortcut) than in Experiment 1 (without the shortcut). Thus, it is not clear whether the shortcut leads to underestimating the needed N. Second, both Experiments 1 and 2 were based on randomly generating parameter values, and therefore might not be well representative of the parameter values which would be found in real-world research.

To address these concerns about validity, we performed a final set of simulation experiments. For each of the six parameter sets in Table 2, and additionally for each of seven empirical examples of fitted LCA models chosen from recent literature, we first imagined that the proposed or estimated model was exactly true for the population. We imagined that an investigator was planning to gather data from this population to test whether there were K or K −1 classes, where K was the number of classes in the published work. We used the following empirical examples. The alcohol model is taken from an analysis in Lanza et al. (2007, p. 687) of data from Monitoring the Future (Johnston, Bachman, O’Malley, & Schulenberg, 2004), original N = 2490. The delinquency model is from Collins and Lanza (2010, p. 12), original N = 2087, based on Wave I data from the National Longitudinal Study of Adolescent Health (Udry, 2003). The depression model is from Lanza, Flaherty, and Collins (2003, p. 687), original N = 1892. The eating model is from Lanza, Savage, and Birch (2010, p. 836), original N = 197. The health risks model is from Collins and Lanza (2010, p. 39), original N = 13840, using Youth Risk Behavior Survey (2005) data. The nicotine withdrawal model is from Xian and colleagues (2005, p. 414), original N = 4112. The psychosis model is from Shevlin and colleagues (2007, p. 105), original N = 5893.⁷ Each of these models is based on dichotomous items, typically representing the presence or absence of some symptom or behavior, as is fairly common in psychological and medical research.

For each dataset, we calculated w and KL based on the population parameters, and then calculated the required N according to Table 4 to obtain a power of .80 at α = .05 for that w or KL (i.e., we imagined that the hypothetical experimenter guesses the effect size exactly right). We then simulated 1000 datasets of size N from this hypothetical population, and performed the bootstrap test (without the computational shortcut) for each one. We did this separately for N_w, the sample size obtained using w and Equation (7), and for N_KL, the sample size obtained using KL and Equation (8). Finally, we also did a set of simulations for 1.15N_KL, for reasons described below. The total computational time required was 221 days. Results are shown in Table 6.

Table 6.

Agreement with target power for K-class versus (K − 1)-class models in Experiment 3

Scenario	Items	Classes	Effect Sizes		Using Nw		Using NKL		Using 1.15NKL
			w	KL	N	Power	N	Power	N	Power
Scenarios from Hypothetical Models
Model 1	5	3	0.06	0.002	4071	0.82	3571	0.76	4107	0.82
Model 2	5	3	0.11	0.006	1314	0.77	1163	0.72	1338	0.78
Model 3	5	3	0.17	0.014	559	0.77	494	0.74	569	0.79
Model 4	5	3	0.27	0.038	216	0.81	188	0.74	217	0.80
Model 5	5	3	0.35	0.061	131	0.87	117	0.82	135	0.88
Model 6	5	3	0.51	0.141	62	0.93	51	0.87	59	0.91
Scenarios from Published Empirical Results
alcohol	7	5	0.27	0.040	312	1.00	230	0.97	265	0.98
delinquency	6	4	0.18	0.015	586	0.77	531	0.71	611	0.79
depression	8	5	0.23	0.025	491	0.79	428	0.69	493	0.79
eating	14	4	0.58	0.140	191	0.98	124	0.87	143	0.94
health risks	12	5	0.30	0.028	537	0.77	534	0.77	615	0.85
nicotine	12	4	0.18	0.014	1524	0.95	1075	0.78	1237	0.86
psychosis	13	4	0.11	0.005	4639	0.98	3219	0.84	3702	0.87

Note. w and KL refer to the calculated effect sizes for each model. N_w, N_KL, and 1.15N_KL refer to sample size N chosen using each of the three ways described in the text for calculating needed sample size (using w, using KL, or using KL and then multiplying the result by 1.15). For each combination of model and sample size calculation method, “N” refers to the sample size recommended by that method in order to obtain a predicted power of .80, and “Power” refers to the simulated power actually achieved for samples of that size from that model. Thus, a highly accurate method of predicting power would have entries very close to .80 in its Power column.

Ideally, we would hope that the simulated power for each of these 13 scenarios would be close to .80. This would indicate that the results of Experiment 2 were generalizable to parameter sets other than those used in Experiment 2. Table 6 shows that the sample sizes chosen to afford a power of .80 do obtain power reasonably near .80, although how near seems to depend on the method as well as the scenario. N_w is seldom too small (providing power of at least 0.77 for all of the models) but often needlessly large (power higher than .99 in one instance). N_KL provides power which is is very close to .80 on average, and seems to be a more precise estimate than the estimate from w. Thus, KL might potentially be a more useful measure than w for sample size planning.

However, there is an important caveat: notice that N_KL is sometimes too small (in one case a power of only .69 is obtained for a target power of .80). In many cases, an underestimation of the needed sample size may be more harmful than an overestimation (i.e., it is better to err by expending slightly more resources than is needed to attain one’s goals, than to fail to attain them at all by expending slightly too little). Thus, perhaps an unbiased estimate of the required sample size is not really desirable, but instead it would be better to have an estimate which is purposefully slightly biased in the direction of caution. This might be done by first obtaining an N estimate from KL but then multiplying this estimate by some constant slightly greater than 1. We found that the multiplier 1.15 seems to work well,⁸ in that the selected N’s now provided simulated power ranging from about .8 to about .9. That is, using 1.15N_KL gave power values that were never much lower than .80, although they were often slightly higher.

The correct selection rates by other analysis methods besides the α = .05 bootstrap were also observed, and are compared in Table 7. For simplicity we show only results using N_w since relative patterns will be the same regardless. The values for the BLRT in Table 7 can be considered to represent statistical power. The term “power” is not quite correct for AIC, BIC or adjusted BIC since they are not designed to be hypothesis tests with fixed α levels (although they are being used like tests in this case, in that a larger model is being compared to a smaller). However, it is still enlightening to compare their behavior. Decreasing α for the BLRT from .05 to .01 noticeably reduces power, although increasing α to .10 does not increase it as much. The rejection rates of the too-small model by the information criteria varied, with AIC being the most liberal or sensitive (hence least likely to result in underextraction) and BIC being by far the most conservative, parsimonious, or specific (most likely to result in underextraction). Although this is important information, decisions about what selection method to use should not be made on the basis of Table 7 alone, since it only deals with the case in which H₁ is true. If overextraction (the equivalent of Type One error) were being considered, then the reverse would have been seen, with BIC becoming more likely to be correct than AIC, and a BLRT with a low nominal α becoming more likely to be correct than one with a higher one (see Dziak et al., 2012).

Table 7.

H₀ rejection probability of different methods in Experiment 3, using N determined from w and Equation (7)

	N	Proportion Correctly Selecting K-class Over (K − 1)-Class Model
		BLRT With			Information Criteria
		α = .01	α = .05	α = .10	AIC	BIC	Adj. BIC
Hypothetical Scenarios
Model 1	4071	0.58	0.82	0.87	0.92	0.01	0.17
Model 2	1314	0.50	0.77	0.86	0.91	0.02	0.40
Model 3	559	0.57	0.77	0.87	0.90	0.05	0.60
Model 4	216	0.55	0.81	0.89	0.92	0.13	0.88
Model 5	131	0.67	0.87	0.92	0.92	0.19	0.96
Model 6	62	0.78	0.93	0.96	0.94	0.38	1.00
Scenarios from Published Empirical Results
alcohol	312	0.89	1.00	1.00	0.89	0.00	0.67
delinquency	586	0.54	0.77	0.83	0.88	0.02	0.54
depression	491	0.57	0.79	0.87	0.95	0.00	0.62
eating	191	0.94	0.98	0.99	0.99	0.08	0.98
health risks	537	0.57	0.77	0.85	0.96	0.00	0.56
nicotine	1524	0.84	0.95	0.97	1.00	0.00	0.49
psychosis	4639	0.92	0.98	0.99	1.00	0.00	0.24

Note. BLRT=bootstrap likelihood ratio test, AIC=Akaike information criterion (Akaike, 1973), BIC=Bayesian information criterion (Schwarz, 1978), Adj. BIC = Adjusted BIC (see Sclove, 1987).

Recommendations

Using the results in Table 4, a predicted sample size requirement can be obtained for powering a test to select the K-class model over the corresponding (K −1)-class model, at least under the assumption that there are no more than K classes. This may be useful in planning the needed N for observational studies based on consideration of one or more hypothetical population structures. It may also be useful in evaluating the adequacy of available datasets prior to doing an LCA analysis. Using KL seems to be a slightly better choice than using w, but w also works fairly well. In order to err on the side of caution, we recommend multiplying the estimated required N by 1.15.

As illustrated in Table 8, recommended N depends heavily on the assumed effect size. Cohen (1988) provided benchmarks of .1, .3, or .5 for low, medium or high w, but these were for a classic χ² fit test, not for LCA. We are unaware of any similar benchmarks for KL at all. The average values in Table 5 could be used, but these estimates might be too pessimistic because they are based on random numbers rather than interesting and well-measured real-world datasets.

Table 8.

Sample size recommendations for power=.80 assuming different values of w

J	Assuming Benchmark Values of w			Assuming Median Observed w From Random Datasets In Experiment 2 Given a Number of Classes
	(w=.1)	(w=.3)	(w=.5)	(2 classes)		(3 classes)		(4 classes)		(5 classes)		(6 classes)
	N	N	N	w	N	w	N	w	N	w	N	w	N
4	1480	164	59	0.15	632	0.05	5920	low	high	low	high	low	high
5	1620	180	65	0.28	202	0.11	1415	0.04	13224	low	high	low	high
6	1850	206	74	0.44	96	0.11	1424	0.06	5694	0.04	12163	low	high
7	2200	244	88	0.63	55	0.20	545	0.10	2115	0.06	5543	0.04	14464
8	2640	293	106	0.48	116	0.23	482	0.10	2537	0.12	1774	0.06	8727
9	3080	342	123	0.76	53	0.33	290	0.16	1218	0.13	1768	0.08	4813
10	3550	394	142	0.88	low	0.39	229	0.20	870	0.17	1273	0.11	3044
11	4040	449	162	1.05	low	0.46	192	0.26	593	0.16	1502	0.14	2121
13	5460	607	218	1.09	low	0.62	144	0.38	386	0.32	550	0.20	1379
15	7430	826	297	2.30	low	0.84	107	0.54	256	0.40	462	0.30	842

Note. J represents the number of items. K represents the number of classes for the recommendations that use median values from Experiment 2. The number of classes does not matter for the recommendations that simply use the benchmark value. The estimated required sample size N for a given value of w was calculated using Equation (7) and the $m_{80}^{(w^2)}$ constants from Table 4 here, without multiplying by our proposed conservative factor of 1.15. To apply the conservative factor, simply multiply the N values above by 1.15.

Table 6 may provide a better guide to reasonable effect size values than Table 5, since it is based on published estimates rather than random data. However, in some cases it might be better for a researcher to construct one or more scenarios deemed reasonable for the true parameters, as in Table 2, and then calculate w or KL from each of them using the pseudo-population approach described earlier in the paper; a macro for doing this is provided at http://methodology.psu.edu/LcaEffectSizes/.

In summary, the required sample size for an LCA BLRT can be estimated as follows. First, specify an estimated effect size (either w or KL). One way to obtain such an estimate is to specify a H₁ model (including the number of items, supposed number of classes, and supposed γ and ρ values), and calculate the effect size for testing this model against the H₀ number of classes (a SAS macro is available for easily doing so in the case of comparing a K versus K −1 class model). A conservative approach would be to consider several reasonable models and choose the smallest effect size among them. After obtaining the effect size, one can use expression (7) or (8) to estimate the required N without needing to do simulations. If desired, one could optionally justify this estimate further by simulating datasets with that N and calculating the power as we did in Experiment 3.

Discussion

In this paper we empirically addressed the question of how large a sample size is needed to avoid underextraction when using the BLRT test to choose a number of classes in LCA. We proposed a method for doing so, based on first specifying a proposed effect size in terms of w or KL, and then using the tables compiled from our simulations to calculate the power needed to detect that effect size with adequate probability. Our simulations involved generating many scenarios with random characteristics, calculating the effect size measures, and empirically estimating the power of the BLRT on many simulated datasets for each scenario. This provided a feasible, though time-consuming, way to get around the lack of an analytic power formula for the LCA BLRT: namely, empirically plotting simulated power against simulated effect size in order to tabulate the required sample sizes. The tables can now be used by investigators without having to do simulations themselves. We studied only the case of dichotomous items, but the approach may be extended in the future to more general datasets.

An obvious limitation of the current paper is that we considered only a fairly simple application of LCA, involving dichotomous items and no covariates. Our study of even this simple case required a very large investment of computation time, so it is not clear how future research on more complicated models should be done. It is not known how polytomous items would affect power. It is reasonable to expect that informative covariates might improve power (Wu, 2009, p. 116), but this would require further study, as would the question of predicting power to detect relationships between covariates and the latent class variable.

Another important caveat is that the results in this paper are better used for prospective planning prior to doing an analysis, and may not be meaningful if applied in a post hoc way after doing an LCA (just as with classical power and sample size formulas; see, e.g., Hoenig & Heisey, 2001; Lenth, 2007). For example, in Table 6, the required N was always calculated as less than the N that was used in the original study. However, this cannot be interpreted as evidence that the original studies successfully found “all” of the classes of interest in their population, even if the classes are considered to be real phenomena and not just convenient abstractions in a model. Similarly, it cannot be interpreted as evidence that past LCA studies have used large enough N, or too large N, according to some objective standard. Either conclusion would involve circular reasoning, since by doing the computation we had already assumed that the results of the original study were accurate. Thus, although our results may be useful in planning empirical studies, or even in deciding whether to do an LCA analysis on an existing dataset, they should not be used to attempt to quantify confidence in a fitted LCA model.

Also, although we have treated model selection as closely related to testing, they are not the same (see, e.g., Burnham & Anderson, 2002). By focusing on testing in this paper, we gloss over some complications, especially the possibility that neither model might be correct. This is relevant even in classic significance testing but is very obvious in the context of class extraction. Nonetheless, the familiar paradigm of the power of a statistical test provides a simple and tractable way to begin to explore required N. In practice, researchers might take a stepwise approach to LCA model selection, such as comparing a 1-class solution to a 2-class, then a 2-class solution to a 3-class, and so on. If a researcher compares each pair of model sizes with a penalized likelihood criterion such as AIC (Akaike, 1973) or BIC (Schwarz, 1978), choosing the best one according to this criterion, then this is algebraically exactly the same as comparing each pair of models using a naïve likelihood ratio test, with an α level determined indirectly by the penalty weight of the criterion (see Foster & George, 1994; Leeb & Pötscher, 2005; Teräsvirta & Mellin, 1986). Thus, our approach based on ideas of hypothesis testing seems to be reasonable. However, there is not enough information to comprehensively compare approaches such as the information criteria to the BLRT. In Tables 1, 3, and 7, it is clear that AIC has a much higher probability of rejecting the inadequate model than BIC does. Reliance on the BIC is likely to result in the choice of overly simple models if N is not large.⁹ However, we do not necessarily recommend AIC as a substitute for BIC, because that might replace the underextraction problem with an overextraction problem. It is known that when using AIC or BIC to choose between two models, AIC will be more likely to overfit and BIC will be more likely to underfit (Dziak et al., 2012; Lin & Dayton, 1997). Rather than choosing one extreme or the other, it might be better to consider both AIC and BIC together (Collins & Lanza, 2010). Using BIC alone, however, involves a serious underfitting risk.¹⁰

We have only explored tests of the form (2), i.e., K −1 classes versus K classes, and have not explored what would happen if we replace H₀ in (2) with “The population consists of K −1 or fewer latent classes.” However, there might not be much of a difference. That is, if a (K −2)-class model is not rejected by the BLRT against a K-class alternative, then a (K −1)-class model should not be rejected either, assuming enough random starts have been used to find a global optimum likelihood for each size. A more fundamentally different case is what to do if one wishes to test broader alternative hypotheses. For example,

$$\begin{array}{l}{H}_0:\text{The}\text{population}\text{consists}\text{of}\text{at}\text{most}K-1\text{latent}\text{classes}.\\ H_1:\text{The}\text{population}\text{consists}\text{of}K\text{or}\text{more}\text{latent}\text{classes}.\end{array}$$ (9)

Such hypotheses may be of interest in confirmatory or goodness-of-fit analyses with LCA. However, the approach taken in the current paper does not apply well to them because of the lack of a specific H₁. The test in (9) is best viewed as a test of goodness of fit of the K − 1 class model, that is, of whether the local independence assumption implicit in Model (1) holds (see Collins et al., 1993; Collins & Lanza, 2010; Vermunt & Magidson, 2004, 2005), rather than as a comparison of two specific candidate values of K. Thus, since the test is different, the appropriate procedure for power or sample size planning would presumably also have to be different, and might be based on trying to determine the power to detect a certain amount of residual correlation.

Despite these limitations, in this study we have found that two proposed effect size measures, w and KL, were strongly related to the power of the LCA BLRT across thousands of simulated datasets. Based on this, we have compiled power tables for LCA class extraction, which has not been done before to our knowledge. We hope that this will help applied researchers in planning studies when latent classes are posited to exist.

Appendix 1. Calculating the Effect Size Measures

Formulas (3) and (4), for the w and KL effect size measures, suggest that to calculate effect size one needs to calculate P₀ and P₁ values for each of the cells in the contingency table of possible responses (of which there are 2^J if J dichotomous items are being analyzed). Fortunately, this is not as burdensome as it sounds. All that is required are proposed theoretical values for the class sizes γ and response probabilities ρ for H₁. All of the P₀ and P₁ can then be calculated as outlined below. For dichotomous items, this can be done automatically using a SAS macro provided at http://methodology.psu.edu/LcaEffectSizes/, but we provide an outline and the rationale for the procedure below.

1. Take a set of proposed γ values and a set of proposed ρ values provided by the investigator. These values specify the K-class H₁ model which is assumed to be true for calculating power.

2. Given theseH₁ parameters, calculate P₁ for each of the cells using expression (1).

3. Create a synthetic dataset having size approximately P₁ for each cell. We do this by first creating a dataset with one line for each cell (e.g., [1, 1, 1, 1, 1], [1, 1, 1, 1, 2], etc.) and then giving each cell a frequency weight proportional to the P₁ for that cell. This dataset now represents the population probability distribution specified by H₁, and could be considered a “pseudo-population.”

4. Do a (K − 1)-class LCA on the pseudopopulation (even though the pseudopopulation was generated under a K-class model). Do this LCA very carefully (with many random start values) to try to find the global maximum likelihood solution. Intuitively, the γ and ρ parameters from this solution now provide a fitted (K − 1)-class model which approximates the fit of the true K-class model about as well any (K − 1)-class model can do. This in turn approximates the bootstrapped distribution used by the BLRT.

5. Using the calculated best H₀ parameters, calculate P₀ for each of the cells by again using expression (1).

6. Now that P₀ and P₁ values are available for all cells, the effect size can be calculated directly using Formulas 3 and 4.

In the outline above, one might ask why we calculate the H₀ probabilities indirectly from the H₁ probabilities, instead of asking the investigator for γ and ρ values for H₀ as well. In other words, why are H₀ and H₁ being treated so differently, and why is the elaborate step of constructing a pseudopopulation necessary? The answer is that this corresponds to the way the BLRT test is done in practice. When doing a BLRT in practice, the bootstrap H₀ datasets are simulated not from a pre-specified set of parameters, but from the best fitting (K − 1)-class parameters to the observed data. Thus, to be realistic, after we propose a particular assumed set of H₁ parameters for calculating P₁, we should not also propose another arbitrary set of H₀ parameters for calculating P₀. Instead, we need to find the set of H₀ parameters which give P₀ values which are, in general, as close as possible to P₁. This sounds difficult but is easy: as described above, one can just use existing LCA software to fit a (K − 1)-class model to a sample of fake data having cell proportions equal to the P₁. Since these steps are automated, the process is actually much simpler for the user than having to specify separate theoretical values for both the H₀ model and the H₁ model.

Appendix 2

Appendix 2 is provided online at http://methodology.psu.edu/media/LcaEffectSizes/AppendixDziakLanzaTan.pdf.