Automated structure prediction of weakly homologous proteins on a genomic scale

Abstract

We have developed tasser, a hierarchical approach to protein structure prediction that consists of template identification by threading, followed by tertiary structure assembly via the rearrangement of continuous template fragments guided by an optimized C_α and side-chain-based potential driven by threading-based, predicted tertiary restraints. tasser was applied to a comprehensive benchmark set of 1,489 medium-sized proteins in the Protein Data Bank. With homologues excluded, in 927 cases, the templates identified by our threading algorithm prospector_3 have a rms deviation from native <6.5 Å with ≈80% alignment coverage. After template reassembly, this number increases to 1,172. This shows significant and systematic improvement of the final models with respect to the initial template alignments. Furthermore, significant improvements in loop modeling are demonstrated. We then apply tasser to the 1,360 medium-sized ORFs in the Escherichia coli genome; ≈920 can be predicted with high accuracy based on confidence criteria established in the Protein Data Bank benchmark. These results from our unprecedented comprehensive folding benchmark on all protein categories provide a reliable basis for the application of tasser to structural genomics, especially to proteins of low sequence identity to solved protein structures.

Despite considerable effort, the prediction of the native structure of a protein from its amino acid sequence remains an outstanding unsolved problem. In this postgenomic era, because protein structure can assist in functional annotation, the need for progress is even more crucial (1, 2). Historically, protein structure prediction divides into three categories: comparative modeling (CM) (3, 4), threading (5, 6), and new fold prediction (7–9). In CM, the protein structure is predicted by aligning the target sequence to an evolutionarily related, solved template structure. Threading goes beyond CM in that it is designed to match sequences to proteins adopting similar folds, where the target and template sequences need not be evolutionarily related. Finally, for new folds, the target sequence could adopt a structure not seen before and modeling should be done ab initio. This is the hardest category with the lowest prediction accuracy.

As the most robust of the protein structure prediction approaches, there are three main issues involved in CM/threading methods. First, a necessary precondition for their success is the completeness of the library of solved structures in the Protein Data Bank (PDB) (10). Recently, it was demonstrated that the PDB library is most likely complete for single domain protein structures at low to moderate resolution (11); e.g., for any given protein up to 100 residues, regardless of whether it is evolutionarily related to other solved protein structures, there is at least one already solved structure existing in the PDB that has a rms deviation (rmsd) from native <4 Å for 90% of its residues. This strongly suggests that the protein structure prediction problem can in principle be solved by using CM/threading methodologies and that new fold approaches may not be necessary. However, an effective fold recognition algorithm must be developed to identify these correct template proteins and alignments.

Second, having a threading template with gapped alignments and average coverage, it is nontrivial to build a complete model that is useful for functional studies. Most successful structure predictions are still dictated by the evolutionary relationship between target and template proteins. For proteins having >50% sequence identity to their templates, models built by CM techniques (3, 4) can have up to a 1-Å rmsd from native for their backbone atoms. For proteins with 30–50% sequence identity to their templates, the models often have ≈85% of their core regions within a rmsd of 3.5 Å from native, with errors mainly in loops (2, 4). When the sequence identity drops below 30%, the “twilight” zone (about two-thirds of known protein sequences), modeling accuracy sharply decreases because of the lack of significant threading hits and substantial alignment errors. Until recently, for all sequence identity ranges, improvement from the initial alignment has not been consistently demonstrated (12) and the ability to accurately predict the conformation of the intervening loops between aligned regions has been rather limited (4, 12). Therefore, the development of an effective automated technology that can deal with proteins in the twilight zone of sequence identity and then build refined models that are closer to the native structure than their initial template alignments with reasonably accurate loop conformations is essential.

Third, the large-scale benchmarking and validation of any given structure prediction methodology are of key importance. Previously, most approaches treated a relatively small number of proteins, which made it difficult to establish their generality. Indeed, one of the goals of CASP (13), the Critical Assessment of Techniques for Protein Structure Prediction, has been to introduce objectivity into the protein structure prediction field. However, the number of CASP targets has been relatively small, making it difficult to fully establish general trends.

To address these issues, we develop a structure prediction methodology called threading assembly refinement (tasser) that has the capacity to recognize the majority of nonevolutionarily related folds in the PDB library, to significantly refine the structures with respect to their initial template, and to generate good predictions for the loops. To assess its generality, we present folding results based on a large-scale benchmark of all representative single-domain proteins in the PDB where structural templates of >30% sequence identity to the targets are excluded. To demonstrate the generality of the conclusions and as an example of tasser's application to structural genomics, we describe the structure prediction results on all small and medium size ORFs in the Escherichia coli genome.

Methods

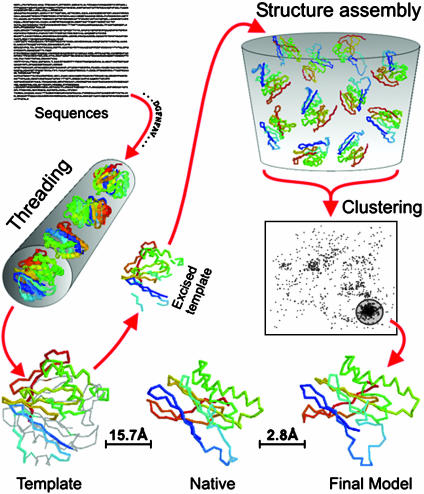
The tasser methodology consists of template identification, structure assembly, and model selection; an overview is presented in Fig. 1.

Fig. 1.

Overview of the tasser structure prediction methodology that consists of template identification by the prospector_3 threading algorithm (6), CAS fragment assembly, and fold selection by spicker clustering (18). The entire process for 1ayyD is shown as an example.

Threading. The structure templates for a target sequence are selected from the PDB library (10) by our iterative threading program prospector_3 (6), designed to identify analogous as well as homologous templates. The scoring function of prospector_3 includes close and distant sequence profiles, secondary structure predictions from psipred (14), and side chain contact pair potentials extracted from the alignments in previous threading iteration. Alignments are generated by using a Needleman–Wunsch global alignment algorithm (15). Based on score significance, target sequences are classified into three categories: if prospector_3 has at least one significant hit with Z score (the energy in standard deviation units relative to mean) >15 or if it has at least two consistent hits of Z score >7, these templates have high confidence to be correct and the target is assigned to the “easy set.” In practice, the majority of “easy” cases have a correct template and good alignments. [We note that easy does not mean that they are trivially identified; indeed, in the benchmark set, see below, prospector_3 correctly assigns more than twice the number of targets to their correct templates as psi-blast (16) does.] Those sequences that either hit a single template with 7 < Z < 15 or hit multiple templates lacking a significant consensus region are assigned to the “medium set”; these have the correct fold identified in most cases, but the alignment may be incorrect. Finally, those sequences that cannot be assigned by prospector_3 to a template belong to the “hard set,” and from the point of view of the algorithm are new folds, although according to the finding of the completeness of the PDB (11), (almost) all proteins should be assigned to either the easy or medium set by a “perfect” threading algorithm.

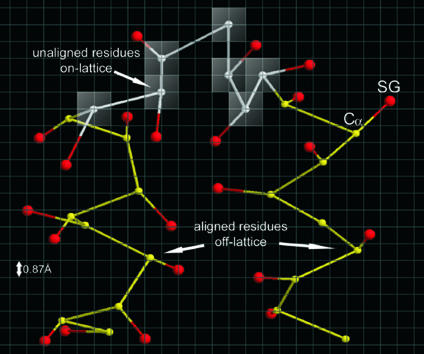
On-and-Off Lattice C-Alpha Side Chain Based (CAS) Model. A protein is represented by its C_α atoms and side chain centers of mass (SG), called the CAS model. Based on the threading alignment, the chain is divided into continuous aligned regions (more than five residues) whose local conformation is unchanged during assembly and gapped ab initio regions. For computational efficiency, the C_α values of these ab initio residues lie on an underlying cubic lattice, whereas the C_α values of aligned residues are excised from the threading template and are off-lattice for maximum accuracy. SGs are always off-lattice. A representative chain fragment is shown in Fig. 2. The CAS potential includes predicted secondary structure propensities from psipred (14), backbone hydrogen bonds, consensus predicted side chain contacts from prospector_3, and statistical short-range correlations and hydrophobic interactions (9). The combination of energy terms was optimized by maximizing the correlation between the rmsd of decoy structures to native and energy for 100 nonhomologous training proteins (extrinsic to the benchmark set used here), each with 60,000 decoys. Optimization resulted in a funnel-like energy landscape for training proteins, with an average correlation coefficient of 0.69 between the energy and rmsd to native (9).

Fig. 2.

Schematic representation of a piece of polypeptide chain in the on- and off-lattice CAS model. Each residue is described by its C_α and side chain center of mass (SG). Whereas C_α values (white) of unaligned residues are confined to the underlying cubic lattice system with a lattice space of 0.87 Å, C_α values (yellow) of aligned residues are excised from templates and traced off-lattice. SG values (red) are always off-lattice and determined by using a two-rotamer approximation (9).

Template Assembly and Refinement. For a given threading template, an initial full-length model is built by connecting the continuous template fragments by a random walk of C_α–C_α lattice bond vectors. If a template gap region cannot be spanned by the unaligned residues, a long C_α–C_α bond remains, and a spring-like external force that draws sequential fragments together is used until a physically reasonable bond length is achieved. Initial models are submitted to parallel hyperbolic Monte Carlo sampling (17) for assembly/refinement with two kinds of conformational updates: off-lattice movements involve rigid fragment translations and rotations whose amplitude is normalized by the fragment length so that the acceptance rate is approximately constant for different size fragments. Lattice confined residues are subject to two to six bond movements and multibond sequence shifts (9).

Certainly, the idea of assembling tertiary structure from protein fragments pieces is not new. For example, rosetta (8) uses small fragments (approximately three to nine residues). Because the conformational search is carried out by using large-scale moves (by switching between different local segments), the acceptance rate significantly decreases with increasing fragment size. Here, movement consists of scaled continuous translations and rotations, allowing for the successful movement of all size substructures. Because our threading-based fragments are much longer (≈20.7 residues on average), the conformational entropy is significantly reduced and more native-like interactions are retained.

Structure Selection. The Monte Carlo simulations employ 40 replicas, and the structures generated in the 14 lowest temperature replicas are submitted to an iterative structural clustering program, spicker (18). The final models are combined from the clustered structures and ranked by structure density.

Folding Results on a Comprehensive PDB Benchmark. To undertake a comprehensive test of the methodology, we developed an exhaustive benchmark set of all PDB structures with 41–200 amino acids. This set contains 1,489 nonhomologous single domain proteins with a maximum 35% pairwise sequence identity to each other. A total of 448, 434, and 550 targets are α, β, αβ proteins, respectively (the remaining 57 targets either have only C_α atoms in their solved structures or irregular secondary structures). Twenty targets are transmembrane proteins.

Among the 1,489 target sequences, prospector_3 assigns 877 to the easy set, with an average rmsd to native of 4.4 Å, and 87% alignment coverage (Table 1); 84% of these templates have a rmsd to native <6.5 Å (a statistically significant cutoff; ref. 19). In 799 cases, the top two scoring templates have a consensus region with 67% coverage and an average rmsd of 3.3 Å. This consensus region serves as an additional artificial template in the structure assembly of easy set proteins. There are 605 proteins assigned to the medium set, with an average rmsd to native of 9.7 Å and 62% alignment coverage. Of these, 191 have a rmsd <6.5 Å. For both the easy and medium sets, the average target/template sequence identity is ≈22%.

Table 1. Summary of threading results from prospector_3 and optimization by tasser.

				〈rmsd to native〉, ŧ			Nfold¶
	Ntargets*	Template selected†	〈covali〉, %‡	Tali	Mali	Ment	Tali	Mali	Ment
Easy set	877 (59%)	Top-2 + consensus	87	4.4	3.1	3.7	736 (84%)	819 (93%)	769 (88%)
Medium set	605 (40.5%)	Top-5 (Z score > 7)	62	9.7	6.3	8.0	191 (32%)	348 (58%)	216 (36%)
Hard set	7 (0.5%)	Top-20	75	11.3	6.0	6.3	0 (0%)	5 (71%)	5 (71%)
Total	1,489 (100%)		77	6.7	4.4	5.5	927 (62%)	1,172 (79%)	990 (66%)

^*Number and percentage of the target proteins in each category

^†Number of templates used in the assembly procedure. For easy targets, we used the top-2 templates of highest Z score and an artificial template consisting of the consensus region of these two templates if identified; for medium targets, up to five hits with Z score > 7; for hard targets, up to 20 templates, all having weak scores

^‡Alignment coverage on average for the best template that has the lowest rmsd to native

^§rmsd to native on average for the best initial templates and the best of top five models. T_ali, template structures with rmsd calculated over aligned residues; M_ali, model with rmsd calculated over the aligned residues; M_ent, model with rmsd calculated over the entire chain

^¶Number of targets with rmsd to native < 6.5 Å. The value in parentheses is the fraction of targets in the specific category set

Combining the easy and medium set results, 63% (927 of 1,482) of the targets have an acceptable template on the basis of the prospector_3 alignment (with rmsd <6.5 Å over 80% average coverage). Furthermore, if we ask whether a related fold is identified on the basis of structure alignment, 91% (1,348 of 1,482) of the proteins have a rmsd <6.5 Å with 72% average coverage. Thus, with respect to the ability of prospector_3 to identify related folds, it fails in ≈10% of the target sequences, although the alignment accuracy needs to be improved for one-third of the targets. Note that there are only seven proteins in the hard set where no global template is predicted. The average results for the threading templates, as well as the corresponding final models, are summarized in Table 1.

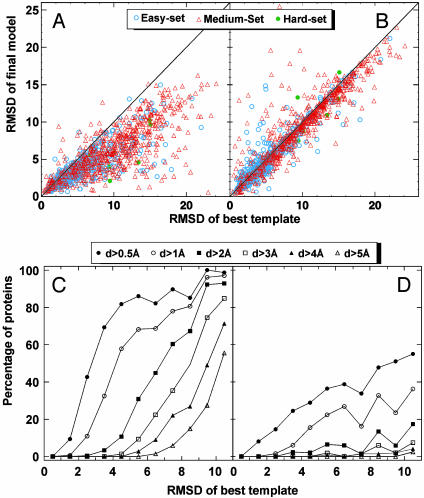
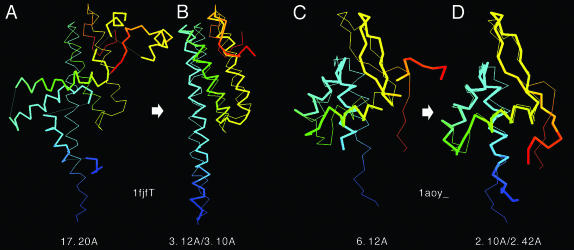
In Fig. 3A, we show the rmsd to native of the best model in the top five clusters selected by spicker compared to the initial alignments provided by prospector_3. Exactly the same aligned regions are used in both rmsd calculations. There are obvious improvements for almost all quality templates, with the biggest absolute rmsd improvement for the poorer quality targets (initial rmsd >8 Å), which mainly belong to the medium (Fig. 3A, red triangles) and hard (Fig. 3A, green circles) sets. These substantial rmsd reductions are mainly caused by the conversion from unphysical template alignments given by prospector_3 to geometrically acceptable models. A medium set example, 1fjfT, is shown in Fig. 4 A and B. Here, the template has substantial gaps (Fig. 4A) with high-quality local substructures, but a large deviation of global topology from native. By moving these rigid fragments and reassembling them into physically realistic models, a dramatic reduction of rmsd results (Fig. 4B).

Fig. 3.

(A) Scatter plot of rmsd to native for final models by tasser versus rmsd to native for the initial templates from prospector_3 (6). The same aligned region is used in both rmsd calculations. (B) Similar data as in A, but the models are from modeller. (C) Fraction of targets with a rmsd improvement d by tasser approach greater than some threshold value. Here, d = “rmsd of template” - “rmsd of final model.” Each point in C is calculated with a bin width of 1 Å; however, the last point includes all templates with rmsd > 10 Å. (D) Similar data as in C, but the models are from modeller.

Fig. 4.

Representative examples showing the improvement of final models with respect to the initial templates. The thin lines are native structures; the thick lines signify initial templates or final models. Blue to red runs from the N terminus to the C terminus. To guide the eye, the thinner lines connect contiguous template segments. (A and B) Medium/hard set example. (A) The template (from 1a5kC) superimposed on native structure of 1fjfT with an initial rmsd of 17.2 Å. (B) The optimized model for 1fjfT superposed on the native with rmsd of 3.1 Å (3.12 Å over aligned residues). (C and D) Easy set example. (C) The template (from 1b4aA) superimposed onto the native structure of 1aoy_, with an initial rmsd of 6.12 Å. (D) The optimized model for 1aoy_ superimposed on native with rmsd of 2.42 Å (2.1 Å over aligned residues).

As shown in the Fig. 3C, the fraction of targets having a rmsd improvement above the given threshold value is plotted as a function of the initial rmsd of the aligned residues. For initial models with an ≈4- to 5-Å rmsd, 58% of targets improve by at least 1 Å. Similarly, 43% of very good templates, ≈2- to 3-Å initial rmsd, have at least a 0.5-Å improvement. Thus, many distant CM targets are brought into the range of more traditional CM results (30–50% identity) on a systematic basis. For most initially good templates, mainly from the easy set (Fig. 3A, open cyan circles), with an initial rmsd of ≈2–6 Å to native, there is consistently an ≈1- to 3-Å improvement because of the better packing of local structures and side chain groups after CAS optimization. A representative example, 1aoy_, is shown in Fig. 4 C and D. Here, the global topology of the initial template is quite similar to the native structure (6.1-Å rmsd with 83% coverage) with local fragments in the initial alignment having different orientations from native. After tasser refinement, the final model has a rmsd of 2.4 (2.1) Å over the entire chain (aligned regions).

There are a few cases where refinement made the models worse (see Fig. 3A). Most are nonglobular proteins. For example, 1gl2C, the worst case spoiled by CAS refinement, is a 60-residue long single helix from a coiled coil. prospector_3 has a weak hit (Z = 4.9) to a gapped long helical template, 1bu0C, with a rmsd of 2.8 Å to native. Ideally, there should be no tertiary contacts in this protein. However, because of some spurious contact predictions (47 in total) collected from other weak scoring templates, the assembly procedure drives the structure to a two-helix bundle with a rmsd of 9.4 Å to native. A simple solution is to perform in parallel a pure ab initio simulation without restraints (9); this gives a final model having a rmsd of 2.9 Å to native.

In Fig. 3 B and D, we also show the comparison of the initial templates and optimized final models from a widely used CM tool, modeller (3, 4). As expected, because the structure given by modeller is obtained by optimally satisfying tertiary restraints from templates, threading template quality mainly dictates the final result (see Fig. 3D). In contrast, in tasser, because the relative orientations of template fragments are allowed to move, the strong reliance on the initial alignment is alleviated, and the final models can be significantly different, especially when the alignment is very gapped and the CAS potential does not favor the initial alignment. For good templates (mostly easy set targets), the alignments are much less gapped and the tertiary contact restraints from prospector_3 are much more consistent. This way, tasser tends to automatically “select” better templates and “refine” worse templates. Overall, for 1,349 targets, the final model is closer (with smaller rmsd) to native compared to the initial template within the aligned region, often significantly so.

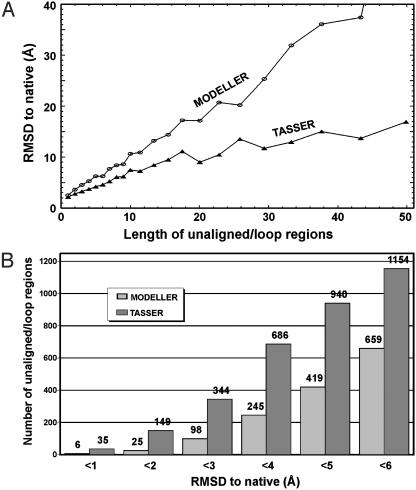
There are 6,101 continuous regions (ranging from 1 to 170 residues long and mainly on loops and tails) in the 1,489 targets where prospector_3 does not have coordinates aligned, and tasser needs to build the fragments by ab initio CAS approaches. In Fig. 5A, we show the average rmsd of the unaligned/loop regions as a function of length. Here, the rmsd between modeled loops and native was calculated based on the superposition of up to five neighboring stem residues on both sides of the loops. Although modeling accuracy decreases with increasing loop length in both modeller and tasser, the tasser ab initio procedure has on average a better control of the loop configurations, especially for the longer loops. In Fig. 5B, we show the histogram of 1,968 unaligned/loop regions that have length ≥4 residues. The average rmsd for these loops by tasser and modeller are 6.7 Å and 14.9 Å, respectively. If we consider for example a rmsd cutoff of <4 Å, modeller gives successful results in 12% (245 of 1,968) of the cases, whereas tasser ab initio modeling is successful in 35% (686 of 1,968) of the cases.

Fig. 5.

(A) Average rmsd to native of all unaligned/loop regions by tasser and modeller (3) as a function of loop length. The rmsd is calculated based on the superposition of up to five neighboring stem residues on both sides of the loop. (B) Histogram of the rmsd for the unaligned/loop regions with ≥4 residues (1,968 in total) modeled by tasser and modeller.

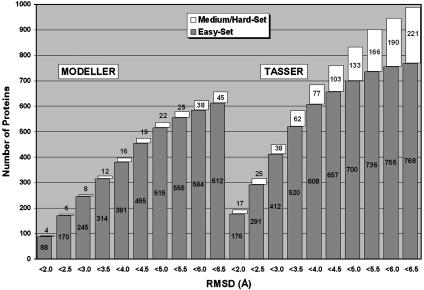
Fig. 6 summarizes the rmsd distribution of the full-length models by tasser and modeller, both starting from the same prospector_3 alignments. For the easy targets, tasser outperforms modeller, although the differences are smaller, as compared to the medium and hard sets, where the difference is even more pronounced. This comparison may not be entirely fair because modeller was designed to fold homologous proteins, and homologous templates have been excluded from our template library. However, this difference shows the utility of using tasser. Overall, the average rmsd of the best models to native are 12.16 Å and 5.49 Å for modeller and tasser, respectively (this significant difference is partially due to the fact that modeller generates random structures in some hard targets that have very short alignment templates); in 1,403 cases, tasser has a lower rmsd, and in 85 cases, modeller does.

Fig. 6.

Histograms of foldable proteins using modeller (3) and tasser based on the same templates and alignments from prospector_3 (6).

If we define foldable cases as those where one of the top five structures has a rmsd to native <6.5 Å, as shown in the last column of Table 1, the overall success rate for tasser full-length models is 66% (990 of 1,489). The total number of templates having an rmsd <6.5 Å in the aligned regions increases from 927 (62%) to 1,172 (79%) after tasser refinement. Among the 20 transmembrane proteins, nine (45%) of them (1a91_, 1bccH, 1f16A, 1fftC, 1jb0J, 1k3kA, 1kzuB, 1lghB, and 1qleD) are foldable, with an average rmsd of 3.8 Å. Furthermore, in contrast to many previous approaches (7–9), tasser does not show significant bias to secondary structure class: the success rates for α, β, and αβ proteins are 311 of 448 (69%), 265 of 434 (61%), and 380 of 550 (69%), respectively. Nevertheless, a weak dependence on protein size exists. For targets <120 residues, the success rate is 73% (642 of 884); but for targets >120 residues, it is 58% (348 of 605). All results, including threading templates, structure trajectories, and final combined models for each of targets, are available on our web site, www.bioinformatics.buffalo.edu/abinitio/1489.

Structure Predictions for the E. coli Genome. As an example of a genomic application of tasser, we apply here the approach to all 1,360 ORFs in the E. coli genome (20) ≤200 residues in length. prospector_3 assigns 829 (61%) to the easy set, 521 (38%) to the medium set, and 10 (0.7%) to the hard set. These threading assignment results are quite similar to that of the PDB benchmark, with a slightly larger portion of targets assigned to the easy set in E. coli, which may be due to the fact that homologues are not excluded.

It should also be mentioned that genome scale structure predictions have been performed by many authors on different organisms (21–27). Most are based on homology modeling or sequence comparison techniques, which require solved homologous structures. For example, the study by Peitsch et al. (22) produced comparative models for ≈10–15% of proteins in the entire E. coli genome. Using psi-blast (16), Hegyi et al. (25) assigned 28% of all E. coli ORFs to SCOP domains. In the PEDANT database (27), Frishman et al. showed that 50% of E. coli ORFs have a psi-blast hit to PDB structures, but the assignment rate is 31% for ORFs of <200 residues. In GTOP (26), Kawabata et al. used the reverse psi-blast (28) and aligned 53% of all E. coli ORFs (35% for those <200 residues) to the solved structures in PDB. Thus, prospector_3 alone is seen to perform significantly better than psi-blast.

As an indicator of likelihood of success for blind structure predictions, we noticed that: (i) the Z score of the template indicates the significance of the threading alignment; (ii) the degree of structure convergence in CAS assembly strongly correlates with the quality of models in spicker clustering (18). Thus, we define a confidence score, C-score, for tasser models by

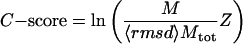[1]

where M is the multiplicity of structures in a spicker cluster, M_tot is the total number of structures submitted for clustering, and 〈rmsd〉 denotes the average rmsd of the structures to the cluster centroid.

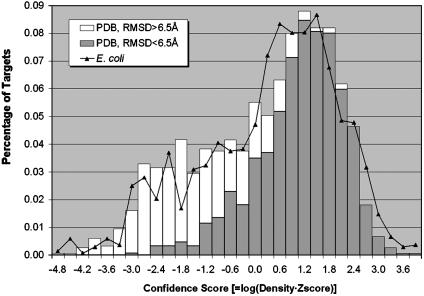
In Fig. 7, we show the C-score distribution of rank-one clusters generated for E. coli ORFs as well as that for the PDB benchmark proteins. The benchmarking data indeed show the significant sensitivities of the C score to the prediction success rate. For example, if we use a C-score threshold of -0.5 for the rank-one clusters, the false positive (negative) rate is 12.4% (14.7%). The C-score distribution of E. coli ORFs is consistent with the PDB benchmark, except for the slightly more targets distributed at high negative C-score regions for E. coli ORFs due to the fact that we did not exclude homologous proteins. If we assume that tasser has similar C-score sensitivity in E. coli as that in the PDB benchmark, we would expect ≈920 (68%) ORFs to have acceptable models.

Fig. 7.

Histogram distributions of the C-score (defined in Eq. 1) for the PDB benchmark proteins and E. coli genome. The targets of the best rmsd in top five clusters below and above 6.5 Å for PDB benchmark are shown in different color.

Around 23% (309 of 1,360) of these ORFs belong to membrane proteins according to memsat (29) predictions. This rate is slightly lower than the estimate of 26% by Jones (30) for the entire set, which may be due to the fact that we here only focus on the small ORFs with length ≤200 residues. In all rank-one models of transmembrane proteins, there is at least one long (putative transmembrane) helix occurring, which shows the consistency of our modeling with the memsat prediction. If we define the confidence level based on the C-score of the predicted models, there are 56% (174 of 309) of the membrane proteins that have >60% probability for the predicted models to have rmsd <6.5 Å; 47% (146 of 309) have >80% probability for the models with a rmsd <6.5 Å. The predicted models for all of the ORFs with corresponding C-scores and confidence indexes are available on our web site: www.bioinformatics.buffalo.edu/genome/ecoli.

We did not mask out signal peptide residues from the ORF sequences in our modeling. Actually, we found 149 cases having annotated signal peptides in the swiss-prot database (31). Because of their distinct sequences, the majority of the signal peptide residues are not aligned in the prospector_3 alignments. In all of the resulting, full-length, rank-one models, the signal peptide segments are outside the compact core structure because of the lack of predicted contact restraints between the signal peptide and the core regions. Therefore, the signal peptide sequence does not exert much of an influence on the core regions of tasser modeling. Indeed, one possibility to be pursued is to use this method to predict signal sequences.

Conclusions

We have developed tasser, an algorithm for protein tertiary structure assembly that spans the range from CM to ab initio folding. To establish its generality, we applied the methodology to a comprehensive benchmark set of 1,489 medium-sized proteins that covers the whole PDB at the level of 35% sequence identity. Consistent with our finding that the PDB is a complete set of single domain protein structures at low resolution (11), we can identify significant templates for >90% of such proteins. Furthermore, in a large-scale test, the results presented here demonstrate that threading alignments can be significantly improved by moving and rearranging rigid fragments. Three factors contribute to this success: the requirement of chain connectivity, improved tertiary structure packing of the native like secondary fragments due to an optimized force field, and the set of predicted tertiary contacts from threading. A success rate of around two in three is expected for the proteins of sequence identity <30% (on average 22% identity) to known structures. Based on tasser's confidence criteria established in the PDB benchmark, comparable performance is obtained for the E. coli genome. Although significant improvements in tasser are still being developed, nevertheless the ability to fold two-thirds of all non- and weakly homologous proteins of <200 residues represents encouraging progress on the protein structure prediction problem.