Distributions of Angles in Random Packing on Spheres

Abstract

This paper studies the asymptotic behaviors of the pairwise angles among n randomly and uniformly distributed unit vectors in ${\mathbb{R}}^p$ as the number of points n → ∞, while the dimension p is either fixed or growing with n. For both settings, we derive the limiting empirical distribution of the random angles and the limiting distributions of the extreme angles. The results reveal interesting differences in the two settings and provide a precise characterization of the folklore that “all high-dimensional random vectors are almost always nearly orthogonal to each other”. Applications to statistics and machine learning and connections with some open problems in physics and mathematics are also discussed.

1. Introduction

The distribution of the Euclidean and geodesic distances between two random points on a unit sphere or other geometric objects has a wide range of applications including transportation networks, pattern recognition, molecular biology, geometric probability, and many branches of physics. The distribution has been well studied in different settings. For example, Hammersley (1950), Lord (1954), Alagar (1976) and García-Pelayo (2005) studied the distribution of the Euclidean distance between two random points on the unit sphere ${\mathbb{S}}^{p-1}$. Williams (2001) showed that, when the underlying geometric object is a sphere or an ellipsoid, the distribution has a strong connection to the neutron transport theory. Based on applications in neutron star models and tests for random number generators in p-dimensions, Tu and Fischbach (2002) generalized the results from unit spheres to more complex geometric objects including the ellipsoids and discussed many applications. In general, the angles, areas and volumes associated with random points, random lines and random planes appear in the studies of stochastic geometry, see, for example, Stoyan, et al. (1995) and Kendall and Molchanov (2010).

In this paper we consider the empirical law and extreme laws of the pairwise angles among a large number of random unit vectors. More specifically, let X₁, ⋯, X_n be random points independently chosen with the uniform distribution on ${\mathbb{S}}^{p-1}$, the unit sphere in ${\mathbb{R}}^p$. The n points X₁, ⋯, X_n on the sphere naturally generate n unit vectors ${\overrightarrow{\mathbf{OX}}}_i$ for i = 1,2 ⋯, n, where O is the origin. Let 0 ≤ Θ_ij ≤ π denote the angle between ${\overrightarrow{\mathbf{OX}}}_i$ and ${\overrightarrow{\mathbf{OX}}}_j$ for all 1 ≤ i < j ≤ n. In the case of a fixed dimension, the global behavior of the angles Θ_ij is captured by its empirical distribution

$${\mu }_n=\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i<j\le n}{\delta }_{{\Theta }_{\mathit{ij}}},n\ge 2.$$ (1)

When both the number of points n and the dimension p grow, it is more appropriate to consider the normalized empirical distribution

$${\mu }_{n,p}=\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i<j\le n}{\delta }_{\sqrt{p-2}(\frac{\pi }{2}-{\Theta }_{\mathit{ij}})},n\ge 2,p\ge 3.$$ (2)

In many applications it is of significant interest to consider the extreme angles Θ_min and Θ_max defined by

$${\Theta }_{\min }=\min \{{\Theta }_{\mathit{ij}};1\le i<j\le n\};$$ (3)

$${\Theta }_{\max }=\max \{{\Theta }_{\mathit{ij}};1\le i<j\le n\}.$$ (4)

We will study both the empirical distribution of the angles Θ_ij, 1 ≤ i < j ≤ n, and the distributions of the extreme angles Θ_min and Θ_max as the number of points n → ∞, while the dimension p is either fixed or growing with n.

The distribution of minimum angle of n points randomly distributed on the p-dimensional unit sphere has important implications in statistics and machine learning. It indicates how strong spurious correlations can be for p observations of n-dimensional variables (Fan et al., 2012). It can be directly used to test isotropic of the distributions (see Section 4). It is also related to regularity conditions such as the Incoherent Condition (Donoho and Huo, 2001), the Restricted Eigenvalue Condition (Bickel et al., 2009), the ℓ_q-Sensitivity (Gautier and Tsybakov, 2011) that are needed for sparse recovery. See also Section 5.1.

The present paper systematically investigates the asymptotic behaviors of the random angles {Θ_ij;1 ≤ i < j ≤ n}. It is shown that, when the dimension p is fixed, as n → ∞, the empirical distribution μ_n converges to a distribution with the density function given by

$$h\left(\theta \right)=\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}\cdot {\left(\sin \theta \right)}^{p-2},\theta \in [0,\pi ].$$

On the other hand, when the dimension p grows with n, it is shown that the limiting normalized empirical distribution μ_n,p of the random angles Θ_ij, 1 ≤ i < j ≤ n is Gaussian. When the dimension is high, most of the angles are concentrated around π/2. The results provide a precise description of this concentration and thus give a rigorous theoretical justification to the folklore that “all high-dimensional random vectors are almost always nearly orthogonal to each other,” see, for example, Diaconis and Freedman (1984) and Hall et al. (2005). A more precise description is given in Proposition 5 later in terms of the concentration rate.

In addition to the empirical law of the angles Θ_ij, we also consider the extreme laws of the random angles in both the fixed and growing dimension settings. The limiting distributions of the extremal statistics Θ_max and Θ_min are derived. Furthermore, the limiting distribution of the sum of the two extreme angles Θ_min + Θ_max is also established. It shows that Θ_min + Θ_max is highly concentrated at π.

The distributions of the minimum and maximum angles as well as the empirical distributions of all pairwise angles have important applications in statistics. First of all, they can be used to test whether a collection of random data points in the p-dimensional Euclidean space follow a spherically symmetric distribution (Fang et al., 1990). The natural test statistics are either μ_n or Θ_min defined respectively in (1) and (3). The statistic Θ_min also measures the maximum spurious correlation among n data points in the p-dimensional Euclidean space. The correlations between a response vector with n other variables, based on n observations, are considered as spurious when they are smaller than a certain upper quantile of the distribution of |cos(Θ_min)| (Fan and Lv, 2008). The statistic Θ_min is also related to the bias of estimating the residual variance (Fan et al., 2012). More detailed discussion of the statistical applications of our studies is given in Section 4.

The study of the empirical law and the extreme laws of the random angles Θ_ij is closely connected to several deterministic open problems in physics and mathematics, including the general problem in physics of finding the minimum energy configuration of a system of particles on the surface of a sphere and the mathematical problem of uniformly distributing points on a sphere, which originally arises in complexity theory. The extreme laws of the random angles considered in this paper is also related to the study of the coherence of a random matrix, which is defined to be the largest magnitude of the Pearson correlation coefficients between the columns of the random matrix. See Cai and Jiang (2011, 2012) for the recent results and references on the distribution of the coherence. Some of these connections are discussed in more details in Section 5.

This paper is organized as follows. Section 2 studies the limiting empirical and extreme laws of the angles Θ_ij in the setting of the fixed dimension p as the number of points n going to ∞. The case of growing dimension is considered in Section 3. Their applications in statistics are outlined in Section 4. Discussions on the connections to the machine learning and some open problems in physics and mathematics are given in Section 5. The proofs of the main results are relegated in Section 6.

2. When The Dimension p Is Fixed

In this section we consider the limiting empirical distribution of the angles Θ_ij, 1 ≤ i < j ≤ n when the number of random points n → ∞ while the dimension p is fixed. The case where both n and p grow will be considered in the next section. Throughout the paper, we let X₁, X₂, ⋯, X_n be independent random points with the uniform distribution on the unit sphere ${\mathbb{S}}^{p-1}$ for some fixed p ≥ 2.

We begin with the limiting empirical distribution of the random angles.

Theorem 1 (Empirical Law for Fixed p)

Let the empirical distribution μ_n of the angles Θ_ij, 1 ≤ i < j ≤ n, be defined as in (1). Then, as n → ∞, with probability one, μ_n converges weakly to the distribution with density

$$h\left(\theta \right)=\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}\cdot {\left(\sin \theta \right)}^{p-2},\theta \in [0,\pi ].$$ (5)

In fact, h(θ) is the probability density function of Θ_ij for any i ≠ j(Θ_ij’s are identically dis tributed). Due to the dependency of Θ_ij’s, some of them are large and some are small. Theorem 1 says that the average of these angles asymptotically has the same density as that of Θ₁₂.

Notice that when p = 2, h(θ) is the uniform density on [0, π], and when p > 2, h(θ) is unimodal with mode θ = π/2. Theorem 1 implies that most of the angles in the total of $\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)$ angles are concentrated around π/2. This concentration becomes stronger as the dimension p grows since (sinθ)^p–2 converges to zero more quickly for θ ≠ π/2. In fact, in the extreme case when p → ∞, almost all of $\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)$ angles go to π/2 at the rate $\sqrt{p}$. This can be seen from Theorem 4 later.

It is helpful to see how the density changes with the dimension p. Figure 1 plots the function

$$\begin{array}{cc}\hfill h_p\left(\theta \right)& =\frac{1}{\sqrt{p-2}}h\left(\frac{\pi }{2}-\frac{\theta }{\sqrt{p-2}}\right)\hfill \\ \hfill & =\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)\sqrt{p-2}}\cdot {\left(\cos \frac{\theta }{\sqrt{p-2}}\right)}^{p-2},\theta \in [0,\pi ]\hfill \end{array}$$ (6)

which is the asymptotic density of the normalized empirical distribution μ_n,p defined in (2) when the dimension p is fixed. Note that in the definition of μ_n,p in (2), if “$\sqrt{p-2}$” is replaced by “$\sqrt{p}$”, the limiting behavior of μ_n,p does not change when both n and p go to infinity. However, it shows in our simulations and the approximation (7) that the fitting is better for relatively small p when “$\sqrt{p-2}$” is used.

Figure 1.

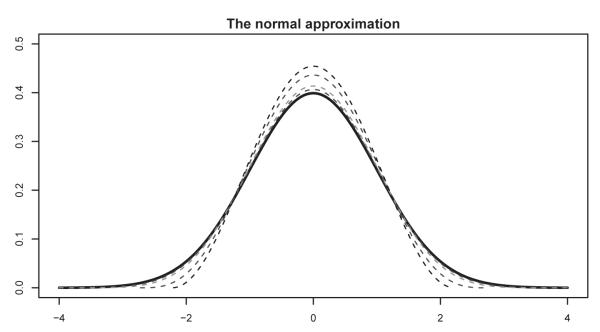
Functions h_p(θ) given by (6) for p = 4, 5, 10 and 20. They are getting closer to the normal density (thick black) as p increases.

Figure 1 shows that the distributions h_p(θ) are very close to normal when p ≥ 5. This can also be seen from the asymptotic approximation

$$h_p\left(\theta \right)\propto \exp \left((p-2)\log \left\{\cos \right(\frac{\theta }{\sqrt{p-2}}\left)\right\}\right)\approx e^{-{\theta }^2∕2}.$$ (7)

We now consider the limiting distribution of the extreme angles Θ_min and Θ_max.

Theorem 2 (Extreme Law for Fixed p)

Let Θ_min and Θ_max be defined as in (3) and (4) respectively. Then, both n^2/(p–1)Θ_min and n^2/(p–1)(π − Θ_max) converge weakly to a distribution given by

$$F\left(x\right)=\{\begin{array}{cc}1-e^{-{\mathit{Kx}}^{p-1}},\hfill & \mathit{if}x\ge 0,\cdot \hfill \\ 0,\hfill & \mathit{if}x<0,\hfill \end{array}\phantom{\}}$$ (8)

as n → ∞, where

$$K=\frac{1}{4\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p+1}{2}\right)}.$$ (9)

The above theorem says that the smallest angle Θ_min is close to zero, and the largest angle Θ_max is close to π as n grows. This makes sense from Theorem 1 since the support of the density function h(Θ) is [0,π].

In the special case of p = 2, the scaling of Θ_min and π − Θ_max in Theorem 2 is n². This is in fact can also be seen in a similar problem. Let ζ₁, ⋯, ζ_n be i.i.d. U[0,1]-distributed random variables with the order statistics ζ₍₁₎ ≤ ⋯ ≤ ζ_(n). Set W_n: = min_{1≤i≤n – 1}(ζ_(i+1) − ζ_(i)), which is the smallest spacing among the observations of ζ_i’s. Then, by using the representation theorem of ζ_(i)’s through i.i.d. random variables with exponential distribution Exp(1) (see, for example, Proposition 4.1 from Resnick (2007)), it is easy to check that n²W_n converges weakly to Exp(1) with the probability density function e^–xI(x ≥ 0).

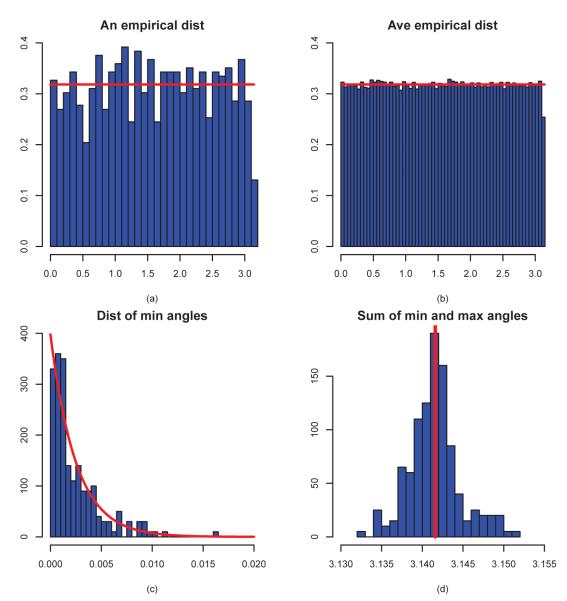
To see the goodness of the finite sample approximations, we simulate 200 times from the distributions with n = 50 for p = 2,3 and 30. The results are shown respectively in Figures 2–4. Figure 2 depicts the results when p = 2. In this case, the empirical distribution μ_n should approximately be uniformly distributed on [0,π] for most of realizations. Figure 2 (a) shows that it holds approximately truly for n as small as 50 for a particular realization (It indeed holds approximately for almost all realizations). Figure 2(b) plots the average of these 200 distributions, which is in fact extremely close to the uniform distribution on [0,π]. Namely, the bias is negligible. For Θ_min, according to Theorem 1, it should be well approximated by an exponential distribution with K = 1/(2π). This is verified by Figure 2(c), even when sample size is as small as 50. Figure 2(d) shows the distribution of Θ_min + Θ_max based on the 200 simulations. The sum is distributed tightly around π, which is indicated by the red line there.

Figure 2.

Various distributions for p = 2 and n = 50 based on 200 simulations. (a) A realization of the empirical distribution μ_n; (b) The average distribution of 200 realizations of μ_n; (c) the distribution of Θ_min and its asymptotic distribution exp(−x/(2π))/(2π); (d) the distribution of Θ_min + Θ_max; the vertical line indicating the location π.

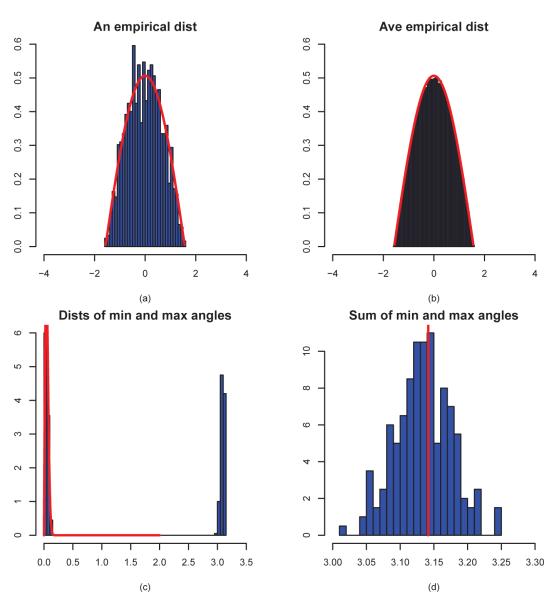
Figure 4.

Various distributions for p = 30 and n = 50 based on 200 simulations. (a) A realization of the normalized empirical distribution μ_n,p given by (2); (b) The average distribution of 200 realizations of μ_n,p; (c) the distribution of Θ_min and its asymptotic distribution; (d) the distribution of Θ_min + Θ_max; the vertical line indicating the location π.

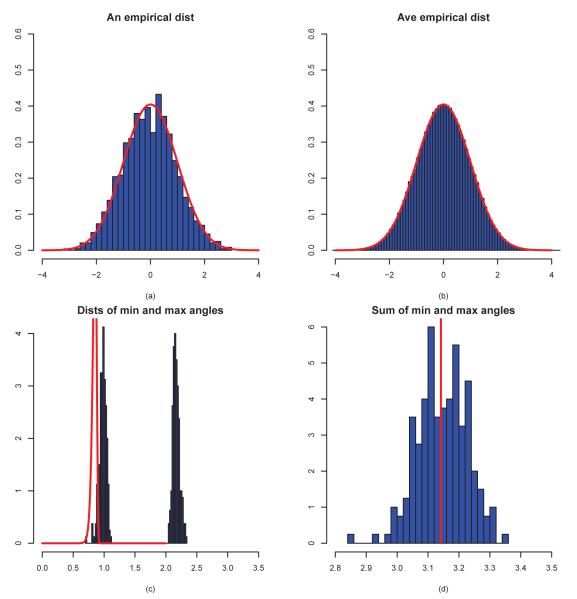
The results for p = 3 and p = 30 are demonstrated in Figures 3 and 4. In this case, we show the empirical distributions of $\sqrt{p-2}(\pi ∕2-{\Theta }_{\mathit{ij}})$ and their asymptotic distributions. As in Figure 1, they normalized. Figure 3(a) shows a realization of the distribution and Figure 3(b) depicts the average of 200 realizations of these distributions for p = 3. They are very close to the asymptotic distribution, shown in the curve therein. The distributions of Θ_min and Θ_max are plotted in Figure 3(c). They concentrate respectively around 0 and π. Figure 3(d) shows that the sum is concentrated symmetrically around π.

Figure 3.

Various distributions for p = 3 and n = 50 based on 200 simulations. (a) A realization of the normalized empirical distribution μ_n,p given by (2); (b) The average distribution of 200 realizations of μ_n,p; (c) the distribution of Θ_min and its asymptotic distribution; (d) the distribution of Θ_min + Θ_max; the vertical line indicating the location π.

When p = 30, the approximations are still very good for the normalized empirical distributions. In this case, the limiting distribution is indistinguishable from the normal density, as shown in Figure 1. However, the distribution of Θ_min is not approximated well by its asymptotic counterpart, as shown in Figure 4(c). In fact, Θ_min does not even tends to zero. This is not entirely surprising since p is comparable with n. The asymptotic framework in Section 3 is more suitable. Nevertheless, Θ_min + Θ_max is still symmetrically distributed around π.

The simulation results show that Θ_max + Θ_min is very close to π. This actually can be seen trivially from Theorem 2: Θ_min → 0 and Θ_max → π in probability as p → ∞. Hence, the sum goes to π in probability. An interesting question is: how fast is this convergence? The following result answers this question.

Theorem 3 (Limit Law for Sum of Largest and Smallest Angles)

Let X₁, X₂, ⋯, X_n be independent random points with the uniform distribution on ${\mathbb{S}}^{p-1}$ for some fixed p ≥ 2. Let Θ_min and Θ_max be defined as in (3) and (4) respectively. Then, n^2/(p–1)(Θ_max + Θ_min − π) converges weakly to the distribution of X – Y, where X and Y are i.i.d. random variables with distribution function F(x) given in (8).

It is interesting to note that the marginal distribution of Θ_min and π − Θ_max are identical. However, n^2/(p–1)Θ_min and n^2/(p–1)(π − Θ_max) are asymptotically independent with non-vanishing limits and hence their difference is non-degenerate. Furthermore, since X are Y are i.i.d., X – Y is a symmetric random variable. Theorem 3 suggests that Θ_max + Θ_min is larger or smaller than π “equally likely”. The symmetry of the distribution of Θ_max + Θ_min has already been demonstrated in Figures 2–4.

3. When Both n and p Grow

We now turn to the case where both n and p grow. The following result shows that the empirical distribution of the random angles, after suitable normalization, converges to a standard normal distribution. This is clearly different from the limiting distribution given in Theorem 1 when the dimension p is fixed.

Theorem 4 (Empirical Law for Growing p)

Let μ_n,p be defined as in (2). Assume lim_n→∞ p_n = ∞. Then, with probability one, μ_n,p converges weakly to N(0,1) as n → ∞.

Theorem 4 holds regardless of the speed of p relative to n when both go to infinity. This has also been empirically demonstrated in Figures 2–4 (see plots (a) and (b) therein). The theorem implies that most of the $\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)$ random angles go to π/2 very quickly. Take any γ_p → 0 such that $\sqrt{p}{\gamma }_p\to \infty$ and denote by N_n,p the number of the angles Θ_ij that are within γ_p of π/2, that is, $\mid \frac{\pi }{2}-{\Theta }_{\mathit{ij}}\mid \le {\gamma }_p$. Then $N_{n,p}∕\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)\to 1$. Hence, most of the random vectors in the high-dimensional Euclidean spaces are nearly orthogonal. An interesting question is: Given two such random vectors, how fast is their angle close to π/2 as the dimension increases? The following result answers this question.

Proposition 5

Let U and V be two random points on the unit sphere in ${\mathbb{R}}^p$. Let Θ be the angle between $\overrightarrow{\mathbf{OU}}$ and $\overrightarrow{\mathbf{OV}}$. Then

$$P(\mid \Theta -\frac{\pi }{2}\mid \ge \epsilon )\ge K\sqrt{p}{\left(\cos \epsilon \right)}^{p-2}$$

for all p ≥ 2 and ε ∈ (0,π/2), where K is a universal constant.

Under the spherical invariance one can think of Θ as a function of the random point U only. There are general concentration inequalities on such functions, see, for example, Ledoux (2005). Proposition 5 provides a more precise inequality.

One can see that, as the dimension p grows, the probability decays exponentially. In particular, take $\epsilon =\sqrt{\left(c\log p\right)∕p}$ for some constant c > 1. Note that cosε ≤ 1 – ε²/2+ε⁴/24, so

$$P\left(\mid \Theta -\frac{\pi }{2}\mid \ge \sqrt{\frac{c\log p}{p}}\right)\le K\sqrt{p}{\left(1-\frac{c\log p}{2p}+\frac{c^2{\log }^{2}p}{24p^2}\right)}^{p-2}\le K^{\prime }{p}^{-\frac{1}{2}(c-1)}$$

for all sufficiently large p, where K’ is a constant depending only on c. Hence, in the high dimensional space, the angle between two random vectors is within $\sqrt{\left(c\log p\right)∕p}$ of π/2 with high probability. This provides a precise characterization of the folklore mentioned earlier that “all high-dimensional random vectors are almost always nearly orthogonal to each other”.

We now turn to the limiting extreme laws of the angles when both n and p → ∞. For the extreme laws, it is necessary to divide into three asymptotic regimes: sub-exponential case $\frac{1}{p}$ logn → 0, exponential case $\frac{1}{p}$ logn → β ∈ (0,∞), and super-exponential case $\frac{1}{p}$ logn → ∞. The limiting extreme laws are different in these three regimes.

Theorem 6 (Extreme Law: Sub-Exponential Case)

Let p = p_n → ∞ satisfy $\frac{\log n}{p}\to 0$ as n → ∞. Then

1. ${\max }_{1\le i<j\le n}\mid {\Theta }_{\mathit{ij}}-\frac{\pi }{2}\mid \to 0$ in probability as n → ∞;

2. As n → ∞, 2plogsinΘ_min + 4logn − loglogn converges weakly to the extreme value distribution with the distribution function F(y) = 1 – e^−Key/2, $y\in \mathbb{R}$ and $K=1∕\left(4\sqrt{2\pi }\right)$. The conclusion still holds if Θ_min is replaced by Θ_max.

In this case, both Θ_min and Θ_max converge to π/2 in probability. The above extreme value distribution differs from that in (8) where the dimension p is fixed. This is obviously caused by the fact that p is finite in Theorem 2 and goes to infinity in Theorem 6.

Corollary 7

Let p = p_n satisfy ${\lim }_{n\to \infty }\frac{\log n}{\sqrt{p}}=\alpha \in [0,\infty )$. Then p cos² Θ_min – 4logn+loglogn converges weakly to a distribution with the cumulative distribution function $\exp \{-\frac{1}{4\sqrt{2}\pi }{e}^{-(y+8{\alpha }^2)∕2}\},y\in \mathbb{R}$. The conclusion still holds if Θ_min is replaced by Θ_max.

Theorem 8 (Extreme Law: Exponential Case)

Let p = p_n satisfy $\frac{\log n}{p}\to \beta \in (0,\infty )$ as n → ∞, then

1. ${\Theta }_{\min }\to {\cos }^{-1}\sqrt{1-e^{-4\beta }}$ and ${\Theta }_{\max }\to \pi -{\cos }^{-1}\sqrt{1-e^{-4\beta }}$ in probability as n → ∞;

2. As n → ∞, 2plogsinΘ_min + 4logn − loglogn converges weakly to a distribution with the distribution function

   $$F\left(y\right)=1-\exp \left\{-K\left(\beta \right)e^{(y+8\beta )∕2}\right\},y\in \mathbb{R},\mathit{where}K\left(\beta \right)={\left(\frac{\beta }{8\pi (1-e^{-4\beta })}\right)}^{1∕2},$$

   and the conclusion still holds if Θ_min is replaced by Θ_max.

In contrast to Theorem 6, neither Θ_max nor Θ_min converges to π/2 under the case that (logn)/p → β ∈ (0,∞). Instead, they converge to different constants depending on β.

Theorem 9 (Extreme Law: Super-Exponential Case)

Let p = p_n satisfy $\frac{\log n}{p}\to \infty$ as n → ∞. Then,

1. Θ_min → 0 and Θ_max → π in probability as n → ∞;

2. As n → ∞, 2plogsin${\Theta }_{\min }+\frac{4p}{p-1}\log n-\log p$ converges weakly to the extreme value distribution with the distribution function F(y) = 1 – e^−Key/2, $y\in \mathbb{R}$ with $K=1∕\left(2\sqrt{2\pi }\right)$. The conclusion still holds if Θ_min is replaced by Θ_max.

It can be seen from Theorems 6, 8 and 9 that Θ_max becomes larger when the rate β = lim(logn)/p increases. They are π/2, $\pi -{\cos }^{-1}\sqrt{1-e^{-4\beta }}\in (\pi ∕2,\pi )$ and π when β = 0, β ∈ (0,∞) and β = ∞, respectively.

Set $f\left(\beta \right)=\pi -{\cos }^{-1}\sqrt{1-e^{-4\beta }}$. Then f(0) = π/2 and f(+∞) = π, which corresponds to Θ_max in (i) of Theorem 6 and (i) of Theorem 9, respectively. So the conclusions in Theorems 6, 8 and 9 are consistent.

Theorem 3 provides the limiting distribution of Θ_max + Θ_min − π when the dimension p is fixed. It is easy to see from the above theorems that Θ_max + Θ_min − π → 0 in probability as both n and p go to infinity. Its asymptotic distribution is much more involved and we leave it as future work.

Remark 10

As mentioned in the introduction, Cai and Jiang (2011, 2012) considered the limiting distribution of the coherence of a random matrix and the coherence is closely related to the minimum angle Θ_min. In the current setting, the coherence L_n,p is defined by

$$L_{n,p}=\underset{1\le i<j\le n}{\max }\mid {\rho }_{\mathit{ij}}\mid$$

where ${\rho }_{\mathit{ij}}={\mathbf{X}}_i^T{\mathbf{X}}_j$. The results in Theorems 6, 8 and 9 are new. Their proofs can be essentially reduced to the analysis of max_1≤i<j≤n ρ_ij. This maximum is analyzed through modifying the proofs of the results for the limiting distribution of the coherence L_n,p in Cai and Jiang (2012). The key step in the proofs is the study of the maximum and minimum of pairwise i.i.d. random variables {ρ_ij; 1 ≤ i < j ≤ n} by using the Chen-Stein method. It is noted that {ρ_ij; 1 ≤ i < j ≤ n} are not i.i.d. random variables (see, for example, p.148 from Muirhead (1982)), the standard techniques to analyze the extreme values of {ρ_ij; 1 ≤ i < j ≤ n} do not apply.

4. Applications to Statistics

The results developed in the last two sections can be applied to test the spherical symmetry (Fang et al., 1990):

$$H_0:\mathbf{Z}\text{is spherically symmetric in}{\mathbb{R}}^p$$

based on an i.i.d. sample ${\left\{{\mathbf{Z}}_i\right\}}_{i=1}^n$. Under the null hypothesis H₀, Z/∥Z∥ is uniformly distributed on ${\mathbb{S}}^{p-1}$. It is expected that the minimum angle Θ_min is stochastically larger under the null hypothesis than that under the alternative hypothesis. Therefore, one should reject the null hypothesis when Θ_min is too small or formally, reject H₀ when

$$n^{2∕(p-1)}{\Theta }_{\min }\le c_{\alpha },$$

where the critical value c_α, according to Theorem 2, is given by

$$c_{\alpha }={(-K^{-1}\log (1-\alpha \left)\right)}^{1∕(p-1)}$$

for the given significance level α. This provides the minimum angle test for sphericity or the packing test on sphericity.

We run a simulation study to examine the power of the packing test. The following 6 data generating processes are used:

• Distribution 0: the components of X follow independently the standard normal distribution;

• Distribution 1: the components of X follow independently the uniform distribution on [−1,1];

• Distribution 2: the components of X follow independently the uniform distribution on [0,1];

• Distribution 3: the components of X follow the standard normal distribution with correlation 0.5;

• Distribution 4: the components of X follow the standard normal distribution with correlation 0.9;

• Distribution 5: the components of X follow independently the mixture distribution 2/3exp(−x)I(x ≥ 0) + 1/3exp(x)I(x ≤ 0).

The results are summarized in Table 1 below. Note that for Distribution 0, the power corresponds to the size of the test, which is slightly below α = 5%.

Table 1.

The power (percent of rejections) of the packing test based on 2000 simulations

Distribution	0	1	2	3	4	5
p = 2	4.20	5.20	20.30	5.55	10.75	5.95
p = 3	4.20	6.80	37.20	8.00	30.70	8.05
p = 4	4.80	7.05	64.90	11.05	76.25	11.20
p = 5	4.30	7.45	90.50	18.25	99.45	11.65

The packing test does not examine whether there is a gap in the data on the sphere. An alternative test statistic is μ_n or its normalized version μ_n,p when p is large, defined respectively by (1) and (2). A natural test statistic is then to use a distance such as the Kolmogrov-Smirnov distance between μ_n and h(θ). In this case, one needs to derive further the null distribution of such a test statistic. This is beyond the scope of this paper and we leave it for future work.

Our study also shed lights on the magnitude of spurious correlation. Suppose that we have a response variable Y and its associate covariates ${\left\{X_j\right\}}_{j=1}^p$ (for example, gene expressions). Even when there is no association between the response and the covariate, the maximum sample correlation between X_j and Y based on a random sample of size n will not be zero. It is closely related to the minimum angle Θ_min (Fan and Lv, 2008). Any correlation below a certain thresholding level can be spurious—the correlation of such a level can occur purely by chance. For example, by Theorem 6(ii), any correlation (in absolute value) below

$$\sqrt{1-n^{-4∕p}{\left(\log \right(n\left)\right)}^{1∕p}}$$

can be regarded as the spurious one. Take, for example, p = 30 and n = 50 as in Figure 4, the spurious correlation can be as large 0.615 in this case.

The spurious correlation also helps understand the bias in calculating the residual σ² = var(ε) in the sparse linear model

$$Y={\mathbf{X}}_S^T{\beta }_S+\epsilon$$

where S is a subset of variables {1,⋯ p}. When an extra variable besides X_S is recruited by a variable selection algorithm, that extra variable is recruited to best predict ε (Fan et al., 2012). Therefore, by the classical formula for the residual variance, σ² is underestimated by a factor of 1 – cos²(Θ_min). Our asymptotic result gives the order of magnitude of such a bias.

5. Discussions

We have established the limiting empirical and extreme laws of the angles between random unit vectors, both for the fixed dimension and growing dimension cases. For fixed p, we study the empirical law of angles, the extreme law of angles and the law of the sum of the largest and smallest angles in Theorems 1, 2 and 3. Assuming p is large, we establish the empirical law of random angles in Theorem 4. Given two vectors u and v, the cosine of their angle is equal to the Pearson correlation coefficient between them. Based on this observation, among the results developed in this paper, the limiting distribution of the minimum angle Θ_min given in Theorems 6-9 for the setting where both n and p → ∞ is obtained by similar arguments to those in Cai and Jiang (2012) on the coherence of an n × p random matrix (a detailed discussion is given in Remark 10). See also Jiang (2004), Li and Rosalsky (2006), Zhou (2007), Liu et al. (2008), Li et al. (2009) and Li et al. (2010) for earlier results on the distribution of the coherence which were all established under the assumption that both n and p → ∞.

The study of the random angles Θ_ij’s, Θ_min and Θ_max is also related to several problems in machine learning as well as some deterministic open problems in physics and mathematics. We briefly discuss some of these connections below.

5.1 Connections to Machine Learning

Our studies shed lights on random geometric graphs, which are formed by n random points on the p-dimensional unit sphere as vertices with edge connecting between points X_i and X_j if Θ_ij > δ for certain δ (Penrose, 2003; Devroye et al., 2011). Like testing isotropicity in Section 4, a generalization of our results can be used to detect if there are any implanted cliques in a random graph, which is a challenging problem in machine learning. It can also be used to describe the distributions of the number of edges and degree of such a random geometric graph. Problems of hypothesis testing on isotropicity of covariance matrices have strong connections with clique numbers of geometric random graphs as demonstrated in the recent manuscript by Castro et al. (2012). This furthers connections of our studies in Section 4 to this machine learning problem.

Principal component analysis (PCA) is one of the most important techniques in high-dimensional data analysis for visualization, feature extraction, and dimension reduction. It has a wide range of applications in statistics and machine learning. A key aspect of the study of PCA in the high-dimensional setting is the understanding of the properties of the principal eigenvectors of the sample covariance matrix. In a recent paper, Shen et al. (2013) showed an interesting asymptotic conical structure in the critical sample eigenvectors under a spike covariance models when the ratio between the dimension and the product of the sample size with the spike size converges to a nonzero constant. They showed that in such a setting the critical sample eigenvectors lie in a right circular cone around the corresponding population eigenvectors. Although these sample eigenvectors converge to the cone, their locations within the cone are random. The behavior of the randomness of the eigenvectors within the cones is related to the behavior of the random angles studied in the present paper. It is of significant interest to rigorously explore these connections. See Shen et al. (2013) for further discussions.

5.2 Connections to Some Open Problems in Mathematics and Physics

The results on random angles established in this paper can be potentially used to study a number of open deterministic problems in mathematics and physics.

Let x₁, ⋯, x_n be n points on ${\mathbb{S}}^{p-1}$ and R = {x₁, ⋯, x_n}. The α-energy function is defined by

$$E(R,\alpha )=\{\begin{array}{cc}\sum _{1\le i<j\le n}{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^{\alpha },\hfill & \text{if}\alpha \ne 0;\hfill \\ \sum _{1\le i<j\le n}\log \frac{1}{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert },\hfill & \text{if}\alpha =0,\hfill \end{array}\phantom{\}}$$

and $E(R,-\infty )={\min }_{1\le i<j\le n}\frac{1}{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }$ where ∥·∥ is the Euclidean norm in ${\mathbb{R}}^p$. These are known as the electron problem (α = 0) and the Coulomb potential problem (α = 1). See, for example, Kuijlaars and Saff (1998) and Katanforoush and Shahshahani (2003). The goal is to find the extremal α-energy

$$\epsilon (R,\alpha )≔\{\begin{array}{cc}{\inf }_{R}E(R,\alpha ),\hfill & \text{if}\alpha \le 0,\hfill \\ {\sup }_{R}E(R,\alpha ),\hfill & \text{if}\alpha >0,\hfill \end{array}\phantom{\}}$$

and the extremal configuration R that attains ε(R,α). In particular, when α = −1, the quantity ε(R,−1) is the minimum of the Coulomb potential

$$\sum _{1\le i<j\le n}\frac{1}{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }.$$

These open problems, as a function of α, are: (i) α = −∞: Tammes problem; (ii) α = −1: Thomson problem; (iii) α = 1: maximum average distance problem; and (iv) α = 0: maximal product of distances between all pairs. Problem (iv) is the 7th of the 17 most challenging mathematics problems in the 21st century according to Smale (2000). See, for example, Kuijlaars and Saff (1998) and Katanforoush and Shahshahani (2003), for further details.

The above problems can also be formulated through randomization. Suppose that X₁, ⋯, X_n are i.i.d. uniform random vectors on ${\mathbb{S}}^{p-1}$. Suppose R = {x₁, ⋯, x_n} achieves the infinimum supremum in the definition of ε(R,α). Since P(max_1≤i≤n ∥X_i – x_i∥ < ε) > 0 for any ε > 0, it is easy to see that ε(R,α) = ess · inf(E(R,α)) for α ≤ 0 and ε(R,α) = ess · sup(E(R,α)) for α > 0 with R = {X₁, ⋯, X_n}, where ess · inf(Z) and ess · sup(Z) are the essential infinimum and the essential maximum of random variable Z, respectively.

For the Tammes problem (α = −∞), the extremal energy ε(R,−∞) can be further studied through the random variable Θ_max. Note that ∥x_i – x_j∥² = 2(1 – cosθ_ij), where θ_ij is the angle between vectors ${\overrightarrow{\mathbf{Ox}}}_i$ and ${\overrightarrow{\mathbf{Ox}}}_j$. Then

$$\frac{1}{2E{(R,-\infty )}^2}=\underset{{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_n\in {\mathbb{S}}^{p-1}}{\max }(1-\cos {\theta }_{\mathit{ij}})=1-\cos {\tilde{\Theta }}_{\max },$$

where ${\tilde{\Theta }}_{\max }=\max \{{\theta }_{\mathit{ij}};1\le i<j\le n\}$. Again, let X₁, ⋯, X_n be i.i.d. random vectors with the uniform distribution on ${\mathbb{S}}^{p-1}$. Then, it is not difficult to see

$$\frac{1}{2\epsilon {(R,-\infty )}^2}=\underset{R}{\sup }\frac{1}{2E{(R,-\infty )}^2}=\underset{R}{\sup }(1-\cos {\tilde{\Theta }}_{\max })=1-\cos \Delta$$

where Δ:= ess · sup(Θ_max) is the essential upper bound of the random variable Θ_max as defined in (4). Thus,

$$\epsilon (R,-\infty )=\frac{1}{\sqrt{2(1-\cos \Delta )}}.$$ (10)

The essential upper bound Δ of the random variable Θ_max can be approximated by random sampling of Θ_max. So the approach outlined above provides a direct way for using a stochastic method to study these deterministic problems and establishes connections between the random angles and open problems mentioned above. See, for example, Katanforoush and Shahshahani (2003) for further comments on randomization. Recently, Armentano et al. (2011) studied this problem by taking x_i’s to be the roots of a special type of random polynomials. Taking independent and uniform samples X₁, ⋯, X_n from the unit sphere ${\mathbb{S}}^{p-1}$ to get (10) is simpler than using the roots of a random polynomials.

6. Proofs

We provide the proofs of the main results in this section.

6.1 Technical Results

Recall that X₁,X₂, ⋯ are random points independently chosen with the uniform distribution on ${\mathbb{S}}^{p-1}$, the unit sphere in ${\mathbb{R}}^p$, and Θ_ij is the angle between ${\overrightarrow{\mathbf{OX}}}_i$ and ${\overrightarrow{\mathbf{OX}}}_j$ and ρ_ij = cosΘ_ij for any i ≠ j. Of course, Θ_ij ∈ [0,π] for all i ≠ j. It is known that the distribution of (X₁,X₂, ⋯) is the same as that of

$$\left(\frac{{\mathbf{Y}}_1}{\Vert {\mathbf{Y}}_1\Vert },\frac{{\mathbf{Y}}_2}{\Vert {\mathbf{Y}}_2\Vert },\cdots \right)$$

where {Y₁,Y₂, ⋯} are independent p-dimensional random vectors with the normal distribution N_p(0,I_p), that is, the normal distribution with mean vector 0 and the covariance matrix equal to the p × p identity matrix I_p. Thus,

$${\rho }_{\mathit{ij}}=\cos {\Theta }_{\mathit{ij}}=\frac{{\mathbf{Y}}_i^T{\mathbf{Y}}_j}{\Vert {\mathbf{Y}}_i\Vert \cdot \Vert {\mathbf{Y}}_i\Vert }$$

for all 1 ≤ i < j ≤ n. See, for example, the Discussions in Section 5 from Cai and Jiang (2012) for further details. Of course, ρ_ii = 1 and |ρ_ij| ≤ 1 for all i, j. Set

$$M_n=\underset{1\le i<j\le n}{\max }{\rho }_{ij}=\cos {\Theta }_{\min }.$$ (11)

Lemma 11

((22) in Lemma 4.2 from Cai and Jiang (2012)) Let p ≥ 2. Then {ρ_ij; 1 ≤ i < j ≤ n} are pairwise independent and identically distributed with density function

$$g\left(\rho \right)=\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\left(\frac{p-1}{2}\right)}\cdot {(1-{\rho }^2)}^{\frac{p-3}{2}},\mid \rho \mid <1.$$ (12)

Notice y = cosx is a strictly decreasing function on [0,π], hence Θ_ij = cos⁻¹ ρ_ij. A direct computation shows that Lemma 11 is equivalent to the following lemma.

Lemma 12

Let p ≥ 2. Then,

1. {Θ_ij; 1 ≤ i < ≥ j ≤ n} are pairwise independent and identically distributed with density function

   $$h\left(\theta \right)=\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}\cdot {\left(\sin \theta \right)}^{p-2},\theta \in [0,\pi ].$$ (13)

2. If “Θ_ij” in (i) is replaced by “π − Θ_ij”, the conclusion in (i) still holds.

Let I be a finite set, and for each α ∈ I, X_α be a Bernoulli random variable with p_α = P(X_α = 1) = 1–P(X_α = 0) > 0. Set W = ∑_α∈I X_α and λ = EW = ∑_α∈I p_α. For each α ∈ I, suppose we have chosen B_α ⊂ I with α ∈ B_α. Define

$$b_1=\sum _{\alpha \in I}\sum _{\beta \in B_{\alpha }}{p}_{\alpha }{p}_{\beta }\text{and}{b}_2=\sum _{\alpha \in I}\sum _{\alpha \ne \beta \in B_{\alpha }}P(X_{\alpha }=1,X_{\beta }=1).$$

Lemma 13

(Theorem 1 from Arratia et al. (1989)) For each α ∈ I, assume X_α is independent of {X_β; β ∈ I – B_α}. Then |P(X_α = 0 for all α ∈ I)–e^−λ| ≤ b₁ + b₂.

The following is essentially a special case of Lemma 13.

Lemma 14

Let I be an index set and {B_α,α ∈ I} be a set of subsets of I, that is, B_α ⊂ I for each α ∈ I. Let also {η_α,α ∈ I} be random variables. For a given $t\in \mathbb{R}$, set λ = ∑_α∈I P(η_α > t). Then

$$\mid P(\underset{\alpha \in I}{\max }{\eta }_{\alpha }\le t)-e^{-\lambda }\mid \le (1\wedge {\lambda }^{-1})(b_1+b_2+b_3)$$

where

$$\begin{array}{cc}\hfill b_1=& \sum _{\alpha \in I}\sum _{\beta \in B_{\alpha }}P({\eta }_{\alpha }>t)P({\eta }_{\beta }>t),b_2=\sum _{\alpha \in I}\sum _{\alpha \ne \beta \in B_{\alpha }}P({\eta }_{\alpha }>t,{\eta }_{\beta }>t),\hfill \\ \hfill b_3=& \sum _{\alpha \in I}E\mid P({\eta }_{\alpha }>t\mid \sigma ({\eta }_{\beta },\beta \notin B_{\alpha }\left)\right)-P({\eta }_{\alpha }>t)\mid ,\hfill \end{array}$$

and α(η_β, β ∉ B_α) is the α-algebra generated by {η_β, β ∉ B_α}. In particular, if η_α is independent of {η_β, β ∉ B_α} for each α, then b₃ = 0.

Lemma 15

Let p = p_n ≥ 2. Recall M_n as in (11). For {t_n ∈ [0,1]; n ≥ 2}, set

$$h_n=\frac{n^2{p}^{1∕2}}{\sqrt{2\pi }}{\int }_{t_n}^1{(1-x^2)}^{\frac{p-3}{2}}\mathit{dx}.$$

If lim_n→∞ p_n = ∞ and lim_n→∞ h_n = λ ∈ [0,∞), then lim_n→∞ P(M_n ≤ t_n) = e^−λ/2.

Proof

For brevity of notation, we sometimes write t = t_n if there is no confusion. First, take I = {(i, j); 1 ≤ i < j ≤ n}. For u = (i, j) ∈ I, set B_u = {(k, l) ∈ I; one of k and l = i or j, but (k, l) ≠ u}, η_u = ρ_ij and A_u = A_ij = {ρ_ij > t}. By the i.i.d. assumption on X₁, ⋯, X_n and Lemma 14,

$$\mid P(M_n\le t)-e^{-{\lambda }_n}\mid \le b_{1,n}+b_{2,n}$$ (14)

where

$${\lambda }_n=\frac{n(n-1)}{2}P\left(A_{12}\right)$$ (15)

and

$$b_{1,n}\le 2n^{3}P{\left(A_{12}\right)}^2\text{and}{b}_{2,n}\le 2n^{3}P\left(A_{12}{A}_{13}\right).$$

By Lemma 11, A₁₂ and A₁₃ are independent events with the same probability. Thus, from (15),

$$b_{1,n}\vee b_{2,n}\le 2n^{3}P{\left(A_{12}\right)}^2\le \frac{8n{\lambda }_n^2}{{(n-1)}^2}\le \frac{32{\lambda }_n^2}{n}$$ (16)

for all n ≥ 2. Now we compute P(A₁₂). In fact, by Lemma 11 again,

$$P\left(A_{12}\right)={\int }_t^{1}g\left(x\right)\mathit{dx}=\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}{\int }_t^1{(1-x^2)}^{\frac{p-3}{2}}\mathit{dx}.$$

Recalling the Stirling formula (see, for example, p.368 from Gamelin (2001) or (37) on p.204 from Ahlfors (1979)):

$$\log \Gamma \left(z\right)=z\log z-z-\frac{1}{2}\log z+\log \sqrt{2\pi }+O\left(\frac{1}{x}\right)$$

as x = Re(z) → ∞, it is easy to verify that

$$\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}\sim \sqrt{\frac{p}{2}}$$ (17)

as p → ∞. Thus,

$$P\left(A_{12}\right)\sim \frac{p^{1∕2}}{\sqrt{2\pi }}{\int }_t^1{(1-x^2)}^{\frac{p-3}{2}}\mathit{dx}$$

as n → ∞. From (15), we know

$${\lambda }_n\sim \frac{p^{1∕2}{n}^2}{2\sqrt{2\pi }}{\int }_t^1{(1-x^2)}^{\frac{p-3}{2}}\mathit{dx}=\frac{h_n}{2}$$

as n → ∞. Finally, by (14) and (16), we know

$$\underset{n\to \infty }{\lim }P(M_n\le t)=e^{-\lambda ∕2}\text{if}\underset{n\to \infty }{\lim }{h}_n=\lambda \in [0,\infty ).$$

6.2 Proofs of Main Results in Section 2

Lemma 16

Let X₁,X₂, ⋯ be independent random points with the uniform distribution on the unit sphere in ${\mathbb{R}}^p$.

1. Let p be fixed and μ be the probability measure with the density h(θ) as in (5). Then, with probability one, μ_n in (1) converges weakly to μ as n → ∞.

2. Let p = p_n and {φ_n(θ); n ≥ 1} be sequence of functions defined on [0,π]. If φ_n(Θ₁₂) converges weakly to a probability measure ν as n → ∞, then, with probability one,

   $${\nu }_n≔\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i<j\le n}{\delta }_{{\phi }_n\left({\Theta }_{\mathit{ij}}\right)}$$ (18)

   converges weakly to ν as n → ∞.

Proof

First, we claim that, for any bounded and continuous function u(x) defined on $\mathbb{R}$,

$$\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i<j\le n}\left[u\right({\phi }_n\left({\Theta }_{\mathit{ij}}\right))-\mathit{Eu}({\phi }_n\left({\Theta }_{\mathit{ij}}\right)\left)\right]\to 0a.s.$$ (19)

as n → ∞ regardless p is fixed as in (i) or p = p_n as in (ii) in the statement of the lemma. For convenience, write u_n(θ) = u(φ_n(θ)). Then u_n(θ) is a bounded function with M: = sup_Θ∈[0,π] |u_n(θ)| < ∞. By the Markov inequality

$$\begin{array}{cc}\hfill & P\left(\mid \sum _{1\le i<j\le n}\left(u_n\right({\Theta }_{\mathit{ij}})-{\mathit{Eu}}_n({\Theta }_{\mathit{ij}}\left)\right)\mid \ge \epsilon \left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)\right)\hfill \\ \hfill \le & \frac{1}{{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^2{\epsilon }^2}E{\mid \sum _{1\le i<j\le n}\left(u_n\right({\Theta }_{\mathit{ij}})-{\mathit{Eu}}_n({\Theta }_{\mathit{ij}}\left)\right)\mid }^2\hfill \end{array}$$

for any ε > 0. From (i) of Lemma 12, {Θ_ij; 1 ≤ i < j ≤ n} are pairwise independent with the common distribution, the last expectation is therefore equal to $\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)\mathrm{Var}\left(u_n\right({\Theta }_{12}\left)\right)\le \left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)M^2$. This says that, for any ε > 0,

$$P\left(\mid \sum _{1\le i<j\le n}\left(u_n\right({\Theta }_{\mathit{ij}})-{\mathit{Eu}}_n({\Theta }_{\mathit{ij}}\left)\right)\mid \ge \epsilon \left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)\right)=O\left(\frac{1}{n^2}\right)$$

as n → ∞. Note that the sum of the right hand side over all n ≥ 2 is finite. By the Borel-Cantelli lemma, we conclude (19).

1. Take φ_n(θ) = θ for $\theta \in \mathbb{R}$ in (19) to get that

   $$\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i<j\le n}u\left({\Theta }_{\mathit{ij}}\right)\to \mathit{Eu}\left({\Theta }_{12}\right)={\int }_0^{\pi }u\left(\theta \right)h\left(\theta \right)d\theta a.s.$$

   as n → ∞, where u(θ) is any bounded continuous function on [0,π] and h(θ) is as in (5). This leads to that, with probability one, μ_n in (1) converges weakly to μ as n → ∞.
2. Since φ_n(Θ₁₂) converges weakly to ν as n → ∞, we know that, for any bounded continuous function u(x) defined on $\mathbb{R}$, $\mathit{Eu}\left({\phi }_n\right({\Theta }_{12}\left)\right)\to {\int }_{-\infty }^{\infty }u\left(x\right)d\nu \left(x\right)$ as n → ∞. By (i) of Lemma 12, Eu(φ_n(Θ_ij)) = Eu(φ_n(Θ₁₂)) for all 1 ≤ i < j ≤ n. This and (19) yield

   $$\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i<j\le n}u\left({\phi }_n\right({\Theta }_{\mathit{ij}}\left)\right)\to {\int }_{-\infty }^{\infty }u\left(x\right)d\nu \left(x\right)a.s.$$

   as n → ∞. Reviewing the definition of ν_n in (18), the above asserts that, with probability one, ν_n converges weakly to ν as n → ∞.

Proof of Theorem 1

This is a direct consequence of (i) of Lemma 16.

Recall X₁, ⋯, X_n are random points independently chosen with the uniform distribution on ${\mathbb{S}}^{p-1}$, the unit sphere in ${\mathbb{R}}^p$, and Θ_ij is the angle between ${\overrightarrow{\mathbf{OX}}}_i$ and ${\overrightarrow{\mathbf{OX}}}_j$ and ρ_ij = cosΘ_ij for all 1 ≤ i, j ≤ n. Of course, ρ_ii = 1 and |ρ_ij| ≤ 1 for all 1 ≤ i ≠ j ≤ n. Review (11) to have

$$M_n=\underset{1\le i<j\le n}{\max }{\rho }_{\mathit{ij}}=\cos {\Theta }_{\min }.$$

To prove Theorem 2, we need the following result.

Proposition 17

Fix p ≥ 2. Then n^4/(p–1)(1 – M_n) converges to the distribution function

$$F_1\left(x\right)=1-\exp \{-K_1{x}^{(p-1)∕2}\},x\ge 0,$$

in distribution as n → ∞, where

$$K_1=\frac{2^{(p-5)∕2}}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p+1}{2}\right)}.$$ (20)

Proof

Set t = t_n = 1 – xn^−4/(p–1) for x ≥ 0. Then

$$t\to 1\text{and}{t}^2=1-\frac{2x}{n^{4∕(p-1)}}+O\left(\frac{1}{n^{8∕(p-1)}}\right)$$ (21)

as n → ∞. Notice

$$P\left(n^{4∕(p-1)}\right(1-M_n)<x)=P(M_n>t)=1-P(M_n\le t).$$

Thus, to prove the theorem, since F₁(x) is continuous, it is enough to show that

$$P(M_n\le t)\to e^{-K_1{x}^{(p-1)∕2}}$$ (22)

as n → ∞, where K₁ is as in (20).

Now, take I = {(i, j); 1 ≤ i < j ≤ n} For u = (i,j), ∈ I, set B_u = (k,l) ∈ I; one of k and l = i or j, but (k, l) ≠ u}, η_u = ρ_ij and A_u = A_ij = {ρ_ij > t}. By the i.i.d. assumption on X₁, ⋯, X_n and Lemma 14,

$$\mid P(M_n\le t)-e^{-{\lambda }_n}\mid \le b_{1,n}+b_{2,n}$$ (23)

where

$${\lambda }_n=\frac{n(n-1)}{2}P\left(A_{12}\right)$$ (24)

and

$$b_{1,n}\le 2n^{3}P{\left(A_{12}\right)}^2\text{and}{b}_{2,n}\le 2n^{3}P\left(A_{12}{A}_{13}\right).$$

By Lemma 11, A₁₂ and A₁₃ are independent events with the same probability. Thus, from (24),

$$b_{1,n}\vee b_{2,n}\le 2n^{3}P{\left(A_{12}\right)}^2\le \frac{8n{\lambda }_n^2}{{(n-1)}^2}\le \frac{32{\lambda }_n^2}{n}$$ (25)

for all n ≥ 2. Now we evaluate P(A₁₂). In fact, by Lemma 11 again,

$$P\left(A_{12}\right)={\int }_t^{1}g\left(x\right)\mathit{dx}=\frac{1}{\pi }\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}{\int }_t^1{(1-x^2)}^{\frac{p-3}{2}}\mathit{dx}.$$

Set $m=\frac{p-3}{2}\ge -\frac{1}{2}$. We claim

$${\int }_t^1{(1-x^2)}^m\mathit{dx}\sim \frac{1}{2m+2}{(1-t^2)}^{m+1}$$ (26)

as n → ∞. In fact, set s = x². Then $x=\sqrt{s}$ and $\mathit{dx}=\frac{1}{2\sqrt{s}}\mathit{ds}$. It follows that

$$\begin{array}{cc}\hfill {\int }_t^1{(1-x^2)}^m\mathit{dx}& ={\int }_{t^2}^1\frac{1}{2\sqrt{s}}{(1-s)}^m\mathit{ds}\hfill \\ \hfill & \sim \frac{1}{2}{\int }_{t^2}^1{(1-s)}^m\mathit{ds}=\frac{1}{2m+2}{(1-t^2)}^{m+1}\hfill \end{array}$$

as n → ∞, where the fact lim_n→∞t = lim_n→∞t_n = 1 stated in (21) is used in the second step to replace $\frac{1}{2\sqrt{s}}$ by $\frac{1}{2}$. So the claim (26) follows.

Now, we know from (24) that

$$\begin{array}{cc}\hfill {\lambda }_n\sim \frac{n^2}{2\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}{\int }_t^1{(1-x^2)}^{\frac{p-3}{2}}\mathit{dx}& \sim \frac{n^2}{2\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{(p-1)\Gamma \left(\frac{p-1}{2}\right)}{(1-t^2)}^{(p-1)∕2}\hfill \\ \hfill & =\frac{1}{4\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p+1}{2}\right)}{\left(n^{4∕(p-1)}(1-t^2)\right)}^{(p-1)∕2}\hfill \end{array}$$

as n → ∞, where (26) is used in the second step and the fact Γ(x + 1) = xΓ(x) is used in the last step. By (21),

$$n^{4∕(p-1)}(1-t^2)=2x+O\left(\frac{1}{n^{4∕(p-1)}}\right)$$

as n → ∞. Therefore,

$${\lambda }_n\to \frac{2^{(p-5)∕2}}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p+1}{2}\right)}{x}^{(p-1)∕2}=K_1{x}^{(p-1)∕2}$$

as n → ∞. Finally, by (23) and (25), we know

$$\underset{n\to \infty }{\lim }P(M_n\le t)=e^{-K_1{x}^{(p-1)∕2}}.$$

This concludes (22).

Proof of Theorem 2

First, since M_n = cosΘ_min by (3), then use the identity $1-\cos h=2{\sin }^2\frac{h}{2}$ for all $h\in \mathbb{R}$ to have

$$n^{4∕(p-1)}(1-M_n)=2n^{4∕(p-1)}{\sin }^2\frac{{\Theta }_{\min }}{2}.$$ (27)

By Proposition 17 and the Slusky lemma, $\sin \frac{{\Theta }_{\min }}{2}\to 0$ in probability as n ∞ ∞. Noticing 0 ≤ Θ_min ≤ π, we then have Θ_min → 0 in probability as n → ∞. From (27) and the fact that ${\lim }_{x\to 0}\frac{\sin x}{x}=1$ we obtain

$$\frac{n^{4∕(p-1)}(1-M_n)}{\frac{1}{2}{n}^{4∕(p-1)}{\Theta }_{\min }^2}\to 1$$

in probability as n → ∞. By Proposition 17 and the Slusky lemma again, $\frac{1}{2}{n}^{4∕(p-1)}{\Theta }_{\min }^2$ converges in distribution to F₁(x) as in Proposition 17. Second, for any x > 0,

$$\begin{array}{cc}\hfill P(n^{2∕(p-1)}{\Theta }_{\min }\le x)& =P\left(\frac{1}{2}{n}^{4∕(p-1)}{\Theta }_{\min }^2\le \frac{x^2}{2}\right)\hfill \\ \hfill & \to 1-\exp \{-K_1{(x^2∕2)}^{(p-1)∕2}\}=1-\exp \{-{\mathit{Kx}}^{p-1}\}\hfill \end{array}$$ (28)

as n → ∞, where

$$K=2^{(1-p)∕2}{K}_1=\frac{1}{4\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p+1}{2}\right)}.$$ (29)

Now we prove

$$n^{2∕(p-1)}(\pi -{\Theta }_{\max })\text{converges weakly to}F\left(x\right)\text{as}n\to \infty .$$ (30)

In fact, recalling the proof of the above and that of Proposition 17, we only use the following properties about ρ_ij:

1. {ρ_ij; 1 ≤ i < j ≤ n} are pairwise independent.

2. ρ_ijj has density function g(ρ) given in (12) for all 1 ≤ i < j ≤ n.

3. For each 1 ≤ i < j ≤ n, ρ_ij is independent of {ρ_kl; 1 ≤ k < l ≤ n; {k, l} ⋂ {i, j} = ∅.

   By using Lemmas 11 and 12 and the remark between them, we see that the above ties properties are equivalent to

   (a) {Θ_ij; 1 ≤ i < j ≤ n} are pairwise independent.

   (b) Θ_ij has density function h(θ) given in (13) for all 1 ≤ i < j ≤ n.

   (c) For each 1 ≤ i < j ≤ n, Θ_ij is independent of {Θkl; 1 ≤ k < l ≤ n; {k, l} ⋂ {i, j} = ∅}.

   It is easy to see from (ii) of lemma 12 that the above three properties are equivalent to the corresponding (a) , (b) and (c) when “Θ_ij” is replaced by “π — Θ_ij” and “Θ_kl” is replaced by “π Θ_kl.” Also, it is key to observe that min{π − Θ_ij; 1 ≤ i < j ≤ n} = π − Θ_max. We then deduce from (28) that

   $$P\left(n^{2∕(p-1)}\right(\pi -{\Theta }_{\max })\le x)\to 1-\exp \{-{\mathit{Kx}}^{p-1}\}$$ (31)

   as n → ∞, where K is as in (29).

Proof of Theorem 3

We will prove the following:

$$\underset{n\to \infty }{\lim }P(n^{2∕(p-1)}{\Theta }_{\min }\ge x,n^{2∕(p-1)}(\pi -{\Theta }_{\max })\ge y)=e^{-K(x^{p-1}+y^{p-1})}$$ (32)

for any x ≥ 0 and y ≥ 0, where K is as in (9). Note that the right hand side in (32) is identical to P(X ≥ x, Y ≥ y), where X and Y are as in the statement of Theorem 3. If (32) holds, by the fact that Θ_min, Θ_max, X,Y are continuous random variables and by Theorem 2 we know that $Q_n≔\left((n^{2∕(p-1)}{\Theta }_{\min },n^{2∕(p-1)}(\pi -{\Theta }_{\max })\right)\in {\mathbb{R}}^2$ for n ≥ 2 is a tight sequence. By the standard subsequence argument, we obtain that Q_n converges weakly to the distribution of (X,Y) as n → ∞. Applying the map h(x,y) = x – y with $x,y\in \mathbb{R}$ to the sequence {Q_n; n ≥ 2} and its limit, the desired conclusion then follows from the continuous mapping theorem on the weak convergence of probability measures.

We now prove (32). Set t_x = n^−2/(p–1)x and t_y = π – n^−2/(p–1)y. Without loss of generality, we assume 0 ≤ t_x < t_y < ∞ for all n ≥ 2. Then

$$\begin{array}{cc}\hfill & P(n^{2∕(p-1)}{\Theta }_{\min }\ge x,n^{2∕(p-1)}(\pi -{\Theta }_{\max })\ge y)\hfill \\ \hfill =& P(t_x\le {\Theta }_{\mathit{ij}}\le t_y\text{for all}1\le i<j\le n)\hfill \\ \hfill =& P(X_u=0\text{for all}u\in I)\hfill \end{array}$$ (33)

where I:= {(i, j); 1 ≤ i < j ≤ n} and

$$X_u≔\{\begin{array}{cc}1,\hfill & \text{if}{\Theta }_u\notin [t_x,t_y];\hfill \\ 0,\hfill & \text{if}{\Theta }_u\in [t_x,t_y].\hfill \end{array}\phantom{\}}$$

For u=(i, j) ∈ I, set B_u ={(k, l) ∈ I; one of k and l = i or j, but (k, l) ≠ u}. By the i.i.d. assumption on X₁, ⋯, X_n and Lemma 13

$$\mid P(X_u=0\text{for all}u\in I)-e^{-{\lambda }_n}\mid \le b_{1,n}+b_{2,n}$$ (34)

where

$${\lambda }_n=\frac{n(n-1)}{2}P\left(A_{12}\right)\text{and}{A}_{12}=\{{\Theta }_{12}\notin [t_x,t_y\left]\right\}$$ (35)

and

$$b_{1,n}\le 2n^{3}P{\left(A_{12}\right)}^2\text{and}{b}_{2,n}\le 2n^{3}P\left(A_{12}{A}_{13}\right)=2n^{3}P{\left(A_{12}\right)}^2$$ (36)

by Lemma 12. Now

$$P\left(A_{12}\right)=P({\Theta }_{12}<t_x)+P({\Theta }_{12}>t_y).$$ (37)

By Lemma 12 again,

$$\begin{array}{cc}\hfill P({\Theta }_{12}>t_y)& =\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}{\int }_{t_y}^{\pi }{\left(\sin \theta \right)}^{p-2}d\theta \hfill \\ \hfill & =\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}{\int }_0^{n^{-2∕{(p-1)}_y}}{\left(\sin \eta \right)}^{p-2}d\eta \hfill \end{array}$$ (38)

by setting η = π – θ. Now, set ν = cosη for η ∈ [0,π]. Write (sinη)^p–2 = −(sinη)^p–3(cosη)’. Then the integral in (38) is equal to

$${\int }_{v_y}^1{(1-v^2)}^{(p-3)∕2}\mathit{dv}$$

where

$$v_y≔\cos \left(n^{-2∕(p-1)}y\right)=1-\frac{y^2}{2n^{4∕(p-1)}}+O\left(\frac{1}{n^{8∕(p-1)}}\right)$$

as n → ∞ by the Taylor expansion. Trivially,

$$v_y^2=1-\frac{y^2}{n^{4∕(p-1)}}+O\left(\frac{1}{n^{8∕(p-1)}}\right)$$

as n → ∞. Thus, by (26),

$${\int }_{v_y}^1{(1-v^2)}^{(p-3)∕2}\mathit{dv}\sim \frac{1}{p-1}{(1-v_y^2)}^{(p-1)∕2}=\frac{y^{p-1}}{(p-1)n^2}\left(1+O\left(\frac{1}{n^{4∕(p-1)}}\right)\right)$$

as n → ∞. Combining all the above we conclude that

$$\begin{array}{cc}\hfill P({\Theta }_{12}>t_y)& =\frac{\Gamma \left(\frac{p}{2}\right)}{\sqrt{\pi }(p-1)\Gamma \left(\frac{p-1}{2}\right)}\frac{y^{p-1}}{n^2}(1+o(1\left)\right)\hfill \\ \hfill & =\frac{\Gamma \left(\frac{p}{2}\right)}{2\sqrt{\pi }\Gamma \left(\frac{p+1}{2}\right)}\frac{y^{p-1}}{n^2}(1+o(1\left)\right)\hfill \end{array}$$ (39)

as n → ∞. Similar to the part between (38) and (39), we have

$$\begin{array}{cc}\hfill P({\Theta }_{12}<t_x)& =\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}{\int }_0^{n^{-2∕{(p-1)}_x}}{\left(\sin \theta \right)}^{p-2}d\theta \hfill \\ \hfill & =\frac{\Gamma \left(\frac{p}{2}\right)}{2\sqrt{\pi }\Gamma \left(\frac{p+1}{2}\right)}\frac{x^{p-1}}{n^2}(1+o(1\left)\right)\hfill \end{array}$$

as n → ∞. This joint with (39) and (37) implies that

$$P\left(A_{12}\right)=\frac{\Gamma \left(\frac{p}{2}\right)}{2\sqrt{\pi }\Gamma \left(\frac{p+1}{2}\right)}\frac{x^{p-1}+y^{p-1}}{n^2}(1+o(1\left)\right)$$

as n → ∞. Recalling (35) and (36), we obtain

$$\underset{n\to \infty }{\lim }{\lambda }_n=K(x^{p-1}+y^{p-1})$$

and b_1,n $\vee b_{2,n}=O\left(\frac{1}{n}\right)$ as n → ∞, where K is as in (9). These two assertions and (34) yield

$$\underset{n\to \infty }{\lim }P(X_u=0\text{for all}u\in I)=e^{-K(x^{p-1}+y^{p-1})}.$$

Finally, this together with (33) implies (32).

6.3 Proofs of Main Results in Section 3

Proof of Theorem 4

Notice (p – 2)/p → 1 as p → ∞, to prove the theorem, it is enough to show that the theorem holds if “μ_n,p” is replaced by “$\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}{\sum }_{1\le i<j\le n}{\delta }_{\sqrt{p}(\frac{\pi }{2}-{\Theta }_{\mathit{ij}})}$.” Thus, without loss of generality, we assume (with a bit of abuse of notation) that

$${\mu }_{n,p}=\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i<j\le n}{\delta }_{\sqrt{p}(\frac{\pi }{2}-{\Theta }_{\mathit{ij}})},n\ge 2,p\ge 2.$$

Recall p = p_n. Set $Y_n≔\sqrt{p}(\frac{\pi }{2}-{\Theta }_{12})$ for p ≥ 2. We claim that

$$Y_n\text{converges weakly to}N(0,1)$$ (40)

as n → ∞. Assuming this is true, taking ${\phi }_n\left(\theta \right)=\sqrt{p}(\frac{\pi }{2}-\theta )$ for θ ∈ [0,π] and ν = N(0,1) in (ii) of Lemma 16, then, with probability one, μ_n,p converges weakly to N(0,1) as n → ∞.

Now we prove the claim. In fact, noticing Θ₁₂ has density h(θ) in (13), it is easy to see that Y_n has density function

$$\begin{array}{cc}\hfill h_n\left(y\right):& =\frac{1}{\sqrt{\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}\cdot {\left[\sin \left(\frac{\pi }{2}-\frac{y}{\sqrt{p}}\right)\right]}^{p-2}\cdot \mid -\frac{1}{\sqrt{p}}\mid \hfill \\ \hfill & =\frac{1}{\sqrt{p\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}\cdot {\left(\cos \frac{y}{\sqrt{p}}\right)}^{p-2}\hfill \end{array}$$ (41)

for any $y\in \mathbb{R}$ as n is sufficiently large since lim_n→∞ p_n = ∞. By (17),

$$\frac{1}{\sqrt{p\pi }}\frac{\Gamma \left(\frac{p}{2}\right)}{\Gamma \left(\frac{p-1}{2}\right)}\to \frac{1}{\sqrt{2\pi }}$$ (42)

as n → ∞. On the other hand, by the Taylor expansion,

$${\left(\cos \frac{y}{\sqrt{p}}\right)}^{p-2}={\left(1-\frac{y^2}{2p}+O\left(\frac{1}{p^2}\right)\right)}^{p-2}\to e^{-y^2∕2}$$

as n → ∞. The above together with (41) and (42) yields that

$$\underset{n\to \infty }{\lim }{h}_n\left(y\right)\to \frac{1}{\sqrt{2\pi }}{e}^{-y^2∕2}$$ (43)

for any $y\in \mathbb{R}$. The assertions in (41) and (42) also imply that ${\sup }_{y\in \mathbb{R}}\mid h_n\left(y\right)\mid \le C$ for n sufficiently large, where C is a constant not depending on n. This and (43) conclude

Proof of Proposition 5

By (i) of Lemma 12,

$$P(\mid \Theta -\frac{\pi }{2}\mid \ge \epsilon )=C_p{\int }_{\mid \theta -\frac{\pi }{2}\mid \ge \epsilon }{\left(\sin \theta \right)}^{p-2}d\theta =C_p{\int }_{\epsilon \le \mid t\mid \le \pi ∕2}{\left(\cos t\right)}^{p-2}\mathit{dt}$$

by making transform $t=\theta -\frac{\pi }{2}$, where $C_p≔\frac{1}{\sqrt{\pi }}\Gamma \left(\frac{p}{2}\right)∕\Gamma \left(\frac{p-1}{2}\right)$. The last term above is identical to

$$2C_p{\int }_{\epsilon }^{\pi ∕2}{\left(\cos t\right)}^{p-2}\mathit{dt}\le \pi C_p{\left(\cos \epsilon \right)}^{p-2}.$$

It is known that lim_x→+∞ Γ(x+a)/(x^aΓ(x)) = 1, see, for example, Dong, Jiang and Li (2012). Then $\pi C_p\le K\sqrt{p}$ for all p ≥ 2, where K is a universal constant. The desired conclusion then follows.

Proof of Theorem 6

Review the proof of Theorem 1 in Cai and Jiang (2012). Replacing |ρ_ij|, L_n in (2) and Lemma 6.4 from Cai and Jiang (2012) with ρ_ij, M_n in (11) and Lemma 15 here, respectively. In the places where “n – 2” or “n – 4” appear in the proof, change them to “p – 1” or “p – 3” accordingly. Keeping the same argument in the proof, we then obtain the following.

(a) M_n → 0 in probability as n → ∞.

(b) Let $T_n=\log (1-M_n^2)$. Then, as n → ∞,

$${\mathit{pT}}_n+4\log n-\log \log n$$

converges weakly to an extreme value distribution with the distribution function F(y) = 1 – e^−Key/2, $y\in \mathbb{R}$ and $K=1∕\left(2\sqrt{8\pi }\right)=1∕\left(4\sqrt{2\pi }\right)$. From (11) we know

$$M_n=\underset{1\le i<j\le n}{\max }{\rho }_{\mathit{ij}}=\cos {\Theta }_{\min }\text{and}{\Theta }_{\min }\in [0,\pi ];$$ (44)

$$T_n=\log (1-M_n^2)=2\log \sin {\Theta }_{\min }.$$ (45)

Then (a) above implies that Θ_min → π/2 in probability as n → ∞, and (b) implies (ii) for Θ_min in the statement of Theorem 6. Now, observe that

$$\underset{1\le i<j\le n}{\min }\{\pi -{\Theta }_{\mathit{ij}}\}=\pi -{\Theta }_{\max }\text{and}\sin (\pi -{\Theta }_{\max })=\sin {\Theta }_{\max }.$$ (46)

By the same argument between (30) and (31), we get π – Θ_max → π/2 in probability as n → ∞, that is, Θ_max → π/2 in probability as n → ∞. Notice

$$\begin{array}{cc}\hfill & \underset{1\le i<j\le p}{\max }\mid {\Theta }_{\mathit{ij}}-\frac{\pi }{2}\mid \hfill \\ \hfill \le & \mid {\Theta }_{\max }-\frac{\pi }{2}\mid +\mid {\Theta }_{\min }-\frac{\pi }{2}\mid \to 0\hfill \end{array}$$

in probability as n → ∞. We get (i).

Finally, by the same argument between (30) and (31) again, and by (46) we obtain

$$2p\log \sin {\Theta }_{\max }+4\log n-\log \log n$$

converges weakly to F(y) = 1 – e^−Key/2, $y\in \mathbb{R}$ and $K=1∕\left(4\sqrt{2\pi }\right)$. Thus, (ii) also holds for Θ_max.

Proof of Corollary 7

Review the proof of Corollary 2.2 from Cai and Jiang (2012). Replacing L_n and Theorem 1 there by M_n and Theorem 6, we get that

$${\mathit{pM}}_n^2-4\log n+\log \log n$$

converges weakly to the distribution function $\exp \{-\frac{1}{4\sqrt{2\pi }}{e}^{-(y+8{\alpha }^2)∕2}\},y\in \mathbb{R}$. The desired conclusion follows since M_n = cosΘ_min.

Proof of Theorem 8

Review the proof of Theorem 2 in Cai and Jiang (2012). Replacing |ρ_ij|, L_n in (2) and Lemma 6.4 from Cai and Jiang (2012) with ρ_ij, M_n in (11) and Lemma 15, respectively. In the places where “n – 2” and “n – 4” appear in the proof, change them to “p – 1” and “p – 3” accordingly. Keeping the same argument in the proof, we then have the following conclusions.

1. $M_n\to \sqrt{1-e^{-4\beta }}$ in probability as n → ∞.

2. (ii) Let $T_n=\log (1-M_n^2)$. Then, as n → ∞,

   $${\mathit{pT}}_n+4\log n-\log \log n$$

   converges weakly to the distribution function

   $$F\left(y\right)=1-\exp \left\{-K\left(\beta \right)e^{(y+8\beta )∕2}\right\},y\in \mathbb{R},$$

   where

   $$K\left(\beta \right)=\frac{1}{2}{\left(\frac{\beta }{2\pi (1-e^{-4\beta })}\right)}^{1∕2}={\left(\frac{\beta }{8\pi (1-e^{-4\beta })}\right)}^{1∕2}.$$

   From (44) and (45) we obtain

   $${\Theta }_{\min }\to {\cos }^{-1}\sqrt{1-e^{-4\beta }}\text{in probability and}$$ (47)

   $$2p\log \sin {\Theta }_{\min }+4\log n-\log \log n$$ (48)

   converges weakly to the distribution function

   $$F\left(y\right)=1-\exp \left\{-K\left(\beta \right)e^{(y+8\beta )∕2}\right\},y\in \mathbb{R},\text{where}K\left(\beta \right)={\left(\frac{\beta }{8\pi (1-e^{-4\beta })}\right)}^{1∕2}$$ (49)

   as n → ∞. Now, reviewing (46) and the argument between (30) and (31), by (47) and (48), we conclude that ${\Theta }_{\max }\to \pi -{\cos }^{-1}\sqrt{1-e^{-4\beta }}$ in probability and 2plogsinΘ_max + 4logn − loglogn converges weakly to the distribution function F(y) as in (49). The proof is completed.

Proof of Theorem 9

Review the proof of Theorem 3 in Cai and Jiang (2012). Replacing |ρ_ij|, L_n in (2) and Lemma 6.4 from Cai and Jiang (2012) with ρ_ij, M_n in (11) and Lemma 15, respectively. In the places where “n – 2” or “n – 4” appear in the proof, change them to “p – 1” or “p – 3” accordingly. Keeping the same argument in the proof, we get the following results.

1. M_n → 1 in probability as n → ∞.

2. As n → ∞,

   $${\mathrm{pM}}_n+\frac{4p}{p-1}\log n-\log p$$

   converges weakly to the distribution function F(y) = 1 – e^−Key/2, $y\in \mathbb{R}$ with $K=1∕\left(2\sqrt{2\pi }\right)$. Combining i), ii), (44) and (45), we see that, as n → ∞,

   $$\begin{array}{cc}\hfill & {\Theta }_{\min }\to 0\text{in probability};\hfill \\ \hfill & 2p\log \sin {\Theta }_{\min }+\frac{4p}{p-1}\log n-\log p\text{converges weakly to}\hfill \end{array}$$

   F(y) = 1 – e^−Key/2, $y\in \mathbb{R}$ with $K=1∕\left(2\sqrt{2\pi }\right)$. Finally, combining the above two convergence results (46) and the argument between (30) and (31), we have

   $$\begin{array}{cc}\hfill & {\Theta }_{\max }\to \pi \text{in probability};\hfill \\ \hfill & 2p\log \sin {\Theta }_{\max }+\frac{4p}{p-1}\log n-\log p\text{converges weakly to}\hfill \end{array}$$

   F(y) = 1 – e^−Key/2, $y\in \mathbb{R}$ with $K=1∕\left(2\sqrt{2\pi }\right)$.