Abstract
The census tract-based residential segregation literature rests on problematic assumptions about geographic scale and proximity. We pursue a new tract-free approach that combines explicitly spatial concepts and methods to examine racial segregation across egocentric local environments of varying size. Using 2000 census data for the 100 largest U.S. metropolitan areas, we compute a spatially modified version of the information theory index H to describe patterns of black-white, Hispanic-white, Asian-white, and multi-group segregation at different scales. The metropolitan structural characteristics that best distinguish micro-segregation from macro-segregation for each group combination are identified, and their effects are decomposed into portions due to racial variation occurring over short and long distances. A comparison of our results to those from tract-based analyses confirms the value of the new approach.
The historical roots of sociological interest in racial and ethnic residential segregation can be traced to Robert Park's famous dictum that spatial patterns reflect social relations (Park 1926). For many scholars, however, the standard Chicago School rationale no longer suffices. Beyond its role as an indicator of the social distance between majority and minority groups, segregation is now considered an important force contributing to racial inequality more generally in American society. Recent evidence links high levels of segregation to minority deficits in safety, health, education, and employment, among other outcomes (Acevedo-Garcia et al. 2003; Card and Rothstein 2006; Cutler and Glaeser 1997; Ellen 2000; Peterson, Krivo, and Browning 2006). Similarly, the neighborhood effects literature incorporates segregation in localized form, exploring how racial isolation and related aspects of concentrated disadvantage both heighten exposure to problems and reduce access to resources and opportunities (Brooks-Gunn, Duncan, and Aber 1997; Sampson, Morenoff, and Gannon-Rowley 2002; Wilson 1987, 1996).
Most segregation investigators have turned to the decennial census for their data. The resulting literature offers valuable insights not only into the consequences of racial segregation but, more often, into its patterns and antecedents (Farley and Frey 1994; Iceland, Weinberg, and Steinmetz 2002; Lieberson 1980; Logan, Stults, and Farley 2004; Massey and Denton 1993; Taeuber and Taeuber 1969). Here we are concerned with a practice common to this census-based research: relying on a single type of spatial unit—typically the census tract (although sometimes the block group or block)—when computing segregation measures such as the index of dissimilarity. The tract is officially defined as a compact, recognizable, and homogeneous territorial unit with relatively permanent boundaries and an optimum population of about 4,000 (U.S. Census Bureau 1997).1 Its popularity can be traced in part to its convenience and to the belief that it approximates a “real” neighborhood. One difficulty with the latter justification lies in the elastic nature of the neighborhood concept; urban dwellers' perceptions of the name, size, and boundaries of the same residential environment can vary markedly (Chaskin 1994; Lee and Campbell 1997; Sastry, Pebley, and Zonta 2002). While the congruence, or lack thereof, between a subjectively meaningful neighborhood and a census tract is hardly a trivial matter, we speak to this issue in only indirect fashion.
More crucial for our purposes is that sole reliance on the tract (or block group or block) as the unit of analysis precludes appreciation of the geographic scale of residential segregation. The concept of scale refers to the geographic level at which any phenomenon of interest is organized, experienced, or observed (Smith 2000). Residential segregation is inherently spatial; hence, a complete understanding of the phenomenon must be attentive to its scale in addition to its magnitude (Kaplan and Holloway 2001). We contend, however, that conventional census studies, in which tracts are treated as discrete residential turfs, rest on two problematic assumptions about scale and a third about proximity. Although the third assumption has been widely discussed in the segregation measurement literature (Dawkins 2004; Massey and Denton 1988; Morrill 1991; White 1983; Wong 1993), the two about scale have received less scrutiny.
The first of these is the implicit assumption that the tract constitutes an appropriately-sized spatial unit for capturing segregation. This assumption obscures potential variation among regions (e.g., metropolitan areas) in the scale of segregation since tract measures cannot distinguish regions where racial composition changes over short distances from those where differences in composition occur between large subareas. The second assumption, actually a corollary of the first, is that the scale to which the census tract corresponds can in fact be ascertained, thanks to the standardized, stable nature of tracts. As we show below, substantial variation exists in the territorial size of tracts within and across metro areas, which means that the “scale” of tract-based segregation measures remains ambiguous. The third assumption is that all persons sharing a tract, whether located in the core of the tract or near its edges, have no proximity to residents outside of the tract but are equally proximate to everyone within its boundaries. This assumption inheres less in the tract-level data used by conventional studies than in their treatment of tracts as spatially autonomous, disregarding how close to or far from each other tracts are.
Our aim is to reduce the need for these assumptions via a spatially refined strategy in which scale and proximity are handled in a more flexible manner. We begin by explicating the assumptions with reference to current tract-based research on racial segregation. Following Reardon and colleagues (Reardon et al. forthcoming; Reardon and O'Sullivan 2004), we argue that segregation be reconceptualized as variation in the racial composition of the egocentric local environments inhabited by individual residents, where the definition of “local” may be manipulated to evaluate segregation at a range of geographic scales. We also introduce the segregation profile as a method for summarizing the extent of segregation across local environments of differing territorial size. Simply put, the proposed approach treats scale as a variable rather than a constant and takes proximity seriously.
In the analysis proper, we apply spatial techniques of measuring segregation to 2000 census data for the 100 largest U.S. metropolitan areas. A spatially weighted version of the information theory index (H) serves as the primary segregation measure throughout. Our initial analytic objectives are to describe average levels of segregation for combinations of racial groups (black-white, Hispanic-white, etc.), to observe how these levels vary when we use different definitions of local environment size, and to relate large- and small-environment patterns with a tool known as the macro-micro segregation ratio. We then disaggregate segregation patterns by metropolitan area, given that rankings of the most and least segregated areas may depend on geographic scale. If the areas most segregated across small local environments are also the most segregated across large ones, a measure of racial segregation at any scale (even at the uncertain scale of the tract) would tell us all that we need to know.
If, on the other hand, the rankings do vary by scale, then not only the patterns but the determinants of segregation are called into question. This possibility guides the second part of our analysis, which explores the cross-scale relevance of a structural perspective on segregation popular in census-based studies (Farley and Frey 1994). A measure of net micro-segregation is computed for each metropolis that allows us to decompose the total segregation among individuals' small local environments into macro- and micro-scale components (i.e., the portions of total segregation due to variation between and within large subregions, respectively). By fitting regression models that incorporate net micro-segregation as one of several scale-specific dependent variables, we can assess the degree to which the metropolitan structural properties examined in conventional research differentially explain macro- and micro-segregation. Finally, we compare our regression results for egocentric local environments to those for tracts. This type of comparison—which we also employ to evaluate descriptive patterns—addresses an overarching issue: in what ways, if any, our scale-sensitive approach advances understanding of racial residential segregation.
PROBLEMATIC ASSUMPTIONS IN CONVENTIONAL RESEARCH
Contemporary evidence on segregation comes from a series of studies undertaken after the release of 2000 census data (Charles 2003; Farrell 2008; Fischer 2008; Glaeser and Vigdor 2003; Iceland et al. 2002; Logan 2003; Logan et al. 2004). One intriguing trend documented by the studies is the convergence of group-specific segregation levels due to pervasive black-white declines and small Hispanic and Asian increases in segregation. That trend has not, however, eliminated the familiar racial hierarchy, with African Americans still the most segregated minority from whites, Asians the least segregated, and Hispanics in-between. To understand inter-metropolitan differences in segregation levels, researchers often employ some version of Farley and Frey's (1994) structural-ecological perspective (also see Frey and Farley 1996). The body of work inspired by the perspective finds variation in segregation to be related to metro area population size, region, functional specialization (e.g., as a military or retirement center), minority group size, and minority socioeconomic status, among other structural characteristics (Farrell 2005; Iceland and Nelson forthcoming; Logan et al. 2004; Timberlake and Iceland 2007; Wilkes and Iceland 2004). Section B of the Online Supplement reviews recent studies of segregation in greater detail.
Such studies share something else besides their conclusions about the patterns and determinants of residential segregation. Despite their nominally spatial orientation, they tend to be aspatial in certain key respects, like the segregation literature in general. With occasional exceptions (Dawkins 2004; Grannis 1998; Jargowsky and Kim 2005; White 1983; Wong 1999, 2005), researchers utilize measures that stress the racial composition of census tracts to the neglect of spatial complexities. In particular, the tract-based computation of dissimilarity (D) and exposure (P*) indexes rests on the assumptions about scale and proximity identified earlier. These assumptions, which we discuss in turn, can foster measurement error in conventional segregation research.
Scale
Concerns about scale provide the primary motivation for our analysis. To assume that tracts constitute a gold standard in the calculation of segregation measures—i.e., that their size is consistently attuned to the spatial texture of racial composition—discounts the likelihood of metropolitan- and group-specific variations in that texture. The topography of a metropolis, the number of municipalities it comprises, the experiences of its minority residents in the local housing market, and a host of other factors can all be expected to contribute to distinctive racial distributions, with some metro areas and groups segregated predominantly at a macro-geographic scale (e.g., black-white segregation in Atlanta and Chicago, where the subregions occupied by each racial group are spatially large) and some at a micro scale (e.g., instances of Asian-white segregation where Asian groups are concentrated in highly localized enclaves). Although the tract may be an appropriate unit when segregation manifests itself between these two extremes, tract-based segregation measures necessarily obscure racial patterns that extend over territorial domains bigger or smaller than tracts. The general point we wish to make is that one size does not fit all.
This conclusion raises a logically prior issue: do census tracts even approximate a uniform size? Despite Census Bureau portrayals of tracts as compact, stable, neighborhood-like units and their reification as such by social scientists, population rather than territory represents the decisive criterion in defining tracts. For the 2000 census, local statistical area committees were instructed to treat 4,000 as the optimum tract population size, with 1,500 and 12,000 as the minimum and maximum thresholds beyond which a formal justification for exemption would be required (U.S. Census Bureau 1997).2 An obvious consequence of linking tract boundaries to population is that the overall density of a metropolitan area will be negatively related to tract spatial size. Among the 25 most densely settled metro areas in our sample, the interquartile range in tract size runs from 1.1 to 6.2 square kilometers (km2), on average. Among the 25 lowest-density metro areas, the interquartile range is 2.5 to 27.8 km2.
Keep in mind that these summary statistics mute the magnitude of contrasts between and within particular metropolises. As an example, median tract size in Little Rock-North Little Rock (16.6 km2) is nearly 80 times greater than that in New York-White Plains-Wayne (.21 km2), and tracts in Riverside-San Bernardino-Ontario and Salt Lake City cover roughly half a square kilometer on the low end to 20,700 and 14,981 km2, respectively, on the high end. More generally, 23 of the 100 largest metropolitan areas have tracts of less than a square mile and of more than 500 square miles (1,300 km2). Intra-metropolitan variation also occurs in tract population, so much so that 45 of the largest metro areas have tracts falling both below and above the prescribed 1,500-12,000 range.
Boundaries are another aspect of tracts that lack consistency. In theory, they are supposed to take a concrete, unambiguous form (as streets, rivers, railroads, and the like), yet certain kinds of invisible political jurisdictions, such as county lines, can double as tract boundaries. Moreover, the ideal of boundary stability is breached quite often, thanks to tract splits, mergers, and irregular shifts in demarcation. One need look no further than the Census Bureau's 1990-2000 census tract relationship files (at www.census.gov/geo/www/relate/rel_tract.html), which show that 29.4% of the 66,304 unique tracts recognized nationwide in the 2000 census qualify as “significantly changed” (i.e., more than 2.5% of their 2000 population would have been located in a different tract based on 1990 boundaries). To its credit, the Census Bureau is careful to acknowledge that it “establishes and maintains census tracts solely for statistical purposes...” (U.S. Census Bureau 1997:16). However, this warning tends to be overridden by a belief in tracts as standardized, quasi-neighborhood units. We maintain the opposite: they are rather arbitrary with respect to spatial size (also see White 1987:286-300).
Proximity
The way in which proximity is handled in conventional segregation research has an element of arbitrariness as well. The difficulty with implicitly assuming that residents of different tracts have no proximity to each other can be seen in the well-known “checkerboard” problem (Massey and Denton 1988; Morrill 1991; White 1983). This refers to the inability of the index of dissimilarity and other common measures to distinguish between the settlement of two groups in racially homogeneous but spatially alternating tracts (giving the metropolis a checkerboard appearance) and a very different situation in which all tracts occupied by each group are clustered in large, separate racial communities (dividing the metropolis into black and white sides of town). The D value calculated across tracts would be identical (equaling 100) for both patterns, despite the likelihood that the everyday lives of residents would diverge under the checkerboard and clustering scenarios (see Section C of the Online Supplement).
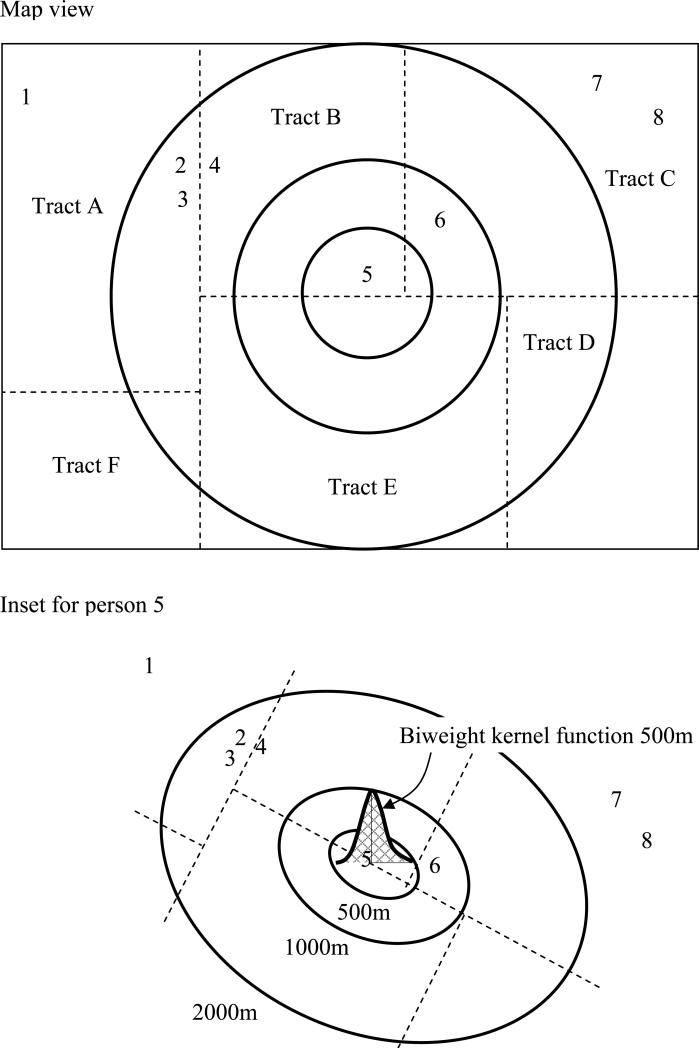
Common segregation measures also fail to distinguish among different locations within a tract. That is, all tract residents are assumed to have equal proximity to each other, even if whites and people of color occupy distinct pockets inside tract boundaries and experience minimal interracial exposure (Allen and Turner 1995). Turning to Figure 1 for illustration, this means that person 1 in tract A is treated as living as close to persons 2 and 3 as the latter two do to each other. Similarly, standard measures such as D and P* ignore differences in the relative locations of 6, 7, and 8 in tract C, considering them equidistant from one another and subject to the same intra-neighborhood racial mix.
Figure 1.
Census Tracts and Local Environments
The special case of people located on opposite sides of a tract boundary brings into sharp relief the potentially misleading nature of the proximity assumption built into most segregation studies. These people may literally live across the street from one another, as 2 and 4 do in tracts A and B of Figure 1, yet they are judged more distant than are individuals who live relatively far apart but within the same tract (such as 4 and 5 in tract B). The resulting measurement error can be understood as a manifestation of the modifiable areal unit problem, or MAUP. The main message from MAUP is that segregation measures which rely on racial population counts for geographic subareas will be sensitive to how subarea boundaries are drawn. Levels of segregation are likely to vary with subarea size (e.g., tracts versus block groups), and they may be responsive to boundary shifts, even if the number and size of subareas are held constant (Openshaw and Taylor 1979; Wong 1997, 2004).
A SPATIAL APPROACH
Local Environments
For our purposes, two important conceptual directions emerge from the foregoing critique. The first is to move beyond arbitrary units such as tracts, which capture the spatial circumstances of racial groups in crude fashion. Following the lead of Reardon and O'Sullivan (2004), we propose that segregation measurement recognize individuals' proximity to each other in residential space. It then becomes possible to think of segregation as the degree to which the local environments of these individuals—their egocentric neighborhoods—differ in racial composition. Every person is assumed to live at the center of a local environment whose population reflects the proximity-weighted average composition of each surrounding point in some larger geographic region of interest. Nearby populations will likely contribute more to the local environment than will distant ones; hence the former are given greater weight. The proximity-weighted racial composition of each individual's local environment provides the basic input for calculating various types of segregation statistics.
To better “see” what we mean by an egocentric local environment, consider the smallest concentric circle drawn around person 5 in Figure 1. This circle approximates person 5's immediate, walkable neighborhood, extending 500 meters (m) in all directions irrespective of tract boundaries. Even within such a modest-sized environment, 5 will probably be more influenced by the neighbors closest to his or her residence, as the surface in the inset portion of the figure depicts. Now envision creating a local environment of the same radius for each of the thousands of individuals living in tracts A-F. The proximity-weighted racial composition of those egocentric environments can be used in place of census tract data to arrive at spatially refined estimates of segregation.
Segregation Profile
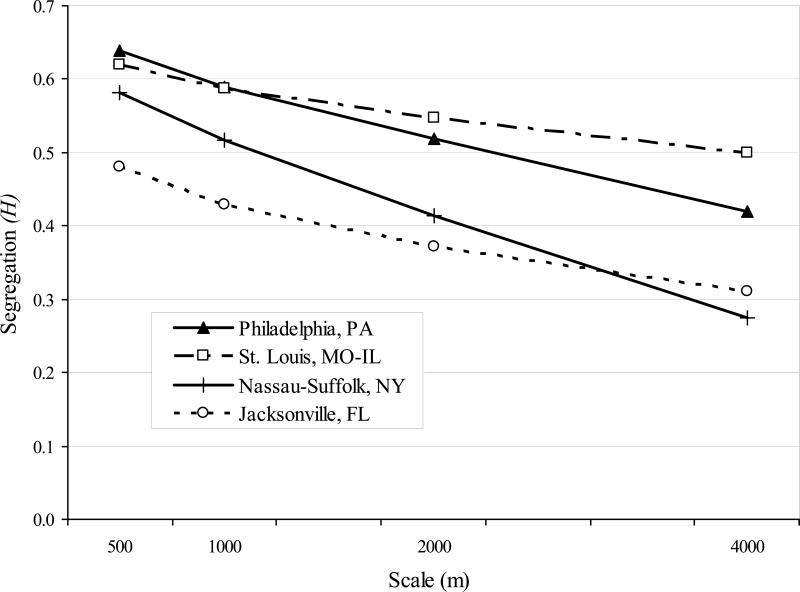
Note that our approach does not hinge on any specific definition of local environment. As shown in Figure 1, person 5 might be positioned in the middle of several nested concentric circles. Thus, a second novel conceptual direction taken here involves examining and comparing segregation across local environments of systematically varying size rather than of a single size.3 Elsewhere Reardon et al. (forthcoming) introduce the segregation profile, a tool well suited to this objective. The profile is a curve that shows the level of segregation by geographic scale in a given metropolitan area. Each point on the horizontal axis of the profile represents a local environment of a distinct radius. Two key properties are conveyed by the profile: the magnitude of segregation at a particular scale (depicted by the height of the profile on the vertical axis), and the extent to which segregation changes with scale (depicted by the slope of the profile). Figure 2 illustrates these properties, presenting black-white profiles for four metropolitan areas.
Figure 2.
Black-White Segregation Profiles for Selected Metropolitan Areas
The value of the segregation profile becomes apparent when one realizes that racial residential patterns vary across metropolitan areas in ways that do not necessarily conform to tract boundaries. Such variation gives rise to differences in what we term micro-segregation and macro-segregation, that is, segregation measured at different geographic scales. In a metropolis where racial composition fluctuates dramatically over short distances, micro-segregation (measured using a small-radius definition of the local environment) will tend to be higher than macro-segregation (measured using a large-radius definition of local) because larger local environments mask the fine-grained racial distributions that exist “on the ground.” However, in a metro area where racial composition changes little over short distances, micro- and macro-segregation levels will be more similar. That is, most of the micro-segregation will be captured by the racial texture of large local environments, so that people experience comparable levels of diversity (or homogeneity) whether close to or far from their homes.4 The slope of the segregation profile sheds light on these scalar relationships. It also serves as the foundation for the macro-micro segregation ratio and the net micro segregation measure, which we formalize in the next section.
In Figure 2, the Philadelphia and St. Louis metropolitan areas both exhibit high levels of black-white micro-segregation, indicating that there is substantial variation in the racial composition of the local (500m radius) environments of individuals within these areas. But St. Louis exhibits higher black-white macro-segregation (4,000m radius) than does Philadelphia. The resulting flatter slope of the St. Louis profile implies that more of the micro-segregation in St. Louis is due to large-scale patterns, with racial composition remaining stable for longer distances. Alternatively, the steeply declining profile for Nassau-Suffolk, NY denotes the primacy of a fine-grained racial landscape over a coarser, large-scale one.
Implications
The information summarized by these profiles bears directly on the conclusions about segregation drawn in descriptive research. Ponder, for example, a question that underlies many studies: which metropolitan areas are the most segregated? Investigators routinely address this question by ranking areas on the basis of their tract-based D scores. Our approach raises the possibility that a single rank order may not provide a satisfactory answer (also see Jargowsky and Kim 2005; Wong 2004). Returning to Figure 2, Philadelphia tops St. Louis, Nassau-Suffolk, and Jacksonville when black-white segregation is measured across small local environments while St. Louis is the most segregated of the four at a large scale. In terms of segregation level, the often-documented racial hierarchy (African American > Hispanic > Asian) could be scale-dependent as well, at least in certain metro areas. Suffice it to say that the task of describing patterns of residential segregation becomes more challenging, but potentially more enlightening, when geographic scale is taken into account.
So does the task of explaining segregation. On one hand, studies of residential preferences (Charles 2005; Farley et al. 1994; Krysan and Farley 2002) seem geared toward micro-segregation, though perhaps unintentionally. By asking survey participants to react to cards which show small (15 housing-unit), hypothetical neighborhoods of varying racial composition, these studies implicitly assume that only the race of people in the immediate vicinity matters as a household decides whether to enter the neighborhood, leave it, or stay put. On the other hand, structural analyses guided by Farley and Frey's (1994) perspective emphasize metropolitan-wide forces such as functional specialization and minority group size and socioeconomic status, which may contribute to macro-segregation instead of (or in addition to) segregation over shorter distances. Other factors, including the local street network (Grannis 1998) and institutional jurisdictions (for schools, shopping centers, churches, etc.), could be relevant at multiple scales. The point here is that investigators ideally should theorize residential segregation with a particular geographic scale in mind. To date, however, little has been learned about what predicts segregation at scales different from that of the tract (whatever the size of a tract happens to be), and especially about whether the predictors of micro- and macro-segregation are distinct or the same.
METHODOLOGY
Data
We use data from the 2000 census to implement our new approach. Counts from Summary File 1 have been extracted to represent four mutually exclusive racial/ethnic groups: non-Hispanic whites, non-Hispanic blacks, non-Hispanic Asians, and Hispanics of any race.5 Our analysis focuses on the segregation of each of the last three groups from whites and on multi-group segregation in the 100 metropolitan areas with the largest populations at the time of the census. OMB metropolitan definitions issued in 2003 are adhered to throughout (Frey et al. 2004), although 11 consolidated metro areas (e.g., San Francisco-Oakland) have been broken down into their primary area parts, which we treat as separate cases. The top 100 areas are listed in Section D of the Online Supplement; they range in size from New York-Wayne-White Plains (2000 population of 11,296,377) to Scranton-Wilkes-Barre, PA (560,625). Substantial proportions of all whites (55.7%), blacks (69.5%), Hispanics (78.2%), and Asians (85.9%) in the U.S. live in the metro areas covered by our sample.
GIS Procedures
Consistent with the conceptual directions proposed above, the construction of local environment-based segregation measures requires that we not rely on tracts. Instead, racial/ethnic counts for blocks—the smallest available census aggregations—provide the raw data from which we estimate the proximity-weighted racial composition of individuals' local environments. By reconfiguring the block data with GIS software (Environmental Systems Research Institute 2006), it becomes possible to specify more precisely the locations of members of the four racial groups relative to one another. A truly sophisticated spatial strategy would forego spatial aggregation altogether, in favor of distances among households (for further discussion, see Section E of the Online Supplement). Due to confidentiality concerns, the Census Bureau is unlikely to release the geographic identifiers needed to pursue this strategy any time soon. We thus seek to approximate it, building local environments around small cells or parcels of each block and assembling racial compositional data from other cells within the concentric circle defined by a given radius, as in Figure 1 (but with cells replacing the numbered persons).
Because the GIS procedures for creating local environments are complicated and have already been described in detail elsewhere (Reardon et al. forthcoming; Reardon and O'Sullivan 2004), we offer only a brief summary. The initial steps involve (1) superimposing a grid of 50m × 50m cells on the census block map for a metropolitan area, (2) using race-specific population densities at the block level to estimate racial group counts for every cell of each block, and (3) smoothing the grid with Tobler's (1979) pycnophylactic method, which softens the sharp changes in counts at block boundaries yet preserves total and race-specific counts within blocks. We then compute the proximity-weighted composition of the local environment of each cell by taking the weighted average population counts of the four racial groups in surrounding cells. In line with White's (1983) recommendation, the particular function that we have selected for this purpose—a two-dimensional biweight kernel function—incorporates a distance-decay dynamic, assigning nearby cells more weight than far ones on the assumption that spatial proximity is correlated with interpersonal exposure and interaction among residents. The biweight kernel function approximates a Gaussian (normal curve) shape, as represented in the Figure 1 inset, but has the practical advantage of being bounded by a fixed radius, reducing computation time. (Section F in the Online Supplement offers additional coverage of technical issues.)
Systematic manipulation of the radius of the proximity function produces racial compositional data on local environments of varying size. Here we calculate segregation levels for environments with radii of 500m, 1,000m, 2,000m, and 4,000m. These radii have been chosen with an eye toward the nested nature of meaningful local environments recognized in the past by community scholars (Suttles 1972; for a review, see Chaskin 1994). The smallest of our environments (500m radius) resembles a pedestrian neighborhood in which most activities—visiting neighbors, walking the dog, taking children to a park or playground—can be managed on foot. At the other extreme, the 4,000m radius translates into a macro-local environment of nearly 20 square miles, larger than many suburban municipalities and approaching (if not surpassing) the maximum of what metropolitan dwellers consider a neighborhood or community. Recent evidence suggests that church participation, shopping, socializing, and high school attendance typically occur within such a radius (Hu and Reuscher 2004; Sastry et al. 2002). The two intermediate local environments correspond in rough fashion to institutional jurisdictions (e.g., a police substation zone, an elementary school or daycare service area). The institutional neighborhood with the 1,000m radius also happens to come closer to census tracts in size (3.1 km2 versus a tract median of 2.6 km2 across the 100 sample metro areas) than do the other environments incorporated in our analysis.
Segregation Measures
The statistic that we use to measure segregation is the spatial information theory index, symbolized by H. Our preference for H is based on two recent evaluations of segregation indices that find both the spatial and aspatial versions of H to be conceptually and mathematically superior to the more popular index of dissimilarity D (Reardon and Firebaugh 2002; Reardon and O'Sullivan 2004).6 Like D, spatial H taps the evenness dimension of segregation, but does so by comparing the proximity-weighted racial composition of individuals' local environments to the racial composition of the metropolitan population as a whole. In particular, H tells us how much less diverse, on average, the former is than the latter. A value of 1 indicates that each person's environment is monoracial (maximum segregation); a value of 0 indicates that each persons' environment has the same racial composition as the metropolis (no segregation). The interpretation of H remains the same regardless of the number of racial groups included in its calculation. Indeed, H is attractive in part because it can be extended in a straightforward manner to multi-group segregation (Theil 1972; for substantive applications with tract data, see Farrell 2008; Fischer et al. 2004; Iceland 2004). This allows us to analyze white-black-Hispanic-Asian H scores in addition to the normal two-group variety.
Following the logic of the segregation profile, we estimate H for combinations of racial groups across the four types of local environments, yielding H500, H1000, H2000, and H4000. We complement these with two measures that relate micro- and macro-scale segregation. The first measure, the macro-micro segregation ratio (H4000/H500) operationalizes the slope of the profile, revealing the proportion of small-environment (500m radius) segregation due to large-environment (4,000m radius) segregation. Our second measure, which we label net micro segregation, is a simple difference score: net micro H = H500 - H4000. The net micro measure indicates what part of the total segregation among individuals' small local environments cannot be attributed to large-environment segregation; that is, it facilitates the decomposition of total small-environment segregation into macro- and micro-scale components. Because of this desirable property, net micro H is featured when we assess potential structural antecedents of segregation, while the H ratio proves most helpful for describing basic segregation patterns. Both measures are intended to distinguish between geographic scales, capturing the degree to which segregation among small environments results from variation in racial composition over short or long distances.
RESULTS
Descriptive Patterns
Table 1 presents mean H values and standard deviations (based on our sample of 100 metro areas) for racial group combinations across the four local environments defined above. By way of illustration, the .447 H value in the upper left corner of the table indicates that, on average, black and white residents live in small local environments (500m radius) that are 44.7% less diverse, or substantially more segregated, in terms of their black-white population mix than is the surrounding metropolis as a whole. A column-by-column reading affirms the traditional racial hierarchy: black-white segregation exceeds Hispanic-white segregation, which in turn exceeds Asian-white segregation. More significant is the finding that geographic scale matters. Looking across the first three rows, one can see that the level of segregation from whites experienced by each minority group declines as scale increases, due to the more heterogeneous populations encompassed by larger local environments.7 In concrete terms, people of color typically encounter more white residents within a 4,000m radius of their homes than within a 500m radius. The scale-segregation relationship applies to the multi-group case as well. According to the bottom row, average white-black-Hispanic-Asian segregation is over one-and-a-half times greater (i.e., multiracial diversity is considerably lower) in the local environment with the 500m radius than in its 4,000m counterpart.
Table 1.
Mean Segregation Levels By Local Environment Size and Racial Group Combinationa
| Group combination | Scale-specific segregation |
Macro-micro segregation ratiob | |||
|---|---|---|---|---|---|
| H500 | H1000 | H2000 | H4000 | ||
| Black-White | .447 (.141) | .403 (.140) | .349 (.132) | .279 (.117) | .611 (.100) |
| Hispanic-White | .282 (.086) | .242 (.086) | .200 (.082) | .154 (.072) | .526 (.148) |
| Asian-White | .212 (.049) | .168 (.047) | .133 (.045) | .103 (.041) | .476 (.112) |
| White-Black-Hispanic-Asian | .343 (.099) | .304 (.096) | .258 (.089) | .204 (.079) | .584 (.094) |
N = 100 metro areas; standard deviations appear in parentheses.
Operationalized as H4000/H500.
If the Hs from the table were plotted as in Figure 2, the segregation profiles for the four combinations of racial groups would appear to parallel one another, all sloping gradually downward from left (500m local environment) to right (4,000m local environment). They would still differ in a notable respect, however. The macro-micro segregation ratios, or H ratios (measured as H4000/H500), in the fifth column of Table 1 are smaller for Hispanic-white (.526) and Asian-white (.476) segregation, translating into modestly steeper slopes. From an interpretive standpoint, a steeper slope tells us that racial composition varies more over short distances, describing a pattern of micro-segregation that is not well accounted for by macro-segregation. In contrast, the black-white combination has the flattest slope (mean H ratio = .611). Segregation drops off less between these two groups because more of the variation in black-white composition occurs over greater distances.
Indeed, it is the substantial level of black-white macro-segregation that appears to underlie the high black segregation regularly documented in conventional tract-based studies. This fact, which is not well known, can be highlighted through a simple hypothetical exercise. Suppose that we could reduce black-white segregation across 4,000m local environments to the same H4000 value observed for Hispanics and whites. Such equalization of black-white and Hispanic-white macro-segregation would remove most of the difference in black-white versus Hispanic-white segregation at smaller scales.8 The influence of large-environment racial patterns is also evident in the mean H ratio for the multi-group combination, which approaches the magnitude of the black-white ratio.
The rough parallelism among the profiles summarized in Table 1 suggests that by knowing how segregated a metropolis is at one geographic scale, we can infer its ranking across the board (i.e., at all scales). Spearman rank-order correlations among H500, H1000, H2000, and H4000, calculated for the metro sample, would seem to support such a conclusion. For each combination of racial groups, most of the correlation coefficients are greater than .9. But for Hispanics and whites the correlation between H500 and H4000 equals .85, and the corresponding Asian-white correlation is .81. These somewhat smaller relationships leave open the possibility that the ranking of metropolitan areas could be affected by the size of the local environment across which segregation is measured. Wong (2004) addresses the same possibility using tracts and blocks (also see Jargowsky and Kim 2005).
Table 2 confirms that judgments about the most segregated places are in fact sensitive to scale for certain group combinations. To conserve room, we limit our attention to metropolises with the 10 highest H scores based on the smallest and largest local environments. The black-white and multi-group panels of the table document some reshuffling of metropolitan areas when H500 and H4000 values are compared, yet also impressive overlap: eight areas show up on both black-white lists and nine on both multi-group lists. In the Hispanic-white panel, however, Essex County, MA, the metropolis with the highest H500 score, drops off the most segregated list at a 4,000m radius, as do four other areas; Los Angeles-Long Beach-Glendale takes over at the head of the H4000 list. Non-trivial shifting also occurs in the Asian-white metropolitan rankings. Beyond the top 10, an assessment of all H500 and H4000 scores reveals extensive flux. The majority of metropolitan areas climb or fall 10 or more ranks in Hispanic-white (58 of 100 areas) and Asian-white (53 of 100) segregation with a jump from a 500m to a 4,000m radius, as foreshadowed by the Spearman correlations in the preceding paragraph.
Table 2.
Most Segregated Metropolitan Areas by Local Environment Size and Racial Group Combination
| Group combination | H500 | H4000 | ||
|---|---|---|---|---|
| Black-White | .767 | Gary, IN | .606 | Gary, IN |
| .737 | Detroit-Livonia-Dearborn, MI | .569 | Detroit-Livonia-Dearborn, MI | |
| .709 | Chicago-Naperville-Joliet, IL | .550 | Chicago-Naperville-Joliet, IL | |
| .683 | Newark-Union, NJ-PA | .509 | Cleveland-Elyria-Mentor, OH | |
| .674 | Milwaukee-Waukesha-West Allis, WI | .502 | Newark-Union, NJ-PA | |
| .666 | New York-White Plains-Wayne, NY-NJ | .500 | St. Louis, MO-IL | |
| .665 | Cleveland-Elyria-Mentor, OH | .498 | Milwaukee-Waukesha-West Allis, WI | |
| .662 | Birmingham-Hoover, AL | .465 | Dayton, OH | |
| .640 | Philadelphia, PA | .463 | Birmingham-Hoover, AL | |
| .620 | St. Louis, MO-IL | .426 | Los Angeles-Long Beach-Glendale, CA | |
| Hispanic-White | .469 | Essex County, MA | .315 | Los Angeles-Long Beach-Glendale, CA |
| .464 | Springfield, MA | .303 | Newark-Union, NJ-PA | |
| .434 | Hartford-West Hartford-East Hartford, CT | .291 | Camden, NJ | |
| .433 | New York-White Plains-Wayne, NY-NJ | .287 | Chicago-Naperville-Joliet, IL | |
| .428 | Philadelphia, PA | .280 | Hartford-West Hartford-East Hartford, CT | |
| .423 | Los Angeles-Long Beach-Glendale, CA | .277 | Philadelphia, PA | |
| .422 | Camden, NJ | .270 | Detroit-Livonia-Dearborn, MI | |
| .420 | Newark-Union, NJ-PA | .263 | Bakersfield, CA | |
| .411 | Providence-New Bedford-Fall River, RI-MA | .259 | Milwaukee-Waukesha-West Allis, WI | |
| .405 | Boston-Quincy, MA | .254 | Oxnard-Thousand Oaks-Ventura, CA | |
| Asian-White | .332 | Baton Rouge, LA | .214 | New Orleans-Metairie-Kenner, LA |
| .323 | Stockton, CA | .209 | Houston-Sugar Land-Baytown, TX | |
| .321 | New Orleans-Metairie-Kenner, LA | .201 | Los Angeles-Long Beach-Glendale, CA | |
| .315 | McAllen-Edinburg-Mission, TX | .200 | Bakersfield, CA | |
| .303 | Houston-Sugar Land-Baytown, TX | .189 | San Diego-Carlsbad-San Marcos, CA | |
| .300 | Bakersfield, CA | .189 | Stockton, CA | |
| .298 | Edison, NJ | .187 | Sacramento--Arden-Arcade--Roseville, CA | |
| .283 | Birmingham-Hoover, AL | .186 | Baton Rouge, LA | |
| .279 | Los Angeles-Long Beach-Glendale, CA | .176 | San Francisco-San Mateo-Redwood City, CA | |
| .277 | Greensboro-High Point, NC | .170 | Edison, NJ | |
| White-Black-Hispanic-Asian | .613 | Detroit-Livonia-Dearborn, MI | .465 | Detroit-Livonia-Dearborn, MI |
| .592 | Birmingham-Hoover, AL | .398 | Gary, IN | |
| .529 | Cleveland-Elyria-Mentor, OH | .396 | Birmingham-Hoover, AL | |
| .520 | Gary, IN | .396 | St. Louis, MO-IL | |
| .520 | Baton Rouge, LA | .395 | Cleveland-Elyria-Mentor, OH | |
| .509 | St. Louis, MO-IL | .364 | Dayton, OH | |
| .499 | Milwaukee-Waukesha-West Allis, WI | .354 | Milwaukee-Waukesha-West Allis, WI | |
| .491 | Chicago-Naperville-Joliet, IL | .338 | Chicago-Naperville-Joliet, IL | |
| .488 | Dayton, OH | .311 | Baton Rouge, LA | |
| .488 | Memphis, TN-MS-AR | .311 | Newark-Union, NJ-PA |
The lesson here, which census tract analyses alone cannot convey, is apparent in the Philadelphia/St. Louis and Nassau-Suffolk/Jacksonville pairs of segregation profiles in Figure 2. Because some metro areas are more segregated at a micro scale while others are more segregated at a macro scale, the slopes of these areas frequently diverge to such an extent that their curves cross. Crossing tends to be easier when the distribution of segregation levels is tightly packed, as in the case of Hispanic-white and Asian-white segregation. In that situation, no one metropolis will qualify as most segregated across all types of local environments. A single candidate (Gary, IN, for black-white segregation or Detroit-Livonia-Dearborn for multi-group segregation) is more likely to surface when profiles are flatter and widely spaced, although specific metro rankings will still vary by scale.
Determinants of Segregation
The scale dependence of racial segregation patterns leads to a logical follow-up question: are the determinants of segregation scale-dependent as well? In search of an answer, we turn to the Farley and Frey (1994) framework. Although the framework has been shown to have some empirical validity for tracts and block groups, it is unclear whether it accounts for levels of segregation measured across different-sized local environments. We initially evaluate the performance of the Farley-Frey structural predictors by regressing H500 through H4000 on them in separate models for the four racial group combinations. We then estimate models in which net micro-segregation, or net micro H, serves as the dependent variable. Combined with the results from the H500 and H4000 models, the net micro H regression coefficients enable us to decompose each predictor's total influence on small-environment segregation into portions associated with racial compositional patterns occurring over short and long distances. We emphasize this decomposition exercise because it offers a novel way to think about the scalar complexities of segregation.
Most of the original Farley-Frey structural characteristics are incorporated in the regression models, along with a few new ones from studies testing revised versions of the framework (Farrell 2005; Iceland and Nelson forthcoming; Iceland and Scopilliti forthcoming; Logan et al. 2004; Timberlake and Iceland 2007; Wilkes and Iceland 2004). Two of the characteristics have proven sufficiently influential in past research to qualify as baseline predictors. First, we tap the regional location of the sample metropolitan areas with Northeast, Midwest, and South dummy variables. The West is an appropriate reference category due to its generally lower levels of segregation and to the longer histories of residential discrimination and exclusion in the other regions. Second, metropolitan size is operationalized as the logarithm (base 10) of total population in 2000. Previous work has shown metro size to be positively related to segregation, perhaps a consequence of the established minority enclaves and more competitive housing markets in larger areas.
We organize the remaining characteristics into four sets of explanatory variables that depict a metro area's racial/ethnic composition, socioeconomic status, housing supply, and functional specialization as of the 2000 census.9 Segregation is hypothesized to rise with minority group size, reflecting preferences for own-group neighbors or, alternatively, the logic of the group threat hypothesis (Blalock 1967). It should fall with minority status advantages (in income and homeownership) and the availability of new housing, which is less likely than housing in older neighborhoods to suffer from a racialized reputation. Finally, segregation should be lower in metropolises specializing in functional domains (e.g., the military, government, higher education) known to value racial equality, but higher when the retirement function dominates, presumably because retirement communities are less affordable to minorities and are occupied by elderly whites who prefer racial homogeneity. Measurement details and descriptive statistics for all 16 predictors are reported in the appendix (Table A-1).
Table A-1.
Description of Predictorsa
| Mean | Standard deviation | Minimum | Maximum | |
|---|---|---|---|---|
| Baseline | ||||
| West (ref.) | .220 | .416 | .000 | 1.000 |
| Northeast | .230 | .423 | .000 | 1.000 |
| Midwest | .200 | .402 | .000 | 1.000 |
| South | .350 | .479 | .000 | 1.000 |
| Metro population (000s) | 1,732 | 1,665 | 561 | 11,296 |
| Racial/ethnic composition | ||||
| % black | .123 | .094 | .004 | .433 |
| % Hispanic | .133 | .159 | .007 | .884 |
| % Asian | .042 | .065 | .005 | .538 |
| % foreign-born | .114 | .091 | .020 | .509 |
| Socioeconomic status | ||||
| Black/white incomeb | .687 | .125 | .475 | 1.103 |
| Hispanic/white incomeb | .759 | .110 | .493 | 1.056 |
| Asian/white incomeb | 1.057 | .181 | .730 | 1.772 |
| Minority/white incomeb | .921 | .088 | .492 | 1.000 |
| Black ownershipc | .423 | .083 | .154 | .649 |
| Hispanic ownershipc | .431 | .116 | .169 | .715 |
| Asian ownershipc | .532 | .087 | .352 | .748 |
| Minority ownershipc | .460 | .090 | .239 | .712 |
| Housing supply | ||||
| % new constructiond | .169 | .078 | .047 | .483 |
| Functional specialization | ||||
| % retiremente | .121 | .031 | .072 | .285 |
| % manufacturingf | .124 | .048 | .032 | .260 |
| % governmentg | .133 | .033 | .081 | .229 |
| % collegeh | .085 | .016 | .038 | .126 |
| % militaryI | .008 | .017 | .000 | .112 |
N = 100 metro areas.
Ratio of racial group's median household income to white median household income.
Group-specific home ownership rate.
Proportion of housing units built during 1990s.
Proportion of population aged 65 and over.
Proportion of labor force (16+ years) employed in manufacturing.
Proportion of labor force (16+ years) employed by local, state, federal government.
Proportion of adult population enrolled in college, grad or professional school.
Proportion of labor force (16+ years) in the armed forces.
Preliminary experimentation has led us to pursue a hybrid model-building strategy. For each combination of racial groups, we regress each scale-specific segregation measure (H500, H1000, H2000, and H4000) on the regional dummies and metropolitan population size simultaneously, then allow predictors representing the other explanations to enter in stepwise mode if they are significant. Any predictor that achieves significance in at least one scale-specific equation is subsequently included in all equations for that particular group combination. Thus, none of the models in Table 3 contains the full complement of structural characteristics, yet the models for each group combination are specified identically and all models throughout the table share the baseline predictors at a minimum. This strategy strikes us as optimal, generating robust results in a parsimonious manner while facilitating comparisons by scale.
Table 3.
Determinants of Segregation by Local Environment Size and Racial Group Combinationa
| Group combination/predictor | Scale-specific segregation |
Net micro-segregationb (Net micro H) |
H500 componentsc |
||||
|---|---|---|---|---|---|---|---|
| Macro (H4000) | Micro (<H4000) | ||||||
| H500 | H1000 | H2000 | H4000 | ||||
| Black-White | |||||||
| Northeast | .109*** | .099*** | .074** | .037 | .072*** | .339 | .661 |
| Midwest | .199*** | .198*** | .185*** | .156*** | .043*** | .784 | .216 |
| South | .070** | .056* | .038 | .019 | .051*** | .271 | .729 |
| Metro population (log10) | .083** | .090** | .093** | .093*** | −.010 | 1.120 | −.120 |
| % black | .873*** | .861*** | .802*** | .712*** | .161*** | .816 | .184 |
| % Hispanic | .110 | .115 | .128* | .135* | −.026 | 1.227 | −.227 |
| % retirement | 1.121*** | 1.070*** | .887** | .570* | .551*** | .508 | .492 |
| % military | −1.650*** | −1.597** | −1.516** | −1.273** | −.377 | .772 | .228 |
| Intercept | −.395* | −.468* | −.501** | −.501** | .106 | 1.268 | −.268 |
| Adjusted R2 | .727 | .708 | .675 | .634 | .646 | ||
| Hispanic-White | |||||||
| Northeast | .064** | .061** | .047* | .022 | .043*** | .344 | .656 |
| Midwest | .000 | −.002 | −.006 | −.015 | .016 | n.a. | n.a. |
| South | .002 | −.016 | −.033 | −.044* | .046*** | −22.000 | 23.000 |
| Metro population (log10) | .049 | .060* | .069** | .067** | −.017 | 1.367 | −.367 |
| % Hispanic | .253*** | .255*** | .244*** | .212*** | .040 | .838 | .162 |
| % black | .238* | .242* | .243* | .241** | −.003 | 1.013 | −.013 |
| Hispanic/white income | −.174* | −.176* | −.156 | −.121 | −.053 | .695 | .305 |
| Hispanic ownership | −.226** | −.169* | −.101 | −.017 | −.209*** | .075 | .925 |
| % manufacturing | .458* | .417* | .364* | .308* | .150 | .672 | .328 |
| % college | −1.289* | −1.123 | −1.012 | −.943 | −.346 | .732 | .268 |
| Intercept | .155 | .027 | −.100 | −.179 | .334*** | −1.155 | 2.155 |
| Adjusted R2 | .423 | .415 | .389 | .346 | .566 | ||
| Asian-White | |||||||
| Northeast | −.009 | −.017 | −.026 | −.035* | .026** | 3.889 | −2.889 |
| Midwest | −.011 | −.017 | −.021 | −.023 | .012 | 2.091 | −1.091 |
| South | .007 | .000 | −.006 | −.011 | .018* | −1.571 | 2.571 |
| Metro population (log10) | −.011 | .007 | .02 | .026* | −.037*** | −2.364 | 3.364 |
| % Asian | .220* | .244** | .228** | .170* | .050 | .773 | .227 |
| % black | .118 | .105 | .090 | .090 | .028 | .763 | .237 |
| Asian/white income | .077** | .065* | .053* | .036 | .041** | .468 | .532 |
| Asian ownership | −.176** | −.153** | −.116* | −.067 | −.109*** | .381 | .619 |
| % new construction | −.118 | −.136 | −.139 | −.125 | .007 | 1.059 | −.059 |
| % retirement | −.264 | −.332* | −.363* | −.349* | .084 | 1.322 | −.322 |
| Intercept | .324** | .187 | .078 | .004 | .319*** | .012 | .988 |
| Adjusted R2 | .181 | .230 | .284 | .314 | .504 | ||
| White-Black-Hispanic-Asian | |||||||
| Northeast | .041* | .027 | .006 | −.019 | .060*** | −.463 | 1.463 |
| Midwest | .104*** | .098*** | .087*** | .066*** | .038*** | .635 | .365 |
| South | .035 | .022 | .007 | −.008 | .043*** | −.229 | 1.229 |
| Metro population (log10) | .028 | .036 | .044* | .051** | −.023* | 1.821 | −.821 |
| % black | .675*** | .656*** | .607*** | .547*** | .128** | .810 | .190 |
| % Hispanic | .208*** | .215*** | .213*** | .206*** | .002 | .990 | .010 |
| % foreign-born | −.375*** | −.363*** | −.344*** | −.324*** | −.051 | .864 | .136 |
| % new construction | −.249** | −.283** | −.287** | −.246** | −.003 | .988 | .012 |
| % retirement | .572** | .537** | .459* | .341 | .231* | .596 | .404 |
| % military | −1.165*** | −1.101*** | −1.009*** | −.839** | −.326* | .720 | .280 |
| Intercept | .047 | −.025 | −.096 | −.162 | .209** | −3.447 | 4.447 |
| Adjusted R2 | .760 | .750 | .724 | .679 | .623 | ||
p<.05
p<.01
p<.001
N = 100 metro areas; entries in columns are unstandardized regression coefficients.
Dependent variable operationalized as H500 – H4000; coefficients equivalent to B500 – B4000.
See text for description of decomposition procedure.
The OLS regressions in the first four columns of Table 3, which exhibit numerous significant coefficients in the hypothesized direction, confirm the broad applicability of the Farley-Frey framework.10 Some predictors, however, do not enter the models for certain group combinations (eight of the 16 are omitted from the black-white models and six of 16 from the rest). And despite the cross-scale importance of many predictors, others achieve statistical significance only at certain scales (e.g., the income and home ownership variables in the Hispanic-white equations and metropolitan population in the multi-group equations). Just two pairs of equations in the table—for black-white H500 and H1000 and for Asian-white H1000 and H2000—include exactly the same significant coefficients with the same signs. The proportions of variance explained in H500 through H4000, which tend to be greatest for the black-white and multi-group combinations, taper off moderately as scale increases. Asian-white R2s constitute the sole exception, growing in magnitude as one moves from small- to large-radius local environments.
Regression Decomposition
Overall, the contrasts in the left half of Table 3 are sharpest between the H500 and H4000 models for all group combinations, whether focusing on R2s or significant predictors. But recall that some portion of the variation in H500 may reflect the macro-scale racial texture of a metropolis. This is where our net micro-segregation measure proves useful. Net micro H refers to the part of total segregation among individuals' small local environments that is not attributable to large-environment segregation (net micro H = H500 - H4000). If we fit the same regression model for net micro H as we already have for H500 and H4000, it can easily be shown that the regression coefficients from the net micro H and H4000 models will sum to the coefficients in the H500 model; that is, for each predictor, B500 = B4000 + net micro B. This allows us to calculate how much of the overall effect of some predictor X on small-environment segregation (B500) is due to the association between X and macro- or large-environment segregation (B4000/B500) and how much is due to the association between X and any micro-segregation existing on top, or net, of the large-environment patterns (net micro B/ B500). These macro and micro components from the decomposition of the H500 coefficients are reported in the last two columns of Table 3, right after the net micro-segregation models in the fifth column (for a proof of the regression decomposition, see Reardon and Yun 2001.).
Selected black-white results (top panel) nicely convey the value added by our decomposition approach, identifying five possible relationships between the predictors of small-environment and large-environment segregation. First, as in the case of metropolitan population size, the significant impact of a predictor on black-white H500 may be completely accounted for by the predictor's association with the large-scale racial patterning manifested in H4000. (Note the insignificance of the metro size coefficient in the net micro-segregation model and the dominance of the macro component over the micro component in columns 6 and 7.) A second possibility is apparent for the proportion black measure, which—like metro size—positively and significantly influences H500 primarily through macro-scale patterns but—unlike metro size—also registers a significant effect on net micro H. Functional specialization as a retirement center represents a third possibility; its effects on both H500 and net micro H are positive and significant, with the former effect consisting of roughly equal macro and micro components. The fourth possible scenario, illustrated by the Northeast dummy variable, occurs when the coefficients in the H500 and net micro H models are significant and comparable in magnitude; this means that the region's influence on H500 is not a product of its association with large-environment segregation. Fifth and finally, a characteristic such as proportion Hispanic may only shape black-white segregation at more macro-geographic scales, having no relevance to either H500 or net micro H.
One key insight from Table 3 concerns the impressive frequency of the first two scenarios, when the impact of a Farley-Frey predictor on small-environment segregation is driven primarily if not entirely by its connection to racial residential patterns evident over greater distances. The multi-group results (bottom panel) communicate this insight most clearly. Of the eight significant predictors of white-black-Hispanic-Asian segregation in the H500 model, three (proportion Hispanic, proportion foreign born, and new housing construction) do not influence net micro-segregation, and another four (Midwest location, proportion black, and retirement and military functional specializations) operate mainly via their association with macro-segregation (see columns 6 and 7). One-half of the significant H500 predictors from both the black-white and Hispanic-white models experience a similar fate.
Measures of metropolitan racial composition stand out because they consistently affect segregation through macro-scale processes. Each minority group appears more segregated from whites within every type of local environment when its members constitute a larger proportion of the metro population, but this relationship can be traced to racial patterns at the macro level. We suspect that sizeable minority concentrations facilitate the development of spatially expansive ghettos, barrios, and enclaves. Similarly, the positive influence of metropolitan population size on smaller-scale segregation is due to its association with macro-segregation (H4000). This finding, which holds across all group combinations, takes an interesting twist in the Asian-white and multi-group cases: the coefficient for metro size in the net micro H model is significantly negative, indicating that bigger metropolitan areas have less micro-scale racial variation than do smaller areas. Perhaps as size increases, fine-grained differentiation of urban space becomes impractical or unnecessary, and racial patterns within subregions give way to differences between them.
What explains variation in net micro-segregation, the portion of H500 not due to the distribution of racial groups across 4,000m environments? According to the results in the right half of Table 3, regional location plays an important role. For all group combinations, metropolitan areas in the Northeast and the South are more micro-segregated than their Western counterparts, usually because of smaller-scale, localized fluctuations in racial composition. The Midwest exhibits higher micro-segregation as well, though the Midwestern influence—limited to black-white and multi-group segregation—has both local (micro) and macro components, with the latter dominating. Minority home ownership is another significant determinant of net micro-segregation among Hispanics and Asians: as the proportion of owners in each group rises, their segregation from whites declines. This negative effect, which confirms the neighborhood access-enhancing benefits of socioeconomic advantage, has both micro- and macro-scale components but is rooted more firmly in the former.11
Net micro-segregation is also influenced by metropolitan functional specialization as a retirement center. Both black-white and multi-group micro-segregation scores tend to be elevated in senior citizen-oriented metro areas, a finding that may reflect the racial attitudes of older whites and the economic selectivity of many retirement communities. Military specialization has the opposite impact, lowering multi-group micro-segregation in metropolises that boast a large military presence. Yet it does so more through its association with large-scale than small-scale racial patterns. Indeed, in the black-white case the negative effect of military specialization on H4000 is sufficiently strong to preclude any significant effect on net micro-segregation. This link to variation in racial composition over greater distances could be a manifestation of how the “equal opportunity” commitment of the armed forces plays out in metropolitan-wide housing markets. Macro-scale processes are further evident from a comparison of the manufacturing coefficients in the Hispanic-white H4000 and net micro-segregation models: manufacturing specialization heightens Hispanics' large-environment segregation (but not micro-segregation) from whites. One tentative interpretation here is that the modest wages from employment in “sweatshop” industries may restrict Hispanics to sprawling working-class residential districts with a heavy co-ethnic presence, as typified by East Los Angeles.
In summary, the models in the fourth and fifth columns of Table 3 allow us to tell a more nuanced story about racial segregation than has heretofore been possible. The Farley-Frey framework explains large-scale segregation (H4000) primarily in terms of metropolitan population size and minority group representation. However, net micro-segregation is due for the most part to regional differences, with home ownership rates of secondary importance for some group combinations. A few forms of functional specialization have scattered effects on micro- and/or macro-segregation. Interestingly, non-trivial proportions of variance wind up being accounted for at both geographic scales, but distinct sets of structural predictors are responsible.12
Comparisons with Aspatial Measures
The worth of any new approach can be weighed in part by comparing it to conventional practice. In the present instance, the issue is whether our analysis of segregation across flexible local environments yields lessons beyond those from research that relies upon fixed spatial units such as census tracts. The most direct comparison would be between results for the spatial version of the information theory index (the H statistic featured in previous sections) and its aspatial counterpart calculated for tracts. But the dominant position of the index of dissimilarity (D) in the residential segregation literature suggests that stacking up spatial H against tract-based D also has merit, even though H and D do not capture the evenness dimension of segregation in identical fashion. To be on the safe side, we pursue both types of comparisons in a brief re-examination of our principal findings.
With respect to segregation patterns, the aspatial H means for each group combination (not shown) closely mirror those for H2000 in Table 1. Likewise, the means for D adhere to the same order that we have already documented for spatial H, with black-white segregation highest, Asian-white lowest, and Hispanic-white intermediate. While Spearman rank-order correlations between spatial H and the two aspatial measures (calculated across metropolitan areas) reveal a strong correspondence overall, H500 and H4000 exhibit few correlation coefficients with aspatial H and D that reach .9. And in race-specific terms, the Asian-white coefficients are consistently more modest than those for the rest of the group combinations, falling in the .77-.89 range.
As the less-than-perfect correlations hint, rankings of individual metro areas differ by type of segregation measure. Proceeding conservatively, we have compared the 10 metropolises with the highest tract-based D scores to the top 10 on H1000 (see Table 2), the scale-specific measure with which D is most strongly associated. The Asian-white rankings from this exercise are instructive. Baton Rouge, the metro area with the highest D, ranks third on H1000, and Boston-Quincy and Pittsburgh (second and third highest Ds) rank 16th and 18th respectively on H1000. Meanwhile, New Orleans, at the top of the H1000 standings, does no better than seventh on D. Similar contrasts in rank exist for other racial group combinations and between spatial and aspatial H top 10 lists. These contrasts grow more pronounced when tract-based D and H values are compared to Hs calculated across the smallest and largest local environments.
Finally, our scale-specific analysis of segregation determinants in Table 3 can be juxtaposed with similar stepwise regressions in which tract-based H and D serve as the dependent variables (see Section G of the Online Supplement). For black-white and Hispanic-white segregation, the results from these tract-based regressions overlap substantially with the H500, H1000, and H2000 models, both in terms of variance explained and predictors identified. More intriguing, however, are the numerous points of divergence. For example, the significant determinants of aspatial H and D bear only limited resemblance to those of either large-environment segregation (H4000) or net micro-segregation for all group combinations. In the Asian-white case, none of our scale-specific models look very much like the aspatial models. Overall explanatory performance diverges as well: the R2s obtained in the Hispanic-white and Asian-white net micro-segregation equations surpass the aspatial H and D R2s for the same groups by five to 15 percentage points. Such comparisons reinforce the value of being able to distinguish between macro-segregation and net micro-segregation, the predictors of which may differ.
CONCLUSION
Our spatially refined treatment of racial segregation offers a promising way to address the scale and proximity challenges faced in research that relies on tracts or other fixed census aggregations. Nevertheless, a critic might reasonably ask whether the new approach is worth the effort, given that many previous conclusions about segregation appear to be supported. In response to the critic, consider the well-known fact that black-white segregation exceeds that of other group combinations. Our analysis confirms this but shows further that it is due mainly to how blacks and whites are distributed across large sub-regions of the metropolis. That is, macro-segregation contributes more to black-white segregation than to Hispanic-white or Asian-white segregation among small local environments. Another amply documented finding, the influence of regional location, proves more complicated upon closer inspection. As hypothesized, segregation tends to be higher outside the West, but our regression decomposition identifies different dynamics at work by region: smaller-scale racial variations are responsible for higher net micro-segregation in Northeastern and Southern metro areas while macro patterns drive Midwestern micro-segregation. Of broader importance are the distinct sets of significant predictors in the fourth and fifth columns of Table 3, which highlight the extent to which the explanation of segregation depends on geographic scale. By proceeding at multiple scales, additional insights can be gained that enrich the results from conventional scholarship.
A critic could also question the practicality of our approach because of its complex, computationally intensive nature. The good news is that we have established a website (www.pop.psu.edu/mss) for anyone who wishes to study segregation with the methods described here. Accessible through a download link at the website are a user guide, estimated run times, and our SpatialSeg program (in Visual Basic for Applications code, with ArcGIS implementation). The program, which requires data and shapefiles as input, offers numerous options for customizing one's analysis, including decisions about local environment size, group combination, and segregation statistic (H, D, P*, etc.). While flexible, the program is not without limitations. It assumes, for example, that all people can move freely throughout their local environments despite the irregular distribution of highways, railroad tracks, parks, bodies of water, and other barriers. Research by Grannis (1998) underscores the fallacy of this assumption, suggesting that discontinuities in local street networks may affect racial housing patterns (for a similar argument about railroad tracks, see Ananat 2007). In principle, the increasing availability of spatial databases, coupled with enhancements to our program, should allow us to incorporate a variety of barriers in the future so that segregation scores can be calculated across more realistic terrains.
Another step toward heightened realism would entail reconceptualizing proximity to better reflect social rather than physical (Euclidian) distance. If social distance is partly a function of metropolitan development patterns, then local environments of identical physical size in, say, New York (a compact, densely settled metropolis) and Nashville (more spread out) may not be directly comparable. On average, more “action” of all kinds—businesses, institutions, and housing units—will be packed into the New York egocentric neighborhood, a fact that could obscure fine-grained variations in racial composition even within a 500m radius. In Nashville, the preponderance of single-unit dwellings and large lots yields fewer potential neighbors (whether of the same or a different race) at every scale. Alternative proximity functions based on population density or travel time could help build social distance into our approach, although implementation of these metrics remains daunting.
An even greater need exists for scale-specific theorizing about segregation, a task beyond the scope of the present paper.13 By way of preview, however, we propose that micro- and macro-segregation (and the relation between the two) be conceived as the product of forces capable of carving up territory inside metropolitan boundaries. A good place to start is the natural environment, the topographic (e.g., hills, valleys, ridges) and hydrologic (rivers, lakes, bays) features of which establish the broad contours within which other, human-generated influences on segregation operate.14 Among the human influences we have in mind are (1) the transportation grid, (2) housing policies and practices (zoning, actions of lenders and real estate agents, etc.), (3) the degree of fragmentation among school districts, municipalities, and similar jurisdictions, (4) the spatial distribution of employment nodes and non-residential land uses, and (5) different types of residential preferences (for neighborhood racial homogeneity, nearness to work, or a particular housing size or style). Like the natural environment, each of these factors differentiates the metropolis to a greater or lesser extent. Finer differentiation—a metropolitan “jigsaw puzzle” comprising numerous small “pieces” of meaningful space—should increase the likelihood that racial composition changes over shorter distances and that micro-segregation prevails. Conversely, fewer bigger puzzle pieces portend a macro-segregated scenario in which variations in the racial mix are manifested across larger local environments, all else equal.
Of course, all else may not be equal. Conventional research and our own results, for instance, demonstrate that when blacks, Hispanics, or Asians constitute a high proportion of the metro population, they are more segregated from whites. But what if we also knew something about how members of a minority group are spread throughout the metropolis? If the group is extensively suburbanized, implying that members have gained entry to desirable housing and neighborhoods, we might anticipate diminished levels of segregation. Moreover, the simple fact of dispersion might produce a segregation profile marked by a flatter slope (assuming that racial composition achieves stability over longer distances) or by a steeper one (assuming that suburbanized group members recongregate in homogeneous yet decentralized enclaves). The message here is that spatially specific information about potential independent variables could be helpful for fleshing out a scale-tuned theory of segregation.
As theoretical work progresses, more thought must be devoted to the consequences as well as the causes of racial segregation by scale. The evidence summarized earlier concerning metropolitan variation in micro- and macro-segregation takes on added significance insofar as the consequences of these types of segregation differ across categories of residents. At the extremes of the age continuum, the restricted mobility of young children and the elderly hints that their exposure to smaller as opposed to larger local environments may have fateful effects on health, safety, and other dimensions of well-being. Teenagers' educational performance and their attitudes and behaviors may be responsive primarily to intermediate-sized local environments that approximate middle school or high school attendance zones. For mobile, working-age adults, the often far-flung nature of jobs should make macro-environments especially salient. Whether most racial groups, or most members of any racial group, experience the same age- and scale-specific outcomes of residential segregation remains an open question. Yet it is this kind of question that should motivate efforts to pursue a spatially nuanced understanding of the phenomenon.
Note that the implications of our approach extend past racial segregation per se. We are currently in the process of developing scale-sensitive measures of income segregation (Reardon et al. 2006), and life cycle segregation deserves attention as well. More generally, the replacement of tracts with egocentric local environments allows investigators to think in a precise manner about the linkages between inequality and neighborhood circumstances: namely, how the nested settings that surround one's home can shape both exposure to risk and access to opportunity. Downey's (2006) GIS-based analysis of racial and income differences in proximity to an environmental hazard (industrial pollution) nicely exemplifies the risk orientation, which could also be applied to crime, undesirable land uses (e.g., vacant lots, abandoned buildings), or similar indicators of disorder. On the opportunity side of the coin, a household's quality of life is likely affected to some extent by the institutional resources (schools, churches, grocery stores, health clinics, daycare centers, etc.) available nearby (Matthews, Detwiler, and Burton 2005; Sastry et al. 2002; Zenk et al. 2005). Determining what “nearby” means in local environment terms for each type of resource (or risk) and social group strikes us as a crucial issue across a range of substantive topics. Fortunately, the prospects for resolving it should continue to improve as spatially flexible concepts and methods of the sort introduced here, along with a growing supply of geocoded data, permit sociologists to move beyond the census tract.
Supplementary Material
Footnotes
Grants from the National Science Foundation (SES-0520400 and SES-0520405) and the Penn State Children, Youth, and Families Consortium have made this research possible. Additional support has been provided by the Penn State Population Research Institute (PRI), which receives core funding from the National Institute of Child Health and Human Development (R24-HD41025). We thank David Pemberton of the U.S. Census Bureau for his insights into census tract history, Steve Graham and Yosef Bodovski of PRI for their programming and technical assistance, and Avery Guest, Nancy Landale, Eric Silver, Katherine White, and the ASR referees and editors for their valuable feedback on previous drafts.
A discussion of how the census tract rose to prominence and why we give it priority over other types of spatial units can be found in Section A of the Online Supplement to this article, accessed at www2.asanet.org/journals/asr/xxx.
A desire to create homogeneous units could lead the committees, consciously or otherwise, to take population composition into account when delineating tract boundaries. This tendency, which has received official Census Bureau encouragement in the past (White 1987:288-98), might serve initially to align census geography with the metropolitan racial landscape. Over time, however, residential mobility and size-induced boundary adjustments erode the original level of compositional coherence, generating significant racial diversity within many tracts (for suggestive evidence, see Allen and Turner 1995; Fasenfest, Booza, and Metzger 2004). And our main criticism still stands: relying on any single type of bounded unit —irrespective of the criteria used to define that unit—obscures issues of scale in segregation research.
Previous investigators have employed multiple territorial units—including some combination of blocks, block groups, tracts, places (e.g., central cities and suburbs), metropolitan areas, states, and regions—to analyze segregation at different scales (Farrell 2008; Fischer et al. 2004; Massey and Hajnal 1995; Wong 2004). Their work, while useful, is restricted to census aggregations, the boundaries of which may or may not adequately encompass the residential patterns of interest. Moreover, as we have seen with tracts, a single type of aggregation can come in many sizes, rendering its “scale” uncertain.
For the sake of illustration, imagine a metro area bisected by a wide river, with all blacks living on one side of the river and all whites on the other. Micro-segregation would be high in this instance: the racial mix of small local environments (either all-black or all-white) differs markedly from that of the metropolis as a whole, even though racial composition on both sides of the river does not change at all over short distances. In sum, there is substantial micro-segregation, but it is due to variation in racial composition over long rather than short distances. Later we describe a decomposition method that separates out that part of micro-segregation attributable to larger-scale segregation.
All other groups, including persons who report two or more races, have been dropped. One drawback of the Summary File 1 data is that they encompass institutionalized as well as non-institutionalized members of each racial group. Given our need for block-level data, however, no alternative exists. (Summary File 3 would allow us to restrict analysis to the non-institutional population, but it only provides counts down to the block-group level.) We use block-level information obtained from GeoLytics (2003).
In general, H is highly correlated with D and has many of the same desirable properties (e.g., scale interpretability, organizational/locational equivalence, group size/density invariance) but better satisfies transfer and exchange criteria, which pertain to how segregation scores should respond to the movement of group members.
Similar aggregation effects for fixed spatial units are reported in Taeuber and Taeuber (1969:220-31), Van Valey and Roof (1976), and Wong (2004).
Our claim here follows from the results in Table 1. For the 100 sample metro areas, the average black-white versus Hispanic-white difference in H4000 is .125. This difference in H across 4,000m local environments constitutes the majority of the difference in H across 500m environments (the mean H500 difference is .165). So it seems plausible that, by setting macro-segregation equal, we could drastically narrow if not eliminate the black-white versus Hispanic-white gap in micro-segregation.
Because degrees of freedom are at a premium in an analysis with only 100 cases, some Farley-Frey characteristics that register few significant effects in past research (such as age of the metropolitan area) have been omitted, and other characteristics are treated in condensed fashion (e.g., a single measure of manufacturing specialization rather than separate durable and non-durable manufacturing indicators).
It is technically inappropriate to use OLS regression for dependent variables such as ours, which have a truncated range of values (0-1). However, an inspection of residual plots for all group combinations reveals no major violations of regression assumptions due to truncation. Also, both histograms and skewness/kurtosis statistics suggest that, with few exceptions, the scale-specific Hs and the net micro H scores approximate normal distributions.
The ratio of minority to white income, a more direct socioeconomic status measure, only shapes Asians' net micro-segregation, and it takes an unexpected (positive) sign. We speculate that relatively affluent Asian populations may self-segregate, insofar as their members are better able to fulfill own-group residential preferences.
The limited overlap among predictors should not come as a great surprise, given the modest correlations between net micro-segregation (net micro H) and macro-segregation (H4000). For blacks and whites, r = .28; for Hispanics and whites, r = .03; for Asians and whites, r = .02; and for the multi-group combination, r = .34. The correlation between net micro H and H500 is larger but still moderate in magnitude (mean r across all group combinations = .57).
This need occasionally receives attention in other substantive areas. Hipp (2007), for example, considers which geographic scale is most appropriate for understanding the effects of neighborhood characteristics on perceived crime and disorder, although his analysis is limited to fixed census units (blocks and tracts).
It seems likely that communities known for their distinctive natural settings (think Seattle, San Francisco, Cincinnati, Pittsburgh, or Boston) will be more micro-segregated and less macro-segregated than their metropolitan counterparts situated on flatter, relatively featureless ground.
Contributor Information
Barrett A. Lee, Pennsylvania State University
Sean F. Reardon, Stanford University
Glenn Firebaugh, Pennsylvania State University.
Chad R. Farrell, University of Alaska-Anchorage
Stephen A. Matthews, Pennsylvania State University
David O'Sullivan, University of Auckland.
REFERENCES
- Acevedo-Garcia Dolores, Lochner Kimberly A., Osypuk Theresa L., Subramanian SV. Future Directions in Residential Segregation and Health Research: A Multilevel Approach. American Journal of Public Health. 2003;93:215–21. doi: 10.2105/ajph.93.2.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen James P., Turner Eugene. Ethnic Differentiation by Blocks Within Census Tracts. Urban Geography. 1995;16:344–64. [Google Scholar]
- Ananat Elizabeth O. NBER Working Paper 13343. National Bureau of Economic Research; Cambridge, MA: 2007. The Wrong Side(s) of the Tracks: Estimating the Causal Effects of Racial Segregation on City Outcomes. [Google Scholar]
- Blalock Hubert M. Toward a Theory of Minority Group Relations. John Wiley; New York: 1967. [Google Scholar]
- Brooks-Gunn Jeanne, Duncan Greg J., Lawrence Aber J., editors. Neighborhood Poverty, Vols. 1 and 2. Russell Sage; New York: 1997. [Google Scholar]
- Card David, Rothstein Jesse. NBER Working Paper 12078. National Bureau of Economic Research; Cambridge, MA: 2006. Racial Segregation and the Black-White Test Score Gap. [Google Scholar]
- Charles Camille Zubrinsky. The Dynamics of Racial Residential Segregation. Annual Review of Sociology. 2003;29:167–207. [Google Scholar]
- Charles Camille Zubrinsky. Can We Live Together? Racial Preferences and Neighborhood Outcomes. In: de Souza Briggs X, editor. The Geography of Opportunity: Race and Housing Choice in Metropolitan America. Brookings Institution Press; Washington, DC: 2005. pp. 45–80. [Google Scholar]
- Chaskin Robert J. Defining Neighborhood: History, Theory, and Practice. Chapin Hall Center for Children. University of Chicago; Chicago: 1994. [Google Scholar]
- Cutler David M., Glaeser Edward L. Are Ghettos Good or Bad? Quarterly Journal of Economics. 1997;112:827–72. [Google Scholar]
- Dawkins Casey J. Measuring the Spatial Pattern of Residential Segregation. Urban Studies. 2004;41:833–51. [Google Scholar]
- Downey Liam. Using Geographic Information Systems to Reconceptualize Spatial Relationships and Ecological Context. American Journal of Sociology. 2006;112:567–612. doi: 10.1086/506418?origin=JSTOR-pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellen Ingrid Gould. Is Segregation Bad for Your Health? The Case of Low Birth Weight. In: Gale WG, Pack JR, editors. Brookings-Wharton Papers on Urban Affairs 2000. Brookings Institution Press; Washington, DC: 2000. pp. 203–38. [Google Scholar]
- Environmental Systems Research Institute . ArcGIS: Release 9.2. ESRI; Redlands, CA: 2006. [Google Scholar]
- Farley Reynolds, Frey William H. Changes in the Segregation of Whites from Blacks During the 1980s: Small Steps Toward a More Integrated Society. American Sociological Review. 1994;59:23–45. [Google Scholar]
- Farley Reynolds, Charlotte Steeh Maria Krysan, Jackson Tara, Reeves Keith. Stereotypes and Segregation: Neighborhoods in the Detroit Area. American Journal of Sociology. 1994;100:750–80. [Google Scholar]
- Farrell Chad R. Ph.D. dissertation. Department of Sociology, Pennsylvania State University; University Park, PA: 2005. Urban Mosaics: Multiracial Diversity and Segregation in the American Metropolis. [Google Scholar]
- Farrell Chad R. Bifurcation, Fragmentation, or Integration? The Racial and Geographic Structure of Metropolitan Segregation, 1990-2000. Urban Studies. 2008;45:467–99. [Google Scholar]
- Fasenfest David, Booza Jason, Metzger Kurt. Living Cities Census Series, Center on Urban and Metropolitan Policy. Brookings Institution; Washington, DC: 2004. Living Together: A New Look at Racial and Ethnic Integration in Metropolitan Neighborhoods, 1990-2000. [Google Scholar]
- Fischer Claude S., Gretchen Stockmayer Jon Stiles, Hout Michael. Distinguishing the Geographic Levels and Social Dimensions of Segregation, 1960-2000. Demography. 2004;41:37–59. doi: 10.1353/dem.2004.0002. [DOI] [PubMed] [Google Scholar]
- Fischer Mary J. Shifting Geographies: Examining the Role of Suburbanization in Blacks’ Declining Segregation. Urban Affairs Review. 2008;43:475–96. [Google Scholar]
- Frey William H., Farley Reynolds. Latino, Asian, and Black Segregation in U.S. Metropolitan Areas: Are Multiethnic Metros Different? Demography. 1996;33:35–50. [PubMed] [Google Scholar]
- Frey William H., Wilson Jill H., Berube Alan, Singer Audrey. Metropolitan Policy Program Report. Washington, DC: 2004. Brookings Institution. Tracking Metropolitan America into the 21st Century: A Field Guide to the New Metropolitan and Micropolitan Definitions. [Google Scholar]
- GeoLytics . Census 2000 Short Form Blocks. GeoLytics, Inc.; East Brunswick, NJ: 2003. [Google Scholar]
- Glaeser Edward L., Vigdor Jacob L. Racial Segregation: Promising News. In: Katz B, Lang RE, editors. Redefining Urban and Suburban America: Evidence From Census 2000, Volume I. Brookings Institution Press; Washington, DC: 2003. pp. 211–34. [Google Scholar]
- Grannis Rick. The Importance of Trivial Streets: Residential Streets and Residential Segregation. American Journal of Sociology. 1998;103:1530–64. [Google Scholar]
- Hipp John R. Block, Tract, and Levels of Aggregation: Neighborhood Structure and Crime and Disorder as a Case in Point. American Sociological Review. 2007;72:659–80. [Google Scholar]
- Hu Pat S., Reuscher Timothy R. Summary of Travel Trends. National Household Travel Survey. Federal Highway Administration, U.S. Department of Transportation; Washington, DC: 2004. p. 2001. [Google Scholar]
- Iceland John. Beyond Black and White: Metropolitan Residential Segregation in Multi-Ethnic America. Social Science Research. 2004;33:248–71. [Google Scholar]
- Iceland John, Anne Nelson Kyle. Hispanic Segregation n Metropolitan America: Exploring the Multiple Forms of Spatial Assimilation. American Sociological Review. Forthcoming.
- Iceland John, Scopilliti Melissa. Immigrant Residential Segregation in U.S. Metropolitan Areas, 1990-2000. Demography. Forthcoming. [DOI] [PMC free article] [PubMed]
- Iceland John, Weinberg Daniel H., Steinmetz Erika. U.S. Census Bureau, Series CENSR-3. Government Printing Office; Washington, DC: 2002. Racial and Ethnic Residential Segregation in the United States: 1980-2000. [Google Scholar]
- Jargowsky Paul A., Kim Jeongdai. Political Economy Working Paper. University of Texas at Dallas; Dallas: 2005. A Measure of Spatial Segregation: The Generalized Neighborhood Sorting Index. [Google Scholar]
- Kaplan David H., Holloway Steven R. Scaling Ethnic Segregation: Causal Processes and Contingent Outcomes in Chinese Residential Patterns. GeoJournal. 2001;53:59–70. [Google Scholar]
- Krysan Maria, Farley Reynolds. The Residential Preferences of Blacks: Do They Explain Persistent Segregation? Social Forces. 2002;80:937–80. [Google Scholar]
- Lee Barrett A., Campbell Karen E. Common Ground? Urban Neighborhoods as Survey Respondents See Them. Social Science Quarterly. 1997;78:922–36. [Google Scholar]
- Lieberson Stanley. A Piece of the Pie: Blacks and White Immigrants Since 1880. University of California Press; Berkeley: 1980. [Google Scholar]
- Logan John R. Ethnic Diversity Grows, Neighborhood Integration Lags. In: Katz B, Lang RE, editors. Redefining Urban and Suburban America: Evidence From Census 2000, Volume I. Brookings Institution Press; Washington, DC: 2003. pp. 235–55. [Google Scholar]
- Logan John R., Stults Brian J., Farley Reynolds. Segregation of Minorities in the Metropolis: Two Decades of Change. Demography. 2004;41:1–22. doi: 10.1353/dem.2004.0007. [DOI] [PubMed] [Google Scholar]
- Massey Douglas S., Denton Nancy A. The Dimensions of Residential Segregation. Social Forces. 1988;67:281–315. [Google Scholar]
- Massey Douglas S., Denton Nancy A. American Apartheid: Segregation and the Making of the Underclass. Harvard University Press; Cambridge, MA: 1993. [Google Scholar]
- Massey Douglas S., Hajnal Zoltan L. The Changing Geographic Structure of Black-White Segregation in the United States. Social Science Quarterly. 1995;76:527–42. [Google Scholar]
- Matthews Stephen A., Detwiler James E., Burton Linda M. Geo-Ethnography: Coupling Geographic Information Analysis Techniques with Ethnographic Methods in Urban Research. Cartographica. 2005;40:75–90. [Google Scholar]
- Morrill Richard L. On the Measurement of Spatial Segregation. Geography Research Forum. 1991;11:25–36. [Google Scholar]
- Openshaw Stanley, Taylor Peter. A Million or So Correlation Coefficients: Three Experiments on the Modifiable Area Unit Problem. In: Wrigley N, editor. Statistical Applications in the Spatial Sciences. Pion; London: 1979. pp. 127–44. [Google Scholar]
- Park Robert E. The Urban Community as a Spatial Pattern and a Moral Order. In: Burgess EW, editor. The Urban Community. University of Chicago Press; Chicago: 1926. pp. 3–18. [Google Scholar]
- Peterson Ruth D., Krivo Lauren J., Browning Christopher R. Segregation and Race/Ethnic Inequality in Crime: New Directions. In: Cullen FT, Wright JP, Blevins KR, editors. Taking Stock: The Status of Criminological Theory. Transaction; New Brunswick, NJ: 2006. pp. 169–87. [Google Scholar]
- Reardon Sean F., Firebaugh Glenn. Measures of Multi-Group Segregation. Sociological Methodology. 2002;32:33–67. [Google Scholar]
- Reardon Sean F., Firebaugh Glenn, O'Sullivan David, Matthews Stephen A. A New Approach to Measuring Socio-Spatial Economic Segregation.. Paper presented at Inter-national Association for Research in Income and Wealth Conference; Joensuu, Finland. August.2006. [Google Scholar]
- Reardon Sean F., Matthews Stephen A., O'Sullivan David, Lee Barrett A., Firebaugh Glenn, Farrell Chad R., Bischoff Kendra. The Geographical Scale of Metropolitan Racial Segregation. Demography. Forthcoming. [DOI] [PMC free article] [PubMed]
- Reardon Sean F., O'Sullivan David. Measures of Spatial Segregation. Sociological Methodology. 2004;34:121–62. [Google Scholar]
- Reardon Sean F., Yun John T. Suburban Racial Change and Suburban School Segregation, 1987-1995. Sociology of Education. 2001;74:79–101. [Google Scholar]
- Sampson Robert J., Morenoff Jeffrey D., Gannon-Rowley Thomas. Assessing ‘Neighborhood Effects’: Social Processes and New Directions in Research. Annual Review of Sociology. 2002;28:443–78. [Google Scholar]
- Sastry Narayan, Pebley Anne, Zonta Michela. CCPR Working Paper 033-04. California Center for Population Research, UCLA; Los Angeles: 2002. Neighborhood Definitions and the Spatial Dimension of Daily Life in Los Angeles. [Google Scholar]
- Smith Neil. Scale. In: Johnston RJ, Gregory D, Pratt G, Watts M, editors. The Dictionary of Human Geography. Blackwell; Oxford, UK: 2000. pp. 724–27. [Google Scholar]
- Suttles Gerald D. The Social Construction of Communities. University of Chicago Press; Chicago: 1972. [Google Scholar]
- Taeuber Karl E., Taeuber Alma F. Negroes in Cities: Residential Segregation and Neighborhood Change. Atheneum; New York: 1969. [Google Scholar]
- Theil Henri. Statistical Decomposition Analysis: With Applications in the Social and Administrative Sciences. North-Holland; Amsterdam: 1972. [Google Scholar]
- Timberlake Jeffrey M., Iceland John. Change in Racial and Ethnic Residential Inequality in American Cities, 1970-2000. City & Community. 2007;6:335–65. [Google Scholar]
- Tobler Waldo R. Smooth Pycnophylactic Interpolation for Geographical Regions. Journal of the American Statistical Association. 1979;74:519–30. doi: 10.1080/01621459.1979.10481647. [DOI] [PubMed] [Google Scholar]
- U.S. Census Bureau . United States Census 2000: Participant Statistical Areas Program Guidelines. U.S. Census Bureau; Washington, DC: 1997. [Google Scholar]
- Van Valey Thomas L., Roof Wade Clark. Measuring Residential Segregation in American Cities: Problems of Intercity Comparison. Urban Affairs Quarterly. 1976;11:453–68. [Google Scholar]
- White Michael J. The Measurement of Spatial Segregation. American Journal of Sociology. 1983;88:1008–18. [Google Scholar]
- White Michael J. American Neighborhoods and Residential Differentiation. Russell Sage; New York: 1987. [Google Scholar]
- Wilkes Rima, Iceland John. Hypersegregation in the Twenty-First Century. Demography. 2004;41:23–36. doi: 10.1353/dem.2004.0009. [DOI] [PubMed] [Google Scholar]
- Wilson William J. The Truly Disadvantaged: The Inner City, the Underclass, and Public Policy. University of Chicago Press; Chicago: 1987. [Google Scholar]
- Wilson William J. When Work Disappears: The World of the New Urban Poor. Alfred A. Knopf; New York: 1996. [Google Scholar]
- Wong David W.S. Spatial Indices of Segregation. Urban Studies. 1993;30:559–72. [Google Scholar]
- Wong David W.S. Spatial Dependency of Segregation Indices. Canadian Geographer. 1997;41:128–36. [Google Scholar]
- Wong David W.S. Geostatistics as Measures of Spatial Segregation. Urban Geography. 1999;20:635–47. [Google Scholar]
- Wong David W.S. Comparing traditional and spatial segregation measures: a spatial scale perspective. Urban Geography. 2004;25:66–82. [Google Scholar]
- Wong David W.S. Formulating a General Spatial Segregation Measure. Professional Geographer. 2005;57:285–94. [Google Scholar]
- Zenk Shannon N., Schulz Amy J., Israel Barbara A., James Sherman A., Bao Shuming, Wilson Mark L. Neighborhood Racial Composition, Neighborhood Poverty, and the Spatial Accessibility of Supermarkets in Metropolitan Detroit. American Journal of Public Health. 2005;95:660–67. doi: 10.2105/AJPH.2004.042150. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.