Abstract
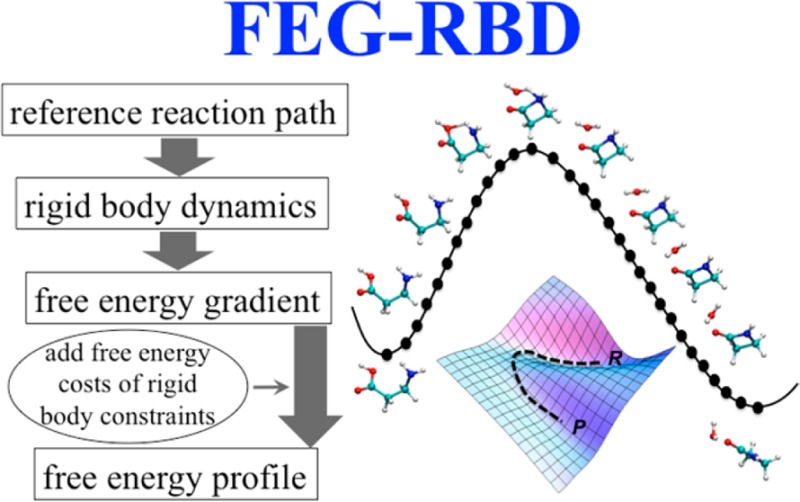
The calculations of potential of mean force along complex chemical reactions or rare events pathways are of great interest because of their importance for many areas in chemistry, molecular biology, and material science. The major difficulty for free energy calculations comes from the great computational cost for adequate sampling of the system in high-energy regions, especially close to the reaction transition state. Here, we present a method, called FEG-RBD, in which the free energy gradients were obtained from rigid body dynamics simulations. Then the free energy gradients were integrated along a reference reaction pathway to calculate free energy profiles. In a given system, the reaction coordinates defining a subset of atoms (e.g., a solute, or the quantum mechanics (QM) region of a quantum mechanics/molecular mechanics simulation) are selected to form a rigid body during the simulation. The first-order derivatives (gradients) of the free energy with respect to the reaction coordinates are obtained through the integration of constraint forces within the rigid body. Each structure along the reference reaction path is separately subjected to such a rigid body simulation. The individual free energy gradients are integrated along the reference pathway to obtain the free energy profile. Test cases provided demonstrate both the strengths and weaknesses of the FEG-RBD method. The most significant benefit of this method comes from the fast convergence rate of the free energy gradient using rigid-body constraints instead of restraints. A correction to the free energy due to approximate relaxation of the rigid-body constraint is estimated and discussed. A comparison with umbrella sampling using a simple test case revealed the improved sampling efficiency of FEG-RBD by a factor of 4 on average. The enhanced efficiency makes this method effective for calculating the free energy of complex chemical reactions when the reaction coordinate can be unambiguously defined by a small subset of atoms within the system.
1. Introduction
The free energy of molecules is an important physical property, as it determines the populations of accessible species (e.g., conformers of reactant and products) in a system, but it is computationally much more expensive to obtain compared to the potential energy. As such, algorithms to calculate the free energy accurately and efficiently1−6 have been under active development in the decades since Kirkwood’s and Zwanzig’s work in 1935 and 1954.7,8 When describing a transition process, e.g., a chemical reaction, it is convenient and often necessary to define one or more reaction coordinates a priori along which the free energy is desired. Using predefined reaction coordinates, a transition or reaction path is computed, and the free energy profile along the path can be obtained with various free energy algorithms. Umbrella sampling is one of the most broadly applied free energy methods to calculate the free energy profile along a reaction path with reference to certain reaction coordinate.9 However, it can be prohibitively expensive to apply umbrella sampling on cases with more than a few degrees of freedom. The use of so-called hyperplane constraints is another useful technique to sample the configuration space within the vicinity of a reference reaction path.10 But caution needs to be paid that the hyperplane constraint is only valid within the region close to the reference path.11 Other methods have been developed to calculate the free energy profile along pathways for target reactions with many degrees of freedom, with a common goal of maximizing sampling along the path and of avoiding wasting computer resources simulating those off-path degrees of freedom that do not contribute significantly to the path free energy.12−15
In contrast to umbrella sampling, in which the free energy gradient can be inferred from the deviation of the ensemble with a restraining harmonic potential, in constrained molecular dynamics the free energy gradient is obtained by computing the constraint force applied during time propagation.16−20 However, the latter has been practical only for simple two body constraints through the use of the popular SHAKE21 algorithm. Nagaoka and co-workers developed free energy gradient based optimization methods22−25 using the pairwise RATTLE algorithm.26 In this work, SHAPE,27 a novel rigid body integrator that is as accurate as SHAKE for two-body constraints but is far more flexible in terms of the number and the types of constraints, is applied in reaction-path free energy calculations based on the constrained molecular dynamics theory. The developed method is referred to as free energy gradient from a rigid body dynamics simulation (FEG-RBD).
Before describing FEG-RBD, let us briefly review the theory of constrained molecular dynamics. For an arbitrary reaction coordinate ξ, the free energy A can be defined as a state function of ξ in a generalized statistical mechanical expression,
| 1 |
where kB is the Boltzmann factor, T is the temperature, and Q is the partition function. The reaction coordinate ξ could be any order parameter that can measure reaction progress unambiguously, such as bond distance, dihedral angle, etc.
According to thermodynamic integration (TI), the free energy difference between two values of the reaction coordinates can be calculated through integrating the derivative of the free energy along the reaction coordinate:
| 2 |
where
| 3 |
The ensemble average of the derivative of the free energy with respect to a general reaction coordinate is also referred to as the mean force. The mean force can be calculated in Cartesian coordinates17 through
| 4 |
The ensemble average ⟨...⟩ in the numerator contains the contribution to the mean force from potential energy term and kinetic energy in term of a logarithmic derivative of the determinant of the Jacobian. V is the potential energy, J is the Jacobian matrix to transform Cartesian coordinates to a set of generalized coordinates including ξ, and Zξ is the so-called metric tensor and defined as
| 5 |
where N is the total number of atoms, mk is the mass of atom k, rk is Cartesian coordinates of atom k, and rk′ is mass-weighted coordinates
| 6 |
Although eq 4 is appealing for its seeming simplicity, the calculation of the right-hand side of this equation is impractical for large systems, because the evaluation of the Jacobian matrix J requires a full set of generalized coordinates.
Equation 4 can be simplified for constrained molecular dynamics in which the reaction coordinate ξ is constrained to a particular value throughout the simulation. The simplified equation reads
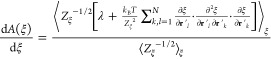 |
7 |
where λ is the Lagrangian multiplier with regard to the constrained reaction coordinate ξ. When using a bond distance as the reaction coordinate, the Lagrangian multiplier λ has the same magnitude as the constrained force with regard to that bond distance. Equation 7 can be generalized for multiple reaction coordinates ξi=1, ..., p, giving eq 8.
| 8 |
Zξ is a p × p matrix defined as
| 9 |
and the Di term reads
| 10 |
Equation 8 provides a theoretical foundation to calculate the mean constrained force for multiple reaction coordinates.
The most straightforward reaction coordinates to be subjected to constraint are bond distances, due to the simplicity and efficiency of using SHAKE21 or similar methods. Simultaneously constraining too many bond distances that are coupled to each other through SHAKE is not practical due to the recursive nature of this method. On the other hand, most complex transitions cannot be properly described merely through several bond distances. It is thus desirable to simultaneously constrain coupled reaction coordinates of various types, such as bond distances, bond angles, and dihedral angles. To the best of our knowledge this has not been practical using any existing method.
2. Method
Constrained dynamics provide an efficient way to sample the potential of mean force. We will apply constraints in the form of a rigid body during the simulation to sample the constraint forces. In the proposed method, the overall reaction is represented as a reaction pathway through a series of structures. Each of the structures is subjected to rigid body molecular dynamics with identified key atoms forming a single rigid body throughout the simulation. Through the use of a rigid body integrator published recently and implemented in the SHAPE module in the CHARMM program package,28 all the degrees of freedom of this rigid body except overall translations and rotations are constrained. The constraint forces for maintaining the rigid body can be integrated to obtain the free energy profile along the reaction pathway.
Consider a system with total N atoms, with M atoms identified as necessary to distinguish between reactant (R) and product (P) structures. If the M atoms form a nonlinear structure, the number of degrees of freedom being constrained is 3M – 6 throughout the simulation with these M atoms constrained as a rigid body. Normally only one or two order parameters are used as reaction coordinates to describe chemical reaction or transition processes. In this case, all 3M – 6 degrees of freedom being constrained are used to describe the reaction process, and therefore considered as implicit reaction coordinates. The transition or reaction between R and P can be represented as a continuous minimum energy pathway (Γ) defined by the M atoms. For any given point on Γ, we have a tangent vector T, and free energy gradient vector F. Both T and F have 3M – 6 components corresponding to the implicit reaction coordinates. Therefore, the free energy difference between R and P can be calculated through a line integral,
| 11 |
This provides a theoretical framework to calculate the free energy profile along the given pathway. Equation 11 can be rewritten with explicit expressions for F and T vectors,
| 12 |
where p, the number of reaction coordinates, is 3M – 6 for a nonlinear rigid body in use.
It is worth noting that in a typical TI calculation, what is being calculated is the free energy difference between two thermodynamic states without having an actual reaction pathway connecting the two states. Usually a coupling parameter λ is used to form a “pathway” to change the simulation from one state to the other alchemically. After TI calculation, no free energy profile can be obtained with free energy reaction barrier information. In the FEG-RBD method, the mean force integration is carried out along an actual reaction pathway with a transition state. The integration of the mean force will provide a complete free energy profile along the pathway, including the reaction barrier information. This is an improvement in FEG-RBD method over the TI calculation.
In practice, the continuous pathway Γ is represented by a series of discrete structures, which can be generated using any chain-of-states methods.29 The integration in eq 12, therefore, can be calculated through summation. All the FEG-RBD simulations in this work were carried out using the CHARMM molecular simulation program and the CHARMM22 force field.30
In this study, each individual FEG-RBD simulation was carried for 10 ns with 1 fs as the time step. To minimize the autocorrelation in the sampled data and collect sufficient amount of data for convergence, the constraint force on a rigid body for every 1000 simulation steps was averaged in each simulation, leading to the mean constraint forces calculated from a total of 10 000 frames in each simulation.
3. Results
3.1. Isosceles Triangle
First, the FEG-RBD method is tested using isosceles triangles composed of three van der Waals (VDW) gas particles (neon was selected arbitrarily). In this case, the two legs of the triangle vary from 2.0 to 5.0 Å with a 0.03 Å step size, while the base is fixed at 2.0 Å. This test case was selected for its simplicity in structure and complexity in reaction coordinate, which corresponds to two order parameters (two legs of the isosceles triangle) with equal values. The theoretical values of the free energy could be calculated as reference due to the structural simplicity of this system. The improved efficiency of FEG-RBD over umbrella sampling could also be demonstrated due to the complexity in the reaction coordinate. In total there were 101 isosceles triangles subjected to FEG-RBD simulations. Each isosceles triangle comprising three neons was subjected to Langevin dynamics at 300 K. In the simulation, the constraint forces are needed to balance the van der Waals interactions among three particles as well as the centrifugal forces with respect to the center of mass of the triangle. The mean constraint forces of each simulation were used to compute the line integral along the reaction path assembled by 101 isosceles triangles to obtain the free energy profile (Figure 1). The simulation for each neon triangle configuration was repeated ten times with different random initial velocities for statistical purposes. The free energy profile was plotted in Figure 1 with error bar calculated from the ten simulations of each configuration. The plotted error bars in Figure 1 are cumulative, which means that the error bars at larger reaction coordinates (i.e., the leg length of the triangle) are the square root of the sum of the variance for each structure with smaller reaction coordinates. The extremely small error bars (which are hardly visible in Figure 1) from only ten simulations of each structure demonstrate the high convergence rate of FEG-RBD method due to its sampling efficiency. Since the line integral of the free energy gradient can only provide the free energy difference, the isosceles triangle with two legs at 5.0 Å was chosen as the reference point with zero free energy.
Figure 1.
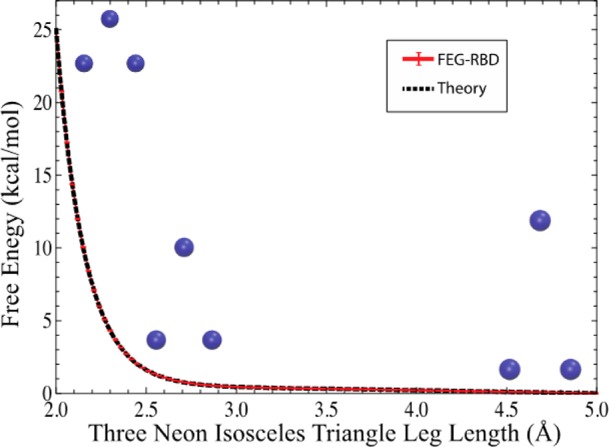
Free energy profile of three neon isosceles triangles.
The theoretical free energy curve with regard to the chosen reaction coordinates is calculated using the following equation of a rigid body,31
| 13 |
where Q is the partition function of the system, h is the Planck constant, A, B, and C are the principal moments of inertia of the rigid body with respect to the center of mass, k is the Boltzmann constant, and T is the temperature. The free energy profile calculated using FEG-RBD method is in excellent agreement within statistical precision with the theoretical results (Figure 1).
Harmonic forces can also be used for free energy sampling as in umbrella sampling, which is one of the most widely applied methods for free energy simulation. It would be helpful if constraint force based and restraint force based free energy methods can be compared for their advantage and disadvantages. Therefore, the free energy difference between two configurations of the three-site VDW system was computed using umbrella sampling and FEG-RBD. For the umbrella sampling simulations the base of the triangle was constrained using SHAKE, while the two equivalent edges were restrained by quadratic potentials. The restraints on two edges actually create two reaction coordinates for free energy sampling, instead of one. This leads to some difficulties in postsimulation analysis, in which only those triangle geometries with the lengths of two edges close to each other enough can be counted.
The force constants were chosen so that the bias potential had a value of one kT directly between bins (ranging from 103 to 759 kcal/mol/Å2). The free energy was evaluated with the WHAM algorithm. The free energy difference between configurations with isosceles edge length 3.0 and 4.5 was computed. To compute the standard error, 15 simulations of 13.3 ns each were executed for every umbrella sampling or FEG-RBD point. To avoid complications with large umbrella sampling force constants, a 0.5 fs time step was used, which will decrease the sampling efficiency by a factor of 2 comparing to a normal 1.0 fs time step.
As shown in Table 1, the standard errors of the FEG-RBD simulations are substantially smaller, on average by a factor of 4. Interestingly, the longer the simulations are, the more significant the improvement of FEG-RBD over umbrella sampling is. This suggests a faster convergence rate of FEG-RBD simulations comparing to the umbrella sampling simulations. Of course, this enhancement will depend to some extent on the binning used by the WHAM procedure,32 essentially, how large a region on the two-dimensional surface is averaged over to approximate the free energy of a point on the path.
Table 1. Standard Errors for the Free Energy Difference between Two Points of the Three-Site van der Waals System from FEG-RBD and Umbrella Sampling Simulations.
| number of simulations | umbrella samplinga | FEG-RBDa | enhanced efficiency |
|---|---|---|---|
| 8 | 0.0098 | 0.0035 | 2.8 |
| 10 | 0.0076 | 0.0027 | 2.8 |
| 12 | 0.0070 | 0.0026 | 2.7 |
| 14 | 0.0090 | 0.0032 | 2.8 |
| 16 | 0.0080 | 0.0020 | 4.0 |
| 18 | 0.0095 | 0.0013 | 7.3 |
| 20 | 0.0081 | 0.0016 | 5.1 |
These errors (in kcal/mol) are lowered with an increasing number of independent simulations without changing the spacing of simulation windows.
Note that each simulation as a recording of ensemble in the isosceles triangles phase space was uncorrelated with the previous one. In a simulation of a system of chemical interest, the standard error of umbrella sampling will likely be determined by a slow correlation time scale of the unconstrained motions. On the other hand, the FEG-RBD removes any possible slow time scale internal processes in addition to more efficient sampling of the path. The most part of the free energy loss resulted from rigid body could be recovered from postprocessing analysis, and will be discussed later in this paper.
3.2. Intramolecular Condensation Reaction of β-Alanine
The FEG-RBD method is then tested using the intramolecular condensation reaction of β-alanine (3-aminopropanoic acid) (see Scheme 1). This system was selected to represent a typical chemical reaction, for which the FEG-RBD method could be an efficient choice for free energy calculations. A minimum energy pathway (MEP) with 58 structures representing this reaction was prepared using the replica path (RPATH) module in the CHARMM program package.28 The energy and gradient of each structure were calculated at the B3PW91/6-31G(d,p) level of theory using the Q-Chem program package33 through an interface within CHARMM.34 The structures along the MEP were solvated in a box of TIP3P35 water molecules separately (the number of water molecules ranges from 354 to 424, see Supporting Information for details) and subjected to the FEG-RBD simulations. Each FEG-RBD simulation was carried out using the NVT ensemble at 298 K.
Scheme 1.
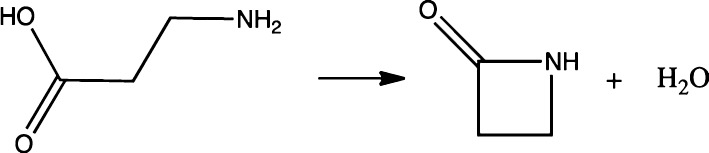
While the minimum energy pathway was obtained from the quantum mechanics/molecular mechanics (QM/MM) reaction pathway calculations, our subsequent FEG-RBD simulations were performed at the level of molecular mechanics only to avoid prohibitively expensive QM calculation for long simulations. For each solute structure, which remains rigid using the SHAPE algorithm, only the VDW parameters and atomic charges were used to capture the solute–solvent interaction in the simulation. Other terms for the solute such as bond stretching, bond angle bending, dihedral angle torsion, were all omitted from the simulation because these terms do not contribute to the solute–solvent interaction. The VDW parameters of solute molecule were obtained from the CHARMM22 force field.30
Gas-phase electrostatic potential (ESP) charges of each structure calculated at B3PW91/6-31G(d,p) level of theory using Gaussian 0936 were used in the FEG-RBD simulations, thus not accounting for the polarization of solute electron structure by the solvent molecules. The polarization of solute by solvent molecules is very important in solvation free energy, but needs QM calculation in simulations. This will make FEG-RBD simulation prohibitively expensive for this test case. However, more methodology development is underway to speed up the QM calculations in FEG-RBD simulations. Overall, during the course of each simulation, all the energy terms between solute and solvent and within solvent molecules are calculated; while all the intramolecular energy terms of the solute were ignored, which remain constant for each FEG-RBD simulation.
The mean constraint forces on solute of each simulation were used to compute the line integral along the MEP as represented by 58 structures to obtain the free energy profile. The simulation for each structure was repeated 10 times with random starting velocities. The free energy profile was plotted as a black line with square symbol and error bar calculated based on 10 simulations of each configuration in Figure 2. Similar to the Case 1, the plotted error bars in Figure 2 for FEG-RBD simulation are cumulative. Considering that these simulations were carried out in explicit solvent, the small error bars from only ten simulations of each structure again demonstrate the high sampling efficiency of the FEG-RBD method. β-Alanine, the first structure on the MEP, was chosen as the reference point with zero free energy. Since the internal energy of solute was removed during the simulation, the free energy contribution mainly comes from the interaction between the solute and solvent, and among the solvent molecules.
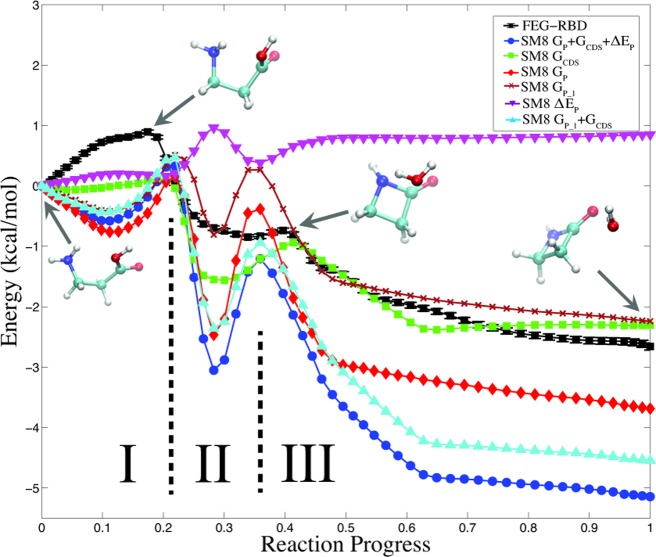
Figure 2.
Solvation free energy profile of intramolecular condensation reaction of β-alanine (3-aminopropanoic acid) through FEG-RBD simulation (black line), and key structures along the reaction pathway. Also shown are relative solvation free energies from the SM8 implicit solvation model (dark blue line), and its three components: GP (red line), GCDS (green line) and ΔEP (purple line). For a direct comparison to FEG-RBD results, the nonpolarizable portion of SM8 solvation free energy, GP_1 + GCDS, is also shown (light blue line). This comparison demonstrates that FEG-RBD simulation was able to capture the detailed solvation effect of solute molecule excluding polarization effects.
The reaction pathway is divided into three steps in Figure 2 reflecting the shape of the free energy contribution. In Step I, the two ends of the solute molecule (β-alanine) move toward each other (Figure 2). This movement reduces the space between the carboxyl and amine groups, leading to a partial desolvation of these two functional groups and understandably to an unfavorable free energy contribution. In Step II, the chemical bonds breaking and forming of the condensation reaction between the carboxyl and amine groups occur (Figure 2), and lead to a favorable free energy contribution. In Step III, all the chemical bonds rearrangements are finished; the forming water molecule moves away from β-lactam as the condensation product, and eventually forms a hydrogen bond with the carbonyl oxygen in the final structure in the reaction pathway. With the FEG-RBD method, the overall solvation contribution to reaction free energy is found to be 2.5 kcal/mol.
To further illustrate the solvation contribution to the free energy calculated in this test case, the structures from the reference reaction pathway were also subjected to single point calculations at B3PW91/6-31+G** using an implicit solvation method, SM8,37 as implemented in Q-Chem. SM8 is chosen because there are separate solvation energy terms, which can be used for comparison purpose. There are three terms in the SM8 solvation free energy: ΔEF is the change of the solute’s internal energy from the gas phase to the solution at the same geometry due to polarization by the solvent; GP is the polarization free energy of a generalized Born formalism; and GCDS is the contribution to the free energy from cavitation (C), dispersion (D) and solvent structural effects (S). SM8 solvation free energy and its three terms along the reference reaction path are also plotted in Figure 2 with reference to the first structure. The free energy profile calculated using FEG-RBD shows some interesting differences and similarities from the SM8 profile along the path (Figure 2). In step I, unlike FEG-RBD, SM8 (dark blue line) predicts an initial favorable change in the solvation free energy as the carboxyl and amine groups move closer. In steps II and III, SM8 qualitatively agrees with FEG-RBD. Quantitatively, the SM8 solvation free energies changes are far steeper.
As mentioned above, the solute is nonpolarizable in our FEG-RBD simulations, because fixed gas-phase ESP charges are used for the solute. So, as a more direct comparison, we can compare it against the nonpolarizable portion of the SM8 solvation free energy: GP_1, which is the polarization free energy from the first self-consistent field (SCF) cycle in the solution phase calculation and is thus based on gas-phase CM4 charges, and GCDS. In other words, we exclude ΔEF (the change in the solute SCF energy due to polarization by the solvent) and the change in GP due to different CM4 charges in the gas-phase and the solution phase. This nonpolarizable portion of the SM8 solvation free energy, GP_1 + GCDS, is shown as the light blue line in Figure 2, and it closely resembles the entire SM8 solvation free energy (dark blue line) as the reaction progresses. At the same time, electron polarization effects account for about 20% of SM8 solvation free energy for this reaction, so the GP_1 + GCDS values are typically ca. 20% smaller, bringing it closer to our FEG-RBD results.
Since SM8 was parametrized against experimental aqueous solvation free energies, the correlation between our FEG-RBD results and SM8 results along the reaction pathway, at least in steps II and III, strongly suggests that our FEG-RBD method captures the nonpolarizable portion of solvation free energy, especially the contribution from cavitation, dispersion, and solvent structural effects. To further capture the solute polarization effect, we need to either adopt a polarizable force field for the solute or, more preferably, treat the solute quantum mechanically during the simulation. The latter (QM/MM) treatment can be rather expensive for the long (10 ns) simulations carried out in this study. Further work is underway to speed up the QM/MM calculation in FEG-RBD simulations.
3.3. Butane
The first two cases demonstrate both accuracy and efficiency of FEG-RBD method. To test the limitation of FEG-RBD method, butane molecule was selected as a third test case using dihedral angle as the main reaction coordinate. The energy profiles of the dihedral angle rotation defined by four carbons in butane are calculated for comparison. The purpose for this selection is testing the effectiveness of FEG-RBD method on dihedral angle rotation, which is a common reaction coordinate, but difficult to deal with in constrained molecular dynamics simulations. The MEP with 73 structures, which corresponds to the rotation of butane backbone dihedral angle, was prepared using the RPATH method available in the CHARMM program package.28 The energy profile of MEP is plotted in Figure 3. The 73 structures of butane on MEP were subjected to two types of FEG-RBD simulations. In the first type simulation (FEG-RBD 1 in Figure 3), the whole butane molecule is kept as rigid body. In the second type (FEG-RBD 2 in Figure 3), only four carbon atoms are kept as rigid body. Both FEG-RBD simulations were repeated 10 times with different random initial velocities for statistical purposes.
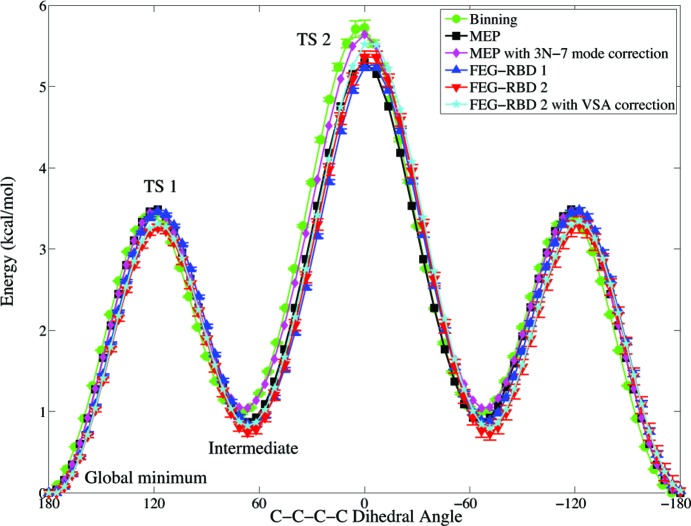
Figure 3.
Energy profiles of dihedral angle rotation associated with central carbon–carbon bond in butane.
To measure the accuracy of our FEG-RBD results, the free energy profiles are also computed in two other ways. First, a total of 1.2 μs standard molecular dynamics simulation time at 300 K were carried out for butane and subjected to distribution (binning) analysis for calculating the free energy, where the results are shown in both Figure 3 and Table 2. The simulation was repeated ten times with different random initial velocities. Second, vibrational analyses were performed on the 73 structures on the MEP to calculate the free energy correction from the 3N – 7 vibrational modes (excluding the backbone torsion and translations/rotations) to the MEP. From Figure 3, clearly, with the exception of the region around TS1, the vibrational correction works remarkably well to reproduce the free energy from the binning analysis.
Table 2. Barriers and Energies of Butane (kcal/mol).
| method | global minimum | TS 1 | intermediate | TS 2 |
|---|---|---|---|---|
| binning | 0.00 | 3.41(±0.0075) | 0.98(±0.011) | 5.72(±0.095) |
| minimum energy path (MEP) | 0.00 | 3.49 | 0.87 | 5.30 |
| FEG-RBD 1 | 0.00 | 3.46(±0.017) | 0.84(±0.022) | 5.24(±0.029) |
| FEG-RBD 2 | 0.00 | 3.27(±0.040) | 0.75(±0.058) | 5.36(±0.074) |
| MEP + vib. corr. | 0.00 | 3.52 | 0.99 | 5.60 |
| FEB-RBD 2 + VSA corr. | 0.00 | 3.31 | 0.82 | 5.52 |
The free energy profile from the FEG-RBD 1 simulations does not show significant difference compared to the MEP profile. With the relative positions between all carbon and hydrogen atoms fixed, FEG-RBD 1 only accounts for the translational and rotational degrees of freedom and the shape and size of the molecule does not change dramatically during the course of the central carbon–carbon bond rotation in butane. TS1, the intermediate, and TS2 all become more stable with FEG-RBD 1. The largest difference occurring at TS2 where the FEG-RBD1 value (5.24 kcal/mol) is 0.06 (±0.029) kcal/mol lower than the MEP value (5.30 kcal/mol), reflecting lower rotational free energy at TS2.
In addition to the translational and rotational degrees of freedom, the hydrogen atoms also become flexible with FEG-RBD 2. This makes TS1 and the intermediate even more stable. On the other hand, the methyl rotations are allowed in FEG-RBD 2 simulations. At TS2, methyl rotations are hindered—this might be the main reason behind the 0.06 (±0.074) kcal/mol increase of the free energy from MEP (5.30 kcal/mol) to FEG-RBD 2 (5.36 kcal/mol).
The binning analysis suggests that the free energy makes TS1 0.08 (±0.0075) kcal/mol more stable comparing to MEP calculations (3.49 to 3.41 kcal/mol). At the same time, the intermediate becomes 0.11 (±0.011) kcal/mol less stable (0.87 to 0.98 kcal/mol), and most significantly, TS2 is 0.42 (±0.095) kcal/mol less stable (5.30 to 5.72 kcal/mol). So, with flexible hydrogen atoms, FEG-RBD 2 reproduces the same trend as the binning analysis at both TS1 and TS2.
The relative free energy of the intermediate from binning analysis is consistently higher than FEG-BRD 2 results: 0.14 (±0.048) kcal/mol (3.41 vs 3.27 kcal/mol) at TS1, 0.23 (±0.069) kcal/mol (0.98 vs 0.75 kcal/mol) at the intermediate, and 0.36 (±0.17) kcal/mol (5.72 vs 5.36 kcal/mol) at TS2. These differences should come from applying the rigid-body constrains in our FEG-BRD 2 simulations, namely, (a) the flexibility of the butane backbone (bond stretching and bond angle bending), which are not accounted for in the rigid body simulation; and (b) the coupling between these backbone motions and the motions of the hydrogen atoms. Observing the accuracy of the vibrational free energy correction to MEP (as compared against the binning analysis), vibrational subsystem analysis (VSA) was performed on the backbone. Here the molecular Hessian is partitioned into a basis that represents the three C–C stretching and two C–C–C angle bending degrees of freedom. As shown in Figure 3 and Table 2, this vibrational subsystem analysis brings FEG-RBD 2 results closer to the binning analysis results. At TS2 the difference was narrowed from 0.36 (±0.17) kcal/mol to 0.20 (±0.095) kcal/mol (5.72 vs 5.52 kcal/mol). For TS1, the difference is 0.10 (±0.0075) kcal/mol, and for the intermediate state 0.16 (±0.011) kcal/mol.
Furthermore, the enthalpic costs of imposing the SHAPE constraints can be readily evaluated by conducting a minimization on the constrained degrees of freedom. This was done by removing the SHAPE constraints from the carbons and then restraining or constraining the other degrees of freedom before conducting an energy minimization. Normally this is very small correction, because a minimum on potential energy surface is close to its counterpart on the corresponding free energy surface. For FEB-RBD2, the enthalpic costs of the SHAPE constraints ranged between 0.0002 and 0.0447 kcal/mol, but the effect on the relative free energy of TS1, TS2, and the intermediate state are below 0.0007 kcal/mol, so the enthalpic contribution of the constraints can be neglected in this particular case.
4. Discussion
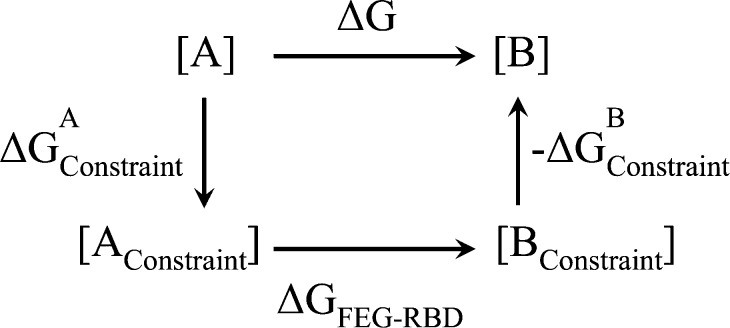
In general, the free energy calculation using rigid body constraint can be represented as a calculation cycle illustrated in Figure 4. Corrections are needed for FEG-RBD results for better free energy information. One source of corrections is that the constrained potential energy surface is not the same as the unconstrained surface in the off-path degrees of freedom. To properly account for such differences, one can calculate or estimate the free energy cost of applying such constraints (ΔGcons). This free energy cost can be accounted for by determining the enthalpy increase (ΔH) and entropy losses (−TΔS) of the constrained degrees of freedom for each snapshot. The enthalpic costs can be estimated by the potential energy difference between the constrained structure and the structure at the local energy minimum of the degree of freedom. This corresponds to using the projections of the gradients g and Hessian H into the constrained degrees of freedom, and performing a one step Newton–Raphson minimization,
| 14 |
where ∥···∥ denotes a sum over all elements.
Figure 4.
Free energy calculation using rigid body constraint.
The entropic costs of the constrained degrees of freedom include both a frequency term and a term based on the metric tensor (Jacobian).38−40 The Jacobian term of the system Js, can be calculated as
| 15 |
where α is the index of atom, N is the total number of atoms, and Jα is the Jacobian factor of each atom, and internal coordinates for each atom are represented as three vectors, siα, sjα, and skα.38 The Jacobian term was estimated to be below 0.01 kcal/mol for the present cases, so it was neglected. However, there might be cases where the Jacobian term is important (e.g., constraining a single bond length that changes by more than 10%). The frequency term can be well estimated using a vibrational subsystem analysis41,42 if the off-path constrained degrees of freedom are primarily harmonic on the unconstrained potential energy surface. This is the case for the bond and angle terms considered in the examples here.
| 16 |
where Λ are the eigenvalues of Hessian matrix.
The free energy change due to releasing all constraints in a free energy simulation is
| 17 |
where ⟨⟩cons denotes an ensemble average using rigid body constrained dynamics. This equation corresponds to the Zwanzig equation, but uses ΔG instead of ΔU.8 More details on how to calculate the corrections for constrained bonds and angles in simulations can be found in a manuscript that has been submitted elsewhere.43
Notably, the above analysis only works for constrained degrees of freedom that can be treated harmonically. This is not true for dihedral angles with multiple rotational states. However, this problem can be addressed using the techniques for treating rotational isomers developed by Straatsma and McCammon.44 If there are n subspaces that together span the entire accessible phase space (i.e., n possible rotational states), the free energy difference can be calculated by
| 18 |
where ΔGi is the free energy difference for one particular subspace or rotational substate. Thus, the free energy difference can be evaluated by performing a rigid body simulation for each possible rotational state. A good approximation may consist in simulating just the lowest energy rotamers if the other states are strongly disfavored.
5. Conclusions
We presented a free energy gradient simulation method employing rigid body dynamics (named FEG-RBD) to enhance sampling efficiency for a reference reaction pathway. In this method, all the atoms that are important (as determined by the user) for a reaction coordinate are selected to form a rigid body, while all the other atoms are free to move during the simulation. The constraint forces associated with the rigid body are averaged over the simulation to obtain the gradient of the free energy. Such a rigid body simulation is carried out for each structure along the reaction path. Finally, the gradients of the free energy from the rigid body simulations are integrated along the reference reaction pathway to obtain the free energy profile.
When using the constrained dynamics concept, three test cases demonstrated both the strengths and weaknesses of the FEG-RBD method. A simple test case with an analytically known free energy was simulated to demonstrate the rigorousness of the method. Using the constrained dynamics concept through rigid body simulation, the convergence rate for free energy simulations is faster than normal molecular dynamics or simulations with restraints, providing an efficient way to calculate free energy from simulation. The FEG-RBD method is the most suitable for complex chemical reactions in solution and biochemical reactions, in which multiple order parameters are essential to define the reaction progress, and entropic contribution from the environment is important for the overall free energy.
The missing contribution to the free energy from the loss of flexibility in the rigid body can be accounted in terms of enthalpy and entropy. The enthalpic correction can be estimated from the energy difference between constrained and unconstrained structures. The entropic correction includes frequency term and Jacobian term. The Jacobian term is normally negligible in most cases. The frequency term can be estimated through vibrational subsystem analysis.41,42 The degrees of freedom that cannot be treated harmonically, such as dihedral angles with multiple rotational states, can be addressed using special techniques for treating rotational isomer.44
The FEG-RBD method with enhanced sampling efficiency comparing to umbrella sampling method by a factor of 4 has potential applications for free energy simulation in many areas, including solvation free energy calculations, enzymatic reaction and many other complex chemical reaction mechanisms. For example, for the solvation free energy calculation, solute molecule can be treated as rigid body in QM/MM dynamics simulation to include polarization effect. Further study in this direction is currently under development.
Acknowledgments
This research was supported by the Intramural Research Program of the U.S. National Institutes of Health (NIH), U.S. National Heart, Lung, and Blood Institute, and startup research fund at Southern Methodist University (SMU). Computational resources and services used in this work were provided by the LoBoS cluster of the NIH and High-Performance Computing Facilities at SMU. We thank Dr. D. Smith for helpful discussions and Dr. W. Horsthemke for critical reading of the manuscript.
Supporting Information Available
Detailed derivation of eq 4, water box information for simulations of β-alanine intramolecular condensation reaction. This material is available free of charge via the Internet at http://pubs.acs.org
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Ackland G. J. Calculation of free energies from ab initio calculation. J. Phys.: Condens. Matter 2002, 14, 2975–3000. [Google Scholar]
- Chipot C.; Pearlman D. A. Free energy calculations. The long and winding gilded road. Mol. Simul. 2002, 28, 1–12. [Google Scholar]
- van Gunsteren W. F.; Daura X.; Mark A. E. Computation of free energy. Helv. Chim. Acta 2002, 85, 3113–3129. [Google Scholar]
- Kofke D. A. Free energy methods in molecular simulation. Fluid Phase Equilib. 2005, 228, 41–48. [Google Scholar]
- Vanden-Eijnden E. Some Recent Techniques for Free Energy Calculations. J. Comput. Chem. 2009, 30, 1737–1747. [DOI] [PubMed] [Google Scholar]
- Christ C. D.; Mark A. E.; van Gunsteren W. F. Basic Ingredients of Free Energy Calculations: A Review. J. Comput. Chem. 2010, 31, 1569–1582. [DOI] [PubMed] [Google Scholar]
- Kirkwood J. G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar]
- Zwanzig R. W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar]
- Kastner J. Umbrella sampling. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar]
- Kudin K. N.; Car R. Free energy profile along a discretized reaction path via the hyperplane constraint force and torque. J. Chem. Phys. 2005, 122, 114108. [DOI] [PubMed] [Google Scholar]
- Johannesson G. H.; Jonsson H. Optimization of hyperplanar transition states. J. Chem. Phys. 2001, 115, 9644–9656. [Google Scholar]
- Hu H.; Yang W. T. Free energies of chemical reactions in solution and in enzymes with ab initio quantum mechanics/molecular mechanics methods. Annu. Rev. Phys. Chem. 2008, 59, 573–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- E W. N.; Vanden-Eijnden E. Transition-Path Theory and Path-Finding Algorithms for the Study of Rare Events. Annu. Rev. Phys. Chem. 2010, 61, 391–420. [DOI] [PubMed] [Google Scholar]
- Rosta E.; Nowotny M.; Yang W.; Hummer G. Catalytic Mechanism of RNA Backbone Cleavage by Ribonuclease H from Quantum Mechanics/Molecular Mechanics Simulations. J. Am. Chem. Soc. 2011, 133, 8934–8941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Branduardi D.; Faraldo-Gómez J. D. String Method for Calculation of Minimum Free-Energy Paths in Cartesian Space in Freely Tumbling Systems. J. Chem. Theory Comput. 2013, 9, 4140–4154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprik M.; Ciccotti G. Free energy from constrained molecular dynamics. J. Chem. Phys. 1998, 109, 7737–7744. [Google Scholar]
- den Otter W. K.; Briels W. J. The calculation of free-energy differences by constrained molecular-dynamics simulations. J. Chem. Phys. 1998, 109, 4139–4146. [Google Scholar]
- den Otter W. K.; Briels W. J. Free energy from molecular dynamics with multiple constraints. Mol. Phys. 2000, 98, 773–781. [Google Scholar]
- Ciccotti G.; Ferrario M. Rare events by constrained molecular dynamics. J. Mol. Liq. 2000, 89, 1–18. [Google Scholar]
- Coluzza I.; Sprik M.; Ciccotti G. Constrained reaction coordinate dynamics for systems with constraints. Mol. Phys. 2003, 101, 2885–2894. [Google Scholar]
- Ryckaert J.; Ciccotti G.; Berendsen H. J. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar]
- Okuyama-Yoshida N.; Nagaoka M.; Yamabe T. Transition-state optimization on free energy surface: Toward solution chemical reaction ergodography. Int. J. Quantum Chem. 1998, 70, 95–103. [Google Scholar]
- Okuyama-Yoshida N.; Kataoka K.; Nagaoka M.; Yamabe T. Structure optimization via free energy gradient method: Application to glycine zwitterion in aqueous solution. J. Chem. Phys. 2000, 113, 3519–3524. [Google Scholar]
- Nagae Y.; Oishi Y.; Naruse N.; Nagaoka M. Hydrated structure of ammonia-water molecule pair via the free energy gradient method: Realization of zero gradient and force balance on free energy surfaces. J. Chem. Phys. 2003, 119, 7972–7978. [Google Scholar]
- Nagaoka M.; Nagae Y.; Koyano Y.; Oishi Y. Transition-state characterization of the ammonia ionization process in aqueous solution via the free-energy gradient method. J. Phys. Chem. A 2006, 110, 4555–4563. [DOI] [PubMed] [Google Scholar]
- Andersen H. C. Rattle: A “velocity” version of the shake algorithm for molecular dynamics calculations. J. Comput. Phys. 1983, 52, 24–34. [Google Scholar]
- Tao P.; Wu X. W.; Brooks B. R. Maintain rigid structures in Verlet based Cartesian molecular dynamics simulations. J. Chem. Phys. 2012, 137, 134110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks B. R.; Brooks C. L.; Mackerell A. D.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; Caflisch A.; Caves L.; Cui Q.; Dinner A. R.; Feig M.; Fischer S.; Gao J.; Hodoscek M.; Im W.; Kuczera K.; Lazaridis T.; Ma J.; Ovchinnikov V.; Paci E.; Pastor R. W.; Post C. B.; Pu J. Z.; Schaefer M.; Tidor B.; Venable R. M.; Woodcock H. L.; Wu X.; Yang W.; York D. M.; Karplus M. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao P.; Larkin J. D.; Brooks B. R.. Reaction Path Optimization and Sampling Methods and Their Applications for Rare Events. In Some Applications of Quantum Mechanics; Pahlavani M. R., Ed.; InTech: Rijeka, Croatia, 2012, 27–66. [Google Scholar]
- MacKerell A. D.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph-McCarthy D.; Kuchnir L.; Kuczera K.; Lau F. T. K.; Mattos C.; Michnick S.; Ngo T.; Nguyen D. T.; Prodhom B.; Reiher W. E.; Roux B.; Schlenkrich M.; Smith J. C.; Stote R.; Straub J.; Watanabe M.; Wiorkiewicz-Kuczera J.; Yin D.; Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- Desloge E. A. Classical partition function of a rigid rotator. Am. J. Phys. 1984, 52, 261–262. [Google Scholar]
- Kumar S.; Bouzida D.; Swendsen R. H.; Kollman P. A.; Rosenberg J. M. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar]
- Shao Y.; Fusti-Molnar L.; Jung Y.; Kussmann J.; Ochsenfeld C.; Brown S. T.; Gilbert A. T. B.; Slipchenko L. V.; Levchenko S. V.; O’Neill D. P.; DiStasio R. A.; Lochan R. C.; Wang T.; Beran G. J. O.; Besley N. A.; Herbert J. M.; Lin C. Y.; Van Voorhis T.; Chien S. H.; Sodt A.; Steele R. P.; Rassolov V. A.; Maslen P. E.; Korambath P. P.; Adamson R. D.; Austin B.; Baker J.; Byrd E. F. C.; Dachsel H.; Doerksen R. J.; Dreuw A.; Dunietz B. D.; Dutoi A. D.; Furlani T. R.; Gwaltney S. R.; Heyden A.; Hirata S.; Hsu C. P.; Kedziora G.; Khalliulin R. Z.; Klunzinger P.; Lee A. M.; Lee M. S.; Liang W.; Lotan I.; Nair N.; Peters B.; Proynov E. I.; Pieniazek P. A.; Rhee Y. M.; Ritchie J.; Rosta E.; Sherrill C. D.; Simmonett A. C.; Subotnik J. E.; Woodcock H. L.; Zhang W.; Bell A. T.; Chakraborty A. K.; Chipman D. M.; Keil F. J.; Warshel A.; Hehre W. J.; Schaefer H. F.; Kong J.; Krylov A. I.; Gill P. M. W.; Head-Gordon M. Advances in methods and algorithms in a modern quantum chemistry program package. Phys. Chem. Chem. Phys. 2006, 8, 3172–3191. [DOI] [PubMed] [Google Scholar]
- Woodcock H. L.; Hodoscek M.; Gilbert A. T. B.; Gill P. M. W.; Schaefer H. F.; Brooks B. R. Interfacing Q-chem and CHARMM to perform QM/MM reaction path calculations. J. Comput. Chem. 2007, 28, 1485–1502. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam N. J.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, 2009. [Google Scholar]
- Cramer C. J.; Truhlar D. G. A universal approach to solvation modeling. Acc. Chem. Res. 2008, 41, 760–768. [DOI] [PubMed] [Google Scholar]
- Herschbach D. R.; Johnston H. S.; Rapp D. Molecular Partition Functions in Terms of Local Properties. J. Chem. Phys. 1959, 31, 1652–1661. [Google Scholar]
- Boresch S.; Karplus M. The Jacobian factor in free energy simulations. J. Chem. Phys. 1996, 105, 5145–5154. [Google Scholar]
- Boresch S.; Karplus M. The role of bonded terms in free energy simulations: 1. Theoretical analysis. J. Phys. Chem. A 1999, 103, 103–118. [Google Scholar]
- Woodcock H. L.; Zheng W.; Ghysels A.; Shao Y.; Kong J.; Brooks B. R. Vibrational subsystem analysis: A method for probing free energies and correlations in the harmonic limit. J. Chem. Phys. 2008, 129, 214109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghysels A.; Miller B. T.; Pickard F. C.; Brooks B. R. Comparing normal modes across different models and scales: Hessian reduction versus coarse-graining. J. Comput. Chem. 2012, 33, 2250–2275. [DOI] [PubMed] [Google Scholar]
- König G.; Brooks B. R.. Correcting for the free energy costs of bond or angle constraints in molecular dynamics simulations. Biochim. Biophys. Acta Submitted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Straatsma T. P.; McCammon J. A. Treatment of rotational isomers in free energy calculations. II. Molecular dynamics simulation study of 18-crown-6 in aqueous solution as an example of systems with large numbers of rotational isomeric states. J. Chem. Phys. 1989, 91, 3631–3637. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.