Assessment of the Density Functional Tight Binding Method for Protic Ionic Liquids

Abstract

Density functional tight binding (DFTB), which is ∼100–1000 times faster than full density functional theory (DFT), has been used to simulate the structure and properties of protic ionic liquid (IL) ions, clusters of ions and the bulk liquid. Proton affinities for a wide range of IL cations and anions determined using DFTB generally reproduce G3B3 values to within 5–10 kcal/mol. The structures and thermodynamic stabilities of n-alkyl ammonium nitrate clusters (up to 450 quantum chemical atoms) predicted with DFTB are in excellent agreement with those determined using DFT. The IL bulk structure simulated using DFTB with periodic boundary conditions is in excellent agreement with published neutron diffraction data.

1. Introduction

Ionic liquids (ILs) are liquids that are comprised entirely of ions, differentiated from typical ionic salts by having melting points below 100 °C.¹ IL melting points are low because electrostatic interactions between component ions are weaker and crystal lattice packing is hindered. This is typically achieved by making at least one of the ions large, unsymmetrical and organic. The physicochemical properties of ILs can be tuned through a judicious choice of ions.²⁻⁵ This “flexibility” has driven wide-ranging research into their use as solvents in “green” chemistry,^1,6 energy,⁷ electrochemical applications,^8,9 pharmaceuticals,¹⁰⁻¹² and lubricants.¹³⁻¹⁵

Protic ILs are formed by proton transfer from a Brønsted acid and a Brønsted base. While molecular liquids like water are structurally homogeneous, many ILs are nanostructured in the bulk¹⁶⁻²⁴ and at interfaces.^14,25−27 Nanostructure in protic ILs is usually spongelike.^3,28−30 IL nanostructure is driven by the amphiphilicity of (usually) the cation, with short-range forces driving the formation of longer-range self-assembled structures. IL nanostructure is a consequence of the solvophobic effect;³¹ strong electrostatic attractions between IL charged groups lead to the assembly of charged (polar) domains. Cation alkyl chains are solvophobically excluded from these charged regions and cluster together to form uncharged (apolar) domains.^16,32 Many IL properties can be correlated with nanostructure, and the short-range interactions within it, such as hydrogen bonding.³³ To fully exploit IL nanostructure for control of physicochemical properties an atomistic understanding of the interactions between IL ions is required. While this cannot currently be achieved using experiments, it can be using classical molecular dynamics,³⁴ab initio molecular dynamics (AIMD),³⁵ as well as static quantum chemical calculations.^36,37

IL simulations generally fall into two categories that balance accuracy and system size. Accurate quantum chemical simulations yield a detailed picture of IL structure at the atomic scale, but are limited in large-scale applications by their computational expense. This means that fundamental aspects of real IL systems, such as self-assembled nanostructure,³⁸⁻⁴⁵ are not captured. One possible approach to circumventing this problem is the use of continuum solvation models,⁴⁶ but this method is complicated by the heterogeneous liquid nanostructure. Noncontinuum solvation methods based on the reference interaction site model (RISM)^47,48 are a possible alternative, but an accurate description of the solvating “bulk” region is still required; this becomes particularly problematic in the case of conformationally flexible ions. Conversely, large-scale model IL systems consisting of hundreds of ion pairs can be studied using classical potentials,^3,35,49−54 though such potentials often lead to reduced accuracy and are invariably IL-specific. If molecular dynamics (MD) is employed, the time scale of the simulation is another parameter limiting accuracy, and this often necessitates smaller systems.

Density functional tight binding (DFTB) is a fast quantum chemical method with great potential for IL simulations. Density functional tight binding has accuracy comparable to density functional theory (DFT), but is 100–1000 times faster. Potentially, therefore, DFTB enables both molecular and nanoscale structures to be captured simultaneously, with quantum chemical accuracy. However, the performance of DFTB in predicting structure and properties of protic ILs has not yet been assessed.

In this work, we compare proton affinities (PAs) computed with DFTB against DFT and electron correlated ab initio calculations, and DFTB-predicted bulk structure against neutron-diffraction data.³ Protic ILs are synthesized by proton transfer from a Brønsted acid to base. Therefore, PAs of component ions provide the best elementary test of the accuracy of a method. We demonstrate that DFTB predicts accurate PA values for a wide range of prototypical IL cations and anions (see Figures 1 and 2),⁵⁵ along with the bulk IL structure. These results indicate that DFTB is an ideal method for efficiently and accurately predicting properties and structure for protic ILs in general, over both molecular-scale and nanoscale domains.

Figure 1.

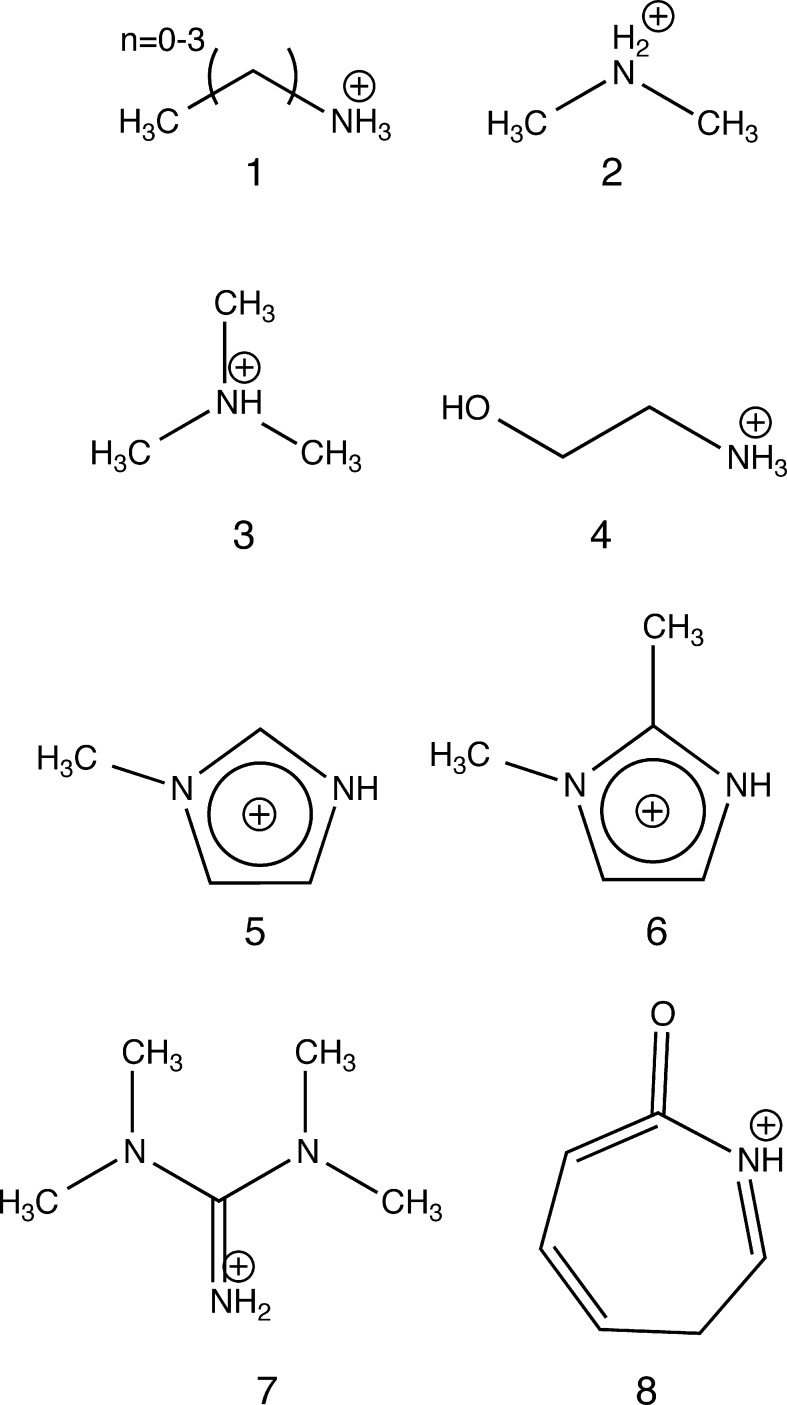
Protic IL cations considered in this work: (1–3) primary, secondary, tertiary n-alkyl amines, (4) ethanolammonium, (5,6) mono, 1,2-dimethyl imidizolium (MIm, 1,2-DMIm), (7) 1,1,3,3-tetramethylguanidine, and (8) caprolactam.

Figure 2.

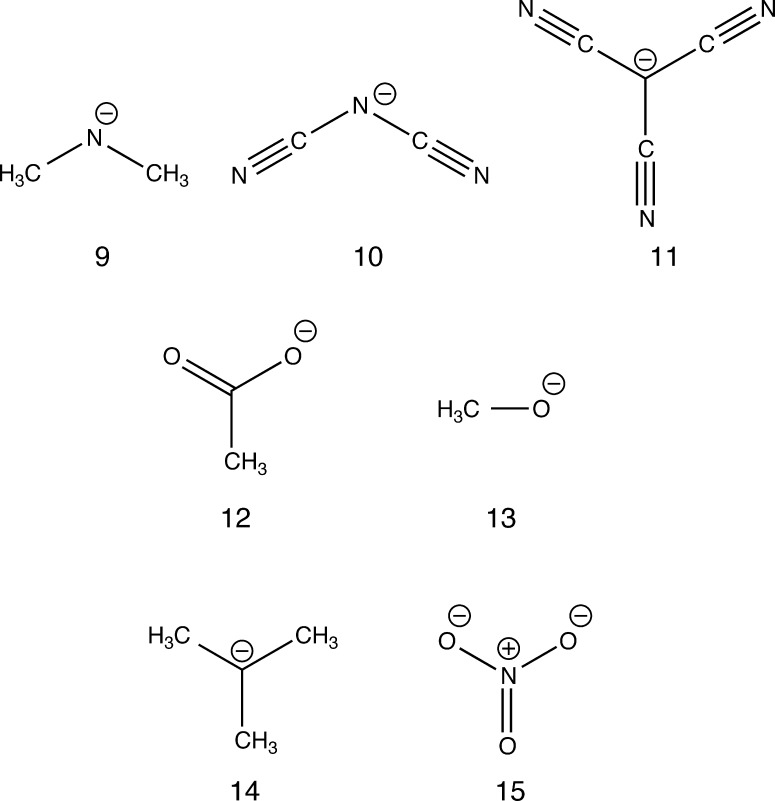
Protic IL anions considered in this work: (9) dimethylamide, (10) dicyanamide (dca), (11) tricyanomethanide (tcm), (12) acetate, (13) methoxy, (14) isobutane, and (15) nitrate.

2. Computational Details

2.1. Density Functional Tight Binding

DFTB is an extended Hückel-like method, parametrized with DFT (see refs (56 and 57) for recent reviews), and consists of electronic and repulsive terms. The DFTB method assumes the Foulkes-Haydock ansatz; the electron density ρ is treated as a reference density ρ⁰ plus a small perturbation (i.e., ρ = ρ⁰ + Δρ), where ρ⁰ is computed using DFT. The exchange-correlation potential can thus be expanded in a Taylor series around some reference density ρ⁰. The DFTB energy can be written as

1

where the first and second terms are the electronic and repulsive terms, respectively. The third term accounts for charge transfer between atoms A and B (γ_AB is a distance-dependent function of the chemical hardness of A and B, and Δq is the difference between an atom’s charge and its charge arising from the reference density ρ⁰), and the fourth term accounts for how each atom’s contribution to the reference density ρ⁰ relaxes in the presence of every other atom (Γ_AB describes how the chemical hardness (γ_AB) changes as a function of the chemical environment due to atoms A and B). The DFTB3 method is the most recent extension to the original DFTB method pioneered by Fraunheim and Seifert,^58,59 and includes all terms up to and including third-order.⁶⁰ The inclusion of third-order effects in the exchange-correlation potential expansion enables an accurate treatment of hydrogen bonding^60,61 and so is particularly important in the context of ILs. In this work, we will consider both the self-consistent charge DFTB method (i.e., the second order expansion in eq 1, DFTB2) and full DFTB3.

All DFTB calculations presented in this work were performed with the DFTB+ program.⁶² As a demonstration of DFTB’s transferability, we rely on the mio-0-1⁶³ and 3ob-1-1 sets,⁶⁴ both of which are already available, and do not develop any new “purpose-built” parameters in this work. Many previous investigations have demonstrated the importance of dispersion forces in IL structure and properties.⁶⁵⁻⁶⁷ Therefore, all DFTB calculations include dispersion forces calculated using a Slater–Kirkwood polarizable atom model;⁶⁸ however, dispersion is anticipated to be significant only for large cluster and bulk calculations.

2.2. Proton Affinities

For each of the ions in Figures 1 and 2, PAs calculated with DFTB2 and DFTB3 were compared with those obtained using DFT and second-order Møller–Plesset perturbation theory (MP2). Density functional theory (DFT) and MP2 calculations were performed in conjunction with the 6-31G(d) and 6-311G(2d,2p) Pople basis sets, in order to assess basis set effects. Addition of diffuse functions (+ and ++) to these basis sets was also investigated. For DFT calculations, the PBE,⁶⁹ B3LYP,^70,71 and M06-2X⁷² DFT functionals were employed. The PBE functional was included because of its use in the parametrization of the electronic term in eq 1, B3LYP was chosen as a hybrid functional and also because of its popularity, and M06-2X was included because, in several previous ILs, it accurately reproduces properties and structure.^54,73

The proton affinity is defined as the negative enthalpy for the reaction A^– + H⁺ → AH in the gas phase. The PA is thus computed via

2

For all DFTB2 and DFTB3 calculations, E^H+ values of 141.90 and 151.04 kcal/mol, respectively, were employed.⁶⁰ For all DFT and MP2 calculations, PAs are based solely on the electronic potential energy and zero-point energy corrections and excluded thermal contributions. DFT, MP2, and DFTB PAs are compared with those determined using the G3B3 method.⁷⁴⁻⁷⁶ All PA calculations reported here (except DFTB) were performed with Gaussian09.⁷⁷

2.3. Bulk and Cluster Nanostructure

The Kick³ stochastic generation algorithm^54,78 was used to determine low-energy structures of ethyl-, propyl-, and butyl-ammonium nitrate (EAN, PAN, and BAN) clusters and the bulk liquid. The power of the Kick³ approach, when it is combined with DFTB3, is that it can be used to quickly and reliably elucidate complex molecular structure in conformationally flexible systems. Clusters consisting of 2–10, 15, and 20 ion pairs were generated, and all ethyl, propyl, and butyl chains were given full conformational flexibility. Between 1000 and 2000 starting structures were generated for cluster sizes of 2–10 ion pairs, whereas, for the larger clusters (15 or 20 ion pairs), 5000 starting structures were generated. This typically afforded ca. 500 “unique” structures for each system. Uniqueness is defined using energetic and geometric criteria. If the DFTB3 energy of two structures differed by less than 1 mE_h, their geometries were compared by computing the centroid of each ion and then computing the root mean square deviation (RMSD) of cation–cation, anion–anion, and cation–anion intercentroid distances. A relatively loose threshold of 1.0 Å is applied to each RMSD, since it is expected that the potential energy surface (PES) will be comparatively flat, particularly for larger clusters. The energetically higher of the two structures is discarded as a duplicate only if all three geometric criteria fall below this threshold.

Each starting structure was optimized using DFTB3-D in conjunction with the mio-0–1 parameter set. Hubbard derivatives were the standard values published by Gaus et al.⁶⁰ To ensure that DFTB3-D provides reliable thermodynamic trends, single-point energies of each unique structure were calculated using M06-2X/6-311G(d,p) at the optimized DFTB3-D geometry. For smaller clusters (fewer than 6 ion pairs), DFTB3-D structures were reoptimized with M06-2X/6-311G(d,p). Harmonic vibrational frequencies were also calculated with M06-2X/6-311G(d,p) to ensure they correspond to a local minimum on the PES. This is consistent with the approach employed in our recent investigation of imidazolium-based IL clusters.

For the bulk structure of EAN, PAN, and BAN, this Kick³ prescreening process was essentially repeated in the presence of cubic periodic boundary conditions. Cubic supercells of 1.58 nm × 1.58 nm × 1.58 nm (i.e., 4 nm³) were filled with 24 (EAN) or 20 (PAN, BAN) ion pairs, yielding densities of 1.077 g/cm³ (EAN), 1.013 g/cm³ (PAN), and 1.129 g/cm³ (BAN). These values correspond approximately to experimental densities.^55,79,80 The absence of interatomic correlations at distances larger than 0.9 nm in previously published neutron diffraction data indicates that the box used here is sufficiently large to capture IL nanostructure.^3,53 Following the Kick³ optimization of each bulk liquid (performed at 0 K), molecular dynamics (MD) with a time step of 1 fs was used to calculate partial g_ij(r) distribution functions for each liquid. An NVT ensemble at 298 K was enforced via a Nosé–Hoover chain thermostat (chain length = 3, coupling strength = 500 cm^–1).^81,82 Each liquid was first equilibrated for 50 ps. Partial g_ij(r) distribution functions were then sampled from a subsequent 50 ps period of simulation. All periodic calculations used 1 × 1 × 1 Monckhorst-Pack sampling (i.e., at the Γ-point only). Partial g_ij(r) distribution functions for EAN and PAN determined using DFTB3-D are compared to experimental data.³

3. Results and Discussion

3.1. Proton Affinities in Protic Ionic Liquids

The most elementary test of any first-principles method in the present context is the prediction of PA; a method incapable of yielding accurate PAs is unlikely to predict accurately larger-scale structures in protic ILs. PAs for cations 1–8 (Figure 1) calculated using DFTB2 and DFTB3 are presented in Table 1. The cation 1 PA value in Table 1 refers to n = 0 (i.e., methylammonium cation); supplementary calculations show that PAs are essentially the same for n = 1–3 (i.e., EA⁺, PA⁺, and BA⁺).

Table 1. Deviations in Computed Proton Affinities from G3B3 Values, for Protic IL Cations 1–8^a.

	Cation Proton Affinity (kcal/mol)
	1 (n = 0)	2	3	4	5	6	7	8	MADb	max dev
6-31G(d)
PBE	12.8	11.2	9.7	–0.4	11.3	11.3	13.4	14.1	10.4	14.1
B3LYP	12.7	11.5	10.2	–0.5	12.0	12.0	13.7	15.6	10.9	15.6
M06-2X	10.4	9.0	7.8	–3.0	8.7	8.5	–0.3	10.2	6.5	10.4
MP2	13.8	13.6	13.4	0.5	14.7	14.6	15.7	17.7	13.0	17.7
6-31+G(d)
PBE	9.2	8.1	6.9	–4.8	7.3	7.3	9.2	9.5	6.6	9.5
B3LYP	8.3	7.7	6.9	–5.7	7.1	7.1	8.7	9.9	6.2	9.9
M06-2X	6.9	6.1	5.2	–7.1	4.9	4.6	6.0	5.6	4.0	6.9
MP2	11.5	11.6	11.5	–2.3	11.5	11.5	12.8	13.9	10.3	13.9
6-31++G(d)
PBE	9.2	8.2	7.0	–4.8	7.4	7.4	9.2	9.5	6.6	9.5
B3LYP	8.3	7.7	6.9	–5.7	7.1	7.1	8.6	9.9	6.2	9.9
M06-2X	6.9	6.2	5.3	–7.1	4.9	4.7	6.0	5.6	4.1	6.9
MP2	11.6	11.8	11.7	–2.3	11.6	11.6	12.8	13.9	10.3	13.9
6-311G(2d,2p)
PBE	12.4	11.4	10.5	–0.8	11.8	11.8	13.2	14.1	10.5	14.1
B3LYP	11.6	11.1	10.5	–1.7	11.8	11.7	12.9	14.8	10.3	14.8
M06-2X	9.5	9.2	8.8	–3.9	8.6	7.8	9.6	9.6	7.4	9.6
MP2	15.8	16.1	16.6	2.5	16.4	16.5	17.2	19.0	15.0	19.0
6-311++G(2d,2p)
PBE	9.7	9.4	8.9	–3.8	9.6	9.7	11.0	11.1	8.2	11.1
B3LYP	8.5	8.7	8.6	–5.1	9.3	9.3	10.4	11.4	7.7	11.4
M06-2X	7.0	7.3	7.3	–6.6	6.5	6.5	7.6	6.9	5.3	7.6
MP2	13.8	14.5	15.2	0.2	14.4	14.6	15.4	16.5	13.1	16.5
DFTB2/mio-0-1	–7.5	–8.6	–9.0	–19.3	5.9	4.7	4.9	0.5	2.7	9.0
DFTB3/mio-0-1	–4.2	–3.0	–1.9	–16.4	13.1	12.0	8.8	6.2	4.1	13.1
DFTB3/3ob-1-1	–1.9	1.1	3.9	–13.8	16.0	14.8	11.1	9.8	5.6	16.0
G3B3	214.2	221.5	226.1	227.8	229.3	234.2	245.5	214.4

^aEnergies are given as E^method – E^G3B3.

^bMean absolute deviation.

Each cation modeled has an acidic nitrogen, and therefore poses a challenge to any minimal basis set or semi-empirical method,⁸³ because of the well-known nitrogen hybridization issue (which leads to large deprotonation errors). This is complicated further by the presence of both sp²- and sp³-hybridized nitrogen atoms in our test set. Table 1 reveals that the mean absolute deviations (MADs) of DFTB-predicted PAs from those determined using G3B3 are within ca. 5 kcal/mol. G3B3 values⁷⁴ deviate from experimental values⁸⁴ by, at most, 2 kcal/mol for these species. Based on previous reports,^60,85 this level of accuracy is acceptable. DFTB3 is more accurate for cations 1–3, which have sp³-hybridized nitrogens (i.e., the alkyl ammonium cations), while DFTB2 provides greater accuracy for the other cations which have sp²-hybridized nitrogens.

For sp³ cations 1–3, DFTB3 is most accurate when the 3ob-1-1 parameter set is used, with maximum errors of 3.9 kcal/mol. This is surprising, because the 3ob-1-1 parameters have previously been shown to be inaccurate in modeling the sp³ nitrogen PAs,⁶⁰ which prompted the development of the NHmod parameter set. However, in this study, the NHmod parameters produced deviations ca. 10 kcal/mol higher than those obtained using 3ob-1-1 for sp³ cations 1–3. The underlying cause of this is a topic of further study. However, we note that for cation 4, NHmod parameters substantially reduce the deviation in PA obtained using 3ob-1-1, from −13.8 kcal/mol to 5.0 kcal/mol. For the sp² cations 5–8, deviations between DFTB3 and G3B3 data are as large as 16 kcal/mol. The most significant deviations occur for the MIm and 1,2-DMIm cations; we attribute this to DFTB’s treatment of charge delocalization in the imidazole ring (similar behavior for DFT has been noted previously for IL anions⁴³).

Table 2 presents PAs for the protic IL anions presented in Figure 2. For anions with acidic oxygen (12, 13, 15), DFTB2-predicted PAs are within ca. 6 kcal/mol of the G3B3 values. PAs are generally reduced by 1–2 kcal/mol using DFTB3 in conjunction with mio-0-1 parameters, but when the 3ob-1-1 parameters are used PAs are underestimated for anions 12 and 14. The charge of the dca and tcm anions (anions 10, 11) is highly localized because of the cyano ligands. For isobutene (anion 14), DFTB2 underestimates the G3B3 PA by −18.1 kcal/mol, but third-order corrections increase accuracy substantially to within −12.8 kcal/mol. In general, however, DFTB PAs deviate from G3B3 values by as much as 25 kcal/mol, since DFTB cannot accurately treat localized charges.⁶¹ DFT suffers this shortcoming also, albeit to a lesser extent;⁴³ deviations from G3B3 PA values are as large as 16 kcal/mol. The smallest deviations for DFT for these anions (<1 kcal/mol) occur with the smallest basis set (6-31G(d)), and this is most likely due to a fortuitous cancellation of errors. Adding a set of diffuse functions (i.e., 6-31+G(d)) increases the MAD by ca. 7 kcal/mol; however, the addition of further diffuse functions to hydrogen atoms (i.e., 6-31++G(d)) provides no further improvement. Similarly, adding diffuse functions to the larger 6-311G(2d,2p) basis set increases DFT MADs by ca. 4 kcal/mol. Conversely, for MP2, adding diffuse functions to the 6-31G(d) and 6-311G(2d,2p) basis sets decreases MAD values to 4.0 kcal/mol (6-31++G(d)) and 0.5 kcal/mol (6-311++G(2d,2p)), respectively.

Table 2. Deviations in Computed Proton Affinities from G3B3 Values, for Protic IL Anions^a.

	Anion Proton Affinity (kcal/mol)
	9	10	11	12	13	14	15	MADb	max dev
6-31G(d)
PBE	–0.6	0.5	–0.4	4.5	2.5	4.4	10.3	3.3	10.3
B3LYP	–0.4	2.0	1.7	5.0	2.7	4.9	11.3	4.0	11.3
M06-2X	–2.3	0.5	0.6	3.2	2.5	2.1	7.5	2.7	7.5
MP2	7.7	4.1	2.6	5.5	7.8	13.4	1.9	6.1	13.4
6-31+G(d)
PBE	–13.5	–8.2	–8.3	–10.4	–13.5	–13.4	–4.9	10.3	13.5
B3LYP	–15.1	–8.6	–8.1	–12.0	–15.3	–15.1	–6.4	11.5	15.3
M06-2X	–14.7	–7.8	–7.0	–10.7	–13.2	–14.9	–6.6	10.7	14.9
MP2	–2.6	–2.7	–3.1	–5.2	–5.5	–0.6	–7.8	3.9	7.8
6-31++G(d)
PBE	–14.6	–8.2	–8.3	–10.4	–14.1	–15.2	–4.8	10.8	15.2
B3LYP	–16.4	–8.5	–8.0	–12.1	–15.9	–17.1	–6.3	12.0	17.1
M06-2X	–15.3	–7.8	–6.9	–10.7	–13.5	–16.2	–6.6	11.0	16.2
MP2	–2.9	–2.7	–3.1	–5.2	–5.6	–1.0	–7.7	4.0	7.7
6-311G(2d,2p)
PBE	–4.4	0.1	–1.9	4.1	1.3	–5.2	14.3	4.5	14.3
B3LYP	–5.0	0.7	–1.0	3.3	0.4	–5.6	14.1	4.3	14.1
M06-2X	–5.3	–0.7	–1.6	2.5	1.7	–6.9	10.6	4.2	10.6
MP2	6.4	4.9	3.3	8.3	9.3	7.6	9.1	7.0	9.3
6-311++G(2d,2p)
PBE	–12.7	–6.0	–7.1	–5.8	–9.9	–15.1	1.4	8.3	15.1
B3LYP	–14.1	–6.3	–7.0	–7.6	–11.7	–16.6	–0.3	9.1	16.6
M06-2X	–12.7	–6.6	–6.5	–6.6	–9.1	–15.3	–1.2	8.3	15.3
MP2	–0.8	–0.5	–1.2	0.4	–0.6	–0.1	0.0	0.5	0.8
DFTB2/mio-0-1	–9.0	13.1	20.0	5.1	–3.2	–18.1	2.1	7.5	18.1
DFTB3/mio-0-1	–6.2	13.7	24.6	2.2	–1.8	–12.8	–3.2	5.3	12.8
DFTB3/3ob-1-1	–4.4	14.3	24.9	–3.4	–5.6	–9.2	–6.1	5.8	9.2
G3B3	412.4	316.6	308.3	361.4	400.4	435.0	329.2

^aEnergies are given as (E^method – E^G3B3).

^bMean absolute deviation.

These results show that comparable, if not greater, accuracy can be obtained systematically with DFTB than can be obtained using the PBE, B3LYP, and M06-2X DFT functionals with either small (6-31G(d)/6-31+G(d)) or large (6-311G(2d,2p)) basis sets. For anions 9–15, DFT calculations with 6-31G(d) and 6-311G(2d,2p) basis sets both produce deviations from G3B3 data that are <5 kcal/mol (however, for the small basis set, this is most likely through a fortuitous cancellation of errors, as noted above). For the cations (1–8), DFT and MP2 with all basis sets typically overestimate PA values, by up to ca. 20 kcal/mol. However, using the 6-31G(d) basis set with a single diffuse function improves accuracy by ∼5 kcal/mol. To improve this accuracy further, thermal/vibrational corrections, and corrections for basis set superposition error (particularly in the case of modest basis sets), are required. Even in small IL clusters, such corrections are computationally intractable. Thus, DFTB represents an efficient and accurate alternative for predicting PAs for both IL anions and cations.

3.2. Structure and Binding in EAN, PAN, and BAN Clusters

The performance of DFTB3 in larger systems is assessed using the n-alkyl ammonium nitrate ILs EAN, PAN, and BAN. These ILs have been chosen, as the bulk structures are known from both neutron diffraction and MD simulations.^3,53 In order to establish that DFTB accurately reproduces the IL nanostructure, the ion arrangements determined by DFTB for clusters will be validated against DFT calculations. Once the cluster structure is established as correct, periodic boundary conditions will be employed to model the bulk liquid, and the structure will be compared to that determined experimentally by comparison of probability distribution functions.

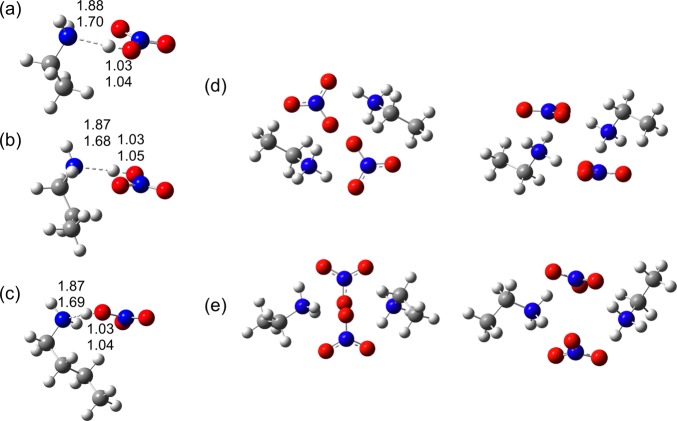
The structure of DFTB ion pairs is first assessed. Previous DFT studies⁸⁶ of n-alkyl ammonium nitrate ILs suggested that, for isolated ion pairs in the gas phase, an ammonium proton is transferred to the NO₃^– anion to form the amine and the acid. This is determined by comparison of the N–H and O–H bond lengths. Figure 3a shows the optimized N–H and O–H bond lengths for EAN, PAN, and BAN ion pairs computed using the M06-2X DFT functional and DFTB3. As per previous studies, both methods predict that the proton resides on the NO₃^– anion, and the O–H bond lengths are in good quantitative agreement, with deviations of <0.02 Å. There is a larger difference between the predicted N–H bond distances, ca. 0.3 Å. However, the distance between the N and H atoms (>1.5 Å) suggests that a bond is not present, accounting for the large variation in “bond” distance. The length of this hydrogen bridge using DFT is sensitive to the choice of functional, but not the basis set. For example, supplementary B3LYP/6-311G(d,p) calculations yield an N–H bond length ca. 0.07 Å larger than the M06-2X/6-311G(d,p) value. MP2/6-311G(d,p) increases this bond length by an additional 0.01 Å. Conversely, this bond length does not change using M06-2X with either a smaller basis set (6-31G(d)) or a larger basis set (aug-cc-pVTZ). Reoptimizing the DFTB/mio-0-1 structure using 3ob-1-1 parameters yields an N–H distance of 1.70 Å. This is a marked improvement over mio-0-1 data, as anticipated,⁶⁴ and is in close agreement with B3LYP and MP2 results. This tendency for proton transfer is eliminated for larger clusters (2 or more ion pairs) (c.f. Figure 3), which is consistent with previous results.⁸⁶ Increased competition between a greater number of hydrogen bonding donor and acceptor sites in larger clusters decreases the acidity of the ammonium group protons, preventing formation of the neutral species.

Figure 3.

DFTB3 equilibrium geometries of (a) EAN, (b) PAN, and (c) BAN monomers. N–H and O–H bond lengths (Å) are shown for DFTB3 (top number) and M06-2X/6-311G(d,p) (bottom number). (d) The most energetically stable EAN dimer structure and (e) an EAN dimer structure 25 kcal/mol higher in energy; both are shown from the top (left) and side (right) views. Structures shown are those optimized with DFTB3.

With structural accuracy established, the energy of the structures is now compared for cluster sizes between 2 and 15 ion pairs. Figure 4a–c plots the DFT and DFTB cluster energies against each other for cluster sizes of 2, 6, and 15 ion pairs for the unique structures identified using the Kick³ search for EAN. Corresponding data for PAN and BAN is presented in the Supporting Information. The closer these data fall to the line of unit gradient, the better the agreement between methods. For the three cluster sizes for EAN, PAN, and BAN, the agreement between models is excellent, except for the highest energy structures (energies >100 kcal/mol), which are not of chemical relevance. The agreement between DFTB3 and M06-2X is corroborated by the cluster binding energy, shown in Figure 4d. The cluster binding energy (BE) for n ion pairs is defined as

3

where E_cluster is the energy of the relaxed cluster, and E_anion and E_cation are the energies of the relaxed isolated anion and cation structures. For M06-2X/6-311G(d,p), E_cluster is the energy at the optimized DFTB3 structure.

Figure 4.

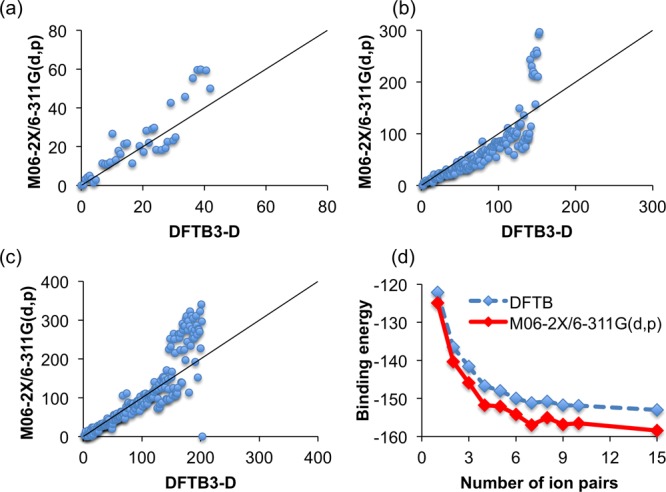
Comparison of relative energies (in kcal/mol) for (a) 2 (39 unique structures), (b) 6 (152 unique structures), and (c) 15 EAN ion-pair clusters (204 unique structures), computed using DFTB3 and M06-2X/6-311G(d,p). DFTB3 energies are fully optimized, M06-2X/6-311G(d,p) are single-point energies. (d) Binding energies (kcal/mol per ion pair) for EAN clusters, as a function of cluster size, computed using DFTB3 and M06-2X/6-311G(d,p). Corresponding data for PAN and BAN are included in the Supporting Information (Figure S1).

Figure 4d shows the BE per ion pair for EAN clusters of between 2 and 15 ion pairs. Corresponding data for PAN and BAN are presented in the Supporting Information (Figure S1). As the number of ion pairs increases, the BE and the form of the data obtained using DFT and DFTB is similar, but the BE for DFTB is ∼10 kcal/mol higher for all cluster sizes. The BE is almost constant for both methods when the cluster size is 7 ion pairs or more, thus providing a confident estimate of the bulk liquid BE per ion pair. Equivalent behavior was observed in our previous work considering imidazolium nitrate-based ILs.⁵⁴ We note that two sources of error are present in these DFT values. Firstly, the values are calculated from single-point energies at the DFTB geometries and thus represent an upper bound to the value that would be obtained were the clusters to be fully optimized using DFT. Secondly, the modest basis set employed is likely to result in some degree of basis set superposition error, which is an error that, by construction, does not affect DFTB.

The binding energies in PAN and BAN also converge to values between −150 and −160 kcal/mol. Since increasing the cation alkyl chain length does not measurably influence the BE, this suggests that the BE is primarily determined by electrostatic interactions between the ammonium and nitrate charge groups. This is consistent with the predicted structures for EAN, PAN, and BAN clusters,^54,86 where the cluster core is enriched in charged groups with n-alkyl chains expelled to an outer shell. The tendency for alkyl chains to be solvophobically expelled from between charged groups toward is evident even in the smallest clusters (c.f. Figures 3d and 3e).

3.3. Bulk Structure in EAN, PAN, and BAN

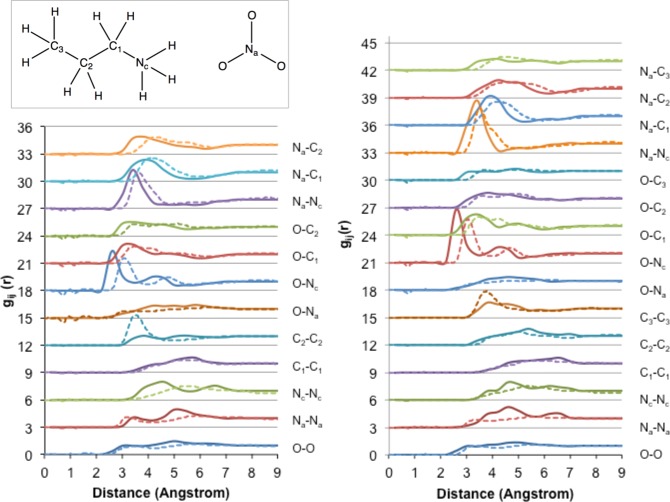
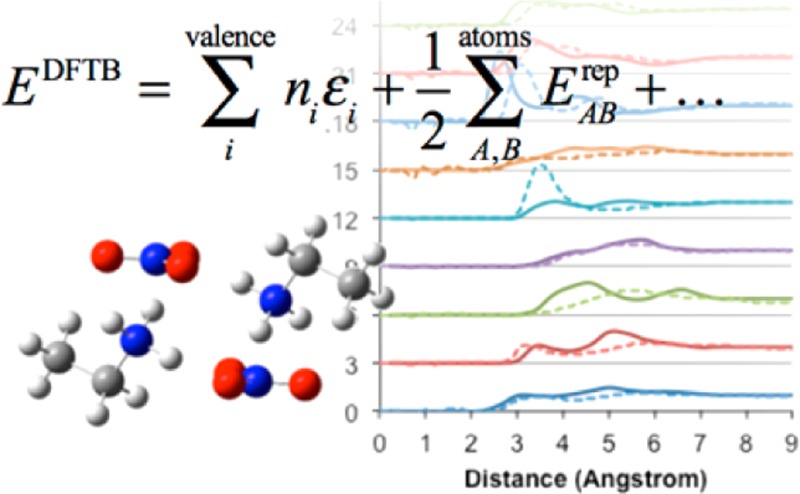
To model the bulk liquid structure rather than a cluster, a 1.58 nm × 1.58 nm × 1.58 nm (i.e., 4 nm³) supercell was filled with 24 ion pairs (EAN), or 20 ion pairs (PAN, BAN) to approximate the EAN, PAN, and BAN liquid densities.⁵⁵ Periodic boundary conditions were employed to allow ions to move in the same way as they would in the bulk fluid, and the supercell volume and temperature were fixed via an NVT ensemble. The accuracy of the bulk structures obtained from DFTB is assessed by comparison of partial g_ij(r) distribution functions with published experimental (EAN and PAN)³ and simulation (BAN) data (c.f. Figures 5 and 6, respectively). The labeling scheme used to identify different atoms is shown in these figures. These DFTB3 simulations employ the mio-0-1 parameter set, and we note here that this should generally be avoided (3ob-1-1 parameters should be used instead). However, at least with respect to bulk structure in EAN, these parameter sets result in essentially identical bulk structures (see Figure S2a in the Supporting Information). All g_ij(r) functions for EAN are in near-perfect agreement, except for the N_a–N_a correlation, which loses the pronounced double-peak structure evident in Figure 5. Near perfect agreement between DFTB2-D/mio-0-1 and DFTB3-D/mio-0-1 bulk structure is also observed (Figure S2b in the Supporting Information).

Figure 5.

Comparison of partial g_ij(r) distribution functions for EAN bulk (left) and PAN bulk (right), computed with DFTB3-D/MD at 298 K (solid lines) and obtained via neutron diffraction³ (dotted lines). The inset shows the labeling scheme. The inset shows the C/N/O labeling scheme for PAN. The same scheme is used for EAN; note that the C₃ carbon and associated H atoms are absent in EA⁺.

Figure 6.

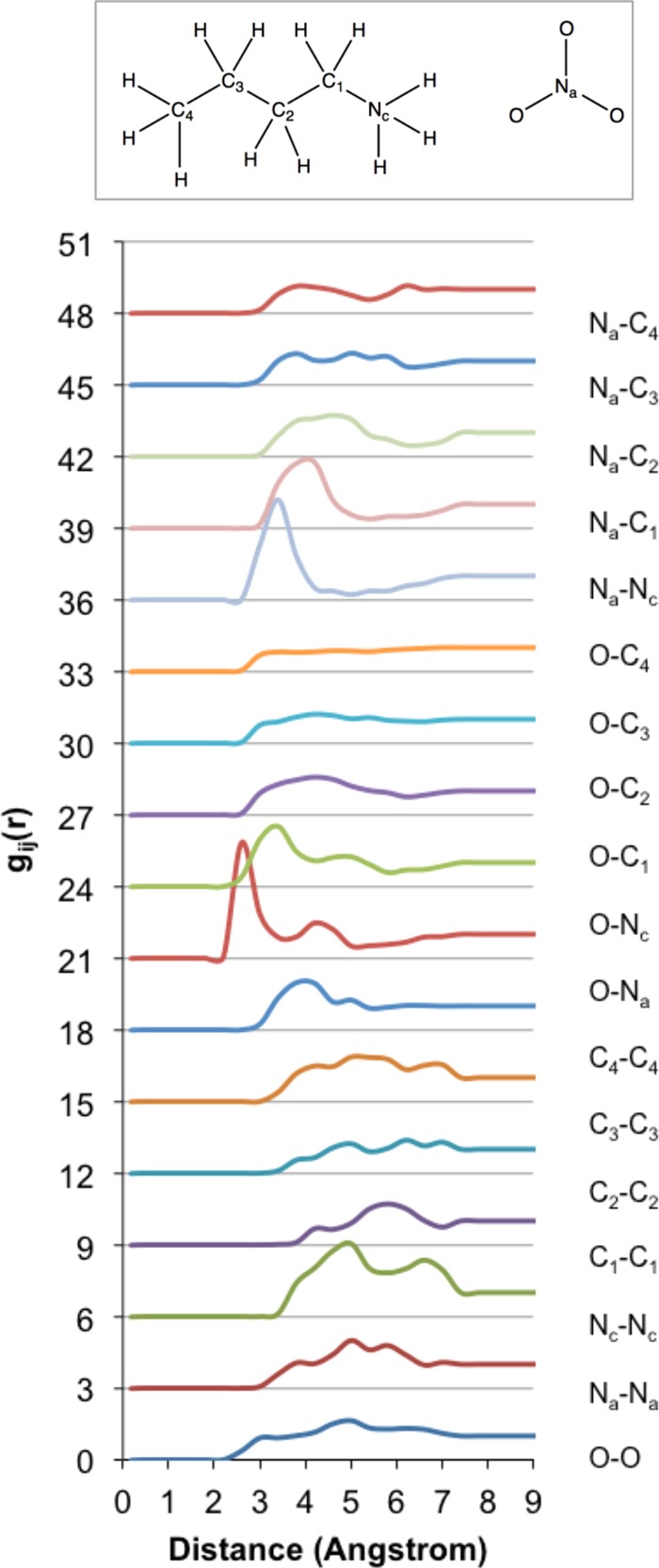
Partial g_ij(r) distribution functions for BAN predicted using DFTB3/MD at 298 K. The inset shows the C/N/O labeling scheme.

For EAN and PAN, agreement between the g_ij(r) distribution functions determined with DFTB3 and neutron diffraction is excellent; any deviations are primarily a consequence of DFTB overbinding effects,⁶⁰ which tend to shift g_ij(r) peaks to shorter distances (usually by ∼0.5 Å). Overbinding here contracts covalent bonds in each ion, resulting in a more localized charge distribution and therefore a stronger electrostatic interaction between ions, causing the observed contraction in g_ij(r) peaks. The fact that simulated and experimental g_ij(r) distribution functions are in such good agreement here also indicates that the simulation box size is sufficient. For instance, if the box size was too small, or the simulated density too high, spurious g_ij(r) peaks not observed experimentally would be obtained, since ions would be forced into unphysical arrangements in the bulk liquid. This is not the case, as can be seen from Figure 5. The agreement between the g_ij(r) distribution functions from experiment and simulation reveals that DFTB3 reproduces the protic IL bulk sponge nanostructure, with segregated polar and apolar domains in the liquid. As such, the best way to assess the accuracy of the simulation is to examine the arrangements of charged and uncharged groups separately.

The accuracy of charge group arrangements can be assessed by examination of the N_a–N_c, N_c–N_c, and N_a– N_ag_ij(r) distribution functions. The primary peak position and height in the N_a–N_cg_ij(r) distribution function is almost perfectly reproduced by DFTB3. For the N_a–N_ag_ij(r), the agreement between the model and the experiment for the peak at short distances is good; however, in the simulation, the second peak is shifted to shorter distances. Similarly, for the N_c–N_cg_ij(r) distribution function peaks, both peaks are shifted to shorter distances.

The correctness of the cation alkyl chain arrangements in the nonpolar domains is determined by comparison of the arrangements C₁–C₁ and C₂–C₂g_ij(r) distribution function from DFTB3 and the experiment. The C₁–C₁g_ij(r) distribution function is in almost exact agreement with the experiment, but for the terminal C₂g_ij(r) (C₃ for PAN), the prominent correlation observed experimentally (3.4 Å) is underestimated by DFTB3. This is also a consequence of the overbinding effect. When charge groups associate more closely (even slightly), the nanostructure “contracts”, such that the space available for alkyl chain packing is reduced. Alkyl chains interdigitate to compensate, leading to the primary peak intensity being reduced in the C₂–C₂g_ij(r) with a concomitant increase in the intensity of the second peak.

Song et al.⁵³ have recently reported on the bulk heterogeneity within primary n-alkyl ammonium nitrate ILs, including BAN, on the basis of X-ray diffraction and classical MD simulations. The prominent features in the simulated BAN g_ij(r) distribution functions are a sharp peak in the N_a–N_c correlation function at 3.18 Å, broad peaks in the O–C₄ and N_a–C₄ correlation functions at 3.7 and 3.99 Å, respectively, and a C₄–C₄ peak at 3.99 Å. The N_c–O correlation function features a double peak, with the first solvation shell located at 3.99 Å. The DFTB3 partial g_ij(r) distribution functions for BAN are presented in Figure 6, and agree well with those reported by Song et al.⁵³ In consideration of the overbinding effect, peaks are generally shifted to shorter distances.

Experimental trends between EAN, PAN, and BAN regarding the extent of aggregation within both charged and uncharged domains are also reproduced here, using DFTB3. As the cation alkyl chain length is increased, the intensity of the correlation between alkyl chain terminal carbons increases. This is consistent with better segregation between charged and uncharged domains, attributed to stronger solvophobic interactions.

4. Conclusions

We have presented a systematic assessment of the density functional tight binding (DFTB) method for protic ionic liquids (ILs). DFTB is an exciting, but as yet underutilized, alternative method for simulating IL structure and IL-related phenomena. However, it is a quantum chemical method; its tight binding formulation enables computational speeds ca. 100–1000 times faster than conventional density functional theory (DFT) (depending on the system in question, and the number of terms included in the expansion of the exchange-correlation potential). A single DFTB3 energy and gradient calculation⁸⁷ on a 15-ion-pair EAN cluster, for example, requires only 37 s. The scaling of DFTB3-D in the current context is shown explicitly in Figure S3 in the Supporting Information for EAN, which shows a near-perfect logarithmic relationship between cluster size and computation time. It is emphasized here that DFTB is also transferable—all calculations presented here have been performed with already available and general-purpose parameters. We note here that, despite recently reported DFTB3 parameters for S and P⁸⁸ and DFTB2 parameters for halogens,⁸⁹ third-order parameters (specifically the derivative of the Hubbard parameter, U) for halogens have not been reported to our knowledge. The application of DFTB3 to aprotic ILs including common anions, such as NTf₂^–, BF₄^–, and PF₆^– (for example), is currently not possible.

For ammonium nitrate ILs, DFTB is capable of predicting (1) the PAs of isolated gas-phase ions with accuracy often exceeding that achieved with both DFT and MP2 using extended basis sets, (2) the structure in IL clusters (with respect to DFT), and (3) the bulk structure (with respect to neutron diffraction data).³ As such, DFTB, and particularly DFTB3, is an efficient and accurate method for studying properties and structure in protic ILs.

Supporting Information Available

Comparison of DFTB and M06-2X/6-311G(d,p) binding energies for PAN and BAN clusters, up to 15 ion pairs. Comparison of radial distribution functions for EAN using DFTB2-D/mio-0-1, DFTB3-D/mio-0-1 and DFTB3-D/3ob-0-1. Computational scaling of DFTB3-D/mio-0-1 for ionic liquid clusters. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States