Abstract
Systematic, high-throughput dissection of causal post-translational regulatory dependencies, on a genome wide basis, is still one of the great challenges of biology. Due to its complexity, however, only a handful of computational algorithms have been developed for this task. Here we present CINDy (Conditional Inference of Network Dynamics), a novel algorithm for the genome-wide, context specific inference of regulatory dependencies between signaling protein and transcription factor activity, from gene expression data. The algorithm uses a novel adaptive partitioning methodology to accurately estimate the full Condition Mutual Information (CMI) between a transcription factor and its targets, given the expression of a signaling protein. We show that CMI analysis is optimally suited to dissecting post-translational dependencies. Indeed, when tested against a gold standard dataset of experimentally validated protein-protein interactions in signal transduction networks, CINDy significantly outperforms previous methods, both in terms of sensitivity and precision.
Introduction
Reverse engineering of gene regulatory networks using gene expression profiles has proven valuable in dissecting the logic of cellular regulation in multiple species [1]–[4] and in elucidating mechanisms governing pathophysiological processes [5]–[7]. However the vast majority of these methods has been developed for the dissection of pairwise relationships between gene-products, for instance by using co-expression [8], information theoretic [3], and Bayesian Network [9] methods. These are well-suited to identify relatively static interactions between transcription factors (TFs) and targets or protein-protein interactions (PPIs) in complexes [10] but fail to capture the more complex dynamic rewiring of regulatory interactions implemented by signal transduction, post-transcriptional regulation, and multi-TF combinatorial regulation. However, most regulatory dependencies, such as regulation of target expression by a TF, are not static but rather depend on additional events, such as the availability of co-factors and microRNAs or on protein modification events such as acetylation, phosphorylation and ubiquitylation, which dynamically rewire the logic of the cell in response to specific exogenous and endogenous signals [11].
These observations provided the original rationale for the development of the Modulator Inference by Network Dynamics (MINDy) algorithm [12]. MINDy was instrumental in the elucidation of novel modulators of oncogene TF activity, such as the STK38 kinase and the HUWE1 ubiquitin ligase as regulators of MYC and MYCN ubiquitin dependent proteasomal degradation, respectively, which were experimentally validated [6], [13]. MINDy relied on information theoretic principles to identify candidate modulators of TF activity, specifically by assessing the difference in mutual information, 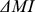 , between a TF and its target genes, when conditioning on the highest and lowest expression of any candidate modulator gene [14]. The algorithm was very effective in predicting novel candidate modulators that could be experimentally validated and associated with regulation of specific post-translational modifications [6], [12], [13], [15]. However, it was never systematically tested across a comprehensive set of established post-translational dependencies and suffers from a relatively high false negative rate. Indeed, use of the
, between a TF and its target genes, when conditioning on the highest and lowest expression of any candidate modulator gene [14]. The algorithm was very effective in predicting novel candidate modulators that could be experimentally validated and associated with regulation of specific post-translational modifications [6], [12], [13], [15]. However, it was never systematically tested across a comprehensive set of established post-translational dependencies and suffers from a relatively high false negative rate. Indeed, use of the 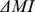 was originally chosen as a heuristic approximation of the theoretically correct analytical formulation. This analytical formulation analyzes the differences in multi mutual information of two different distributions describing two different topologies, one depicting the independent regulation of a target gene (Tg) by a modulator (M) and a TF (
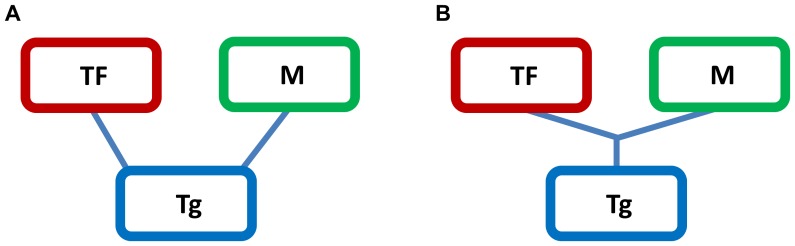
Figure 1A
) and the second one depicting a three-way interaction between the TF, the target gene and the modulator (
Figure 1B
). As proposed in [12], this difference requires estimation of:
was originally chosen as a heuristic approximation of the theoretically correct analytical formulation. This analytical formulation analyzes the differences in multi mutual information of two different distributions describing two different topologies, one depicting the independent regulation of a target gene (Tg) by a modulator (M) and a TF (
Figure 1A
) and the second one depicting a three-way interaction between the TF, the target gene and the modulator (
Figure 1B
). As proposed in [12], this difference requires estimation of:
| (Eq.1) |
for the inference of a three-way interaction, where M is any modulator protein affecting the ability of a transcription factor (TF) to regulate its targets (Tg). Indeed, at the time the algorithm was developed, using the theoretically derived formulation would have been a prohibitive undertaking, both computationally and in terms of data requirements. One of the critical limitations of the 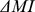 heuristic was that we had to assume
heuristic was that we had to assume 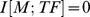 , thus limiting the analysis strictly to modulators whose expression was statistically independent of the TF's, a condition that precluded the analysis of many relevant modulator proteins. This constraint limits the inference of three-way interactions to the conditional interactions, i.e. those between TF and Tg that are conditionally dependent on the expression of M. Inference of true conditional transcriptional interactions requires.
, thus limiting the analysis strictly to modulators whose expression was statistically independent of the TF's, a condition that precluded the analysis of many relevant modulator proteins. This constraint limits the inference of three-way interactions to the conditional interactions, i.e. those between TF and Tg that are conditionally dependent on the expression of M. Inference of true conditional transcriptional interactions requires.
Figure 1. Alternative three-way network topologies including a Transcription Factor (TF), a Target gene (Tg) and a Modulator gene (M).
(A) depicts the independent regulation of the target gene by a modulator and a TF; (B) describes a three-way interaction between the TF, the target gene and the modulator.
| (Eq.2) |
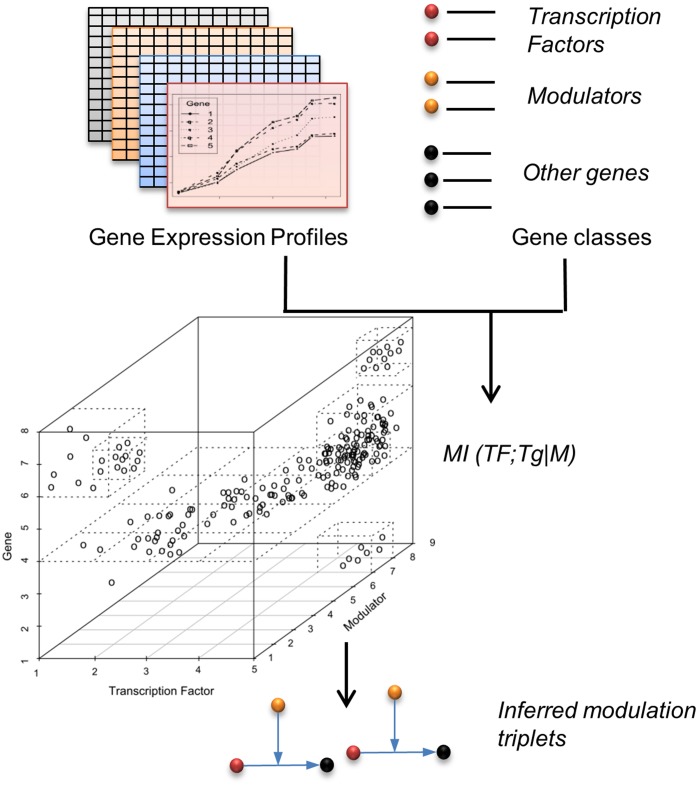
Moreover, the explicit test of independence (i.e. 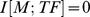 ) increases the false negative rate by not considering the possibility where despite the existence of dependency between M and TF's expression, Eq. 2 is satisfied. To address these problems we now introduce a computationally efficient solution to estimate the full conditional mutual information (CMI), based on adaptive partitioning [16], thus avoiding any heuristics, removing the limitations of the previous formulation, and embracing the correct theoretical model for the dissection of conditional interactions. Adaptive partitioning is a very efficient method for calculating the Shannon entropy of joint gene distributions [16], using a histogram based approach (
Figure 2
). The new approach has been implemented in a novel algorithm for the Conditional Inference of Network Dynamics (CINDy). Elucidating candidate modulators of TF activity is an extremely important problem in biology, as it helps dissect the logic by which signal transduction pathways regulate transcriptional programs. We applied CINDy to two independent datasets and evaluated its precision and sensitivity in predicting experimentally validated post-translational modulators of TF activity. We also compared the performance of CINDy with the original MINDy algorithm. There are virtually no other available algorithms to dissect post-translational dependencies from gene expression profile data. As a result, comparison to MINDy is the most appropriate for the new algorithm.
) increases the false negative rate by not considering the possibility where despite the existence of dependency between M and TF's expression, Eq. 2 is satisfied. To address these problems we now introduce a computationally efficient solution to estimate the full conditional mutual information (CMI), based on adaptive partitioning [16], thus avoiding any heuristics, removing the limitations of the previous formulation, and embracing the correct theoretical model for the dissection of conditional interactions. Adaptive partitioning is a very efficient method for calculating the Shannon entropy of joint gene distributions [16], using a histogram based approach (
Figure 2
). The new approach has been implemented in a novel algorithm for the Conditional Inference of Network Dynamics (CINDy). Elucidating candidate modulators of TF activity is an extremely important problem in biology, as it helps dissect the logic by which signal transduction pathways regulate transcriptional programs. We applied CINDy to two independent datasets and evaluated its precision and sensitivity in predicting experimentally validated post-translational modulators of TF activity. We also compared the performance of CINDy with the original MINDy algorithm. There are virtually no other available algorithms to dissect post-translational dependencies from gene expression profile data. As a result, comparison to MINDy is the most appropriate for the new algorithm.
Figure 2. Schematic representations of the CINDy algorithm.
A collection of gene expression profiles is required to calculate Conditional Mutual Information between lists of modulators, transcription factors and putative target genes, with the final output of inferred modulation events.
Results
First, we tested the performance of the two algorithms (using default parameters) in inferring established modulatory interactions, using two distinct gene expression profile datasets: (a) a B-cell lymphoma dataset containing 226 samples [17] and (b) a lung adenocarcinoma TCGA dataset containing 412 samples [18]. These datasets were specifically selected to evaluate the algorithms' performance and applicability within different contexts and using gene expression profiles from different platforms (Affymetrix U133P2 microarrays and RNASeq, respectively). The results of these analyses are summarized in Table 1 .
Table 1. Default parameters used for running MINDy.
| Parameters | |||||
| Percentage of samples in each tail | MI p-value for independence between modulator and transcription factor | Corrected pvalue threshold for each modulator, transcription factor and target interaction | MI p-value for independence between transcription factor and target | FDR p-value for TF/modulator pair | |
| MINDy | 35% | 10−5 | 0.05 | 10−6 | 0.05 |
| CINDy | NA | NA | 0.05 | NA | 0.05 |
NA: Not applicable.
Briefly, for the MINDy algorithm, for each candidate modulator gene, M, we tested only TFs with expression statistically independent of M, as assessed by the statistical significance of the Mutual Information of their gene expression profiles. We also discarded candidate target genes whose gene expression was highly correlated with that of the associated TF, thus restricting the number of candidate target genes in the analysis. Both of these are a requirement for using the 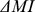 heuristics in place of the full CMI formulation. MINDy proceeds by selecting two non-overlapping sample subsets (
heuristics in place of the full CMI formulation. MINDy proceeds by selecting two non-overlapping sample subsets ( and
and  ) representing 35% highest and 35% lowest expression of M (a heuristically selected threshold). Then, for each TF considered in the analysis, the mutual information
) representing 35% highest and 35% lowest expression of M (a heuristically selected threshold). Then, for each TF considered in the analysis, the mutual information 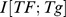 between the TF and each candidate target gene is computed independently from the
between the TF and each candidate target gene is computed independently from the 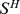 and from the
and from the 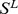 samples and the statistical significance of their difference (i.e.,
samples and the statistical significance of their difference (i.e., 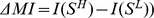 is evaluated using a null model based on sample permutations. For each candidate M
is evaluated using a null model based on sample permutations. For each candidate M  TF interaction, the number of target genes,
TF interaction, the number of target genes, 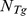 , producing a statistically significant
, producing a statistically significant 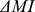 is computed. For CINDy, instead, the full conditional mutual information analysis is performed (see Eq. 2 and
Materials and Methods
).
is computed. For CINDy, instead, the full conditional mutual information analysis is performed (see Eq. 2 and
Materials and Methods
).
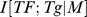 is calculated using an estimation of 3-dimensional probability distribution, whereas
is calculated using an estimation of 3-dimensional probability distribution, whereas 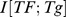 is calculated using an estimation of 2-dimansional probability distribution, therefore numerically
is calculated using an estimation of 2-dimansional probability distribution, therefore numerically 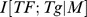 cannot be compared to
cannot be compared to 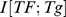 , thus making the calculation of Eq.2 a non-trivial problem. To solve this, we used a null model that is centered around
, thus making the calculation of Eq.2 a non-trivial problem. To solve this, we used a null model that is centered around 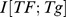 (see
Materials and Methods
). This null model not only eliminates the need to compare
(see
Materials and Methods
). This null model not only eliminates the need to compare 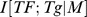 and
and 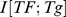 but also assesses the statistical significance of Eq. 2. This eliminates both the
but also assesses the statistical significance of Eq. 2. This eliminates both the 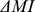 heuristics, as well as the arbitrary parameter controlling the tail sizes used in the MINDy implementation. Again, the number of candidate targets
heuristics, as well as the arbitrary parameter controlling the tail sizes used in the MINDy implementation. Again, the number of candidate targets 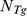 needed to produce a statistically significant CMI for a candidate M
needed to produce a statistically significant CMI for a candidate M  TF interaction is computed. Finally, for both algorithms, significant M
TF interaction is computed. Finally, for both algorithms, significant M  TF interactions are inferred based on the number of statistically significant conditional target interactions, using a statistical model. In brief, for a particular FDR threshold (default FDR = 0.05), the number of affected targets in the null hypothesis is assessed by running both algorithms repeatedly over the same dataset, following random modulator expression assignment. The final result is a list of M
TF interactions are inferred based on the number of statistically significant conditional target interactions, using a statistical model. In brief, for a particular FDR threshold (default FDR = 0.05), the number of affected targets in the null hypothesis is assessed by running both algorithms repeatedly over the same dataset, following random modulator expression assignment. The final result is a list of M  TF pairs and associated p-values.
TF pairs and associated p-values.
To objectively assess the performance of the two algorithms, we compared the modulatory interactions they inferred to a set of validated Protein-Protein Interactions (PPIs) between TFs and candidate modulator proteins (“gold standard dataset,” PPIGold). The latter was generated by taking the union of interactions obtained from four independent databases: for generic PPIs, we combined the interactions in HPRD [19], Y2H db [20] and STRING [21], while for candidate kinase/target pairs, we used the PhosphoSite database [22] (see Materials and Methods and Figure S1). Algorithm performance was evaluated by computing recall rate, defined as the fraction of inferred interactions in the PPIGold, and precision rate, defined as 1 minus the fraction of inferred interactions not present in the PPIGold. An important point to note is that the PPIGold dataset contains only a very small fraction of all true biological PPIs. Therefore, any precision estimates represent highly underestimated values. Indeed, precision should be used only as a comparative metric here such that recall may be computed either at roughly the same or better precision and is not representative of true precision, which can only be assessed from experimental validation.
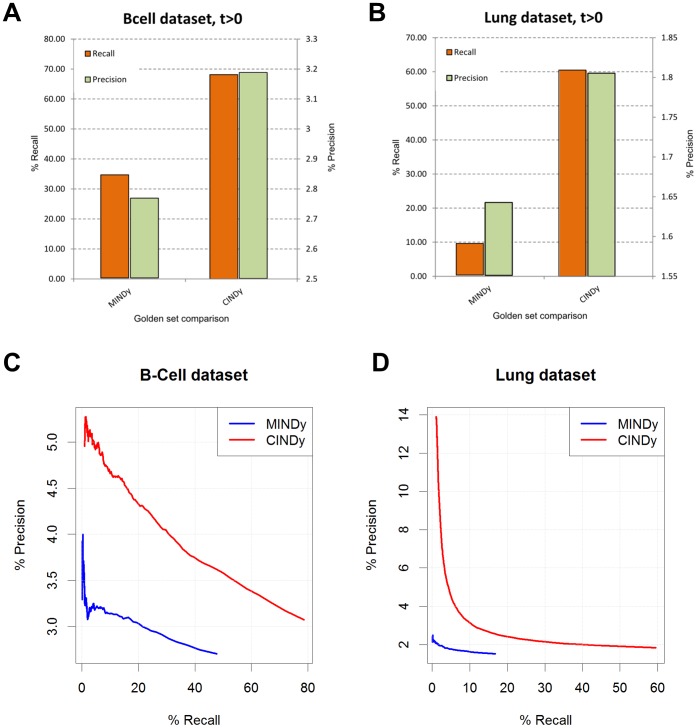
In B-Cell lymphoma ( Figure 3A ), CINDy outperformed MINDy by achieving significantly higher recall and precision. In fact, CINDy achieves roughly twice the recall of MINDY (68.13% vs. 34.37%) while also increasing precision (3.19% vs. 2.76%). Similarly, in lung adenocarcinoma ( Figure 3B ) CINDy achieves a 60.50% recall rate with 1.81% precision, whereas MINDy achieves a dramatically smaller recall of 9.26% at an even lower precision of 1.64%.
Figure 3. Comparative performance of MINDy and CINDy.
Precision and recall values are compared in the B-cell lymphoma dataset (panel A) and Lung Adenocarcinoma dataset (panel B), calculated by matching the predictions with a gold standard dataset set obtained from four different databases of experimentally validated PPIs between modulators and transcription factors. Precision and recall are further compared at different robustness threshold for MINDy (blue line) and CINDy (red line) in the B-cell dataset (panel C) and in the Lung dataset (panel D, see Materials and Methods ).
We also evaluated the performance of both algorithms by changing the stringency of the analysis, i.e., the minimum number of statistically significant (TF, Tg) interactions (i.e., 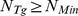 ) required to call a M
) required to call a M  TF modulatory interaction. To simplify the analysis, since the number of significant target interactions is discrete and hence a precise relationship with a meaningful FDR rate is not always possible, we considered
TF modulatory interaction. To simplify the analysis, since the number of significant target interactions is discrete and hence a precise relationship with a meaningful FDR rate is not always possible, we considered 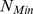 values between 1 and 300, a significant FDR range between 1 and 10−16. As expected, with the increase of the stringency threshold we observed a decrease in recall rate by both methods in both datasets (
Figure 3C–D
). However, at any equivalent recall rate, CINDy significantly outperformed MINDy. As expected, precision was positively correlated with the stringency threshold. Taken together, these findings show that use of the correct conditional mutual information model significantly outperforms the
values between 1 and 300, a significant FDR range between 1 and 10−16. As expected, with the increase of the stringency threshold we observed a decrease in recall rate by both methods in both datasets (
Figure 3C–D
). However, at any equivalent recall rate, CINDy significantly outperformed MINDy. As expected, precision was positively correlated with the stringency threshold. Taken together, these findings show that use of the correct conditional mutual information model significantly outperforms the 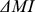 heuristics proposed in [2].
heuristics proposed in [2].
Due to the resulting differences in the analysis, the computational requirements of the algorithms are different (Figure S2). When using identical computational environments, CINDy requires almost double the time of MINDy, mostly due to using the entire dataset rather than just the top and bottom 25%. However, its memory requirements are half of those of MINDy (Figure S2).
Much of the computational requirements for the algorithms are due to the fact that every gene is considered as a candidate TF target by the analysis. To reduce both computation time and memory requirements (Figure S3), one can consider TF targets that are either experimentally assessed from CHIP-Seq and or TF silencing assays [23], [24], inferred by reverse engineering algorithms, such as ARACNe [3], CLR [25], Mider [26], and others [27]–[29], or from sequence specific TF binding sites [30]. Although this provides a significant computational advantage and without decreasing precision, use of pre-determined target genes significantly decreases the number of correctly predicted TF modulators in the gold set, hence increasing the false negative rate (Figure S4 and Table S1).
Finally, we assessed the performance of CINDy by varying the number of gene expression profiles, n. We varied n from 50 to 200 with an interval of 25 and assessed the performance by inferring modulatory interactions for 100 transcription factors and modulators with maximum connection in the gold standard dataset. For a given n we repeated the assessment 100 times by resampling the gene expression profiles. This analysis showed that whereas there is no change in the precision with varying n there is a constant increase in recall rate with increasing n (Figure S5).
CINDy identifies novel modulatory interactions
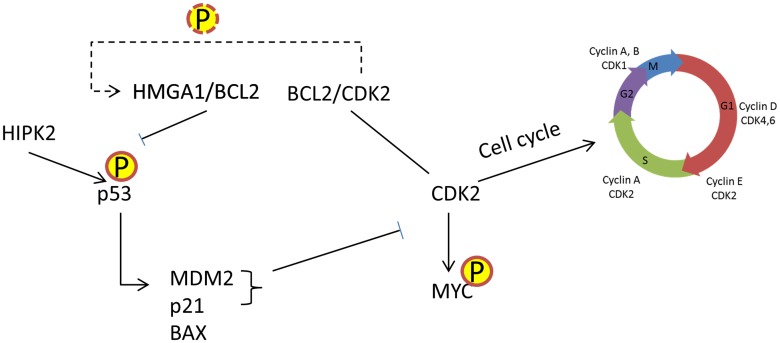
CINDy confirmed previous predictions of modulatory interactions, such as MYC activity modulation by the STK38, MAPK1 and CSNK2A1 proteins in B-cell lymphoma [12], but it also inferred a large number of established post-translational regulatory interactions that could not be detected by MINDy (Table S2), as well as several novel predictions. Among the newly inferred MYC activity modulators, we find many signaling proteins and TFs that are associated with B-lymphoma malignancies, including ATM [31], CDK2 [32], MYC [33], [34], HIF1A [35] [36] and NFKB [37]. In addition, many of the protein pairs inferred only by CINDy are well-known and have been experimentally validated, e.g. GSK3B/MYC [38], IKBKB/NFKB1 [39], MAPK1/MYC [40]. However, when considering post-translational modulators of proteins known to play a causal role in B-lymphoma, such as MYC and BCL6, their CINDy inferred modulators are generally unknown and likely to be experimentally validated, since experimental validation of MINDy prediction has been consistently in the 70% - 80% range. These predictions identify several interesting and potentially biologically relevant links. For instance, the interaction between CDK2 and HMGA1, predicted only by CINDy, may constitute a previously uncharacterized signaling bridge during cell cycle progression. The CDK2 kinase belongs to the family of cyclin-dependent kinases (CDKs) regulating cell cycle [41] and its activity depends on the interactions with other regulatory proteins, A or E-type cyclins, complexes of which are involved in the regulation of G1 and S phase transitions [42], [43]. The functional role of CDK2 in maintaining neoplastic growth was previously reported [44]–[46]. HMGA1 belongs to the family of non-histone chromatin-associated high-mobility group proteins involved in various cellular processes including heterochromatin organization, regulation of gene transcription, DNA replication and it is overexpressed in malignant neoplasms but not in normal adult cells [47]. Causal regulation of HMGA1 activity by CDK2 was never previously reported. However, there are many clues suggesting that such an interaction may be realistic ( Figure 4 ). HMGA1 was shown to contribute to neoplastic transformation by modulating transcriptional activity of p53 leading to inhibition of apoptosis [48], [49]. Transcriptional targets of p53, MDM2 and p21, have been shown to inhibit CDK2 activity and contribute to p53-dependent cell cycle arrest [50]. Both, HMGA1 and CDK2 were shown to interact with BCL2 [51], [52]. Hence it is not unlikely that they may form a functional complex. Thus MINDy provides direct clues leading to experimentally testable hypotheses that may elucidate novel functional interactions in tumorigenesis as previously reported [2], [6], [13].
Figure 4. Example of novel prediction by CINDy.
Proposed mechanism for modulation of HMGA1 by CDK2.
In lung adenocarcinoma, CINDy specifically highlights modulatory interactions that affect epithelial proliferation, such as the direct phosphorylation by the Epidermal Growth Factor Receptor (EGFR) of the STAT1 [53] and STAT3 [54] TFs, a fundamental and well established step in the proliferative signal transduction cascade that was not detected by MINDy. Another modulatory interactions found exclusively by CINDy is the phosphorylation of GATA binding protein 1 (GATA1) by the kinase ERK2/MAPK1 [55]. Other non-phosphorylation dependent modulations, like the transcriptional co-activation of the proliferative transcription factor Forkhead box protein M1 (FOXM1) by the histone acetyltransferase CREB binding protein (CREBBP), show how the algorithm can dissect a variety of regulatory interactions, mediated by diverse post-translational mechanisms and simply undetectable by conventional gene expression analysis [56].
Discussion
The most pressing challenge for Systems Biology is the development of model-based approaches for the veritable interpretation of an avalanche of new biological data. Reverse engineering algorithms provide a key approach to build regulatory models representing the molecular mechanisms that control cell behavior. These models in turn can provide critical novel knowledge about mechanistic control of physiologic processes [57] and their dysregulation in disease [5]–[7], [58]–[62], thus allowing the rapid, genome-wide generation of new testable biological hypotheses. By leveraging broadly available gene expression data, the MINDy algorithm allowed high-fidelity reconstruction of complex post-translational causal dependencies, where a modulator protein can affect the transcriptional activity of a TF on its targets. Replacing the original empirical formulation of the MINDy algorithm with the theoretically correct one, based on the conditional mutual information, the CINDy algorithm dramatically improves both recall and precision, thus virtually doubling the number of candidate modulatory interactions while also decreasing false positives. This allows inference of many interactions that were experimentally established such as the activation of the STAT TFs by EGFR aberrant signals or the activation of MYC by GSK3B, which could not be previously detected. The inclusion of prior knowledge to reduce the search space of CINDy to a subset of the potential TF target genes shows benefit both in terms of increased precision and substantial decrease in computational time, albeit at the price of decreased sensitivity. The dataset size also seems to be affecting the performance of CINDy, since intuitively, more samples drive higher recall rates at comparable precision. Fewer than 100 samples results in very small recall rate and only by using>150 samples does CINDy produce a reasonable recall rate (>20%). Therefore, it is recommended to use CINDy with a minimum of 150 samples. It is foreseeable that in the future with the concurrent increase of broader and more accurate databases for context-specific experimentally validated regulatory networks, more sophisticated CMI-based tools will be developed to integrate weighted evidences coming from different sources, such as novel MI-based reverse engineering methods [63], sequence motif analysis [64], or ChIP-seq data [23]).
Due to its general formulation, CINDy can identify a variety of post-translational interaction mechanisms that go beyond standard post-translational modification (e.g., phosphorylation, or ubiquitylation events), such as recruitment of CREBBP to FOXM1 and consequent transcriptional activation. It is also able to generate novel testable hypotheses for intriguing dependencies, such as regulation of HMGA1 activity by CDK2 ( Figure 4 ).
Importantly, by adopting a theoretically rigorous formulation, CINDy does away with many of the heuristics and parameter choices of the MINDy implementation. For instance, the need to select arbitrary tails of the modulator expression, the somewhat arbitrary thresholds used to evaluate a modulator TF interaction or the statistical dependency between a TF and a candidate target gene, as well as the statistical significance of 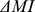 (
Table 1
). CINDy effectively eliminates the requirement to choose nonstandard values for these parameters or eliminates them altogether. Indeed, CINDy requires only the selection of a statistical threshold to evaluate the statistical significance of the CMI, thus making the algorithm extremely robust. Altogether, our finding shows that CINDy is a novel standard tool for inferring genome-wide modulation events affecting transcription factor activity.
(
Table 1
). CINDy effectively eliminates the requirement to choose nonstandard values for these parameters or eliminates them altogether. Indeed, CINDy requires only the selection of a statistical threshold to evaluate the statistical significance of the CMI, thus making the algorithm extremely robust. Altogether, our finding shows that CINDy is a novel standard tool for inferring genome-wide modulation events affecting transcription factor activity.
Materials and Methods
Expression datasets
We ran the CINDy and MINDy algorithms on two independent datasets, called “Lung dataset” and “B-Cell dataset”. The Lung dataset originates from the TCGA gene expression study [18], and it contains genome wide gene expression profiles of 412 RNASeq samples (Synapse v6 release: https://www.synapse.org/#!Synapse:syn395683), RPKM-normalized. The B-Cell dataset derives from human B-cell microarray gene expression experiments [17], and it's constituted by 226 samples profiled on the Affymetrix U133P2 platform.
Transcription factors and modulator genes
Transcription factors and modulator gene lists used to run MINDy in this study were defined as in [12] and then further extended with the current Gene Ontology (GO) annotations [65]. In brief, a “transcription factor” gene was defined as such if annotated in the GO molecular category “transcription factor activity”, while a “modulator” is defined as a gene belonging to any of the following molecular functions: protein kinase activity, phosphoprotein, phosphatase activity, acetyltransferase activity, deacetylase activity or signal transduction. The lists were further manually curated and are available in the Table S3, containing 3,203 candidate modulators and 1,673 transcription factors. 210 of these genes fall in both categories (e.g. CREB1, NFKB1 and TP53), i.e. they have both the transcriptional as well as modulatory function, and were therefore processed in our analyses both as candidate modulators and transcription factors.
Gold standard sets
We collected human PPI interactions from HPRD release 9 (3,637 unique modulator/TF interactions), Y2H (170), Strings v9.0.5 (81,504) and human phosphorylation kinase/target pairs from PhosphoSite (541), totaling 82,160 distinct modulator/TF interactions (Figure S1). We excluded homodimerization interactions and peptides that could not be unambiguously mapped to any Entrez gene id.
Adaptive Partitioning (AP)
AP is an algorithm for dynamic binning of the expression distribution, which can be applied for calculation of mutual information between two or more variables [16], [26]. An initial partitioning is applied, centered on the median of the distributions, and then partitioning proceeds in the quadrants where the sample distribution is significantly non-uniform (assessed by 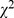 test)
test)
Conditional Mutual Information (CMI)
The CMI between a Transcription Factor (TF) and a Target Gene (Tg), given a putative Modulator (M) is inferred by estimating the conditional probability distribution using an adaptive partitioning approach:
| (Eq.3) |
where p indicates the outcome probability for a given gene expression range.
CMI is therefore analogous to conditional partial correlation for mutual information calculation [66]: the relationship between TF and Tg is assessed while keeping M constant. If this relationship changes significantly depending on the M distribution, MINDy will report M as a putative modulator of the interaction between TF and Tg ( Figure 2 ).
Null Model to estimate significance of CMI
To assess the statistical significance of a particular CMI, we generate a series for null models, each for different ranges of mutual information between TF and Tg. To build this null model, first we randomly select 104 distinct (TF,Tg) pairs and estimate 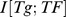 between them using the adaptive partitioning method. Next for each of these pairs we calculate 1000 CMI scores using the randomized expression of modulators. We bin the entire range of
between them using the adaptive partitioning method. Next for each of these pairs we calculate 1000 CMI scores using the randomized expression of modulators. We bin the entire range of 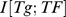 into 100 equi-probable bins, resulting in 100 TF-Tg pairs and 105 CMI values in each bin. Within each bin, we model the distribution of CMI as an extended exponential,
into 100 equi-probable bins, resulting in 100 TF-Tg pairs and 105 CMI values in each bin. Within each bin, we model the distribution of CMI as an extended exponential, 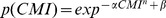 (as described in [67]). To estimate the pvalue of given CMI, we estimate the mutual information between TF and Tg from this CMI to identify the bin and use the extended exponential model from that bin to extrapolate the probability of that CMI.
(as described in [67]). To estimate the pvalue of given CMI, we estimate the mutual information between TF and Tg from this CMI to identify the bin and use the extended exponential model from that bin to extrapolate the probability of that CMI.
Supporting Information
Number of modulator/transcription factor associations in four independent databases, and relative intersections.
(TIF)
Comparative computational performance of MINDy and CINDy. The test was performed on the human B-cell dataset [17] with 100TFs 100 Modulators and 250 samples. Reported are the mean and standard deviations of all the 100 MINDy runs. The performance was assessed on a 16 x Intel Xeon CPU E5-2630 0 @ 2.3 GHz machine with 30,098,316K total RAM.
(TIF)
CINDy performance on a single TF-Modulator pair using increasing number of target genes. The vertical black line to the left indicates the average number of targets in the dataset (97.2). For this particular dataset, on average, MINDY using all genes is almost 130 times slower than using target genes, and requires almost 28 times more RAM.
(TIF)
Benchmark of MINDy runs using a subset of target genes defined by ARACNe [27] (p-value 10e-8). A-B Precision and recall of MINDy, CINDy, intersection and union sets in the B-cell and Lung datasets, calculated over a golden set of four databases of experimentally validated PPIs between modulators and transcription factors. C-D Precision/Recall plots for MINDy (blue points) and CINDy (red points) at different robustness thresholds (see Materials and Methods ).
(TIF)
Effects of sample size on precision and recall in the B-cell dataset (226 samples). The precision/recall curves were calculated using the 100 TFs and modulators with most connections in the gold standard set (Figure S1). The error bars indicate the standard deviation in the estimation of precision and recall obtained by running CINDy over 100 datasets generated by subsampling.
(TIF)
Raw performance information for CINDy and MINDy in the lung adenocarcinoma and B-cell lymphoma datasets, at different thresholds defined by the number of target genes affected by the modulation events.
(XLSX)
Significant modulation events predicted by CINDy and MINDy at standard parameters in the B-Cell and Lung datasets. The number of significant conditional target interactions for each M  TF is also reported.
TF is also reported.
(XLSX)
Gene symbols used in the current manuscript as modulator genes or transcription factors.
(XLSX)
Acknowledgments
We would like to thank Manjunath Kustagi for implementing and packaging CINDy in distributable format.
Data Availability
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper and its Supporting Information files.
Funding Statement
This work was supported by MaGNeT (Multiscale Analysis of Genomic and Cellular Networks - http://magnet.c2b2.columbia.edu/) grant (5U54CA121852) and CTD2 (Cancer Target Discovery and Development - http://ocg.cancer.gov/programs/ctd2) grant (U01CA168426). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Lefebvre C, Rieckhof G, Califano A (2012) Reverse-engineering human regulatory networks. Wiley Interdiscip Rev Syst Biol Med 4: 311–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Wang K, Saito M, Bisikirska BC, Alvarez MJ, Lim WK, et al. (2009) Genome-wide identification of post-translational modulators of transcription factor activity in human B cells. Nat Biotechnol 27: 829–839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Basso K, Margolin AA, Stolovitzky G, Klein U, Dalla-Favera R, et al. (2005) Reverse engineering of regulatory networks in human B cells. Nat Genet 37: 382–390. [DOI] [PubMed] [Google Scholar]
- 4. Giorgi FM, Del Fabbro C, Licausi F (2013) Comparative study of RNA-seq-and Microarray-derived coexpression networks in Arabidopsis thaliana. Bioinformatics 29: 717–724. [DOI] [PubMed] [Google Scholar]
- 5. Carro MS, Lim WK, Alvarez MJ, Bollo RJ, Zhao X, et al. (2010) The transcriptional network for mesenchymal transformation of brain tumours. Nature 463: 318–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Zhao X, D DA, Lim WK, Brahmachary M, Carro MS, et al. (2009) The N-Myc-DLL3 cascade is suppressed by the ubiquitin ligase Huwe1 to inhibit proliferation and promote neurogenesis in the developing brain. Dev Cell 17: 210–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aytes A, Mitrofanova A, Lefebvre C, Alvarez MJ, Castillo-Martin M, et al. (2014) Cross-species analysis of genome-wide regulatory networks identifies a synergistic interaction between FOXM1 and CENPF that drives prostate cancer malignancy. Cancer Cell, in press. [DOI] [PMC free article] [PubMed]
- 8. Schadt EE, Lamb J, Yang X, Zhu J, Edwards S, et al. (2005) An integrative genomics approach to infer causal associations between gene expression and disease. Nat Genet 37: 710–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Friedman N (2004) Inferring cellular networks using probabilistic graphical models. Science 303: 799–805. [DOI] [PubMed] [Google Scholar]
- 10. Zampieri M, Soranzo N, Altafini C (2008) Discerning static and causal interactions in genome-wide reverse engineering problems. Bioinformatics 24: 1510–1515. [DOI] [PubMed] [Google Scholar]
- 11. Luscombe NM, Babu MM, Yu H, Snyder M, Teichmann SA, et al. (2004) Genomic analysis of regulatory network dynamics reveals large topological changes. Nature 431: 308–312. [DOI] [PubMed] [Google Scholar]
- 12. Wang K, Saito M, Bisikirska BC, Alvarez MJ, Lim WK, et al. (2009) Genome-wide identification of post-translational modulators of transcription factor activity in human B cells. Nature biotechnology 27: 829–837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Bisikirska BC, Adam SJ, Alvarez MJ, Rajbhandari P, Cox R, et al. (2012) STK38 is a critical upstream regulator of MYC's oncogenic activity in human B-cell lymphoma. Oncogene. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bansal M, Califano A (2012) Genome-wide dissection of posttranscriptional and posttranslational interactions. Gene Regulatory Networks: Springer. pp. 131–149. [DOI] [PubMed] [Google Scholar]
- 15. Mani KM, Lefebvre C, Wang K, Lim WK, Basso K, et al. (2008) A systems biology approach to prediction of oncogenes and molecular perturbation targets in B-cell lymphomas. Mol Syst Biol 4: 169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Liang K-C, Wang X (2008) Gene regulatory network reconstruction using conditional mutual information. EURASIP Journal on Bioinformatics and Systems Biology 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Basso K, Saito M, Sumazin P, Margolin AA, Wang K, et al. (2010) Integrated biochemical and computational approach identifies BCL6 direct target genes controlling multiple pathways in normal germinal center B cells. Blood 115: 975–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Hammerman P, Lawrence M, Voet D, Jing R, Cibulskis K, et al. (2012) Comprehensive genomic characterization of squamous cell lung cancers. Nature 489: 519–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Prasad TK, Goel R, Kandasamy K, Keerthikumar S, Kumar S, et al. (2009) Human protein reference database—2009 update. Nucleic acids research 37: D767–D772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Yu H, Tardivo L, Tam S, Weiner E, Gebreab F, et al. (2011) Next-generation sequencing to generate interactome datasets. Nature methods 8: 478–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Franceschini A, Szklarczyk D, Frankild S, Kuhn M, Simonovic M, et al. (2013) STRING v9. 1: protein-protein interaction networks, with increased coverage and integration. Nucleic acids research 41: D808–D815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Hornbeck PV, Kornhauser JM, Tkachev S, Zhang B, Skrzypek E, et al. (2012) PhosphoSitePlus: a comprehensive resource for investigating the structure and function of experimentally determined post-translational modifications in man and mouse. Nucleic acids research 40: D261–D270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Lachmann A, Xu H, Krishnan J, Berger SI, Mazloom AR, et al. (2010) ChEA: transcription factor regulation inferred from integrating genome-wide ChIP-X experiments. Bioinformatics 26: 2438–2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Basso K, Saito M, Sumazin P, Margolin AA, Wang K, et al. (2010) Integrated biochemical and computational approach identifies BCL6 direct target genes controlling multiple pathways in normal germinal center B cells. Blood 115: 975–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Faith JJ, Hayete B, Thaden JT, Mogno I, Wierzbowski J, et al. (2007) Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS biology 5: e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Villaverde AF, Ross J, Morán F, Banga JR (2014) Mider: network inference with mutual information distance and entropy reduction. PloS one 9: e96732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Margolin AA, Nemenman I, Basso K, Wiggins C, Stolovitzky G, et al. (2006) ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC bioinformatics 7: S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Opgen-Rhein R, Strimmer K (2007) From correlation to causation networks: a simple approximate learning algorithm and its application to high-dimensional plant gene expression data. BMC systems biology 1: 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Luo W, Hankenson KD, Woolf PJ (2008) Learning transcriptional regulatory networks from high throughput gene expression data using continuous three-way mutual information. BMC bioinformatics 9: 467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Matys V, Kel-Margoulis OV, Fricke E, Liebich I, Land S, et al. (2006) TRANSFAC and its module TRANSCompel: transcriptional gene regulation in eukaryotes. Nucleic acids research 34: D108–D110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Fang N, Greiner T, Weisenburger D, Chan W, Vose J, et al. (2003) Oligonucleotide microarrays demonstrate the highest frequency of ATM mutations in the mantle cell subtype of lymphoma. Proceedings of the National Academy of Sciences of the United States of America 100: 5372–5377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Al-Assar O, Rees-Unwin KS, Menasce LP, Hough RE, Goepel JR, et al. (2006) Transformed diffuse large B-cell lymphomas with gains of the discontinuous 12q12-14 amplicon display concurrent deregulation of CDK2, CDK4 and GADD153 genes. British journal of haematology 133: 612–621. [DOI] [PubMed] [Google Scholar]
- 33. Dalla-Favera R, Martinotti S, Gallo RC, Erikson J, Croce CM (1983) Translocation and rearrangements of the c-myc oncogene locus in human undifferentiated B-cell lymphomas. Science 219: 963–967. [DOI] [PubMed] [Google Scholar]
- 34. Ott G, Rosenwald A, Campo E (2013) Understanding MYC-driven aggressive B-cell lymphomas: pathogenesis and classification. Blood 122: 3884–3891. [DOI] [PubMed] [Google Scholar]
- 35. Evens AM, Sehn LH, Farinha P, Nelson BP, Raji A, et al. (2010) Hypoxia-Inducible Factor-1 α Expression Predicts Superior Survival in Patients With Diffuse Large B-Cell Lymphoma Treated With R-CHOP. Journal of Clinical Oncology 28: 1017–1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Qiao Q, Nozaki Y, Sakoe K, Komatsu N, Kirito K (2010) NF-κB mediates aberrant activation of HIF-1 in malignant lymphoma. Experimental hematology 38: 1199–1208. [DOI] [PubMed] [Google Scholar]
- 37. Gilmore T (1991) Role of rel family genes in normal and malignant lymphoid cell growth. Cancer surveys 15: 69–87. [PubMed] [Google Scholar]
- 38. Grimes C, Jope R (2001) The multifaceted roles of glycogen synthase kinase 3beta in cellular signaling. Prog Neurobiol 65: 391–426. [DOI] [PubMed] [Google Scholar]
- 39. Klapproth K, Sander S, Marinkovic D, Baumann B, Wirth T (2009) The IKK2/NF-κB pathway suppresses MYC-induced lymphomagenesis. Blood 114: 2448–2458. [DOI] [PubMed] [Google Scholar]
- 40. Seth A, Gonzalez FA, Gupta S, Raden DL, Davis RJ (1992) Signal transduction within the nucleus by mitogen-activated protein kinase. Journal of Biological Chemistry 267: 24796–24804. [PubMed] [Google Scholar]
- 41. Fisher RP (2012) The CDK Network Linking Cycles of Cell Division and Gene Expression. Genes & cancer 3: 731–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Morgan DO (1995) Principles of CDK regulation. Nature 374: 131–134. [DOI] [PubMed] [Google Scholar]
- 43. Obaya A, Sedivy J (2002) Regulation of cyclin-Cdk activity in mammalian cells. Cellular and Molecular Life Sciences CMLS 59: 126–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Du J, Widlund HR, Horstmann MA, Ramaswamy S, Ross K, et al. (2004) Critical role of CDK2 for melanoma growth linked to its melanocyte-specific transcriptional regulation by MITF. Cancer cell 6: 565–576. [DOI] [PubMed] [Google Scholar]
- 45. Faber AC, Chiles TC (2007) Inhibition of cyclin-dependent kinase-2 induces apoptosis in human diffuse large B-cell lymphomas. CELL CYCLE-LANDES BIOSCIENCE- 6: 2982. [DOI] [PubMed] [Google Scholar]
- 46. Junk DJ, Cipriano R, Stampfer M, Jackson MW (2013) Constitutive CCND1/CDK2 activity substitutes for p53 loss, or MYC or oncogenic RAS expression in the transformation of human mammary epithelial cells. PloS one 8: e53776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Cleynen I, Van de Ven WJ (2008) The HMGA proteins: A myriad of functions (Review). International journal of oncology 32: 289–305. [PubMed] [Google Scholar]
- 48. Esposito F, Tornincasa M, Federico A, Chiappetta G, Pierantoni G, et al. (2012) High-mobility group A1 protein inhibits p53-mediated intrinsic apoptosis by interacting with Bcl-2 at mitochondria. Cell death & disease 3: e383. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 49. Frasca F, Rustighi A, Malaguarnera R, Altamura S, Vigneri P, et al. (2006) HMGA1 inhibits the function of p53 family members in thyroid cancer cells. Cancer research 66: 2980–2989. [DOI] [PubMed] [Google Scholar]
- 50. Giono LE, Manfredi JJ (2007) Mdm2 is required for inhibition of Cdk2 activity by p21, thereby contributing to p53-dependent cell cycle arrest. Molecular and cellular biology 27: 4166–4178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Crescenzi E, Sannino M, Tonziello G, Palumbo G (2002) Association of Bcl-2 with Cyclin A/Cdk-2 Complex and Its Effects on Cdk-2 Activity. Annals of the New York Academy of Sciences 973: 268–271. [DOI] [PubMed] [Google Scholar]
- 52. Esposito F, Tornincasa M, Chieffi P, De Martino I, Pierantoni GM, et al. (2010) High-mobility group A1 proteins regulate p53-mediated transcription of Bcl-2 gene. Cancer research 70: 5379–5388. [DOI] [PubMed] [Google Scholar]
- 53. Quelle FW, Thierfelder W, Witthuhn BA, Tang B, Cohen S, et al. (1995) Phosphorylation and activation of the DNA binding activity of purified Stat1 by the Janus protein-tyrosine kinases and the epidermal growth factor receptor. Journal of Biological Chemistry 270: 20775–20780. [DOI] [PubMed] [Google Scholar]
- 54. Shao H, Cheng HY, Cook RG, Tweardy DJ (2003) Identification and characterization of signal transducer and activator of transcription 3 recruitment sites within the epidermal growth factor receptor. Cancer research 63: 3923–3930. [PubMed] [Google Scholar]
- 55. Yu Y-L, Chiang Y-J, Chen Y-C, Papetti M, Juo C-G, et al. (2005) MAPK-mediated phosphorylation of GATA-1 promotes Bcl-XL expression and cell survival. Journal of Biological Chemistry 280: 29533–29542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Major ML, Lepe R, Costa RH (2004) Forkhead box M1B transcriptional activity requires binding of Cdk-cyclin complexes for phosphorylation-dependent recruitment of p300/CBP coactivators. Molecular and cellular biology 24: 2649–2661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Lefebvre C, Rajbhandari P, Alvarez MJ, Bandaru P, Lim WK, et al. (2010) A human B-cell interactome identifies MYB and FOXM1 as master regulators of proliferation in germinal centers. Mol Syst Biol 6: 377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Califano A, Butte AJ, Friend S, Ideker T, Schadt E (2012) Leveraging models of cell regulation and GWAS data in integrative network-based association studies. Nat Genet 44: 841–847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Piovan E, Yu J, Tosello V, Herranz D, Ambesi-Impiombato A, et al. (2013) Direct Reversal of Glucocorticoid Resistance by AKT Inhibition in Acute Lymphoblastic Leukemia. Cancer Cell 24: 766–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Della Gatta G, Palomero T, Perez-Garcia A, Ambesi-Impiombato A, Bansal M, et al. (2012) Reverse engineering of TLX oncogenic transcriptional networks identifies RUNX1 as tumor suppressor in T-ALL. Nat Med 18: 436–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Sumazin P, Yang X, Chiu HS, Chung WJ, Iyer A, et al. (2011) An Extensive MicroRNA-Mediated Network of RNA-RNA Interactions Regulates Established Oncogenic Pathways in Glioblastoma. Cell 147: 307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. De Keersmaecker K, Real PJ, Gatta GD, Palomero T, Sulis ML, et al. (2010) The TLX1 oncogene drives aneuploidy in T cell transformation. Nat Med 16: 1321–1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Jang IS, Margolin A, Califano A (2013) hARACNe: improving the accuracy of regulatory model reverse engineering via higher-order data processing inequality tests. Interface focus 3: 20130011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Matys V, Fricke E, Geffers R, Gößling E, Haubrock M, et al. (2003) TRANSFAC: transcriptional regulation, from patterns to profiles. Nucleic acids research 31: 374–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Carbon S, Ireland A, Mungall CJ, Shu S, Marshall B, et al. (2009) AmiGO: online access to ontology and annotation data. Bioinformatics 25: 288–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Reverter A, Chan EK (2008) Combining partial correlation and an information theory approach to the reversed engineering of gene co-expression networks. Bioinformatics 24: 2491–2497. [DOI] [PubMed] [Google Scholar]
- 67. Margolin AA, Wang K, Lim WK, Kustagi M, Nemenman I, et al. (2006) Reverse engineering cellular networks. Nature Protocols 1: 662–671. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Number of modulator/transcription factor associations in four independent databases, and relative intersections.
(TIF)
Comparative computational performance of MINDy and CINDy. The test was performed on the human B-cell dataset [17] with 100TFs 100 Modulators and 250 samples. Reported are the mean and standard deviations of all the 100 MINDy runs. The performance was assessed on a 16 x Intel Xeon CPU E5-2630 0 @ 2.3 GHz machine with 30,098,316K total RAM.
(TIF)
CINDy performance on a single TF-Modulator pair using increasing number of target genes. The vertical black line to the left indicates the average number of targets in the dataset (97.2). For this particular dataset, on average, MINDY using all genes is almost 130 times slower than using target genes, and requires almost 28 times more RAM.
(TIF)
Benchmark of MINDy runs using a subset of target genes defined by ARACNe [27] (p-value 10e-8). A-B Precision and recall of MINDy, CINDy, intersection and union sets in the B-cell and Lung datasets, calculated over a golden set of four databases of experimentally validated PPIs between modulators and transcription factors. C-D Precision/Recall plots for MINDy (blue points) and CINDy (red points) at different robustness thresholds (see Materials and Methods ).
(TIF)
Effects of sample size on precision and recall in the B-cell dataset (226 samples). The precision/recall curves were calculated using the 100 TFs and modulators with most connections in the gold standard set (Figure S1). The error bars indicate the standard deviation in the estimation of precision and recall obtained by running CINDy over 100 datasets generated by subsampling.
(TIF)
Raw performance information for CINDy and MINDy in the lung adenocarcinoma and B-cell lymphoma datasets, at different thresholds defined by the number of target genes affected by the modulation events.
(XLSX)
Significant modulation events predicted by CINDy and MINDy at standard parameters in the B-Cell and Lung datasets. The number of significant conditional target interactions for each M  TF is also reported.
TF is also reported.
(XLSX)
Gene symbols used in the current manuscript as modulator genes or transcription factors.
(XLSX)
Data Availability Statement
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper and its Supporting Information files.