Modelling from the experimental developmental biologist’s viewpoint

1. Introduction

“So what good are models? The foregoing discussion may seem a bit depressing to theoretical biologists: all manner of models produce the same spatial patterns. Thus it is not generally possible to distinguish between models solely from the patterns they generate, and the question I raised at the beginning begs an answer: what good are models of pattern formation?” Oster [1]

The question posed in the above passage was pertinent at the time when George Oster – a theoretician – was writing and it captures an opinion that still persists to a degree among some experimental biologists today. Oster describes a range of different pattern-forming models based on qualitatively different biological phenomena, specifically neural interaction, the reaction between diffusing morphogens, chemotaxis and the mechanical properties of tissues. However, despite the differences in the biological phenomena these different models capture, they all display what are commonly called Reaction-Diffusion (RD), or as Oster refers to it, local activation and lateral inhibition (LALI) dynamics. Indeed, most patterning models at the time Oster was writing displayed such behaviours. Consequently, the types of patterns that these seemingly different models could generate were essentially the same. If different models of pattern formation capturing qualitatively different biological phenomena can generate the same patterns, how can the models inform our understanding of the patterning process?

In subsequent years, particularly the last decade, a number of papers consisting a joint experimental and theoretical approach have shown that models are of the utmost importance to our understanding of biological pattern formation. In this review we will first briefly examine the historical basis for the skepticism around theoretical models. We will then illustrate some recent studies of biological pattern formation focusing on RD type models, as this remains one of the most iconic and influential models in biological pattern formation. While there have been excellent reviews in this area [for example 2, 3], we hope to bring out the importance of a joint theoretical-experimental approach and demystify some of the frustrations each type of practitioner has in appealing to the other.

2. Background

The RD model has its origins in Alan Turing’s seminal 1952 paper [4]. Turing explicitly set out to discuss how well-known physical laws can account for the main phenomena of biological morphogenesis, specifically that of the embryo. While RD models are very familiar now, it is easy to forget how what Turing demonstrated was groundbreaking, and in many way counter-intuitive. He took a system of at least two diffusing chemicals (or morphogens as he named them), reacting with each other as they diffuse through tissue and showed that an initially stable state could be destabilized by the addition of diffusion. Thereby, a system with no spatial order could self-organise into a complex pattern. Of the six different types of spatial patterns that could be generated by such a system, Turing emphasized the set of stationary waves of a fixed period as being the most biologically interesting, noting the similarity of such patterns to the tentacles of a Hydra or patterns of phyllotaxis.

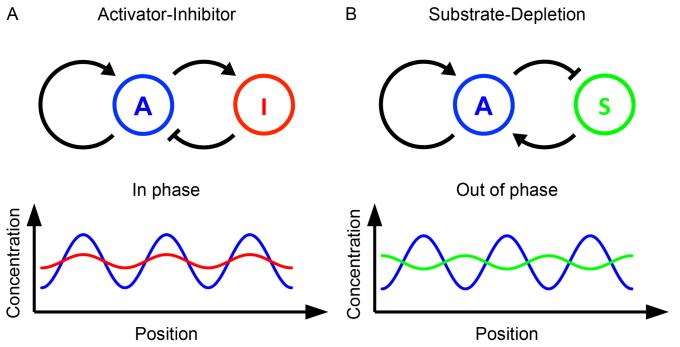
For the following two decades these ideas lay largely dormant until they were rediscovered by Gierer and Meinhardt. Gierer and Meinhardt were considering the role of well-known biological processes in patterning [5]. In particular they were inspired by the idea of lateral inhibition, which was known to operate in arthropod visual systems to amplify differences in signal intensity. Lateral inhibitory fields had previously been implicated in patterning, such as the spacing of leaf primordial and insect bristles [5], however, Gierer and Meinhardt added a second crucial component, namely local autoactivation – in the absence of autoactivation how would the inhibitory field not inhibit itself? They then demonstrated that these two processes – local autoactivation and lateral inhibition – were the essential components for the formation of pattern [6]. This can simply be thought of as a system containing two components: an activator and a faster diffusing inhibitor (Fig. 1A). A small fluctuation in activator level will be amplified by its autocatalytic behavior creating a peak in activator concentration. However, this will also increase levels of the faster diffusing inhibitor, which will spread and suppress the activator in the neighbouring tissue, resulting in regularly spaced peaks of activation.

Figure 1. Two component Reaction-Diffusion models.

(A) and (B) illustrate the two reaction topologies of diffusing morphogens that give rise to RD models. In Activator-Inhibitor models (A) the activator morphogen activates itself and its fast diffusing inhibitor, resulting in in phase waves of activator and inhibitor concentration. In Substrate-Depletion models (B) the activator activates itself and consumes its fast diffusing substrate (i.e. it inhibits its activator), resulting in out of phase waves of activator and substrate concentration. Adapted from [3].

It is important to remember that Gierer and Meinhardt emphasised the generality of their concept. At one level, it can be generated by a number of different network topologies. For example, they propose another two-component system commonly known as substrate-depletion (Fig. 1B). Here the inhibitor can be thought of as a substrate required for autocatalysis of the activator, which thereby locally depletes the substrate. Diffusion of the substrate from surrounding area creates an inhibitory depletion zone around the activator peak. Other systems of more components can be imagined, for example autoactivation through the inhibition of a second local inhibitor [7].

Indeed any system resulting in a local activation and a lateral inhibition has the potential to self-organize (depending on, for example, rates of morphogen diffusion or domain geometry amongst others). This applies to two-component systems as much as to complex networks. Even physical systems such sand dunes can be described in activator-inhibitor terms [8]. Turing’s diffusion driven instability and Gierer and Meinhardt’s concept of local activation and lateral inhibition are mathematically very similar [see references in 5]. However, not all systems describable by this type of mathematics fit Turing’s original concept of diffusing chemical morphogens – an important distinction in terms of the biology of the system. Specifically, we will refer to as specific or “strong” RD examples those cases consisting of systems of diffusing chemical morphogens, as put forward by Turing himself, while we will refer to other cases – those mediated by other, diffusion-like, processes such as chemotaxis or neural interactions – as general or “weak”. While, mathematical analysis of different the LALI systems demonstrate the same pattern forming behaviours [1] it is important to recognize the differences in physical mechanisms that this strong/weak distinction makes, not only from the experimentalist’s point of view, but also because practically speaking more detailed modelling post-Turing/Meinhardt has to take the physical manifestation of the LALI architecture into account.

In the subsequent years, many different formulations of the basic principle of local auto-activation and lateral inhibition were applied to a number of patterning problems. As well as those considering reaction between diffusing morphogens, models based on neural interactions, chemotaxis and mechanical forces were used to explain a range of biological patterns [1]. These ranged from the pigmentation patterns on mollusc shells, to mammalian coat patterns and even the sequence of appearance of alligator teeth.

These studies demonstrated that a theoretical model could simulate a pattern of interest. However, they did not provided any specific support for one model over another that could produce the same range of patterns. This brings us back to Oster’s pessimism. If different models capturing different phenomena predict the same patterns, what use are they? Oster does provide two important points in support of theoretical models. First, it should not be forgotten that while different models can predict the same outcomes, that does not mean that any of these models can predict any outcome – a point overlooked by many experimental biologists. This was elegantly shown by Oster et al [9] in the context of the developing limb. The cartilages of the developing tetrapod limb form in a proximal to distal direction as a series of bifurcations. A LALI model of this process predicts that only a limited number of types of bifurcation can occur. Moreover, other features such as trifurcations are very unlikely under the model. The model does not allow simply any old behaviour. (This is the exact opposite of how some skeptical experimentalists sometimes view mathematical models, namely as a “fudge” – a vehicle where the model can be made to fit reality by a trivial and arbitrary choice of parameters.)

Second, while different models predict the same range of patterns, the qualitatively different nature of the models means that different models would predict different responses to perturbation experiments. For example, as Oster argues, reaction-diffusion (in the strong sense of diffusing morphogens) and neural net models, which have both been proposed for mollusc shell pigmentation, may produce the same possible patterns, but only a neural model would be disrupted by neuroactive drugs. At the time Oster was writing this, the molecular knowledge and technology needed to achieve incisive perturbations were simply not there, and so it is perhaps not surprising that mathematical modelling in developmental biology underwent a decline while the experimental work had to catch up.

Ironically, early molecular genetic explorations of patterning actually appeared to argue against the importance of the elegantly self-organising models that had been prominent in the preceding years: early molecular genetic studies in Drosophila melanogaster showed that the early embryos are not homogeneous systems that need to self-organized to generate patterns [10]. In fact they are highly structured. For example, the periodic pattern of pair rule genes seen in Drosophila is not generated by a self-organizing system, but rather by a hierarchical genetic cascade, which is initially by a set up by a gradient of bicoid protein. This gradient is in turn generated by a maternally localised mRNA. This is very different from an elegant self-organizing system.

Thus, there were two reasons why theory in general and RD models in particular fell into disrepute. On the one hand there was a loss of confidence within the theoretical biology field due to the recognition that most interesting models were under-constraining relative to the then-feasible experimental methods. On the other, there was, ironically, a blossoming of experimental approaches that seemed to trump any theory and, in as far as they addressed it, seemed to show that nature achieved pattern in messier, cruder ways than the beautiful models suggested.

While Turing, Gierer and Meinhardt provided the mathematical “thesis” and the genetics of the 1980s and 1990s launched the experimental “antithesis”, we can now begin to talk about the synthesis between these two. There is increasing recognition that even the apparently simple Bicoid gradient is far from simple and requires some really sophisticated modelling to understand in terms of the underlying physics [11], while better tools and deeper understanding have revived an interest in systems that self-organise more conspicuously than Drosophila. In recent years, in particular the last decade, a joint theoretical-experimental approach has provided compelling support for the role of RD in biological patterning. We will now present a number of recent studies, illustrating how in many systems a combination of theoretical modeling and experimental biology has informed our understanding of biological pattern formation. These are the best examples we know of that confront the theory with experiment.

3. Heterocyst formation

Anabaena is a filamentous bacterium that differentiates specialized nitrogen fixing cells, called heterocysts, under nitrogen limiting conditions. The heterocysts form at regular intervals or approximately every 10 cells – a periodic pattern of the sort generated by RD systems (Fig. 2A). Moreover, as the filament grows new heterocysts differentiate in the increasing gap between existing heterocysts to maintain this periodicity, again consistent with an RD system. The theoretical framework of RD makes strong predictions about the system. Most simply there should be short-range autocatalysis and long-range inhibition.

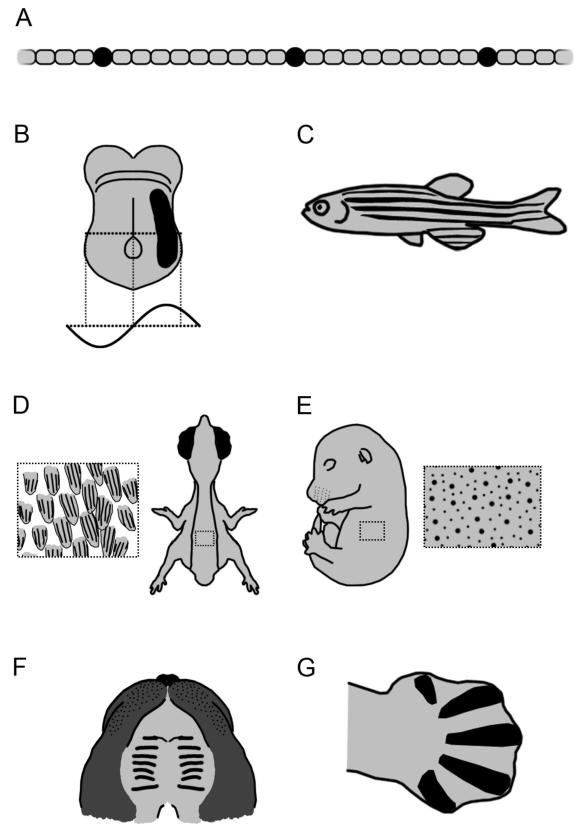
Figure 2. Biological systems patterned by Reaction-Diffusion type dynamics.

Schematics illustrating periodic patterns generated by RD dynamics, with periodic pattern element shown in black. (A) Regular spacing of nitrogen fixing heterocysts (black) in the filament forming bacterium Anabaena. (B) Ventral view of E8 mouse embryo showing expression of Nodal on the left hand side (based on [50]). Asymmetric gene expression creates a diffusion gradient of protein across the embryo, constituting one wave or part of one wave of a periodic pattern. (C) Zebrafish showing periodic pattern of longitudinal stripes of melanophores (black stripes), alternating with stripes of xanthophores. (D) Dorsal view of HH 37 chick embryo, with detail showing periodic spacing of feather buds. Within each feather bud, black lines show periodic spacing of developing feather barb ridges as marked by Sonic Hedgehog expression (based on [51]). (E) E15 mouse embryo with detail showing periodic spacing of primary hair follicles (large black spots) with secondary follicles (small black dots) spaced between (based on [52]). (F) Ventral view of E14 mouse palate with black lines marking out series of palatal ridges (rugae). (G) E12.5 mouse limb showing periodic pattern of forming digits (black) as visualised by Sox9 expression [based on 46].

Genetic studies have implicated a number of genes in the patterning process. Of particular importance are hetR, patS and hetN. Various studies have shown that hetR promotes the formation of heterocysts [12], while patS and hetN inhibit the process [13, 14]– candidates for the activator and inhibitor in an RD system. Molecular studies have further enforced these roles. In particular, the mode of autoactivation of the hetR protein was clearly demonstrated by Huang et al [15]. hetR dimers bind to their own promoter, promoting their own transcription. Moreover, hetR dimers also bind to the promoters of patS and hetN – the activator activates the inhibitor. patS and hetN inhibit hetR activity through the inhibition of DNA binding. They have also been shown to inhibit hetR post-translationally. The inhibition by these proteins has even been localised to a pentapeptide motif, with mutations to the motif relieving inhibition.

In an RD system, an activator acts locally, while the inhibitor acts more broadly. hetR fulfills the criterion of local autoactivation as it is expressed in the protoheterocyst and there is no evidence for its diffusion to neighbouring cells [16] . In contrast, hetN and patS [13] [14] can diffuse to neighbouring cells. The resulting lateral inhibition of the activator was beautifully demonstrated by Risser and Callahan [16]. They examined at the stability of a hetR-GFP ubiquitously expressed under the control of a copper ion-inducible promoter. Gradients of increasing fluorescence levels with increasing distance from the heterocyst demonstrated the range of lateral inhibition. Importantly, such gradients could also form around vegetative cells driving patS and hetN indicating that these proteins, not some other product of the heterocyst were driving the inhibition of hetR. Therefore, detailed molecular analysis has demonstrated how proteins fulfill the criterion of local autoactivation with lateral inhibition.

4. Nodal Lefty

The filamentous structure of Anabaena is a very simple system in terms of its morphology, with the putative RD patterning process essentially occurring in one dimension. There is strong evidence that RD processes are also operating in the more complicated systems of metazoan embryos. One such well-characterised system is the Nodal Lefty system. Nodal and Lefty are members of the TGF-beta superfamily. Nodal is involved in mesendoderm induction and the development of left right asymmetry (Fig. 2B). In these systems Nodal, signalling through so-called activin receptors, has been shown to promote its own transcription and that of Lefty. In contrast, Lefty does not signal though a receptor, but rather is a secreted diffusible Nodal antagonist, dimerising with Nodal to inactivate it and/or competitively binding the same receptors [17].

These characteristics suggested that Nodal and Lefty could act as an RD pair. However, an RD system requires that the inhibitor acts at a long range relative to the activator. To examine whether Nodal and Lefty fulfilled this criterion of an RD system, Chen and Schier [18], examined it in the context of zebrafish mesendoderm induction. In the zebrafish there are two Nodal genes (Cyclops and Squint) and two Lefty genes (lefty1 and lefty2). All are expressed in an overlapping domain adjacent to the prospective mesoderm. Through a series of morpholino and overexpression experiments they demonstrated that the lefty genes restrict the range of nodal activity and can work at long range. This would appear to satisfy the condition of local autoactivation and lateral inhibition.

Subsequent work by Nakamura et al [19], in the context of mouse left right asymmetry, provided further support for Nodal Lefty comprising an RD system. Nodal and two lefty genes lefty1 and lefty2 are expressed on the left side of the node. It is thought that small perturbations generated by beating cilia in the node create an initial asymmetry that is amplified by the local autoactivation, with the lateral inhibitory component inhibiting expression on the right side. Many basic predictions of this model were tested through lipofection and microdissection experiments. The authors then went on to demonstrate that, the relative expression of these genes and the marker of nodal signalling Pitx2 could be recapitulated through an RD simulations of these experiments. What is even more compelling is that the simulation predicted unexpected experimental observations in lateral plate mesoderm, namely specific deletions of FoxHl. Moreover, the model indicates that variation in Pitx2 expression depends on the percent of cells where there has been a deletion.

Our understanding of this RD system has been taken even further, with a recent study examining the basis to the different ranges of the Nodal and Lefty proteins. Working in the zebrafish, Muller et al [20] specifically asked whether the differential ranges of the activators Cyclops and Squint, and the inhibitors lefty1 and lefty2 were based on differential diffusion, or differential clearance. Using FRAP it was shown that while the half lives of lefty1 and lefty2 are slightly larger than those of Cyclops and Squint, there is a considerable increase in diffusion coefficient, supporting a role for differential diffusion.

In one way the Nodal Lefty system might seem to be atypical for an RD system, as the pattern generated is not overtly periodic. There is only one wavelength across the length of the tissue and the system essentially sets up a gradient (Fig. 2B). Interestingly, more examples of axial patterning systems like those under the control Nodal Lefty, are starting to be seen as example of RD systems. For example, the apical organ of the sea anemone, Nematostella vectensis has been shown the be patterned by two FGF ligands Nvfgfa1 and Nvfgfa2 and one receptor NvfgfRa [21]. Nvfgfa1 activates its own expression as well as Nvfgfa2 and NvfgfRa. Similarly, Nvfgfa2 inhibits Nvfgfa1 at the level of the receptor as was seen in the Nodal Lefty system. This may turn out to be a common or even predominant mechanism for establishing monotonic gradients. Importantly, this experimental system should serve as a paradigm for liberating the reputation of Turing and RD models from mere stripes and spots, a reputation not uncommon among skeptical experimentalists.

5. Zebrafish stripes

The pigment stripes in the zebrafish skin are another one of the best-understood RD systems. Zebrafish skin is marked by a series of longitudinal stripes (Fig. 2C). Here, unlike in the case of Nodal Lefty, the output is a periodic pattern – the type of pattern traditionally thought of in the context of RD. However, as will be seen, the zebrafish pigment pattern is an excellent example of what we refer to as a general or weak RD system, namely one that is mediated without diffusing morphogens.

Kondo and Asai [22] initially implicated RD in pigment patterning in the skin of fish. They demonstrated that the dynamic behaviour of stripes in the skin of the Emperor angelfish Pomacanthus imperator could be simulated using an RD model. Experimental support for this model initially came from genetic perturbations and specifically the skin patterns of an allelic series of mutations in the gene leopard (leo) [23]. The variation of skin patterns in an allelic series of leo mutants could be captured by alterations in a single parameter of a basic RD model. Varying the allelic form was essentially tuning a parameter of an RD model. Further support for an RD model came from ablation experiments. The response of the pattern to various stripe ablations could be replicated in an RD simulation [24].

While the response of the pattern to both genetic and physical perturbations showed that the pattern varied within the constraints of an RD system, this did not provide any specific support to any particular form of RD model. Although the authors emphasised this point, they initially favoured a model based on diffusing morphogens. Surprisingly, the genetic studies did not provide support for such a model as the leo gene was shown to be a connexin – a membrane-integral protein involved in making channels between cells in contact, rather than signalling pathways involving secreted morphogens [25].

Subsequent studies into the basis of the autoactivation and lateral inhibition recently demonstrated that this is an excellent example of “weak” RD system where patterning is mediated in the absence of diffusing morphogens. It had long been known that the stripes consisted of two differently pigmented cell types, black melanophores and yellow xanthophores. Through ablating these different cell types Nakamasu et al [26] demonstrated that these interactions constitute a network of short range autoactivation and long range inhibition. Specifically, at short range, ablation of melanophores or xanothophores promotes the other cell type’s survival, indicative of a local mutual inhibition, which is equivalent to a bistable local autoactivation loop. Xanthophore ablation results at long range in melanophore loss. This showed that xanthophores normally promote survival of melanophores at long range, i.e. activating their inhibitor, in effect a long-range auto-inhibitory loop.

The cellular and genetic basis to these interactions is now being elucidated. The short-range autoactivation is mediated by a mutual cell-cell contact-mediated repulsion between the two migratory cell types. When a xanothophore contacts a melanophore, the latter depolarizes and is repelled [27]. The xanothophore sends out pseudopodia and follows the melanophore as part of a “run-and-chase” behaviour, which segregates the cell types. This repulsion is not seen in mutants for leo, or jaguar, a potassium channel, resulting in pattern defects [28]. Long-range signalling is achieved not by morphogen secretion but instead by long cellular projections – filopodia – whose dynamics in effect mimic diffusion [29]. These filopodia on xanthopores express the deltaC and delta-like 4 ligands, while melanophores express their receptors, notch1a and notch2.

The stripes of the zebrafish provide an excellent example of how investigating the basis of a putative RD patterning system (in the general or weak sense) has found strong support for a novel cell-level based network of interactions that mediates the auto-activation and lateral inhibitory behaviours. In some ways, this system offers a particularly “complete” version of an RD system since the description of the cell behaviours and interactions can completely capture the regulatory network and spatial dynamics independently of the underlying molecular participants.

6. Feather buds and hair follicles

The arrangement of skin appendages, in particular mammalian hair follicles and bird feather buds, are another pattern in the vertebrate skin that has long been discussed in the context of RD models. Both hair follicles and feather buds form from regularly spaced epidermal placodes, associated with dermal condensations (Fig. 2D and E). Early studies into these systems examined hair follicle patterning in the context of sheep wool [30]. Regularly spaced hair follicles form in a series of phases, and RD simulations captured this behaviour. As attention turned to molecular genetics and model systems, questions focused on mouse hair follicles and chick feather buds.

The first molecular study into any of these systems was chick feather bud patterning [31]. Feather buds first appear as a pair of tracts of regularly spaced buds along the dorsal midline, with further buds forming at increasingly more lateral positions, at a regular spacing. The authors considered the system in an RD framework, and searched for potential activator and inhibitor molecules. First looking at relative expression patterns they demonstrated that Shh and FGF2, which had previously been proposed as activators, were expressed early in the forming buds, while the proposed inhibitors BMP2 and 4 were expressed later. Application of these proteins via beads supported these activatory and inhibitory roles, by either promoting or inhibiting feather buds locally.

However, subsequent studies suggest that the basis to the local autoactivation and lateral inhibition is likely to be a more complex network involving other factors such as cell migration. For example, a subsequent study by Michon et al [32] implicated both an inhibitory and an activatory role for BMP signalling. They proposed BMP7 as an activator, causing chemotaxis of dermal cells to the placode. In contrast, BMP4 was an inhibitor of this process. Simulating these behaviors with an RD model expanded to include chemotaxis and proliferation, not only did they demonstrate the observed expression patterns and cell densities, but also unexpected results. For example, beads of the BMP7 – the proposed activator in the system – inhibited bud formation in the surrounding area. In terms of the model, increasing levels of activator increases the amount of chemotaxis and therefore depletes cells in the surrounding region, inhibiting bud formation. Similarly, Lin et al [33] also implicate chemotaxis, but as a response to FGF signalling and Erk activation. Clearly, a complete model of the system would require integration of these pathways and Shh, and any effect they may have on cell proliferation and migration.

Studies of hair follicle patterning also seem to be uncovering a non-trivial core activator-inhibitor network, involving different pathways to the feather bud. In contrast to the sequence of appearance of feather buds, mouse hair follicles first appear at an approximately even spacing in an initial phase, with secondary and tertiary phases of formation inserting new follicles between existing ones. Using skin explant cultures Mou et al [34], identified an activatory role for Eda signalling, mediated through autoactivation of the Eda receptor. They also identified BMP signalling as inhibitory. In contrast, Sick et al [35] using a combination of computer simulations and mouse genetic experiments, implicated Wnt signalling as an activator of hair follicle formation and the Wnt antagonists Dkk2 and Dkk4 as inhibitors. Subsequent studies have shown a cross regulation between Wnt and Eda signalling [for example 36], and potential networks integrating the pathways have been proposed [37], although this has not been tested directly. Therefore, it seems that for feather buds and hair follicles, a large network, rather than simply an activator-inhibitor morphogen pair, mediates local activation and lateral inhibition.

7. Other molecularisations

While the complete networks for feather bud and hair follicle patterning have still to be fully elucidated, the discovery of auto-activatory and inhibitory loops clearly puts these systems in the field of RD patterning. An increasing number of other biological patterns are being understood at this level, namely a molecularisation of activatory and inhibitory behaviours.

For example, a recent study looking at the mammalian palate provided strong evidence for an RD system [38]. The palate is marked with a series of regularly spaced ridges, known as rugae (Fig. 2F), which are sequentially added in association with a localised region of tissue growth. The authors tested whether an existing ruga was a source of inhibition by explanting the palate and cutting posterior to a ruga to remove any inhibitory effect. Unexpectedly, removal of a ruga led to bifuration of the next ruga posterior to cut. This behaviour could be simulated in an RD system, and is hard to imagine any other form of patterning system consistent with it. The authors then demonstrated through genetic manipulations and inhibitor studies that FGF signalling has an activatory role and Shh an inhibitory role. However, again, it is important to note that while FGF and Hedgehog signalling appear to form an activator-inhibitor pair, there is evidence for the involvement of other pathways such as the Wnts and possibly the BMPs, so as with the skin appendages, the core circuit mediating the autoactivation and lateral inhibition is likely to involve more than two pathways. In addition, the authors also demonstrated that ruga formation is associated with bursts of proliferation which appear to contribute to tissue growth and therefore pattern element spacing [39]. It is therefore likely that the cellular behaviours need to be considered in the context of this system.

Another intriguing example of the molecularisation of an RD model comes again from skin appendages. Harris et al [40] demonstrated the role of an RD model in the patterning of barb ridges in the developing feather bud (Fig. 2D). In plumulaceous feathers (i.e. downy rather than bladed), feather barbs are fused in a tuft at the base, and form as a series of parallel ridges along the barb, and this pattern of barb formation was recapitulated using an RD simulation. Shh and BMP2 are expressed in overlapping stripes along the length of the feather bud. They then demonstrate using viral vectors three important components of an RD system: the inhibitor (BMP2) inhibits the activator, the activator (Shh) is autocatalytic and that the activator activates the inhibitor. Finally, they demonstrate that the size of the bud correlates with the number of barb ridges, that is to say the wavelength of the pattern is fixed – another feature of an RD system. What is particularly interesting is the case of pennaceous feathers where the barbs attach in a more organized manner to a central shaft called a rachis. This is associated with helical barb ridge growth. While this behaviour cannot be captured by a two-component RD system, it was shown that the addition of a third component – a short range, long duration inhibitor – and a dorsal ventral polarity, can capture the behaviour. Therefore, the RD framework allows strong predictions to be made about the nature of potential extra components, although in this case the specific molecules predicted have not yet been identified.

8. What level of abstraction is necessary?

The molecularising of activatory and inhibitory behaviours brings up an interesting question. What level of detail of the core network is needed to be informative? Indeed, can one even speak about a “core” network, or is there behind many RD-like systems a kind of statistical aggregation of molecular variables that can only be understood on a genomic scale? If examinations of activating and inhibiting pathways brings up multiple sets of activator and inhibitor molecules, do we need to know the complete topology of how these different molecules interact to understand the patterning system?

To have an understanding of the mechanism by which a system pattern, the goal should be to know the topology of the core RD circuit and the basis of the differences in range of activation and inhibition, and to know how the different interactions are mediated. For example, are the distributed interactions mediated purely by diffusion, or by cell movement or by other processes? Indeed, these details can have an impact on the patterning ability of a system. A recent study considering non-diffusive receptor dynamics in an RD network demonstrated that patterning required the receptors to be self-inhibitory [41]. It would be convenient if most of the behaviour of the relevant systems is captured by a relatively small number of active ingredients and pathways, but it is probably fair to say that to date there are very few systems if any for which one can be confident that this is the case.

At a different level, a comprehensive network topology is not necessarily needed at the level of individual molecules or even pathways to gain insight into the working of a patterning model. It is important to remember that as Oster points out, there are constraints on how a model can behave and the types of patterns it can produce. If the responses of the systems to perturbation place the systems firmly in the context of RD as opposed to some other type of patterning system, as in the studies described above, there are only certain ways in which a pattern can be varied through changing parameters in the model. This provides a context to understand variations in the pattern. This is elegantly illustrated by a recent study, again in the context of feather buds.

Mou et al [42] recently examined basis to the Naked neck trait in chickens, where the birds lack feathers on their necks. The Naked neck phenotype was mapped to an insertion affecting the regulation of BMP12 expression and BMP signalling. Adding BMP12 protein to skin explants of wildtype chicken recapitulates the phenotype – on increasing the concentration of BMP 12 applied to explants, the number of feather buds on the neck skin drops off sharply while that from the body does not respond. Given that BMP has been implicated as an inhibitor in the system, RD simulations were run with a differential sensitivity to the inhibitor between two regions. Increasing the background inhibitor production to mimic adding BMP 12, the experimental pattern was recapitulated: where sensitivity to the inhibitor was higher, the number of activator spots dropped off with increasing background inhibitor level. In contrast, reducing inhibitor potency led to a spot to stripe transition on the body (a common feature of RD systems), but less readily on neck, mimicking the effect of BMP inhibitor on cultures. The authors further showed that this difference was due to elevated retinoic acid signalling in neck, sensitizing skin to BMP signals. This establishes a distinction between a periodicity-generating circuitry and something that modulates it. Thus, even in the absence of a complete molecular description of the core RD circuit, the theoretical framework has allowed insights into variation in the pattern.

The vertebrate limb is another example of a system where insight into an RD patterning process has been gained by considering the constraints on the patterns an RD model can produce, even in the absence of a core circuit. This is particularly surprising given that the limb has long been associated with patterning theories predominantly involving positional information. Specifically it was thought that Shh, expressed in the Zone of Polarising Activity (ZPA) at the posterior of the limb, set up a morphogen gradient, and a consequently a counter gradient in the repressor form of Gli3. This was thought to be the basis of positional information that patterned the digits, a finding supported by grafts of the ZPA from the posterior to the anterior of limb buds [43].

In fact, there have been several theoretical papers associating RD theories with the patterning of the limb. Newman and Frisch [44] originally demonstrated that an RD model could simulate the pattern of the metapodials. Genetic perturbations provided further experimental support for an RD system. In the Doublefoot mutant there are supernumerary digits. In particular, there are digits or interdigits that are thinner than normal, a behaviour that can be captured in RD simulations on growing domains with activator saturation [45].

In their recent study Sheth et al [46] convincingly demonstrated the involvement of RD in patterning the digits of the limb (Fig. 2G). It has long been known that Gli3 mutants have polydactyly – a finding that is difficult to reconcile with a positional information systems. Sheth et al demonstrated that progressive deletion of the posterior hox genes progressively increased digit number. Importantly this was done not by increasing the size of the hand plate, but by decreasing the wavelength of the digits – again, a finding that can be explained by an RD patterning system but not if each digit were specified individually by position. Moreover, it was noticed that increased digit number was associated with digit bifurcation, as visualized by the Sox9 expression.

They next simulated patterning in the growing limb bud. As the limb paddle is fan shaped, its anteroposterior length increases along its proximodistal axis. This was captured by modulating the activity of the inhibitor on the activator along the PD axis. Global inhibition of this interaction, to simulate the modulation by the hox genes, not only increased the number of digits (by reducing the wavelength), but also caused digit bifurcations. It should be remembered that the core components of this RD system are not known, and nor is the nature of the Hox gene modulation. Some interaction with the PD FGF gradient is suggested for the latter, but is untested. It is important to note that viewing the system in terms of an RD model has allowed an interpretation of the mutant phenotypes, and thereby given important insights into the patterning processes involved in the limb. Importantly, it uncouples the specification of digits in general from the regulation of their spacing and from the specification of their different identities. It does this by providing separate conceptual frameworks for each of those processes.

9. Final thoughts

To the question “what good are models of biological pattern formation?” we can now provide an answer that puts flesh on the bones of the answer given by George Oster in 1988. In short, quantitative mathematical models have greatly informed our understanding of biological pattern formation by framing it in terms of its moving parts. A crucial element to our understanding has been the ability to test the predictions of the models with biological experiments. On the one hand, experimental investigation has constrained which form of a theoretical model – in terms of the biological processes captured – can be seen to operate in a given system. On the other, the constraints on the patterns a theoretical model can generate provide a basis to interpret the results of biological experiments.

Or, to put it another way, to the experimentalists we say: recognise that mathematical models are not fudge machines, infinitely elastic and therefore trivial simulators of biological pattern formation. Try getting a given model to accurately mimic your system’s pattern and you will see that it wrestles under your grasp in ways that are non-intuitive and informative. To the mathematical modeller, we say beware of the appearance of facile alignment of model and experiment. In this area more than many, it is essential that the sometimes difficult route to the best model and the narrative of challenged and modified assumptions is more useful than the model itself.

As we have seen, some RD systems such as heterocyst formation, the Nodal Lefty system and the stripes of the zebrafish have been characterized to a great level of detail. In these systems investigations have led to an understanding of the molecular basis to not only activation and inhibition, but even their differential effective diffusion ranges. However, we have also seen that in the Naked neck chicken and the vertebrate limb, such a level of understanding is not always needed to give insights into the patterning process.

As to the question “what level of abstraction of the biological system is necessary to understand pattern formation?” there is certainly no simple answer and the next few years of computational-experimental dialogue will establish how much detail is useful. It is conceivable that a fully elucidated series of interactions could allow a realistic set of equations to be written. But is this necessary? The simulations of, for example, the vertebrate limb or zebrafish stripes, were run using various standard RD equations, not ones tailored to the specific system (to some degree this is true of all the studies discussed above), and they produced important insights into how the patterns are generated.

One interesting example where details of the molecular interactions mediating local autoactivation and lateral inhibition have been implicated in the patterning process is the example of axial patterning, such as Nodal Lefty, described above. In these cases inhibition is mediated by inhibition at the level of the receptor. It has recently been shown that including transcriptional delays in RD systems can send the system into oscillations [47]. Meinhardt suggests that inhibition at the level of the receptor avoids a transcriptional delay and thereby avoiding the risk of oscillations [48].

In a similar vein, while different formulations of RD equations can generate the same types of patterns, the ranges of parameter space where this occurs differ [49]. A better understanding of the biological interactions of the RD network may give insight into a realistic structure of the RD equations, and this could give insight into the robustness of different systems to perturbations, something that could conceivably be test experimentally.

Currently, we are not yet at the level of understanding for most systems where RD has been implicated. However, RD has been an important framework for understanding the biological phenomena. It is important to remember what Turing said of his system is applicable to all the models discussed above, namely that they are “a simplification and an idealization, and consequently a falsification”. However, as we have seen the theoretical framework, when constrained by the biological data has provided insight into the patterning process. As Turing went on to say, he hoped that “the features retained for discussion are those of greatest importance in the present state of knowledge”.