An application of conditional logistic regression and multifactor dimensionality reduction for detecting gene-gene Interactions on risk of myocardial infarction: The importance of model validation

Abstract

Background

To examine interactions among the angiotensin converting enzyme (ACE) insertion/deletion, plasminogen activator inhibitor-1 (PAI-1) 4G/5G, and tissue plasminogen activator (t-PA) insertion/deletion gene polymorphisms on risk of myocardial infarction using data from 343 matched case-control pairs from the Physicians Health Study. We examined the data using both conditional logistic regression and the multifactor dimensionality reduction (MDR) method. One advantage of the MDR method is that it provides an internal prediction error for validation. We summarize our use of this internal prediction error for model validation.

Results

The overall results for the two methods were consistent, with both suggesting an interaction between the ACE I/D and PAI-1 4G/5G polymorphisms. However, using ten-fold cross validation, the 46% prediction error for the final MDR model was not significantly lower than that expected by chance.

Conclusions

The significant interaction initially observed does not validate and may represent a type I error. As data-driven analytic methods continue to be developed and used to examine complex genetic interactions, it will become increasingly important to stress model validation in order to ensure that significant effects represent true relationships rather than chance findings.

Background

There is a growing awareness that the failure to replicate single-locus association studies for common complex diseases may be due to an underlying genetic architecture in which interactions between genes are the norm rather than the exception [1,2]. In fact, a recent review of 166 putative single-locus associations found that only six had been consistently replicated [3].

The angiotensin converting enzyme insertion/deletion (ACE I/D) polymorphism has been associated with an increased risk of myocardial infarction (MI) in some but not all studies [4-8]. One possible explanation for the inconsistent results is that interaction with another gene or genes could modify the effect of the ACE DD genotype on the risk of MI. Accumulating evidence suggests that the renin-angiotensin system plays a role in regulating fibrinolytic balance, maintained primarily by the interplay of PAI-1 and t-PA levels [9,10]. Either an increase in PAI-1 levels, which promote thrombosis, or a decrease in t-PA levels, which promote fibrinolysis, shifts the balance towards thrombosis. Hence, we report the results from a recent study to examine possible interactions between the ACE I/D, the plasminogen activator inhibitor-1 (PAI-1) 4G/5G, and the tissue plasminogen activator insertion/deletion (t-PA I/D) polymorphisms on risk of MI. An interaction between the ACE DD genotype and PAI-1 4G allele on risk of MI has been hypothesized as both are associated with increased PAI-1 levels [11-13] and recent evidence suggests an interaction between the two polymorphisms on plasma PAI-1 levels [14]. An interaction between the ACE DD and t-PA II genotypes on risk of MI has also been hypothesized since the ACE DD genotype is associated with an increased breakdown of bradykinin, a potent stimulus for t-PA release [15,16] and the t-PA II genotype has been postulated to interfere with t-PA release [17].

We used data from 343 matched case-control pairs in the Physicians' Health Study (PHS) to examine possible interactions among the bi-allelic ACE I/D, PAI-1 4G/5G, and t-PA I/D polymorphisms on the risk of MI. The standard analysis technique for such study designs is conditional logistic regression (CLR). However, it has been suggested that parameter estimates obtained from a logistic regression model may be unreliable unless 10–20 events (cases) per variable are available [18]. In the current study, a total of 19 parameters must be estimated in the maximum conditional logistic regression model under consideration, which considers all possible main effects and two-way interactions among three polymorphisms with three genotypes each (1 for the intercept, 2 each for the main effects of ACE, PAI-1, and t-PA, and 4 each for the ACE × PAI-1, ACE × t-PA, and PAI-1 × t-PA interactions). With 343 observed cases, this study has approximately 18 events per parameter in the full model and is thus on the outer limit of having an acceptable ratio of events to parameters in the model. Furthermore, even if the sample size is sufficient to provide adequate parameter estimates, the study may suffer from low power to detect clinically relevant interactions. For all of these reasons, when planning the current study, there were concerns regarding whether the planned conditional logistic regression analysis would provide adequate power to detect interactions of interest.

To guard against these concerns, we decided to apply the multifactor dimensionality reduction (MDR) method to this data set as well [19]. The MDR method pools multilocus genotypes into a single dimension with two groups, classified as either high or low risk. The MDR software, described by Hahn et al. [20], will work with datasets that contain up to 500 variables and can examine interactions among as many as 15 genetic and/or environmental factors. The MDR method was inspired by the combinatorial partitioning (CP) method of Nelson et al. [21]. Both methods apply data reduction techniques to address the problems associated with testing for interactions in high dimensional data with modest sample sizes. The two methods differ in the type of outcome variables addressed. The CP method applies when the outcome variable is continuous in nature while the MDR method applies when the outcome is categorical in nature (i.e. disease status).

Ritchie et al. [19] demonstrated that the MDR method was able to detect a high-order interaction in the absence of any statistically significant main effects in both simulated data and among four polymorphisms from three different estrogen-metabolism genes on the risk of sporadic breast cancer. Moore and Williams [1] describe an application of the MDR method for identifying gene-gene interactions in essential hypertension. Although the MDR method is equally applicable to detecting main effects as well as interactions, a major strength of the MDR method is its ability to detect significant interactions in the absence of main effects. Previous examinations in the PHS population had revealed that none of the polymorphisms of interest had significant main effects on the risk of MI [6,22,23]. This lack of main effects make this study an attractive candidate for applying the MDR method.

However, it is well known that models obtained using such data-driven methods are prone to increased type 1 errors [24]. Hence, proper validation of such models is crucial. One of the attractive features of the MDR software is that it provides a prediction error, an estimate of the internal validity of the model, as part of the default output. In this paper, we report our experience of having reported an interaction that was subsequently not confirmed in order to emphasize the importance of using validation measures, such as the prediction error, when building models using data driven approaches. We also investigate whether similar procedures can be used to derive internal prediction errors using conditional logistic regression models.

Results

Conditional logistic regression (CLR) approach

Using CLR with backwards selection to choose a final model, all terms related to t-PA dropped out of the model. In addition, there were no significant differences between the DI and II genotypes for ACE nor between the 4G4G and 4G5G genotypes for PAI-1 on risk of MI. Hence the final model consisted of four groups: the combinations of the ACE polymorphism dichotomized into DD or not DD (DI or II) and the PAI-1 polymorphism dichotomized into at least one 4G allele present or not (4G4G or 4G5G vs. 5G5G). Based on this final model, there was a significant interaction between the ACE and PAI-1 polymorphisms (p = 0.02).

Multifactor dimensionality reduction (MDR) approach

We repeated the analysis using the MDR method with 10-fold cross validation [19,20,25]. The MDR analysis was conducted in two ways: 1) using three separate genotypes for each polymorphism, and 2) using the dichotomous groupings for the polymorphisms suggested by the literature (recessive models for the ACE D and t-PA I alleles and a dominant model for the PAI-1 4G allele).

Table 1 displays the minimum prediction error and cross-validation consistency for the best 2-factor and 3-factor model for each situation. The two-locus model including the ACE and PAI-1 polymorphisms, with the dichotomous groupings suggested by the literature, simultaneously minimized prediction error and maximized the cross-validation consistency. This model had a cross validation consistency of 100%, which was marginally significant with permutation testing (p = 0.09).

Table 1.

Summary of Results for MDR Models Fitting (a) Three separate genotypes for all polymorphisms and (b) Using the dichotomous grouping for the polymorphisms suggested by the literature (ACE DD vs. not DD, PAI-1 presence of 4G allele vs. 5G5G, tPA II vs. not II).

# of Loci	Loci Included in Best Model	Cross-Validation Consistency	Prediction Error
Fitting Three Separate Genotypes for All Polymorphisms:
2	ACE, PAI-1	86%	51%
3	ACE, PAI-1, t-PA	100%	51%
Using Dichotomous Groupings:
2	ACE, PAI-1	100%	46%
3	ACE, PAI-1, t-PA	100%	46%

Figure 2 summarizes the two-locus genotype combinations of ACE and PAI-1 associated with high and low risk for MI. Note that the pattern of high-risk cells for the ACE polymorphism differs across the columns representing the PAI-1 polymorphism. Such differences are evidence of a gene-gene interaction. When the dichotomy suggested by the MDR approach was input into a logistic regression model, those participants classified as "high-risk" had a significantly higher risk of MI compared to those classified as "low-risk" (OR = 1.44, 95% CI: 1.06–1.95).

Figure 2.

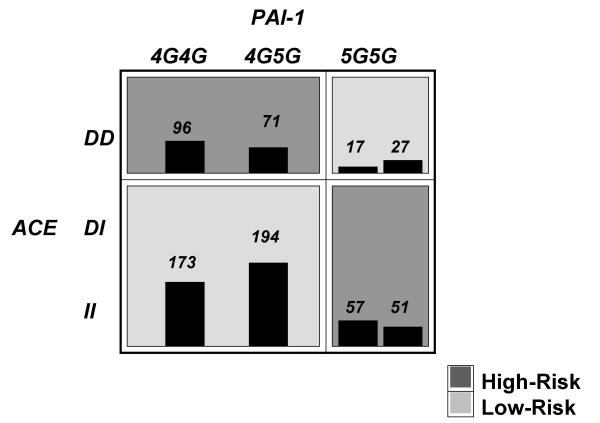
Summary of two-locus ACE I/D and PAI-1 4G/5G genotype combinations associated with high risk and low risk for myocardial infarction from MDR analysis with the lowest prediction error. For each genotype combination, the number of cases is displayed in the left bar while the number of controls is displayed in the right-box. Darker shade indicates the high risk group. Note that the pattern of high and low risk for the ACE polymorphism differs depending on the value of the PAI-1 polymorphism. This is evidence of epistasis or gene-gene interaction.

Comparing the results

Both approaches have substantially reduced the dimensionality of the data, although the amount of dimensionality reduction differs slightly. The final model chosen from the backwards CLR approach reduces the data to a set of four groups while the MDR approach, by definition, reduces the data to two groups. However, the conclusions obtained from the two methods were consistent with both suggesting a possible interaction between the ACE I/D and PAI-1 4G/5G polymorphisms on the risk of MI. Table 2 shows the relationship between the ACE DD genotype (versus not DD) and risk of MI, separately for the two PAI-1 groupings based on both analyses. In both analyses, among those with at least one PAI-1 4G allele, individuals with the ACE DD genotype had a significantly higher risk of MI as compared to those who carried the ACE DI or II genotypes (CLR: OR = 1.50, 95% CI: 1.04–2.17; MDR: OR = 1.44, 95% CI: 1.06–1.95). In contrast, among those with the PAI-1 5G5G genotype, individuals with the ACE DD genotype had a significantly lower risk of MI compared to those who carried the ACE DI or II genotypes only in the MDR analysis (CLR: OR = 0.58, 95% CI: 0.29–1.17; OR = 0.69, 95% CI: 0.51–0.94). This is due to the fact that there is an inverse relationship between the two odds ratios in the MDR analysis (0.69 = 1/1.44) since we are simply reversing the combinations of the ACE polymorphism defined as high and low risk for different combinations of the PAI-1 polymorphism (see Figure 2).

Table 2.

Odds Ratios and 95% Confidence Intervals For ACE DD vs. ACE DI or II, Stratified by PAI-1 Polymorphism Status

			CLR	MDR
		Not DD	ACE DD
PAI-1	5G5G	1.00 Ref.	0.58 (0.29, 1.17)	0.69 (0.51, 0.94)
	4G4G or 4G5G	1.00 Ref.	1.50 (1.04, 2.17)	1.44 (1.06, 1.95)

(CLR = Conditional Logistic Regression, MDR = Multifactor Dimensionality Reduction)

For this example, both approaches would lead to the same model for the prediction of future responses. In a similar data set, we would 'predict' a subject to be a case if they have the combination of a) ACE DD and either PAI-1 4G4G or 4G5G or b) PAI-1 5G5G and either ACE DI or II. Similarly, we would 'predict' someone in a similar data set to be a control if they have the combination of a) ACE DD and PAI-1 5G5G or b) either ACE DI or II and either PAI-1 4G4G or 4G5G. The discrepancy in the number of groups becomes important if we wish to make statements about the excess risk associated with each group. For example, is the amount of excess risk for having an MI the same in the two "high-risk" groups or is the amount of excess risk higher in one group than the other. One way to address this question would be to further divide the high and low risk groups following an MDR analysis. Obviously, this is an important area of future research.

As with all statistical analyses, replication and validity of findings is necessary to separate true relationships from chance findings. One advantage of the MDR method is that it provides the average prediction error, an internal validation measure that protects against finding chance associations in the sample. Although the original analysis suggested a marginally significant interaction between the ACE and PAI-1 polymorphisms on the risk of MI, the minimum prediction error of 46.2% is not significantly lower than the value of 50% that would be expected by chance (p = 0.15). This suggests that the model may not be effective for classification of risk of MI. Concern regarding the failure to obtain a satisfactory prediction error is only exacerbated by the well-known problem of overestimation common to such data-driven analysis methods [18,24].

We had not originally calculated an internal prediction error as part of our CLR analysis. In fact, most standard statistical software packages do not provide such internal validation measures by default with CLR approaches. This motivated us to investigate whether and, if so, by what procedures, we could derive an internal prediction error using CLR models. The SAS macro CVLR [Clinton T. Moore, U.S. Geological Survey, Patuxent Wildlife Research Center, personal correspondence] allows one to perform cross-validation with logistic regression models. However, using the fact that the conditional likelihood for one-to-one matched pairs is the same as the unconditional likelihood for a logistic regression model where the response is always equal to one [26], the CVLR macro allows performing cross-validation with conditional logistic regression models as well. To parallel the internal validation of the MDR approach, ten-fold cross-validation with the CVLR macro was used to determine the prediction error of the final CLR model. The observed prediction error of 42% suggests a limited predictive ability of this model, casting doubt on its clinical utility. This illustrates that the additional effort required to obtain such prediction errors with CLR models can suggest which seemingly significant interactions are not likely to validate in subsequent samples.

External validation sample

After this initial analysis, we were left with a significant gene-gene interaction that did not appear to validate internally. An external validation using an independent data set obtained from a study design as similar as possible to the present study could help gain further insight as to whether or not this significant interaction was scientifically important [27]. Due to the fact that monitoring for cardiovascular events is ongoing in the PHS, after completion of the original study an additional 141 cases, which were not included in the original sample and had been genotyped for the ACE and PAI-1 polymorphisms, became available. For each of these cases, a single control was selected at random from the remaining study participants using the same matching criteria as in the original study. This independent sample of 141 matched case-control pairs was appreciably smaller than the sample in the original study. Hence, concerns regarding adequate power were magnified in this validation sample and failure to validate the significant finding in this sample does not preclude the presence of an effect. Nevertheless, given the failure of the finding to internally validate, computing the prediction error on the external sample may further suggest that the initial significant finding does not validate, particularly since the initial prediction error is typically underestimated.

One complicating factor was that genotyping methods had changed since completion of the initial study. The initial study used assays for each individual polymorphism, which have been described in detail elsewhere [6,22,23]. Multilocus genotyping assays were used for the validation sample [28,29]. However, since the majority of the participants in the initial study (95%) had been re-genotyped using the newer methods, we were able to confirm that the rate of agreement between the two methods was 97% and 93% for the ACE and PAI-1 polymorphisms, respectively. Additionally, we obtained the same conclusions when we repeated the original analysis replacing the original genotyping results with the results using the newer method. Thus, we present results using the original genotyping methods for the initial sample and the multilocus genotyping methods for the validation sample.

Figure 3 summarizes the distribution of cases and controls in the validation sample for the two-locus genotype combinations of ACE and PAI-1. The shading in the figure corresponds to the classification of that genotype combination in the original analysis (darker = high-risk & lighter = low-risk). Each genotype combination contains a nearly even split of cases and controls, with 48.9% of subjects in the validation sample misclassified using the groupings from the original model. This further suggests that the significant interaction observed in the initial sample of 343 matched case-control pairs may not hold up under further scrutiny.

Figure 3.

Summary of two-locus ACE I/D and PAI-1 4G/5G genotype combinations in the independent validation sample. Darker shade indicates those combinations that were classified as high-risk in the original analysis while lighter shade indicates those combinations that were classified as low-risk in the original analysis. Note that each genotype combination contains a nearly even split of cases and controls. Hence the significant interaction observed in the initial dataset does not appear to validate.

Conclusions

For studies attempting to examine possible interactions among two or more genetic polymorphisms, traditional methods such as conditional logistic regression may either prove infeasible due to combinations of factors with no observations or have limited power to detect clinically relevant interactions due to a low number of events per parameter in the model. The MDR method was proposed as a possible solution in such settings. However, this example does not fully illustrate the potential of MDR since it is within the capabilities of standard CLR. In these instances, one would hope that the conclusions obtained from the MDR analysis are consistent with those obtained from the more traditional CLR analysis. In fact, we obtained a significant interaction between the ACE and PAI-1 polymorphisms on risk of MI using both methods. The magnitude of the risk was substantial (1.5-fold increase in risk for those with the combined ACE DD genotype and at least one PAI-1 4G allele) and comparable to that of other risk factors for which interventions are undertaken. The fact that the MDR analysis led to the same conclusions as the more traditional CLR analysis in this example supports the fact that the MDR method is useful for analyzing data in situations where traditional methods cannot be applied. In many instances, researchers might attempt to publish such significant findings. However, the model validation procedures built into the MDR method suggest that, although the model was significant, there was poor internal validation. In addition, applying the MDR method to an independent validation sample drawn from the same study population suggested a lack of external validation as well. This negative result upon cross-validation is informative and serves as a stern warning that researchers should not publish significant results in genetic interaction studies without looking at model validation measures. We strongly feel that the lack of validation in this example arises due to the fact that the initial finding may be a type 1 error. Had we published the initial significant findings without model validation, readers (and future researchers) may have been led to accept a result that, upon further review, may prove to be a type 1 error. This is a serious problem that explains why many published, significant findings are not replicated [30,31].

Although one cannot completely rule out the fact that the lack of validation may be due to an improper modeling method or poor data quality, we feel that this is highly unlikely in this situation. First, the PHS data set is known to be of high quality and has been one of the most widely published studies with regards to genetic determinants of disease. Furthermore, all analyses using PHS data must be verified by an independent statistical reviewer before the PHS team will release the data for publication. Second, although the MDR method is new, it can be shown that the classification method used by MDR once a combination of SNPs has been selected is no different than a Bayes classifier and is equivalent to the gold standard in data mining and machine learning. Finally, application of MDR to real data sets has revealed evidence of gene-gene interactions with statistically significant cross-validation prediction errors as low as 20% in data sets with smaller sample sizes than that analyzed in this study. Due to the reasons stated above, we feel that it is highly unlikely that the negative validation result is due to an improper modeling method or poor data quality.

In the original CLR analysis, we did not initially calculate an internal prediction error as this measure is not routinely reported nor is it included in the output of most standard logistic software packages. Using a special user-written macro to perform cross-validation, we have shown that an internal prediction error may be computed with CLR analyses. Furthermore, we have demonstrated that such internal prediction errors can provide the same information regarding the validity of the model as that obtained using the MDR approach. Although the construction of a prediction error from logistic regression using cross validation is not a novel result, we believe that this deserves wider attention. We recommend that, until prediction error capabilities are added to standard logistic regression software, users consider ways to compute these statistics to facilitate the standard reporting of internal prediction errors when examining genetic interactions in such models.

The primary conclusion of this study is that validation of genetic models using independent samples plays an important role in model-building using data-driven methods such as multifactor dimensionality reduction (MDR). Although there is general agreement regarding the importance of model validation, this problem is too often ignored in published research. As Altman and Royston [18] state, "It is striking that the statistical problem of overoptimistic prediction is mentioned in very few prognostic studies...". They offer several reasons for this, including the fact that correction for overestimation often leads to less significant, and hence less impressive, results. The purpose of research is not to obtain 'significant p-values' (statistical significance), but to uncover relationships between variables and outcomes that can lead to improved treatments, therapies, or understanding of disease processes (scientific, public health, or clinical significance). As data-driven methods are developed to examine complex genetic interactions, it will become increasingly important to stress model validation in order to ensure that significant effects represent true relationships rather than chance findings.

Methods

PHS example

These data are from a nested case-control study involving participants from the PHS, a randomized, double-blind, placebo-controlled trial of aspirin and beta carotene in the prevention of cardiovascular disease and cancer in a cohort of predominantly white, male U.S. Physicians [32]. For the study described in this paper, 343 cases were identified who developed an MI during follow-up and had been genotyped for the ACE, PAI-1, and t-PA polymorphisms. For each case, a single control was selected at random from the subset of study participants who had been genotyped for the three polymorphisms of interest and remained free of cardiovascular disease during the follow-up period. Controls were matched to the cases on age (+/- 1 yr), time since study initiation (+/- 6 months), and smoking history (current, past, never).

Conditional logistic regression approach

Our originally planned analysis utilized CLR models with backwards selection to choose a final model. The 'full model' consisted of the 19 parameters described above. With the exception that we did not allow the removal of main effects terms for a polymorphism until all interaction terms involving that polymorphism had been removed, at each step, the term with the highest p-value (provided it was greater than 0.20) was removed from the model and the model was refit with all remaining terms. This process was continued until no remaining terms could be removed. Furthermore, because the existing literature suggests that any possible effects may be due to the ACE DD genotype [11-13,15,16], the presence of the PAI-1 4G allele [11-13], or the t-PA II genotype [17], we allowed for the collapse of appropriate genotypes if no significant difference was suggested by the model (i.e. we considered a recessive model for the ACE D and t-PA I alleles and a dominant model for the PAI-1 4G allele). After obtaining the 'final model', the primary hypothesis was to test whether the effects of the ACE I/D polymorphism on the risk of MI depends on the presence of the PAI-1 4G/5G or t-PA I/D polymorphisms.

We repeated the backwards selection process including such known MI risk factors as hypercholesterolemia, hypertension, diabetes mellitus, body mass index, exercise, alcohol intake, angina, and randomized treatment assignment to aspirin as factors. Controlling for these known risk factors made no material difference in the odds ratios and corresponding confidence intervals related to the ACE and PAI-1 interaction. Furthermore, although the MDR methods allow the inclusion of covariates, the use of these methods in the presence of known covariates makes it much harder to disentangle the final model. For these reasons, we present only the unadjusted analyses in this manuscript.

MDR approach

Figure 1 illustrates the general steps involved in implementing the MDR method for matched case-control studies. First, a set of genetic and/or discrete environmental factors of interest are identified. Next, the MDR method is applied in the following stepwise manner: 1) The matched pairs are randomly divided into 10 equal subsets. The data are then divided into a training set (e.g. 9/10 of the matched pairs) and an independent holdout set (e.g. 1/10 of the matched pairs) as part of cross-validation. The MDR model is developed on the training sample. 2) Some set of n factors are selected from the pool of all factors. 3) The n factors and their multifactor cells are represented in n-dimensional space. For example, for two polymorphisms with three genotypes each, there are nine two-locus genotype combinations. 4) The ratio of cases to controls is computed in each multifactor cell in n-dimensional space. Each multifactor cell is labeled as "high-risk" if the number of cases exceeds the number of controls. Otherwise, the multifactor cell is labeled as "low-risk". This process reduces the n-dimensional multifactor classes into a one-dimensional model with two multifactor classes: high-risk and low-risk. 5) Steps 2–4 are repeated for all other n factor combinations and the n factor model chosen which has the fewest misclassified individuals in the training set as the 'best' n factor model. 6) The classification from the 'best' n factor model is used to predict disease status for the remaining 1/10 of the data (i.e. the holdout set). By necessity, empty cells in either the training or holdout sample are ignored since there is nothing to predict. The proportion of subjects is computed in the holdout set for which an incorrect prediction was made. The 10-fold cross validation is repeated for each possible 9:1 split of the data.

Figure 1.

Summary of the steps involved in implementing the MDR method.

To protect against chance divisions of the data, the 10-fold cross validation is repeated ten times, i.e. the matched pairs are shuffled 10 times into 10 equal subsets and the cross validation is applied to each possible 9:1 split for each of the 10 shufflings. Finally, for the 'best' n factor model, two statistics are reported: 1) The prediction error is the average of the 100 estimates of the proportion of subjects in the holdout set for which an incorrect prediction is made. 2) The cross-validation consistency is the percentage of times a particular set of n factors are identified across the 100 cross-validation data sets.

The MDR approach first considers all two-factor combinations and chooses the single "best" two-factor model with the lowest prediction error among all two-factor combination models. This process is then repeated among all possible higher order factor combinations, with a "best" model chosen at each step. From the set of best models, we choose the model which minimizes the prediction error and/or maximizes the cross-validation consistency. When several models achieve the same prediction error and cross-validation consistency, the smaller model is chosen for parsimony. For example, in the PHS data, the best two-factor model is chosen from the 3 possible two-factor models (ACE &PAI-1, ACE &t-PA, PAI-1 &t-PA) and compared to the three-factor model containing all three polymorphisms. The model that minimizes the prediction error is chosen as the final model. The significance of the final model is determined using a permutation test. For each of 1000 permutations, the matched pairs are permuted by flipping the case-control status within a pair with a probability of 0.50, a new best model is selected, and the minimum prediction error from the best model is tabulated. This provides an empirical distribution of the average prediction error or cross-validation consistency under the null hypothesis of no association. The p-value for the observed prediction error or cross-validation consistency is computed by comparing its value to this empirical distribution.

Although useful in a wide variety of situations, the MDR method is not without its shortcomings. First, when MDR methods are used in the presence of main effects or known important covariates, it becomes much harder to disentangle the final model. For example, if an MDR analysis suggests that the optimal model contains four factors, in many cases it is not readily clear whether this final model represents a four-way interaction, two separate two-way interactions, two main effects and a two-way interaction, etc. This is clearly an important area of future research. Also, MDR assumes that there is no genetic (locus) heterogeneity. For example, if half of the individuals were affected due to two loci and the other half due to two other loci, there would be a decrease in MDR power since the cross-validation consistency would be lower and the prediction error higher for either pair of loci [25]. Genetic heterogeneity severely impacts power and future research is needed to address this problem.

Authors' contributions

CSC performed the conditional logistic regression analysis, participated in the design of the study, drafted the manuscript, and prepared the final version of the manuscript. PRH participated in the design and coordination of the study as well as the writing of the manuscript. MDR and JHM performed the MDR analysis and participated in the design of the study and writing of the manuscript. HMK provided input on earlier drafts of the manuscript. JMG and PMR provided the PHS data sets for this study. NJB and DEV conceived the original hypothesis for this study. All authors read and approved the final manuscript.