Functional Asymmetry in a Five-Link 3D Bipedal Walker

Abstract

This paper uses a symmetrical five-link 3D biped model to computationally investigate the cause, function, and benefit of gait asymmetry. We show that for a range of mass distributions, this model has asymmetric walking patterns between the left and right legs, which is due to a phenomenon known as period-doubling bifurcation. The ground reaction forces of each leg reflect different roles, roughly corresponding to support, propulsion, and motion control as proposed by the hypothesis of functional asymmetry in human walking. These results suggest that natural mechanics could be responsible for asymmetry in able-bodied walking, rather than neurophysiological mechanisms such as leg dominance.

I. Introduction

Gait asymmetry is commonly observed in impaired walking, but growing evidence suggests that able-bodied walking sometimes exhibits this behavior as well [1]–[4]. Understanding when and why this phenomenon occurs is important to human gait research, where symmetry is commonly assumed in healthy control groups in order to simplify data collection and analysis. Many methods exist for quantifying or defining asymmetry between the right and left sides of the human body, using variables such as stride/step length, joint range of motion, velocity profiles, and ground reaction forces (GRF) [5]. However, the underlying causes of gait asymmetry are still the subject of debate (see [1] for a review).

The hypothesis of functional asymmetry in able-bodied walking distinguishes the primary role of each leg as vertical support/control and anterior-posterior (AP) propulsion [1]. Differences between leg functions were only observed during fast walking trials in [3], suggesting that asymmetry is a strategy for challenging locomotor tasks. This is exemplified by asymmetries reported in athletic race walking [4], which the authors suggested was an artifact of shoes or training on curved tracks. Perhaps the most common explanation for functional asymmetry is leg dominance, but conflicting reports exist for this theory [1].

We proposed in the companion paper [6] that body mechanics, rather than neural control mechanisms, are responsible for functional asymmetry. We previously reported asymmetric ground reaction forces in computational simulations of planar “passive walking” models that use only momentum and gravity to propel forward motion down a shallow slope (kinematic variables were studied in [7], [8]). Although the dynamical equations of motion may yield a stable solution corresponding to a symmetric walking gait, varying model parameters can cause a structural instability at a bifurcation point, after which a new (stable) asymmetric solution emerges from the (unstable) symmetric solution. The symmetrical mechanics of these walking machines admit two families of solutions, one symmetric and one asymmetric, completely independent of motor control. However, this phenomenon has not been shown to extend to high-dimensional 3D walkers that are more characteristic of human dynamics.

This paper examines the cause and function of gait asymmetry in a symmetrical five-link 3D biped. Since most bipeds in 3D do not have passively stable gaits, we adopt the control strategy [9] that exploits passive motion in the sagittal plane. We show that small symmetric changes in leg mass distribution result in the emergence and growth of asymmetry in kinematic and kinetic variables. We study the role of each leg in the asymmetric gaits and find distinct functions roughly corresponding to support, motion control, and propulsion. These results show that under certain conditions gait asymmetry is beneficial for dynamical stability, suggesting that biped mechanics might explain functional asymmetry in human walking.

We first define our dynamical model and gait symmetry.

II. Five-Link 3D Biped Model

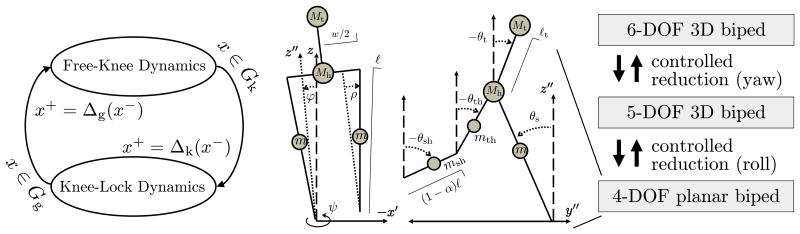
The 3D model in Fig. 1 has two phases during single support: knee-swing with six degrees-of-freedom (DOFs) and knee-lock with five DOFs. The stance knee remains locked through each step cycle. The biped walks on a flat surface with sufficient static friction to prevent slipping at the foot contact point. We model internal/external rotation about the stance leg as an unactuated DOF with passive viscous damping (e.g., from tissue or ground friction). This reflects the fact that the human ankle provides actuation for flexion/extension and inversion/eversion, but internal/external rotation (i.e., yaw) is mostly passive [10].

Fig. 1.

Diagrams of the 3D biped's hybrid system ℋ (left), frontal and sagittal planes (middle), and controlled reduction (right). The control strategy dynamically decouples the 4-DOF dynamics of the sagittal plane by reducing the yaw DOF of the transverse plane and the roll DOF of the frontal plane.

This biped has coordinates q = (ψ, φ, θ^T)^T in configuration space Q = ℝ⁶, where ψ, φ ∈ ℝ are respectively the heading/yaw and roll/lean variables at the stance foot, and vector θ = (θ_s, θ_t, θ_th, θ_sh)^T contains the sagittal-plane (pitch) variables for the stance leg, torso, swing thigh, and swing shank, respectively. Knee-lock phase provides θ_th ≡ θ_sh. The hip abduction/adduction DOFs are fixed at a constant angle ρ to simplify the control problem.

The system state is x = (q^T, q̇^T)^T in domain D ⊂ ℝ¹², the set of all states such that the swing foot height is non-negative. We assume that both knee-strike and ground-strike impact events are instantaneous and perfectly plastic, resulting in transitions between the six and five DOF dynamics according to the hybrid system ℋ of Fig. 1. The ground-strike guard condition G_g is defined as the set of states in D where the swing foot height is zero, and its reset map is Δ_g. The knee-strike guard condition G_K is defined as the set of states in D where θ_th — θ_sh = 0, and its reset map is Δ_K. The dynamics for each single-support phase have the form

$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+N(q)=Bu,$$ (1)

where M ∈ ℝ^{n × n} is the mass/inertia matrix, C ∈ ℝ^{n × n} contains the Coriolis/centrifugal terms, and N ∈ ℝⁿ is the vector of gravitational torques, n ∈ {5, 6}. Control input u ∈ ℝ^{n − 1} and torque map B ∈ ℝ^{n × n − 1} model actuation at every DOF except ankle yaw.

We adopt the geometric feedback control law¹ from [9] (depicted in Fig. 1) to produce 3D walking by effectively decoupling the sagittal plane, thus inheriting the natural passive mechanics. Walking gaits are cyclic and correspond to solution curves x(t) such that x(t) = x(t+T) for all t ≥ 0 and some minimal T > 0. These solutions define isolated closed orbits in state space known as hybrid limit cycles, which correspond to equilibria of the Poincaré return map P : G_g → G_g. The return map represents a hybrid dynamical system as a discrete-time system between impact events, sending state x_j ∈ G_g ahead one step to x_j+1 = P(x_j).

The biped model has bilateral symmetry across the sagittal plane – the hybrid dynamics during left leg stance exactly mirror that of right leg stance (with opposite signs for hip width w and angle ρ). A symmetric periodic solution x(t) has a fixed point x^* = P(x^*), where map P implicitly accounts for bilateral symmetry by flipping the signs of out-of-plane variables (ψ, φ, ψ̇, φ̇) and parameters w, ρ. A periodic solution that is asymmetric has a period greater than one, i.e., x^* ≠ P(x^*), requiring multiple compositions of the return map to find a fixed point x^* = P^k(x^*), for k > 1.

We verify orbital stability of a fixed point x^* of the system

$$x_{j+k}=P^k(x_j),$$ (2)

k ≥ 1, by approximating the linearized map ∇_xP^k(x^*) through simulation [7]. This yields a discrete linear system that is exponentially stable if and only if the magnitudes of the eigenvalues of ∇_xP^k(x^*) are strictly less than one. If any absolute eigenvalue is greater than one, x^* is an unstable solution of (2). This case also corresponds to cyclic walking, but small perturbations can cause large deviations from the solution trajectory (e.g., falling).

For the simulations to follow, we adopt human-like parameters M_h = 14.11 kg, M_t = 17.61 kg, m = 13.5 kg, m_th = μm, m_sh = (1 − μ)m, ℓ_t = 0.55 m, ℓ = 1 m, α = 0.5, w = 0.2 m, and ρ = 0.0564, where μ is the mass distribution between the thigh and shank of each leg. We will vary the parameter μ to obtain asymmetric gaits.

III. Simulation Results

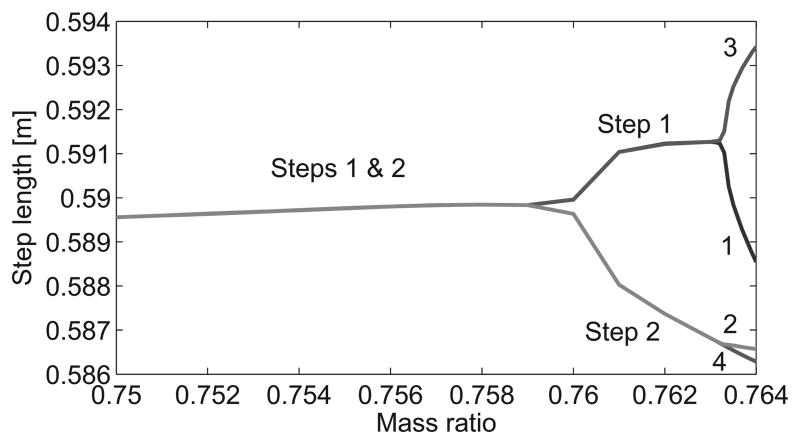
Similar to the passive planar biped considered in the companion paper [6], the mechanics of our 3D biped admit a symmetric and asymmetric family of gaits based on mass ratio μ. The steady-state gait is symmetric and stable for a wide range of ratios less than μ = 0.76. The symmetric gait becomes unstable for ratios larger than μ = 0.76, splitting into a stable asymmetric gait that is cyclic every two steps with a long and short stride. We then observe stable 4-step asymmetric gaits after the second bifurcation at μ = 0.763, where the 2-step family becomes unstable. We observe non-cyclic gaits with eventual falling for μ larger than 0.764.

The functional characteristics of these gaits are visualized in the bifurcation diagrams of Figs. 2-4, which show the steady-state evolution of so-called “gait descriptors” (variables of the stable gait) as μ is varied. We show a limited range of mass ratios around the bifurcation points, where the most interesting behavior occurs. Asymmetric solutions have two or more branches showing the descriptor for each step cycle in the gait, and the averaged descriptors of asymmetric solutions tend to follow the (unstable) symmetric solution.

Fig. 2.

Steady-state step length over mass ratio.

Fig. 4.

Steady-state GRF impulse over mass ratio: vertical (left), anterior-posterior (middle), and absolute mediolateral (right). Impulses are calculated by integrating the GRF vector (over the entire step period for vertical, after midstance for AP and ML) and normalizing by $M_{\text{total}g}\sqrt{\ell /g}$ to be dimensionless.

We see in Fig. 2 that the symmetric solution's step length grows slowly with mass ratio. Gait speed, i.e., step length divided by time period, remains nearly constant in Fig. 3, whereas the impact energy dissipation monotonically increases until the first bifurcation reverses this trend. The total mechanical energy at the end of each step cycle increases monotonically over the entire range. Integrating the GRF vector for each step cycle, we find in Fig. 4 that the AP and vertical impulses follow a monotonic decreasing trend whereas the mediolateral (ML) impulse is approximately sinusoidal over the range of symmetric gaits.

Fig. 3.

Steady-state step velocity (left), total energy (middle), and impact energy dissipation (right) over mass ratio.

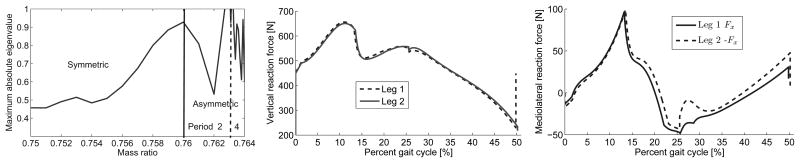
The eigenvalues of the return map between steps characterize a mathematically meaningful definition of gait stability. In fact, the maximum absolute eigenvalue is an inverse scale for stability between zero and one: a smaller value implies faster attenuation of perturbations in some local region around the nominal joint trajectory. We find in Fig. 5 that some asymmetric gaits after the bifurcation point are more stable than symmetric gaits before the bifurcation point (e.g., 0.532 at μ = 0.762 versus 0.673 at μ = 0.757). The maximum absolute eigenvalue of the 4-step asymmetric gait also drops significantly after the 2-step gait becomes unstable at the second bifurcation point. We see that there are multiple local stability minima within the range of walking gaits, where the global minimum resides in the symmetric family.

Fig. 5.

Maximum absolute eigenvalue over mass ratio (left). Vertical (middle) and mediolateral (right) ground reaction forces for the period-2 asymmetric gait of μ = 0.763, where the second step cycle is shifted to coincide with the first step cycle for visual comparison. A supplemental movie of this asymmetric simulation is available at: http://vimeo.com/22420529

IV. Discussion

These simulations show that symmetric changes in physiology can directly cause asymmetry to emerge from bipedal mechanics. We used a control strategy that embraces the natural dynamics of the sagittal plane, so we argue that these passive dynamics are responsible for the asymmetry as with the uncontrolled planar biped of [6].

We find one monotonic relationship between bifurcation parameter and average gait descriptor that agrees with the observations in [6], suggesting that total energy plays a fundamental role in the emergence of asymmetry. Perioddoubling behavior may be a natural way for the body mechanics to compensate for an excess of energy in the gait (e.g., fast walking). This observation is experimentally supported by a test of the functional asymmetry hypothesis [3], where asymmetry was observed in AP impulses only during fast walking. However, a causal relationship is difficult to prove because multi-period solutions to nonlinear hybrid dynamics generally cannot be solved analytically.

The hypothesis of functional asymmetry proposes distinct biomechanical functions of the legs [3], where one contributes more to propulsion and the other to body-weight support/transfer and motion control [1]–[3]. The asymmetric family of solutions in Figs. 3 and 4 shows that each leg contributes different impulses per step cycle and dissipates different energy at double-support transitions. This is manifested in the reaction forces as seen in the asymmetric gait of Fig. 5. The first stance phase provides lean control with a ML impulse 106% greater than the second. We see less distinction in the support and propulsion functions, as the vertical and AP impulses of the second leg are both 1% greater than the first leg (note the clearer distinction for the period-4 gait). This suggests that the function of control might be performed by a distinct leg, whereas support and/or propulsion need not be isolated to one respective leg.

For walking gaits beyond the first bifurcation point, the asymmetric solution is trivially more stable than the unstable symmetric solution (Fig. 5). Both correspond to cyclic walking motion, but walking symmetrically requires a different control strategy to attenuate perturbations. If these characteristics indeed hold for human walking, asymmetries observed in able-bodied studies might be explained in part by humans attempting to maximize stability. The leg corresponding to each biomechanical function may be influenced by limb dominance, but our simulations suggest that an asymmetric walking strategy is dynamically beneficial under certain conditions and human neurophysiology might have developed to exploit this fact.

It is important to note that healthy humans appear to limit gait asymmetry. A study on able-bodied children and young adults did not find any noticeable changes in kinematic and temporal symmetry variables as a function of walking speed [11]. Kinetic asymmetry was only observed during fast walking in [3]. The motor control system may enforce symmetry in all but the most challenging tasks for more than aesthetic reasons – unbalanced strain on joints and muscles over time can lead to musculoskeletal deterioration [5].

V. Conclusions

We observed functional gait asymmetry in simulations of a symmetrical 3D biped after small changes in a mass distribution parameter for both legs. In fact, asymmetric walking was the only stable strategy for a range of physiological conditions. Reaction force impulses of the 2-step asymmetric gaits indicate that the ML control function was mainly provided by one leg, but vertical support and AP propulsion were shared nearly equally by both legs.

This offers insight into the possible divisions of leg function in able-bodied gait: control can be performed by a distinct leg, whereas support and/or propulsion need not be isolated to one leg. Different asymmetric and functional behavior might be observed when varying other parameters (see [6] for a planar environmental case). We argue that period-doubling bifurcation, also known as spontaneous symmetry-breaking, might explain in part the phenomenon of functional asymmetry and why it only appears in certain tasks.

These results motivate a new line of inquiry into the role of human motor control in suppressing gait asymmetry. This also suggests a number of hypotheses for the pathophysiology of abnormal asymmetry, which may inform treatments to restore symmetry. For example, the neurological state change associated with stroke or cerebral palsy might render the motor control system unable to inhibit the natural tendency of biped mechanics to facilitate asymmetry. This motivates investigation of novel therapies that constrain or challenge the subject's control system such that the asymmetric family of gaits is no longer optimal for stability.