Abstract
Purpose
To develop an inversion pulse-based, CEST-like method for detection of 31P magnetization exchanges among all NMR visible metabolites suitable for providing an integrated kinetic analysis of phosphorus exchange reactions in vivo.
Methods
The EKIT sequence (Exchange Kinetics by Inversion Transfer) includes application of a frequency-selective inversion pulse arrayed over the range of relevant 31P frequencies, followed by a constant delay and a hard readout pulse. A series of EKIT spectra, each given by a plot of Z-magnetization for each metabolite of interest versus frequency of the inversion pulse, can be generated from this single data set.
Results
EKIT spectra reflect chemical exchange due to known biochemical reactions, cross-relaxation effects, and relayed magnetization transfers due to both processes. The rate constants derived from EKIT data collected on resting human skeletal muscle were: ATP synthesis via ATP synthase (0.050 ± 0.016 s-1), ATP synthesis via creatine kinase (0.264 ± 0.023 s-1), and cross-relaxation between neighboring spin pairs within ATP (0.164 ± 0.022 s-1).
Conclusion
EKIT provides a simple, alternative method to detect chemical exchange, cross relaxation and relayed magnetization transfer effects in human skeletal muscle at 7T.
Keywords: skeletal muscle, magnetization transfer, NOE, chemical exchange, T1 relaxation time
INTRODUCTION
The ability to probe exchange kinetics between metabolites using 31P NMR magnetization transfer (MT) has long been recognized (1, 2). One subset of these methods, saturation transfer (ST), has been widely applied to measure phosphoryl exchange in skeletal muscle of animals (2, 3) and human subjects (4, 5, 6, 7). More recently, the method has been used to probe mitochondrial function in diseases such as insulin resistance and diabetes (4,8-14). The major advantage of ST is simplicity of extracting unidirectional forward kinetic rate constants such as kPi→γATP or kPCr→γATP from a spin system involving exchange of 31P magnetization among multiple sites. The simplification is technically achieved by irradiating the γ-ATP pool for a sufficient period until the inorganic phosphate (Pi) or phosphocreatine (PCr) signal is reduced to a new steady-state value. Although the simplicity of ST is attractive, some features of some ST observations have been difficult to interpret or quantify mechanistically (6, 7, 15-18). For example, during the saturation of γ-ATP, ST effects have been observed in the β- ATP and α-ATP (7, 18) but have been excluded in a classical exchange model which includes exchanges only between γ-ATP, PCr and/or Pi. The reduction in the β-ATP signal was originally attributed to the near co-resonance of γ-ATP and β-ADP (19, 20) so that saturation of any underlying β-ADP could transfer magnetization to β-ATP at a high rate in tissue with active creatine kinase. An alternative interpretation could be attributed to two cycles of the adenylate kinase reaction (21). However, observation of equal reduction of β-ATP signal in both wild-type mice and double-mutant mice lacking both adenylate kinase and creatine kinase (22, 23) excluded a possible contribution of β-ADP ↔ β-ATP (19) or γ-ATP ↔ β-ADP ↔ β-ATP (21). Instead, nuclear Overhauser effects (NOE), which occur through cross-relaxation between γ- and β-ATP, was suggested to be the underlying mechanism (21). However, the widely-observed ST effect at α-ATP during saturation of γ-ATP cannot be explained by direct NOE between the spatially distant γ- and α- ATP, nor by any known biochemical pathway (18).
Surprisingly, aside from exchange between phosphocreatine (PCr) and γ-ATP mediated by creatine kinase (CK), none of the other exchanges between γ-ATP and Pi, α-ATP, or β-ATP, have been observed using pulsed magnetization transfer techniques such as inversion transfer (18). It has been suggested that these unknown transfers might originate from smaller pools of bound metabolites that are only activated by the prolonged pulses (typically 5-8 s in duration) such as those used in ST experiments (18). Prolonged saturation of a small pool of spins may have an amplified effect on a larger exchanging pool, a phenomenon widely exploited in chemical exchange saturation transfer (CEST) imaging (24-27). An alternative mechanism for the observed ST between γ- and α-ATP may be long range NOE effects though the bonds γ-ATP → β-ATP → α-ATP. Such relayed magnetization transfer effects (28), often seen in large proteins by solution NMR, could become detectable when using prolonged saturation pulses due to transient binding of ATP to macromolecules in vivo. Another possible contribution to apparent transfer between γ- and α-ATP when prolonged pulsed using high power, is off-resonance direct saturation (29, 30), the so-called “spillover” effect. Correction for spillover is normally performed by including a separate control experiment with irradiation at an equal chemical shift but on the opposite side of the observed frequency. This approach implicitly assumes that the control irradiation does not induce unintended saturation of other exchanging metabolites. In practice, it is somewhat challenging to conduct clean control experiments on all high energy phosphates in vivo that might be involved in the exchanges of interest.
Here, we present an alternative pulsed technique to study the kinetics of phosphorous metabolite exchange in human skeletal muscle at 7T. The technique termed Exchange Kinetics by Inversion Transfer (EKIT) uses a variable frequency inversion pulse to initiate transfer of magnetization among all exchanging spins during a fixed delay period after the inversion pulse (Figure 1a). After the inversion pulse, all magnetization transfer effects that are developed during the delay phase can be attributed to either intramolecular NOE or chemical exchange (Figure 1b). EKIT is conceptually similar to CEST except that in CEST, all chemical exchanges take place between chemically specific functional groups (-NH or -OH) and bulk water protons. Hence, the water proton signal is typically the only signal monitored in generating a CEST spectrum. In EKIT, however, transfer of magnetization is monitored among all possible exchanging chemical species simultaneously. A resulting EKIT spectrum, plotted as an array of 31P NMR spectra versus frequency of the inversion pulse, reflects all 31P-31P exchanges detectable on the MR time scale set by the chosen delay times. An analysis of these simple EKIT spectra provides quantitative exchange rates and T1 relaxation times, including auto- and cross-relaxation times for ATP (31), for all observable phosphorus metabolites in human skeletal muscle at 7T.
FIG. 1.
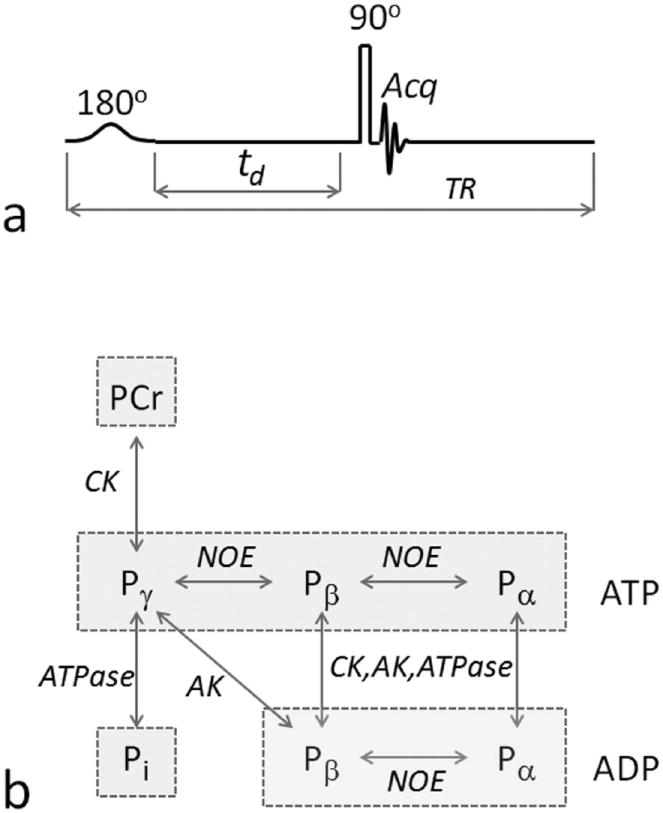
EKIT pulse sequence and 31P magnetization exchange pathways. a: The EKIT pulse sequence consists of a low-power, frequency-sweep inversion pulse, followed by a constant delay period, td, and a hard readout pulse. b: 31P magnetization exchange system in skeletal muscle, showing the various exchange pathways that are possible in skeletal muscle, including phosphorous chemical exchange reactions indicated by vertical arrows, and Nuclear Overhauser Effect (NOE) indicated by horizontal arrows. ATP and ADP are marked by rectangular boxes. A five-pool model including Pi, PCr and ATP but not ADP, was adopted in this work. Abbreviations: AK, adenylate kinase; CK, creatine kinase.
METHODS
Theory
For the five-pool exchange model illustrated in Figure 1b, in the absence of an applied B1 field, the time dependent change in magnetization of each 31P resonance can be written according to Bloch-McConnell-Solomon formalism as:
| [1] |
| [2] |
| [3] |
| [4] |
| [5] |
where a, b, c, d and e denote Pi, PCr, γ-, α- and β-ATP, respectively; (i = a – e) denotes the magnetization of a given spin i at Boltzmann thermal equilibrium; σij (i, j = c – e) denotes rate constant for dipolar cross-relaxation (NOE), with σij = σij > 0; kij (i, j = a – c) denotes pseudo first-order kinetic rate constant for the magnetization exchange process i → j, which relates to the reverse rate constant kji by
| [6] |
R1,i in equations [1-5] is the sum of intrinsic longitudinal relaxation rate (1/T1) of spin i and chemical exchange rate constants that originate from spin i:
| [7] |
| [8] |
| [9] |
| [10] |
| [11] |
Note that in this study the term “intrinsic longitudinal (T1) relaxation” is used for all 31P spins. An alternative term used in the literature is “auto relaxation” (31); this refers to spins which also relax via a dipolar cross-relaxation mechanism (NOE).
The matrix solution to the magnetization equations [1-5] is given by:
| [12] |
in which Mz|t = 0+ represents the initial magnetization immediately after a perturbation by a RF pulse (t = 0+), and
| [13] |
| [14] |
and
| [15] |
Now, consider that the five-pool exchange system is subject to repetitive pulsing by the sequence (180° – td – 90° – τ)n. The initial magnetization before the first 180° pulse is , while the magnetization before each of the following (n-1) 180° pulses is dependent on its recovery in the τ period following the 90° readout pulse:
| [16] |
where I is the identity matrix, and ρ is an experimental parameter, accounting for the effect of the non-selective readout pulse (ρ = 1 for an ideal 90° pulse with zero dead-time, and ρ = 0 if flipping angle is 0°). Due to the difference in initial magnetization between the first scan and the remaining (n-1) scans, the first scan is taken as a preparation scan or dummy scan, and only the remaining (n-1) scans are assumed to be at steady-state magnetization. For these (n-1) scans, the magnetization immediately following the frequency-selective inversion pulse is given by
| [17] |
where αf is an empirical function describing the inversion profile (an inverted pseudo Lorentzian line-shape) observed for the inverted 31P resonances, given by:
| [18] |
where Δδ (= | δinv - δo |) is the difference between the carrier frequency of the inversion pulse (δinv) and center of a given 31P resonance at chemical shift, δo (in ppm); β and γ are coefficients which define the linewidth and shape of the inverted peak, and α is a coefficient that reflects the magnitude of the inverted peak, with 0 ≤ α ≤ 1. For full on-resonance inversion (Δδ = 0), α = 1 and αf = −1.
The magnetization of inverted signals continues to evolve in the delay time (td) as follows (combining Equations [12] and [17]):
| [19] |
After the td period, a 90° readout pulse is applied and the magnetization is detected. An EKIT spectrum is defined as a plot of Mz (for clarity, the superscript of is omitted) versus δinv (as given by αf), or versus δinv in a normalized EKIT spectrum, where represents the maximal magnetization developed in the (τ + td) period (αf = 1 and combining Equations [16] and [19]):
| [20] |
Note that the inversion pulse in this work was frequency-selective (hyperbolic secant shaped), which has virtually no inversion effect on any isolated resonance beyond Δδ ≥ 2 ppm, i.e. , thus giving rise to a flat regions flanking the inverted peak with steady-state Mz independent of Δδ. But if the resonance experiences magnetization exchanges with other spins in the td period, Mz will be reduced and manifested as an inverted peak in its EKIT spectrum. By fitting EKIT spectra of all observed 31P metabolite resonances collected at variable delay times, td, one can solve Equations [14-20] to determine the nine independent, unknown variables which govern the size of various exchange peaks, including five intrinsic T1 values, two rate constants for chemical exchange and two cross-relaxation rates, and the ρ, α, β, and γ parameters.
Human Subjects
The protocol was approved by the Institutional Review Board of the University of Texas Southwestern Medical Center. Prior to the MRS study, informed written consent was obtained from all participants. Seven subjects (2 male and 5 female), aged 28 ± 4 yr and BMI 24 ± 1, participated the study, all healthy with no history of peripheral vascular, systemic or myopathic diseases. To avoid possible exercise-associated physiological variations among subjects, all subjects were asked to refrain from any physical activity of moderate or high intensity for 24 hours prior to the study, and subjects sat at rest for 20 minutes prior to the scan. Heart rate and blood oxygen saturation level were monitored during the scan. The study was well-tolerated by all subjects.
MRS Protocol
All subjects were positioned feet-first and supine in the MRI scanner (7T Achieva, Philips Healthcare, Cleveland, OH), with the right calf muscle positioned parallel to the magnetic field and directly on the detection coil (Philips Healthcare, Cleveland, OH). The coil was a partial volume, double-tuned 1H/31P quadrature TR coil consisting of two tilted, partially overlapping 10 cm loops for 31P detection. The center of the coil was positioned approximately 1/3 of the distance along the leg from the knee to the heel. Axial, coronal, and sagittal T2-weighted turbo spin echo images were acquired for voxel planning. Typical imaging parameters included field-of-view 180 × 180 mm (FOV), repetition time (TR) 2 s, echo time (TE) 75 ms, turbo factor 16, in-plane spatial resolution 0.6 × 0.7 mm2, slice thickness 4 mm, gap 2 mm, bandwidth 517 Hz, number of acquisitions (NA) one, and acquisition time 1.2 min. 2nd order 1H-based automatic volume shimming was applied prior to 31P spectral acquisition. FID-based 31P spectra were acquired from calf muscle for each subject with the following parameters: 1) td/TR = 0/4 seconds; 2) td/TR = 1/5 seconds; 3) td/TR = 2/6 seconds and 4) td/TR = 3/7 seconds, which led to td-dependent data acquisition time of 10, 12.5, 15, 17.5 min, respectively, and a total scan time of 55 min for the entire EKIT data collection. In all experiments, the delay time after the readout pulse remained the same (TR – td = 4 second). The other NMR parameters are bandwidth 4 kHz, 4096 points. The inversion pulse was hypersecant-shaped pulse of 15 ms duration which yielded an effective inversion bandwidth of 150 Hz. The offset frequency of the inversion pulse (δinv) was swept over the entire 31P spectral region from 1400 to -2350 Hz in 25 Hz steps, yielding 150 dynamic spectra. The offset frequency of inversion pulse and the chemical shift of the 31P spectra were referenced to PCr at 0 ppm. Each 31P NMR spectrum was Fourier transformed, processed with Gaussian apodization (6 Hz) using the scanner software (SpectroView, Philips Healthcare), and further analyzed using Matlab (Mathworks) routines.
31P Spectral Analysis
Relative magnetization in EKIT spectra was measured by signal intensity of each metabolite. The 31P signal integral area was measured from NMR spectra acquired with NA = 1 to yield magnetization at equilibrium . Signal postprocessing, EKIT spectral fitting, and statistics were done in Matlab (The Mathworks, Natick, MA). EKIT data acquired at all four delay times (td = 0, 1, 2 and 3) from all five spins (Pi, PCr, ATP α-, β- and γ spins) were fitted simultaneously. The fitting was based on a least squares algorithm (Matlab function lsqcurvefit) to minimize the sum of squared difference between experimental and calculated magnetization values, . The excitation profile of EKIT signals was characterized by an inverted pseudo-Lorentz shape (Equation [18], Theory Section) with fitting parameters α = 0.75 ± 0.03 (Pi), 0.75 ± 0.07 (PCr), 0.70 ± 0.04 (γ-ATP), 0.72 ± 0.03 (α-ATP) and 0.67 ± 0.04 (β-ATP), and β = 5.98 ± 0.26 and γ = 2.86 ± 0.19 for all 31P resonances, and the effect of hard non-selective readout pulse was characterized by fitting parameter ρ = 0.90 ± 0.03 (Equation [16]) for all 31P resonances.
RESULTS
A typical EKIT spectrum acquired from calf muscle of a healthy female subject is shown in Figure 2b. Here, the residual Mz magnetization in PCr is plotted as a function of the frequency of the applied inversion pulse, δinv, over a range of 3,750 Hz in steps of 25 Hz (150 spectra). In addition to the inverted PCr resonance which had partially relaxed after the inversion pulse and the 1 s delay, two additional exchange peaks were observed, one at -2.4 ppm which reflects the well-known exchange between γ-ATP and PCr and another at -16.0 ppm (see Fig 2b inset) which reflects a reduction in the PCr signal that occurred after inversion of the β-ATP resonance. Such a small change in signal could be easily missed in a conventional 31P spectrum, but the well-defined lineshape of this small exchange peak clearly distinguishes it from the baseline spectra due to excellent S/N ratio (~1:150). These features were common and highly reproducible among different subjects, with an averaged variability of 5%.
FIG. 2.
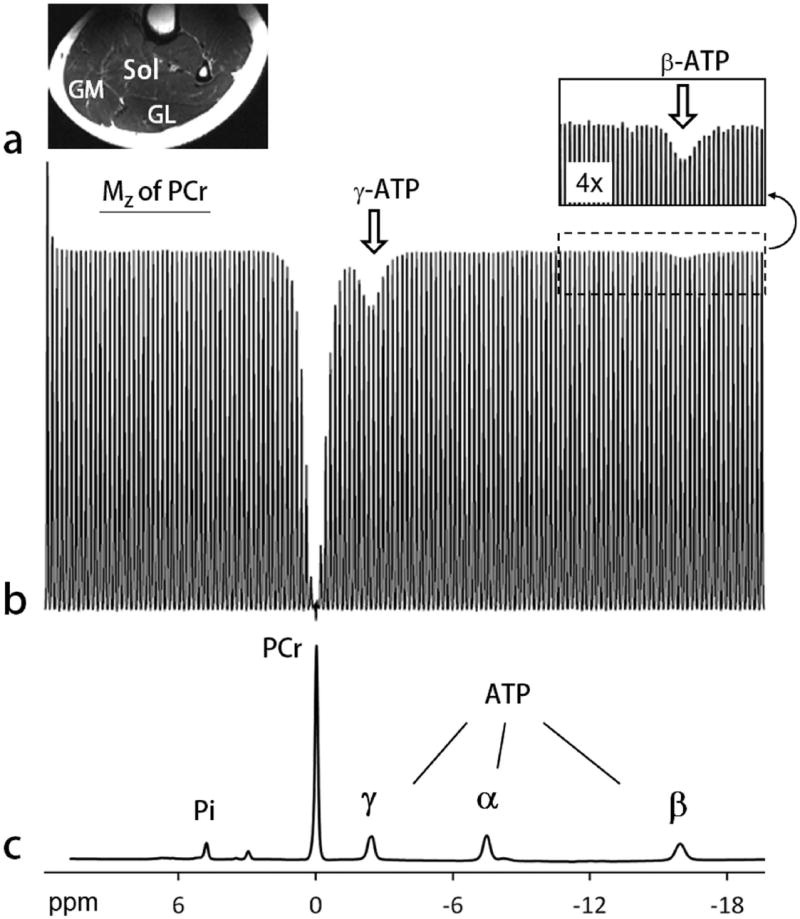
EKIT spectrum of human calf skeletal muscle. a: A typical T2w MR image acquired from human calf using a partial volume coil. Abbreviations: Sol, soleus; GM, gastrocnemius medial; GL, gastrocnemius lateral. b: The EKIT spectrum illustrated here reflects the intensity of PCr signal plotted as a function of frequency of the inversion pulse (150 different frequencies) acquired from calf of a 25 yr healthy female with a BMI = 22.2 kg/m2. Other 31P MRS acquisition parameters: TR 5 second, td 1 second, scan time 12.5 min. Note that PCr magnetization is attenuated after inversion of either γ ATP (white arrow) or β ATP (insert). c: A conventional 31P MR spectrum acquired showing the full chemical shift region of calf muscle 31P resonances, with the chemical shift aligned with that of sweeping inversion pulse used in the EKIT spectrum b.
Alternative displays of EKIT data are shown in Figures 3 and 4 for all 31P signals (Pi, PCr, α- β- and γ-ATP), arrayed to provide an intuitive view of all exchanges occurring between each metabolite. The three-dimensional EKIT spectrum (Figure 3a) was generated by plotting the intensity of each 31P signal against δinv in the first dimension, and the chemical shift δobs of all 31P resonances in the second dimension. The appearance of multiple exchange peaks for ATP can be seen in the enlarged 3D spectrum (Figure 3a) and in a 2D contour plot where the inversion-induced change in signal intensity is plotted as δinv versus δobs (Figure 3b). Although this later plot has 2 chemical shift axes and cross peaks, it was not generated from a conventional 2D NOE experiment (see Discussion).
FIG. 3.
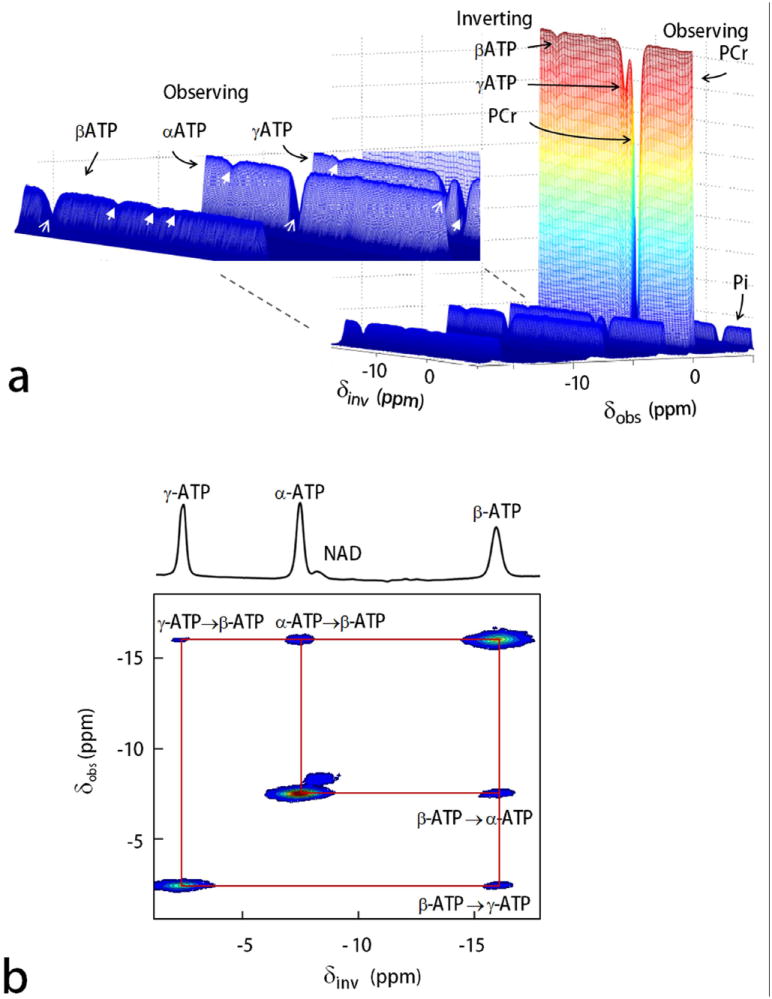
3D and 2D display of EKIT spectra of resting human calf muscle. a: 3D EKIT spectrum plotted by arraying the entire 31P MR spectra acquired using a series of offset inversion frequencies (PCr as reference at 0 ppm), with an enlarged region (inset) showing EKIT exchange peaks among the ATP spins (exchange effects marked by arrows with solid head, on-resonance inversion signals marked by arrows with thin lines). b: 2D contour plot showing ATP cross-relaxation (NOE) generated from subtraction spectra with off-resonance inversion as baseline. Note that the NAD peak which lies along the diagonal of this plot shows no exchange effect with ATP in resting skeletal muscle.
FIG. 4.
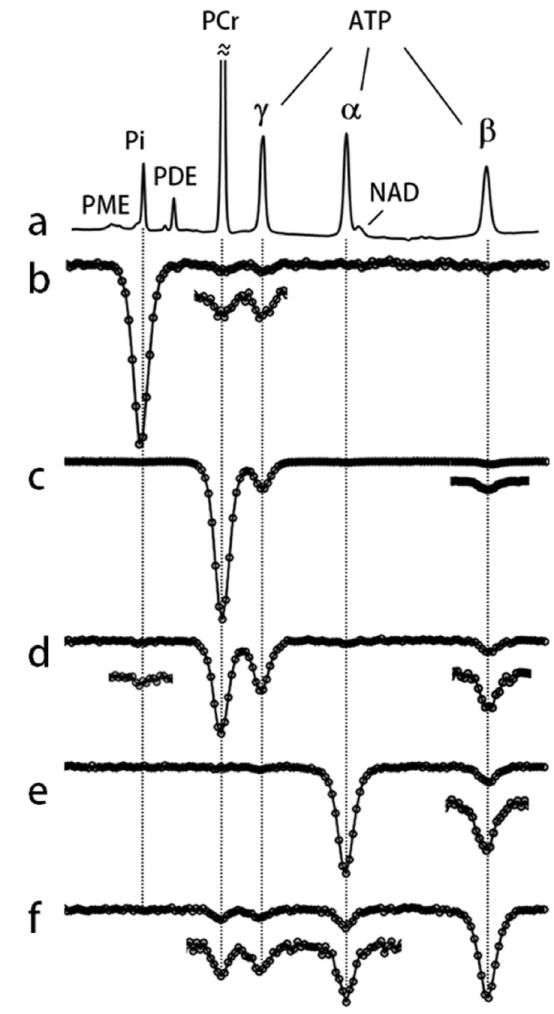
EKIT spectra of resting human calf muscle. a: A conventional 31P MR spectrum and (b-f) EKIT spectra with observation resonance at b: Pi, c: PCr, d: γ-ATP, e: α-ATP, and f: β-ATP acquired from resting human calf muscle at td = 1 s. These spectra represent averages from 7 subjects. In some spectra, small exchange peaks were enlarged 3-fold.
The EKIT spectra shown in Figure 4 were generated for all major 31P metabolite signals (Pi, PCr, α- β- and γ-ATP) by plotting normalized signal intensity against δinv. These individual EKIT spectra feature one large peak due to on-resonance inversion (δinv = δo), plus one or more additional exchange peaks arising from exchange effects due to inversion of other resonances. These exchange peaks are typically 3 to 10-fold weaker than the corresponding on-resonance peak with one exception; in case of γ-ATP (Figure 4d), an even larger decrease in γ-ATP magnetization was observed upon inversion of PCr followed by a 1 s delay than that seen in inversion of γ-ATP itself (Figure 4d).
The exchange peaks seen in these spectra can be classified into three subgroups. One subgroup arises as a consequence of the creatine kinase catalyzed reaction (PCr ↔ γ ATP); this includes the PCr exchange peak at 0 ppm in γ ATP spectrum (Figure 4d) and the γ-ATP exchange peak at -2.4 ppm in PCr spectrum (Figure 4c). A second subgroup arises as a consequence of ATP synthesis (Pi ↔ γ-ATP); this includes the γ-ATP exchange peak at -2.4 ppm in Pi spectrum (Figure 4b) and barely detectable Pi exchange peak at 4.9 ppm in γ-ATP spectrum (Figure 4d). The third subgroup arises as a consequence of NOE effects between neighboring spins within the ATP molecule; these include the β-ATP exchange peak at -16.0 ppm in γ- and α-ATP spectra (Figures 4d and 4e) and the γ- and α-ATP exchange peaks (-2.4 and -7.4 ppm) in β-ATP spectrum (Figure 4f).
Some EKIT signals cannot be attributed solely to either chemical exchange or NOE effects. Three other “exchange peaks” can be detected that must arise from a combination of two mechanisms. The exchange peak at 0 ppm in the Pi spectrum (Figure 4b) reflects magnetization transfer between PCr and Pi that occurs as a result of two chemical exchange reactions: PCr ↔ γ-ATP and γ-ATP ↔ Pi. Exchanges also appear between β-ATP and PCr (Figures 4c and 4f) which reflect a combination of chemical exchange (PCr ↔ γ-ATP) and NOE between γ- ↔ β-ATP spins. These long-range effects between two spins are relayed exclusively through γ-ATP. No chemical exchanges were detected in PDE signal in EKIT spectra of PCr, ATP and Pi (Figures 4b-f) so this pool of phosphorus was excluded from exchange considerations in the model (Figure 1b).
To further explore the quantitative nature of these exchange effects, EKIT data were acquired using various delay times, td = 0, 1, 2 and 3 s. The resulting EKIT spectra are compared in Figures 5 and 6. A simultaneous fitting of all EKIT spectra (5 spectra collected at 4 different delay times = 20 data sets) yielded values for the intrinsic T1 of each metabolite resonance (Table 1), the unidirectional rate constants for chemical exchanges (PCr ↔ γ-ATP and Pi ↔ γ-ATP) and the cross relaxations (NOE) within ATP (Table 2). The 5-pool model fit all EKIT spectra with high precision (solid curves, Figures 5a-e and 6a-d). Both the experimental and fitted data illustrate that the magnitude of the chemical exchange peaks depend upon the length of the delay period following the inversion pulse. No exchange peaks were observed in the td = 0 spectra (Figures 5a-e) with one exception; the PCr peak was slightly inverted in the γ-ATP spectrum (Figure 5c). This indicates that chemical exchange between PCr and γ-ATP is so fast that even a small amount of signal reduction in γ-ATP develops during inversion of PCr and subsequent excitation pulse. This small peak reduction in the td spectrum was used to correct the intensities in the remaining spectra (td ≠ 0). Interestingly, while all exchange peaks representing chemical exchanges appear to reach a maximum near td = 1 s and then decrease with longer delay times, the long-range relayed exchange effects, such as that between PCr and β-ATP or PCr and Pi (Figures 5a, 5b, and 5e) either increase or remain nearly invariant between td = 1 – 3 s. For example, a maximum was observed near td = 2 s in the PCr spectrum (Figure 5b) for the long-range relayed exchange peak between PCr and α-ATP due to successive pathways (α-ATP → β-ATP → γ ATP → PCr).
FIG. 5.
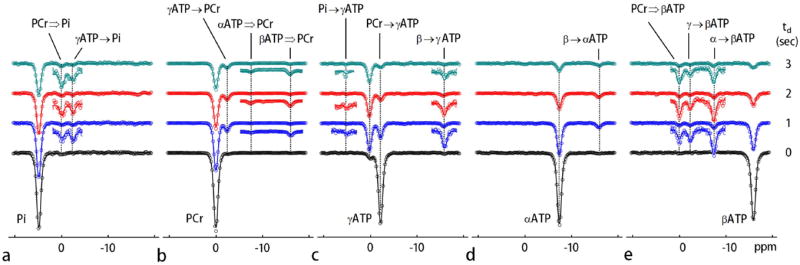
EKIT spectra and data fitting. EKIT spectra for observation of a: Pi, b: PCr, c: γ-ATP, d: α-ATP, and e: β-ATP at inversion delays of 0, 1, 2, and 3 seconds. The EKIT data were acquired from resting human calf muscle averaged for 7 subjects. The major chemical exchange reactions are indicated by solid black arrows while the effects of relayed MT are marked by the hollow arrows. The smaller EKIT exchange peaks were vertically enlarged (x4). The solid curves represent the least-squares fitting of all data to a five-pool kinetic exchange model shown in FIG. 1b.
FIG. 6.
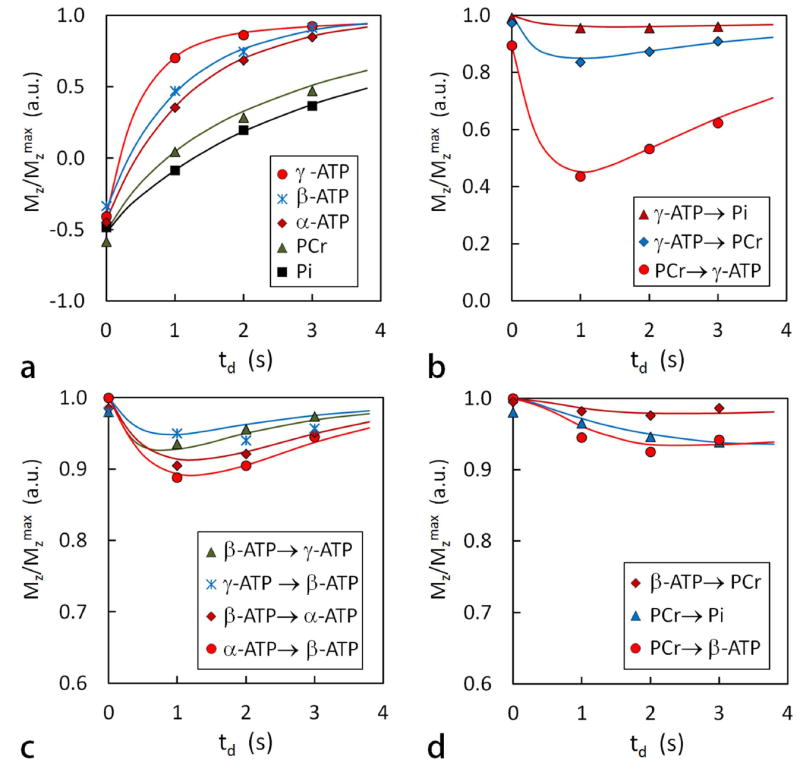
Plots of normalized EKIT peak intensity versus delay time td for several exchange processes. a: plots of Mz/Mz max after an on-resonance inversion pulse for several metabolites, b: for chemical exchanges mediated by CK and ATPase, c: for NOE within ATP, and d: for relayed MT effects. These data are identical to those shown in FIG. 5 with the solid lines showing the best fit of the data to the exchange model.
Table 1.
31P T1 relaxation times in resting human calf muscle at 7T
| T1 (sec)
|
||
|---|---|---|
| EKIT (5-pool Model) | Non-selective inversiona | |
| Pi | 7.34 ± 0.82 | 6.3 ± 1.0 |
| PCr | 5.30 ± 0.33 | 4.0 ± 0.2 |
| γ-ATP | 1.70 ± 0.21 | 3.3 ± 0.2 |
| α-ATP | 1.30 ± 0.09 | 1.8 ± 0.1 |
| β-ATP | 1.13 ± 0.10 | 1.8 ± 0.1 |
Bogner, et al. (ref 37) measured by non-selective inversion of all metabolite resonances followed by recovery at 7T. Each metabolite data set was fit to a mono-exponential decay function.
Table 2.
Forward kinetic rate constants (k) and ATP cross-relaxation rate constants (σ) in resting human calf muscle.
| Mechanism |
k or σ (sec-1)
|
||
|---|---|---|---|
| EKIT (5-pool model) | ST (2-pool Model) | ||
| Pi → γ-ATP | Chemical exchange | 0.050 ± 0.016 | 0.057(Gastroc)a; |
| 0.059(soleus)a; 0.11b | |||
| PCr → γ-ATP | Chemical exchange | 0.264 ± 0.023 | 0.26c; 0.29d; 0.34b |
| γ-ATP ↔ β-ATP | Cross relaxation (NOE) | 0.163 ± 0.019 | |
| α-ATP ↔ β-ATP | Cross relaxation (NOE) | 0.165 ± 0.022 | |
The two most widely studied 31P reactions have been flux through creatine kinase and ATP synthase. The quantitative kinetic results obtained by fitting the EKIT spectra are summarized in Table 2, and compared with previous literature values measured using ST methods. The rate of ATP turnover through creatine kinase, calculated by the product of kPCr→γATP (0.264 sec-1) and total tissue PCr (23.3 mmol/kg ww (ref. 4)) is 369.1 mmol/kg ww/min. Similarly, the ATP turnover rate was found to be 7.44 mmol/kg ww/min, as estimated by the product of kPi→γATP (0.050 sec-1) and total tissue Pi (2.48 mmol/kg ww).
DISCUSSION
The approach presented here for measuring exchange kinetics for all phosphorus-containing metabolites borrows on the concept of incrementing the frequency of an applied pulse from 1H-based CEST techniques (24-27). 31P-based CEST techniques have also been explored by Koretsky et al in biochemical solutions as early as 1985 and recently in vivo by our group. As with CEST, an inherent advantage of EKIT is the observation of all exchanging metabolites in a multiple spin system by simple visual inspection of the entire spectrum. This approach also offers a number of practical and conceptual advantages compared to conventional single-site saturation transfer (ST) or non-selective broadband inversion transfer (IT) measurements. In particular, no assumptions are necessary about which pools may or may not be in exchange since the entire system is interrogated in a single experiment. As with any IT method, EKIT offers a 2-fold larger dynamic range over a ST experiment ( for IT and EKIT versus for ST), although the actual dynamic range can vary depending upon on the properties of NMR spin and characteristics of the inversion pulse. Perhaps more importantly, EKIT data analysis is simplified because only the Mz components need to be considered so all forward and reverse exchanges plus T1 effects are embedded in a single exchange matrix. There is no need for separate T1 measurements (7, 32, 33, 37-45). Unlike ST, the EKIT method is insensitive to small invisible pools of metabolites that may be present such as protein-bound ATP (18). Although this information is of interest, unambiguous identification of the contribution of small pools to ST data is difficult due to presence of confounding factors in vivo (18,22,23). Furthermore, it is not a trivial task to include small pools in the exchange model for quantitative analysis since the NMR properties of small pools are usually less-well defined compared to those of the larger visible pools of metabolites. Finally, given that a single pulse is used for inversion, the EKIT sequence is also easy to implement on human scanners. The frequency-selective inversion pulse used in EKIT is about 250 to 400-fold shorter than saturation duration in a typical ST experiment (5 – 8 sec), and followed by an exchange-labeling period free of B1 pulsing (td: 1 – 4 sec), so one can expect minimal spillover effects and consistent instrument performance (7). Certainly, this EKIT approach benefited from the excellent S/N achieved by the high field and relatively larger coil.
As shown in Figures 2-5, the EKIT peaks observed under current conditions are symmetric, well-resolved and do not require an asymmetry analysis as often used in CEST methods (25). This allows unambiguous identification of small and fine exchange effects such as relayed magnetization transfer. The EKIT fitting quantitatively confirms that, even without direct chemical or cross-relaxation effects (i.e. setting k = 0 and σ = 0), exchange effects can still occur between unconnected spin pairs such as PCr ↔ β-ATP and PCr ↔ α-ATP. These EKIT results data indicate that, in resting human muscle, the relayed MT effect can arise from a result of two different metabolic pathways (CK- and ATPase-mediated reactions as in PCr → γ-ATP → Pi, Figures 4b, 5a and 6d) or two distinct MT mechanisms (chemical exchange and NOE as in β-ATP → γ-ATP → PCr, Figures 4c, 5b and 6d). It is unexpected but not surprising that the relayed MT effect can propagate from α-ATP to β-ATP to γ-ATP to PCr (Figure 5c) because both the experimental conditions and biomolecular NMR properties (td, k, σ , and T1) are favored at this field.
The observation of cross-peaks between neighboring ATP 31P spins in human skeletal muscle (Figure 3c) supports previous assignments of NOEs in animal models (22,23,28). However, without quantitative and integrated analysis, this well-observed but less-recognized mechanism can be a confusing factor in interpretation of the MT effects, as previously illustrated by the ST effects observed at β- and α-ATP upon saturation of γ-ATP (18,22,23,28). It has been suggested that the magnetization changes detected in β-ATP during irradiation of γ-ATP was due to continuous saturation of β-ADP (which co-resonates with γ-ATP (34)) followed by conversion of ADP to ATP. In parallel, a decrease in intensity of β-ATP during irradiation of γ-ATP could also be caused by cross relaxation between β- and γ-ATP (NOE) and/or by reactions mediated by adenylase kinase (Figure 1b). Intramolecular NOEs within ATP are clearly indicated by the magnetization exchange between β- and α-ATP (Figures 3b, 4e, 4f, 5d and 5e), since no known biological reaction would lead to chemical exchange between these two spins (Figure 1b). The observed magnetization exchange between β- and γ-ATP (Figures 3b, 4d, 4f, 5c and 5e) is likely due to the same NOE mechanism. It should be noted that NOE between γ- and β-ATP has not been observed in ATP in water (19), or in a media containing a high concentration of agarose (28). Given that changes in β-ATP magnetization upon saturation of γ-ATP have only been detected in the presence of creatine kinase (1), it seemed reasonable to attribute this to ADP ↔ ATP conversions mediated by creatine kinase. However, this assignment is not consistent with the observation of identical changes in β-ATP magnetization observed in skeletal muscle of wild-type and mutant mice lacking cytosolic isomers of creatine and adenylate kinases (23). Thus, one must conclude that NOE is the dominant mechanism and it likely occurs during transient immobilization of ATP by binding to large biomolecules (23). Quantitatively, the dimensionless NOE factor η ( = σ T1) by EKIT is 18.5% for β-ATP, matching well the corresponding ST result by Nabuurs et al (23) in mouse skeletal muscle where a ~20% of signal reduction was observed for β-ATP upon steady-state saturation of γ-ATP.
Despite the many differences between ST and EKIT described above, both techniques yielded similar forward kinetic rate constants in resting human skeletal muscle. This was particularly evident for the CK-mediated reaction, PCr → γ-ATP, the dominant exchange process in the system (Table 2). For the ATPase-mediated reaction, Pi → γ-ATP, EKIT yielded a rate constant of 0.050 s-1, nearly identical to the values reported for soleus (0.059 s-1) and gastrocnemius (0.057 s-1) by Befroy et al (7) using ST methods, and about half of that reported by Valkovic et al (32). The present result lies at the lower end of all values measured in other ST studies (0.04 - 0.12 s-1) as reviewed by Kemp and Brindle (6). In terms of the rate of ATP synthesis (Pi → ATP), EKIT yielded a value of 7.44 ± 2.38 mmol/kg ww/min, as compared to ST results of 7.50 ± 0.77 mmol/kg ww/min at 2.1T by Petersen et al. (12) and 9.42 ± 1.73 mmol/kg ww/min at 3T by Schmid et al (5). Hence, there is general consistency between MT-measured ATP synthesis rates for resting human skeletal muscle, regardless of which MT scheme was used. This seems to suggest that, in some of the reported ST studies, the smaller bound, MR invisible pools may not contribute significantly to the ST-measured rate of ATP synthesis from Pi → γ-ATP pathway. However, the possibility of a small pool contribution cannot be ruled out in other ST studies where the ATP rate constant is much higher. The existence of such 31P MR invisible pools has been suggested by Koretsky et al (34) in the study of CK solutions containing ADP, ATP, PCr and Cr using frequency stepped ST. Given its potential physiological importance, whether and how much the small exchanging pools play a role in ST effect in vivo warrant a more comprehensive quantitative analysis (probably with inclusion of all relevant terms).
It should be noted that the MR-derived chemical exchange rate constants as given in Table 2 and shown in Equations [1-3] have been called pseudo first order rate constants (19) on the basis that the exchange flux determined by 31P NMR is determined only by visible metabolites of a chemical reaction which generally contain multiple other reactants (including NMR invisible metabolites). For example, for the exchange reaction PCr ↔ γ-ATP, the MR-measured fluxes are kbc[PCr] for forward exchange and kcb[γ-ATP] for reverse exchange, while the actual chemical reaction is more complex, described by PCr + MgADP + H+ ↔ MgATP + Creatine, with forward flux described by kf[PCr][MgADP][H+] and reverse reaction by kr[MgATP][Creatine], in which kf and kr denote the true first order chemical rate constants. This yields the following relationship kbc = kf[MgADP][H+] and kcb = kr[Creatine], indicating that MR-measurable kbc and kcb, unlike chemical kf and kr, are pseudo first order in nature.
Because of the large chemical shift dispersion at 7T, all 31P metabolites yielded symmetric and well-resolved EKIT peaks with an inversion bandwidth of 150 Hz. EKIT resolution could be further improved by utilizing pulses of lower RF power with longer duration, but at expense of decreased inversion efficacy, especially on spins with short T2s (such as ATP spins, (37)). Typically, to invert a given signal, the MR pulse must produce a frequency bandwidth ≫ 1/πT2. For γ-ATP (T2: 29 ms (37)), a rough estimate of the bandwidth is 100 Hz. With an inversion bandwidth of 150 Hz in this study, the measured inversion efficacy, in terms of Mz/Mzmax, is 41% for γ-ATP (Figure 6a), in comparison to 34% for β-ATP (linewidth 50% broader than γ-ATP), 45% for α-ATP (linewidth 6% narrower than γ-ATP), 49% for Pi (T2 109 ms (37)) and 58% for PCr (T2 217 ms (37)). For practical reasons, this study adopted an empirical symmetric function (Equation [18]) to fit EKIT peaks, instead of a theoretical approach by convoluting the shaped inversion pulse and individual MR signals. In fact, the linewidth of EKIT peaks is mainly governed by the bandwidth of the inversion pulse (150 Hz), which is multifold broader than the linewidth of individual 31P NMR peaks (Figures 2b-c).
Using the current EKIT experimental conditions (25 Hz step-size), the EKIT peaks are well defined by an average of 13 data points (Figures 4b-f and Figures 5a-e). Dense sampling by use of smaller intervals could improve the resolution of an EKIT spectrum but only if a narrower band inversion pulse is used. On the other end, overly sparse sampling with large step intervals (for example > 75 Hz) may compromise the kinetic analysis due to poorly-profiled EKIT peaks. One way to reduce the total time to collect an EKIT spectrum while reserving its capability of profiling all exchange peaks might be to eliminate all data points 2 ppm on either side of the center of all EKIT peaks.
The plots shown in Figure 6 indicate that, to buildup sizable EKIT peaks suitable for NMR detection, the delay time td must be sufficiently long, at least 200 ms. The exchange effects appear rapidly as td value approaches 1 s, then become less apparent at longer td values. For the fast CK-mediated reaction (forward kPCr↔γ-ATP 0.264 s-1), the appearance of the maximum effect near td ~ 1 was obvious, but less obvious for the slower ATPase-mediated reaction (forward kPi↔γ-ATP 0.050 s-1). Slower kinetic reactions yielded smaller EKIT peaks, as evidenced by the much smaller magnetization reduction at Pi than at PCr upon inverting γ-ATP (Figure 6b). It can be estimated that the EKIT peak would be too small to be reliably characterized if the Pi rate constant is below 0.02 s-1 under the current conditions. A possible strategy to improve the detection limit is to increase the number of acquisitions and sparse the data using largely on-resonance inversions.
2D EXCSY/NOESY could be an alternative option for measuring kinetics as described previously in the study of exchange between ATP and PCr in CK solutions by Koretsky et al (34) and ATP flux in the leg and head of the anesthetized rat by Balaban et al (46). This later method differs from EKIT by replacing the frequency-sweeping soft 180° pulse in EKIT with two hard 90° pulses (90°-t1-90°) spaced by t1, the evolution time. Here, magnetization transfer appears as cross peaks in a 2D spectrum (46), similar to the 2D plot in Figure 3b. In a system crowded with many exchange pairs, EXCSY/NOESY could be advantage, especially when the exchanging species are too close in resonance frequency to allow selective inversion. However, one would not be able to visualize the 2D results unless the scan is fully completed. In contrast, real-time monitoring of EKIT result sweep-by-sweep is generally accessible in a conventional MRI scanner with MRS capabilities.
As a final point, under the current experimental conditions, the total scan time required to collect a four complete EKIT data sets (four different td values) was 55 min. With multiple td values, the evolution of all EKIT peaks with td can be clearly illustrated (Figures 5 and 6), from which multiple parameters (T1s, NOEs and chemical exchange rates) can be determined simultaneously from a single matrix equation (Equation 19). Theoretically, quantitative analysis of all these parameters requires at least two td series. However, given the non-linearity of EKIT peaks at various td values and the large range of variation in T1 and k values, not all exchange peaks develop optimally at similar td values. Thus, three to four td series are ideal to reasonably quantify all the targeted parameters. If the T1 values were known a priori and the inversion pulse pre-calibrated, one single set of td data could be used to solve for the remaining unknowns. Nevertheless, even with 4 td data series, the EKIT data acquisition time in this study is similar to that required in a typical ST study to measure a single forward reaction, Pi → ATP (~ 1 hr, ref 7). The time required for an EKIT analysis can potentially be reduced multiple-fold by sampling only the “on-resonance” data (Δδ = 0), and using multiple acquisitions to increase S/N.
In summary, using the proposed EKIT approach, an integrated quantitative study has been conducted on the kinetic exchange system of high energy phosphates for measurements of not only ATP turnover rates, but also of T1 relaxation times and NOEs as well. Unlike a conventional 31P MR spectrum which detects all metabolites on the basis of differences in chemical shift, an EKIT spectrum detects connections between exchanging spins of MR visible pools. From the intensities of these exchange signals, one can extract valuable metabolic information pertinent to the activities of endogenous enzymes such as creatine kinase and ATP synthase, as well as dynamic information in vivo through NOEs. Hence, it is expected that EKIT could become a useful tool for studying energy metabolism under alternated physiology and diseases, with potential applications extendable to other organs such as brain and heart where relevant enzymes are expected to be more active.
Acknowledgments
The authors are grateful for the technical support with Dr. Ivan Dimitrov (Philips Medical Systems), Salvador Pena for operational assistance. Jeannie Davis and Janet Jerrow recruited and managed the human subjects. This project was supported by the National Center for Research Resources and the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health through P41EB015908, DK081186, R37HR034557, P01DK058398 and RO1AR050597, Department of Defense Grant W81XWH-06-2-0046.
References
- 1.Brindle KM, Radda GK. Measurements of exchange in the reaction catalysed by creatine kinase using 14C and 15N isotope labels and the NMR technique of saturation transfer. Biochim Biophys Acta. 1985;829(2):188–201. doi: 10.1016/0167-4838(85)90188-8. [DOI] [PubMed] [Google Scholar]
- 2.Brindle KM, Blackledge MJ, Challiss RA, Radda GK. 31P NMR magnetization-transfer measurements of ATP turnover during steady-state isometric muscle contraction in the rat hind limb in vivo. Biochemistry. 1989;28(11):4887–93. doi: 10.1021/bi00437a054. [DOI] [PubMed] [Google Scholar]
- 3.Shoubridge EA, Briggs RW, Radda GK. 31p NMR saturation transfer measurements of the steady state rates of creatine kinase and ATP synthetase in the rat brain. FEBS Lett. 1982;140(2):289–92. doi: 10.1016/0014-5793(82)80916-2. [DOI] [PubMed] [Google Scholar]
- 4.Lebon V, Dufour S, Petersen KF, Ren J, Jucker BM, Slezak LA, Cline GW, Rothman DL, Shulman GI. Effect of triiodothyronine on mitochondrial energy coupling in human skeletal muscle. J Clin Invest. 2001;108:733–737. doi: 10.1172/JCI11775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schmid AI, Schrauwen-Hinderling VB, Andreas M, Wolzt M, Moser E, Roden M. Comparison of measuring energy metabolism by different (31) P-magnetic resonance spectroscopy techniques in resting, ischemic, and exercising muscle. Magn Reson Med. 2012;67(4):898–905. doi: 10.1002/mrm.23095. [DOI] [PubMed] [Google Scholar]
- 6.Kemp GJ, Brindle KM. What do magnetic resonance-based measurements of Pi→ATP flux tell us about skeletal muscle metabolism? Diabetes. 2012;61(8):1927–34. doi: 10.2337/db11-1725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Befroy DE, Rothman DL, Petersen KF, Shulman GI. 31P-magnetization transfer magnetic resonance spectroscopy measurements of in vivo metabolism. Diabetes. 2012;61(11):2669–78. doi: 10.2337/db12-0558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jucker BM, Dufour S, Ren J, Cao X, Previs SF, Underhill B, Cadman KS, Shulman GI. Assessment of mitochondrial energy coupling in vivo by 13C/31P NMR. Proc Natl Acad Sci U S A. 2000;97(12):6880–4. doi: 10.1073/pnas.120131997. Erratum in: Proc Natl Acad Sci U S A 2001;98(6):3624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Szendroedi J, Schmid AI, Chmelik M, Toth C, Brehm A, Krssak M, Nowotny P, Wolzt M, Waldhausl W, Roden M. Muscle Mitochondrial ATP Synthesis and Glucose Transport/Phosphorylation in Type 2 Diabetes. PLoS Med. 2007;4(5):e154. doi: 10.1371/journal.pmed.0040154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lowell BB, Shulman GI. Mitochondrial dysfunction and type 2 diabetes. Science. 2005;307:384–387. doi: 10.1126/science.1104343. [DOI] [PubMed] [Google Scholar]
- 11.Petersen KF, Dufour S, Befroy D, Garcia R, Shulman GI. Impaired mitochondrial activity in the insulin-resistant offspring of patients with type 2 diabetes. N Engl J Med. 2004;350:664–671. doi: 10.1056/NEJMoa031314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Petersen KF, Befroy D, Dufour S, Dziura J, Ariyan C, Rothman DL, DiPietro L, Cline GW, Shulman GI. Mitochondrial dysfunction in the elderly: Possible role in insulin resistance. Science. 2003;300:1140–1142. doi: 10.1126/science.1082889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Petersen KF, Dufour S, Shulman GI. Decreased insulin-stimulated ATP synthesis and phosphate transport in muscle of insulin-resistant offspring of type 2 diabetic parents. PLoS Med. 2005;2(9):e233. doi: 10.1371/journal.pmed.0020233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rabøl R, Boushel R, Dela F. Mitochondrial oxidative function and type 2 diabetes. Appl Physiol Nutr Metab. 2006;31(6):675–83. doi: 10.1139/h06-071. [DOI] [PubMed] [Google Scholar]
- 15.From AH, Ugurbil K. Standard magnetic resonance-based measurements of the Pi→ATP rate do not index the rate of oxidative phosphorylation in cardiac and skeletal muscles. Am J Physiol Cell Physiol. 2011;301(1):C1–11. doi: 10.1152/ajpcell.00345.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brindle KM. NMR methods for measuring enzyme kinetics in vivo. Progress in NMR Spectroscopy. 1988;20:257–93. [Google Scholar]
- 17.Uğurbil K, Petein M, Maidan R, Michurski S, From AH. Measurement of an individual rate constant in the presence of multiple exchanges: application to myocardial creatine kinase reaction. Biochemistry. 1986;25(1):100–7. doi: 10.1021/bi00349a015. [DOI] [PubMed] [Google Scholar]
- 18.Balaban RS, Koretsky AP. Interpretation of 31P NMR saturation transfer experiments: what you can’t see might confuse you. Focus on “Standard magnetic resonance-based measurements of the Pi→ATP rate do not index the rate of oxidative phosphorylation in cardiac and skeletal muscles”. Am J Physiol Cell Physiol. 2011;301(1):C12–5. doi: 10.1152/ajpcell.00100.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Le Rumeur E, Le Tallec N, Kernec F, de Certaines JD. Kinetics of ATP to ADP beta-phosphoryl conversion in contracting skeletal muscle by in vivo 31P NMR magnetization transfer. NMR Biomed. 1997;10(2):67–72. doi: 10.1002/(sici)1099-1492(199704)10:2<67::aid-nbm451>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- 20.Neeman M, Rushkin E, Kaye AM, Degani H. 31P-NMR studies of phosphate transfer rates in T47D human breast cancer cells. Biochim Biophys Acta. 1987;930(2):179–92. doi: 10.1016/0167-4889(87)90030-9. [DOI] [PubMed] [Google Scholar]
- 21.Gupta RK. Saturation transfer 31P NMR studies of the intact human red blood cell. Biochim Biophys Acta. 1979;586(1):189–195. [Google Scholar]
- 22.Nabuurs CI, Hilbers CW, Wieringa B, Heerschap A. Letter to the editor: “Interpretation of 31P NMR saturation transfer experiments: do not forget the spin relaxation properties”. Am J Physiol Cell Physiol. 2012;302(10):C1566–7. doi: 10.1152/ajpcell.00409.2011. [DOI] [PubMed] [Google Scholar]
- 23.Nabuurs C, Huijbregts B, Wieringa B, Hilbers CW, Heerschap A. 31P saturation transfer spectroscopy predicts differential intracellular macromolecular association of ATP and ADP in skeletal muscle. J Biol Chem. 2010;285(51):39588–96. doi: 10.1074/jbc.M110.164665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ward KM, Aletras AH, Balaban RS. A new class of contrast agents for MRI based on proton chemical exchange dependent saturation transfer (CEST) J Magn Reson. 2000;143(1):79–87. doi: 10.1006/jmre.1999.1956. [DOI] [PubMed] [Google Scholar]
- 25.van Zijl PC, Jones CK, Ren J, Malloy CR, Sherry AD. MRI detection of glycogen in vivo by using chemical exchange saturation transfer imaging (glycoCEST) Proc Natl Acad Sci U S A. 2007 Mar 13;104(11):4359–64. doi: 10.1073/pnas.0700281104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ren J, Trokowski R, Zhang S, Malloy CR, Sherry AD. Imaging the tissue distribution of glucose in livers using a PARACEST sensor. Magn Reson Med. 2008 Nov;60(5):1047–55. doi: 10.1002/mrm.21722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Woessner DE, Zhang S, Merritt ME, Sherry AD. Numerical solution of the Bloch equations provides insights into the optimum design of PARACEST agents for MRI. Magn Reson Med. 2005;53(4):790–9. doi: 10.1002/mrm.20408. [DOI] [PubMed] [Google Scholar]
- 28.Du F, Zhang Y, Chen W. Relayed magnetization transfer from nuclear Overhauser effect and chemical exchange observed by in vivαo 31P MRS in rat brain. Magn Reson Imaging. 2012;30(5):716–21. doi: 10.1016/j.mri.2012.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kingsley PB, Monahan WG. Corrections for off-resonance effects and incomplete saturation in conventional (two-site) saturation-transfer kinetic measurements. Magn Reson Med. 2000;43(6):810–9. doi: 10.1002/1522-2594(200006)43:6<810::aid-mrm6>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- 30.Baguet E, Roby C. Off-Resonance Irradiation Effect in Steady-State NMR Saturation Transfer. J Magn Reson. 1997;128(2):149–60. doi: 10.1006/jmre.1997.1230. [DOI] [PubMed] [Google Scholar]
- 31.Kowalewski J, Maler L. Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications (Series in Chemical Physics) New York: CRC Pres; 2006. pp. 195–287. [Google Scholar]
- 32.Valkovič L, Chmelík M, Just Kukurova I, Krššák M, Gruber S, Frollo I, Trattnig S, Bogner W. Time-resolved phosphorous magnetization transfer of the human calf muscle at 3 T and 7 T: a feasibility study. Eur J Radiol. 2013;82(5):745–51. doi: 10.1016/j.ejrad.2011.09.024. [DOI] [PubMed] [Google Scholar]
- 33.Du F, Zhu XH, Qiao H, Zhang X, Chen W. Efficient in vivo 31P magnetization transfer approach for noninvasively determining multiple kinetic parameters and metabolic fluxes of ATP metabolism in the human brain. Magn Reson Med. 2007;57(1):103–14. doi: 10.1002/mrm.21107. [DOI] [PubMed] [Google Scholar]
- 34.Koretsky AP, Basus VJ, James TL, Klein MP, Weiner MW. Detection of exchange reactions involving small metabolite pools using NMR magnetization transfer techniques: relevance to subcellular compartmentation of creatine kinase. Magn Reson Med. 1985;2(6):586–94. doi: 10.1002/mrm.1910020610. [DOI] [PubMed] [Google Scholar]
- 35.Widmaier S, Hoess T, Jung WI, Staubert A, Dietze GF, Lutz O. 31P NMR studies of human soleus and gastrocnemius show differences in the J gamma beta coupling constant of ATP and in intracellular free magnesium. MAGMA. 1996;4(1):47–53. doi: 10.1007/BF01759779. [DOI] [PubMed] [Google Scholar]
- 36.Lei H, Ugurbil K, Chen W. Measurement of unidirectional Pi to ATP flux in human visual cortex at 7 T by using in vivo 31P magnetic resonance spectroscopy. Proc Natl Acad Sci U S A. 2003;100(24):14409–14. doi: 10.1073/pnas.2332656100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bogner W, Chmelik M, Schmid AI, Moser E, Trattnig S, Gruber S. Assessment of (31)P relaxation times in the human calf muscle: a comparison between 3 T and 7 T in vivo. Magn Reson Med. 2009;62(3):574–82. doi: 10.1002/mrm.22057. [DOI] [PubMed] [Google Scholar]
- 38.Meyerspeer M, Krssak M, Moser E. Relaxation times of 31P-metabolites in human calf muscle at 3 T. Magn Reson Med. 2003;49:620–625. doi: 10.1002/mrm.10426. [DOI] [PubMed] [Google Scholar]
- 39.Bottomley PA, Ouwerkerk R, Lee RF, Weiss RG. Four-angle saturation transfer (FAST) method for measuring creatine kinase reaction rates in vivo. Magn Reson Med. 2002;47(5):850–63. doi: 10.1002/mrm.10130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Thomsen C, Jensen KE, Henriksen O. In vivo measurements of T1 relaxation times of 31P-metabolites in human skeletal muscle. Magn Reson Imaging. 1989;7:231–234. doi: 10.1016/0730-725x(89)90709-1. [DOI] [PubMed] [Google Scholar]
- 41.Buchthal SD, Thoma WJ, Taylor JS, Nelson SJ, Brown TR. In vivo T1 values of phosphorus metabolites in human liver and muscle determined at 1.5 T by chemical shift imaging. NMR Biomed. 1989;2:298–304. doi: 10.1002/nbm.1940020520. [DOI] [PubMed] [Google Scholar]
- 42.Brown TR, Stoyanova R, Greenberg T, Srinivasan R, Murphy-Boesch J. NOE enhancements and T1 relaxation times of phosphorylated metabolites in human calf muscle at 1.5 Tesla. Magn Reson Med. 1995;33:417–421. doi: 10.1002/mrm.1910330316. [DOI] [PubMed] [Google Scholar]
- 43.Newcomer BR, Boska MD. T1 measurements of 31P metabolites in resting and exercising human gastrocnemius/soleus muscle at 1.5 Tesla. Magn Reson Med. 1999;41:486–494. doi: 10.1002/(sici)1522-2594(199903)41:3<486::aid-mrm10>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- 44.Schär M, El-Sharkawy AM, Weiss RG, Bottomley PA. Triple repetition time saturation transfer (TRiST) 31P spectroscopy for measuring human creatine kinase reaction kinetics. Magn Reson Med. 2010;63(6):1493–501. doi: 10.1002/mrm.22347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bottomley PA, Ouwerkerk R. The dual-angle method for fast, sensitive T-1 measurement in-vivo with low-angle adiabatic pulses. J Magn Reson Ser B. 1994;104:159–167. [Google Scholar]
- 46.Balaban RS, Kanto HL, Ferretti JA. In vivo flux between phosphocreatine and adenosine triphosphate determined by two-dimentional phosphorous NMR. J Biol Chem. 1983;258(21):12787–89. [PubMed] [Google Scholar]


