A Test of Transitive Inferences in Free-Flying Honeybees: Unsuccessful Performance Due to Memory Constraints

Abstract

We asked whether honeybees, Apis mellifera, could solve a transitive inference problem. Individual free-flying bees were conditioned with four overlapping premise pairs of five visual patterns in a multiple discrimination task (A+ vs. B-, B+ vs. C-, C+ vs. D-, D+ vs. E-, where + and - indicate sucrose reward or absence of it, respectively). They were then tested with the nonadjacent pairs A vs. E and B vs. D. Preference of B to D is consistent with the use of the implicit hierarchy A > B > C > D > E. Equal choice of B and D supports choice based on the associative strength of the stimuli. The bees' choice was determined by their memory constraints: experience with the last premise pair (D+ vs. E-) predominated. In the tests, bees preferred A to E and chose equally B and D. An analysis of the performance in terms of a reward/penalty ratio showed that B had a higher associative strength than D. Thus, bees do not establish transitive inferences but, rather, guide their choices by the joint action of a recency effect and the associative strength of the stimuli. The former supports choice of D, whereas the latter supports choice of B, thus determining equal choice of B and D in the tests.

Transitive inference (A > B; B > C; then A > C) is a problem that is commonly used to study logical reasoning and knowledge manipulation (Potts 1974; Trabasso and Riley 1975; Woocher et al. 1978; Acuna et al. 2002). Preference for A over C in this context can be explained by two essential strategies: (1) deductive reasoning (von Fersen et al. 1991) in which the experimental subjects construct and manipulate a unitary and linear representation of the implicit hierarchy A > B > C (Acuna et al 2002); (2) responding as a function of reinforced and not reinforced experiences (Terrace and McGonigle 1994), in which case animals choose among stimuli based on their associative strength, that is, on the effective number of reinforced and nonreinforced experiences with the stimuli. Several models based on associative theory have been postulated to account for responding in a transitive inference paradigm (von Fersen et al. 1991; Zentall and Sherburne 1994; Zentall et al. 1996; Delius and Siemann 1998).

The common experimental design used to test transitive inference responding implies training subjects with five different stimuli A, B, C, D, and E in a multiple discrimination task A+ versus B-, B+ versus C-, C+ versus D-, D+ versus E-, where + and - indicate reinforcement and absence of it, respectively. Training involves, therefore, overlapping of adjacent premise pairs (A > B, B > C, C > D, D > E), which underlie a linear hierarchy A > B > C > D > E. After training, the critical test presents B versus D, a nonadjacent pair of stimuli that were never explicitly trained together. In terms of associative theory, B and D are supposed to be equivalent as they are, in principle, equally associated with reinforcement or absence of it along training. Thus, subjects guiding their choices by the associative strength of each stimulus should choose randomly between B and D. If, however, subjects use a mental representation of the hierarchy implicit in the training, they should prefer B to D, despite their equal associative strengths.

Up to now, the capacity of solving a transitive inference problem has been studied exclusively in vertebrate species, which are characterized by their well-known learning abilities. It has been shown that pigeons (von Fersen et al. 1991; Wynne et al. 1992; Siemann and Delius 1994; Wynne 1997), pinyon jays (Bond et al. 2002), rats (Davis 1992; Dusek and Eichenbaum 1997), squirrel monkeys (McGonigle and Chalmers 1977, 1992), macaques (Treichler and van Tilburg 1996), and chimpanzees (Gillan 1981; Boysen et al. 1993) can solve this problem. When trained in a multiple instrumental discrimination task A+ versus B-, B+ versus C-, C+ versus D-, D+ versus E-, these animals prefer B to D in subsequent tests. Associated to the study of this problem in vertebrates is the assumption that specific regions of the vertebrate brain subserve such a cognitive capacity. In particular, transitive inference has been related to the hippocampal structure (Dusek and Eichenbaum 1997), which processes and mediates storage of critical relationships among items and events, permitting the flexible use of memories in novel situations.

Focusing on vertebrates exclusively neglects the power of invertebrate models to answer specific questions about learning and memory processes. In particular, the fact that invertebrates possess a simpler and accessible nervous system makes the search of the neural basis of complex learning processes possible. In the present work, we raised the question of whether honeybees, Apis mellifera, are also capable of solving a transitive inference problem. We focused on the honeybee because it constitutes a classical model for the study of learning and memory at the behavioral, cellular, and molecular level (for reviews, see Menzel 1999; Menzel and Giurfa 2001; Giurfa 2003a). This insect exhibits not only elemental associative forms of learning but also nonelemental, higher-order learning phenomena (for reviews, see Menzel and Giurfa 2001; Giurfa 2003b). Bees offer additionally an invaluable opportunity to study the neural basis of complex forms of learning, as their nervous system is accessible to the experimenter through a variety of technical approaches (Giurfa 2003a). The small brain of the honeybee supports cognitive performances that could be related to identified, specific neuropiles and neuronal networks (Menzel and Giurfa 2001; Giurfa 2003b). It has been postulated, for example, that the mushroom bodies, a prominent central neuropile in the bee brain that acts as a multisensory integration center, could support nonelemental forms of learning (Menzel and Giurfa 2001; Giurfa 2003a,b). Thus, studying problem-solving in honeybees, such as in the case of transitive inferences, has the advantage that the search of a neuronal substrate for such capacities could be, in principle, possible.

Here we chose visual pattern learning as our experimental frame to study transitive inferences in honeybees. Pattern learning by bees has been intensively studied since the pioneer work of Karl von Frisch (1915). Free-flying bees can learn different kinds of achromatic (black and white) patterns associated with a reward of sucrose solution, and they can discriminate different kinds of rewarded from nonrewarded patterns (for reviews, see Srinivasan 1994; Giurfa and Lehrer 2001). Different neuronal elements tuned to recognize specific pattern features have been proposed in the honeybee. In particular, it has been shown that bees possess an orientation detection system based on the existence of at least three orientation detectors whose tuning curves are separated by 60° (Yang and Madess 1997). Such a system allows discriminating between different grating orientations such as vertical (0° with respect to the vertical) versus horizontal (90° with respect to the vertical; van Hateren et al 1990; Srinivasan et al. 1994; Giger and Srinivasan 1997). Additionally, radial and concentric filters have also been proposed, which allow responding to radial (star-like) and concentric (ring) patterns, respectively (Horridge and Zhang 1994).

We therefore chose five different patterns that free-flying bees learn and discriminate efficiently from each other and trained bees in an operant paradigm to fly into a Y-maze to obtain a reward of sucrose solution on one of two different patterns presented simultaneously. Different premise pairs were used during training to answer whether or not honeybees can solve a transitive inference problem. Underlying this question was the implicit goal of unraveling the strategies used by bees to solve a serial discrimination problem such as that involved in transitive inference solving.

RESULTS

Experiment 1

Free-flying honeybees, Apis mellifera L., were marked with a colored spot on the thorax or the abdomen and individually trained to fly into a wooden Y-maze to collect 50% sucrose solution on one of two patterns presented on the back walls of the maze (Fig. 1A). Five different patterns were used to establish the four overlapping premise pairs (Fig. 1B). The performance of two groups of six bees was studied in this experiment. One group (group I) was trained with the four adjacent premise pairs A+ versus B-, B+ versus C-, C+ versus D-, and D+ versus E-, whereas the other group (group II) was trained with the same pairs but with inversed contingencies (A- versus B+, B- versus C+, C- versus D+, and D- versus E+). For both groups, A and E were the only stimuli without interfering associations. For group I, A was always rewarded while E was always nonrewarded. For group II, it was the opposite.

Figure 1.

The experimental setup (A) and the stimuli (B) used in the transitive inference experiment. (A, left) Front view of the Y-maze; (right) view from above and dimensions of the setup. A marked bee flew to the entrance chamber of the maze, which could be closed with a sliding door to prevent the access of other bees, and then, entered the decision chamber by passing through a circular aperture. Once in the decision chamber, the bee could see two black-and-white patterns, presented vertically on the back walls of the maze. One was rewarded with sucrose solution and the other not. The whole apparatus was covered with an ultraviolet-transmitting Plexiglas ceiling. (B) Stimuli used in the three experiments. (From left to right) Concentric pattern, radial pattern, checkerboard pattern, and horizontal and vertical grating.

Bees were trained along 160 trials. Each premise pair was trained in an uninterrupted block of 40 trials. The first day, bees had to learn the first two adjacent premise pairs (group I: A+ vs. B- and B+ vs. C-; group II: A- vs. B+ and B- vs. C+). The second day, bees had to learn the remaining two premise pairs (group I: C+ vs. D- and D+ vs. E-; group II: C- vs. D+ and D- vs. E+). After the last training trial with the last premise pair (D vs. E), bees received a refreshment training in which each of the four premise pairs was presented. Bees were then tested with the nonadjacent pairs A versus E and B versus D in extinction conditions (no reward was provided).

A three-factorial ANOVA for repeated measurements yielded a significant variation along blocks of training (F_3,120 = 64.7, p < 0.0001) and between premise pairs (F_3,40 = 4.16, p < 0.05) but not between both groups of bees (F_1,40 = 3.73, NS). Thus, the performances of groups I and II were pooled. Figure 2A shows the correct choices per premise pair as a function of training block. For simplicity, we decided to adhere to the notation of group I throughout (A+ vs. B-, B+ vs. C-, C+ vs. D-, D+ vs. E-) even if the performance shown corresponds to the pooled choices of groups II and I.

Figure 2.

Acquisition (A), refreshment trials (B), and performance in the tests (C) of Experiment 1. (A) Acquisition of the premise pairs trained successively, expressed as percentage of correct choices per training block. Each block consisted of 10 visits to the apparatus. For simplicity, we decided to adhere to the notation of group I throughout (A+ vs. B-, B+ vs. C-, C+ vs. D-, D+ vs. E-) even if the performance shown corresponds to the pooled choices of groups II and I (see text for details). Bees (N = 12) learned to respond correctly to the rewarded pattern within each premise pair. For all four curves, performance in the first block differed significantly from that in the third (Tukey HSD, p < 0.05) and in the fourth block (p < 0.001). Learning differed between pairs, with the first pair (A+ vs. B-) being learned better than the second one (B+ vs. C-; p < 0.05). (B) Percentage of correct choices during the refreshment trials prior to the tests with the nonadjacent pairs (N = 12 bees). Stars connecting bars show significant differences in choice performance (Tukey HSD, ^* p < 0.05; ^** p < 0.001). Stars at the bottom of bars show significant deviation from a theoretical choice percentage of 50% (Mann-Whitney U test). Performance in the refreshment trials is consistent with a preference for the last rewarded stimulus (D) in the sequence. (C) Performance in the tests with the nonadjacent pairs (pairs not experienced during the training) A versus E and B versus D (N = 12 bees). (Black bars) First choice made by the bees, expressed in terms of percentage of choices (binomial test, ^* p < 0.05). (Gray bars) Cumulative choices made during the test, expressed in terms of percentage of choices (touches; see text for detail; Mann-Whitney, ^* p < 0.05). Number of cumulative choices (n) recorded: A versus E: n = 247; B versus D: n = 352. Bees were able to discriminate the nonadjacent stimuli A and E, which were unambiguously associated with reward and with the absence of it. Choice between B and D was not consistent with transitive responding.

For each pair, we found a significant effect of training (one-factorial ANOVA for repeated measurements: A+ versus B-: F_{3, 33} = 13.02, p < 0.0001; B+ versus C-: F_{3, 33} = 19.90, p < 0.0001; C+ versus D-: F_{3, 33} = 11.42, p < 0.0001; D+ versus E-: F_{3, 33} = 27.40, p < 0.0001). In all cases, the performance in the first and the last training blocks of each pair was significantly different (post hoc Tukey HSD comparison; p < 0.05). This indicates that bees learned, consecutively, the four different premise pairs. However, the pairs were not equally learned. The first pair (A+ vs. B-) was significantly better learned than the second one (B+ vs. C-; Tukey test; p < 0.05). This difference is partially consistent with a so-called end-anchoring effect (the first and the last pairs are better learned than the two intermediate pairs), which has been repeatedly reported in transitivity results in humans (Breslow 1981) and animals (Gillan 1981; von Fersen et al. 1991; McGonigle and Chalmers 1992). In our case, no improved performance for the last pair (D+ vs. E-) was found when considering its acquisition curve.

Such improvement was, however, found when analyzing the results of the refreshment trials performed just before the tests. Figure 2B shows the performance of the bees in such trials. We found significant differences between premise pairs in refreshment trials (F_{3, 33} = 6.70, p < 0.05); the level of correct choices was significantly different between A+ versus B- and C+ versus D- pairs, between B+ versus C- and D+ versus E- pairs and between C+ versus D- and D+ versus E- pairs (Tukey test: p < 0.05 in all three cases). Moreover, we compared the choice proportion recorded for each premise pair in the refreshment trials with a theoretical proportion of 50%. We found that bees performed above random level for the last pair (D+ vs. E-) and significantly preferred D to E (Mann-Whitney, p < 0.05); this was not the case for the first (A+ vs. B-) and the second (B+ vs. C-) pairs. Performance with the former pair was not different from a random choice proportion of 50%, whereas it was marginally nondifferent with the latter pair (Mann-Whitney, p = 0.08, NS). Performance with the third pair (C+ vs. D-) was significantly lower than 50% as bees chose repeatedly D, the last rewarded stimulus in the training sequence (Mann-Whitney, p = 0.01). Thus, performance in the refreshment trials exhibited a concave trend (Fig. 2B), which is also consistent with the end-anchoring effect mentioned above.

Figure 2C shows the performance of the bees in the tests with the nonadjacent pairs A versus E and B versus D. The black bars represent performance in terms of the first choice performed by the bees during the tests; the gray bars represent it in terms of the cumulative choice frequency recorded during the entire tests. In the case of the pair A versus E, the analysis of the first choice yielded a preference for A which was marginally nonsignificant (binomial test, p = 0.07, NS). Taking into account the cumulative choices recorded during the entire test treated as a single data point, we found a preference for A, which was significantly different from a theoretical value of 50% (one-sided Mann-Whitney, p = 0.00003). Taken together, these results show that honeybees were able to discriminate the nonadjacent stimuli A and E, which were unambiguously associated with reward and with the absence of it. In this test, bees might have therefore chosen A, but also avoided E, the last nonrewarded stimulus. In the case of the pair B versus D, the analysis of the first choice yielded a significant preference for D (binomial test, p = 0.01), which goes against transitive ordering of stimuli and supports choice in terms of recency (D was the last rewarded stimulus in the complete training sequence). Taking into account the cumulative choices recorded during the entire test, no difference was found between the proportion of choices recorded and a theoretical value of 50% (one-sided Mann-Whitney, NS). Thus, no evidence for transitive responding was found in Experiment 1.

Experiment 2

This experiment was conceived to reduce the impact of the recency effect detected in the previous experiment. As in the first experiment, the two groups of bees (n = 6 in each group) were trained over 2 d with the four overlapping premise pairs until completing 160 trials. Shorter blocks of 10 trials were used such that the four premise pairs were trained four times along 40 trials. In the first day, each bee received the complete sequence A versus B, B versus C, C versus D, D versus E twice and consecutively (i.e., the bee had a total of 20 trials per premise pair). In the second day, the complete training sequence was repeated twice until completing 40 trials per premise pair. After the last training trial with the last premise pair (D vs. E), and before the tests, bees received a refreshment training in which each of the four premise pairs was presented. Bees were then tested with the nonadjacent pairs A versus E and B versus D in extinction conditions (no reward was provided).

A three-factorial ANOVA for repeated measurements yielded a significant difference between blocks (F_3,120 = 9.18, p < 0.0001), but differences were found neither between groups of bees (F_1,40 = 0.66, NS) nor between premise pairs (F_3,40 = 0.26, NS). Thus, performance of both groups was pooled. Again, we adhere to the notation of group I throughout (A+ vs. B-, B+ vs. C-, C+ vs. D-, D+ vs. E-) even if the performance shown corresponds to the pooled choices of groups II and I.

Figure 3A shows the correct choices per premise pair as a function of training block. No significant variation was found for the pairs A+ versus B-, B+ versus C-, and D+ versus E-; only a significant effect was found for the pair C+ versus D- (F_3,33 = 6.3, p < 0.05), in which performance in the first and the third training blocks was significantly different (Tukey test, p < 0.05). Thus, contrarily to Experiment 1, bees did not learn to discriminate the premise pairs when these were trained along shorter blocks.

Figure 3.

Acquisition (A), refreshment trials (B), and performance in the tests (C) of Experiment 2. Shorter blocks of 10 trials were used in training such that the four premise pairs were trained four times along 40 trials. (A) Acquisition, expressed as percentage of correct choices per training block. For simplicity, we decided to adhere to the notation of group I throughout (A+ vs. B-, B+ vs. C-, C+ vs. D-, D+ vs. E-) even if the performance shown corresponds to the pooled choices of groups II and I (see text for details). Bees (N = 12) did not learn to respond correctly to the rewarded pattern within each premise pair. For all four curves, performance in the first block did not differ significantly from that in the fourth block (Tukey HSD). (B) Percentage of correct choices during the refreshment trials prior to the tests with the nonadjacent pairs (N = 12 bees). In no case was a significant deviation from a theoretical proportion of 50% found. Only in the case of the last pair (D+ vs. E-), a marginally nonsignificant difference was found. These results corroborate that bees had difficulties learning the premises pairs in this experiment. (C) Performance in the tests with the nonadjacent pairs (pairs not experienced during the training) A versus E and B versus D (N = 12 bees). (Black bars) First choice made by the bees, expressed in terms of percentage of choices. (Gray bars) Cumulative choices made during the test, expressed in terms of percentage of choices (touches; see text for detail; Mann-Whitney, ^*p < 0.05). The number of cumulative choices (n) recorded: A versus E: n = 255; B versus D: n = 323. Bees were able to discriminate the nonadjacent stimuli A and E, which were unambiguously associated with reward and with the absence of it. Choice between B and D was not consistent with transitive responding.

We next analyzed the results of the four kinds of refreshment trials, which were performed just before the tests (Fig. 3B). We found no significant differences between premise pairs in refreshment trials (F_3,33 = 1.94, NS). When we compared the choice proportion recorded in each refreshment trial with a theoretical proportion of 50%, we found no significant differences. Only in the case of the last pair (D+ vs. E-), the one-sided Mann-Whitney test yielded a difference that was marginally nonsignificant (p = 0.08) and that indicates that, even under these circumstances, recency could influence the choice behavior of the bees. These results corroborate the conclusion raised on the basis of the acquisition curves, namely, that bees had difficulties learning the premises pairs with this kind of training.

Figure 3C shows the performance of the bees when tested with the nonadjacent pairs A versus E and B versus D. The black bars represent performance in terms of the first choice performed by the bees during the tests; the gray bars represent it in terms of the cumulative choice frequency recorded during the entire tests. In the case of the pair A versus E, the analysis of the first choice yielded a preference for A, which was marginally nonsignificant (binomial test, p = 0.08, NS). Taking into account the cumulative choices recorded during the entire test, we found a preference for A, which was significantly different from a theoretical value of 50% (one-sided Mann-Whitney, p = 0.00003). Therefore, in spite of the bad acquisition observed, bees were able to discriminate the nonadjacent stimuli A and E, which were unambiguously associated with reward and with the absence of it. In this test, bees might have avoided E, the last nonrewarded stimulus. In the case of the pair B versus D, the analysis of the first choice as well as of the cumulative choices yielded nonsignificant differences. Therefore, no evidence for transitive responding was found in Experiment 2 for the obvious reason that bees seemed not to be able to master the complete discrimination problem. Obviously, this result precluded the use of randomized (or pseudorandomized) premise pair training in which even shorter blocks (if any) of training would be used.

Experiment 3

This experiment was identical to Experiment 1 except that the tests with the nonadjacent pairs (A vs. E and B vs. D) were done, not on the second day just after finishing the training, but on a third day, following the two days of training. Refreshment trials with each premise pair were performed on the third day, just before the tests. In this way, we tried to reduce the impact of the recency effect, which may bias the choice of the bees toward the last reinforced stimulus of the training sequence. Two reciprocal groups of bees (n = 5 in group I and n = 3 in group II) were trained with 40 consecutive trials per premise pair (i.e., 160 training trials in total).

As in Experiment 1, a three-factorial ANOVA for repeated measurements yielded a significant variation along blocks of training (F_3,72 = 79.16, p < 0.0001) and between premise pairs (F_3,24 = 4.21, p < 0.05) but not between groups of bees (F_1,24 = 0.15, NS). Thus, the performance of groups I and II was pooled. Figure 4A shows the correct choices per premise pair as a function of training block. Again, we adhered to the notation of group I throughout (A+ vs. B-, B+ vs.C-, C+ vs.D-, D+ vs.E-) even if the performance shown corresponds to the pooled choices of groups II and I.

Figure 4.

Acquisition (A), refreshment trials (B), and performance in the tests (C) of Experiment 3. (A) Acquisition of the premise pairs trained successively, expressed as percentage of correct choices per training block. Each block consisted of 10 visits to the apparatus. For simplicity, we decided to adhere to the notation of group I throughout (A+ vs. B-, B+ vs. C-, C+ vs. D-, D+ vs. E-) even if the performance shown corresponds to the pooled choices of groups II and I (see text for details). Bees (N = 8) learned to respond correctly to the rewarded pattern within each premise pair. For all four curves, performance in the first block differed significantly from that in the third (Tukey HSD, p < 0.05) and in the fourth block (p < 0.001). Learning differed between pairs, with the first pair (A+ vs. B-) being learned better than the second one (B+ vs. C-) and the last one (D+ vs. E-; Tukey test, p < 0.05). (B) Percentage of correct choices during the refreshment trials prior to the tests with the nonadjacent pairs (N = 8 bees). Stars at the bottom of bars show significant deviation from a theoretical choice percentage of 50% (Mann-Whitney U test). Performance in the refreshment trials is consistent with a preference for the last rewarded stimulus (D) in the sequence. (C) Performance in the tests with the nonadjacent pairs (pairs not experienced during the training) A versus E and B versus D (N = 8 bees). (Black bars) First choice made by the bees, expressed in terms of percentage of choices (binomial test, ^*p < 0.05). (Gray bars) Cumulative choices made during the test, expressed in terms of percentage of choices (touches; see text for details; Mann-Whitney, ^*p < 0.05). The number of cumulative choices (n) recorded: A versus E: n = 165; B versus D: n = 219. Bees were able to discriminate the nonadjacent stimuli A and E, which were unambiguously associated with reward and with the absence of it. Choice between B and D was not consistent with transitive responding.

For each premise pair (Fig. 4A), we found a significant effect of training (A+ vs. B-: F_3,21 = 0.0002; B+ vs. C-: F_3,21 = 0; C+ vs. D-: F_3,21 = 0.000005; D+ vs. E-: F_3,21 = 0.000005). In all four cases, performance in the first and the last training blocks was significantly different (post hoc Tukey HSD comparison; p < 0.05 in all cases). Thus, as in Experiment 1, bees learned to master successively the discriminations of the four premise pairs. The four pairs were not, however, equally learned. The first pair (A+ vs. B-) was significantly better learned than the second (B+ vs. C-; Tukey test, p < 0.05) and the last one (D+ vs. E-). These differences are again partially consistent with an end-anchoring effect.

We next analyzed the results of the four kinds of refreshment trials, which were performed just before the tests on the third day of the experiment (Fig. 4B). We found no significant differences between premise pairs in such trials (F_3,21 = 1.95, NS). Only, the proportion of choices recorded in the case of the pair D+ versus E- was significantly higher than 50% (one-tailed Mann-Whitney, p = 0.012). Thus, despite the introduction of a third day in the experiment, bees remembered the last training pair better than the previous ones.

Figure 4C shows the performance of the bees tested with the nonadjacent pairs A versus E and B versus D. The black bars represent performance in terms of the first choice performed by the bees during the tests; the gray bars represent it in terms of the cumulative choice frequency recorded during the entire tests. In the case of the pair A versus E, the analysis of the first choice yielded a significant preference for A (binomial test, p = 0.04). Taking into account the cumulative choices recorded during the entire test, we also found a preference for A, which was significantly different from a theoretical value of 50% (one-sided Mann-Whitney, p = 0.0003). Taken together, these results show that honeybees were able to discriminate the nonadjacent stimuli A and E, which were unambiguously associated with reward and with the absence of it. In the case of the pair B versus D, the analysis of the first choice yielded no significant preference (binomial test). Taking into account the cumulative choices recorded during the entire test, no difference was found between the proportion of choices recorded and a theoretical value of 50% (one-sided Mann-Whitney, NS). Thus, no evidence for transitive responding was found in Experiment 3.

Analysis of Performance in Terms of Reward/Penalty Ratios

The rationale of a transitive inference experiment is that, in a B versus D test, animals should in principle exhibit a choice behavior consistent with one of two alternatives: B should be preferred to D in case of hierarchy building, or B should be equally chosen as D in case of associative strength evaluation as B and D are equally reinforced and nonreinforced throughout training. The latter argument can, however, be fallacious in the case of an operant paradigm in which the animal freely moves and decides between options, such as in our Y-maze. In this case, the bee may quickly learn to avoid nonreinforced alternatives such that the effective amount of nonreinforced experience is, in fact, less than planned a priori by the experimenter. It is, therefore, important to compute the effective reinforcement history of stimuli B and D throughout training to understand the outcome of the critical test of a transitive inference paradigm. We thus calculated the reward/penalty ratios experienced by bees during training for stimuli B and D (Delius and Siemann 1998). For each of these stimuli, we divided the percentage of choices recorded when the stimulus was rewarded (correct choices) by the percentage of choices recorded when it was nonrewarded (incorrect choices). For all three experiments, the ratio was calculated over the complete experiment and for the last block of training. The reward/ penalty ratio cannot be calculated for the test stimuli belonging to the other nonadjacent pair (A vs. E) as A was never nonrewarded and E was never rewarded. A Spearman correlation analysis was performed to determine whether choice performance in the test B versus D was affected by such a reward/penalty ratio.

For stimuli B and D, the reward/penalty ratios (R_B and R_D, respectively) calculated for Experiments 1 to 3 were as follows: Experiment 1: R_B = 1.68, R_D = 1.23; Experiment 2: R_B = 1.14, R_D = 1.02; Experiment 3: R_B = 2.16, R_D = 1.36. In the last block of training, the ratios were as follows: Experiment 1: R_B = 5.56, R_D = 2.76; Experiment 2: R_B = 1.26, R_D = 1.10; Experiment 3: R_B = 2.32, R_D = 2.13. Thus, in all cases, we found that R_B was larger than R_D. In terms of associative strength, bees should have shown a consistent preference for B in the test with the nonadjacent pair B versus D.

To determine more precisely the impact of this factor, we made four correlation analyses: (1) between the reward/penalty ratios of the complete training and the first choices observed during the B versus D tests; (2) between the reward/penalty ratios of the last training block and the first choices observed during the B versus D tests; (3) between the reward/penalty ratios of the complete training and the percent of touches (cumulated choices) observed during the B versus D tests; and (4) between the reward/penalty ratios of the last training block and the percent of touches observed during the B versus D tests. None of these correlations was significant: (1) R = -0.54, p = 0.27; (2) R = -0.09, p = 0.87; (3) R = -0.26, p = 0.62; (4) R = -0.09, p = 0.87.

Thus, pure associative theory was not able to explain the performance of bees in our experiments. Such a theory can, however, explain the choice of the unambiguous stimuli A and E. Bees always preferred stimulus A that was unambiguously associated with reward and they avoided stimulus E that was unambiguously associated with the absence of reward. It thus seems that in the case of stimuli B and D, a recency effect that supports choice of D counterbalanced the stronger associative strength of B.

DISCUSSION

In these experiments, we asked whether or not honeybees are capable of transitive inference reasoning. No evidence for transitive inference was found, as bees never preferred B to D during the critical test with the nonadjacent pair B versus D. In fact, bees seemed to be incapable of simultaneously mastering the four overlapping discriminations of our experimental design. Therefore, it seems that in these experimental conditions, bees are not able to build and manipulate the implicit hierarchy A > B > C > D > E underlying training. However, our results allow elucidating the strategy followed by bees in solving a serial discrimination problem. Memory constraints seem to underlie the inefficiency in learning multiple overlapping discriminations. We found that bees assign more weight to the last discrimination, which then drives posterior choices. The behavior of bees is therefore guided by a recency effect. We also found that bees evaluate the associative strength of the stimuli, a fact that is reflected by their clear preference for A to E, the two stimuli that were associated unambiguously with reward and absence of it, respectively. Clearly, the fact that bees in such a test prefer A and avoid E is also influenced by a recency effect as E is the last nonrewarded stimulus of the sequence.

Our results are only partially consistent with algebraic models based on conditioning mechanisms proposed to explain transitive inference building (for review, see Delius and Siemann 1998). In these models, the associative strength of a stimulus is increased if its choice is rewarded, and decreased if its choice is not rewarded. These models explain transitive inference by the associative strength gained during training by each stimulus. To determine if associative strength fully explains the performance of bees in our tests, we analyzed the “reward/penalty” ratios for the stimuli B and D. We did not find any correlation between these ratios and the performances observed during the tests. The evaluation of the associative strength of the stimuli was, however, clearly visible in the case of the stimuli that were unambiguously associated with the reward or the absence of it (A+ vs. E-). The fact that the choice of bees was partially guided by the associative strength of the stimuli suggests that they evaluate, during their foraging trip, the positive and negative experiences with a particular stimulus, and that the overall balance of these experiences determines their subsequent choices. However, such choices are also affected by a recency effect, which can act, as in this paradigm, in the opposite direction of preference. One possible explanation for our results is, therefore, that the stronger associative strength of B measured through the calculation of the reward/penalty ratios, was counteracted by the recency effect of the last premise pair in which D was rewarded. The joint action of both factors would determine a random choice between B and D in the tests.

The calculation of the reward/penalty ratios reveals a potential pitfall of the experimental design underlying the transitive inference problem, which can arise when the subjects control the effective amount of reinforcements and nonreinforcements obtained throughout the experiment. In all cases, we found that R_B > R_D, a result that should support a preference for B in the tests. Although, for the reasons mentioned above, we did not find such a preference, preference for B would have been difficult to interpret in the light of the two disputing hypotheses on transitive inference solving. It would be, in fact, consistent with deductive reasoning on the one hand, but also with an evaluation of the stimulus associative strength. Deciding between true “deductive reasoning” and choice based on associative strength of the stimuli would then be difficult. In this context, classical conditioning paradigms, in which the experimenter fully controls the reinforcement schedule experienced by the animal, could be useful to address the question of transitive inference solving.

The recency effect observed in our serial discrimination problem reveals how sequential memories resulting from this task may control the choice behavior of the bees. Our results show that the information of the last training pair dominates over that of previous pairs and drives the performance of the bees. Menzel (1967) showed that free-flying bees trained with a given color stimulus establish a stable memory after three rewarded experiences on it. Such a memory seems to be erased by successive training with different color stimuli (Menzel 1968) such that color choice is driven by the information last learned. A similar mechanism seems to act in our experiments. When shorter blocks of training are used (Experiment 2), dominance of the last memory (last trained pair) diminishes and bees cannot master the discrimination task anymore. In a theoretical experiment with completely randomized premise pair training, the recency effect should disappear. However, Experiment 2 clearly shows that such randomization would not yield discrimination, thus making the procedure useless (see Fig 3A). Therefore, the transitive inference task confronts us with a circular problem: honeybees have to learn to discriminate the different premise pairs in order to be tested with the critical test B versus D. To this end, consecutive blocked training with each pair (no randomization) has to be performed. But such training will promote the use of other strategies, simpler than true deductive reasoning, which will guide the choice of bees. In this case, the last premise pair memory will drive the bees' behavior.

Associated to the topic of transitive inference building in a foraging context is the question of relative or absolute evaluation of stimulus properties. Our experiments were not aimed to answer this question, as our paradigm does not allow deciding between these two options. Shafir (1994) raised this question in the case of bees foraging on pairs of flowers varying in color (A, B, C, D). In his design, different flower types presented the same ratio “amount of sucrose solution offered/tube length,” but larger rewards were associated with longer flowers. Shafir (1994) assumed that shorter flowers should yield a higher utility than longer ones, as the cost of climbing down to reach the nectar in longer flowers should be higher. Under this assumption, his design could be summarized as A > B > C > D. As reward was always present in all flower types, it is not pertinent to compare Shafir's design and our design. In Shafir's experiments (1994), bees were confronted with A versus D to decide between absolute and relative evaluation of options. Even if bees preferred A to D in the majority of the cases (10 out of 15 bees), it is impossible to discern whether choices were driven by true transitive inference building or by the associative strength of the stimuli. This is because a test opposing A versus D presents to the bees the two extremes of the sequence, which were unambiguous in terms of their utility and thus in terms of their associative strength (A > D), but also in terms of their place in the hierarchy (A > D). This is not the case in a theoretical experiment on transitive inferences using five stimuli A, B, C, D, E in which a test B versus D confronts stimuli that are ambiguous in terms of their associative strength (B = D) but not in terms of their place in the hierarchy (B > D).

In a natural context, the foraging activity of bees follows the principle of flower constancy (Grant 1951; Chittka et al. 1999). Bees are flower-constant because they exploit only one flower species as long as it offers a profitable reward. This temporal specialization can be assimilated to the design of our Experiment 1 in which bees forage successively on different rewarded stimuli. In others words, honeybees do not forage simultaneously on different flower species, a behavior that would correspond to an experimental design with a complete randomization of the premise pairs. This means that the natural organization of honeybee foraging will lead to a choice behavior determined by the last rewarded experience and the associative strength of the stimuli experienced rather than by deductive reasoning. It could, therefore, be argued that the building of transitive inferences is irrelevant considering the biology of bees. However, transitive inferences could intervene to classify different patches of the same species according to their productivity and spatial distribution. Plants of the same species may grow on different kinds of soils, thus presenting differences in their nutritious values, or in different places with different environmental conditions affecting their nectar production. In this scenario, it could be useful building a hierarchy of locations allowing optimizing foraging efficiency.

We believe that our results are important, not only because they uncover the strategies used by bees in a serial discrimination problem, but also because they allow defining a specific cognitive constraint of our model. Despite their alleged developed cognitive capacities (Menzel and Giurfa 2001; Giurfa 2003a,b), honeybees could not solve the transitive inference problem. In comparative studies about animal cognition, it is crucial, not only to establish what animals can do, but also what they cannot do (Giurfa 2003a,b). In this sense, we hope that our results are enlightening for further discussions on the cognitive complexity of honeybees.

MATERIALS AND METHODS

Free-flying honeybees, Apis mellifera L., were trained to collect 30% (w/w) sucrose solution on a feeder distant ∼30 m from the hive. Foragers were individually marked with a colored spot on the thorax or the abdomen and trained to fly into the experimental setup to collect 50% sucrose solution therein.

Experimental Setup

The setup was a wooden Y-maze with a UV-transparent Plexiglas ceiling to ensure natural daylight conditions within the maze (Fig. 1A). A sliding door guaranteed that only one bee at time could enter the maze. Once in the maze, the bee had to pass through an entrance hole (5 cm in diameter) in the middle of a frontal panel to enter into the decision chamber. In this chamber, the bee had to choose between the two arms of the maze. On their back walls (20 × 20 cm), a visual stimulus was presented. Only one of the two stimuli was reinforced with sucrose solution. A hidden drop of solution was given in a micropipette in the middle of the rewarded pattern. The nonreinforced stimulus presented a similar but empty micropipette in its center. The diameter of the micropipette container was 6 mm and could not be detected by the bee's visual system from the decision chamber (Giurfa et al. 1996).

Stimuli

Five achromatic patterns (Fig. 1B), which address different proposed visual filters in the honeybee (see above), were used as training stimuli: a vertical grating, a horizontal grating, a checkerboard pattern, a radial (star-like) pattern, and a concentric pattern. Previous work has shown that bees learn and discriminate these patterns very well and to a similar extent (van Hateren et al. 1990; Horridge and Zhang 1994). Each stimulus occupied the whole back wall (20 × 20 cm) and contained the same amount of white and black surface (200 cm²). Stimuli were placed at 20 cm from the entrance hole leading into the decision chamber. At that point, the patterns subtended a visual angle of 53° to the bee's eye. Gratings had stripes, which were 2 cm wide; similarly, squares in the checkerboard pattern were 2 × 2 cm; finally, the rings of the concentric pattern were also 2 cm wide. These coincident values correspond to a visual angle of 5.7°, which is perfectly resolvable for the bee's eyes (Srinivasan and Lehrer 1988). Sectors in the radial pattern were also perfectly visible to the bees. In its larger extension, each sector covered 5 cm. Thus, the five patterns used could be perfectly resolved by the visual system of a honeybee that had to choose between them.

Training

We performed only individual training and testing, which implies that a single bee was present in the apparatus at a time. In this way, the exact amount of reinforcement and nonreinforcement that each individual bee obtained throughout the training was controlled. Each honeybee was trained with four adjacent premise pairs (A+ vs. B-, B+ vs. C-, C+ vs. D-, D+ vs. E-, or A- vs. B+, B- vs. C+, C- vs. D+, D- vs. E+), where + indicates the presence of sucrose solution (reinforcement) and - the absence of it. The position (right or left) of the reward was pseudorandomized to avoid learning in terms of positional cues. The five patterns were assigned in a balanced way to each hierarchical position A, B, C, D, and E. Thus, each pattern was trained at least once at each position A, B, C, D, and E. When the bee chose the rewarded pattern, it could drink the sucrose solution ad libitum (∼60 μL) and resumed afterward its foraging trip, thus returning to the hive. When the bee chose the nonrewarded pattern, it was gently tossed away from the arm such that it had to re-enter the maze to get the sucrose solution. The procedure was repeated until the bee chose the rewarded stimulus in that foraging bout. Only the first choice was considered for computation of acquisition curves.

Bees in our setup were trained in a differential conditioning procedure in which they had to learn to choose one stimulus and avoid the alternative one. Under such training, bees learn the global properties of patterns and not local, isolated cues (Giurfa et al. 1999). We performed preliminary experiments (data not shown), which demonstrated that, under these circumstances, 40 trials are necessary for a bee to learn a B+ versus C- discrimination after having learned an A+ versus B- discrimination. Therefore, a fixed number of 40 trials for each pair of stimuli was chosen for all the experiments.

In each experiment, two groups of bees were trained, one being the reciprocal of the other. One group (group I) was trained with the sequence A+ versus B-, B+ versus C-, C+ versus D-, D+ versus E- (where the implicit hierarchy is A > B > C > D > E), whereas the other group (group II) was trained with the sequence A- versus B+, B- versus C+, C- versus D+, D- versus E+ (where the implicit hierarchy is A < B < C < D < E). These two groups acted as reciprocal controls for the change in contingency associated with a particular stimulus. In the first group, the change in contingency for a given stimulus was from nonrewarded (-) to rewarded (+); in the second group the change was opposite. Pooling of the data from the two groups was done if there were no significant differences between them. To this end, within each symmetric premise pair (e.g., A+B- and A-B+), we pooled the choices for the rewarded stimuli (A+ and B+) and for the nonrewarded ones (B- and A-). Three experiments were performed using this basic principle; the only difference between them being the amount of consecutive, uninterrupted training trials with each adjacent premise pair. In the three experiments, each bee received 160 training trials in total. Bees that did not complete the training schedule were discarded. This high number of trials implies studying the same individual during 2 d for Experiments 1 and 2, and three days for the third experiment.

Tests

Tests were performed after completing training and were identical for all three experiments. Bees were tested in extinction conditions (no reward offered) with two nonadjacent pairs of stimuli that were never experienced together during training: A versus E and B versus D. The A versus E test allowed us to control that bees could indeed discriminate and respond differently to two stimuli with unambiguously different associative strengths (i.e., for group I, A was always rewarded while E was always nonrewarded; for group II, it was the opposite). The B versus D test was performed to determine whether bees responded according to a transitive inference principle, in which case they should prefer the higher stimulus in the hierarchy (B to D in group I and D to B in group II) despite their equivalent associative strengths, or according the associative strength inculcated by training, in which case they should show theoretically no preference between B and D.

Both tests were repeated twice, alternating the sides of each stimulus from one test to the next. In this way, we could detect position biases, which might affect the choice performance during the test. Between each test, four refreshment trials were given, in which each premise pair was presented once. The purpose of refreshment trials was to keep the bees' motivation to visit the maze high after they were exposed to the extinctions conditions of the tests. Fresh stimuli were used in all tests to ensure that test performances were not influenced by scent marks.

Each test lasted 2 min (Experiment 1) or 1 min (Experiments 2 and 3). This difference was due to different motivational levels in the bees of Experiments 2 and 3, which were more active than those of Experiment 1. During each test, we recorded the first choice of the bee and the number of touches for each stimulus (flights toward a target that ended with a contact of the target with the antennae of the bee; Giurfa et al. 1999).

Analysis of Performance in Terms of Reward/Penalty Ratios

We calculated the reward/penalty ratios experienced by bees during training for stimuli B and D (Delius and Siemann 1998). For each of these stimuli, we divided the percentage of choices recorded when it was rewarded (correct choices) by the percentage of choices recorded when it was nonrewarded (incorrect choices). For all three experiments, the ratio was calculated over the complete experiment and for the last 10 trials of training with the premise pairs in which the stimulus was involved (e.g., for B, it was calculated in the last 10 trials of A+ versus B- and of B+ versus C-). The reward/penalty ratio cannot be calculated for the test stimuli belonging to the other nonadjacent pair (A vs. E) as A was never nonrewarded and E was never rewarded. A Spearman correlation analysis was performed to determine whether choice performance in the test B versus D was affected by such a reward/penalty ratio.

Statistics

Proportion data were transformed using the arcsin 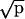transformation to test statistical variation by means of repeated measurement Analysis of Variance. We performed a three-factor ANOVA (factor 1: group, with two levels; factor 2: premise pair, with four levels; and factor 3: trial block, with four levels) to determine whether performance changed significantly according to the factors studied. Post hoc comparisons were done by means of the Tukey HSD test. For each premise pair, we also performed a one- factor repeated-measurement ANOVA to observe the evolution of the acquisition throughout blocks of training.

Performance in refreshing trials was analyzed by means of one-factor repeated measurement ANOVA (factor 1: premise pair, with four levels). For each pair, we compared the performance of the bees with a theoretical proportion of 50% by means of a one-sided Mann-Whitney U test. This procedure was also applied to the cumulative performance recorded during the tests with the nonadjacent pairs. In this case, a proportion was recorded for each bee tested with a nonadjacent pair, and the difference between the proportion sample and a proportion of 50% was tested by means of a one sided Mann-Whitney U test. Performance in tests was also analyzed taking into account the first choice performed by each bee with a given nonadjacent pair. In this case, a one-sided binomial test was performed. α was set at 0.05 in all cases.