Energy-based analysis of biochemical cycles using bond graphs

Abstract

Thermodynamic aspects of chemical reactions have a long history in the physical chemistry literature. In particular, biochemical cycles require a source of energy to function. However, although fundamental, the role of chemical potential and Gibb's free energy in the analysis of biochemical systems is often overlooked leading to models which are physically impossible. The bond graph approach was developed for modelling engineering systems, where energy generation, storage and transmission are fundamental. The method focuses on how power flows between components and how energy is stored, transmitted or dissipated within components. Based on the early ideas of network thermodynamics, we have applied this approach to biochemical systems to generate models which automatically obey the laws of thermodynamics. We illustrate the method with examples of biochemical cycles. We have found that thermodynamically compliant models of simple biochemical cycles can easily be developed using this approach. In particular, both stoichiometric information and simulation models can be developed directly from the bond graph. Furthermore, model reduction and approximation while retaining structural and thermodynamic properties is facilitated. Because the bond graph approach is also modular and scaleable, we believe that it provides a secure foundation for building thermodynamically compliant models of large biochemical networks.

1. Introduction

Oh ye seekers after perpetual motion, how many vain chimeras have you pursued? Go and take your place with the alchemists.

Leonardo da Vinci, 1494

Thermodynamic aspects of chemical reactions have a long history in the physical chemistry literature. In particular, the role of chemical potential and Gibb's free energy in the analysis of biochemical systems is developed by, for example, Hill [1], Beard & Qian [2] and Keener & Sneyd [3]. As discussed by, for example, Katchalsky & Curran [4] and Cellier [5, ch. 8], there is a distinction between classical thermodynamics which treats closed systems which are in equilibrium or undergoing reversible processes and non-equilibrium thermodynamics which treats systems, such as living organisms, which are open and irreversible.

Biochemical cycles are the building-blocks of biochemical systems; as discussed by Hill [1], they require a source of energy to function. For this reason, the modelling of biochemical cycles requires close attention to thermodynamical principles to avoid models which are physically impossible. Such physically impossible models are analogous to the perpetual motion machines beloved of inventors. In the context of biochemistry, irreversible reactions are not, in general, thermodynamically feasible and can be erroneously used to move chemical species against a chemical gradient thus generating energy from nothing [6]. The theme of this paper is that models of biochemical networks must obey the laws of thermodynamics; therefore, it is highly desirable to specify a modelling framework in which compliance with thermodynamic principles is automatically satisfied. Bond graphs provide one such framework.

Bond graphs were introduced by Henry Paynter (see [7] for a history) as a method of representing and understanding complex multi-domain engineering systems such as hydroelectric power generation. A comprehensive account of bond graphs is given by Gawthrop & Smith [8], Borutzky [9] and Karnopp et al. [10] and a tutorial introduction for control engineers is given by Gawthrop & Bevan [11].

As discussed by, for example, Palsson [12,13], Alon [14] and Klipp et al. [15], the numerous biochemical reactions occurring in cellular systems can be comprehended by arranging them into networks and analysing them by graph theory and using the associated connection matrices. These two aspects of biochemical reactions—thermodynamics and networks—were brought together some time ago by Oster et al. [16]. A comprehensive account of the resulting network thermodynamics is given by Oster et al. [17]. As discussed by Oster & Perelson [18] such thermodynamic networks can be analysed using an equivalent electrical circuit representation; but, more generally, the bond graph approach provides a natural representation for network thermodynamics [17,19,20]. This approach was not widely adopted by the biological and biochemical modelling community and may be considered to have been ahead of its time. Mathematical modelling and computational analysis of biochemical systems have developed a great deal since then, and now underpins the new disciplines of systems biology [21], and ‘physiome’ modelling of physiological systems [22–25], where we are faced with the need for physically feasible models across spatial and temporal scales of biological organization.

In particular, there has been a resurgence of interest in this approach to modelling as it imposes extra constraints on models, reducing the space of possible model structures or solutions for consideration. This has been applied from individual enzymes [26,27] and cellular pathways [28] up to large-scale models [29–31], as a way of eliminating thermodynamically infeasible models of biochemical processes and energetically impossible solutions from large-scale biochemical network models alike (see [32] for a review). Additionally, there is new impetus into model sharing and reuse in the biochemical and physiome modelling communities which has garnered interest in modular representations of biochemical networks and has promoted development of software, languages and standards and databases for models of biochemical processes. Model representation languages such as CellML and SBML promote model sharing through databases such as the Physiome Model Repository and BioModels Database. Descriptions of models in a hierarchical and modular format allows components of models to be stored in such databases and assembled into new models. Rather than revisiting the detailed theoretical development, therefore, our aim is to refocus attention on the bond graph representation of biochemical networks for practical purposes such as these. First we briefly review the utility of the bond graph approach with these aims in mind.

Bond graph approaches have also developed considerably in recent years, in particular, through the development of computational tools for their analysis, graphical construction and manipulation, and modularity and reuse [33–37,38], which are key preoccupations for systems biology and physiome modelling. Our focus is on how kinetics and thermodynamic properties of biochemical reactions can be represented in this framework, and how the bond graph formalism allows key properties to be calculated from this representation. In addition, bond graph approaches have been extended in recent years to model electrochemical storage devices [39] and heat transfer in the context of chemical reactions [40]. Cellier [5] extends network thermodynamics beyond the isothermal, isobaric context of Oster et al. [17] by accounting for both work and heat, and a series of papers [37,41] shows how multi-bonds can be used to model the thermodynamics of chemical systems with heat and work transfer and convection and to simulate large systems. Thoma & Atlan [42] discuss ‘osmosis as chemical reaction through a membrane’. LeFèvre et al. [43] model cardiac muscle using the bond graph approach.

Bond graphs explicitly model the flow of energy through networks making use of the concept of power covariables: pairs of variable whose product is power. For example, in the case of electrical networks, the covariables are chosen as voltage and current. As discussed in earlier studies [1,5,44,45], chemical potential is the driving force of chemical reactions. Hence, as discussed by Cellier [5], the appropriate choice of power covariables for isothermal, isobaric chemical reaction networks is chemical potential and molar flow rates. As pointed out by Beard et al. [30], using both mass and energy balance ensures that models of biochemical networks are thermodynamically feasible. Modelling using bond graphs automatically ensures not only mass balance but also energy balance; thus models of biochemical networks developed using bond graphs are thermodynamically feasible.

As discussed by Hill [1], biochemical cycles are the building-blocks of biochemical systems. Bond graph models are able to represent thermodynamic cycles and therefore appropriately represent free energy transduction in biochemical processes in living systems.

Living systems are complex, and therefore a hierarchical and modular approach to modelling biochemical systems is desirable. Bond graphs have a natural hierarchical representation [46] and have been used to model complex network thermodynamics [5,37,41]. Complex systems can be simplified by approximation: the bond graph method has a formal approach to approximation [8,10,11] and the potential algebraic issues arising from such approximation [47]. In particular, complex systems can be simplified if they exhibit a fast and slow timescale; a common feature of many biochemical (for example, Michaelis–Menten enzyme kinetics) and cell physiological systems (for example, slow–fast analysis of the membrane potential of electrically excitable cells). A bond graph approach to two-time-scale approximation has been presented by Sueur & Dauphin-Tanguy [48].

As well as providing a thermodynamically consistent model of a dynamical system suitable for simulation, representation of a biochemical system using the bond graph approach enables a wide range of properties and characteristics of the system to be represented. A number of key physical properties can be derived directly from the bond graph representation. For example, chemical reactions involve interactions between species which preserve matter; the number of moles of each species in a reaction must be accounted for.

As discussed by Oster et al. [17], §5.2, the kinetics of biochemical networks become particularly simple near thermodynamic equilibrium. However, as discussed by Qian & Beard [49], it is important to consider the behaviour of biochemical networks in living systems far from equilibrium. In particular, the analysis of non-equilibrium steady states (where flows are constant but non-zero and states are constant) is important [2,50].

Using elementary reactions as examples, §2 shows how biochemical networks may be modelled using bond graphs. The bond graph is more than a sketch of a biochemical network; it can be directly interpreted by a computer and, moreover, has a number of features that enable key physical properties to be derived from the bond graph itself. For example, §3 shows how the bond graph can be used to examine the stoichiometric properties of biochemical networks. Section 4 discusses the role of bond graphs in the structural approximation of biochemical networks. Section 5 discusses two biochemical cycles, an enzyme catalysed reaction and a biochemical switch, to illustrate the main points of the paper. Section 6 discusses software aspects of the bond graph approach and how it could be integrated into preexisting hierarchical modelling frameworks. Section 7 concludes the paper.

2. Bond graph modelling of chemical reactions

Bond graphs are an energy-based modelling approach. This section introduces the bond graph methodology in the context of biochemical reactions using the reactions listed in figure 1. The section is organized to emphasize the key aspects of bond graph modelling which make it a powerful approach to the modelling of biochemical systems.

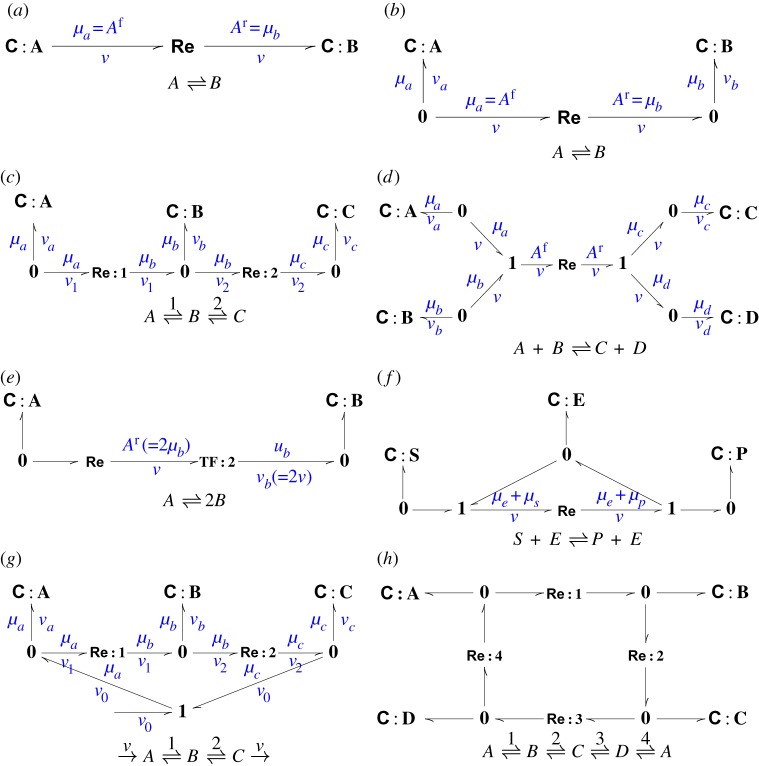
Figure 1.

Simple reactions and their bond graphs. (a) The simple binary reaction is represented by a bond graph using a C component for each substance and an Re component to explicitly represent the reaction. (b) An alternative representation using 0 (common potential) junctions to allow connections. (c) Two reactions in series extending (b). (d) A single reaction between four substances requires a single Re component, one C component for each substance and two 1 (common flow) connections. (e) The stoichiometric coefficient 2 can be incorporated using the bond graph TF component. (f) A simple enzyme-catalysed reaction. The enzyme E appears on each side of the formula thus creating a cycle in the bond graph (see §5a). (g) The same as (c) but with an externally imposed flow that adds molecules of A while subtracting the same number of molecules of C thus allowing a non-equilibrium steady state. (h) A simple biochemical cycle. (Online version in colour.)

(a). Energy flow, storage and dissipation in a simple reversible reaction

Figure 1a shows the simple interconversion of two molecular species, A and B. As mentioned above, a thermodynamically consistent representation of biochemical processes demands consideration of reversible reactions, and so we consider this simple interconversion as the simplest possible reaction. This interconversion is represented by bonds of the form $\underset{v}{\overset{\mu }{\rightharpoondown }}$ each of which is associated with two variables:¹ the chemical potential μ (J mol⁻¹) and a molar flow rate v (mol s⁻¹).² The product of these two variables is energy flow or power P=μ×v (W). The bonds represent the transmission of power in the system and do not create, store or dissipate power. The half-arrow on the bond indicates the direction in which power flow will be regarded as positive and thus defines a sign convention.

In figure 1a, the pools of chemical species A and B are represented by C components. These components reflect the amount of each species present (and hence determine the chemical potential of each species).³ C:A contains x_a moles of species A and the rate of decrease is equal to the molar flow v; C:B contains x_b moles of species B and the rate of increase is v. Thus

$${\dot{x}}_a=-v\mathrm{and}{\dot{x}}_b=v.$$ 2.1

Each C component is associated with a chemical potential μ which, assuming a dilute system within a volume V , is given by Keener & Sneyd [3], §1.2:

$${\mu }_a={\mu }_a^0+\mathrm{RT}\ln \frac{x_a}{V}{\mu }_b={\mu }_b^0+\mathrm{RT}\ln \frac{x_b}{V},$$ 2.2

where ${\mu }_a^0$ is the standard chemical potential for species A, and similarly for species B. It is convenient to rewrite equations (2.2) as

$${\mu }_a=\mathrm{RT}\ln K_a{x}_a,{\mu }_b=\mathrm{RT}\ln K_b{x}_b,\hspace{0.17em}\text{where }{K}_a=\frac{1}{V}\hspace{0.17em}{\mathrm{e}}^{{\mu }_a^0/\mathrm{RT}}\text{and}{K}_b=\frac{1}{V}\hspace{0.17em}{\mathrm{e}}^{{\mu }_b^0/\mathrm{RT}}.$$ 2.3

Each C component stores but does not create or dissipate energy. The corresponding energy flow is described through the bond to which it is connected.

The reversible reaction between chemical species A and B is represented by a single Re (Reaction) component which relates the reaction flow v to the chemical affinities (weighted sum of chemical potentials) for the forward and reverse reactions A^f=μ_a and A^r=μ_b. As discussed by Van Rysselberghe [51] and Oster et al. [17], §5.1, the reaction rate, or molar flow, is given by the Marcelin–de Donder formula:

$$v=v^{+}-v^{-},\hspace{0.17em}\text{where }{v}^{+}=\kappa \hspace{0.17em}{\mathrm{e}}^{A^{\mathrm{f}}/\mathrm{RT}}\text{and}{v}^{-}=\kappa \hspace{0.17em}{\mathrm{e}}^{A^{\mathrm{r}}/\mathrm{RT}},$$ 2.4

where κ is a constant which determines reaction rate. This can be rewritten in two ways. The de Donder formula [52], eqn(11):

$$\frac{v^{+}}{v^{-}}={\mathrm{e}}^{A/\mathrm{RT}},\text{where }A=A^{\mathrm{f}}-A^{\mathrm{r}}$$ 2.5

and the Marcelin formula [53], eqn(1):

$$v=\kappa ({\mathrm{e}}^{A^{\mathrm{f}}/\mathrm{RT}}-{\mathrm{e}}^{A^{\mathrm{r}}/\mathrm{RT}}).$$ 2.6

This latter formulation is used in the sequel. The Re component dissipates but does not create or store, energy.

In the particular case of figure 1a, substituting the chemical potentials of equations (2.3) into equations (2.4) recovers the well-known first-order mass-action expressions:

$$v^{+}=\kappa K_a{x}_a\mathrm{and}{v}^{-}=\kappa K_b{x}_b,v=\kappa (K_a{x}_a-K_b{x}_b).$$ 2.7

We note that this notation clearly demarcates parameters relating to thermodynamic quantities (K_a,K_b) from reaction kinetics (κ) and that the equilibrium constant is given by K_b/K_a.

Equations (2.7) can also be written in the conventional rate constant form as

$$v^{+}=k^{+}{x}_a\mathrm{and}{v}^{-}=k^{-}{x}_b,v=v^{+}-v^{-}=k^{+}{x}_a-k^{-}{x}_b,$$ 2.8

where the forwards and backwards first-order rate constants are

$$k^{+}=\kappa K_a\text{and}{k}^{-}=\kappa K_b.$$ 2.9

The thermodynamic quantities and reaction kinetics are no longer distinguished in the rate constant formulation of equations (2.8).

(b). Modularity: coupling reactions into networks

A key feature of bond graph representations is to construct and analyse models of large-scale systems from simpler building blocks. The bond graph of figure 1a cannot be used as a building block of a larger system as there are no connections available with which to couple to other reactions. However, the bond graph approach is, in general, modular and provides two connection components for this purpose: the 0 junction and the 1 junction. Each of these components transmits but does not store, create or dissipate energy. In figure 1b, the representation of the simple reversible reaction in figure 1a is expanded to include two 0 junction connectors. This representation is identical to that in figure 1a except that it makes explicit the junctions through which other reactions involving species A and B can be coupled to this reaction. The bond graph of figure 1c makes use of the right-hand 0 junction of figure 1b to build two connected reactions; where species B is also reversibly interconverts with species C.

The connector in this case is a 0 junction. The 0 junction can have two or more impinging bonds. In the case of the central 0 junction of figure 1c, there are three impinging bonds: one $\left(\underset{v_1}{\overset{{\mu }_b}{\rightharpoondown }}\right)$ pointing in and two $(\underset{v_b}{\overset{{\mu }_b}{\rightharpoondown }}$ and $\underset{v_2}{\overset{{\mu }_b}{\rightharpoondown }})$ pointing out. As indicated in figure 1c, the 0 junction has two properties:

• (i) the chemical potentials or affinities (efforts) on all impinging bonds are constrained to be the same, (the 0 junction is therefore a common potential connector) and

• (ii) the molar flows on the impinging bonds sum to zero, under the sign convention that a plus sign is appended to the flows corresponding to inward bonds and a minus sign for outward bonds:

  $$v_1-v_b-v_2=0\text{or}{v}_b=v_1-v_2.$$ 2.10

These two properties imply a third: the power flowing out of a 0 junction is equal to the power flowing in (the 0 junction is power-conserving):

$$P_a+P_2={\mu }_b{v}_b+{\mu }_b{v}_2={\mu }_b(v_b+v_2)={\mu }_b{v}_1=P_1.$$ 2.11

In a similar manner, the left-hand 0 junction implies that v_a=−v₁ and the right-hand 0 junction implies that v_c=v₂. Figure 1c can easily be extended to give a reaction chain of arbitrary length.

By contrast, in order to represent the reaction of figure 1d we introduce the 1 junction, which has the same power-conserving property as the 0 junction but which represents a common flow connector.⁴ In particular, with reference to the left-hand 1 junction in figure 1d:

• (i) the molar flows on all impinging bonds are constrained to be the same and

• (ii) the affinities on the impinging bonds sum to zero when a plus sign is appended to the efforts corresponding to inward bonds and a minus sign for outward bonds:

  $${\mu }_a+{\mu }_b-A^{\mathrm{f}}=0\text{or}{A}^{\mathrm{f}}={\mu }_a+{\mu }_b.$$ 2.12

Similarly, the right-hand 1 junction implies that:

$$A^{\mathrm{r}}-{\mu }_c-{\mu }_d=0\text{or}{A}^{\mathrm{r}}={\mu }_c+{\mu }_d$$ 2.13

substituting the chemical potentials of equations (2.12) and (2.13) into equations (2.4) gives the well-known second-order mass-action expression:

$$v=\kappa (K_a{x}_a{K}_b{x}_b-K_c{x}_c{K}_d{x}_e)=k^{+}{x}_a{x}_b-k^{-}{x}_c{x}_d,$$ 2.14

where

$$k^{+}=\kappa K_a{K}_b\text{and}{k}^{-}=\kappa K_c{K}_d.$$ 2.15

Once again, we note that this notation clearly demarcates parameters relating to thermodynamic quantities (K_a,K_b,K_c,K_d) from reaction kinetics (κ).

(c). Incorporating stoichiometry into reactions

The reaction of figure 1e has one mole of species A reacting to form two moles of species B. The corresponding bond graph uses the TF⁵ component to represent this stoichiometry. The TF component transmits but does not store, create or dissipate energy. Hence, the power out equals the power in. Thus. in the context of figure 1e:

$$A^{\mathrm{r}}v={\mu }_b{v}_b$$ 2.16

(noting that in this case A^r is the ‘unknown’ as μ_b is determined by the 0 junction).

A TF component with ratio n is donated by TF:n and is defined by the power conserving property and that the output flow is n times the input flow. As power is conserved, it follows therefore that the input effort is n times the output effort. In the context of figure 1e

$$A^{\mathrm{r}}=2{\mu }_b\mathrm{and}{v}_b=2v.$$ 2.17

Noting that A_f=μ_a it follows from equations (2.4) that:

$$v=\kappa (K_a{x}_a-{(K_b{x}_b)}^2)=k^{+}{x}_a-k^{-}{x}_b^2,\hspace{0.17em}\text{where}\hspace{0.17em}{k}^{+}=\kappa K_a\text{and}{k}^{-}=\kappa K_b^2.$$ 2.18

(d). Non-equilibrium steady states: reactions with external flows

As has been discussed by many authors, in cells biochemical reactions are maintained away from thermodynamic equilibrium through continual mass and energy flow through the reaction. The reaction of figure 1g corresponds to the reaction in figure 1c except that an external flow v₀>0 has been included. This corresponds to adding molecules of A and removing molecules of C at the same fixed rate. As discussed by Qian et al. [50], the reaction has a non-equilibrium steady-state (NESS) corresponding to v₁=v₂=v₀. This is a steady state because the flows v_a=v_b=v_c=0 and hence ${\dot{x}}_a={\dot{x}}_b={\dot{x}}_c=0$; it is not a thermodynamic equilibrium because v₁≠0 and v₂≠0.

(e). Thermodynamic compliance

The bond graph approach ensures thermodynamic compliance: the model may not be correct, but it does obey the laws of thermodynamics. To illustrate this point, consider the biochemical cycle of figure 1h. As discussed by, for example, Qian et al. [50], a fundamental property of such cycles is the thermodynamic constraint that

$$\frac{k_{+1}{k}_{+2}{k}_{+3}{k}_{+4}}{k_{-1}{k}_{-2}{k}_{-3}{k}_{-4}}=1.$$ 2.19

This property arises from the requirement for detailed balance around the biochemical cycle. However, as is now shown, the thermodynamic constraint of equation (2.19) is automatically satisfied by the bond graph representation of figure 1h.

Similar to equation (2.8), the four reaction flows can be written as

$$v_1={\kappa }_1(K_a{x}_a-K_b{x}_b),\dots ,v_4={\kappa }_4(K_d{x}_d-K_a{x}_a).$$ 2.20

Alternatively, the four reaction flows of equations (2.20) can be rewritten as

$$v_1=(k_{+1}{x}_a-k_{-1}{x}_b),\dots ,v_4=(k_{+4}{x}_d-k_{-4}{x}_a),$$ 2.21

where

$$k_{+1}={\kappa }_1{K}_a,\dots ,k_{+4}={\kappa }_4{K}_d,k_{-1}={\kappa }_1{K}_b,\dots ,k_{-4}={\kappa }_4{K}_a.$$ 2.22

Hence

$$\frac{k_{+1}{k}_{+2}{k}_{+3}{k}_{+4}}{k_{-1}{k}_{-2}{k}_{-3}{k}_{-4}}=\frac{{\kappa }_1{K}_a{\kappa }_2{K}_b{\kappa }_3{K}_c{\kappa }_4{K}_d}{{\kappa }_1{K}_b{\kappa }_2{K}_c{\kappa }_3{K}_d{\kappa }_4{K}_a}.$$ 2.23

As each factor of the numerator on the right-hand side of equation (2.23) appears in the denominator, and vice versa, then equation (2.19) is satisfied.

3. Stoichiometric analysis of reaction networks

Stoichiometric analysis is fundamental to understanding the properties of large networks [12,13,54]. In particular, computing the left and right null space matrices leads to information about pools and steady-state pathways [55–58]. For example, when analysing reaction networks such as metabolic networks, one may seek to determine for measured rates of change of metabolite concentrations, what are the reaction rates in the network. This question is addressed below. Initially, we will address the inverse problem: for given reaction velocities, what are the rates of change of concentrations of the chemical species? In bond graph terms, this asks the question: ‘given the reaction flows V , what are the flows $\dot{X}$ at the C components?’. This can be addressed directly from the bond graph using the concept of causality.

The bond graph concept of causality [8,10,11] has proved useful for generating simulation code, detecting modelling inconsistencies, solving algebraic loops [47], approximation, inversion [59–61] and analysis of system properties [62]. This section shows how the bond graph concept of causality can be used to examine the stoichiometry of networks of biochemical reactions. As in §2, this is done by analysis of particular examples. However, as discussed in §6, this approach scales up to arbitrarily large systems.

(a). The stoichiometric matrix

Figure 2a is similar to the bond graph of figure 1a except that two lines have been added perpendicular to each bond; these lines are called causal strokes. It is convenient to distinguish between the flows on each side of the Re component by relabelling them as v^f and v^r (v^f=v_r=v) and this is reflected in the annotation. The implications of the causal stroke are twofold:

• (i) the bond imposes effort on the component at the stroke end of the bond and

• (ii) the bond imposes flow on the component at the other end of the bond.

Figure 2.

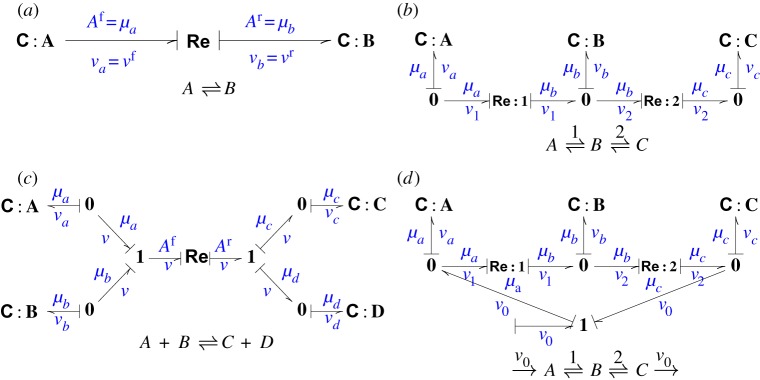
Causal strokes and the stoichiometric matrix. The bond graph notion of causality provides an algorithm for determining the stoichiometric matrix by explicitly showing how the Re flows propagate to the C flows. (a) The C components impose a potential onto the Re component; the Re component imposes a flow into the C components. (b) As (a) and note that exactly one bond imposes a potential on to each 0 (common potential) junction. (c) As (a) and note that exactly one bond imposes a flow on to each 1 (common flow) junction. (d) As the external flow v₀ impinges on to 0 junctions, it does not affect the causality of the parts in common with (b). (Online version in colour.)

Thus, as indicated on the bond graph:⁶ the flows are given by

$${\dot{x}}_a=-v_a=-v^{\mathrm{f}}=-v\mathrm{and}{\dot{x}}_b=v_b=v^{\mathrm{r}}=v$$ 3.1

and the efforts by

$$A_{\mathrm{f}}={\mu }_a\mathrm{and}{A}_{\mathrm{r}}={\mu }_b.$$ 3.2

In general, the reaction flows can be composed into the vector V , and the state derivatives into the vector X and these are related by the stoichiometric matrix N:

$$\dot{X}=NV.$$ 3.3

In the case of figure 2a:

$$X=\left(\begin{array}{c}{x}_a\\ x_b\end{array}\right)V=v\text{and}N=\left(\begin{array}{c}-1\\ 1\end{array}\right).$$ 3.4

The system of figure 2b has three C components and the state X can be chosen as

$$X={(x_a{x}_b{x}_c)}^{\mathrm{T}}.$$ 3.5

There are two reaction flows v₁ and v₂ corresponding to Re:1 and Re:2, respectively. The flow vector V can be chosen as

$$V={(v_1{v}_2)}^{\mathrm{T}}.$$ 3.6

Following the causal strokes and observing the sign convention at the 0 junction

$${\dot{x}}_a=v_a=-v_1,{\dot{x}}_b=v_b=v_1-v_2\mathrm{and}{\dot{x}}_c=v_c=v_2.$$ 3.7

Using (3.5) and (3.6), it follows that

$$\dot{X}=NV,\text{where }N=\left(\begin{array}{cc}-1& 0\\ 1& -1\\ 0& 1\end{array}\right).$$

The system of figure 2d is similar to that of figure 2b but with an additional input v₀ and so V is defined as

$$V={(v_0{v}_1{v}_2)}^{\mathrm{T}}.$$ 3.8

Using the summing rules at the left and right 0 junctions, it follows that:

$$\dot{X}=NV,\text{where }N=\left(\begin{array}{ccc}1& -1& 0\\ 0& 1& -1\\ -1& 0& 1\end{array}\right).$$

The system of figure 2c has 4 C components and the state X can be chosen as

$$X={(x_a{x}_b{x}_c{x}_d)}^{\mathrm{T}}.$$ 3.9

There is one reaction flows v corresponding to Re. The flow vector V is thus scalar in this case:

$$V=v.$$ 3.10

Following the causal strokes and observing the sign convention at the 0 junction,

$${\dot{x}}_a=v_a=-v,{\dot{x}}_b=v_b=-v,{\dot{x}}_c=v_c=v\mathrm{and}{\dot{x}}_d=v_d=v.$$ 3.11

Using (3.5) and (3.6), it follows that

$$\dot{X}=NV,\text{where }N={(-1-111)}^{\mathrm{T}}.$$ 3.12

In bond graph terms, this particular arrangement of causal strokes is known as integral causality. Naturally, this analysis extends to arbitrarily large systems and can be carried out algorithmically in automated software.

(b). Stoichiometric null spaces

The causal analysis of §3a asks the question: ‘given the reaction flows V , what are the flows $\dot{X}$ at the C components?’. This section looks at the inverse question: ‘given the flows $\dot{X}$ at the C components, what are the reaction flows V ?’

With this in mind, the causal stroke on the bond impinging on the C:A component in figure 3a is now at the C end of the bond, thus imposing flow on the Re component and so v^f=v_a. There is now a causal issue: as v_r=v_f, it follows that v_r is also determined by the C:A component and v_r=v_a. Hence the flow on the bond impinging on C:B is determined and the causality must be as shown. Thus causal considerations show that the flow v_a determines the flow v_b which therefore cannot be independently chosen. In bond graph terms, this particular arrangement of causal strokes is known as derivative causality. To summarize,

$$v=v_a=-{\dot{x}}_a\mathrm{and}{\dot{x}}_b=v=-{\dot{x}}_a.$$ 3.13

Figure 3.

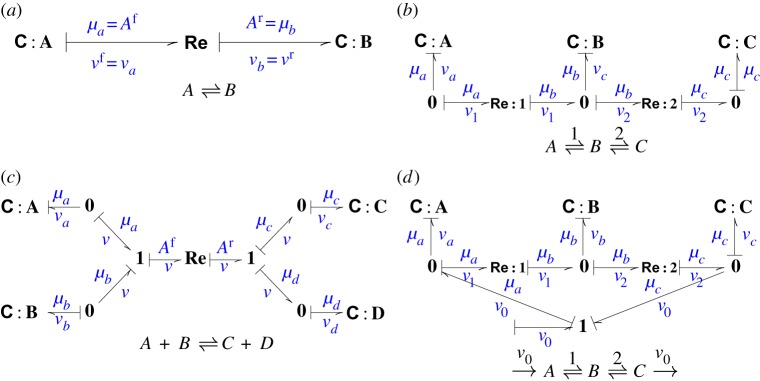
Causal strokes and the stoichiometric matrix subspaces. The bond graph notion of causality provides an algorithm for determining the subspaces of the stoichiometric matrix by explicitly showing how the C flows propagate to other C flows and to the Re flows. (a) C:A imposes a flow into Re which in turn imposes a flow into C:B. (b) C:A imposes a flow into Re:1 and thence, together with C:B. imposes a flow into the 0 junction and thence into Re:2 and C:C. (c) C:A imposes a flow into the 1 junction and thence into C:B and Re;Re in turn imposes a flow into the 1 junction and thence into C:C and C:D. (d) As the external flow v₀ impinges on to 0 junctions, it does not affect the causality of the parts in common with (b). (Online version in colour.)

The system of figure 3a has two C components and

$$X={(x_a{x}_b)}^{\mathrm{T}}.$$ 3.14

It is convenient to decompose X into two components: x the independent part of X and X^d the dependent part of X. In particular,

$$x=x_a=L_{xX}X,\text{where }{L}_{xX}=(10)$$ 3.15

and

$$X^d=(x_b)=L_{dX}X,\text{where }{L}_{dX}=(01).$$ 3.16

The full state X can be reconstructed from x and X^d using

$$X=L_{xX}^{\mathrm{T}}x+L_{dX}^{\mathrm{T}}{X}^d.$$ 3.17

Using this decomposition, equations (3.13) can be written as

$${\dot{X}}^d=L_{dx}\dot{x},$$ 3.18

where

$$L_{dx}=(-1).$$ 3.19

Combining these equations,

$${\dot{X}}^d=L_{dX}\dot{X}=L_{dx}\dot{x}=L_{dx}{L}_{xX}\dot{X}.$$ 3.20

Defining

$$G=L_{dX}-L_{dx}{L}_{xX}$$ 3.21

it follows that the state dependency can also be expressed as

$$G\dot{X}=GNV=0,$$ 3.22

where, in this case

$$G=(01)+(10)=(11).$$ 3.23

As discussed in the earlier studies, as (3.22) is true for all V

$$GN=0$$ 3.24

and thus G is a left null matrix of N. In this particular case, $G\dot{X}=0$ corresponds to

$${\dot{x}}_a+{\dot{x}}_b=0\text{or}{x}_a+x_b=\text{const.}$$ 3.25

Thus, the total amount of A and B is constant.

The system of figure 3b has three C components and

$$X={(x_a{x}_b{x}_c)}^{\mathrm{T}}.$$ 3.26

Following the same arguments as for figure 3a, it follows that

$$x=\left(\begin{array}{c}{x}_a\\ x_b\end{array}\right)=L_{xX}X,\text{where }{L}_{xX}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)$$ 3.27

and

$$X^d=(x_c)=L_{dX}X,\hspace{0.17em}\text{where }{L}_{dX}=(001)\text{and}{L}_{dx}=(-1-1).$$ 3.28

In this case,

$$G=L_{dX}-L_{dx}{L}_{xX}=(001)-(-1-1)\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)=(111).$$ 3.29

In this particular case, $G\dot{X}=0$ corresponds to

$${\dot{x}}_a+{\dot{x}}_b+{\dot{x}}_c=0\text{or}{x}_a+x_b+x_c=\text{const.}$$ 3.30

Thus, the total amount of A, B and C is constant.

The system of figure 3c has four C components and

$$X={(x_a{x}_b{x}_c{x}_d)}^{\mathrm{T}}.$$ 3.31

Following the same arguments as for figure 3a, it follows that

$$x=(x_a)=L_{xX}X,\text{where}\hspace{0.17em}{L}_{xX}=(1000)$$ 3.32

and

$$X^d={(x_b{x}_c{x}_d)}^{\mathrm{T}}=L_{dX}X,$$ 3.33

where

$$L_{dX}=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\hspace{0.17em}\end{array}\right)\text{and}{L}_{dx}=\left(\begin{array}{c}1\\ -1\\ -1\end{array}\right).$$ 3.34

In this case,

$$G=L_{dX}-L_{dx}{L}_{xX}=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\hspace{0.17em}\end{array}\right)-\left(\begin{array}{c}1\\ -1\\ -1\end{array}\right)(1000)=\left(\begin{array}{cccc}-1& 1& 0& 0\\ 1& 0& 1& 0\\ 1& 0& 0& 1\end{array}\right).$$ 3.35

In this particular case, $G\dot{X}=0$ corresponds to

$$x_b=x_a+\text{const.,}{x}_a+x_c=\text{const.}\mathrm{and}{x}_a+x_d=\text{const.}$$

Thus, the amount of B equals the amount of A plus a constant, the total amount of A and C is constant and the total amount of A and D is constant.

Continuing the analysis of the system of figure 3b but including the extra input of figure 3d, the flow vector has an extra component v₀ and can be defined as

$$V={(v_0{v}_1{v}_2)}^{\mathrm{T}},$$ 3.36

where v₁ and v₂ are the two reaction flows. It is convenient to decompose V into two components: v the independent part of V and V ^d part of V dependent on $\dot{X}$ and v. In particular,

$$v=v_0=K_{vV}V,\text{where }{K}_{vV}=(100)$$ 3.37

and

$$V^d=\left(\begin{array}{c}{v}_1\\ v_2\end{array}\right)=K_{dV}V,\text{where }{K}_{dV}=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\end{array}\right).$$ 3.38

Moreover, following the causal strokes in figure 3d the flow vector V can be written in terms of the state derivative $\dot{X}$ and the independent flow v as

$$V=K_{VX}\dot{X}+K_{Vv}v,$$ 3.39

where

$$K_{VX}=\left(\begin{array}{ccc}0& 0& 0\\ -1& 0& 0\\ -1& -1& 0\end{array}\right)\text{and}{K}_{Vv}=\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right).$$ 3.40

In the particular case that the system is in a steady state and so $\dot{X}=0$:

$$V=Kv,\text{where }K=K_{Vv}$$ 3.41

Substituting into equation (3.3) it follows that NKv=0. As this must be true for all v, it follows that NK=0 and thus K is a right null matrix of N.

(c). Reduced-order equations

The stoichiometric analysis of §3a,b has many uses; one of these, reducing the order of the ordinary differential equations (ODEs) describing a system,⁷ is given here. Reducing system order gives a smaller set of equations to solve and may avoid numerical problems, for example, arising from failure to recognize conserved moieties in a reaction system.

From equation (3.18), the derivatives ${\dot{X}}^d$ of the dependent state X^d can be written as linear transformation of the derivatives $\dot{x}$ of the independent state x as

$${\dot{X}}^d=L_{dx}\dot{x}.$$ 3.42

Integrating this equation gives

$$X^d-X^d(0)=L_{dx}(x-x(0)),$$ 3.43

where X^d(0) and x(0) are the values of X^d and x at time zero. Using equations (3.15), (3.16) and (3.21), equation (3.43) can be rewritten as

$$X^d=L_{dx}x+X^d(0)-L_{dx}x(0)=L_{dx}x+(L_{dX}-L_{dx}{L}_{xX})X(0)=L_{dx}x+GX(0).$$ 3.44

Using equation (3.17) to reconstruct X from X^d given by equation (3.44) and x gives

$$X=(L_{xX}^{\mathrm{T}}+L_{dX}^{\mathrm{T}}{L}_{dx})x+L_{dX}^{\mathrm{T}}GX(0)=Lx+G_{X}X(0),$$ 3.45

where

$$L=L_{xX}^{\mathrm{T}}+L_{dX}^{\mathrm{T}}{L}_{dx}\text{and}{G}_X=L_{dX}^{\mathrm{T}}G.$$ 3.46

Equation (3.44) gives an explicit expression for reconstructing the full state X from the independent state x and the initial state X(0).

From equation (3.3), the state X is given by the system ODE as

$$\dot{X}=NV(X,u),$$ 3.47

where u represents external flows (for example, v in figure 3d). Using equations (3.15) and (3.45), the ODE in X of equation (3.47) can be rewritten as the reduced order ODE in x as

$$\dot{x}=L_{xX}NV(Lx+G_{X}X(0),u)$$ 3.48

and the full state reconstructed using equation (3.45).

4. Model reduction and approximation of reaction mechanisms

As discussed in the Introduction, complex systems can be simplified by approximation. However, it is crucial that such approximation does not destroy the compliance with thermodynamic principles reflected in the original system.

In their analysis of the sodium pump, which transports sodium ions out of electrically excitable cells such as cardiomyocytes, Smith & Crampin [26] consider simplification of the linear chain of reactions:

$$\cdots X_1;\stackrel{k_1^{-}}{\underset{k_1^{+}}{\rightleftharpoons }}\hspace{0.17em}{X}_2\stackrel{k_2^{-}}{\underset{k_2^{+}}{\rightleftharpoons }}\hspace{0.17em}{X}_3\stackrel{k_3^{-}}{\underset{k_3^{+}}{\rightleftharpoons }}{X}_4\cdots ,$$ 4.1

where the middle reaction in the chain is fast relative to the other reactions. The three reactions have flows v₁…v₃ given by

$$v_1=k_1^{+}{X}_1-k_1^{-}{X}_2,v_2=k_2^{+}{X}_2-k_2^{-}{X}_3\mathrm{and}{v}_3=k_3^{+}{X}_3-k_3^{-}{X}_4.$$ 4.2

Reaction (4.1) corresponds to the bond graph of figure 4a which has the flows of equations (4.2), where

$$\begin{array}{rl}{k}_1^{+}& ={\kappa }_1{K}_1,k_1^{-}={\kappa }_1{K}_2,\end{array}$$ 4.3

$$\begin{array}{rl}{k}_2^{+}& ={\kappa }_2{K}_2,k_2^{-}={\kappa }_2{K}_3,\end{array}$$ 4.4

and

$$\begin{array}{rl}{k}_3^{+}& ={\kappa }_3{K}_3,k_3^{-}={\kappa }_3{K}_4.\end{array}$$ 4.5

Figure 4.

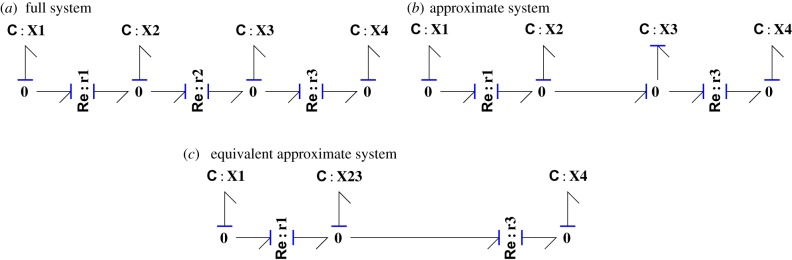
Approximation of unimolecular reactions [26], §3.1. The reaction chain (a) is approximated in (b) by assuming that the reaction represented by Re:r2 is fast (1/κ₂≈0) and so may be removed. (c) is exactly equivalent to (b) except that the adjacent C:X2 and C:X3 are replaced by the composite component C:X23 with coefficient K₂₃ given by equation (4.12). (Online version in colour.)

If κ₂≫κ₁ and κ₂≫κ₃, equation (4.4) can be rewritten as

$${\kappa }_2=\frac{1}{ϵ},$$ 4.6

where ϵ is a small positive number. v₂ (4.2) and (4.4) can then be rewritten as

$$ϵv_2=K_2{X}_2-K_3{X}_3$$ 4.7

assuming non-zero v₂ this means that as $ϵ\to 0$, X₂ and X₃ are in equilibrium and

$$X_3=\rho X_2,\text{where }\rho =\frac{K_2}{K_3}.$$ 4.8

This also means that the difference in affinities associated with reaction 2 is zero

$$A_2^{\mathrm{f}}-A_2^{\mathrm{r}}=K_2{X}_2-K_3{X}_3=0.$$ 4.9

Thus, the corresponding reaction component Re:r3 can be removed from the bond graph to give figure 4b. This implies that the C:X3 component is in derivative causality and thus the bond graph represents a differential-algebraic equation and an ordinary differential equation. However, as discussed by Gawthrop & Bevan [11], as C:X2 and C:X3 are on adjacent 0 junctions, they may be replaced by the single C:X23 component as in figure 4c.

Figure 4c represents the same system as figure 4b if C : X23 contains the same molar mass as C : X2 and C : X3. Moreover, using equations (4.8)

$$X_{23}=X_2+X_3=(1+\rho )X_2.$$ 4.10

The equilibrium constant K₂₃ of C:X23 must also correspond to those of C:X2 and C:X3 so that

$$K_2{X}_2=K_3{X}_3=K_{23}{X}_{23}$$ 4.11

hence

$$K_{23}=\frac{K_2}{1+\rho }=\frac{\rho K_3}{1+\rho }.$$ 4.12

The bond graph of figure 4c corresponds to the reaction scheme [26], §3.1:

$$\cdots X_1\stackrel{{\alpha }_1^{+}}{\underset{{\alpha }_1^{-}}{\rightleftharpoons }}{X}_{23}\stackrel{{\alpha }_3^{+}}{\underset{{\alpha }_3^{-}}{\rightleftharpoons }}{X}_4\cdots$$ 4.13

where

$$\begin{array}{rl}{\alpha }_1^{+}& ={\kappa }_1{K}_1=k_1^{+}{\alpha }_1^{-}={\kappa }_1{K}_{23}={\kappa }_1\frac{K_2}{1+\rho }=\frac{k_1^{-}}{1+\rho }\\ \text{and}{\alpha }_3^{+}& ={\kappa }_3{K}_{23}={\kappa }_1\frac{\rho K_3}{1+\rho }=\frac{\rho k_3^{+}}{1+\rho }=\frac{k_3^{+}}{1+(1/\rho )}{\alpha }_3^{-}={\kappa }_3{K}_4=k_3^{-}.\end{array}\}$$ 4.14

Noting that ‘K₂’ in Smith & Crampin [26], §3.1 corresponds to ‘ρ’ in this paper, equations (4.14) correspond to eqn (18) of Smith & Crampin [26].

In general, a chain of N C components and N−1 Re components where all of the reactions are fast may be approximately replaced by a single C component with

$$K=\frac{1}{1/K_1+1/K_2\dots 1/K_N}=\frac{1}{\sum _{i=1}^N(1/K_i)}.$$ 4.15

This procedure is extended to bimolecular reactions in the electronic supplementary material, §B.

5. Biochemical cycles

Many biochemical processes central to cellular physiology represent biochemical cycles: including enzyme catalysed reactions, transport processes and signalling cascades. A very simple, but practically important, biochemical cycle is the enzyme-catalysed reaction of figure 1f. This reaction is closely related to that of figure 1d with the important difference that the enzyme E appears on both sides of the reaction creating the ‘loop’ in the bond graph corresponding to a biochemical cycle. Moreover, in figure 1f, the net flow into E is zero and thus ${\dot{x}}_e=0$ and x_e=e₀, where e₀ is a constant. It follows that

$$v=\kappa (K_e{x}_e{K}_s{x}_s-K_e{x}_e{K}_p{x}_p)={\kappa }_e(K_s{x}_s-K_p{x}_p),$$ 5.1

where

$${\kappa }_e=\kappa K_e{e}_0.$$ 5.2

(a). Example: enzyme-catalysed reaction cycles

As noted above, the enzyme-catalysed reaction of figure 1f simplifies to a simple reaction with a modified reaction constant κ_e=κK_ee₀. However, it is known from experiments that this simple model of an enzyme-catalysed reaction fails for high reaction flows. For this reason, as discussed in [2,3,15], an intermediate complex C is introduced so that the reaction

$$S+E\rightleftharpoons P+E$$ 5.3

is replaced by

$$S+E\stackrel{1}{\rightleftharpoons }C\stackrel{2}{\rightleftharpoons }P+E.$$ 5.4

This reaction may then be replaced by various versions of the Michaelis–Menten approximation. As discussed by Gunawardena [6], this approximation has been much misused. In particular, it is used in circumstances which violate the fundamental law of thermodynamics.

Using the bond graph approach, this section derives a Michaelis–Menten approximation which is thermodynamically compliant. In particular, the aim of the approximation is, as for the simple case of figure 1f, to replace the enzyme-catalysed reaction by a single Re component with an equivalent gain κ_e. But, unlike the simple case, κ_e is not a constant but rather an nonlinear function of the forward and backward affinities.

Figure 5a shows the enzyme-catalysed reaction (with complex C). The substrate S and product P are omitted from the bond graph as they do not form part of the approximation. This is a more general approach than usual as the result to be derived holds for any biochemical network giving rise to A^f and A^r. As already stated, the aim of the approximation is to replace the bond graph of figure 5a by a single Re component of figure 5b. As, by definition, the Re component has the same flow on each port, it is natural to approximate the bond graph of figure 5a by enforcing this constraint at the outset. To do this, the flow component Sf:v is used to impose a flow v on each port thus generating the corresponding forward A^f and backward A^r affinities.

Figure 5.

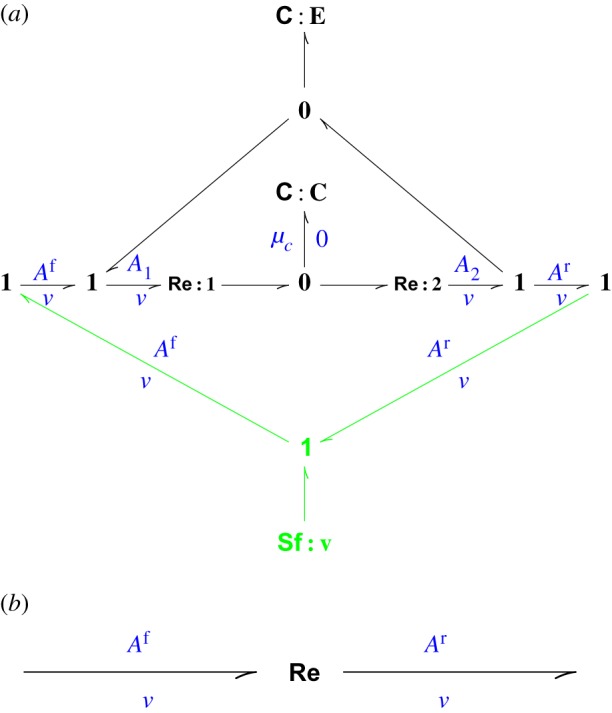
(a,b) The Michaelis–Menten approximation: (a) full, (b) approximate. (Online version in colour.)

With reference to figure 5a, and using equation (2.6), the equation describing the left-hand Re component may be rewritten as

$${\mathrm{e}}^{A_1/\mathrm{RT}}={\mathrm{e}}^{{\mu }_c/\mathrm{RT}}+\frac{v}{{\kappa }_1}=K_c{x}_c+\frac{v}{{\kappa }_1}$$ 5.5

hence

$$A_1=\mathrm{RT}\ln (K_c{x}_c+\frac{v}{{\kappa }_1})\mathrm{and}{A}_2=\mathrm{RT}\ln (K_c{x}_c-\frac{v}{{\kappa }_1}).$$ 5.6

It follows that A^f is given by

$$A^{\mathrm{f}}=A_1-{\mu }_e=A_1-\mathrm{RT}\ln K_e{x}_e=\mathrm{RT}\ln \frac{K_c{x}_c+v/{\kappa }_1}{K_e{x}_e}$$ 5.7

and, similarly

$$A^{\mathrm{r}}=\mathrm{RT}\ln \frac{K_c{x}_c-v/{\kappa }_1}{K_e{x}_e}.$$ 5.8

It is convenient to transform A^f and A^r into $v_0^{+}$ and $v_0^{-}$, where:

$$v_0^{+}={\mathrm{e}}^{A^{\mathrm{f}}/\mathrm{RT}}\mathrm{and}{v}_0^{-}={\mathrm{e}}^{A^{\mathrm{r}}/\mathrm{RT}}$$ 5.9

giving

$$v_0^{+}=\frac{K_c{x}_c+v/{\kappa }_1}{K_e{x}_e}\mathrm{and}{v}_0^{-}=\frac{K_c{x}_c-v/{\kappa }_2}{K_e{x}_e}.$$ 5.10

Subtracting these equations gives

$$v_0^{+}-v_0^{-}=\frac{1/{\kappa }_1+1/{\kappa }_2}{K_e{x}_e}v$$ 5.11

hence

$$v=\overline{\kappa }{K}_e{x}_e{\delta }_v,\hspace{0.17em}\text{where }\overline{\kappa }=\frac{{\kappa }_1{\kappa }_2}{{\kappa }_1+{\kappa }_2}\text{and}{\delta }_v=v_0^{+}-v_0^{-}.$$ 5.12

Multiplying equations (5.10) by κ₁ and κ₂, respectively, and adding gives

$${\kappa }_1{v}_0^{+}+{\kappa }_2{v}_0^{-}=({\kappa }_1+{\kappa }_2)\frac{K_c{x}_c}{K_e{x}_e}$$ 5.13

hence

$$x_c=\frac{K_e}{K_c}{\sigma }_v{x}_e,\text{where }{\sigma }_v=\frac{{\kappa }_1{v}_0^{+}+{\kappa }_2{v}_0^{-}}{{\kappa }_1+{\kappa }_2}=\frac{{\kappa }_1\hspace{0.17em}{\mathrm{e}}^{A^{\mathrm{f}}/\mathrm{RT}}+{\kappa }_2\hspace{0.17em}{\mathrm{e}}^{A^{\mathrm{r}}/\mathrm{RT}}}{{\kappa }_1+{\kappa }_2}.$$ 5.14

Using the feedback loop implied by x_e=e₀−x_c and equation (5.14)

$$x_e=\frac{e_0}{1+(K_e/K_c){\sigma }_v}.$$ 5.15

Substituting equation (5.15) into equation (5.12) gives

$$v=\overline{\kappa }\frac{K_e{e}_0}{1+(K_e/K_c){\sigma }_v}{\delta }_v=\overline{\kappa }\frac{K_c{e}_0}{K_c/K_e+{\sigma }_v}{\delta }_v.$$ 5.16

There are two special cases of interest κ₁=κ₂ and κ₁≫κ₂. In these two cases, σ_v is given by

$${\sigma }_v=\{\begin{array}{ll}\frac{v_0^{+}+v_0^{-}}{2}=\frac{{\mathrm{e}}^{A^{\mathrm{f}}/\mathrm{RT}}+{\mathrm{e}}^{A^{\mathrm{r}}/\mathrm{RT}}}{2}& {\kappa }_1={\kappa }_2\\ v_0^{+}={\mathrm{e}}^{A^{\mathrm{f}}/\mathrm{RT}}& {\kappa }_1\gg {\kappa }_2.\end{array}$$ 5.17

Hence the enzyme-catalysed reaction can be approximated by the Re component with equivalent gain κ_e given by

$${\kappa }_e=e_0\frac{\overline{\kappa }{K}_c}{k_m+{\sigma }_v},\text{where }{k}_m=\frac{K_c}{K_e}.$$ 5.18

In contrast to the expression for the simple case (5.2) κ_e is, via σ_v (5.17), a function of the affinities A^f and A^r. The fact that σ_v>0 ensures that the Re component corresponding to equation (5.18) is thermodynamically compliant.

In both equations (5.2) and (5.18), the expression for κ_e has a factor e₀, the (constant) sum of x_e and x_c. In many biochemical situations, the enzyme E is the product of another reaction. Although equation (5.18) is derived for a constant e₀, a further approximation would be to allow e₀ to be time varying e₀=x_E where x_E is the enzyme concentration from an external reaction. This leads to the concept of the modulated Re, or mRe component of figure 5c. The additional modulating bond carries two signals: the effort μ_E, where

$${\mu }_{\mathrm{E}}={\mathrm{e}}^{x_e/\mathrm{RT}}$$ 5.19

and a zero flow. The zero flow means that the modulating bond does not transmit power. The mRe component is used to approximate the system of §5b.

(b). Example: a biochemical switch

Beard & Qian [2], §5.1.1 discuss a biochemical switch described by

$$\begin{array}{rl}S+\mathrm{ATP}+K\stackrel{1}{\rightleftharpoons }& KSKS\stackrel{2}{\rightleftharpoons }{S}^{\star }+\mathrm{ADP}+K\\ \text{and}{S}^{\star }+P\stackrel{3}{\rightleftharpoons }& S^{\star }P{S}^{\star }P\stackrel{4}{\rightleftharpoons }S+\mathrm{Pi}+P.\end{array}\}$$ 5.20

These reactions represent a phosphorylation/dephosphorylation cycle. Protein S is phosphorylated by kinase K and is dephosphorylated by phosphatase P, where S^⋆ represents the phosphorylated (active, perhaps) state of the protein. The corresponding bond graph appears in figure 6a where the external flow v_a necessary to top up the ATP reservoir is included. This system contains nine states and four reactions with mass-action kinetics. Using the approximation of §5a, figure 5, this system can be approximated by the bond graph of 6b. The approximate system has five states and two reactions with the reversible Michaelis–Menten kinetics of §5a. It has the further advantage that the dynamics are explicitly modulated by the concentrations x_k and x_p of K and P, respectively.

Figure 6.

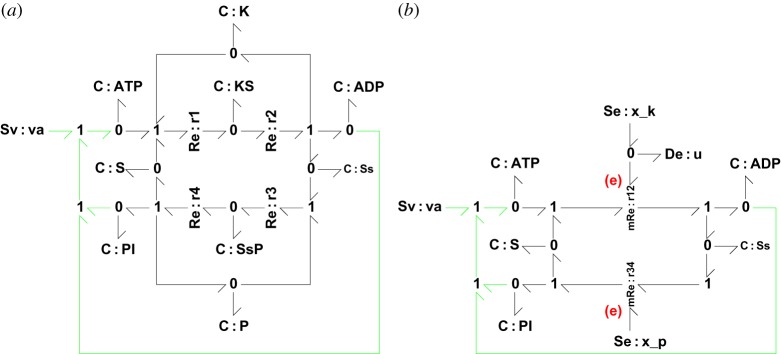
A biochemical switch. (a) The bond graph of the biochemical switch of Beard & Qian [2] has four reactions Re:r1–Re:r4 and nine substances. The external flow v_a of ATP is required for the long-term operation of the switch which consumes ATP. (b) This switch can be approximated using the approximation of figure 5 while retaining thermodynamic compliance. (Online version in colour.)

The bond graph of 6b clearly shows a biochemical cycle. Its behaviour can be understood as follows. When x_k is large, ATP drives S though the reaction component Re:r12 to create S^⋆; and this flow is greater than that though Re:r34 and so the amount of S^⋆ increases at the expense of S. However, when x_k is small the flow though Re:r12 becomes less than that though Re:r34 and amount of S^⋆ decreases.

For the purposes of illustration, the following parameter values were used. With reference to equation (5.18), k_m=0 and $\overline{\kappa }{K}_c=100$ for both reactions. With reference to equations (2.3), K_ATP=10 and K_S=K_S*=K_ADP=K_PI=1. The initial states were x_ATP=10, x_S=x_ADP=1 and x_S*=x_PI=0.

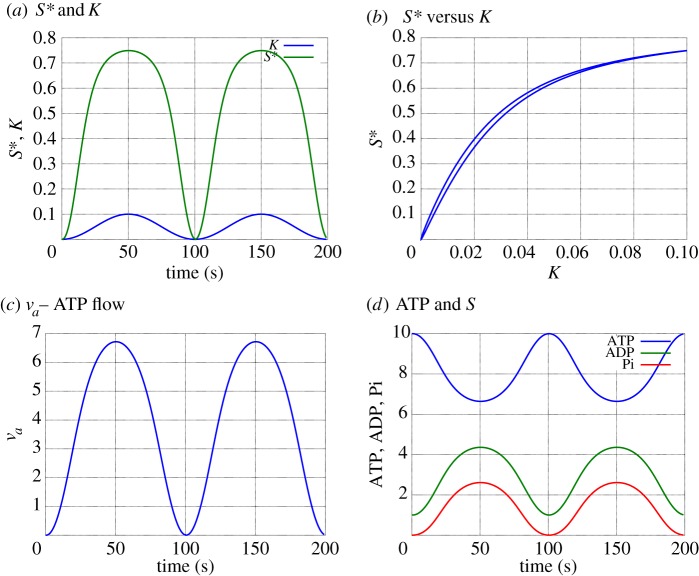
Figure 7 shows a simulation of the biochemical switch when ATP is replenished by setting

$$v_a=g_a(w_{\mathrm{ATP}}-x_{\mathrm{ATP}}),\hspace{0.17em}\text{where }{g}_a=2\text{and}{w}_{\mathrm{ATP}}=10.$$ 5.21

Equation (5.21) represents simple proportional feedback; in vivo, this would correspond to a cellular control system. Figure 7a shows the response of the amount of S^⋆ to a sinusoidal variation in the amount of K. The biochemical switch both amplifies and distorts the signal. This effect is further shown in figure 7b where the amount of S^⋆ is plotted against the amount of K. This is basically a high-gain saturating function. The hysteresis is due to the time constant of the feedback loop implied by equation (5.21); the hysteresis reduces if either g_a is increases or the frequency of the input sinusoid decreased. All biochemical cycles require free-energy transduction [1]. Figure 7c shows the molar flow of ATP into the system (and, as indicated in figure 6b, the outflow of ADP and Pi) as a function of time; the ON state of the switch induces a flow of ATP using equation (5.21) to replenish the ATP consumed by the cycle. Figure 7d shows the corresponding amounts of ATP, ADP and Pi. The controller does not exactly hold ATP at the desired level of w_ATP=10; a higher gain controller would reduce the control error. As discussed by Beard & Qian [2], §5.1.1: ‘… a biochemical switch cannot function without a free energy input. No energy, no switch’. This can be simulated by setting g_a=0 in equation (5.21) and forms the electronic supplementary material, figure S1 of §A.

Figure 7.

A biochemical switch: simulation. (a) The time response of the amount of S^⋆ to a sinusoidal variation in the amount of K. The biochemical switch both amplifies and distorts the signal. Panel (b) plots S^⋆ against K to show the nonlinear amplification effect. (c) The corresponding molar flow of ATP into the system and (d) the corresponding amounts of ATP, ADP and Pi. (Online version in colour.)

Approximate models of signalling network components have been advocated by Kraeutler et al. [68] and Ryall et al. [69] as an approach to understanding the behaviour of complex signalling networks. The models developed in this section could also be used for such a purpose, but with the advantage that the resulting model is thermodynamically compliant.

Model reduction of an enzymatic cycle model of the SERCA pump [70] is discussed in the electronic supplementary material, §c.

6. Hierarchical modelling of large systems

One of the objectives of systems biology is to represent the network of biochemical reactions taking place in cells by computational models. Large-scale models of cellular metabolic and signalling networks have been constructed; for example, cardiac cell models which integrate electrophysiology, metabolism, signalling and cellular mechanics have been developed in order to study cell physiology in normal and disease conditions [71].

In order to facilitate the development and reuse of such models, XML-based markup languages such as CellML [72] and SBML [73] have been created. These languages enable mathematical descriptions of biological processes to be stored in machine-readable formats, but put relatively little restriction on the formulation of the models themselves.

For example, CellML, which was originally developed in order to share models of cardiac cell dynamics, represents models as a number of component elements, each of which contains a number of variables (for example, representing cell membrane potential, or an ionic concentration), the mathematical relationship between these variables (for example, the Nernst potential given as a function of the concentrations) expressed in MathML, and associated parameters. Such components can be connected to one another to form a model.

This construction allows a modular approach to modelling in which cellular processes and reactions can be broken down into components, which are then connected to form a model of the system under study [74]. However, there is no requirement that components adhere to the principles of conservation of mass, conservation of charge or thermodynamic consistency. Nor is there currently any framework which would ensure thermodynamic consistency, or mass or charge conservation, for a model created by connecting components in this modular fashion, even if the components themselves were constructed as thermodynamic cycles.

The bond graph approach which we have outlined here provides such a framework for modular representation of components of biological systems, which can be assembled so as to preserve thermodynamic properties, charge and mass conservation, both in the individual components and in the overall system. Furthermore, the development of the bond graph markup language (BGML) by Borutzky [35] for the exchange and reuse of bond graph models, and associated software, provides the tools through which integration with representations such as CellML may be achieved.

The stoichiometric analysis of §3, and its relationship to causality, is illustrated by simple systems. However, the notion of bond graph causality, and the corresponding propagation of causality using the sequential causality assignment procedure [10], ch. 5, is applicable to arbitarily large systems.

7. Conclusion

Based on the seminal work of Oster et al. [16], the fundamental concepts of network thermodynamics have been combined with more recent developments in the bond graph approach to system modelling to give a new approach to building dynamical models of biochemical networks within which compliance with thermodynamic principles is automatically satisfied. As noted in the Introduction, the bond graph is more than a sketch of a biochemical network; it can be directly interpreted by a computer and, moreover, has a number of features that enable key physical properties to be derived from the bond graph itself. It has been shown that stoichiometric properties, including the stoichiometric matrix N and the left and right null-space matrices G and K, can be directly derived from the bond graph using the concept of causality associated with bond graphs. The corresponding causal paths, when superimposed on the bond graph, directly indicate both pools (conserved moieties) and steady-state flux paths. The bond graph methodology includes a framework for approximating complex systems while retaining compliance with thermodynamic principles and this has been illustrated in two contexts: chains of reactions and the Michaelis–Menten approximation of enzyme-catalysed reactions.

As emphasized by Beard & Qian [2], living organisms are associated with non-equilibrium steady states. For this reason, this paper has emphasized the role of external inputs to biochemical networks modelled by bond graphs. In particular, the example of §5b, models a biochemical switch where the role of ATP as a power source is explicitly integrated into the bond graph model.

The bond graph approach is naturally modular in that networks of biochemical reactions can be connected by bonds while retaining compliance with thermodynamic principles. Modularity has been illustrated by simple examples and future work will develop appropriate software tools to build on this natural modularity.

Biochemical networks have nonlinear dynamics which generate phenomena which cannot be generated by linear systems. Nevertheless, useful information can be obtained from linear models obtained by linearization of nonlinear systems. In the context of engineering systems theory, linearization has been considered within the framework of sensitivity theory [75,76]. In the context of biochemical networks, metabolic control analysis (MCA) [77] is based on the sensitivity analysis of stoichiometric networks. The relationship of MCA to engineering concepts of sensitivity has been examined by Ingalls & Sauro [64], Ingalls [65] and Sauro [66]. Ingalls [65] has shown that standard engineering sensitivity theory can be applied to biochemical networks to derive frequency responses with respect to small perturbations in system parameters. Sensitivity and linearization of systems described by bond graphs has been considered in earlier studies [78–80]. The bond graph approach has the advantage of retaining the system structure. Future work will look at bond graph-based linearization in the context of biochemical networks.

This paper has focused on deriving thermodynamically compliant biochemical reaction networks, and their thermodynamically compliant approximations, from elementary biochemical equations. It would be interesting to look at the inverse problem: Is a given ODE model of a system of biochemical reactions with non-mass-action kinetics thermodynamically compliant and does it have a bond graph representation?

In addition to stoichiometric analysis, the bond graph approach can be used to directly investigate structural properties of dynamical systems such as controllability [62,81] and invertibility [59,61,82,83]. Future work will look at bond graph-based structural analysis in the context of biochemical networks.

The bond graph approach is based on the notion of power flow. For this reason, it has been much used for modelling multi-domain engineering systems with appropriate transducer models to interface domains. Thus, for example: an electric motor or a piezo-electric actuator couples electrical and mechanical domains and a turbine or pump couples hydraulic and mechanical domains. We will build on the work of LeFèvre et al. [43] on chemo-mechanical transduction and the work of Karnopp [39] on chemo-electrical transduction to interface biochemical networks with systems involving muscle and excitable membranes.

We believe that, when combined with modern software tools, the bond graph approach provides a significant alternative hierarchical and modular modelling framework for complex biochemical systems in which compliance with thermodynamic principles is automatically satisfied.

Funding statement

This research was in part conducted and funded by the Australian Research Council Centre of Excellence in Convergent Bio-Nano Science and Technology (project no. CE140100036), and by the Virtual Physiological Rat Centre for the Study of Physiology and Genomics, funded through NIH grant P50-GM094503. P.J.G. thanks the Melbourne School of Engineering for its support via a Professorial Fellowship.