BEYOND STATISTICAL SIGNIFICANCE: CLINICAL INTERPRETATION OF REHABILITATION RESEARCH LITERATURE

Abstract

Evidence‐based practice requires clinicians to stay current with the scientific literature. Unfortunately, rehabilitation professionals are often faced with research literature that is difficult to interpret clinically. Clinical research data is often analyzed with traditional statistical probability (p‐values), which may not give rehabilitation professionals enough information to make clinical decisions. Statistically significant differences or outcomes simply address whether to accept or reject a null or directional hypothesis, without providing information on the magnitude or direction of the difference (treatment effect). To improve the interpretation of clinical significance in the rehabilitation literature, researchers commonly include more clinically‐relevant information such as confidence intervals and effect sizes. It is important for clinicians to be able to interpret confidence intervals using effect sizes, minimal clinically important differences, and magnitude‐based inferences. The purpose of this commentary is to discuss the different aspects of statistical analysis and determinations of clinical relevance in the literature, including validity, significance, effect, and confidence. Understanding these aspects of research will help practitioners better utilize the evidence to improve their clinical decision‐making skills.

Level of evidence:

5

INTRODUCTION

Evidence‐based practice is supposed to affect clinical decision‐making, but interpreting research is often difficult for some clinicians. Clinical interpretation of research on treatment outcomes is important because of its influence on clinical decision‐making including patient safety and efficacy. Publication in a peer‐reviewed journal does not automatically imply proper study design or statistics were used, or that the author's interpretation of the data was appropriate. Furthermore, statistically significant differences between data sets (or lack thereof) may not always result in an appropriate change in clinical practice. Clinical research is only of value if it is properly interpreted.

From a clinical perspective, the presence (or absence) of statistically significant differences is of limited value. In fact, a non‐significant outcome does not automatically imply the treatment was not clinically effective because small sample sizes and measurement variability can influence statistical results.¹ Other factors, such as treatment effect calculations and confidence intervals offer much more information for clinicians to assess regarding the application of research finding, including both the magnitude and direction of a treatment outcome.

The purpose of this clinical commentary is to discuss the different aspects of statistical analysis and determinations of clinical relevance in the literature, including validity, significance, effect, and confidence. Understanding these aspects of research will help practitioners better utilize the evidence to improve their clinical decision‐making skills.

VALIDITY

Clinicians should be able to critically evaluate research for both internal and external validity in order to determine if a study is clinically applicable. Internal validity reflects the amount of bias within a study that may influence the research results. Proper study design and statistical analysis are important factors for internal validity. For additional information on proper research design, the reader is referred to the article “Research Designs in Sports Physical Therapy”.²

The research question drives the research design and statistical analysis. General clinical research designs include clinical trials, cohort studies, and case reports; each providing different levels of evidence.³ Systematic reviews and randomized clinical trials (RCT) are the highest level of research design. Cohort studies include pre‐post designs, epidemiological, and descriptive research. Case reports are among the lowest level of evidence. (Table 1) A recent systematic review found nearly one half of clinical sports medicine literature is comprised of level 1 and level 2 studies, as compared to just 20% of the literature 15 years ago.⁴

Table 1.

Levels of Evidence, adapted from the Oxford Center for Evidence‐based

I*	Systematic review of randomized trials
II*	Randomized trial or observational study with dramatic effect
III*	Non‐randomized controlled cohort / follow‐up studies
IV*	Case series, case control studies, or historical control trials
V*	Mechanism‐based reasoning

^*Level may be graded up or down on the basis of study quality, consistency between studies, or effect size

OCEBM Levels of Evidence Working Group. "The Oxford 2011 Levels of Evidence".

Clear explanation of the population, recruitment, randomization, and blinding are important considerations when evaluating internal validity to identify potential bias. The PEDro scale (http://www.pedro.org.au/english/downloads/pedro‐scale/) for rating clinical trials is a valid tool that can be used to analyze clinical trials for quality⁵ and bias. Detailed description of the intervention and control groups is crucial for both internal and external validity. External validity is the ability of a study to be generalized and applied in clinical situations. While “clinical research” should include patient populations, healthy populations are sometimes used to answer clinical questions such as electromyographical (EMG) analysis of exercises. Practitioners should be cautious when applying results of studies with healthy cohorts to a patient population. Similarly, it is important to differentiate between studies on ‘elite” athletes and recreational athletes in the exercise literature.⁶

In addition to considering the applicability of the study population to clinical practice, other factors can affect external validity, including the complexity of the protocol and cost effectiveness of the intervention. A repeatable protocol is important in order to reproduce the results of a study in clinical practice. If an intervention is not cost‐effective, it may not be feasible in practice. Studies with the highest level of design and high internal validity may still lack external validity, thereby limiting their clinical use.

STATISTICAL SIGNIFICANCE

Traditional research uses statistical hypothesis testing in order to infer something about a population using a representative sample. Statistics are used to answer questions of probability, generally using the scientific method, in order to determine if a hypothesis can be accepted or rejected. Statistical significance only addresses a hypothesis about whether or not differences exist, statistically, between groups. As stated previously, the statistical analysis of a study is driven by the research design, which is determined by the research question.

Statistical significance is based on several assumptions. The sample tested should be representative of the entire clinical population. Inferential statistics assume a normal distribution, represented by a bell‐shaped curve (Figure 1). A normal distribution is represented by standard deviation (σ) from the mean (μ) value. One standard deviation (SD) represents 68% of the population (in both directions from the mean) while 95% of the population is represented by +2 SDs.

Figure 1.

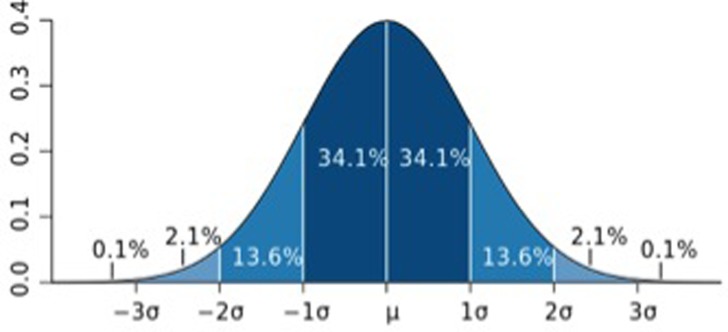
Normal distribution bell‐shaped curve with standard deviations (From http://en.wikipedia.org/wiki/File:Standard_deviation_diagram.svg)

Determination of whether statistically significant differences exist or not is centered on accepting or rejecting a “null” or “alternative” hypothesis. A null hypothesis (represented by H₀) assumes no difference between groups (or no effect of treatment). An alternative hypothesis (represented by H₁) is what the researcher expects to find from the study, and can be directional or non‐directional. A non‐directional hypothesis, based on rejecting the null hypothesis, provides a reference value for the outcome parameter. A directional hypothesis provides a minimal value for the expected outcome parameter. For example, a directional hypothesis for an intervention that decreases pain by a minimal clinical value may be represented by H₁ > 2.

Statistically significant differences are determined using a certain level of probability (the “p‐level”, or α) that the researcher chooses, to ensure that one does not incorrectly reject the null hypothesis due to chance, when the null hypothesis is in fact accepted (Type I error). The generally accepted p‐level of α =0.05 suggests there is a 95% probability that the researchers correctly rejects the null hypothesis when there is no difference between groups. Therefore, the p‐value is only the chance that the researcher makes the correct “yes” or “no” decision regarding a hypothesis.

Statistically significant differences alone should not be the primary influence for clinical interpretation of a study's outcome for application to patient care. Statistically significant differences do not provide clinical insight into important variables such as treatment effect size, magnitude of change, or direction of the outcome. In addition, whether results achieve statistically significant differences is influenced by factors such as the number and variability of subjects, as well as the magnitude of effect. Therefore, p‐values should be considered along with effect size, sample size, and study design.⁷ Evidence based practitioners should examine research outcomes for their clinical significance rather than just statistical significance. Several measures can be used to determine clinical relevance, including clinical significance, effect sizes, confidence intervals, and magnitude‐based inferences.

Clinical Significance

While most research focus on statistical significance, clinicians and clinical researchers should focus on clinically significant changes. A study outcome can be statistically significant, but not be clinically significant, and vice‐versa. Unfortunately, clinical significance is not well defined or understood, and many research consumers mistakenly relate statistically significant outcomes with clinical relevance. Clinically relevant changes in outcomes are identified (sometimes interchangeably) by several similar terms including “minimal clinically important differences (MCID)”, “clinically meaningful differences (CMD)”, and “minimally important changes (MIC)”.

In general, these terms all refer to the smallest change in an outcome score that is considered “important” or “worthwhile” by the practitioner or the patient⁸ and/or would result in a change in patient management^9,10. Changes in outcomes exceeding these minimal values are considered clinically relevant. It is important to consider that both harmful changes and beneficial changes may be outcomes of treatment; therefore, the term “clinically‐important changes” should be used to identify both minimal and beneficial differences, but also to recognize harmful changes.

Unfortunately, there are no standards for calculating clinically important changes in outcomes. Clinicians and researchers sometimes have different values for clinically important changes, and minimal changes may be specific to the individual patient. There is some subjectivity in determining clinical significance because of the paucity of research determining clinically significant values, and variations in patient status and goals and clinician experience. Minimal clinically important differences are generally calculated by comparing the difference in an outcome score before and after treatment with an “anchor” score such as global perceived effect score or another measure of the patients perceived change in an outcome.

Some researchers have identified MIC, MCID, and CMD with various outcome measures. It is important to determine clinical significance in a patient population with similar diagnoses and pain levels. For example, a clinically important change in pain in shoulder pain patients varies between patients with intact rotator cuffs and those with a ruptured rotator cuff.¹¹ Patients with acute pain or higher levels of pain intensity may require less change in pain than chronic pain patients for their changes to be considered clinically important.¹²

Some researchers have suggested that clinically significant changes can be determined using the standard deviation or standard error of the mean (SEM) within a study. Minimal important changes must be beyond the error of the measuring device to ensure clinical changes were not due to measurement error. Wyrwich¹³ reported that the MIC in musculoskeletal disorders was 2.3 or 2.6 times the SEM. To calculate the MCID, Lemieux et al.¹⁴ suggested multiplying the pooled baseline standard deviation scores by 0.2, which corresponds to the smallest effect size. For example, if the pooled baseline standard deviation is +/‐ 10, then the MCID is (0.2 × 10) equal to 2. Therefore, a mean difference between groups that is higher than the MCID of 2 is clinically relevant. However, more research is needed on the method of calculating clinically important changes and on quantifying these changes in patient populations.

EFFECT

The most fundamental question of clinical significance is usually, “Is the treatment effective, and will it or should it change my practice?” Some studies use the terms “efficacy” and “effectiveness” interchangeably; however, these terms should be differentiated. Efficacy is the benefit of an intervention compared to control or standard treatment under ideal conditions, including compliant subjects only. Effectiveness is the benefit of an intervention in a “real‐world” defined population, including non‐compliant subjects. Treatment efficacy is evaluated using compliant subjects,^15,16 while treatment effectiveness includes an ‘intent‐to‐treat’ analysis of all patients enrolled in the trial, by including subjects who dropped out in the final analysis, thus providing more clinically‐relevant outcomes.

The effect size is one of the most important indicators of clinical significance. It reflects the magnitude of the difference in outcomes between groups; a greater effect size indicates a larger difference between experimental and control groups. Standardized effect sizes (or standardized mean differences) are important when comparing treatment effects between different studies, as commonly seen in the performance of meta‐analyses. Clinical researchers should include standardized effect sizes in their results.

Cohen¹⁷ established traditional calculation of effect values based on group differences (change score), divided by the pooled standard deviation in the following equation:

$$\begin{array}{ccc}\frac{\text{Change}\text{in}\text{Experimental}\text{Group}\text{vs}\text{.}\text{control}}{\text{Standard}\text{Deviation}\text{of}\text{both}\text{groups}}& =& \frac{6}{10}\\ & =& 0.6\text{Cohen}\end{array}$$

Cohen quantified effect sizes that have been operationally described in ranges: <0.2= trivial effect; 0.2‐0.5 = small effect; 0.5‐0.8 = moderate effect; > 0.8= large effect. Cohen's effect sizes may be positive or negative, indicating the direction of the effect. For example, the effect size of 0.6 above would be a “moderate positive effect.” If the effect size were negative (‐0.6), the resulting effect would be “moderately negative”.

Treatment effect may also be determined by using “relative risk” or “odds ratio” analysis. The relative risk or “risk ratio” (RR) is the probability of an outcome occurring in a treatment group divided by the probability of an outcome occurring in a comparison group. The odds ratio (OR) is the proportion of subjects in the treatment group with an outcome divided by the proportion of subjects in a comparison group with the outcome. A RR or OR of 1 indicates no difference between the treatment and comparison groups. Values greater than 1 favor the treatment group, while values less than 1 favor the comparison group.

Relative risk (RR) can also be used to identify clinical effectiveness of an intervention. If a clinician assumes that a 10% improvement in a patient is clinically meaningful, then the number of subjects with at least 10% improvement can be compared to those not reaching the minimal (10%) improvement. Therefore, the relative clinical effectiveness (assuming an intent‐to‐treat analysis) would be defined using the following equation:

$$\text{Relative}\hspace{0.17em}\text{clinical}\hspace{0.17em}\text{effectiveness} = \frac{\% \text{subjects} \text{with} \text{clinically} \text{meaningful} \text{outcome}}{\% \text{subjects} \text{without} \text{clinically} \text{meaningful} \text{outcome}}$$

The number needed to treat (NNT) provides the number of patients who need to be treated before seeing one patient improve who would not have improved without the intervention. The NNT can infer clinical effectiveness: a high NNT indicates a less effective treatment, and may render the intervention prohibitive. For more information on the NNT and how to calculate it, the reader is referred to: http://en.wikipedia.org/wiki/Number_needed_to_treat

Effect size, statistical power, and sample size are inter‐related. The power analysis determines the number of subjects needed in a study to detect a statistically significant difference with an appropriate effect size. Statistical power of 80% (0.8) is generally accepted, meaning that 80% of the time, the researcher will avoid Type 2 error (β), where the researcher fails to reject the null hypothesis when there is a difference between groups. Power analysis is usually based on the results of previous studies when the mean differences and SDs are known. In some cases, statistical power can be determined after conclusion of a study in a “post hoc” manner, although determining statistical power before a study begins in an “a priori” manner to estimate sample size is preferred and expected.

A small sample size may demonstrate a lack of statistically significant different results, but still provide results with clinical significance. Even a study powered at 80% still has a 1 in 5 chance of creating a Type 2 error (false negative).⁷ A small sample size limits statistical power; while larger sample sizes provide more power to detect statistically significant differences. While larger sample sizes are obviously preferred in a clinical study to capture a true representation of the clinical population being studied, larger samples sizes can lead to statistically significant differences that remain clinically insignificant.

Confidence Intervals

One of the most meaningful, yet misunderstood and underutilized statistics in interpreting clinical research may be the confidence interval (CI). The CI is the certainty that a range (interval) of values contains the true, accurate value of a population that would be obtained if the experiment were repeated. Fortunately, more researchers and reviewers are using CIs to report results of clinical trials in the literature; however, clinicians need to understand the clinical interpretation and value of reporting the CI.

Confidence intervals are appropriate for reporting the results of clinical trials because they focus on confidence of an outcome occurring, rather than accepting or rejecting a hypothesis.¹⁸ In addition, the CI provides information about the magnitude and direction of an effect, offering more clinical value than answering a hypothesis‐based question. Greenfield et al¹⁹ noted that CIs “are statements about belief in the statistical process and do not have probability implications.” Rather, probability would be determined by interpretations of statistical significance. In contrast, CIs offer more precision of the estimate of the true value of an unknown because it includes the range of uncertainty.

The CI represents the researchers level of confidence that the true value in a representative population is contained within the interval. From a clinical perspective, the CI is the likely range containing the value of a true effect of treatment in an average subject.⁶ A CI is reported as a range or interval describing the lower and upper values (“boundaries”) of uncertainty, also known as the “margin of error.” While some clinicians assume that the CI represents the range of scores (i.e., subjects improved by up to the value of the upper boundary or declined by the value of the lower boundary), this is not correct. Furthermore, the CI should not be confused with standard deviation, which is used to describe the variability of a mean score within a sample. CIs are reported with a “point estimate” (PE) from the sample tested from the population. The PE is a specific value (which may be a sample mean, difference score, effect size, etc), but does NOT represent a “true” value; rather, it represents the “best estimate” of the true value from the average of the sample²⁰ and should be viewed in consideration of the range of the CI. CIs are based on a specific level of confidence. Most CIs are calculated using 95% confidence, meaning if the experiment were repeated 100 times, the true value would be obtained within that interval 95 times. However, Hopkins⁶ recommends using a CI of 90%, which provides a wider interval and greater margin of error.

In the literature, researchers report the PE and interval, and a range of uncertainty (CI) with a confidence level, which may be reported by, “mean value = 0.3 (95% CI, ‐0.1 to 0.7)”. A CI may also be reported as a “+/‐” value, such as 0.3 +/‐ 0.4. Clinically interpreted, these notations would infer: The between group difference in this study sample was 0.3, with the true value represented in a range of ‐0.1 to 0.7 in the population. Subsequent notations within a manuscript may simply report the point estimate and CI, as in, “0.3(‐0.1,0.7).” Clinical researchers are encouraged to clearly report descriptive means and standard deviations along with mean differences, effect sizes, and CIs, as suggested in Table 2.

Table 2.

Suggested format for reporting data in clinical studies

	Mean ± SD
	Pre	Post	Mean Diff ± SD	% Diff	Effect Size	CI (95%)	p‐value
Experimental
Control

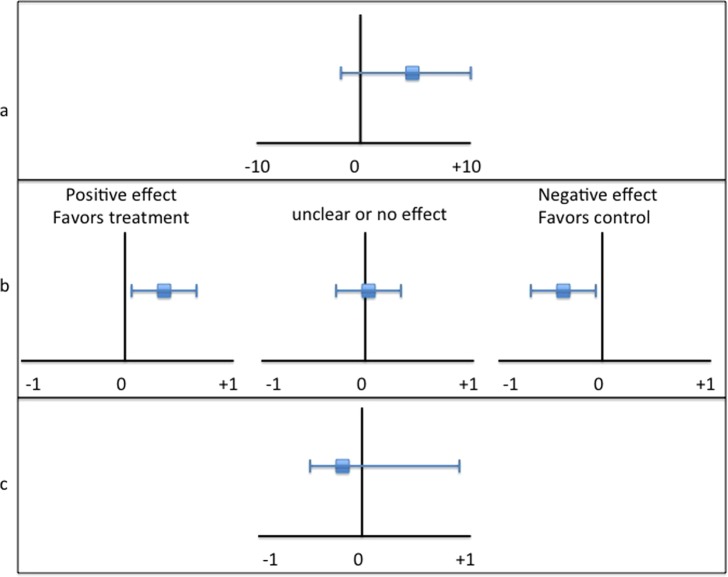
Graphical representation of CIs often helps demonstrate their clinical value and interpretation. Figure 2 provides and example of several types of graphs representing point estimates and CIs. A line graph (Figure 2b) is typically recommended because of its ease of interpretation and comparison.

Figure 2.

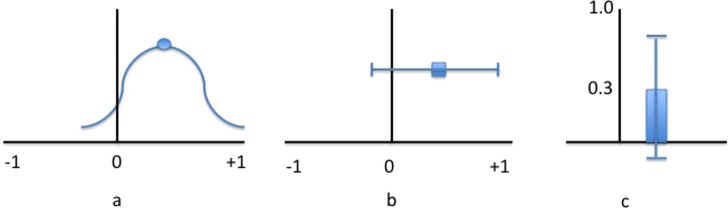
Confidence intervals presented as a curve graph (a), line graph (b), and bar graph (c), each representing a point estimate and CI of 0.3(‐0.1,0.7).

Unfortunately, some authors do not report CIs; however, several free calculators are available online, including one from PEDro (http://www.pedro.org.au/english/downloads/confidence‐interval‐calculator/). The CI is calculated from the representative sample value (PE), the standard error of the mean, and the “confidence coefficient,” which is determined from the z‐value corresponding to sample size and a specific confidence level (for example, a 95% CI generally has a 1.96 confidence coefficient value). The CI is determined by using the formula:

CI = Point estimate +/‐ confidence coefficient * standard error.

Therefore, the upper and lower bounds of the CI represent the equivalent “+/‐” of the confidence values. The standard error is calculated by the standard deviation divided by the square root of the sample size. The smaller the standard error of the mean, the narrower the confidence interval, and the more accurate the estimate.

There are several things to consider when evaluating a CI for assessments of clinical significance, including the type of point estimate; value and location of the point estimate and CI relative to zero; harm/benefit potential; the width and symmetry of the CI; and the MCID.

Type of point estimate

Point estimates and CIs can be used to demonstrate several types of outcome values, including sample means, group differences, effect sizes, and odds/risk ratios (Figure 3). It's important to note what the PE represents when interpreting a CI. Evaluating a mean difference within a CI is different than evaluating an effect size with a CI.

Figure 3.

Graphical representation of different types of CI: point estimate (a); effect size (b); odds ratio (c).

For example, interpreting the CI of a mean value of a sample is relatively straight‐forward; the CI represents the range of possible values containing the true value of the population. For CIs representing effect sizes and differences between groups, interpretation requires more considerations. The PE of an effect size provides the context to help determine if the result is strong or weak, as well as whether it is clinically useful¹⁹. The location and size of the CI also are important to consider.

Point estimate and CI relative to 0

The relationship of the point estimate and CI to zero provides valuable information in CIs representing effects or group differences. Obviously, point estimates further from 0 represent more effect or difference, either positive or negative. Similarly, the closer to 0, the less group difference or effect. Interestingly, CIs can be used with hypothesis testing and are therefore related to statistical significance. If the CI of a mean difference, effect size, OR, or RR does not contain a value of 0, the results are significant. Other types of point estimates, such as sample means, may contain 0 and still be significant statistically. It's important to note that studies with large effect sizes and small CIs that do not cross zero have the most clinical significance.

Harm/Benefit potential

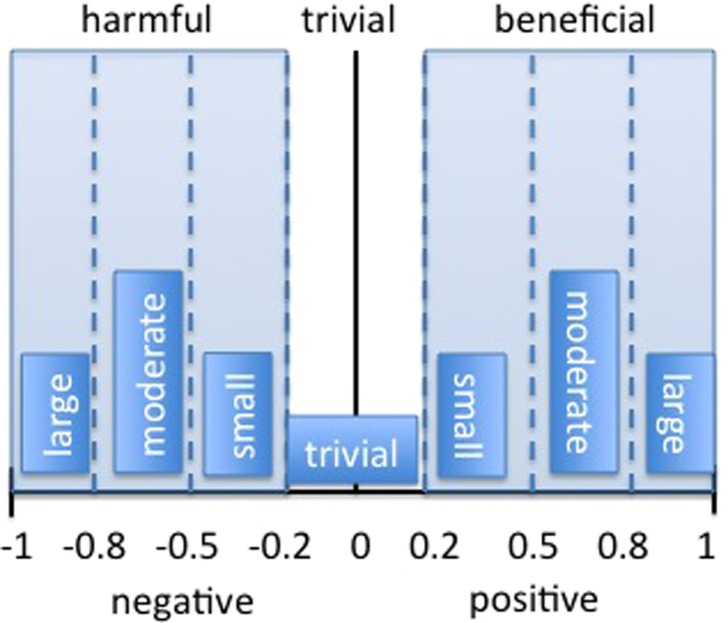
Using Cohen's d‐value (discussed earlier) or standardized effect sizes, the PE and CI can provide information on the magnitude and direction of the effect as well as potentially beneficial or harmful effects. The location of the point estimate determines if the outcome is considered harmful, beneficial, or trivial¹ (Figure 4). A positive effect size greater than 0.2 is considered beneficial, while a negative effect size less than ‐0.2 is considered harmful. Effect sizes between ‐0.2 and 0.2 are trivial in size.

Figure 4.

Harmful, trivial, and beneficial ranges within a CI representing effect sizes. Adapted from Batterham & Hopkins².

Width and symmetry of the CI

The width of the CI provides clarity regarding the magnitude of the treatment effect or group differences. A wide CI (usually representing a small sample size) has more uncertainty and may suggest that study findings are unclear if it spans all 3 levels of magnitude (harmful, trivial and beneficial). With small sample sizes, CIs are more important than examination for statistically significant differences, which are affected by sample size. In contrast, large samples yield narrow CIs, which help clinicians determine the smallest amount of benefit to justify therapy within a smaller margin of error. When interpreting a study result with CIs, an outcome may be statistically insignificant and yet clinically significant in a wide CI. For example, consider a between group difference CI of 0.8(‐3,19) in a small population. While the CI contains 0 (statistically insignificant), the CI remains relatively large, particularly in the positive range; therefore, the conclusion should be that the intervention might be beneficial, but larger sample sizes are needed.

While the difference between the point estimate and the upper and lower boundaries is usually equal (the “+/‐” value), the CI may not be symmetrical. For example, when the CI of odds ratios are reported, there is a natural skew in the interval because the CI is calculated on a natural log value. In this case, the actual upper and lower boundaries of the CI would be reported, rather than using a “+/‐” value with the point estimate.

MCID

It's helpful to know the MCID when interpreting the CI. By comparing the treatment outcome with the MCID, clinicians can determine if the treatment will be beneficial or harmful to their patients. Combining the MCID with the CI is a very valuable strategy to be utilized for clinical interpretation, especially when hypothesis testing reveals no statistically significant differences.

If the MCID falls within the CI, the treatment may be clinically effective regardless of the PE. Recall that the CI represents the range of values in which the true value exists within a population if the study were repeated. Obviously, if the PE exceeds the MCID, the treatment was effective. In the between group differences CI example described previously, 0.3(‐0.1, 0.7), if the MCID is known to be 0.2, the treatment may be clinically effective since it exceeds the point estimate. If the MCID falls within the CI, yet remains below the point estimate, the clinician needs to decide if the treatment is appropriate or not. In an example of a clinical trial, two groups of patients with shoulder pain were compared: one received traditional therapy (control group) for 6 weeks, while another group (experimental) received a different therapy for 6 weeks. A primary outcome of shoulder external rotation range of motion (ROM) was measured before and after the treatment and compared within and between groups (Repeated‐Measures ANOVA for statistically significant differences). The experimental group increased in their external rotation ROM on average from 60 to 68 degrees (a difference of 8 degrees), while the control group increased from 60 to 64 degrees (a difference of 4 degrees); therefore, the mean difference between groups is 4 degrees. The statistical analysis revealed no significant difference between groups; however, clinical interpretation of the results may lead to a different conclusion.

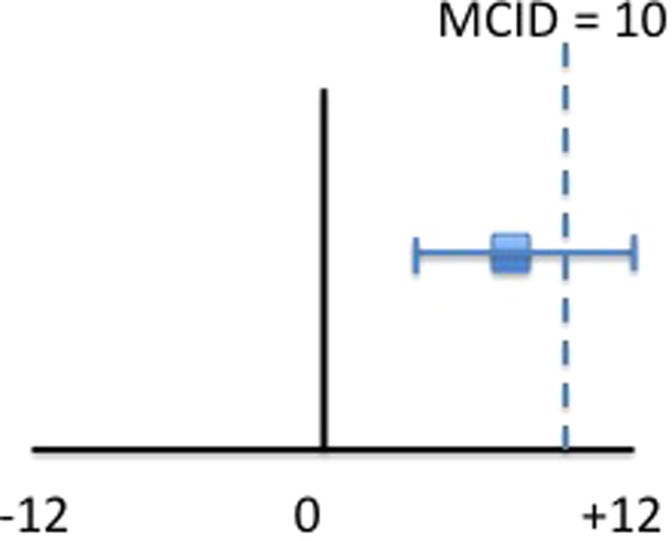
Assume an increase of 10 degrees of external rotation ROM would be the MCID to convince a clinician to change their treatment. In the clinical example above, the mean increase in external rotation ROM in the experimental group was 8 degrees, falling below the MCID, which may not be enough for a clinician to change their treatment. However, if the CI was (4,12), note that the MCID (10 degrees) still falls within the CI; thus it is possible for some patients to reach and even exceed the MCID to 12 degrees (the upper bound of the CI) (Figure 5). If the confidence interval is not harmful and beyond trivial, clinicians might consider the treatment in some patients. The clinician may consider that while the point estimate of the sample did not reach minimal clinical importance, the CI still contains the MCID within the true population, and further research with larger samples are warranted.

Figure 5.

Line graph of CI 8(4,12) and MCID of 10. Note that the CI still contains the MCID; therefore, the treatment may be beneficial but a larger sample is needed.

It is important to consider the population being studied when interpreting CIs. For example, Hopkins et al²¹ discussed how competitive elite athletes value very small percentages of improvement for performance enhancement: a 1% increase in speed during a 100 meter sprint may be the difference between first and second place. They suggested that laboratory‐based studies or studies on non‐elite athlete cohorts cannot be generalized for performance enhancement of elite athletes, and recommended reporting percent changes as well as confidence intervals for utilization in performance enhancement outcomes. For example, if a 1% improvement is meaningful, and a RCT shows no significant difference between two groups of elite athletes, but the CI contains the meaningful improvement (eg, 0.5 to 1.5%), there exists a possibility that an athlete would benefit from the intervention. In contrast, a CI that does not contain the meaningful difference (eg, 0.1 to 0.9%) may not be worthy of using even if the results were statistically significant.

Meta‐analyses use CIs to describe the effectiveness of treatments by pooling data from several homogenous studies in an effort to pool standardize effect sizes, often using Cohen's d‐value or other standardized difference. Most meta analyses use a “forest plot” rather than a bell‐shaped curve to graphically represent the effects of various studies. Forest plots use lines or bars to represent various CIs of different studies and a “summary point estimate,” representing the overall effect of the pooled studies. This type of graphical representation (Figure 6) is often useful to get the “total picture” of the multiple studies contained within in a meta‐analysis.

Figure 6.

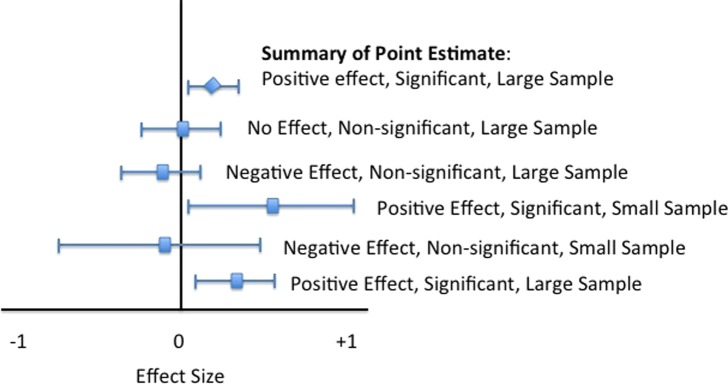
Forest plot used in meta‐analysis studies to summarize the effects of different studies.

MAGNITUDE‐BASED INFERENCES

Because of the aforementioned limitations of hypothesis testing in clinical research, researchers are slowly moving away from relying solely on hypothesis testing to interpretation of other outcomes in clinical studies. Magnitude‐based inferences (MBI) are now being used to avoid limitations of traditional statistical analysis (null and directional hypothesis testing) in relation to clinical significance.⁶

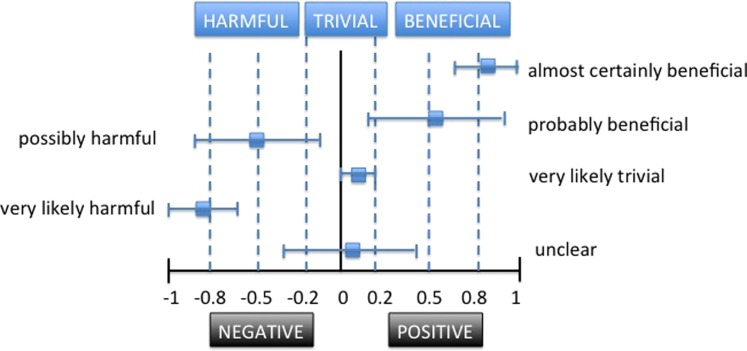
Magnitude‐based inferences use qualitative rather than statistical descriptions of study outcomes. Confidence intervals can provide magnitude of differences or effect through MBI. As stated earlier, Batterham and Hopkins¹ suggest three levels of magnitude of change: harmful, trivial, and beneficial. Obviously, these three levels are important for clinicians to consider when making evidence‐based decisions; the location and width of the CI on an outcome continuum can be clinically interpreted using these three levels. The outcome continuum should include the threshold value for beneficial (MCID, MIC, etc) as well as harmful outcomes.

Hopkins et al⁶ recommend more qualitative statements (such as “probably,” “possibly,” and “likely”) to reflect the uncertainty of the true value, while avoiding the use of “statistical jargon.” These qualitative terms can be combined with the three levels of magnitude (beneficial, harmful, trivial) in order to further refine the possible outcome value represented by the CI (Figure 7). Traditional statistical packages do not provide magnitude‐based inferences; instead a spreadsheet can be used to assess and infer the clinical magnitude.²² Obviously, the MBI that represent harmful or beneficial outcomes provide more clinical information for decision‐making than simply stating, “There was no statistically significant difference.”

Figure 7.

Using Magnitude‐based inferences to describe CIs and clinical relevance.

In their article, Batterham and Hopkins¹ summarize the value of MBI in clinical interpretation of research:

“A final decision about acting on an outcome should be made on the basis of the quantitative chances of benefit, triviality, and harm, taking into account the cost of implementing a treatment or other strategy, the cost of making the wrong decision, the possibility of individual response to the treatment, and the possibility of harmful side effects.”

CLINICAL INTERPRETATION

Understanding and interpreting CIs can help clinicians make better decisions. As opposed to laboratory experiments when conditions and variables are well‐controlled, clinical research is often confounded by subject variability, measurement error, and smaller sample sizes, among other factors. Therefore, reliance on hypothesis testing is of limited value in clinical research. A more practical and useful method of analysis in clinical research utilizes confidence intervals and magnitude‐based inferences. Table 3 provides a checklist for clinical interpretation of rehabilitation research.

Table 3.

Checklist for clinical interpretation of rehabilitation research

	Internal Validity	Appropriate research design Review for sources of bias
	External Validity	Protocol explained and reproducible Relevant Population
	Statistical Power	Adequate sample size reported
	Outcome Measures	Valid & Reliable measures Minimal clinically important differences noted
	Descriptive Statistics	Mean, standard deviation, percent change and standardized values reported
	Effect Sizes	Standardized and reported
	Confidence Intervals	CI used to report means, group differences, effect sizes and/or odds ratios
	Magnitude Based Inferences	Outcomes reported in terms of trivial, harmful, or beneficial using MBI descriptors

Suggestions for researchers and clinicians to improve clinical interpretation of published research include:

1. For validity, provide details on study design, especially specific treatment protocols that are reproducible, including the prescription and progression. Use the PEDRO scale (http://www.pedro.org.au/english/downloads/pedro‐scale/) to guide internal validity.

2. Provide power analysis (preferably a priori) to ensure appropriate sample size to avoid a Type 2 error.

3. Report magnitude of change in percentages as well as absolute and standardized values.

4. Report effect sizes using standardized mean differences (Cohen's d), odds ratio, or risk ratio calculations using representative terms such as trivial, small, moderate, and large.

5. Use CIs to report point estimates including mean differences and treatment effect. Rather than simply stating, “p<.05”, state, “the treatment improved ROM by an average of 10 degrees with a 95% CI between 5 and 15 degrees.”

6. Provide clinical interpretation of the CI with regards to the point estimate and width. For example, “While statistically insignificant, the findings are unclear and larger study samples are needed.”

7. Provide results relative to clinically meaningful differences or minimal clinically important changes.

8. Provide results in terms of magnitude‐based inferences where possible, using terms relative to harmful, beneficial, or trivial, including qualitative terms such as “probably” and “almost certainly.”

CONCLUSION

Clinical researchers need to present clinically meaningful results, and clinicians need to know how to interpret and implement those results in their evidence‐based approach to clinical decision making. Interpretation of clinical research outcomes should not be based solely on the presence or absence of statistically significant differences. Because of the heterogeneity of patient samples, small sample sizes, and limitations on hypothesis testing, clinicians should consider other clinically‐relevant measures such as effect size, clinically meaningful differences, confidence intervals, and magnitude‐based inferences.