Water-tight membranes from neuronal morphology files

Abstract

We present an algorithm to form watertight 3D surfaces consistent with the point-and-diameter based neuronal morphology descriptions widely used with spatial electrophysiology simulators. Such morphology descriptions are readily available online and may come from light-microscopy tracings or from an artificial cell grown algorithmically. These files contain only limited information about a neuron’s full three-dimensional shape, as they consist mostly of a list of points and diameters with connectivity data. This representation is well-suited for electrophysiology simulations, where the space constants are larger than geometric ambiguities. However, the simple interpretations used for pure electrophysiological simulation produces geometries unsuitable for multi-scale models that also involve three-dimensional reaction-diffusion, as such models have smaller space constants. Although one cannot exactly reproduce an original neuron’s full shape from point-and-diameter data, our new Constructive Tessellated Neuronal Geometry (CTNG) algorithm uses constructive solid geometry to define a plausible reconstruction without gaps or cul-de-sacs. CTNG then uses “constructive cubes” to produce a watertight triangular mesh of the neuron surface, suitable for use in reaction-diffusion simulations. CTNG provides the correspondence between internal voxels and surface triangles, needed to make connections between cytoplasmic and membrane mechanisms. Optimization of the underlying marching cubes algorithm and distance calculations optimized the performance of constructive cubes for a neuronal geometry, where a large number of small objects sparsely occupy a large volume.

1 Introduction

¹ Neural dynamics involves continuous interactions of chemical and electrical changes, both of which depend on the morphology of the neuron. Although researchers have been creating digital mappings of neuronal morphologies for decades, and recently began sharing them in databases such as NeuroMorpho.Org, these mappings have generally focused on the measures needed for replicating electrical activity (diameters and lengths) and have not focused on more detailed measures required for detailed chemical simulation. This neglect is a natural consequence of the history of computational neuroscience, which has focused on electrical activity, putting aside the more complex and inaccessible chemical signaling.

The traditional interpretation of these measures effectively reconstructs a neuron as a series of truncated cones, or frusta, based on interpolations between the points where diameter measurements were made. These measures directly provide 1-dimensional distance and topological connectivity. Higher-dimensional derived values, surface areas and volumes, are then calculated based on the frustum assumption. Importantly, this assumption does not provide any definition of the shape of a branch point, of the soma, or of how the dendrites arise off of the soma. Such details are not needed for electrical simulation where small variation in diameter has less effect on longitudinal conductance than diameter measurement error, and where any error in branching angle will have no effect at all.

By contrast, simulations that also incorporate intracellular chemical diffusion must utilize far smaller space constants and will be more affected by local geometry [16]. The most accurate simulations in this domain utilize detailed reconstructions of neurites based on serial electron microscopic (EM) sectioning. Although techniques are improving, technical complexities typically limit such reconstructions to portions of neurons instead of whole cells. Even with extensive reconstruction, detailed chemical simulation is difficult due to the heavy computational loads required to manage multiple chemical species which may interact after moving a few nanometers across spaces that are measured in microns and tens of microns. The space constants are very small relative to the spanned spaces. For this reason, detailed reaction-diffusion simulators such as MCell (mcell.cnl.salk.edu), Smoldyn (www.smoldyn.org), and STEPS (steps.sourceforge.net) are typically applied to small volumes. Thus an alternative strategy is needed for incorporating large-scale reaction-diffusion phenomena in electrophysiology models.

Here we describe an algorithm, Constructive Tessellated Neuronal Geometry (CTNG), that provides such an intermediate reconstruction for when no full EM reconstruction is available. CTNG defines a watertight surface (and therefore volume) consistent with point-and-diameter data from light microscopy tracings. Note that a neuron’s cross-sections are in general not convex, and the actual surface contains arbitrary dips, protrusions, and irregularities. These cannot be reconstructed by CTNG or any other algorithm as not only are these not recorded in the source data but they cannot be recorded as they are smaller than the resolution of light microscopy. Instead, we use a general notion of smoothness to determine the adequacy of a particular reconstruction. As such, CTNG’s reconstructions are appropriate for simulations when the underlying dynamics are insensitive to such variations.

For mesoscale simulations studying chemical-electrical interactions in full neurons or networks of neurons, simply abutting frusta as is often done for pure electrophysiology simulations is inadequate: that approach defines a volume plagued with gaps, overlaps, and extrusions. Some simulators avoid these continuity issues by discretizing the frusta independently and logically connecting the compartments at the end faces. This preserves continuity but loses the details of angles at dendritic joins, and at the joins between soma and dendrites. Cellular chemical dynamics often happens on a spatial scale of the same order as these variations [9]. Like changes in electrical impedance that occurs with widening and narrowing of a cable (whether real or an artifact of measurement error), geometry variations will alter the dynamics of reaction-diffusion signaling [8].

CTNG avoids these issues via a two step process. In the first step, it defines a shape connecting two consecutive points not just on their point-and-diameter information, but also on the information from their neighbors. This shape is similar to, but slightly more complex than, the frusta used by electrophysiology simulators and is expressed using constructive solid geometry. In the second step, a variant of constructive cubes approximates the neuronal surface, expressed as the union of a set of oriented triangles.

CTNG’s detailed constructive solid geometry approach (connecting frusta, adding ball-wedges, intersecting with half-spaces) may seem overly fastidious given the low accuracy of diameter measurement, missing raw-data detail at branch points, and the rarely-circular cross-sections of dendrites. We can expect morphology information to become progressively more detailed with development of improved light and electron microscopy and greater use of automated methods. However, there will continue to be a need to develop heuristics for dendritic branch morphologies for the foreseeable future, and we will enhance CTNG as such information becomes available. By determining morphological structure prior to numerical discretization, CTNG makes it convenient to determine, and then reduce, numerical discretization errors by varying spatial discretization without modifying the fixed geometrical structure.

2 Methods

Morphologies were either specified manually or imported via NEURON’s Import3D tool from reconstructions available at NeuroMorpho.Org [1]. Surfaces as defined in the following sections were calculated in custom code written in a combination of C, Python, and Cython; they were triangulated with the marching cubes algorithm [13] and rendered with Mayavi (code.enthought.com/projects/mayavi).

Timings were performed in a VirtualBox (virtualbox.org) virtual machine running Linux Mint 13 (linuxmint.com) with access to six Intel Core i7 860 cores (2.8 GHz) and 5.9 GB of RAM running in a Windows 7 Host with 8 GB total memory.

Surfaces computed by NETGEN (www.hpfem.jku.at/netgen) were exported to STL and rendered with STL Viewer(stlviewer.sourceforge.net). Multiple views were saved and then combined in GIMP (gimp.org) to form the final image.

3 Results

In this section we give an overview of the Constructive Tesselated Neuronal Geometry (CTNG) algorithm. Subalgorithms for individual steps are given in moderate detail in the following sections. While going through the detailed algorithm, the reader may find it helpful to come back to this section or to the code to be reminded of where a particular piece stands in the context of the algorithm as a whole. The commented code, available at ModelDB (senselab.med.yale.edu/modeldb/ShowModel.asp?model=146950), has comment-keys that reference the subsections of the paper (order of presentation is slightly altered for explanatory ease). These comment-keys can be are of the form CTNG:main, a string that can searched for in the code (comment-keys are used instead of line numbers since the latter will shift with future bug fixes and enhancements).

CTNG provides one possible path for reconstruction of a consistent, continuous surface from the stylized point-and-diameter neuronal morphology data produced by manual or automated tracing from light-microscopic images [7], or created using synthetic generation [2, 6]. Such neuronal morphologies can be obtained from online databases such as NeuroMorpho.Org [1]. The traditional interpretation of point-and-diameter morphology utilizes a frustum for each pair of consecutive points. The basic frusta rule produces a volume suitable for electrical simulations which do not depend too strongly on small errors in the geometry. It does not however describe a physically-realizable volume. Wherever two non-parallel frusta share a common face center point, some of the same points will lie in both objects, the union of their boundaries will contain points inside the union of the volumes, and the union of the boundaries will not be water-tight due to a gap between the frusta end-faces.

The overall algorithm is a two step process, either of which could potentially be used independently, and both of which will be somewhat familiar from computer animation. The first step is to define a three-dimensional geometry from a stylized representation. We use a technique called constructive solid geometry (CSG) which represents a geometry as the unions and intersections of three-dimensional graphics primitives; this representation is also used in computer graphics [19]. The second step is to tessellate the surface with a triangular mesh using a variant of constructive cubes [5]. At this point we diverge from video games since we are interested in the integrity of the continuous surface whereas video games need only concern themselves with surface that is visible from a particular viewpoint.

Our CSG rules start with the standard frusta, but utilize novel join rules to avoid boundary-union discrepancies. With the traditional approach, each frustum is considered in isolation; this does not permit creation of meaningful joins. Instead, we must consider two adjacent frusta as a unit. Therefore, instead of considering only the two points that define the individual frustum, we consider three at a time: the common join-point between neighboring frusta and the points on either side. Two key join conditions allow us to choose the shape of the join between the frusta. First, acute angle bends need to be treated differently from non-acute bends. Second, we must consider the projection of the frusta onto the plane defined by the three points, and count the number of exterior corners at the join. Having classified the joins, we can then either connect exterior corners with a ball-wedge or by intersecting the frustum with a half-space (set of points on one side of a plane). This choice is fairly complicated and is described in detail below.

Unlike the point-and-diameter tracing used with dendrites, cell somas are traced around a two-dimensional contour and must therefore be reconstructed differently. These are reconstructed from the outline using sheared frusta. We slice the outline orthogonally to its major axis at even intervals. We interpret each slice line as a diameter of a circle lying orthogonal to the outline’s major axis. Finally, we connect consecutive pairs of circles with a sheared frustum. As the circles lie in parallel planes, the sheared frusta connect without gaps or overlaps.

Although we now have a neuronal volume that is described as unions and intersections of objects – frusta, sheared frusta, cylinders, wedges of balls, and half-spaces – we have still not entirely solved the problem. We still have to locate the neuronal surface by locating the boundaries of these objects. While doing this, we have to distinguish those parts of the boundary surfaces that form the neuron surface from those parts that are superfluous and end up laying inside. To do this, we use a specialized version of a constructive cubes algorithm. Constructive cubes generates a scalar field of signed distances to the surface of an object, in this case a neuron. It then uses marching cubes, an algorithm for constructing a triangular mesh of a surface of constant value within a scalar field, to find the locations where the distance is zero; this set is the surface. A full-volume marching cube process is untenable because the full neuron can be thousands of times longer than its smallest dendrite, generating an enormous set of sample points. We therefore utilize a two-step optimization. Step 1: we locate voxels containing the boundaries of the objects defining the neuron. Starting with one such boundary voxel, we do a flood fill on the boundary. The neuron’s surface is contained entirely in a subset of these voxels, so any others need not be tested by marching cubes. This process eliminates over 99.9% of voxels from consideration. Step 2: we simplified the remaining distance calculations needed for marching cubes by dividing the space into rectangular prisms to identify which objects nontrivially intersect which prisms. In the interior of a given prism, only those objects that intersect that prism can contribute to neuronal surface; all other objects can be safely ignored when calculating the distance field.

After application of marching cubes, we now have a triangularized water-tight representation of the neuron’s surface. From this representation, we can easily determine surface areas which are essential for calculating the magnitude of ion fluxes across the membrane and relate these fluxes to changes in concentration in the underlying cytoplasm. The water-tight nature of our surface also allows the use of meshless stochastic diffusion simulators without the risk of ions leaking out of the cell.

3.1 Inadequacy of frusta

Neuronal tracing methods remain largely manual. For this reason, data collection is restricted to relatively sparse fiduciary points – a transformation to a tree structure where each node of the tree has a location and a diameter (point-and-diameter representation). The operator scans along a neurite, marking locations when the operator subjectively feels that the degree of curvature or change in diameter warrants it. Branch points are also noted. Depth measurements, normal to the plane of section, are grossly made by using depth-of-focus, allowing the operator to follow neurites up and down. Measurement in depth is both less accurate and more difficult than measurements made in the plane. Therefore diameter is always measured only in the plane, with no effort to determine rotational asymmetries. The final data gathered from this process is a discrete sampling of the tree in which each sample is the (x, y, z) location of the center of a dendrite and its diameter. These sparse data are subsequently processed by algorithms that to a greater or lesser degree preserve the original area, shape, and geometrical consistency. The traditional approach is to concatenate frusta, each of which corresponds to a segment of neurite possessing a central axis with linear interpolation between 2 different diameters (a cylinder if the diameters are the same).

This approximation becomes a problem when one wishes to use the traced structures for simulation of reaction-diffusion problems. Numerical simulation of a reaction-diffusion problem requires a fully-defined geometry. Gaps in the geometry, produced by inadequacies in gridding, become artifactual diffusion barriers. Holes become sinks. Given the spottiness of the geometrical dataset, we require a geometry that is both consistent with the data and free of gaps and holes. Ideally this geometry would also 1. conform to the general appearance of neurons (a gestalt or aesthetic criterion that can be partially expressed as reducing the magnitude of discontinuities in the first spatial derivative); 2. be well-suited to gridding of both the volume and the surface; 3. prepare the association between the volume and surface grids. Although it is possible to use overlapping grids [14], the most straightforward simulation algorithms rely on non-overlapping meshes where each point in the domain belongs in only one compartment. Although any attempt to invert the transformation from neuroanatomy to point-and-diameter dataset is necessarily an approximation, well-defined external boundaries are necessary for either integration strategy. We now describe our rule for creating such a boundary.

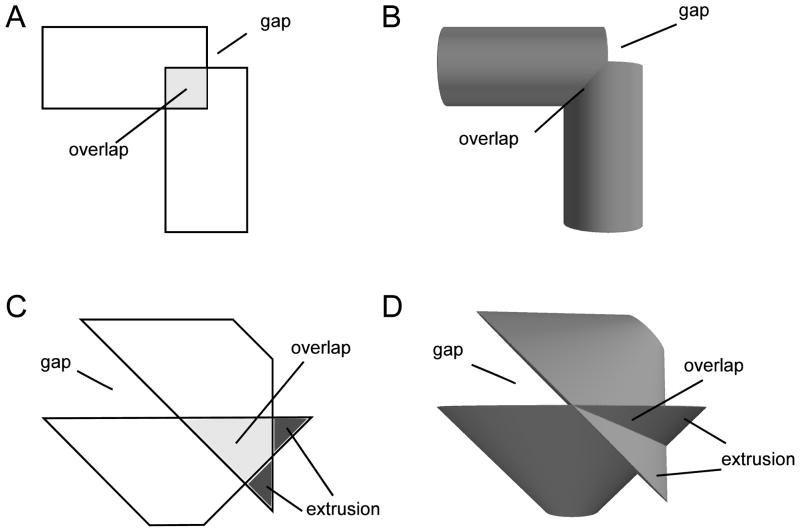
Given three consecutive points P, Q, and R, we create a frustum with axis $\overrightarrow{PQ}$ and a frustum with axis $\overrightarrow{QR}$. If P, Q, and R, are collinear, then the axes are parallel, and the frusta share faces at Q. In that case, the frusta define a consistent geometry. However, if P, Q, and R are not collinear, then the frusta’s boundary planes at Q intersect at an angle. Now the frusta have a non-trivial intersection and a union with a gap where the boundary face of one frustum is not directly connected to the neighboring face (Fig. 1). Projecting to the plane that passes through Q with normal vector $\overrightarrow{PQ}\times \overrightarrow{RQ}$, the frusta become isosceles trapezoids (Fig. 1C). In this projection, certain values of join angle and tapers will produce an overhang or extrusion where one or both of the non-gap join corners do not lie inside the other trapezoid.

Figure 1.

Gaps, overlaps, and extrusions arise in both 2D (isosceles trapezoids: A, C) and 3D (frusta: B, D). The measured join location is shared by the face center points of both objects. When two non-parallel sections with constant radii meet (A, B), some portions of the sections necessarily overlap; in other spots the edges will fail to meet, leaving a gap that exposes the face. If the radii decrease away from a non-parallel join (C, D), in addition to the gap and overlap problems, some portions of the sections may extrude beyond the other section.

When longitudinal electrical conductance values and transmembrane conductance and capacitance are derived from these shapes, ambiguities at the joins have negligible effect, although these do show up as discrepancies of voltage traces using different simulators (e.g., compare the pyramidal cells in the Fortran and NEURON (www.neuron.yale.edu) implementations of senselab.med.yale.edu/ModelDB/ShowModel.asp?model=45539). Such deviations are minimal because electrical joins are made through zero-resistance connections that reach across any gap between locations where the adjoining frusta are determined to end. Hence, discrepancies only occur due to different interpretation of the degree of tapering at an end. For electrical simulation, variations of the rule as to how far the one frustum should be extended into the space occupied by the other will only change longitudinal conductance by very small amounts. By contrast, choices of join morphology will have profound effects on reaction-diffusion simulation and may render the simulation invalid. For example, an extrusive cul-de-sac will provide an artifactual small space which will bring reactants together. Conversely, an artificial barrier will prevent diffusion and reduce reaction. Redundant space, from double-counting at overlaps, will make it impossible to assign substance flux correctly.

3.2 Filling gaps and removing overhangs and extrusions

Interpreting branch points where three or more frusta meet as the union of all pairwise joins reduces the higher-order problem of constructions of the neuron’s surface to the problem of creating two-frusta joins without gaps, overhangs, or extrusions. We further simplify by assuming a uniquely defined diameter at any point. This neglects both the possibility of non-circular dendrite cross-sections and the ambiguities introduced at branch points, where each branch may have been independently measured, resulting in nonuniformity due to measurement error. If no measurements were made immediately adjacent to a bifurcation, then these bifurcation diameters are undefined and must be estimated based on the diameter nearest to the bifurcation. If the unique diameter assumption is not satisfied, bifurcations may be transformed by resetting the diameters to the largest diameter, generally the parent dendrite. The other dendrites then quickly taper to their intrinsic diameter by the next measured point which is typically within a few microns. This transformation prevents any unrealistic abrupt changes in the local membrane area: in a Y-shaped branch, the sum of the areas of the child branches near the branch point will be approximately the same as the area of the parent branch near the branch point. The areas of the children near the branch are thus about half the area of the cones, which is intuitively clear as the other half would lie inside the other child. For simulations with 1D electrophysiology coupled to 3D reaction-diffusion, the local 1D membrane area should thus be based off of the CTNG results and not the cones, as the cones would overstate the local membrane area. CTNG will still produce a water-tight surface at branch points with multiply defined diameters, but in this case, the local area may change abruptly at the branch point, leading to flat faces that fill in the gaps. This issue is illustrated in Fig. 2.

Figure 2.

(A) If the diameters are not unique at a join, a flat face fills in the missing area, but this is a diffusion barrier and increases the local surface area. (B) If the diameters are made unique by taking the largest surface area, there is still a increase in the local surface area as CTNG connects the pieces, but abrupt discontinuities are avoided.

Given the single diameter assumption, two parallel frusta meeting at a join have identical faces: there is no gap, overhang, or extrusion problem at that join. Problems arise when the frusta are not parallel. Suppose frusta f_l runs from p₀ to p₁ and f_r from p₁ to p₂ with r_i the radius at point p_i. Let a_ℓ = (p₁ − p₀)/|p₁ − p₀| and a_r = (p₂ − p₁)/|p₂ − p₁| be the normalized axes. Let A be the plane containing the axes. Then the vector n = a_ℓ × a_r is nonzero as the frusta are nonparallel and lies perpendicular to each axis: n is the vector normal to plane A at p₁. The cross-sections of the frusta in A are overlapping isosceles trapezoids. The vectors r_ℓ = (n × a_ℓ)/|n × a_ℓ| and r_r = (n × a_r)/|n × a_r| lie in the plane A normal to the axes a_l and a_r, respectively. Thus the corners of the bases of the trapezoids near the join are c_ℓ,± = p₁ ± r₁ a_ℓ and c_r,± = p₁ ± r₁ a_r, respectively.

In our algorithm, two frusta are joined according to rules that depend solely on the shape of their projection frusta on A. Remarkably, the 2D projection adequately describes all cases and makes it easier to see how each can be individually handled. Additionally, the two-dimensional join problem of trapezoids on A is interesting in itself. We begin by focusing on what happens on the plane, and then demonstrate that these rules extend naturally to the third dimension.

3.3 Two dimensional solution

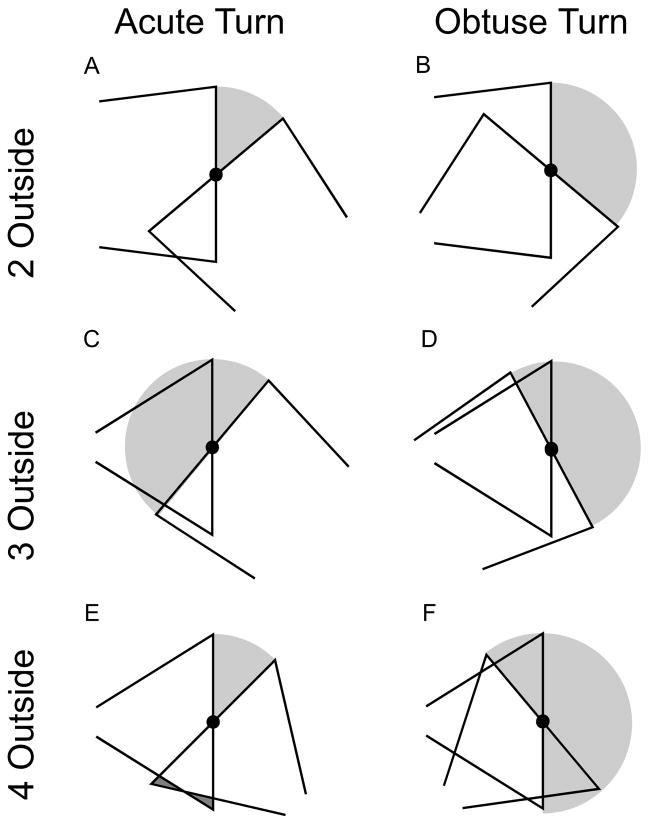
We can classify joins based on two properties: 1. the sign of the dot product between the axes (CTNG:joinangle), and 2. the number of corners lying outside the other trapezoid (Fig. 3) (CTNG:outsidecorners). If a_ℓ · a_r is positive, this corresponds to an obtuse turn (Fig. 3A–C). If the dot produce is negative, it is an acute turn (Fig. 3D–F). If a_ℓ · a_r = 0, (right angle), we process it as if it was positive. Note that these vectors are defined in the direction away from the soma so that the acute angle (positive dot product) corresponds to an obtuse turn – the more common case.

Figure 3.

Representative join for 6 classes of joins in 2D based on the bend sharpness (acute or obtuse), and # of external corners (2, 3, 4 outside). Additional connecting volume added by our rules in light gray; removed extrusions in dark gray (E). See text for details.

There is a gap between the trapezoids anytime there is a non-zero angle between the frusta, so each trapezoid always has at least one external corner and no more than two at a join, leaving three cases for corners at the join: 1. two outside corners (one from each; Fig. 3A,B), 2. three outside corners (two from one, one from the other; Fig. 3C,D), and 3. four outside corners (two from each; Fig. 3E,F). To fill gaps, we use the intersection of a disk of radius r₁ centered at p₁ with the inside of the half planes whose edge planes pass through p₁ with outward normal vectors a_r and −a_ℓ. This is sufficient to solve the two 2-outside-corner cases (Fig. 3A,B) (CTNG:2outside).

Alternative choices of disks to use for joins may produce more aesthetically pleasing isolated segments, but are less effective in the general join case. The primary weakness of this join rule is that the disks do not lie tangent to the trapezoid edges except when the trapezoid is also a rectangle. We tried two strategies to guarantee tangency and found them both lacking: first, for each trapezoid at the join we used the unique disk lying tangent to the trapezoid sides at c_ℓ,± or c_r,±, as appropriate. If both trapezoids are wider at the join than away from the join, the disks will extend past each other, creating a new form of extrusions. If both trapezoids are smaller at the join, then the disks will not meet smoothly. Our second approach was to modify the trapezoids to lie tangent to the disks at each face, however such trapezoids are only guaranteed to exist if the face centers are more than the sum of the radii apart.

The 3-outside-corner obtuse case (Fig. 3C) is slightly more complicated due to the possibility of two situations which depend on the taper of the 2-corner trapezoid: whether the 2-corner side (right-side intersector of Fig. 3C) is narrowing or widening into the join. If it widens away from the join, then the tangent disk is often smaller than the half-disk (or in any case will stick out less), giving the advantage of a smooth boundary. For either subcase, we can assume, without loss of generality, the left-right orientation shown in Fig. 3C. The rules for each subcase were then chosen to create a smaller join area. The points here are ordered such that a_r (which points from p₁ to p₂) is the axis of the trapezoid with two outside corners at the join. If r₂ ≤ r₁, as shown, then we join with the disk centered at p₁ with radius r₁ intersected with the half plane through p₁ with outward normal vector a_r and intersected with the half plane through p₀ with outward normal vector −a_ℓ. This second intersection is necessary to prevent the disk from extending beyond the other trapezoid if the distance between p₀ and p₁ is less than r₁. If a non-join corner of the trapezoid with axis a_ℓ is within r₁ of p₁, then this second intersection will create a flat face, but such a geometry is extremely rare in practice. If, instead, r₁ < r₂, we start with a disk centered at the intersection c of the line through p₁ and p₂ with the normal through q₁ = p₁ + r₁a_r to the trapezoid side that runs from q₁ to q₂ = p₂ + r₂a_r and radius |c – q₁|. By construction, the boundary of this disk lies tangent to the trapezoid sides at q₁ and q₂. We join with the intersection of this disk with the half plane through p₀ with outward normal −a_ℓ and with the half plane through p₂ with outward normal a_r (CTNG:3outobtuse).

For the acute 3-outside acute case (Fig. 3D), we again use a disk to eliminate the overhang. With p₀, p₁, and p₂ ordered as for the obtuse 3-corner case, we use the intersection of the disk of radius r₁ centered at p₁ with the half-plane through p₁ with outward normal vector a_r (CTNG:3outacute).

For the obtuse 4-outside case (Fig. 3E), we remove the two extrusions by only including the portions of a trapezoid that lie either in the half-plane through p₁ in the direction away from the other trapezoid or lie in the intersection of the two trapezoids. That is, the trapezoid with axis a_r is intersected with the union of the trapezoid through a_ℓ and the half-plane through p₁ with outward normal vector −a_ℓ. Likewise, the trapezoid with axis a_ℓ is intersected with the union of the trapezoid through a_r and the half-plane through p₁ with outward normal vector a_r (CTNG:4outobtuse). This is the only join-rule that modifies the trapezoids. Since a trapezoid is joined on up to two ends, it can be clipped on zero, one, or two sides by this rule.

Finally, for the acute 4-outside case (Fig. 3F), we absorb the extrusions into the capping disk. We do this by joining with a disk centered at p₁ with radius r₁ intersected with the union of the half-planes through p₁ with outward normals a_r and − a_ℓ (CTNG:4outacute).

3.3.1 Into the third dimension

The two-dimensional join rules extend naturally to three dimensions. To join two frusta, we look at their trapezoidal projections onto the plane A containing their axes. We use the same rules as described in the previous section, except we join with balls, the geometric term for the interior of a sphere which is the three-dimensional analog of a disk. We then intersect against half-spaces instead of against half-planes.

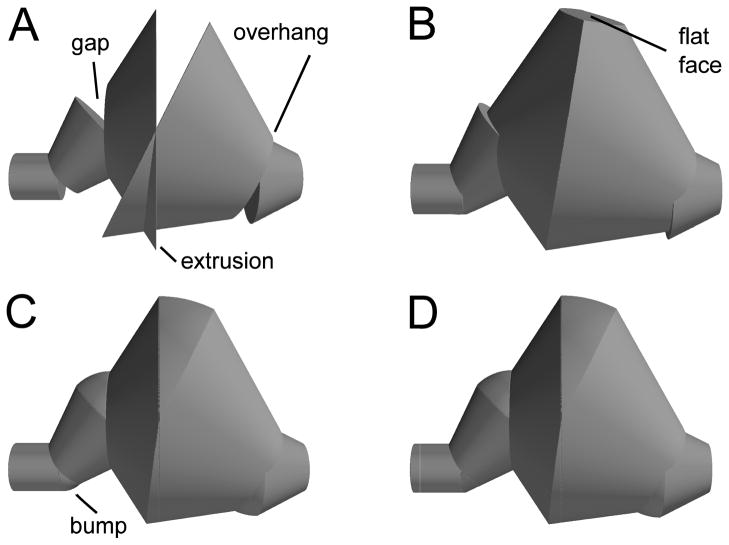
The object in Fig. 4 has obtuse frusta joins with 2-, 3-, and 4-outside type joins, where outside corner counts continue to be based on the trapezoidal projection. Fig. 4A shows the original frusta, revealing the same gaps, overhangs, and extrusions, now in three dimensions. A simpler solution to the gap and overhang problem is to continue neighboring frusta exactly until they intersect. Unfortunately this approach adds substantially to the volume if the angle or taper is strong. Fig. 4B shows that clipping such a join at the plane orthogonal to A that just touches the trapezoids in the projection prevents excessive join volume, but reintroduces flat faces. The results of the algorithm described in the current section are shown in Fig. 4C.

Figure 4.

Sequence of improvements for interpreting joins. (A) Simple frusta join shows gaps, overhangs, and extrusions; (B) Clipping to plane connecting frusta; creates overhang in 2nd join, and flat face in 3rd (rotated to show flat face); (C) Joining sphere wedges leaves small bumps; (D) Bumps resolved by clipping spheres.

A hybrid approach, combining the 2 shown in Fig. 4B,C turned out to be most successful (CTNG:hybrid). A problem with the use of balls to join objects is that a ball need not lie tangent to its neighboring frusta, creating bumps in the surface. To reduce this problem, when possible we intersect the joining balls with the extension of their neighboring frusta into cones (Fig. 4D, note elimination of bump from Fig. 4C). Specifically, if a ball or portion of a ball is used to join frusta f₁ and f₂, then we further intersect that ball with the infinite cone corresponding to f₁ if both join corners of the trapezoid for f₂ lie inside the cone. The cone corresponding to f₂ is handled similarly (CTNG:trimsphere). In a case where the corners do not lie inside the cone, the intersection would not connect both gap corners, since at least one would not lie inside the intersection. Fig. 5 shows examples of routine and non-routine branch points as computed by CTNG.

Figure 5.

Example joins. (A) Y-branch. (B) Sharp angle. (C) Join of four sections.

3.4 Soma outlines

Sophisticated file formats, such as those used by Neurolucida (www.mbfbioscience.com/neurolucida), support outlines for the soma, a structure that is approximately pyramidal or spheroidal rather than thin and long like a dendrite (Fig. 6). Rarely source files may contain multiple outlines representing multiple slices of the soma at different z depths. Although tracing software does not enforce two dimensionality, tracing in depth is difficult. Therefore, tracings are two-dimensional with some wrinkles where focus was slightly changed in order to follow an outer perimeter. We therefore consider here only a single outline, a set of (x, y) points tracing a two dimensional path around a feature.

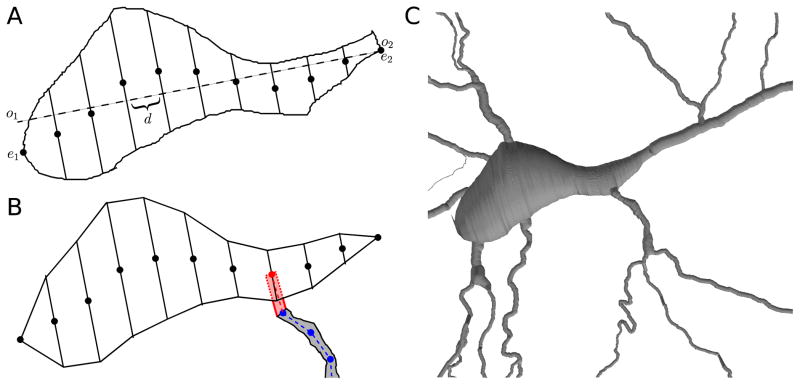
Figure 6.

(A) Sliced soma outline: major axis (dashed); centers of skew frusta ends (dots). (B) Due to measurement and reconstruction errors, a dendrite (gray) defined by a set of nodes (blue) might not touch the reconstructed soma. To fix this, CTNG adds an additional point (red) to the dendrite definition chosen from the centers of the skew frusta faces (black dots). Conceptually this adds the pink region to the dendrite definition, however only the portions lying outside the soma contribute additional surface area and volume due to the constructive cubes approach. (C) CTNG’s 3D interpretation with dendritic attachments.

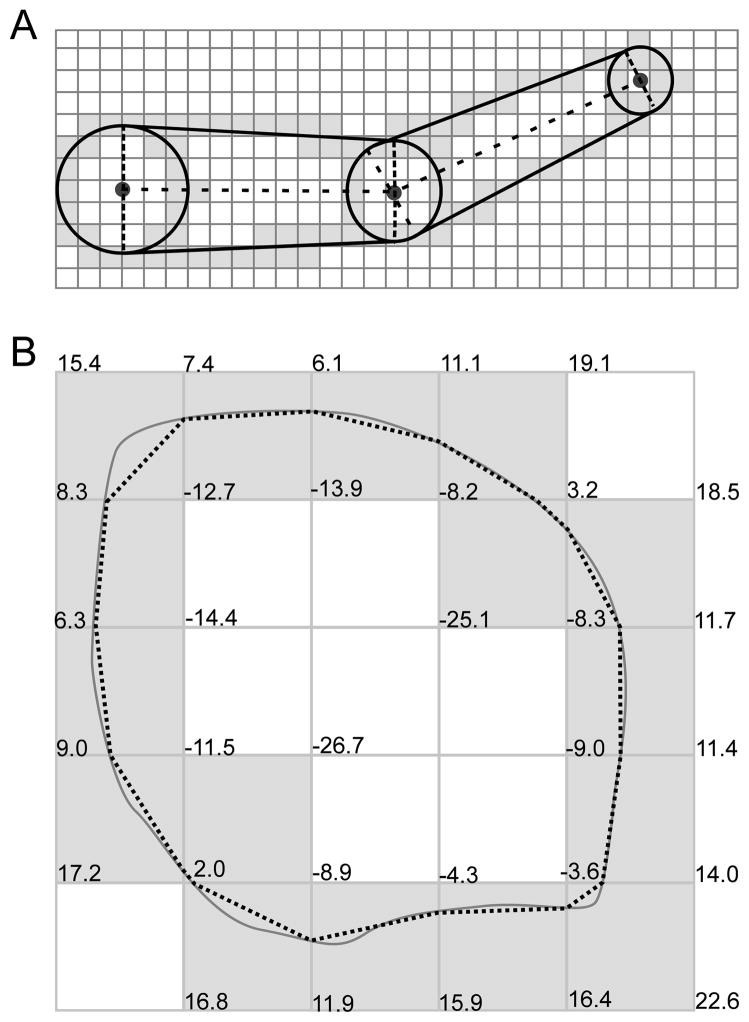
We begin processing soma outlines by rediscretizing their paths to use evenly spaced points; this step ensures all parts of the outline are weighted equally. From these rediscretized points, we compute an approximate centroid and a single linear major axis (CTNG:majoraxis). We then identify the two points e₁ and e₂ on the soma outline whose orthogonal projections o₁ and o₂ onto the major axis are the furthest apart (Fig. 6A; CTNG:somaextrema). All other points have orthogonal projections lying between these two extrema of the outline. For each of the n + 1 test points q_i = o₁ + i · d for i = 0, 1, … n, where d = (o₂ − o₁)/n is the spacing between test points, we consider the line in the outline’s plane orthogonal to the major axis through q_i. We define diameter D_i at q_i to be the maximum distance between points where the outline intersects the line and to be 0 if there are not at least two such points (CTNG:slicesoma). We then define the center c_i as the midpoint of the two extreme points on the line.

We then reconstruct a three-dimensional surface from these 2-dimensional data by using n sheared frusta (Fig. 6). Each of these is a frustum whose end faces have diameters D_i−1 and D_i. The axis of the sheared frustum is parallel to the major axis due to a translation that leaves one end face in place with center at c_i−1, and shears the other end face to a center at c_i. In this way both faces remain perpendicular to the major axis. Neighboring sheared frusta share faces, so there are no problems with gaps, joins or overlaps.

Connecting reconstructed dendrites to the soma must now take into account proximity of the nearest measured end of each loose dendrite to the approximate 3-D elaboration of the soma based on the 2-D tracing. Specific dendrites are not contiguous with the soma since the first dendritic measurement was made some finite distance away from the soma where a dendritic diameter could be measured. Additionally, the file format does not show parent-child logical connectivity for the soma outline in the way that it does between dendrites. To reattach dendrites, we begin them with an extra point p̂ ∈ {c₀, c₁, … c_n}where p̂ is chosen such that the distance between p̂ and the dendrite’s original initial point is at a minimum (CTNG:connectdends). We assume that the dendrite’s diameter at p̂ is equal to its diameter at the first measured point. This process is illustrated in Fig. 6B.

3.5 Preprocessing to reduce measurement artifacts

By preprocessing the data, we can further improve the quality of the reconstruction at the cost of reduced fidelity to the original data. For example, many reconstructions feature points sampled very close together relative to the diameter. At these small distances, measurement error may cause neighboring frusta to have radically different orientations. NMO_02699’s apical [15] presents an extreme case, as in places there are two y values for each (x, z) pair. Directly rendering these frusta produces a mesh-like structure, whereas our algorithm produces a solid but slightly bumpy surface. If we instead preprocess the apical by discarding all but one y value for each (x, z) pair, our algorithm then produces a solid, smooth surface as demonstrated in Fig. 7.

Figure 7.

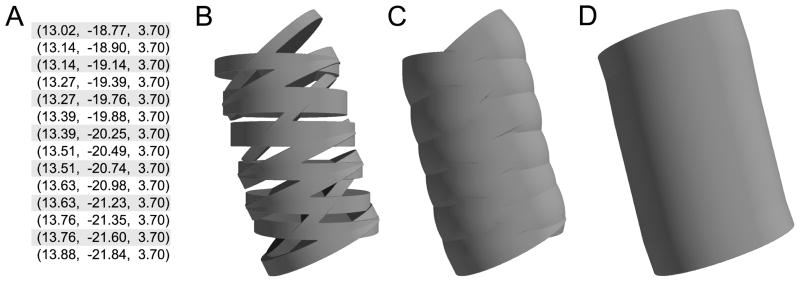
Section of apical dendrite from mouse somatosensory pyramidal cell (NeuroMorpho.Org ID NMO 02699) (A) (x, y, z) points from point-and-diameter data (diameters all 1.97 μm) For each (x, z) pair in the interior of this set, two y values were provided. (B) Direct rendering creates a mesh; (C) Geometry rendered by CTNG; (D) CTNG combined with preprocessing by discarding unshaded data points.

3.6 Locating the surface using marching cubes

Thus far we have followed a constructive solid geometry (CSG) approach, describing the reconstructed geometry as the union and intersection of three-dimensional graphics primitives: balls, frusta, sheared frusta, and half-spaces. Because pieces of these primitives lie within other primitives, and hence within the neuron, only a subset of the primitives’ surfaces define the neuron’s surface. Therefore, we have not yet solved the problem; we still must isolate a unique neuronal surface. Because this complex construction represents the unions and intersections of primitives and not simply a concatenation of individual graphics primitives, we must calculate distances to unions (the minimum of distance to any member) and intersections (the maximum of these distances). If relevant pieces fail to be considered when working with the union, we end up getting remnants of the neural interior which are continuations of the other pieces. If we don’t process the structure as a union, we end up with remnants sticking into the neural interior, falsely identified as surface constituents.

We initially tried interpreting our CSG via the open-source program NETGEN (www.hpfem.jku.at/netgen) to assess a large neuron from ModelDB model #20212 (senselab.med.yale.edu/ModelDB/ShowModel.asp?model=20212 [17]): 5341 3D points distributed across 181 sections, making 5341 – 181 = 5160 frusta. NETGEN stalled, which we tracked to an inability to resolve cusps between 3 intersecting cylinders. We simplified this aspect by using join-balls whose diameters were 2% larger than the dendrites at these branch points, and simplified the join rules by connecting unintersected frusta with full spheres. Since the joins are only a small portion of the geometry, this alteration would have only a small effect on total surface area and volume. However, NETGEN then ran out of memory. After turning off concurrent rendering, the program ran further but then produced a segmentation fault. In order to make sure we were using the program correctly, we reran with only 2.4% of the morphology (126 frusta), again using the simplified joins and enlarged balls. In this situation, NETGEN was able to mesh the surface in 15.75 seconds.

We thus augmented CTNG to produce the surface meshing using the constructive cubes algorithm [5], optimized for our problem (CTNG:constructivecubes). Constructive cubes imposes a regular Cartesian grid over a volume containing the neuron. At each grid point, it calculates the signed distance (outside is positive, inside is negative) to the neuron’s surface. Constructive cubes concludes by using the marching cubes algorithm [13, 18], explained below, to create a triangular mesh of the zero isosurface (a surface of points all having the same value) of this scalar field, which is by definition the set of points with no distance from the surface; i.e., the resulting points are the neuron’s surface.

Marching cubes is a technique to approximate an arbitrary isosurface given a regularly sampled scalar field. It does this by individually considering each cube or voxel whose vertices are neighboring grid points, and estimating how the surface must pass through that voxel. It marches through each of the eight vertices in order, checking if they have a value lower than the isovalue, and uses the resulting truth values to form an eight bit binary number (CTNG:domarch). The number and approximate position of the triangles representing the surface passing through the voxel is then obtained from a lookup table keyed by this number (CTNG:tritable). All vertices of the triangles thus described lie on edges of the voxel, and an edge contains a triangle’s vertex exactly when one of the edge’s end points is lower than the isovalue and the other end point is not. The vertex of a triangle on an edge is placed at the approximate location of the isovalue as determined by linearly interpolating from the edge’s end points (CTNG:interpedge). Marching cubes is a fast algorithm as it consists only of a table lookup and some linear interpolations. Furthermore, it is an example of an embarrassingly-parallel algorithm, as each voxel can be processed independently of every other voxel.

It follows from the definition of marching cubes that an exact signed distance is not required, only a function that is approximately linear near the neuron’s surface. We use this flexibility to simplify the processing of sheared frusta. We must, however, provide continuous approximations of the distance instead of a simple binary inside/outside indicator to avoid a stair-step appearance in the resulting surface.

We begin by computing signed distances to the neuron, following the arbitrary convention that distance is positive if the point is outside and negative if it is inside. Since we defined the neural surface as the union of parts of balls and frusta, it follows that the distance from a point to the neural surface is equal to the minimum of the individual distances to the nearby nearby constitutive objects (CTNG:uniondist). The distance to an intersection of objects is the maximum of the distances to the objects (CTNG:intdist). Signed distance to a ball is the distance to the center minus the radius (CTNG:balldist). Distance to a half-space is simply distance to the plane defining that half-space, which follows from the definition of a scalar projection: distance from a point is given as (n⃗ · x⃗) – (n⃗ · p⃗) where x is the point, and the plane is defined by unit outward normal vector n⃗ and a point p in the plane (CTNG:planedist). Because the second dot product does not depend on the point being tested, it only needs to be calculated once. The more complicated case is the distance to a frustum, which is handled using the the algorithms for distance to cylinders (CTNG:cyldist) and frusta (CTNG:frustumdist) given in [3]. For sheared frusta, we approximate distance to a point by applying the inverse of the shear transformation to the point and then computing the distance from this transformed point to the original (unsheared) frustum: For the frustum from P to Q where the Q end is sheared to R, we define $\overrightarrow{s}=\overrightarrow{QR}/\mid \overrightarrow{PQ}\mid$. We then use the distance from p′ – d s⃗ to the (unsheared) frustum from P to Q, where p′ is the location of p in the unsheared space, d is the distance from p′ to the plane through P with normal vector $\overrightarrow{PQ}$. This gives an adequate approximation of the signed distance from p in the original coordinate space to the sheared frustum (CTNG:shearfrustdist).

3.7 Discretization

Refinement of the scalar distance grid reduces error at the cost of increased computation time and memory usage. Discretization needs to be at least fine enough so that no cross-section lies entirely within a single voxel; otherwise, marching cubes will fail to locate the corresponding surface. Due to light microscopic resolution, the thinnest measurable dendrites have diameters of ~ 0.40 microns, so 0.15 microns is often an adequate discretization step, although CTNG works with any user-specified resolution. The Poirazi et al. neuron [17] is contained in a box 431.45 × 740.76 × 412.47 microns (132 nl). A 0.15 micron grid produces ~ 39 × 10⁹ voxels, of which only ~ 0.01% contain any surface. It is therefore extremely inefficient to apply marching cubes over a neuron’s entire bounding box. Full marching cubes on a Y-branch of 110,000 voxels, ~0.04% of a neuron, took 32.78s to run.

Fortunately, neurons occupy only a tiny fraction of their bounding box, so we reduce computation time by not applying marching cubes to voxels that are not candidates for containing neuronal surface. That is, we eliminate any voxel that we know lies more than one voxel away from the surface. As the neuron is a union of simpler objects, it follows that we can eliminate voxels that are more than one voxel outside of all of the constituent objects. In particular, if a given voxel or group of voxels does not intersect any of the bounding boxes of the neuron’s constituent objects, then it cannot contain any of the neuron’s surface because it will not be close to any object.

We refine this idea by noting that any point on the surface of the union is necessarily on the boundary of one of its constituent objects. The converse is false: the set of voxels containing object boundaries is a larger set than the set of voxels containing neuron surface. However, the set of object-boundary voxels is still vastly smaller (typically less than 0.1%, although this depends on voxel size) than the set of all voxels in the neuron’s bounding box. We can thus proceed by locating the subset of voxels containing object boundaries, and then perform marching cubes on that small subset to locate the neuron’s surface.

Efficient localization of voxels containing object boundaries is nontrivial and must take into account the variety of object shapes being used. Even where one can readily generate an expression for the voxels containing a boundary, there remains greater difficulty in actually constructing the voxel set. Consider, as a simplified case, the unintersected ball centered at the origin of radius r. Its boundary is the set B = {(x, y, z) : x² + y² + z² = r} and thus the voxels containing boundary are those with indices in V = {v(b) : b ∈ B} where v(x, y, z) = (⌊(x − x₀)/dx⌋, ⌊(y − y₀)/dx⌋, ⌊(z − z₀)/dx⌋) where x₀, y₀, and z₀ are the origin of the voxel grid, dx is the isotropic discretization, and ⌊·⌋ is the floor function.

Now, we must generate the voxel set from the function. One straightforward approach is to parameterize the boundary and use a regular gridding. In the case of a sphere, we can use polar coordinates {(r cos θ sin φ, r sin θ sin φ, r cos φ) : 0 ≤ θ < 2π, 0 ≤ φ ≤ π}, and sample on an even grid along (θ, φ) space. Unfortunately, this approach is very inefficient; δθ must be small to ensure we sample every voxel along the equator (φ = π/2). As one approaches the poles the gridding becomes increasingly redundant till every value of θ returns the same point at φ = 0 and φ = π. Developing adaptive griddings across the various shapes provides additional algorithmic complexities. Missing even one voxel is unacceptable as the final boundary would no longer be water-tight. Intersecting the balls and frusta with other objects increases the complexity both of the boundary parameterization and of choosing an efficient sampling of the boundary.

Due to these difficulties, we adapted a flood-fill algorithm for building the voxel set (CTNG:floodfill). Note that flood-fill is used on the object’s boundary, not its volume. The method is more efficient, and considerably faster, than gridding because it never repeats voxels. It also has the advantage of being general: the same code can process any shape efficiently, with no a priori parameterization required. The algorithm can start from any voxel that is known to contain boundary. It then checks the voxel’s neighbors to see if they contain boundary. Any such voxel is added to the set. The process then checks previously unchecked neighbors of voxels in the growing set, repeating until no further boundary members can be found. At this point, all voxels containing the object’s boundary have been located. These voxels are only needed because they may contain neuron surface; there is no need to determine a triangularized representation of the object’s boundary. Note that this algorithm requires the ability to detect if a voxel contains boundary. Fortunately, there is a simple sufficient condition based on the distance function and the intermediate value theorem: if any one vertex of the voxel lies outside the object (has positive distance to the object; distance here is to the object rather than to the neuron) and one vertex lies inside (has negative distance), then by continuity the boundary must pass through the voxel.

The problem of creating the object’s voxel set is thus reduced to the problem of locating a single voxel such that one corner is outside and one corner is inside of the object. Fortunately, each object is either 1. a frustum, possibly intersected through the center of a face by one or more half-spaces with face centers that then always lie on the boundary; or 2. a ball intersected by one or more half-spaces through its center with the center of the ball becoming a point on the boundary after the intersection. A problem arises in cases where the object is the narrow ball wedge used to join two frusta. In these cases it may be so narrow that all of its corners are within the containing voxel, so that another voxel must be found. We would then search within 2 voxels of the initial point or, in the case of balls, within two voxels of the initial point shifted by a radius in each cardinal direction. In the case of the neuron of [17], we found that this procedure was sufficient to locate all but 97 out of 10744 constitute objects. For the remainder, we systematically search within the object’s bounding box until the first boundary point is located. Despite being 1% of the surface, this brute force search accounted for most of the boundary location time (CTNG:systemsearch). Subsequent refinements use the object parameterization as the fallback mechanism to guide this search and improve overall performance.

For the Poirazi neuron, the process of locating the potential surface voxels eliminates about 99.99% of the bounding box, leaving only 3,994,837 voxels to examine. Similarly, processing NeuroMorpho.Org’s neuron NMO_02699 [15] with a 0.07 micron grid gives a nearly 99.98% reduction down to only 6,034,455 candidate surface voxels.

Although this procedure removes most candidate voxels from consideration, it still leaves a large number of distances to calculate for marching cubes. We can simplify the calculation further by utilizing an observation about the distance metric. The distance from a point to the neuron, a union of thousands of objects, is by definition the minimum of the set of distances between that point and the objects individually. Hence, the distance from a point to the neuron is the same as the distance from that point to the closest object. More generally, the distance is the same as the distance from a point to any subset of the neuron’s objects that contains the closest object. This last generalization is important as we do not normally know a priori which object is the closest to any given point.

For any rectangular prism or box of space, we can identify a subset of the objects guaranteed to contain the closest object for every point lying within one voxel of the neuron within that prism; there is no need to compute a new subset for every point. For a point to be near the neuron, it must be near some constituent object, so we consider only those objects that pass near our prism. For an object to be within one voxel of the prism, its bounding box must be within one voxel of the prism; this test is quick, requiring at most six comparisons per object (CTNG:testbb). Any object not satisfying this condition is not relevant to distance calculations within the prism. We note, however, that an object’s bounding box may come close to the prism even if the object does not. For example, the bounding box of a cylinder whose axis lies 45° from each coordinate axis intersects more space than the bounding box of a cylinder of the same size with an axis that lies parallel to a coordinate axis.

We thus apply a second, more computationally expensive test, to those objects whose bounding boxes intersect our rectangular prism of interest. This test derives from the observation that an object that has nontrivial intersection with a set S necessarily has nontrivial intersection with any superset of S. In particular, an object passing no more than a voxel away from a prism nontrivially intersects any ball containing all points within a voxel of the prism. We test with the smallest such ball, namely the ball centered at the prism center whose diameter is equal to the diameter of the prism after it has been expanded by one voxel width on all sides (CTNG:testball). The intersection condition is satisfied exactly when the distance from the ball center to the object is less than or equal to the ball radius, so this test requires one distance calculation per object per prism. Any object not satisfying this intersection condition may be safely neglected when calculating distances within the prism.

Sub-voxel sized bumps in the surface, due to numerical error from slight variations in round-off between the distance functions, can arise where an intersected ball meets a frustum. These errors can typically be eliminated in cases where the frustum expands away from the join or has constant radius by allowing the balls to enter the frustum, and then intersecting them with the half-space perpendicular to the axis through the center of the far face, instead of intersecting them with a plane through the center of the join. With this modification of our rules, the intersection of the ball with the half-space is now far from the join and no longer affects the local distance calculations. As most reconstructions exhibit constant radii on most segments, this rule removes most such numerical artifacts.

3.8 Validating with surface area and volume comparisons

To check the validity of our surface reconstructions, we compared our estimate of somatic surface area (CTNG:surfacearea), with estimates from two standard tools: NeuroMorpho.Org and NEURON. The results are summarized in Table 1. We calculate surface area and volume from our triangularization with linear algebra: the area of a triangle PQR is $\mid \overrightarrow{PQ}\times \overrightarrow{PR}\mid /2$ and the volume of a region bounded by a set of oriented triangles {P_iQ_iR_i} is $\frac{1}{6}\mid \sum (P_i·Q_i\times R_i)\mid$.

Table 1.

Comparison of CTNG, frustum, and NeuroMorpho.Org surface area and volume measurements for multiple neurons taken from original morphologies from NeuroMorpho.Org. There is typically closer agreement between CTNG and frustum values than between either of them and NeuroMorpho.Org. Frustum area and volumes are based on the frustums instantiated by NEURON’s Import3D tool. CTNG data and runtimes are based on a 0.15 μm discretization. The CTNG surface area includes end caps on the tips of dendrites, while the frustum surface areas do not.

NeuroMorpho.Org ID		NMO 00240	NMO 00863	NMO 02699	NMO 04506
Type		Basket	Purkinje	Pyramidal	Granule
Area (μm2)	NeuroMorpho.Org	25467	23086.1	8345.85	990.4
	Frustum	26184	23819.8	8825.56	1128.2
	CTNG	25377	23775.1	8593.61	1126.3
Volume (μm3)	NeuroMorpho.Org	3117.5	7776.3	1911.66	263.59
	Frustum	4458.0	10499.0	3650.42	476.14
	CTNG	4240.0	10794.9	3589.89	475.80
Runtime (s)	CTNG	198.6	290.4	162.2	24.1

Using NcuroMorpho.Org’s NMO_02699 [15] as a test soma, CTNG calculated a surface area of 939 μm². In contrast, the area calculator at NeuroMorpho.Org substantially overestimated the surface area (1499 μm²) by approximating with the surface area of the soma as a sphere with radius equal to the average distance of the soma outline from the center (neuromorpho.org/neuroMorpho/SomaFormat.html). NEURON, using soma processing similar to ours, slightly underestimated surface area, giving a value of 876 μm². The key difference is that after slicing the soma, NEURON slides each thin disk slice so that it is centered on the major axis. This shifting artificially straightens the soma, thereby reducing its surface area.

4 Discussion

We have developed a method for defining water-tight three-dimensional neuronal reconstructions from point-and-diameter data. These reconstructions cannot match the original neuron exactly since the point-and-diameter data is a fairly abstract representation. We obtain reconstructions that are physically possible: the same space cannot be occupied by different matter, the surface must not have holes, and the surface must never lie inside the neuron. We also require solutions to be biologically plausible: no portion of a dendrite may extend past its neighbor. We found that the standard frustum-based interpretation fails all of the physical conditions anytime the morphology is not perfectly straight and sometimes fails the biologically plausible condition. We identified six different classes of relationships between three consecutive point-and-diameter data points which allowed us to develop constructive solid geometry (CSG) rules. We also developed CSG rules for somas, which are specified by their two-dimensional outlines. We then developed a variant of the constructive cubes algorithm optimized for sparse neuronal geometries to construct water-tight triangularly tessellated surfaces from our CSG descriptions.

CTNG works with cubic voxels and directly provides the voxel-mesh correspondence required at the surface interface. Therefore, CTNG is optimized for handling a Cartesian-mesh finite-volume simulation method. As compared to other discretization schemes, a Cartesian grid offers the most well-understood rules for bounding numerical error. Some care is needed to do finite volumes correctly at the point where a cube is divided by the surface. In these cases, the algorithm needs to take account of 1. the proportion of the cube’s volume that lies within the surface, 2. the area of the surface contained in the cube, and 3. the areas of the intersections of each of the cube’s faces with the surface. These values can be made readily calculable by using a simulation spatial step-size that is an integer multiple of the voxel discretization provided by CTNG. In this way, no surface triangles cross simulation grid boundaries.

We found that existing CSG-enabled meshing programs could not handle our domain due to the sparseness of the problem: a dendritic tree fills very little of the large space that it spans. We informally tried several meshing programs, and intensively tested NETGEN to locate the surface. NETGEN triangularly tessellates the surface with an adaptive mesh. One problem with use of this program was that the triangularization produced was not aligned with an underlying Cartesian mesh, which would make it complicated to establish volume-surface (cytoplasm-membrane) correspondence. More importantly, NETGEN could not handle the problem, even after simplification of the surface.

Another algorithmic alternative would be to build boundary representations from a point cloud. In this approach, one generates a large number of points and outward normal vectors on the surface of each object. Points lying inside of another object could then be discarded. Connecting these points to form a water-tight surface is nontrivial, but is handled by the software package CGAL (cgal.org). Use of this algorithm would again leave us with difficulties in establishing volume-surface correspondence. Additionally, parallelization of this algorithm remains a work in progress (www.cgal.org/in_progrcss.html) [4].

We therefore developed our own algorithm, optimizing a constructive cubes algorithm. We used marching cubes on only a subset of points so to avoid the problem of neuronal sparseness. Marching cubes can run in parallel across multiple processors or GPUs [10]. It also naturally provides correspondence between internal voxels and surface pixels. In addition to the importance of cytoplasm-membrane correspondence, a good approximation of a neuron’s surface is essential in order to adequately estimate fluxes through ion channels and pumps. Misestimation of surface area will lead to channel discrepancies that will alter local and global dynamics.

The vertices of each triangle are ordered so that when viewed from outside, every triangle is traced in the same rotational direction. This property is essential as some visualization, volume-calculation, and simulation techniques require knowing the outward normal. Since our algorithm constructs the triangles from signed distances, the exterior face (and hence the appropriate ordering) is known at triangle-creation time and requires no additional computational effort.

4.1 Comparison with other software packages

Many whole cell multi-compartment neurosimulation packages (e.g., GENESIS (genesis-sim.org), MOOSE (moose.sourceforge.net), NEURON (www.neuron.yale.edu)) use point-and-diameter data to define the morphology for electrophysiology simulations. In this domain, either frusta or cylinders can provide adequate approximations, as the space constant is far larger than any resulting errors in the geometry. PSICS (Parallel Stochastic Ion Channel Simulator; psics.org) provides simulation at a lower scale, hence requires a more detailed interpretation of the point-and-diameter data. When possible, PSICS places balls at each measured point, and it connects consecutive balls with a frustum that lies tangent to each at the points of intersection. Joins constructed in this way are necessarily gapless as each frusta at the join shares the same spherical cap. Unfortunately, these frusta need not exist if the diameter changes rapidly relative to the distance between the end points. As an extreme example, one ball may end up lying strictly inside of the other.

The stochastic reaction-diffusion simulator NeuroRD (krasnow1.gmu.edu/CENlab/software.html) is a reaction diffusion simulator that can construct three-dimensional discretizations from point-and-diameter morphologies. NeuroRD discretizes each frustum independently in three dimensions using a local cylindrical coordinate system, then connects these pre-discretized compartments to their radial or longitudinal neighbors. This approach is very similar to that used by the NEURON simulator. The compartment from the last slice of a parent segment is logically connected to the first slice of each child segment for diffusion. In this way, a pair of child segments are connected as though they continued in line with the parent, even though the morphology file shows them at an angle. Because the discretization is done first, the geometry may show compartment overlaps and gaps: the numerical simulation is unaffected since the morphology is an approximation of the discretization, rather than the other way around. Detailed morphological information is lost, precluding investigation of branch angles and of connections from soma to dendrites. It is hypothesized that realistic three-dimensional morphology is important not only for technical accuracy, but also because details of geometry can fundamentally alter the interaction between reaction-diffusion dynamics in a volume and interaction with pumps and channels on an adjoining membrane [9]. Analogously to how impedance mismatches impair electrical signaling, geometric changes can block chemical signaling [8].

Simulators, as well as independent neural viewers (Neuronvisio, neuronvisio.org; CVAPP, github.com/pgleeson/Cvapp-NeuroMorpho.org; NLMorphologyViewer, neuronland.org), visualize the neuron’s surface. Except for ICING (PSIC’s renderer), these generally render frusta or cylinders and are not careful about joins, as can be easily seen by doing a zoom-in and noting discontinuities and overlaps. With a few notable exceptions, such as NEURON’s fiat projection based approach, these tools provide the appearance of constructing a surface; in reality, they only render a surface. The key difference is that rendering a surface does not require locating the actual surface; the boundary of each frusta (or ball, in the case of PSIC’s renderer ICING) is located and displayed independently of all the other objects. To display the collection of objects, the graphics card uses z-buffering or some other hidden surface removal algorithm which produces the illusion of a well-defined surface. These algorithms render pixel-by-pixel for a specific view angle; they do not reshape triangles that are partly hidden, and they do not distinguish between not-currently visible triangles and never-visible triangles that lie on the interior. Thus while the user never sees any internal membranes, they continue to exist, making the tessellated surfaces used for rendering unsuitable for surface area calculations.

Lasserre et al. [11] also produce a watertight mesh from point-and-diameter data. Their method starts with a point on the neuron and grows the dendrites from that point to pass through each data point. This introduces a non-local dependence to all stages of the triangularization, whereas after the constructive geometry is defined in CTNG, each voxel can be processed independently. Since the Lasserre method is tracing a tree, it requires the existence and correctness of a logical connectivity tree; CTNG makes connections based on (x, y, z) coordinates. Finally, the Lasserre method makes dendrites with square cross-sections while CTNG makes circular cross-sections like the traditional cylindrical and conical approximations used by electrophysiology simulators like GENESIS, MOOSE, and NEURON.

The marching cubes algorithm has been previously used to locate neuron surfaces [18]. The fundamental difference between our approach and theirs is that they require a more complete dataset, a stack of laser-scanning microscopy images, rather than from sparse point-and-diameter data. With the extra data, they can faithfully reproduce non-circular dendritic cross-sections and other details.

4.2 Enhancements and future directions

Our algorithm could be accelerated by reducing the number of objects identified as possible contributors to the distance from a given point to the neuron. By reducing the number of objects, we reduce the number of calculations required to compute distances. We currently identify separate subsets of objects for several regions of space. By reducing region size, we can reduce the number of objects in each region at the cost of increasing the number of object subsets that we must identify. This cost would be reduced using a recursive approach: identify the set of objects that contribute to the distance function in a large region, then divide that region into smaller regions, testing only those objects that matter in the bigger region. This recursion would stop when no more than one object lies near the region or the region only contains one voxel. A still more sophisticated approach would trace the surface of the neuron and identify those portions of dendrites that lie far from joins, locations where the surface of the neuron is the boundary of the corresponding frustum.

Another refinement would be to use an adaptive grid size: divide total volume into regions and choose a different mesh size in each, based on the size of the smallest feature within the given region. Using larger grids reduces the number of voxels to process, thereby speeding up calculations and reducing memory usage. The trade-off with this approach is that surfaces will not, in general, line up at the boundary between regions of different resolutions, creating holes that then have to be filled in. The graphics community is developing solutions for patching such regions together, but this is an area of continuing research [12].

External morphology precision could be improved somewhat with the use of existing file formats and programs by taking care to make measurements immediately adjacent to joins so as to provide the most information about the diameters leading up to those points. In future, it might be possible to slightly augment these file formats by providing additional fiduciary points surrounding joins, something that could now be done with some difficulty by switching back and forth from the tracing function used for somas. In the more distant future, we can hope to see these measurements fully automated, providing whatever level of detail is desired. At that point, it might be advisable to revisit the standard file format to determine what other information about joins would be valuable in order to generate accurate surfaces. Although the use of electron microscopy might be an eventual ideal, it is likely that a great deal of detail could be provided by using confocal and other forms of modern light microscopy.

Our algorithm bridges the world between point-and-diameter morphologies and realistic three-dimensional simulation. Point-and-diameter morphologies are likely to remain common: it is much simpler to measure points and diameters than to obtain full three-dimensional data, something that ultimately requires electron microscopy. Although CTNG was designed for compatibility with Cartesian mesh discretizations, it is not limited to this simulation approach. CTNG can be readily used by simulators needing tetrahedral meshes, such as STEPS. In this case, CTNG would be followed by a postprocessing that would construct a set of tetrahedra, something which can be done with an advancing front method; a key advantage of a tetrahedral discretization over cubic is that tetrahedra can be chosen so that their faces precisely match a triangulated surface. CTNG can also be readily used with meshless simulators such as MCell and Smoldyn, which require an initial surface representation as an input to establish their boundary conditions.

Figure 8.

2D representation of the constructive cubes process. (A) Locating voxels containing boundaries of constituent objects (shaded). (B) Computation of distance from each corner of each cube to figure surface (solid curve) with interpolation to find crossing locations. Connecting resultant crossing points forms approximation of the surface (dashed).