Estimating Anatomically-Correct Reference Model for Craniomaxillofacial Deformity via Sparse Representation

Abstract

The success of craniomaxillofacial (CMF) surgery depends not only on the surgical techniques, but also upon an accurate surgical planning. However, surgical planning for CMF surgery is challenging due to the absence of a patient-specific reference model. In this paper, we present a method to automatically estimate an anatomically correct reference shape of jaws for the patient requiring orthognathic surgery, a common type of CMF surgery. We employ the sparse representation technique to represent the normal regions of the patient with respect to the normal subjects. The estimated representation is then used to reconstruct a patient-specific reference model with “restored” normal anatomy of the jaws. We validate our method on both synthetic subjects and patients. Experimental results show that our method can effectively reconstruct the normal shape of jaw for patients. Also, a new quantitative measurement is introduced to quantify the CMF deformity and validate the method in a quantitative approach, which is rarely used before.

Introduction

Craniomaxillofacial (CMF) surgeries involve the surgical treatment of congenital and acquired conditions of the head and face. In the United States, a significant number of patients (17 million) suffer from CMF deformity and require CMF surgery [1]. The basic principles of CMF surgery involve repositioning all the displaced bones to their normal positions, and replacing the missing skeletal parts with bone grafts or alloplasts if needed. The success of CMF surgery depends not only on the surgical techniques, but also upon accurate surgical plans. However, CMF surgical planning is extremely challenging due to the complexity of deformity and the absence of a patient-specific reference model. In the conventional CMF surgical planning, a surgeon virtually cuts a 3D model, and moves and rotates the bony segments to a desired position based on the “averageness” of normal population (so called normal values). However, the outcome is often subjective and highly dependent on the surgeon’s experience. We hypothesize that if a surgeon preoperatively knows what the normal CMF shape of the patient should be, the surgical planning process will be more objective and personalized.

To this end, we present a novel method for preoperatively and automatically estimating what the patient-specific normal CMF shape should be for individuals with CMF deformities. The estimated explicit patient-specific shape model can be used as a reference to guide the surgical planning. Surgeons will be able to determine the difference between the original patient deformed shape and the reference shape, and then generate a feasible surgical plan. In this paper, our method is focused on a common type of CMF surgery, the orthognathic surgery, in which the patient’s deformity is non-syndromic and limited to the jaws, i.e., only the maxilla and mandible are involved in surgery while the midface (the level at zygoma and above) is anatomically correct and does not need a surgery. Fig. 1 shows a typical patient requiring a double-jaw orthognathic surgery. The midface (marked in cyan) is anatomically correct, while the upper and lower jaws (marked in yellow) need to be surgically corrected.

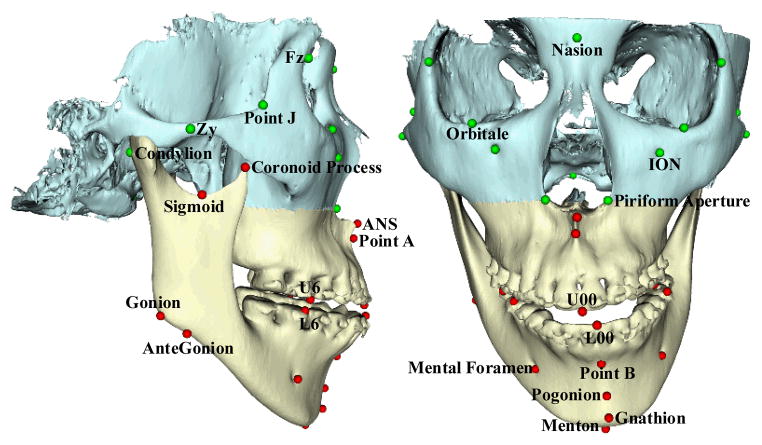
Fig. 1.

Surface models and landmarks. The skull surface is divided into two parts: the midface and the jaws. Midface model S_mid is marked in cyan, which remains unchanged during the surgery. Deformed jaw surface S_jaw is marked in yellow, which need to be corrected during the surgery. The landmarks are accordingly partitioned into two groups: midface landmarks L_mid (green spheres) and jaw landmarks L_jaw (red spheres).

To estimate a patient-specific jaw reference model, we use a data-driven method based on sparse shape composition [2]. Given a dictionary of normal subjects, we first use the sparse representation [2–4] to approximately represent the midface by the corresponding regions of the normal subjects in the dictionary. Then, the derived sparse coefficients are used to reconstruct a patient-specific reference jaw shape. Unlike previous Statistical Shape Model (SSM) based methods [5–7], sparse shape composition allows us to explicitly employ the shapes of normal subjects as prior.

Method

The overall flowchart of the proposed method is shown in Fig. 2. Given a patient with CMF deformity, we first generate the bony surface model that includes two structures: midface surface S_mid and deformed jaw surface S_jaw. As described above, orthognathic surgery only involves the jaws while leaving the midface untouched. Therefore, based on the patient’s midface surface, we can estimate a patient-specific jaw reference model that indicates what the normal-looking shape of the patient’s jaws should be.

Fig. 2.

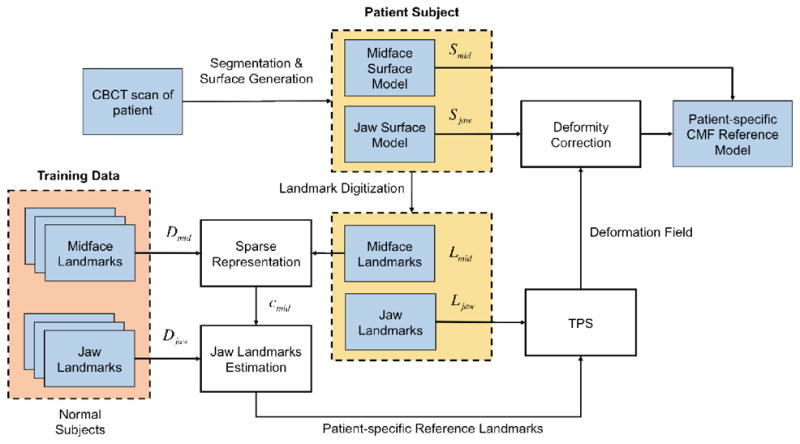
Flowchart of proposed method.

In order to effectively and efficiently utilize the surface model, anatomical landmarks are digitized (placed) on the midface and jaw surface models. The advantages of using landmarks include: 1) it is computationally efficient based on a small set of landmarks, instead of tens of thousands of vertices on a discretized surface model (with triangle mesh); 2) it is easier and more reliable to establish the surface correspondences among different surface models; 3) the use of landmark is clinically relevant since all the cephalometric analysis (a collection of measurements used for orthognathic surgery and orthodontics to quantify the deformity) are landmark-based. In our method, we select a subset of bony landmarks [8] after the 3D model is positioned in the reference system [9]. Since we divide the surface model into midface and jaws, we accordingly partition the landmarks into the midface landmarks L_mid and jaw landmarks L_jaw (Fig. 1). In addition, the landmarks on mandibular condyles are static along with L_mid for the calibration of jaws.

Using digitized anatomical landmarks, we employ the sparse representation technique to estimate the patient-specific jaw reference model by referring to the subjects with normal jaw shape. Specifically, we first linearly align all normal subjects onto the current patient space based on their corresponding midface landmarks. For each normal subject and patient, all the coordinates of its midface landmarks are arranged into a column vector. By gathering all the midface landmarks from all the aligned normal subjects, we can build a dictionary matrix D_mid, where each column is the vector of midface landmarks of a normal subject. To represent the vector of midface landmarks L_mid of the patient by the dictionary D_mid, its sparse coefficients C can be estimated by minimizing a l1 Lasso problem [10] as defined below:

$$\mathit{arg}{min}_C{\Vert D_{\mathit{mid}}C-L_{\mathit{mid}}\Vert }^2+\lambda {\Vert C\Vert }_1$$ (1)

where ||·||² and ||·||₁ are the l2 and l1 norms of vector, respectively, and λ is a parameter controlling the sparsity of representation. Specifically, the first term is the data fitting term, and the second term is the l1 regularization term used to enforce the sparsity of coefficients C.

Then, with the estimated sparse coefficients C, the patient-specific jaw reference landmarks $L_{\mathit{jaw}}^{\prime }$ can be estimated as

$$L_{\mathit{jaw}}^{\prime }=D_{\mathit{jaw}}C$$ (2)

where D_jaw is the matrix containing all column vectors of jaw landmarks from the aligned normal subjects. With the estimation of these patient-specific jaw reference landmarks $L_{\mathit{jaw}}^{\prime }$, we can further interpolate the dense deformation field (equally dense correspondences) based on correspondences between the deformed patient jaw landmarks L_jaw and the estimated patient-specific reference jaw landmarks $L_{\mathit{jaw}}^{\prime }$ by using the thin-plate-spline (TPS) [11]. Thus, by applying the estimated dense deformation field to the original jaw surface model of patient, we can derive the patient-specific jaw reference surface model. Finally, we combine patient-specific jaw reference model with the assumed-normal midface model to get the whole patient-specific CMF reference model, based on which surgeons can use for guiding their decision-making during surgical planning.

Experiments and Results

3.1 Subjects and Preprocessing

In our experiments, the training data (library) consists of 20 multi-slice CT (MSCT) scans of normal subjects. All the MSCT scans were acquired by a 64-slice GE scanner following a standard clinical protocol: a matrix of 512×512, a field of view of 25 cm, and a slice thickness of 1.25 mm. The patient data consists of 11 CBCT scans of patients with CMF deformity who had already undergone double-jaw orthognathic surgery. They were randomly selected from our clinical archive database. The CBCT scans were acquired using an iCAT scanner (Imaging Sciences Int LLC, Hatfield, PA) following the standard 0.4mm isotropic voxel scanning protocol. All MSCT and CBCT scans are automatically segmented to generate the midface and CMF surface model [12], while their landmarks are annotated manually.

3.2 Qualitative Validation: Patient-specific Reference Model Reconstruction

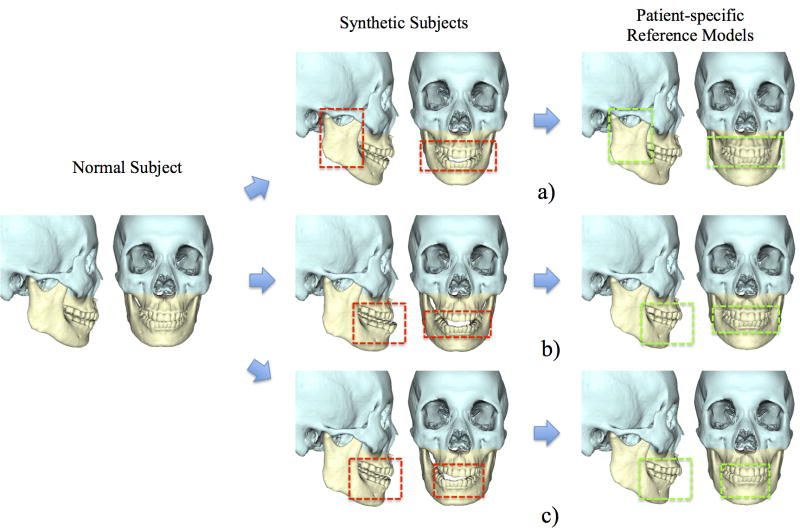
We validated our method using both synthetic subjects and patients. In the validation with synthetic subjects, 3 types of the jaw deformity were created from a randomly selected normal subject: a) Mandibular hypoplasia with severe anterior open-bite; b) Mandibular hyperplasia; c) Mandibular asymmetry (vertical unilateral condylar hyperplasia) (Fig. 3). The original normal models served as the ground truth. Our method was then used to estimate their normal jaw shapes. It is important to note that the normal subject which was used to generate synthetic models was excluded from our dictionary during the step of sparse representation. The experimental results showed that all 3 deformed jaws were successfully recovered to the shape with normal appearance by using our method. More importantly, all estimated reference models are very similar to the ground truth no matter what type of deformity is (mean error of the landmarks: 4.38mm). Note that only the jaws marked in yellow were “deformed” and “recovered”, mimicking a real orthognathic surgery. The midface marked in blue is left untouched.

Fig. 3.

Experimental results on synthetic subjects. The left column shows a normal subject, the middle column shows 3 synthetic patients created from the same subject, and the right column shows our estimated patient-specific reference models. Red frames highlight the jaw deformity, and green frames highlight the corresponding regions on the reference models. The types of simulated deformity include a) Mandibular hypoplasia; b) Mandibular hyperplasia; and c) Mandibular asymmetry.

In the validation using patient data, all 20 normal subjects were included in the dictionary. Fig. 4 showed 2 representative patient models. The diagnosis of the patient in Fig. 4a is maxillary hypoplasia, mandibular hyperplasia and severe anterior open-bite - a typical Class III patient. The diagnosis of the patient in Fig. 4b is unilateral condylar hyperplasia. This is a more complex in which right condyle is larger than the other, resulting in a severe mandibular asymmetry. The original and estimated patient-specific reference models are shown in the right column of Fig. 4, respectively. The results show the deformed jaws were “restored” to the normal shape based on the subject’s midface structure.

Fig. 4.

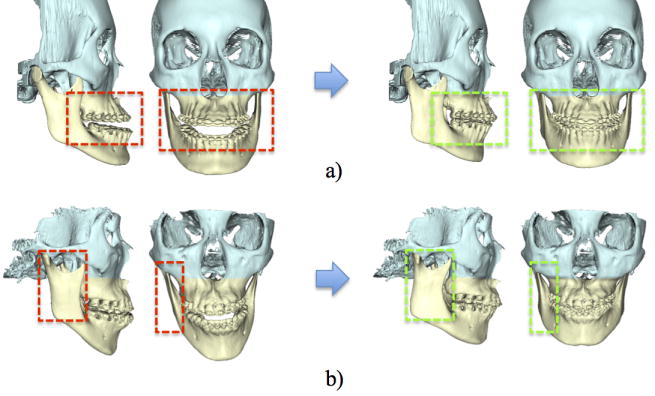
Experiments using patient data. Red frames highlight the jaw deformity, and green frames highlight the corresponding region on the reference models. The diagnoses of these two patients are: a) mandibular hyperplasia and maxillary hypoplasia, and b) vertical unilateral condylar hyperplasia, respectively.

3.3 Quantitative Validation: Normality Score

To quantitatively validate our method, we introduce a measurement, namely normality score, to quantify the deformity of a subject, which ranges from 0 to 1. A higher normality score indicates the patient is more likely to be normal, and vice versa. This score is computed via sparse representation, similar as described in Section 2. The dictionary includes both normal and patient subjects, in which each subject is associated with a score (Score “1” denotes the normal subjects, while score “0” denotes the patients). If a new subject is mainly represented by normal subjects in the dictionary, the subject’s jaw shape tends to be more normal. However, if a new subject is mainly represented by patient subjects, its jaw shape more tends to be deformed. To compute the normality score, we first linearly align all training subjects into a common space based on the landmarks and construct a dictionary D_all by column-wisely stacking all landmarks of training subjects together. To calculate the normality score of a new subject, we first linearly align the landmark of the subject to the common space. Then, dictionary D_all can be used to sparsely represent this new subject, thus obtaining a sparse coefficient C. Finally, the sparse coefficient C can be used as weight to average the scores from the corresponding training subjects for deriving the normality score of this new subject, i.e., C^Tv, where v is the score vector with each entry denoting the score (0 or 1) of one training subject. We calculate normality score on three groups of subjects, including 20 normal subjects, 11 patients, and their corresponding patient-specific reference models, in a leave-one-out manner, i.e., the testing subject is not included in the construction of dictionary D_all.

The statistics of the normality scores from the three groups is summarized in the table within Fig. 5. Statistics shows that typically normal subjects have scores greater than 0.6, while patients have scores less than 0.6. This indicates that the proposed normality score can effectively and quantitatively separate the patients from the normal subjects. The bar graph in Fig. 5 compares the normality scores of each patient with his/her corresponding reference model. It clearly shows that most reconstructed patient-specific reference models have much higher normality scores than the original patient models. This reflects the effectiveness of our method for constructing a normal-looking patient-specific reference model. Furthermore, an interesting observation is that the normality scores of the reference models are even slightly better than those of the normal subjects. This is due to the fact that human face has about 5% of fluctuating asymmetry even in normal population with a possible less than 2mm upper dental midline deviation, while our reference models are “recovered” to have a perfect symmetry with upper dental midline right on the midsagittal plane.

Fig. 5.

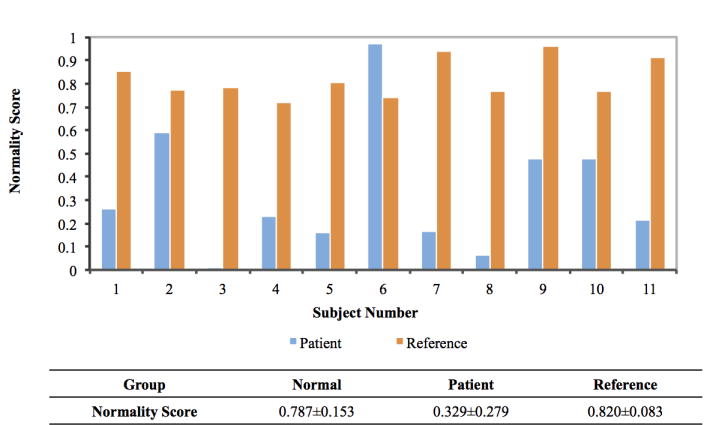
A summary of normality scores for three groups of subjects. The table shows the mean and standard deviation of the normality scores for the Normal subjects, the Patients, and the corresponding patient-specific Reference models. The bar graph shows the comparison between normality scores of patients and their reference models.

Discussion and Future Work

We have presented a novel method to automatically estimate a patient-specific reference model for the patient suffering from CMF deformity. Specifically, we employ the sparse representation technique to preoperatively estimate a patient-specific CMF reference surface model on what the “normal” jaw shape should be. In addition, a quantitative concept to measure the extent of normality of patient, i.e., the normality score, is introduced to validate our method in a quantitative approach.

It is important to note that the estimated patient-specific reference model can only serve as a guide to surgeons, because jaw can only undergo rigid transform and cannot be elastically deformed to match the shape of reference model. In addition, the proposed method is only applicable to orthognathic surgery where midface is assumed normal. Moreover, the accuracy of the normality score can be further improved if more patient samples are added into the dictionary, which may avert the error of patient #6’s score in Fig. 5. Our future work will include validation using more patient data and integration of the proposed method into CMF surgical planning, and further development for syndromic craniofacial deformities, in which all cranial base, midface and jaws are all deformed.