A Pipeline for Copy Number Variation Detection based on Principal Component Analysis

Abstract

DNA copy number variation (CNV), an important structural variation, is known to be pervasive in the human genome and the determination of CNVs is essential to understanding their potential effects on the susceptibility to diseases. However, CNV detection using SNP array data is challenging due to the low signal-to-noise ratio. In this study, we propose a principal component analysis (PCA) based approach for data correction, and present a novel processing pipeline for reliable CNV detection. Tested data include both simulated and real SNP array datasets. Simulations demonstrate a substantial reduction in the false positive rate of CNV detection after PCA-correction. And we also observe a significant improvement in data quality in real SNP array data after correction.

I. INTRODUCTION

Copy number variation (CNV) is a type of genetic variation caused by large segmental insertions or deletions in a DNA sequence. Considering the affected nucleotides, CNVs may account for more overall inter-individual genetic variations than single nucleotide variants combined [1]. While the majority may be mildly deleterious, specific CNVs have been identified to be associated with cancer [2], HIV infection [3], autism [4, 5], and schizophrenia [6, 7].

One commonly used technology to assess genomic CNVs is through genomic single nucleotide polymorphism (SNP) arrays [8-11]. Typically, the Log R Ratio (LRR) and B allele frequency (BAF) are measured for each SNP marker. LRR represents the normalized overall fluorescent intensity from both alleles in a log 2 format, while the BAF measures the fluorescent intensity ratio between two alleles. With the developing high throughput genotyping technique, genomic SNP arrays can provide high density profiles. For instance, the Illumina 1M array has a median spacing of 2.5Kbp between adjacent markers [11]. However, the reduced length of probes may result in a low signal-to-noise ratio (SNR) of hybridization [12], which makes the reliable detection of CNVs challenging. As noted by Scherer et al. [13], the consistency of CNV detection results in the literature is quite low. Therefore, quality improvement emerges as a crucial need for the outputs of the high-resolution arrays. In LRR data, one major source of noise has been identified to be GC-percentage (i.e. the percentage of nitrogenous bases on a DNA molecule that are either guanine or cytosine), whose effect can be eliminated using a regression-based method [14, 15].

In this paper, we propose a data correction approach using principal component analysis (PCA) and present a processing pipeline with PCA-correction incorporated, aiming at improving the reliability of CNV detection through imposing stringent controls on false positives. The performance of the PCA-correction was evaluated through simulations from multiple perspectives, including variance of the raw data, false positive rate (FPR) and false negative rate (FNR) of CNV detection. Furthermore, we applied PCA-correction to a real SNP array dataset, and conducted CNV detection via the proposed pipeline process.

II. METHODOLOGY

The suggested pipeline is illustrated in Figure 1. For LRR data, we first perform outlier smoothing, and then apply PCA-correction to eliminate variations induced by potential confounding factors. Samples are excluded if they fail the quality control after PCA-correction. The corrected data are then segmented using a circular binary segmentation (CBS) algorithm and a hidden Markov model (HMM) algorithm independently. Those segments reported by both algorithms are flagged as potential CNVs, whose qualities are further investigated through SNR. A CNV segment is called only when its SNR passes the preselected threshold. Finally we exclude outlier samples with excessive number of CNVs.

Figure 1.

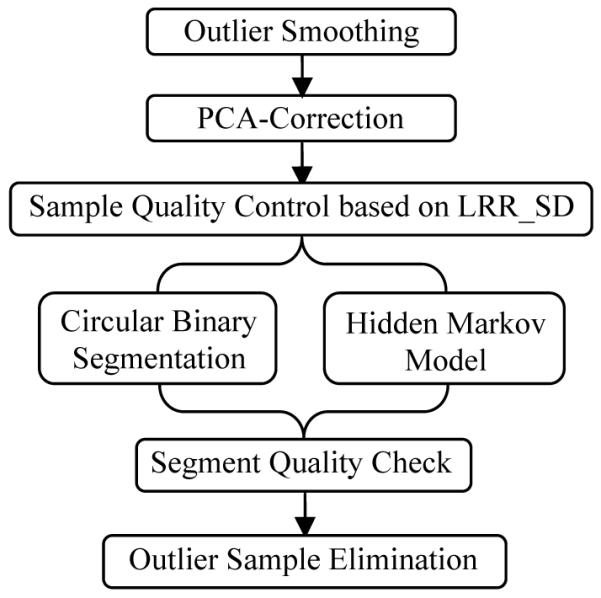
Flowchart of the proposed processing pipeline

A. PCA-correction

A PCA-correction scheme is proposed to remove the variations in the LRR data induced by potential confounding factors. Using PCA, LRR data are decomposed into a linear combination of underlying principal components (PCs), with each PC accounting for a certain amount of variance. If the PC reflects some confounding factor such as scanner artifacts or GC-percentage, then the data quality can be theoretically improved by removing the effect of this PC.

PC extraction is based on singular value decomposition, as shown in (1). X is the LRR dataset composed of m markers and n samples. Each column of V is the projection of a PC, or loadings. S is a diagonal matrix with each diagonal element being a singular value, which is proportional to the square root of the variance represented by the corresponding component. Here, r denotes the number of components. U is the counterpart of V, or the representation of X in the principal component space.

$$X_{m\times n}=U_{m\times r}{S}_{r\times r}{V}_{n\times r}^T(m⪢n)$$ (1)

Pearson correlation or analysis of variance (ANOVA) is used to assess the association of PCs with all the potential continuous or categorical confounding factors. The association test is either evaluated on U, when the factor is a genomic feature along marker space such as GC-percentage, or on V when the factor is a sample feature along sample space such as batch effect. A PC with a significant association after Bonferroni correction is identified to represent a confounding factor and removed as presented in (2). X can be written as a linear combination of r components. If, for example, the k^th component has been identified representing a confounding factor, we simply subtract X_k from the original X to eliminate the variations induced by that factor, and obtain the corrected dataset X_c,

$$X={\Sigma }_{i=1}^r{u}_i{\sigma }_i{\nu }_i^T;X_k=u_k{\sigma }_k{\nu }_k^T;X_c=X-X_k$$ (2)

B. Processing pipeline

Outlier smoothing

Outliers manifest as large negative or positive values appearing at only one marker location. An isolated outlier can affect the regional LRR mean, resulting in incorrectly assigned segments. Here we adopt the method introduced by Olshen et al. [16] for outlier smoothing. Briefly speaking, it is to replace any local maximum or minimum, which is 4-standard deviation (SD) away from its nearest neighbor in the local 5-marker window, using the value of 2-SD plus the median.

Sample quality control

After the outlier smoothing and PCA-correction, the data quality can still vary dramatically from sample to sample. Therefore, samples with standard deviation of LRR data (LRR_SD) greater than 0.28, as recommended in [17, 18], are considered as bad samples, and excluded from subsequent analysis.

Segmentation

Segmentation is performed with two independent algorithms: CBS [16] implemented in MATLAB; and HMM segmentation implemented in PennCNV [14]. The default settings are chosen for both algorithms. A segment is flagged as a potential CNV only when it is detected by both algorithms.

Segment quality check

We further evaluate the qualities of potential CNVs based on SNR. For each potential CNV, we extract a number of neighboring markers to cover a comparable length of base pairs, serving as a reference. Then the SNR is evaluated as the ratio of LRR mean difference between the potential CNV and the reference over the LRR_SD of the reference. A potential CNV is finally validated if its SNR is greater than 1.4 in case of insertions, or greater than 2 in case of deletions, where the thresholds are estimated empirically based on the LRR means of single insertions and deletions, respectively.

Outlier Sample Elimination

Finally based on the detected CNVS, we eliminate those outlier samples for which an excessive number of CNVs are detected (> 3SD).

III. SIMULATION DESIGN

Synthetic SNP array data were prepared to evaluate the effectiveness of the PCA-correction. To closely represent the real data characteristics, we inherited the chromosome 1 markers’ names and positions in the Illumina Human-1M Duo SNP array (97964 markers), and simulated three types of noise effect: GC-percentage [15], batch effect (scanner and processing date) and random noise. A total of 200 samples were generated.

GC-percentage effect

The baseline LRR data were first constructed to incorporate GC-percentage induced noise. For each marker, we computed the GC-percentage G_j, based on UCSC gc5base table (http://genome.ucsc.edu), and applied a linear regression model to create the baseline of LRR data. As noted in (3), L_ij represents the baseline LRR at the j^th marker of the i^th sample; β_i0 and β_i1 are the intercept and the slope, varying across samples and following normal distributions; ε_ij is the normally distributed residual imposed to randomize the GC-percentage effect in each sample.

$$L_{ij}={\beta }_{io}+{\beta }_{i1}\times G_j+{∊}_{ij}(j=1,2,\cdots M)$$ (3)

Batch effect

A common LRR genomic profile was superimposed onto each sample with different weights, to emulate the batch effect. The 2^nd PC extracted from real data was used as the common LRR profile. As shown in (4), the baseline LRR (L_ij) was adjusted by adding the genomic profile with a different weight (α_i) for each sample. We simulated four experiment batches with different weights.

$$L_{ij}^{\prime }=L_{ij}+{\alpha }_i\times P{C}_j(j=1,2,\cdots M)$$ (4)

Gaussian noise

Zero-mean Gaussian noise with various SDs was imposed on each sample to reflect variations induced by unknown factors. We simulated two groups with low-SD and high-SD Gaussian noise, respectively.

True CNVs, including both segment insertions and deletions, were superimposed onto each sample’s adjusted LRR profile. The number of imposed CNVs ranged from 1 to 14 across samples, with a median of 6.

The final simulated LRR data consisted of imposed CNVs and three types of noise. The GC-percentage effect varied across samples (|r_LRR-GC| ranging from 0.01 to 0.74 with a median of 0.28). The overall LRR_SD of each sample ranged from 0.20 to 0.39 with a median of 0.27.

For the purpose of evaluating the effectiveness of PCA-correction, we chose to only apply PennCNV algorithm, instead of the whole pipeline, which requires less computation yet proves the concept. FPR and FNR were calculated by comparing the PennCNV results with the true imposed CNVs. The detection accuracy was evaluated based on the full simulated dataset without excluding bad samples.

IV. EXPERIMENTS

A. Participants

The study was conducted according to the principles expressed in the declaration of Helsinki, approved by the institutional review board of University of New Mexico. A total of 326 healthy participants between the ages of 21 and 55 were recruited, including 100 females age 32.62 ± 10.47 and 226 males age 31.58 ± 9.38. Participants had a minimum alcohol consumption of two binge drinking days per week. Demographic information and behavioral assessment scores were obtained through self-reporting questionnaires administered during interviews with participants. All participants provided written informed consent for data collection and subsequent analysis.

B. DNA genotyping

Participants were instructed to deliver 5 ml of saliva into a sterile 50 ml conical centrifuge tube. DNA was then extracted from saliva, purified, bisulfite converted and hybridized. The Illumina Human-1M Duo BeadChip was used to detect 1,199,187 genome-wide SNP and CNV markers. A focus on autosomes (chromosome 1 – 22), reduced the number of loci to 1,147,842. 13,567 additional loci with missing measurements were also removed. The final dataset included 326 samples and 1,134,275 markers.

V. RESULTS

A. Simulations

Ten independent datasets were tested and results indicated consistent performance. Using PCA-correction, the first two components were identified as representing GC-percentage and batch effect, summarized in Table 2a. After correcting for these two types of noise effects, the number of bad samples decreased from 76 to 40 in the high noise group and 10 to 4 in the low noise group, resulting in improved detection accuracy, as shown in Table 2b and 2c, where we can see a significant improvement of FPR in CNV detection, as well as a slight improvement of FNR. Finally, a performance comparison was made between PCA-correction and regression-based correction [15], as shown in Table 2d. The results indicated comparable detection accuracies, with PCA-correction showing a slight improvement.

Table 1.

PCA and data quality evaluation (simulation)

Table 2a. PCA-correction
Designed feature	GC-percentage		Date and scanner
Identified Component	1st		2nd
P-value	<1E-23		<1E-23
Table 2b. Evaluation of data quality
Data Quality	High noise		Low noise
	σLRR	Nsub_ex	σLRR	Nsub_ex
Uncorrected	0.30±0.03	76	0.25±0.03	10
Corrected (Comp. 1)	0.28±0.02	46	0.23±0.02	4
Corrected (Comp. 1,2)	0.28±0.02	40	0.22±0.02	4
Table 2c. Detection Accuracy: PCA-correction
Total generated markers with CNVs: 75867
PennCNV results	Overall FPR		Overall FNR
Uncorrected	0.6220		0.1374
Corrected (comp. 1)	0.0389		0.0940
Corrected (comp. 1,2)	0.0351		0.0886
Table 2d. Detection Accuracy: regression-based correction
PennCNV results	Overall FPR		Overall FNR
GC-percentage corrected	0.0389		0.0944

Note: high/low noise: group with high-SD/low-SD Gaussian noise, each containing 100 samples; σ_LRR: overall standard deviation of the simulated LRR data for each sample; N_{sub_ex}: number of bad samples failed by quality control; FPR and FNR are calculated with regard to the total number of markers with CNVs.

To separately investigate the influences of different types of noise on CNV detection, further analysis is limited to the GC-percentage corrected data.

We observed a significant group difference between high and low Gaussian noise, in terms of false negatives, as illustrated in Table 3. A further comparison was made among three independent datasets, different only in the level of GC-percentage effect, measured by the absolute correlation between GC-percentage and the simulated LRR data (|r_GC-LRR|). The ANOVA test showed a significant group difference among these three datasets in terms of false positives, as shown in Table 4. However, after correcting for GC-percentage using PCA, the FPRs all went down to a low level around 0.04 and no group difference was observed.

Table 3.

Evaluation of false positives vs. GC-percentage

Uncorrected	GC1	GC2	GC3
|rLRR-GC|	0.35±0.21	0.30±0.18	0.25±0.17
FPs	444±678	236±407	155±334
ANOVA	P-value = 2.34E-08
Overall FPR	GC1	GC2	GC3
Uncorrected	1.1710	0.6220	0.4090
Corrected	0.0413	0.0389	0.0317

Note: GC1, GC2 and GC3 represent the three datasets with different levels of GC-percentage effect, each dataset containing 200 samples. |r_LRR-GC|: absolute correlation between LRR data and GC-percentage.

Table 4.

PCA and data quality evaluation (experiment)

Factor	Component	P-value
GC-percentage	1st 4th 6th 7th	< 1E-23
Gender	7th	6.42E-5
Data Quality	Uncorrected	Corrected
σLRR	0.25± 0.08	0.18 ± 0.05
Nsub_ex	68	14

B. Experiments

In the real SNP array data, four components representing GC-percentage and gender were corrected using PCA. Table 5 lists the PCA results and the data quality evaluation, where 54 samples are saved by PCA-correction. Due to the unavailability of the ground truth, no evaluation was made on FPR and FNR for real SNP array data. After 14 samples were excluded by the quality control, the 312-sample dataset were sent for segmentation and CNV calls. Based on CNVs confirmed through the pipeline, an additional 7 samples were determined to be outliers due to the larger numbers of detected CNVs, and thus excluded. Table 6 demonstrates the final CNV calls from 305 samples. The median number and size of CNVs were comparable to previous reports (~22 CNVs per sample with a median size of 13Kbp) [14].

Table 5.

Statistics of detected CNVs

5228 CNVs: 2220 insertions vs. 3008 deletions
CNV Statistics	Min	Median	Max
NcNv (per sample)	2	17	43
LCNV (Kbp)	0.5	10.5	2916

Note: 305 samples. N_CNV: number of CNVs; L_CNV CNV length.

VI. DISCUSSIONS AND CONCLUSIONS

PCA-correction

PCA-correction provides a complete data decomposition, which allows a non-parametric data correction helping CNV detection by significantly reducing FPR and slightly reducing FNR. Compared to the previously proposed regression-based method [15, 19], PCA-correction shows a slight improvement in detection accuracy for corrected data. More important is the flexibility of PCA-correction which can be extended to correct other categorical confounding factors along sample space, such as the batch effect or input DNA quantity values [20], whose influences on the data may be difficult to isolate otherwise.

FPR vs. FNR

These two measures are employed to evaluate the accuracy of CNV detection. While FPR is greatly reduced after eliminating the variations induced by GC-percentage (Table 2c), a slight improvement is observed in FNR for corrected dataset. The results imply a stronger influence from GC-percentage effect on FPR than on FNR. The ANOVA test in Table 3 shows a significant group difference in the false negatives, but not in the false positives, between the two groups with different levels of Gaussian noise, indicating that it is more likely to miss a true CNV when Gaussian noise level is higher. Further tests on three different levels of GC-percentage effect datasets confirm with previous conclusions. As shown in Table 4, false positives significantly differ among the three uncorrected datasets. After correction, no group difference is observed in either false positives or false negatives. This provides more evidence that GC-percentage induced variations strongly affect false positives.

GC-percentage vs. Gaussian noise

These two factors influence two types of errors in different ways. GC-percentage induces oscillations in the LRR data. Since the CNV detection tries to locate regions with significant alternations in LRR, it is sensitive to oscillatory noise, which explains the higher FPR when GC-percentage effect is stronger. On the other hand, with increased variations induced by Gaussian noise, the difference in LRR between aberrant and normal regions becomes less significant, which leads to false negatives.

CNV call

Final CNV calls incorporate reports from both CBS and HMM methods. The use of two detecting algorithms is a conservative approach. Together with the subsequent segment SNR evaluation, it imposes a highly stringent control on false positives, which is expected to improve the reliability of the confirmed CNV regions and avoid the inflation of CNV calls.

In summary, we propose a PCA-based correction for LRR data, and incorporate outlier smoothing, quality control, two segmentation algorithms and a final SNR evaluation into the processing pipeline for CNV detection. Both simulation and experiment results show that PCA-correction significantly decreases the fluctuations in LRR data, and simulations further confirm that PCA-correction leads to a significant improvement in FPR, along with a slight improvement in FNR. More undesired factors can be corrected through PCA-correction if necessary. Overall, the PCA-correction incorporated pipeline is designed to work with existing CNV detecting algorithms to reduce the false positives in detection and enhance the validity of resulting CNV calls.

Table 2.

Evaluation of false negatives vs. Gaussian noise

Corrected	High noise	Low noise
σ Gaussian	0.28±0.02	0.22±0.01
FNs	21±32	6±11
ANOVA	P-value = 4.92E-06

Note: σ_Gaussian denotes the standard deviation of the imposed Gaussian noise.