Putative Ancestral Origins of Chromosomal Segments in Individual African Americans: Implications for Admixture Mapping

Abstract

Theoretically, markers that distinguish European from West African ancestry can be used to examine the origin of chromosomal segments in individual African Americans. In this study, putative ancestral origin was examined by using haplotypes estimated from genotyping 268 African Americans for 29 ancestry informative markers spaced over a 60-cM segment of chromosome 5. Analyses using a Bayesian algorithm (STRUCTURE) provided evidence that blocks of individual chromosomes derive from one or the other parental population. In addition, modeling studies were performed by using hidden real marker data to simulate patient and control populations under different genotypic risk ratios. Ancestry analysis showed significant results for a genotypic risk ratio of 2.5 in the African American population for modeled susceptibility genes derived from either putative parental population. These studies suggest that admixture mapping in the African American population can provide a powerful approach to defining genetic factors for some disease phenotypes.

Admixture mapping methods have the potential power to map susceptibility genes in complex genetic diseases and phenotypes (Briscoe et al. 1994; McKeigue et al. 2000; Hoggart et al. 2003). These methods should be applicable when the distributions (locations) of susceptibility genes are different in the founding populations and the susceptibility genes have remained linked with alleles or haplotypes relatively unique to one of the founding populations. Theoretically, under these conditions the admixed proband population will show a larger than expected contribution from one parental population.

Previous studies have demonstrated that strong linkage disequilibrium (LD) in the admixed African American (AA) populations can be detected between markers separated by >15 cM (Lautenberger et al. 2000; Parra et al. 2001; Rybicki et 2002; Collins-Schramm et al. 2003). In particular, the ability to detect this long-range linkage disequilibrium appears to be strongly correlated with the ability of the markers to distinguish ancestry (Collins-Schramm et al. 2003). The demonstration of long-range linkage disequilibrium provides support for the application of admixture mapping to complex genetic disease in the AA population. The large linkage disequilibrium intervals theoretically translate into less demanding requirements for both marker saturation and sample size for admixture mapping studies compared with standard association studies using nonadmixed populations (Stephens et al. 1994; McKeigue 1998).

Furthermore, the ability to define ancestry of chromosomal segments in admixed individuals may provide additional power over directly examining linkage disequilibrium. Conceptually, this approach examines the probability of linkage of a trait with the ancestry of a chromosomal location. Theoretically, the ancestral derivation of a particular chromosomal location can be inferred from combining information from multiple loci in the surrounding genome. Because markers separated by >50 kb are unlikely to be in linkage disequilibrium in the parental populations, the ancestry information can be combined by algorithms that condition on linkage disequilibrium created by admixture. Recent studies have developed such computational algorithms and have provided preliminary confirmation that the implementation of this approach in the program STRUCTURE can uncover ancestry relationships (Falush et al. 2003).

The current study was initiated to further investigate the ability to assign ancestry for a chromosomal segment in the AA population by using a dense set of ancestry informative markers (AIMs) similar to what can be reasonably achieved in genome-wide studies. For this investigation, we applied the program STRUCTURE to examine the probability of ancestry in unrelated individuals using estimated haplotype data. This differs from the initial STRUCTURE studies of Falush et al. (2003), in which largely unselected markers at wide intervals and without estimation of haplotypes were used. In addition, in the current study, genotyping data from loci excluded from ancestry analysis were used to simulate cases and controls for risk genes derived from each of the parental populations. The results suggest that current resources can provide estimates of ancestry useful for mapping ancestry-linked disease genes of modest genotypic risk ratios (GRRs) in the admixed AA population.

RESULTS

Estimating Haplotypes in European American (EA), African (AF), and African American (AA) Subjects

Previous studies in our laboratory identified and characterized 14 diallelic EA/AF AIMs that were included within a 60-cM segment of human chromosome 5. We reasoned that haplotypes and chromosomal segment structure analysis would be enhanced by the inclusion of additional AIMs. Review of The SNP Consortium (TSC; http://snp.cshl.org/) and Applied Biosystems (https://myscience.appliedbiosystems.com/) databases suggested that additional SNP AIMs in this region could be easily confirmed by using Assay on Demand SNPs and reagents. As shown in Table 1, an additional 15 AIMs were validated by typing >90 AF and >90 EA subjects. Together, 29 markers (mean EA/AF δ = 0.57; mean EA/AF f = 0.37) spanning a 61-cM distance from 100 to 160.6 cM were selected for the subsequent haplotype and structure studies. The median distance between adjacent markers was 1.2 cM and 1.5 Mb.

Table 1.

Marker Characteristics

			Population Frequenciesd			EA/AFe
Markera	cMb	Mbc	EA	AF	AA	δ	f
MID-1683	100.0	90.3	0.79	0.12	0.22	0.67	0.46
MID-737	106.5	97.6	0.39	0.00	0.08	0.39	0.24
CV3163022	114.8	107.5	0.15	0.77	0.72	0.62	0.38
MID-1272	118.0	109.4	0.89	0.06	0.25	0.83	0.69
MID-883	118.8	110.5	0.23	0.87	0.76	0.64	0.42
MID-1848	119.5	111.3	0.16	0.65	0.50	0.49	0.25
MID-879	120.7	111.8	0.58	0.02	0.17	0.56	0.38
CV118646	121.5	112.2	0.32	0.95	0.83	0.63	0.43
TSC0232289	123.7	113.5	0.00	0.30	0.29	0.30	0.18
MID-739	126.5	115.4	0.65	0.19	0.28	0.46	0.21
MID-1191	126.7	115.5	0.51	0.03	0.12	0.48	0.28
TSC0569173	127.7	116.8	0.63	0.06	0.19	0.57	0.36
MID-1937	128.6	117.8	0.66	0.14	0.29	0.62	0.28
CV2060865	130.8	120.9	0.63	0.10	0.22	0.53	0.30
CV15965557	131.2	121.4	0.20	0.62	0.42	0.42	0.18
MID-990	131.5	121.9	0.31	0.04	0.08	0.27	0.12
TSC0237153	132.3	123.2	0.95	0.40	0.58	0.55	0.34
CV3167763	132.4	123.3	0.91	0.46	0.57	0.45	0.23
CV11532818	133.1	125.6	0.14	0.90	0.72	0.76	0.57
MID-1013	133.7	126.4	0.78	0.34	0.38	0.44	0.19
CV1561700	134.2	127.3	0.63	0.10	0.22	0.53	0.30
MID-768	135.8	130.8	0.82	0.10	0.24	0.72	0.53
MID-1102	136.1	131.6	0.88	0.07	0.22	0.81	0.66
CV8844618	137.1	132.4	0.00	0.25	0.24	0.25	0.14
MID-719	139.1	134.0	0.85	0.31	0.45	0.54	0.30
CV8958376	139.3	134.4	0.12	0.59	0.49	0.48	0.25
CV2083528	142.0	138.5	0.65	0.09	0.18	0.56	0.33
CV1989090	145.0	142.1	0.07	0.93	0.70	0.85	0.73
CV1675518	148.0	146.2	0.62	0.03	0.15	0.59	0.40
CV3220692	151.0	149.9	0.92	0.27	0.41	0.65	0.44
MID-1348	160.6	157.7	0.72	0.21	0.39	0.51	0.26

^aData for markers designated with asterisks were previously published (Collins-Schramm et al. 2003). MID numbers designate Marshfield insertion/deletions (http://research.marshfieldclinic.org/genetics), TSC numbers are as designated by The SNP Confortium (see http://snp.cshl.org/), and CV numbers are as designated by Applied Biosystems (https://myscience.appliedbiosystems.com/).

^bGenetic map positions based on Marshfield map positions. These were interpolated based on the sequence location of genetic markers on this map located within short physical distances flanking the physical location of the markers in the sequence assembly.

^cThe approximate megabase position for each marker was determined by use of the Human Genome Browser (J. Kent, University of California, Santa Cruz, CA), based on the June 2002 human-genome draft assembly, http://genome.ucsc.edu/.

^dAllele frequencies for allele 1 (shorter polymorphism for diallelic indels, and α order of SNPs in forward direction).

^eThe standard variance (also known as the Wahlund variance and shown as the f value or Fst) of each marker (see Methods).

AF, EA, and AA subjects were genotyped for these markers, and the haplotypes were estimated for each individual in each population separately by using the PHASE program (Stephens et al. 2001). The mean probability for the haplotype assignments in each individual was 0.966, 0.954, and 0.933 for the AF, EA, and AA populations, respectively.

Examining Ethnic Ancestry Across a Chromosomal Region

To examine ancestry over this region of chromosome 5, the STRUCTURE program was used under the linkage model. The Bayesian algorithm implemented under this condition examines the correlations between linked markers in addition to using a clustering model to estimate both ancestry of the individual and, importantly for the current study, the ancestry of a particular genomic segment (Falush et al. 2003). First, the estimated haplotypes from the 268 AA individuals were examined together with the phased data from the 90 EA and 90 AF subjects under the condition of two major populations (which are randomly defined as either population 1 or population 2 by the program). The STRUCTURE output file provided the probability that each locus on each haplotype derived from either population 1 or population 2. These data were then expressed as the Ln of the probability ratio (LnPR) that the locus derived from population 1 or population 2. The results provided evidence that blocks of individual chromosomes derived from either one or the other population (Fig. 1).

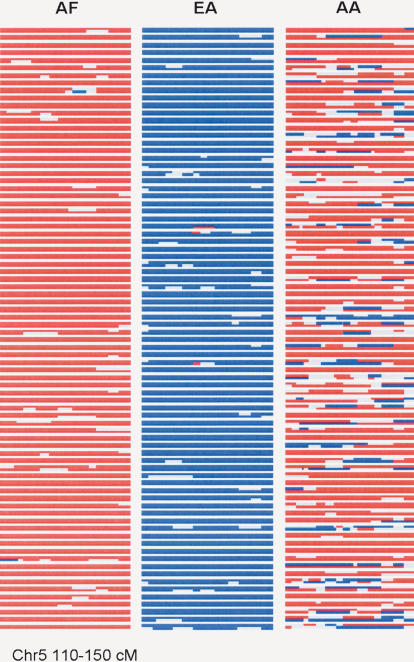
Figure 1.

STRUCTURE analysis of a 40-cM segment of chromosome 5 in EA, AF, and AA. The calculated probable ethnic origin for both chromosomes of 80 subjects from each population on each chromosome is shown with proportional segment length. Chromosome pairs are depicted with spaces between individual subjects. The Ln of the ratio of the probability that each locus on each haplotype in each individual derived from either AF or EA was determined for each individual and coded as red (Ln AF/EA > 2.0), blue (Ln AF/EA < –2.0), or gray lines (LN AF/EA < 2.0, > –2.0). The data shown is from a 40-cM region (110–150) that is derived from the analysis of a 61-cM segment (100–160.6) region using 268 AA, 90 AF, and 90 EA subjects for the locus-by-locus estimation of population ancestry using the program STRUCTURE, version 2.0. The 80 subjects graphically depicted were chosen randomly. The central 40 cM is shown because the ancestry assignments for the ends of the examined segment are less certain. For these analyses, STRUCTURE was run under the linkage model by using 50,000 burn-in and 50,000 replications, with K = 2, phased data, and infer-α.

For the parental populations, the STRUCTURE analysis showed an overwhelming predominance of chromosomal segments derived from population 1 (positive Ln ratios) for the AF subjects and population 2 (negative Ln ratios) for the EA subjects (Fig. 1). For the AF subjects, only four of 90 individuals showed any chromosomal blocks with LnPR <–2.0. Conversely, there were only two chromosomal blocks from the 180 EA chromosomes that appeared to derive from population 1. For AF subjects, the LnPR for 95% of the loci of individual chromosomes exceeded 2.0; for 70%, exceeded 5.0. Similarly in EA, >95% of the loci showed LnPR <–2.0, and 65% were <–5.0.

In contrast to the results for the putative parental population, the AA haplotypes showed substantial contributions from both populations (Fig. 1). As expected, the contribution from population 1 (corresponding to the putative AF population) was much greater than that from population 2 (corresponding to the putative EA population). The mean contribution of ancestry from population 1 was 78%; from population 2, 22%. For many of the chromosomal loci, the probability of correct ancestry determination was high: LnPR >5.0 for 33% of the loci and LnPR <–5 for 5% of the loci. For the majority of loci, the LnPR was either >2.0 (66%) or <–2.0 (13%). Because there were many segments for which ancestry was uncertain, it is difficult to precisely define the length of the segments in AA derived from each population. The vast majority of chromosomal blocks that were derived from each population were >15 cM: For the 268 AA subjects, there was a total of 29 segments derived from population 2 (EA) that were <15 cM (distance defined as the length of continuous LnPR of <–2.0). A recombination frequency between ancestry assignments was estimated at 0.0685 in the AA population, suggesting that, on average, an admixture event took place 6.9 generations ago, assuming a hybrid isolation model (see Discussion).

The AA haplotypes were also examined without the putative parental populations by using the same STRUCTURE parameters. The results were nearly the same, with a similar distribution and ancestry probability of the chromosomal segments. However, without putative parental information, the specific ancestry (African or European) of each chromosomal segment cannot be assigned without the additional analyses (inspection of specific genotypes in the context of parental allele frequency information). In contrast, when these analyses were performed with fewer AIMs (20 rather than 29), the number of ambiguous segments was substantially greater when AA haplotypes were examined without the EA and AF haplotypes (data not shown). When the number of AIMs was decreased even further (<15), the segment assignments for the AA haplotypes were much more ambiguous, with >30% of the chromosomal segments showing absolute LnPRs <2.0 even when the EA and AF parental haplotypes were included.

Admixture Mapping Using Simulated Cases and Controls

To further evaluate the assignment of ancestry and the applicability of these results to admixture mapping, cases and controls were simulated from the 268 AA subjects. The simulations were performed by using the typing results of two diallelic markers to model susceptibility genes originating in the two different parental populations (AF and EA). Marker CV8844618 (AF allele 1, 0.25; EA allele 1, 0.00; map position, 137.1 cM) was used to model an AF susceptibility gene (model 1). Marker MID-990 (AF allele 1, 0.04; EA allele1, 0.31; map position; 131.5 cM) was used to model an EA susceptibility gene (model 2). Setting GRRs of 2.5 and 4.0 in the AA population, 500 cases and 500 controls were selected from the 268 AA subjects that had been genotyped. Haplotypes for the cases and controls for each GRR and model were then separately estimated by using PHASE (Stephens et al. 2001). The genotyping data that were used for haplotype estimation or subsequent STRUCTURE analysis did not include either of the markers used for the models. The simulated haplotypes were analyzed with STRUCTURE by using the same parameters described above. The putative parental haplotypes (90 EA and 90 AF subjects) were included in this analysis because the ability to assign ancestry by STRUCTURE is improved by including members of the parental ethnicities (see above).

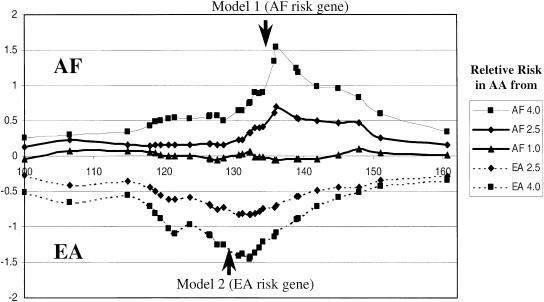
For both the EA and AF susceptibility models, there were peaks in the respective LnPRs (cases minus controls) at the chromosomal location of the modeled markers (Fig. 2). Evidence for the 2.5 RR models was not as strong as for the 4.0 RR models but was still detectable. The peaks were close to the modeled loci: For model 1, hidden locus location was 137.1 and peak probability ratio was 136 cM; for model 2, hidden locus location was 131.5 and peak probability ratio was 131.2 cM.

Figure 2.

Plot of the ancestry probability for both AF and EA susceptibility gene models for a segment of chromosome 5 in AA subjects. The Ln of the probability AF versus EA ancestry is shown on the ordinate and the cM position on the abscissa. The arrows indicate the position of the modeled susceptibility loci, and the symbols and graphs correspond to the relative risk models shown in the legend. The data were derived from results of 268 AA genotyped with 31 diallelic EA/AF AIMs. Two of the markers in the interval were used for determining the cases and controls for each model according to relative risk set for the AA population. These two markers were not included in either the subsequent haplotype or ancestry estimations; 500 cases and 500 control subjects were generated from the 268 typed individuals to conform to the various risk models using a computational algorithm set to the inheritance model and based solely on the two selected markers. The haplotypes of each sample group were estimated by using PHASE (Stephens et al. 2001). The haplotypes of cases and controls for each model were then analyzed together with haplotypes estimated from 90 AF and 90 EA subjects for the locus-by-locus estimation of population ancestry using the program STRUCTURE, version 2.0 (http://pritch.bsd.uchicago.edu/software/readme/readme). The Ln of the ratio of the probability that each locus on each haplotype in each individual was derived from either AF or EA was determined for each sample set and used to calculate the mean probability in each sample set. The confidence levels for identification of the modeled susceptibility genes in each model are discussed in the text.

For these models, the P values were assessed by a comparison of the Ln odd ratio (OR) score between cases and controls using the Wilcoxon rank sum test. Median P values were determined from 100 random samplings of 300 cases and 300 controls from the 500 simulated cases and 500 simulated controls for each model. This assessment of the P value was chosen to minimize aberrant results from sampling variation. For model 1 (AF susceptibility gene) and a sample size of 300 cases and 300 controls, the P values at the best location for RR 4.0 and RR 2.5 (136 cM; Fig. 2) were 2.1 × 10^–14 and 2.8 × 10^–5, respectively. For model 2 (EA susceptibility gene) the P values for RR 4.0 and 2.5 were 2.3 × 10^–10 and 3.7 × 10^–5 at the best location (131.2 cM). These P values are still highly significant after conservative Bonferroni adjustment for the 29 loci examined. Examination of flanking markers showed that the P values, as expected, decreased with the distance from the maximum case-control LnPR. An interval defined by a two order of magnitude decrease in the confidence limit was 12 cM for the AF model RR 2.5 and 21 cM for the EA model RR 2.5. As noted in the Discussion, the P values provided here may be substantially lower than a true data set due to the limitation in the original sample number (268 typed AA subjects) and the resampling of multiple subjects in the simulations.

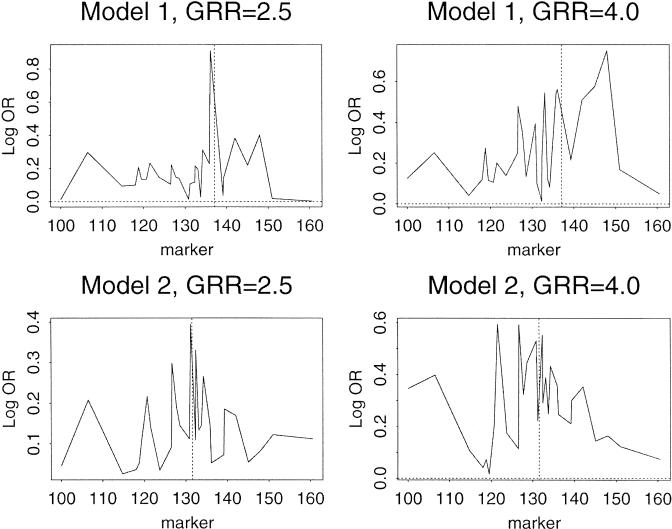
Finally, we examined the results obtained for the same models when LD is examined rather than putative assignment of ancestry. For these analyses the log odds ratio was determined by comparing the alleles of each of the 29 markers in the 500 simulated cases with the 500 simulated controls (Fig. 3). In contrast to the results obtained by using the ancestry estimations, the analysis showed inconsistent results. For example, although a strong signal was observed for model 1 RR = 2.5 at the correct location, the peak signal for model 1 RR-4.0 was >10 cM from the simulated susceptibility gene.

Figure 3.

Log odds ratio comparing the alleles of simulated cases and controls. The panels show the results for each of the 29 markers and the same models described in Figure 2. The alleles for each marker were compared between the cases and controls for each of the models. The log odds ratio of the associated allele (either allele 1 or allele 2) is shown on the ordinate and the cM position on the abscissa. The position of the markers used for model 1 and model 2 are as indicated by the vertical dashed line.

DISCUSSION

In the current study, we show that the West African or European ancestry of chromosomal blocks can be assigned with high probability in the admixed AA population. By using unrelated AA individuals with or without parental information, haplotypes estimated from AIMs typing data were translated into chromosome blocks of ancestral inheritance by using a program, STRUCTURE, which uses clustering algorithms. This is the first demonstration of such chromosomal blocks, although their theoretical existence has been the basis of significant effort in developing admixture mapping tools and techniques. Simulations of cases and controls based on hidden markers provided strong evidence of the accuracy of ancestry assignment as well as the applicability of these methods to admixture mapping of ancestry-linked traits.

The ability to assign ancestry to chromosomal segments in an admixed population is dependent on (1) markers with large frequency differences between the contributing ancestral populations, (2) approximation of the number of generations and/or model of admixture, and (3) a sufficiently dense map of informative markers. These conditions are not independent because, for example, the number of generations since admixture and the information content of each marker will determine the density of markers required to accurately assign ancestry to chromosomal blocks.

With respect to the first condition, previous studies as well as the current study have demonstrated that markers that distinguish very large ancestry differences can be readily identified and characterized (Shriver 1997; Smith 2001; Collins-Schramm et al. 2002a,b; Weber et al. 2002). Recent studies suggest that the world's population can be grouped into six major ancestral groups, five of which correspond to major geographic regions (Rosenberg 2002). Furthermore, our previous studies have suggested that there are only small differences within these major populations (Collins-Schramm et al. 2002a,b). For AIMs distinguishing AF and EA populations, only small differences were observed within divergent African populations (e.g., Bantu-speaking compared with Pygmy ethnic groups; Collins-Schramm et al. 2002a). Finally, both historical evidence as well as DNA studies consistently show that AAs are an admixed population that has contributions from two major ancestral populations: AF and EA (Chakraborty et al. 1992; Shriver et al. 1997; McKeigue et al. 2000; Collins-Schramm et al. 2002a,b). These include modeling studies using AIMs data and initial evaluations of admixture in individual AA (Pfaff et al. 2001; Collins-Schramm et al. 2002a,b). Additional studies in our laboratory are currently addressing this issue, including possible Amerindian contribution to the AA population.

Second, the history of admixture including the number of events over multiple generations and the number of generations since admixture is a critical variable in defining the ancestry of chromosomal blocks. A previous study has provided support for a continuous gene flow model to explain admixture in AA when this model is compared with hybrid isolation for an admixture event occurring 15 generations ago (Pfaff et al. 2001). The current STRUCTURE analysis of our data implied that the overall AA population examined was the result of an admixture event occurring ∼7 generations ago. However, these algorithms assume a hybrid isolation model. Thus, this result is more consistent with the continuous gene flow model because historical evidence would suggest that initial admixture events occurred >10 generations ago. The result is also consistent with a previous study examining the association of ancestry between the Duffy locus (FY) and AT3 locus on chromosome 1 that suggested that on average European gene flow occurred five to nine generations ago (McKeigue et al. 2000) and is not inconsistent with a recent genome-wide study using wide intermarker intervals that provided an estimate of seven to 13 generations (Falush et al. 2003). Further refinement of these estimations and perhaps algorithms to account for individual admixture history may improve the resolution of chromosomal blocks. Regardless, the current data provide empiric support for the ability to define ancestry of chromosomal blocks in AA using the approach described here.

Third, the current study provides some empirical guidelines with respect to the practical requirements for AIM density and informativeness for initial characterization of chromosomal blocks in the AA population. For the studies herein, with the exception of the extreme ends of the chromosomal segment examined, for each 10-cM or 10-Mb block a cumulative f > 1.5 was achieved. When this density was reduced by ∼30% by decreasing the number of AIMs, the ambiguous assignment of chromosomal blocks was greatly increased. These results are not inconsistent with previous estimates by McKeigue et al. (2000) suggesting that ∼1000 biallelic markers with an average f-value of 0.4 would be required for admixture mapping. As discussed, the current results suggest that, on average, presumably due to continuous gene flow, a lower number of generations since admixture is applicable for the AA population and, hence, a lower requirement for information content density. The marker informativeness and density achieved in the current study should be obtainable for genome-wide studies in AA using current resources.

It is also worth noting that the best map position of AIMs in a specific admixed population may not be as simple as defining the megabase position or the interpolated genetic map position within the commonly used Genethon or Marshfield map. Hot and cold regions for meiotic recombination favor the use of genetic maps. However, these maps are largely or totally based on analyses of European or EA families and may not accurately reflect the meiotic recombination in other ethnic groups. For the current study, the results obtained using centimorgan or megabase positions were nearly the same, suggesting this may not be critical (data not shown). However, it is not clear whether this may be a critical factor in other genomic regions.

As part of the current study, we used the assignment of ancestry blocks in simulated cases and controls to both support the validity of these assignments as well as to test a potential method for admixture mapping of traits. In these analyses, a GRR of 2.5 in the AA population could be linked to chromosomal blocks both for a locus modeled for a risk gene originating in AF, present in 25% in AF and 0% in EA, and similarly for a risk gene originating in the EA, present in 4% in AF and 31% in EA. It is, of course, uncertain what the actual frequency of risk genes will be in the two populations for different diseases or traits. However, current evidence suggests that many regions of the genome contain sequence variation between major ethnicities that may be the result of selection in one or both populations (Akey et al. 2002). Thus, large differences in the allele frequencies may be present in the admixed population.

In the current study, very similar results could be obtained without using putative parental population haplotypes. At first, this finding appears surprising given the difficulty in assessing admixture proportions in mixed populations without parental genotypic information. However, in the current study the markers were all tightly linked, presumably allowing the STRUCTURE clustering algorithm to more correctly assign ancestry under the linkage model conditions used. This linkage model, by grouping the linked alleles that must come from the same population, can provide more accurate estimates of the ancestry vector (Falush et al. 2003). When markers were more widely spaced, the ability to define the putative ancestral segments without parental haplotypes was, in fact, greatly impaired (data not shown).

This study also had several limitations. First, the study examined only a single genomic region. Second, the uncertainty in haplotype assignment was not accounted for in the STRUCTURE analysis. Notably, the simulated model examined also showed similar results when genotype data rather than the estimated haplotypes were analyzed. However, the genotype data do not provide an explicit examination of ancestry of both chromosomes for a given chromosomal segment but rather estimate the probability for the population of origin of the maternal and paternal alleles. Under the genotype model, the ancestry haplotype of the segment cannot be derived. At present, it is unclear whether estimation of haplotypes will improve the power of admixture mapping, and this issue, including an approach to account for uncertainty in marker haplotypes, is under further investigation.

The third, and perhaps most important, limitation is that the simulations were based on the typing results of only 268 subjects and thus required multiple sampling of the same subjects to obtain the sample sizes used for the 500 simulated cases and 500 simulated controls for each model. For the 2.5 GRR models, a total of 209 and 222 of the 268 were represented in the cases for the two models, respectively, compared with 267 and 268 of the 268 subjects that were represented in the simulated controls for these models. Of more potential concern, due to chance, 10 of the subjects were represented >5 times (maximum, nine times) for the cases in model 1, and 14 of the subjects were represented >5 times (maximum, 10 times) for the case in model 2. Thus the P values presented in this article are likely to be larger than with real data sets due to this limitation. Thus, additional and more extensive studies of multiple genomic regions will be needed to prove the general applicability of the current results.

In the current study, the linkage of modeled susceptibility genes to the estimated ancestry of chromosomal segments provided a much more powerful approach than did examination of LD to specific markers. The latter was inconsistent, presumably based on the limited information provided by each marker and the chance that some individual markers will not be in strong LD with the modeled susceptibility gene. For example, in model 2, GRR = 4.0, the marker closest to the modeled susceptibility gene showed a log OR of 0.25, whereas a marker 10 cM proximal to the modeled susceptibility gene showed a log OR of ∼0.6. In contrast, the linkage to ancestral segments uses only the ancestry information and does not rely on individual marker LD. Because presumably all of the LD is the result of admixture rather than true disease LD within the original population, the correct assignment of ancestry would capture all information.

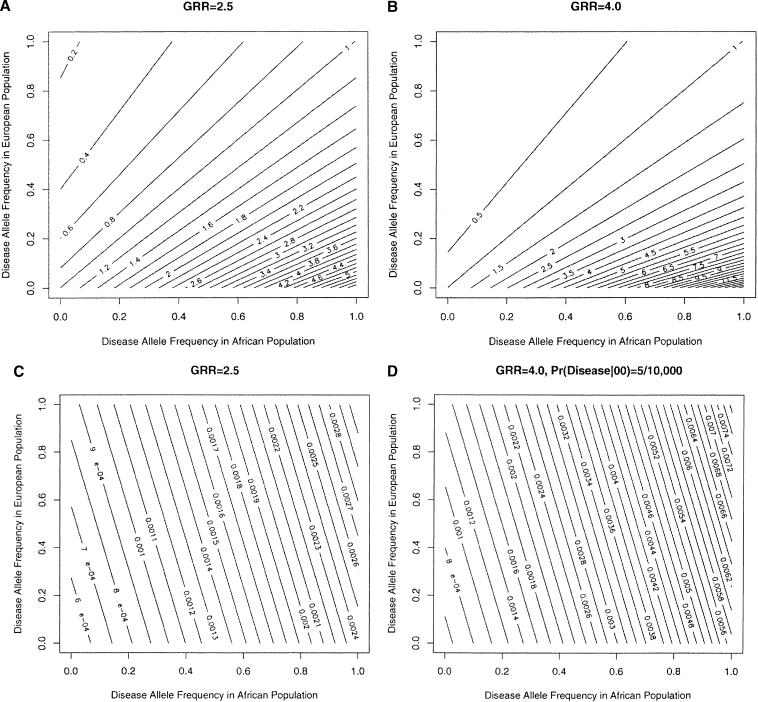
Previous studies have examined the potential power of admixture with respect to population risk ratios (McKeigue 1998). As shown in Figure 4, A and B, population risk ratios can be related to different GRRs in the admixed population by examining the disease allele frequencies in the two parental populations. In the current study for the models simulated on real typing data, the GRRs of 2.5 and 4.0 correspond to population risk ratios of ∼2.0 and ∼3.0, respectively. These results therefore provide additional support for the feasibility of admixture mapping in scenarios in which the population risk ratios are moderate. In practice, this method could be applied to a whole-genome study, in which case a genome-wide significance can be evaluated by methods similar to those used by other genome-wide linkage studies (Lander and Kruglyak 1995).

Figure 4.

Contour plots show the relationship between genotypic risk ratio in the admixed population and disease allele frequencies in two parental populations. In panel A (GRR = 2.5) and panel B (GRR = 4.0), the contour lines show the population risk ratios corresponding to the disease allele frequencies. In panel C (GRR = 2.5) and panel D (GRR = 4.0), the contour lines show the disease prevalence in the admixed population attributed to the susceptibility gene as a function of the disease allele frequencies in the parental populations.

GRRs in the admixed population and disease allele frequencies in the parental populations can also be related to disease prevalence that can be attributed to the putative susceptibility genes provided that a probability of disease in noncarriers is estimated (Fig. 4C,D). If we assume a disease probability in noncarriers of 5 × 10^–4, the simulated disease locus for model 1 GRR2.5 and model 1 GRR4 correspond to disease prevalences of 9 × 10^–4 and 1.5 × 10^–3, respectively. For model 2 GRR 2.5 and GRR 4.0, the corresponding disease prevalences are 6 × 10^– 4 ⁴, respectively. Thus, under certain disease allele fre- and 8 × 10^– quencies, the current study supports the ability of the admixture mapping approach to define susceptibility genes that can account for relatively small differences in disease prevalence.

In this study, a possible method for admixture mapping in a case/control study is illustrated. Other methods of admixture mapping are currently under development in several laboratories. These include (1) a method in which linkage is examined by conditioning on the estimated admixture of both parents by using a multipoint analysis of the marker data informative for ancestry, even when parental data is missing (McKeigue 1998; McKeigue et al. 2000); (2) a multipoint linkage disequilibrium method (Zheng and Elston 1999); and (3) a likelihood approach being developed by our group (C. Chang, K. Chen, M.F. Seldin, and H. Li, in prep.). The current study and the likelihood approach we are developing differ from the other approaches by explicitly using estimated haplotypes in determining the ancestral affiliation of chromosomal blocks. Also, in contrast to the parental conditioning approach, these methods do not condition on admixture but rather provide evidence that favors one chromosomal region compared with other regions. An extension of this type of approach, in which the evidence for linkage in cases alone is examined by comparing the ancestry of different chromosomal regions, is currently being developed. Future studies comparing the power of these different approaches will be useful in the practical application of genome-wide admixture mapping to complex human diseases in recently admixed populations.

METHODS

Populations and Samples

Blood- or buccal-cell samples were obtained from all individuals, according to protocols and informed-consent procedures approved by institutional review boards and were labeled with an anonymous code number. DNA samples were prepared from blood or buccal-cells as previously described (Bali et al. 1999). None of the individuals were first-degree relatives of each other, and ethnicities were self-described. The EA and AA individuals were random volunteers from northern California. AF samples were Bantu-speaking members of the Edo (Bini) ethnic group as previously described (Collins-Schramm et al. 2002a).

Markers and Conditions

A panel of 14 diallelic indel and 15 SNP AIMs was used to examine the population structure of a segment of chromosome 5, and an additional two markers were used for modeling. These included 14 markers previously published (Collins-Schramm et al. 2003) and an additional 15 markers characterized in this study (Table 1). Two additional markers, CV8844618 and MID-990, were used in the modeling studies (Table 1). Physical map positions were determined from the Human Genome Browser (J. Kent, University of California, Santa Cruz, CA), based on the June 2002 human-genome draft assembly (see the Web site of the UCSC Human Genome Project Working Draft). The genetic map positions were based on Marshfield map positions (see Web site of The Marshfield Center for Medical Genetics). These were interpolated based on the sequence location of genetic markers on this map that were located within short physical distances flanking the physical location of the markers in the sequence.

The indel markers were amplified by using a standard PCR protocol previously reported (Collins-Schramm et al. 2002b) in a 9700 GeneAmp PCR System. PCR products were electrophoresed on a 3700 DNA Analyzer and analyzed with Genotyper software (PE Applied Biosystems).

Fourteen of the SNPs were genotyped by TaqMan assays scanned on an ABI 7900 Analyzer (PE Applied Biosystems). For 12 of the SNPs, the manufacturer's conditions and reagents for Assays-on-Demand were used (PE Applied Biosystems, CV numbers provided in Table 1). For TSC0569173 ABI Primers-by-Design (PE Applied Biosystems) were obtained and assayed by using the same condition as the Assays-on-Demand SNPs. The TaqMan assays were analyzed by using software (SDS v.2.0) provided by the manufacturer (PE Applied Biosystems).

The TSC0232289 and TSC0237153 SNPs were assayed by a primer extension method using the ABI Prism SNaPshot Multiplex System kit (PE Applied Biosystems) and the ABI 3700 DNA Analyzer. The PCR primers for TSC0232289 were as follows: forward, 5′-CCAACCCCTTTACTAGGCACAT-3′; reverse, 5′-GG GAATCCCAGGGAATACGTTA-3′. The primer used for the extension reaction was AAACTAACAAAACACACCCTAAATGCA TCTAA. The PCR primers for TSC0237153 were as follows: forward, 5′-GACCAAAGACAGCAGGTTTGC-3′; reverse, 5′-TAGCCCTGCTAAGTAGTCCATTCC-3′. The primer used for the extension reaction was AAAAAAAAAAAAAAGCCTTTCCA GAATCTCTGAGGTCA. The primer extension data was analyzed by using the GeneScan and Genotyper software from ABI.

Estimation of Haplotypes

Haplotypes for each population were separately estimated by using PHASE (Stephens et al. 2001). PHASE was run under the default parameters (10,000 iterations, 100 thinning intervals, and 10,000 burn ins).

Statistical Analyses of Chromosomal Segment Structure

Estimated haplotypes were examined for ancestral population structure by using STRUCTURE 2.0 (Pritchard et al. 2000; http://pritch.bsd.uchicago.edu/software/readme/readme.html). This program uses a Bayesian clustering algorithm to examine the population structure of each individual. The analyses used a linkage model option that implements a model allowing for admixture linkage disequilibrium. The analysis was performed without prior assignment of population affinity and was run under the condition of phased data, two populations, and an independent α, and using 50,000 replicates during both the burn-in and simulation phases. Nearly identical results were obtained for multiple runs by using these conditions. The results were expressed as the natural LnPR that the locus derived from population 1 or population 2.

Statistical Analyses of Population Variances

The standard variance (also known as the Wahlund variance [Wahlund 1928] or Wright's F statistic and shown as the f value or Fst) of each marker was calculated between populations. It is calculated by the following formula, in which μ_x is the frequency of allele 1 in population x and μ_y is the frequency of allele 1 in population y:

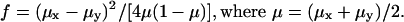This value is a measure of the ethnic information provided by a marker, and ranges from zero (noninformative) to one (completely informative). For each population comparison, the f values of all markers were averaged to obtain the mean standard variances.

Disease Model Simulations

Sampling from the 268 genotyped individuals was performed under multiplicative models of GRR of 2.5 or 4.0 for the modeled markers by using a probability of disease in noncarriers [Pr (disease|11)] = 0.000625. The markers used for modeling were CV8844618 (AF allele 1, 0.25; EA allele 1, 0.00) and MID-990 (AF allele 1, 0.04; EA allele1, 0.31) for AF and EA susceptibility genes, respectively.

Wilcoxon Rank Test

A Wilcoxon rank sum test was used to provide a statistical test for the identification of a susceptibility gene using the estimated ancestry probabilities. The rationale is that we would expect a difference in the ancestry probability between cases and controls in the region close to the disease locus. This test was performed by comparing the median LnPr(AF)/Pr(EA) between cases and controls, where Pr(AF) is estimated by STRUCTURE. We applied this nonparametric test to each locus and comparing all individual cases with all controls with respect to ancestry distribution. Because this test is based on the rank position of the probabilities, the extreme probabilities (∞ and –∞) define the maximum and minimum rank. This provides a more robust test than do alternative tests, such as a t test, for comparing the mean of the LnPR or a logistic regression analysis, each of which requires a parametric distributional assumption. One hundred random samplings of 300 cases and 300 controls from the 500 simulated cases and 500 simulated controls were examined for each model. The median P value from the Wilcoxon test of these samplings was then used as the P value. This assessment of the P value was chosen to minimize aberrant results from sampling variation. The alternative approach of simulating multiple data sets was not used owing to the laborious procedure (individual PHASE and STRUCTURE runs) necessary for analyzing each data set separately.