Building Genomic Profiles for Uncovering Segmental Homology in the Twilight Zone

Abstract

The identification of homologous regions within and between genomes is an essential prerequisite for studying genome structure and evolution. Different methods already exist that allow detecting homologous regions in an automated manner. These methods are based either on finding sequence similarities at the DNA level or on identifying chromosomal regions showing conservation of gene order and content. Especially the latter approach has proven useful for detecting homology between highly divergent chromosomal regions. However, until now, such map-based approaches required that candidate homologous regions show significant collinearity with other segments to be considered as being homologous. Here, we present a novel method that creates profiles combining the gene order and content information of multiple mutually homologous genomic segments. These profiles can be used to scan one or more genomes to detect segments that show significant collinearity with the entire profile but not necessarily with individual segments. When applying this new method to the combined genomes of Arabidopsis and rice, we find additional evidence for ancient duplication events in the rice genome.

The comparison of genomic sequences across species provides valuable insights into many aspects of their biology. Apart from a better understanding of the various biological processes through the comparative analysis of the genes involved, the availability of an ever-increasing amount of genomic sequences from a large variety of organisms also makes it possible to study the processes that drive the evolution of genomes. To study the organization and evolution of genomes, homologous regions within or between genomes need to be identified. However, owing to different types of rearrangements (e.g., inversions, translocations, and transpositions), gene duplications, and gene loss, their identification is not always obvious.

In the past years, several methods have been developed to detect homologous genomic segments based on different strategies. Generally, these methods can be divided into either alignment methods that align primary genomic DNA sequences or map-based methods that compare genetic or physical maps of genomic fragments. Alignment methods have the advantage that they can detect homology at the highest resolution possible, that is, at the nucleotide level. Both pairwise (e.g., DOTTER, Sonnhammer and Durbin 1995; MUMmer, Delcher et al. 2002; PipMaker, Schwartz et al. 2000; SSAHA, Ning et al. 2001; BLAT, Kent 2002; BLASTZ, Schwartz et al. 2003b; AVID, Bray et al. 2003; LAGAN, Brudno et al. 2003) and multiple (Multi-LAGAN, Brudno et al. 2003; MultiPipmaker, Schwartz et al. 2003a) sequence alignment tools have been developed for the comparison of genomic sequences at the DNA level. However, when there is considerable sequence divergence, it becomes difficult to detect similarity at the nucleotide level and thus to infer homology using a direct sequence comparison approach.

On the other hand, map-based methods such as LineUp (Hampson et al. 2003), FISH (Calabrese et al. 2003), or ADHoRe (Vandepoele et al. 2002a) allow detecting homology even between highly divergent genomic sequences. Rather than identifying primary sequence similarity, map-based methods look for statistically significant conservation of gene content and order, which is commonly referred to as collinearity. Obviously, these methods depend on the availability of a genetic map or an annotation of a genomic sequence. Because genetic maps, based on molecular markers, only provide limited resolution, physical maps derived from completely annotated genome sequences are preferred when looking for inter- or intragenomic homology. Map-based approaches have already proven their importance in analyzing the rate and patterns of chromosomal rearrangements (see, e.g., Coghlan and Wolfe 2002; Pevzner and Tesler 2003) and greatly aided in uncovering the genomic duplication past of different eukaryotic organisms such as yeast (Wolfe and Shields 1997; Wong et al. 2002), human (McLysaght et al. 2002; Lundin et al. 2003), Arabidopsis (Simillion et al. 2002; Bowers et al. 2003), and rice (Vandepoele et al. 2003).

Recently, we have shown that homologous relationships between two genomic segments that, at present, no longer show any significant collinearity, can still be recognized through comparison with a third segment (Simillion et al. 2002; Vandepoele et al. 2002b). If two segments show collinearity with the same third segment, but not with each other, these two segments, through transitivity, must be homologous as well. Inferring such higher-order relationships is important when determining the actual number of duplication events a genomic segment has undergone, as was previously demonstrated for Arabidopsis (Simillion et al. 2002). Although considering such transitive homologies allows the identification of many, previously undetectable, homologous genomic segments (Simillion et al. 2002), it is still required that each of the homologous segments shows significant collinearity with at least one other segment so that they can be identified by direct segment-to-segment comparison.

Obviously, this is not always the case. Indeed, one can imagine a homology detection problem in which within a set of mutually homologous segments (referred to as a multiplicon; Simillion et al. 2002), one or more segments have diverged so much from the others in gene content and order that they no longer show any significant collinearity with any of the other segments. Such occurrences of segments that are “in the twilight zone” of homology have already been demonstrated (Ku et al. 2000; Zhu et al. 2003).

In these cases, homology could only be inferred by comparing the gene content and order of such a single highly diverged sequence segment with the combined gene content and order of the other segments in the multiplicon. However, at present there are no methods available to automatically identify such homology relationships. Consequently, there is a clear need for an algorithm that is able to uncover homology between segments by comparing the total gene content and order of a group of mutually homologous segments with that of an individual segment (Ku et al. 2000; Zhu et al. 2003). Here, we present a new software tool called i-ADHoRe (iterative Automatic Detection of Homologous Regions) that has been especially developed to address this need. We demonstrate that, by constructing “profiles” that combine gene content and gene order information from their constituting homologous segments, additional heavily degenerated but homologous segments can still be identified.

METHODS

Preparation of the Input Data

The input for i-ADHoRe consists of a set of genomic fragments (entire chromosomes, contigs, or BAC sequences) from any number of organisms. Of these fragments, only the gene products and their strand orientation are considered. Because of this, we further refer to these genomic fragments as “gene lists.” Within the total set of gene products from all gene lists, pairs of homologous genes are determined after conducting an all-against-all BLAST search using the method of Rost (1999). Briefly, this method uses an empirical function based on the length of the alignable region and the number of identical residues between two protein sequences to determine if these two sequences are homologs or not. Next, tandemly duplicated genes (i.e., consecutive series of homologous genes on a gene list) are remapped onto the member with the lowest index in the gene list.

Construction of the Gene Homology Matrices (GHMs)

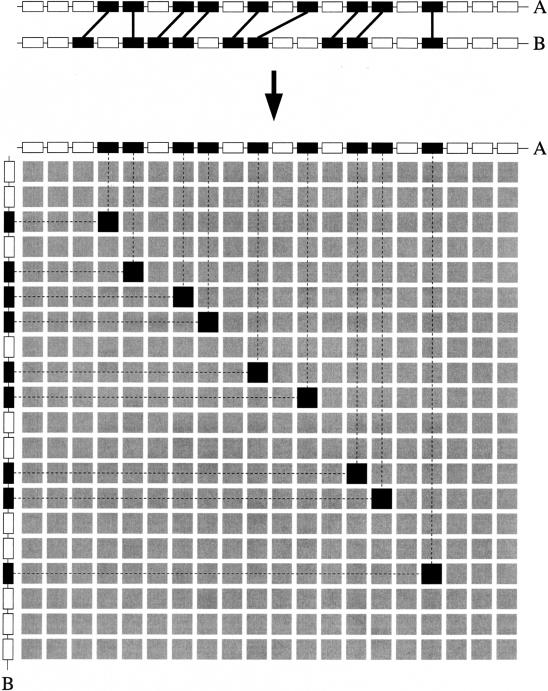
After the preparation steps described above, the entire data set (i.e., the complete set of gene lists) is scanned for segments that are homologous to each other. This is done by constructing a “gene homology matrix” (GHM) for every pair of gene lists in the data set. In this GHM matrix, the rows and columns correspond to the positions of the gene products in their respective gene lists. A cell will contain a nonzero value if the gene products of the corresponding row and column are homologous to each other. In addition, a cell will be marked as positive when both gene products involved are transcribed on the same DNA strand and as negative if they have opposite transcriptional orientations. In such a GHM, segments that are homologous between the two genomic fragments become apparent as series of diagonally arranged nonzero elements in the matrix (see Fig. 1). Because these nonzero elements represent pairs of homologous genes, a series of diagonally arranged elements depicts a pair of regions that show conserved gene content and order, that is, form a pair of collinear regions. A set of homologous genomic segments is referred to as a multiplicon (Simillion et al. 2002), whereas the multiplication level of a multiplicon denotes the number of segments the multiplicon contains. Nonzero, that is, homologous elements in the GHM are referred to as anchor points. The boundaries of the segments that form a multiplicon are determined by considering the coordinates of the extreme-most anchor points in the cluster (Vandepoele et al. 2002a).

Figure 1.

Construction of a gene homology matrix (GHM). The top section shows two collinear genomic segments A and B. Every box denotes a gene. The black boxes connected by lines represent pairs of homologous genes (anchor points). The bottom section shows the actual GHM derived from these two segments. Every column represents a gene of segment A, whereas every row corresponds to a gene of segment B. A cell will contain a nonzero value (i.e., is marked in black) if the gene products of the corresponding row and column are homologous to each other.

Detection and Statistical Validation of Level 2 Multiplicons

Once the GHMs are constructed for every possible pair of gene lists in the data set (thus n(n – 1)/2 pairs for n gene lists), each matrix is presented to the previously described ADHoRe algorithm (Vandepoele et al. 2002a). This algorithm automatically detects all level 2 multiplicons present in the data set as clusters of minimum three anchor points in the GHM. In short, this is achieved by clustering neighboring anchor points in the GHM using a special distance function (diagonal pseudodistance, or DPD). This function returns a lower distance measure for diagonally arranged elements in a matrix than for horizontally or vertically arranged elements (see Fig. 2) and is given by:

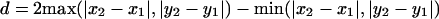(1)

In this way, elements that fit onto the same diagonal line are clustered together. The process is controlled by two parameters: G, the maximum DPD distance between two anchor points in a cluster, and Q, the degree to which the anchor points in a cluster must fit on a single diagonal line (Vandepoele et al. 2002a).

Figure 2.

The diagonal pseudodistance (DPD) for a given cell in the matrix to the central cell marked by the black dot. The DPD is smaller for diagonally arranged cells (gray boxes) than for elements deviating from the diagonal. Note that hatched cells are considered to be on an infinite distance from the central cell because in a GHM nonempty cells on these positions denote tandemly duplicated genes.

To assess which of the detected multiplicons reflect true homology and which ones are likely to be generated by chance, a new statistical method was developed. Again, this method considers a multiplicon as a cluster of anchor points in the GHM. It starts from the observation that a cluster that was generated by chance generally contains fewer anchor points than a real significant cluster, whereas also the average DPD distance between these anchor points is greater (Vandepoele et al. 2004). In other words, the more anchor points a cluster contains and the closer these anchor points are located to each other, the less likely it is that this cluster was generated by chance.

Consider a GHM with dimensions m × n and i nonempty cells. The probability to find a nonempty cell corresponds to the density of that matrix and is given by:

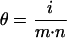(2)

Next, consider cluster C containing the anchor points {(x₁, y₁),..., (x_n, y_n)}. Let us assume that these anchor points are sorted by their x-coordinates so that for every anchor point (x_i, y_i), with 1 ≤ i < n, x_i ≤ x_i+1. Let d_i be the DPD distance between (x_i, y_i) and (x_i+1, y_i+1). The total number of cells in a matrix that lies within a DPD range of d_i from the anchor point (x_i, y_i) and for which x > x_i and y > y_i is then given by (see Fig. 3):

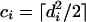(3)

Note that ⌈...⌉ brackets mean “if the number inside the brackets is not an integer, round up to the next integer.”) This number corresponds to the number of cells the ADHoRe algorithm had to search to detect, starting from anchor point (x_i, y_i), the anchor point (x_i+1, y_i+1). Using the binomial distribution, the probability of observing a single anchor point within a distance d_i of (x_i, y_i) is then given by:

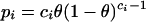(4)

Figure 3.

Detection of a level 2 multiplicon (i.e., containing two homologous segments). For every anchor point, the area of cells the algorithm has to search to detect the next anchor point is marked. Thus, starting from the upper left anchor point, the algorithm detects four additional anchor points.

Thus, when ADHoRe starts searching from the first anchor point (x₁, y₁), it detects n – 1 anchor points in an area of c = Σ_i c_i cells. The probability of observing such a pattern by chance is given by:

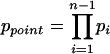(5)

In other words, equation 5 above expresses the probability to find, starting from one anchor point (x₁, y₁) a cluster of n – 1 additional anchor points within a total area of c = Σ_ic_i cells by chance. However, ADHoRe tries to make clusters starting from every potential anchor point (every nonzero element) present in the GHM. In other words, if there are p such elements in the GHM, there will be p attempts to find cluster C. Therefore,

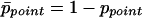(6)

expresses the probability not to find cluster C from a given anchor point. The probability not to find C from any of the p anchor points is then given by:

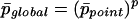(7)

The final probability to find cluster C in our entire GHM is finally given by:

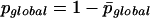(8)

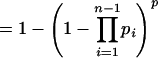(9)

In other words, the value of p_global depends on both the number n of anchor points in cluster C and the overall density of anchor points in the matrix θ. If, now, for a given cluster C in the GHM, p_global exceeds a user-defined threshold value (e.g., 0.0001), then this cluster/multiplicon is considered to be generated by chance and discarded.

Detection of Higher-Level Multiplicons

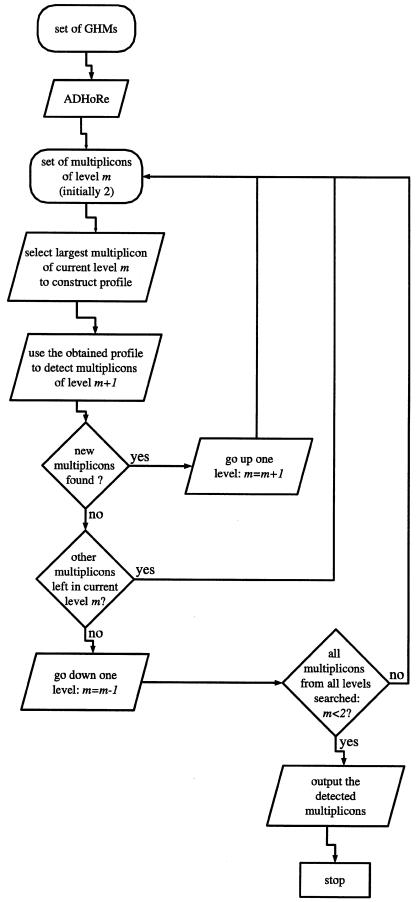
At this point, the algorithm has detected a set of statistically valid multiplicons with a multiplication level of 2. It now enters an iterative loop, where it tries to add additional segments to these multiplicons and thus to increase the initial multiplication level. This is done by sorting all the multiplicons of the current multiplication level (initially 2) according to the number of anchor points they contain. Next, the largest multiplicon (i.e., containing the most anchor points) is selected, and its constituting segments are used to construct a profile that combines the gene order and content information of those segments. Here, a profile is simply a multiplicon of which the constituting segments have been aligned so that pairs of homologous genes, if possible, are placed at the same position. The exact alignment procedure is described below. This profile is then used to “scan” (see below) all gene lists present in the data set for segments that are homologous to the profile. The segments that are already contained in the profile are masked.

From these homologous segments, again the largest one is selected and added to the multiplicon, thereby increasing its multiplication level, and updating the corresponding profile. As a result, the profile will now become more sensitive to detect homology relationships (see Fig. 6 below), because it combines information from more segments. Therefore, it is used again to scan the entire data set for additional homologous segments. This process is repeated until for a given multiplicon no more additional segments can be found. Then, the algorithm selects the next largest multiplicon from the previous multiplication level to repeat the entire process. The algorithm stops when no more segments can be found that are homologous to any of the profiles. An overview of the entire procedure is given in Figure 4.

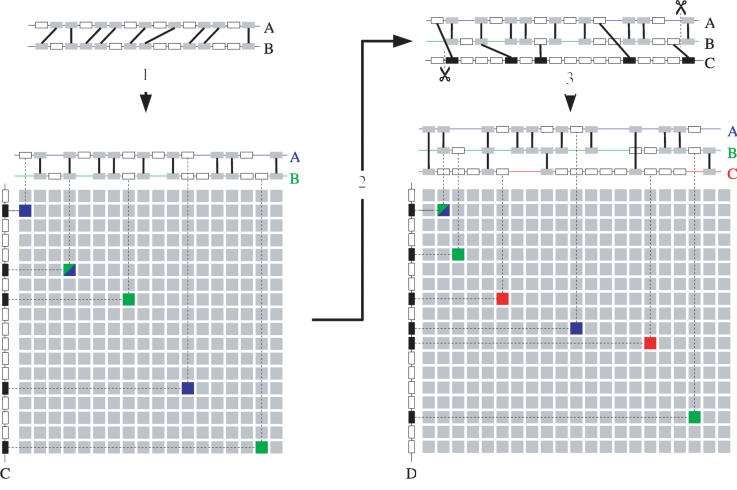
Figure 6.

Detection of homology with a genomic profile. (1) An initially detected level 2 multiplicon (a pair of homologous chromosomal segments) is aligned to form a profile as described. The gray boxes connected by lines represent pairs of homologous genes (anchor points) between the two segments. Note that, as a consequence of the alignment procedure, sets of nonhomologous genes (empty boxes) too can be placed on the same position in the profile. A homology matrix can now be constructed by comparing this profile with the genes of a chromosomal segment (segment C on the left of the matrix). Anchor points in the matrix are detected whenever a gene of this chromosomal segment is homologous to one of the genes in any of the segments in the profile. The blue squares represent anchor points between segments A and C, the green between B and C. A blue-green square denotes an anchor point between the three segments. Note that segments A and B each individually only have three anchor points with segment C but when combined in a profile, A and B together have five anchor points with C (counting the common anchor point only once). (2) The multiplicon is extended with the newly detected segment C. The extremities of the multiplicon or segment that are beyond the outermost anchor points are stripped (indicated by dashed lines). (3) Next, the new segment is aligned against the existing profile and consequently added to it. This new profile can again be compared against another segment D. Again, anchor points with segments A en B are shown in blue and green, respectively, whereas anchor points with segment C are shown in red. Note that segment D has only two (segments A and C) or three (segment B) anchor points with each segment in the profile individually but a total of six anchor points with the profile as a whole.

Figure 4.

Flowchart of the entire i-ADHoRe algorithm.

Multiplicon Alignment and Profile Construction

As mentioned above, the profiles that are used to detect higher-level (>2) multiplicons are constructed by aligning the homologous segments of the multiplicon. This is done progressively as, starting from an initial alignment of two segments, each additional segment is aligned separately to the existing alignment and consequently added to it. As mentioned before, the aim of this alignment procedure is to position as many genes as possible from the same gene family in the same column.

Because the objects that need to be aligned are segments of gene lists, that is, sequences of genes, rather than sequences of nucleotides or amino acids, this procedure is somewhat different from traditional multiple alignment algorithms. First, the alphabet size or the total number of “characters” possible in the alignment is typically far greater here than in nucleotide or amino acid sequence alignments because every set of homologous genes or gene family in the data set is considered as a different character. Second, although in both types of alignment the aligned sequences are evolutionarily related, the events that cause the sequences to diverge from each other differ. Indeed, insertions and deletions aside, nucleotide and amino acid sequences mainly undergo substitutions in which one character (residue) changes (mutates) into another. This is not the case for sequences of genes because a gene of one gene family cannot change into a gene of another gene family. On the other hand, a sequence of genes often undergoes rearrangements, thereby changing the original order of genes in the sequence. In turn, this kind of rearrangement event does not occur in nucleotide or amino acid sequences.

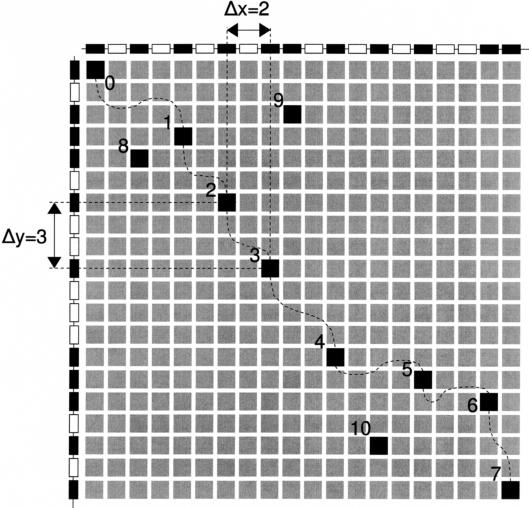
Because rearrangements can disturb the original gene order between the segments in a multiplicon, the multiplicon alignment procedure must be able to cope with this phenomenon. This is done as follows. Consider two homologous segments A and B that need to be aligned. When constructing the GHM between these segments, the algorithm looks for a maximum number of anchor points that run from top to bottom of the GHM and in which each subsequent anchor point is positioned lower than and to the right of the previous anchor point and with a minimum distance to the previous anchor point (see Fig. 5).

Figure 5.

Construction of alignment guides from a GHM between two homologous segments. The anchor points 0 to 7 are included in the alignment guide. Anchor points 8, 9, and 10 are not considered because their inclusion makes the alignment guide invalid because of the implicit requirement that every subsequent anchor point must be lower and to the right of the previous one. The values of Δx and Δy (the number of positions between two subsequent anchor points in the alignment guide; see text) have been indicated for anchor points 2 and 3.

Such an optimal series of anchor points is called the alignment guide for the segments A and B. To align two such segments, the difference between the number of positions on the x-axis (Δx) and the number on the y-axis (Δy) between two subsequent anchor points in the alignment guide must be zero (see Fig. 5). This is accomplished by inserting gap positions on any of the two segments where needed so that there is always an equal number of positions between genes that form subsequent anchor points in the alignment guide. This way, all gene pairs that form anchor points in the alignment guide used are at the same position in the alignment.

The entire construction of the alignment and corresponding profile now proceeds as follows. After the initial detection of a level 2 multiplicon (see previous section), the two segments that form this multiplicon are aligned as described above. Using the obtained alignment as a profile, a new type of GHM can be constructed in which the rows again correspond to the positions of the gene products in their respective gene lists but where the columns correspond this time to specific positions of the profile. A cell will now be nonempty if the gene product of its corresponding row is homologous to any of the genes aligned on the position of the alignment of the corresponding column (see Fig. 6). Once this GHM is constructed, it is again presented to the basic ADHoRe algorithm, which again will detect clusters of anchor points. The same statistical validation as described above is used, except that a Bonferroni correction is applied by multiplying the initial probability of the cluster with the multiplication level of the profile used. This time, however, the obtained clusters will not reveal homology between two individual segments but between the two segments inside the multiplicon and a third segment. Because this type of GHM combines gene content and order information of the different segments in the profile, it is possible to detect homology relationships with a third segment that could not be recognized by directly comparing any of the segments of the multiplicon individually with this third segment.

If such a third segment is detected, it is added to the multiplicon, thereby increasing its multiplication level, and updating the corresponding profile by aligning the new segment to it (see Fig. 6). This is done in the same way as aligning two segments, except that the x-coordinates in the GHM used to infer the alignment guide now represent positions in the already existing alignment. Thus, instead of inserting gaps in a single segment, gaps are now inserted into the entire alignment. If the third segment is homologous to only a part of the profile, then only this part will be used in the new alignment and profile. The entire detection process can now be repeated with the newly obtained multiplicon (see also Fig. 4).

Preparation of Arabidopsis and Rice Data Sets

In this study, we used the same Arabidopsis thaliana annotation as in Simillion et al. (2002). We retrieved the TIGR annotation of the A. thaliana genome (version of August 2001) and extracted the amino acid sequences, the relative chromosome position, and strand orientation for a total of 25,439 protein-encoding genes.

For rice (Oryza sativa), the TIGR annotation for the 12 chromosomes was downloaded from the TIGR ftp-site at ftp://ftp.tigr.org/pub/data/Eukaryotic_Projects/o_sativa/annotation_dbs/pseudomolecules/. Amino acid sequences, relative chromosome position, and strand orientation were retrieved for 57,221 protein-encoding genes (Yuan et al. 2003).

From the Arabidopsis and rice data sets, respectively, 667 and 12,553 genes that showed significant similarity to (retro-)transposons were removed.

The obtained protein sets of Arabidopsis and rice were BLASTed against themselves and against each other, using BLASTP (Altschul et al. 1997). From the resulting query–hit pairs, all pairs of intragenomic and intergenomic homologous genes were determined using the method of Rost (1999).

Consequently, i-ADHoRe was run on the Arabidopsis and rice data sets separately and on a combined Arabidopsis–rice data set. We used a gap size of 30, a quality factor of 0.9, and a probability cutoff of 0.0001 as parameters for all analyses.

Randomization Tests

To validate our method, two different simulation tests were conducted. First, to assess the accuracy of our statistical validation method, we constructed 1000 randomized data sets. For each of these data sets, all the genes present in the combined Arabidopsis–rice data set were pooled together, and 10 pseudochromosomes of 4069 genes each (the average number of genes per Chromosomes for the combined Arabidopsis–rice data set) were constructed by randomly picking genes from the pooled set. Next, i-ADHoRe was run on every data set. Obviously, every multiplicon detected in these data sets has arisen by chance. When using a probability cutoff of 0.0001, 1051 multiplicons of level 2 were detected and 11 clusters of level 3. Although the number of detected level 2 multiplicons might seem rather high at first sight, this number is to be expected considering the huge number of GHMs evaluated. Indeed, as explained above, when presented a data set consisting of n genomic fragments, i-ADHoRe starts by constructing GHMs for all n(n + 1)/2 possible pairs of fragments and subsequently detecting level 2 multiplicons within these GHMs. Thus, for 1000 data sets of 10 pseudochromosomes each, this results in a total of 55,000 GHMs that needs to be evaluated. Because numerous candidate multiplicons are detected and evaluated in each GHM, it can therefore be expected that from that total number of candidate multiplicons evaluated, still a considerable number of multiplicons arisen by chance has a probability score lower than 0.0001. Thus, using this probability cutoff results on average only in 1.05 false-positive multiplicons of multiplication level 2 and only in 0.011 of level 3, which justifies the use of this value in our analysis of real data sets.

Secondly we tested whether the detection of multiplicons using profiles could result in too many false positives. This was done by first running i-ADHoRe on the real Arabidopsis–rice data set to detect all valid level 2 multiplicons from which profiles were built. Next, all genes in the data set that were not contained in the detected multiplicons were pooled together, and 1000 pseudochromosomes were constructed from this pooled set. Each of the constructed profiles was then scanned against all 1000 pseudochromosomes. For 261 out of 270 profiles used, not a single false-positive level 3 multiplicon was detected. With the remaining nine profiles, 10 false-positive level 3 multiplicons were found. This corresponds to an average false-positive rate of 0.0003 false-positive multiplicons per profile and per pseudochromosome. When again constructing profiles from these 10 multiplicons and subsequently scanning the pseudochromosomes, only one false-positive level 4 multiplicon is found, which is still only a false-positive rate of 0.0001 per profile per pseudochromosome.

RESULTS

To evaluate the performance of our profile-building approach, i-ADHoRe was run on three different data sets. First, we reanalyzed the genomes of Arabidopsis and rice separately to compare the new results with our previous analyses (Simillion et al. 2002; Vandepoele et al. 2003). Additionally, we ran i-ADHoRe on a combined data set of Arabidopsis and rice. The results of the analyses of the individual genomes are shown in Table 1; the results of the analysis combining both genomes are shown in Table 2.

Table 1.

i-ADHoRe Results for the Rice and Arabidopsis-Only Data Sets

	O. sativa
Multiplication level	2	3	4
Chromosome 1	21.76%	0%	0%
2	28.14%	1.62%	0%
3	10.67%	0%	0%
4	25.01%	3.70%	0%
5	28.39%	0%	0%
6	16.64%	1.59%	0%
7	8.75%	0%	0%
8	16.13%	0%	0%
9	20.19%	0%	0%
10	9.49%	0%	0%
11	34.81%	9.45%	1.82%
12	27.53%	7.55%	0.86%
Entire genome	20.59%	1.78%	0.18%
	A. thaliana
Multiplication level	2	3	4	5	6
Chromosome 1	87.63%	49.44%	36.60%	26.22%	24.67%
2	74.23%	53.40%	43.64%	35.59%	25.87%
3	85.68%	50.15%	39.87%	24.00%	17.41%
4	85.63%	59.40%	49.68%	29.31%	24.19%
5	78.72%	38.32%	27.81%	17.30%	11.21%
Entire genome	82.72%	49.11%	38.29%	25.66%	20.19%
Multiplication level	7	8	9	10
Chromosome 1	9.86%	8.81%	4.77%	3.45%
2	16.95%	14.61%	10.30%	5.17%
3	12.93%	11.27%	6.43%	1.65%
4	15.36%	12.63%	9.41%	8.26%
5	9.36%	6.82%	3.87%	1.93%
Entire genome	12.32%	10.34%	6.47%	3.72%

The fraction of the genes that occurs in a multiplicon with a multiplication level X or more is given for each chromosome individually as well as for the entire genome.

Table 2.

i-ADHoRe Results for the Combined Rice and Arabidopsis Data Sets

	O. sativa
Multiplication level	2	3	4	5
Chromosome 1	26.98%	5.66%	1.64%	1.64%
2	28.35%	3.90%	1.54%	1.32%
3	19.75%	4.46%	0%	0%
4	24.88%	5.89%	1.33%	1.13%
5	32.92%	4.19%	0.99%	0.37%
6	18.39%	1.59%	0%	0%
7	11.69%	1.80%	0%	0%
8	18.60%	0%	0%	0%
9	24.11%	0%	0%	0%
10	9.22%	0%	0%	0%
11	37.30%	18.04%	4.97%	2.55%
12	31.04%	14.81%	4.60%	3.38%
Entire genome	23.80%	4.98%	1.22%	0.88%
	A. thaliana
Multiplication level	2	3	4	5	6
Chromosome 1	88.45%	60.81%	52.54%	33.67%	30.34%
2	77.03%	58.65%	51.49%	46.88%	43.08%
3	85.44%	51.92%	42.12%	37.20%	32.24%
4	87.12%	73.25%	66.78%	51.50%	47.18%
5	80.60%	52.21%	42.32%	32.33%	28.07%
Entire genome	83.99%	58.51%	49.99%	38.83%	34.73%
Multiplication level	7	8	9	10	11
Chromosome 1	23.23%	17.86%	12.87%	9.37%	3.16%
2	37.39%	25.95%	13.28%	7.21%	2.19%
3	26.63%	18.50%	8.46%	5.28%	1.95%
4	38.12%	31.02%	20.89%	9.11%	2.09%
5	20.54%	16.06%	6.94%	4.48%	0.40%
Entire genome	27.77%	20.82%	11.85%	7.02%	1.96%

The fraction of the genes that occurs in a multiplicon with a multiplication level X or more is given for each chromosome individually as well as for the entire genome.

When analyzing the genome of Arabidopsis separately, we detect 946 multiplicons with multiplication levels ranging from 2 to 10; 82.72% of the genes of Arabidopsis reside in duplicated regions. This result is very similar to our previous study (Simillion et al. 2002), in which we reported that 82.19% of the genome is duplicated. However, considering the fraction of the genome that is part of multiplicons with a multiplication level of 5 or more, we see that using i-ADHoRe this number increases from 8.22% to 25.66%. Given this figure and the fact that only 6.47% of the genome has a multiplication level greater than 8, our original conclusion that Arabidopsis has undergone three genome-wide duplication events in its evolutionary past and an additional, more local event gains considerable support (Simillion et al. 2002). Bowers et al. (2003) also independently confirmed the hypothesis of three large-scale duplication events.

For rice, we see that, using i-ADHoRe, 20.59% of the genome is found in duplicated regions. Multiplicons with a multiplication level of up to 4 are observed, but the majority of the duplicated fraction of the rice genome has only a multiplication level of 2. Considering each individual chromosome, we see that the dispersion of duplicated segments is not uniform throughout the genome. Indeed, the duplicated fraction per chromosome ranges from 8.75% for Chromosome 7 up to 34.81% for Chromosome 11. Thus, our previous conclusion (Vandepoele et al. 2003) that rice is an ancient aneuploid is largely confirmed, despite the larger overall fraction of duplicated segments observed in this study. This is mainly because of large duplicated fractions on Chromosomes 11 and 12. Furthermore, the vast majority of anchor points (78%; data not shown) that involve these chromosomes are formed by gene pairs between these two chromosomes themselves, and these fractions are therefore most likely the result of another local duplication event. The existence of a duplicated region between Chromosomes 11 and 12 has been described before (Nagamura et al. 1995; Wu et al. 1998). The fact that these duplicated regions were not detected in our previous study (Vandepoele et al. 2003) is probably because of the more complete assembly and annotation that were used here.

The presence of multiplicons with multiplication levels up to 4 indicates that at least one additional duplication event must have occurred (Simillion et al. 2002). However, because only a very small fraction (1.78%) of the genome consists of multiplicons with a multiplication level >2 and the chromosomal distribution of the segments in these multiplicons is again highly nonuniform, there is little indication that these higher levels are the remnants of a large, genome-wide duplication event.

Combining the data sets of Arabidopsis and rice and building profiles including segments from both genomes reveals a different picture for both genomes. For Arabidopsis, we now find that 83.99% of the genome is duplicated and a significant increase of segments with multiplication levels of 5 and/or 8. Indeed, when analyzing the combined data set, 38.83% of the genome of Arabidopsis has a multiplication level of 5 or more, compared with 25.66% in the Arabidopsis-only data set.

For rice, we observe that 23.80% of the genome is duplicated and that 4.98% has a multiplication level of 3 or more. In addition, we observe multiplicons with multiplication levels up to 5 (compared with 4 in the rice-only data set). Also, 14.02% of the rice genome shows collinearity with 29.71% of the Arabidopsis genome. Note, however, that this includes collinearity between segments and profiles rather than collinearity between two individual segments.

The complete results of these analyses can be viewed on our Web site http://www.psb.ugent.be/bioinformatics/.

DISCUSSION

Genomic Profiles Uncover Additional Homology

The massive silencing of duplicated loci after large-scale gene duplication events (Song et al. 1995; Lynch and Conery 2000; Mittelsten Scheid et al. 2003) causes two duplicated chromosomal segments, which are initially identical in gene order and content, to diverge from each other. In the extreme, this divergence can come to the point where these two segments do not share any similarity at all. However, because these two segments are the result of a duplication event, they are homologous. As mentioned above, one may be able to uncover such degenerated homologies as “hidden” or “ghost” (Simillion et al. 2002; Vandepoele et al. 2002b) relationships, but this strategy still requires that both segments involved show significant collinearity with at least one other segment.

By constructing genomic profiles that combine gene content and order information from multiple homologous segments, it becomes possible to detect heavily degenerated homology relationships between segments that no longer show significant collinearity with any of the segments contained in the profile. The strength of this approach is clearly illustrated by the fact that we observe a considerable increase of multiplicons with multiplication levels of 5 or more in the genome of Arabidopsis when compared with the traditional approach (see Results). Detecting higher multiplication levels is important when one wants to infer the number of duplication events that have occurred in the evolutionary past of an organism. Indeed, given a maximum observed multiplication level of n, the number of duplications occurred is given by d = ⌈log₂(n)⌉ (take the log₂ of n and round up to the next integer; Simillion et al. 2002).

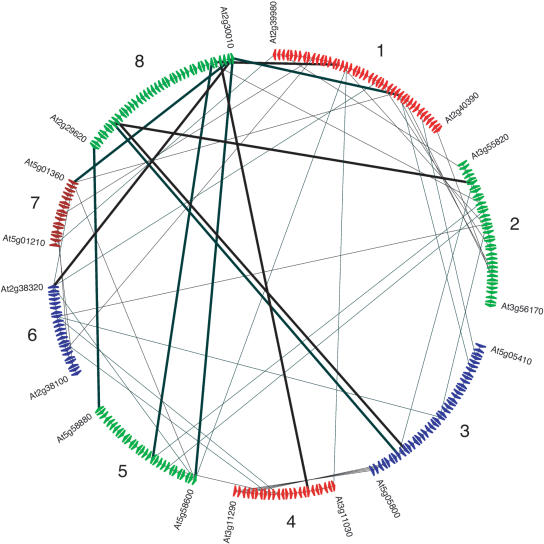
An example of an Arabidopsis multiplicon detected by i-ADHoRe is given in Figure 7. The segments on this figure are shown clockwise in the order in which they were added to the multiplicon. Thus, segments 1 and 2 were detected first as a pair of collinear segments that were consequently aligned to create a profile. This profile was then used to detect segment 3, which, in turn, was aligned and added to the profile. Using the updated profile, segment 4 was detected, and so on, until after adding segment 8 no other homologous segments could be found. When considering the homology relationships between segment 8 and the other segments of the multiplicon, this segment shares three homologous genes with segment 5 over quite a large distance and only one or two genes with any of the other segments. It is obvious that, based on the similarities with any of the other individual segments, the homology with segment 8 is far from statistically significant because there are too few anchor points and the number of intervening genes is too high. However, if we consider the seven other segments in the multiplicon (of which the mutual homology has already been established) together as a profile, we see that segment 8 shares in total eight genes with the profile. This is, given the length of the segment, statistically significant so that segment 8 can be considered to be homologous to the other segments in the multiplicon.

Figure 7.

Example of a multiplicon with a multiplication level of 8 in the genome of Arabidopsis. Each colored triangle on a segment represents a gene. The different segments in this multiplicon are indicated with the locus numbers of their first and last gene. The segments are displayed in the chronological order in which they were added to the multiplicon. See the Discussion section for more details. The lines connect pairs of homologous genes; the homology relations with segment 8 are indicated with thick lines.

A homology relationship between a single segment and a set of mutually homologous segments (a multiplicon) based on only eight anchor points (pairs of homologous genes) shared with seven different segments may at first sight seem not very significant. However, given that these eight anchor points were detected in a GHM using a profile, the order in which the eight homologous genes occur in the segment is the same as their counterparts occur in the profile (see Fig. 8). In other words, although the collinearity (conservation of both gene order and content) between the individual segments in a multiplicon can be completely degenerated, each segment is still significantly collinear to the entire profile that combines all the other segments in it. Moreover, as the number of segments and consequently the number of genes in the profile increases, the overall density of anchor points in the GHM, θ (see equation 2 in the Methods section) also increases because more pairs of homologous genes will be observed in the GHM. As a consequence, a candidate cluster of anchor points will have to be more densely spaced and/or contain more anchor points to be considered statistically significant (see equation 4 in the Methods section).

Figure 8.

Gene homology matrix (GHM) for the multiplicon shown in Figure 7. The segment numbers correspond to the same segments as in Figure 7. The boxes on the segments represent genes. Genes of the same color are homologs. Tandemly duplicated genes have been remapped (data not shown). Segments 1–7 (above the matrix) are aligned to form a profile. Empty positions on the segments denote gaps in the aligment (see Methods section for details). Using this profile, the homology relationship between segment 8 (left of the matrix) and the other segments in the profile/multiplicon can be established because segment 8 is clearly homologous to the profile (see Discussion for more details).

Although the method described here allows the identification of heavily degenerated collinear relationships, it still depends on the initial presence of pairs of clearly collinear regions that can be used to form a profile to detect more degenerated homologies. For genomes that have undergone a relatively recent genome-wide duplication event like Arabidopsis, this is not a problem. Of course, not every genome has undergone such a large-scale duplication event of which the remnants are readily detectable. However, one can still look for degenerated homologies in these genomes by incorporating genomes of relatively related other organisms. When pairs of collinear regions can be detected between different genomes, these regions can also be used to create profiles and subsequently scan the genome of interest.

Is There Evidence for an Ancient Duplication Prior to the Divergence of Monocots and Dicots?

The power of this comparative approach is clearly illustrated with our analysis of the rice genome. Indeed, in a recent study in which both hidden and ghost (using the Arabidopsis genome) duplications were considered (Vandepoele et al. 2003), we found that only 1.3% of the genome of rice is part of multiplicons with a level of more than 2, suggesting that at least one additional duplication event must have happened, apart from the reported monocot-specific aneuploidy event, but with very little indication about the nature of this event. When we apply our new method to the rice-only data set, we detect that 20.59% of the genome is duplicated, with 1.78% in multiplicons with a multiplication level of 3 or 4 (see Table 1). Based on these results, we can only conclude that, during its most recent past, the previously reported aneuploidy event (Vandepoele et al. 2003) and the segmental duplication between Chromosomes 11 and 12 must have occurred. However, when incorporating collinearity between the Arabidopsis and rice genomes using the Arabidopsis–rice data set, the duplicated portion of the genome increases to 23.80%, with 4.98% in multiplicons of level 3 up to 5, distributed over a much wider fraction of the genome. For some chromosomes, that is, 1 and 5, the fraction that has a multiplication level of more than 3 even goes up from 0% to 5.66% and 4.19%, respectively. Also for Chromosomes 3 and 9 we observe a net increase of 9.08% and 3.92%, respectively, of the total duplicated fraction (see Table 2).

The fact that including intergenomic homologies with Arabidopsis significantly increases the fraction of the genome of rice with multiplication levels of 3 up to 5 as well as the overall duplicated fraction, indicates that the additional duplication event observed here is most likely an ancient one. Indeed, one expects that, should a more recent duplication event have occurred, its remnants would be more readily detectable and therefore the rice-only data set would be expected to give the same results as the mixed Arabidopsis–rice data set.

It has been suggested that the oldest of three duplication events in Arabidopsis has occurred before the monocot–dicot split (Bowers et al. 2003), which means that remnants of this duplication event should be present in the genomes of monocots as well. Until now, from analyzing the rice genome, there is little evidence for such an ancient duplication event (Vandepoele et al. 2003). However, because including intergenomic homology with Arabidopsis increases the amount of duplication found for a large part of the genome, it could be possible that these duplicated segments originated before the monocot–dicot split.

On the other hand, the overall number of duplicated segments with a multiplication level of more than 2 in the rice genome is far too low, at least when compared with Arabidopsis, to conclude that this event is indeed the result of a genome-wide duplication. It has been shown that the genome of rice has been relatively stable since the divergence of the Poaceae (Ilic et al. 2003). It is therefore unlikely that the remnants of such a genome-wide duplication event would have been obliterated by extensive rearrangements during this period. Nevertheless, the fact that only 14.02% of the rice genome is collinear to 29.71% of Arabidopsis indicates that still a considerable amount of rearrangement must have occurred since the monocot–dicot divergence. Adding to this the observation that in Arabidopsis still 38.83% of the genome shows remnants of the oldest duplication event, it could be possible that the rice genome was highly rearranged after the monocot–dicot split but before the divergence of the Poaceae. Alternatively, because the pattern of duplication is still nonuniform all over the rice genome, there is also the possibility that these observed segmental duplications are the result of several local and independent duplication events. A further, more detailed dating study should give more indications about the nature and exact time of origin of this older duplication event(s) in rice.

For Arabidopsis too, we see that including the rice genome in the analysis increases the performance of i-ADHore in detecting degenerated genomic homologies. Apart from a significant increase of the portion of the genome with a multiplication level of 5 or more (38.83%), we also detect multiplicons with multiplication levels of up to 11. Because these multiplicons span only 1.96% of the genome, they are most likely also the result of the additional more local duplication event discussed previously (Simillion et al. 2002).

In conclusion, using profiles built by aligning sets of collinear genomic segments to detect highly degenerated homology relationships allows us to gain more insight into the structural past of today's genomes. Especially when combining gene order and content information of different genomes, we are now able to uncover segmental homologies that, up to now, were impossible to detect. With more and more complete genome data becoming available, it can be expected that, using this method, a more complete understanding of the structural genome evolution of eukaryotic organisms will be obtained.

The i-ADHoRe software is freely available from the authors upon request.