Discriminative Brain Effective Connectivity Analysis for Alzheimer’s Disease: A Kernel Learning Approach upon Sparse Gaussian Bayesian Network

Abstract

Analyzing brain network from neuroimages is becoming a promising approach in identifying novel connectivity-based biomarkers for the Alzheimer’s disease (AD). In this regard, brain “effective connectivity” analysis, which studies the causal relationship among brain regions, is highly challenging and of many research opportunities. Most of the existing works in this field use generative methods. Despite their success in data representation and other important merits, generative methods are not necessarily discriminative, which may cause the ignorance of subtle but critical disease-induced changes. In this paper, we propose a learning-based approach that integrates the benefits of generative and discriminative methods to recover effective connectivity. In particular, we employ Fisher kernel to bridge the generative models of sparse Bayesian network (SBN) and the discriminative classifiers of SVMs, and convert the SBN parameter learning to Fisher kernel learning via minimizing a generalization error bound of SVMs. Our method is able to simultaneously boost the discrimination power of both the generative SBN models and the SBN-induced SVM classifiers via Fisher kernel. The proposed method is tested on analyzing brain effective connectivity for AD from ADNI data. It demonstrates significant improvements over the state-of-the-art: classification accuracy increased above 10% by our SBN models, and above 16% by our SBN-induced SVM classifiers with a simple feature selection.

1. Introduction

As the most common form of dementia, Alzheimer’s disease (AD) is a fatal and progressive neurodegenerative disease that has caused serious socioeconomic problems in developed countries. Early diagnosis of AD may benefit the patients with disease-interrupted therapies when the dementia is still mild. Neuroimaging techniques are important in AD study because they may provide more sensitive and consistent measures than traditional cognitive assessment.

Currently, neuroimage analysis has evolved from studying local morphometry to complex relationships and interactions across brain regions. This is because the brain is, by nature, a complex network of many interconnected regions. A brain network is usually modeled by a graph with each node corresponding to a brain region and each edge corresponding to the connectivity between regions. The connectivity could be statistical dependencies (functional connectivity) or causal relationships (effective connectivity) [15], represented by undirected or directed graph, respectively. This paper focuses on brain effective connectivity analysis, which has gradually accumulated attentions due to its ability to analyze the directional effect of one brain region over another. Effective connectivity analysis has been applied to fMRI [6], PET [2], and gray matter morphology in structural MRI [7], and has exhibited its promising potential in identifying novel connectivity-based biomarkers for AD.

With sparse learning techniques, effective connectivity analysis has been able to handle medium to large scale brain network. A remarkable recent work is from Huang, et al. [2, 1], where a sparse Gaussian Bayesian network (SGBN) is recovered from more than 40 brain regions in fluorodeoxyglucose PET (FDG-PET) images for AD analysis. That approach learns the Bayesian network (BN) structure and parameters simultaneously in one step, which demonstrates a more accurate network recovery than the conventional two-stage approaches in sparse BN learning (such as LIMB-DAG [14], MMHC [17], TC and TC-bw [10], etc.). Despite the effectiveness in network representation, the above methods (including [2, 1]) are all generative methods. As known, generative methods focus on representing an individual group, thus may not be discriminative. When analyzing brain network, they are prone to over-emphasizing major structures within an individual group, and neglecting the subtle disease-induced structural changes across different groups. Therefore, generative methods are usually inferior in prediction compared with the discriminaitve methods that focus on the class boundary (such as Support Vector Machines (SVMs)). However, discriminative methods are not amenable for interpretation, which is critical in exploratory research aiming at both the understanding and the diagnosis of the disease. Therefore, we aim to integrate the merits of generative and discriminative methods to learn BNs that are not only representative but also discriminative. Recent progress in [11, 12] for learning discriminative BNs follows the conventional two-stage approach and works for discrete variables. They may not suit for brain network analysis where the brain regional measurements are usually continuous variables.

To achieve our goal, we improve the model of the SGBN in [2], and further boost its discrimination power via a kernel learning approach that links the generative SGBN with the SVM classifiers. The contribution of this paper includes: 1) We propose an augmented SGBN model (A-SGBN) by revisiting the method in [2]. A-SGBN fits the underlying distribution more precisely, therefore bringing better prediction. 2) By inducing Fisher kernel on our A-SGBN models, we provide a way to obtain subject-specific SGBN-induced feature vectors that can be used by discriminative classifiers such as SVMs. Through this, we integrate the generative and discriminative models. 3) More significantly, we convert the learning of SGBN parameters to the learning of discriminative Fisher kernels, which simplifies the optimization. Specifically, we jointly learn the SGBN parameters and the separating hyperplane of SVMs over Fisher kernel by minimizing a generalization error bound of SVMs. 4) We apply our method on ADNI ¹ data to analyze brain effective connectivity for AD from both T1-weighted MRI and FDG-PET images. Our method significantly improves the discrimination power of the generative SGBN and the discriminative SVM classifier simultaneously. 5) By Fisher kernel, we obtain a new kind of features that reflect the changing rate of connection strength, which have not been investigated in conventional approaches.

2. Related Work

2.1. Gaussian Bayesian Network

Gaussian Bayesian network (GBN) is the fundamental tool that we use to learn effective brain connectivity in this paper. It is therefore briefed here, together with the definition of symbols used throughout the paper.

Let x = [x₁, x₂, … , x_m] be a sample of m features (variables). Let $\mathbf{D}\in {\mathbb{R}}^{n\times m}$ be a data matrix of n samples. The i-th row of D represents a sample x_i. The j-th column of D, denoted as f_j, represents a realization of the j-th variable x_j on the n samples.

A Bayesian network (BN) $\mathcal{G}$ is a directed graph that expresses the factorization property of a joint distribution p(x). With each variable correponding to a node in $\mathcal{G}$, the joint distribution is factorized as $p\left(\mathrm{x}\right)={\prod }_{i=1,\cdots ,m}p(x_i\mid \mathbf{Pa}(x_i\left)\right)$, where Pa(x_i) denotes the parent nodes of x_i. A GBN assumes that p(x_i∣Pa(x_i)) follows a Gaussian distribution. Each node x_i is regressed over its parent nodes $\mathbf{Pa}\left(x_i\right):x_i={\theta }_i^{⊺}\mathbf{Pa}\left(x_i\right)+{\epsilon }_i$, where the vector θ_i is the regression coefficients, and ${\epsilon }_i\sim \mathcal{N}(0,{\sigma }_i^2)$. The matrix Θ = [θ₁, … , θ_m] are called the parameters of a GBN. A BN has to be a directed acyclic graph (DAG), in which there must be no directed cycles. In this paper, following [2], a p × p matrix G is used to represent network structure, in which, if there is a direct edge from x_i to x_j, G_ij = 1; otherwise, G_ij = 0. In addition, another p × p matrix P is also kept to record all the directed pathes in the structure. If there is a directed path from x_i to x_j, P_ij = 1; otherwise P_ij = 0.

2.2. Sparse Gaussian Bayesian Network

The state-of-the-art work for brain causal relationship analysis in [2, 1] underpins our study in this paper. In [2, 1], it is proposed to learn a sparse GBN (SGBN) for brain effective connectivity analysis utilizing FDG-PET images. Compared with the conventional BN methods that learn the network structure and parameters in two steps, SGBN simultaneously learns the structure and parameters by enforcing sparseness constraint on a GBN. This one-step learning approach outperforms the conventional two-step methods with higher accuracies for the network edge recovery. In particular, it is proposed in [2, 1] to solve a constrained least-square fitting problem:

$$\begin{array}{cc}\hfill & \underset{\theta }{\min }\sum _{i=1}^m{\Vert {\mathbf{f}}_i-{\theta }_i^{⊺}\mathbf{Pa}\left({\mathrm{x}}_i\right))\Vert }_2+{\lambda }_1{\Vert {\theta }_i\Vert }_1\hfill \\ \hfill & s.t.\mid {\Theta }_{\mathit{ji}}\mid \times {\mathbf{P}}_{\mathit{ij}}=0,\forall i,j=1,\cdots ,m,i\ne j.\hfill \end{array}$$ (1)

Here f_i and θ_i are defined as above. The i-th row of the matrix Pa(x_i) correpond to the parent nodes of x_i, which are initially set as all the nodes other than x_i, and further filtered implicitly by the sparseness constraint over their regression coefficients θ_i. In BN learning, a difficult problem is how to enforce the DAG property to ensure the validity of the resulting BN. In [2] it is proved that a sufficient and necessary condition for a DAG is ∣Θ_ji∣ P_ij = 0 for all i and j. The P_ij is computed by a Breadth-first search on G with x_i being the root node. For more details, please read [2, 1].

3. Our Method

In this paper, we study brain networks from two sources. The first source is gray matter morphology from T1-weighted MRI. It has been reported that the covariation of gray matter morphology might be related to the anatomical connectivity [16]. Studying brain morphology as a network can take the advantage of statistical tools from graph theory. The second source is FDG-PET images. The retention of tracer in FDG-PET is analogue to the glucose uptake, thus reflecting the tissue metabolic activity.

Building brain network includes identifying network nodes and reconstructing the connectivity. This paper focus on the latter. Therefore, after briefing how network nodes are defined in our method in Section 3.1, we concentrate on how to infer the effective connectivity that is both representative (Section 3.2) and discriminative (Section 3.3).

3.1. Determine Network Nodes

MRI

This study involves 120 subjects including 50 MCI (mild cognitive impairment, a prodromal of AD) patients and 70 NC (normal controls) from the publicly accessible data of ADNI. The T1-weighted MR images are segmented into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) using FAST in the FSL² package after intensity correction, skull stripping, and cerebellum removal. These tissue-segmented images are spatially normalized into a template space by HAMMER ³, and partitioned into 100 Region of Interest (ROI) via an ROI atlas [4]. We use the GM volumes of each ROI as network nodes, and select 40 ROIs that have the highest correlation with class labels into our study. The ROI names are provided in the supplementary material.

PET

This study involves 103 subjects including 51 AD patients and 52 NC whose FDG-PET and MR images are downloaded from ADNI. We first co-register the MR images into a template space and partition them into ROIs as mentioned above. Then the PET images are aligned with their MR images from the same subject by a rigid transformation. The average tracer uptakes within each ROI are used as network nodes. Similarly, we select 40 ROIs that are most discriminative with regards to AD (see the supplementary material).

3.2. Augment SGBN in [2, 1]

A simple way to use generative BNs for prediction is to train each class a BN and classify a new sample x_i by assigning it to the class with a higher likelihood ratio. The more precisely the BN model reflects the underlying distribution, the more accurate the prediction. The comparison of the likelihood must be conducted in the same space, which means the data should not be normalized separately for each class as in [2] where a single population is focused.

Regression of a node x_i over all other nodes leads to an estimated expectation $\widehat{\mathbb{E}}\left[x_i\right]={\theta }_i^{⊺}\mathbb{E}\left(\mathbf{Pa}\right(x_i\left)\right)$. This agrees with the true $\mathbb{E}\left[x_i\right]$ in [2] if the sparseness constraint is not considered, because every feature (node) has been normalized to have a zero mean, and a unit standard deviation. However, $\widehat{\mathbb{E}}\left[x_i\right]$ may largely deviate from $\mathbb{E}\left[x_i\right]$ when the normalization cannot be performed or the underlying data relationship is not linear.

To handle this, we introduce a bias term x₀ in the regression, i.e., $x_i={\theta }_i^{⊺}\left[\mathbf{Pa}\right(x_i),x_0]+{\epsilon }_i$. Accordingly, in the graph $\mathcal{G}$, a bias node is added, which has no parent but being the parent of all the other nodes. If originally $\mathcal{G}$ is a DAG, adding x₀ in this way will not cause the violation of DAG. To be distinguished from SGBN in [2], we call ours A-SGBN. Intuitively, there may be two reasons to include a bias node into a brain network: i) there possibly exist some latent variables related to the disease, which are not included into the current study, and their influences may be absorbed by the bias node; or ii) the state of a node may depend not only on the interactions with other nodes, but also on the prior of itself. Our experiment in Section 4 indicates that A-SGBN may be a more precise model than SGBN (smaller fitting errors for both the training and the test data), thus improve the classification. Despite the advantage of A-SGBN over SGBN, in the following we show that actively learning the discrimination can further boost the classification performance.

3.3. Discriminatively Learn SBN via Fisher Kernel

Both SGBN and A-SGBN learn the brain network for AD or NC separately. This may ignore some subtle but important network differences that distinguish the two classes. We argue that the parameters of the generative model should be learned from the two classes jointly to keep the essential discrimination. This can be achieved by maximizing the posterior probability p(y∣x), where y is the class label of x. Although conceptually direct, this approach often leads to complicated optimization problems. This paper takes another approach. Specifically, we employ Fisher kernel to extract feature vectors from the SGBN models of two classes, and then convert the model parameter learning to Fisher kernel learning with SVMs. We find that the SGBN-induced Fisher vector (see below) is a linear function of parameters θ, which well simplifies the optimization.

3.3.1 Induce Fisher Vectors from SGBN

Below we introduce how to use Fisher kernel on SGBNs to obtain feature vectors used for kernel learning.

Fisher kernel provides a way to compare samples induced by a generative model. It maps a sample to a feature vector in the gradient space of the model parameters. The intuition behind is that similar objects induce similar log-likelihood gradients of the model parameters. Fisher kernel is computed as $K(\mathrm{x},{\mathrm{x}}^{\prime })={\mathrm{g}}_{\mathrm{x}}^{⊺}{\mathbf{U}}^{-1}{\mathrm{g}}_{{\mathrm{x}}^{\prime }}$, where the Fisher vector g_x = ▿_θ log(p(x∣θ)) describes the changing direction of parameters to better fit the model. The Fisher information metric U weights the similarity measure, but is often set as an identity matrix in practice [3].

Fisher kernel has recently witnessed successful applications in image categorization [13, 5] for inducing feature vectors from Gaussian Mixture Model (GMM) of a visual vocabulary. Despite its success, to the best of our knowledge, Fisher kernel has not been applied to BN for brain connectivity analysis. More importantly, in the applications above, there is no discriminative learning for Fisher kernel as in this paper. The advantage of discriminative Fisher kernel has also been confirmed by a very recent study that uses a different learning criterion within a different context [9].

Following [2, 1], we only consider Θ as parameters and predefine σ. Let $\mathcal{L}(\mathrm{x}\mid \Theta )=\log \left(p\right(\mathrm{x}\mid \Theta )$ denote the log likelihood. Our Fisher vector for each sample x is ${\Phi }_{\Theta }\left(\mathrm{x}\right)={[{\nabla }_{{\Theta }_1}\mathcal{L}{(\mathrm{x}\mid {\Theta }_1)}^{⊺},{\nabla }_{{\Theta }_2}\mathcal{L}{(\mathrm{x}\mid {\Theta }_2)}^{⊺}]}^{⊺}$, where Θ₁ and Θ₂ are the parameters of the SGBNs for the two class (y = 1, 2), respectively. Recall that, using a BN, the probability p(x∣Θ) can be factorized as $p(\mathrm{x}\mid \Theta )={\prod }_{i=1,\cdots ,m}p(x_i\mid \mathbf{Pa}(x_i),{\theta }_i)$. Therefore, it holds that

$$\begin{array}{cc}\hfill \mathcal{L}(\mathrm{x}\mid \Theta ))& =\sum _{i=1}^m\log p(x_i\mid \mathbf{Pa}(x_i),{\theta }_i)\hfill \\ \hfill & =\sum _{i=1}^m\frac{-{(x_i-{\theta }_i^{⊺}\mathbf{Pa}(x_i\left)\right)}^2}{2{\sigma }_i^2}-m\log \left(2\pi \sqrt{{\sigma }_i}\right).\hfill \end{array}$$ (2)

Taking partial derivative over θ_i, we have

$$\begin{array}{cc}\hfill \frac{\partial \mathcal{L}(\mathrm{x}\mid \Theta )}{\partial {\theta }_i}& =-\frac{\mathbf{Pa}\left(x_i\right)\mathbf{Pa}{\left(x_i\right)}^{⊺}}{{\sigma }_i^2}{\theta }_i-\frac{x_i\mathbf{Pa}\left(x_i\right)}{{\sigma }_i^2}\hfill \\ \hfill & \triangleq \mathbf{S}\left(x_i\right){\theta }_i+{\mathrm{s}}_0\left(x_i\right),\hfill \end{array}$$ (3)

where S(x_i) is a matrix and s₀(x_i) is a vector. As shown, Ф_Θ(x) is a linear function of Θ. This simple form of Ф_Θ(x) significantly facilitates our further kernel learning.

3.3.2 Learn Discriminative Fisher Kernel via SVM

As each Fisher vector is a function of the SGBN parameters, discriminatively learning these parameters can thus be converted to learning discriminative Fisher kernels. We require that the learned SGBN models possess the following properties. Firstly, the Fisher vectors induced by the learned SGBN model should be well separated between classes. Secondly, the learned SGBN models should maintain reasonable capacity of group representation. Thirdly, the learned SGBN models should not violate DAG.

We use the following strategies to achieve our goal. Firstly, to obtain a discriminative Fisher kernel, we jointly learn the parameters of SGBN and the separating hyperplane of SVMs with Fisher kernel. Radius-margin bound, the upper bound of the Leave-One-Out error, is minimized to keep good generalization of the SVMs. Secondly, to maintain reasonable representation, we explicitly control the fitting errors of the learned model during optimization. Thirdly, we enforce the DAG constraint in [2] to ensure the validity of the graph. For convenience, we call our method DL-A-SGBN. More details are given below.

In order to use radius-margin bound, ${\mathcal{L}}_2$-SVM with soft margin has to be employed, which optimizes

$$\begin{array}{cc}\hfill & \underset{\mathrm{w},\xi }{\min }\frac{1}{2}{\Vert \mathrm{w}\Vert }_2^2+C{\xi }^{⊺}\xi \hfill \\ \hfill s.t.& y_i\left({\mathrm{w}}^{⊺}\Phi \right({\mathrm{x}}_i)+b)\ge 1-{\xi }_i,{\xi }_i\ge 0,\forall i\hfill \end{array}$$ (4)

Following the convention in SVMs, x_i is the i-th sample with class label y_i, w the normal of separating plane, b the bias term, ξ the slack variables and C the regularization parameter. $\mathcal{L}2$-SVM can be rewritten as SVM with hard margin by slightly modifying the kernel K := K + I/C, where I is identity matrix. For convenience, in the following, we redefine $\Phi \left({\mathrm{x}}_i\right)≔\left[\Phi \right({\mathrm{x}}_i){\mathrm{e}}_i∕\sqrt{C}]$. The vector e_i has the value of 1 at the i-th element, and 0 elsewhere.

Incorporating radius information leads to solving

$$\begin{array}{cc}\hfill & \underset{\mathrm{w}}{\min }\frac{1}{2}{R}^2{\Vert \mathrm{w}\Vert }_2^2\hfill \\ \hfill s.t.& y_i\left({\mathrm{w}}^{⊺}\Phi \right({\mathrm{x}}_i)+b)\ge 1,\forall i,\hfill \end{array}$$ (5)

where R² denotes the radius of Minimal Enclosing Ball (MEB). It has been observed that when the sample size is small, the estimation of R² may become noisy and unstable. Therefore, it has been proposed to use trace-based scatter matrix instead for such cases [8]. We optimize

$$\begin{array}{cc}\hfill & \underset{\theta ,\mathrm{w}}{\min }\frac{1}{2}\mathrm{tr}\left({\mathbf{S}}_T\right){\Vert \mathrm{w}\Vert }_2^2\hfill \\ \hfill s.t.& y_i\left({\mathrm{w}}^{⊺}{\Phi }_{\Theta }\right({\mathrm{x}}_i)+b)\ge 1,\forall i\hfill \\ \hfill & h({\mathbf{D}}_1,{\Theta }_1)\le T_1,h({\mathbf{D}}_2,{\Theta }_2)\le T_2,\hfill \\ \hfill & {\Theta }_1\in \mathit{DAG},{\Theta }_2\in \mathit{DAG}.\hfill \end{array}$$ (6)

Here tr(S_T) is the trace of the total scatter matrix S_T, where ${\mathbf{S}}_T={\sum }_{i=1}^n{({\mathrm{x}}_i-m)}^{⊺}({\mathrm{x}}_i-\mathrm{m})$, and m is the mean of total n samples. It can be shown that tr(S_T ) = tr(K) − 1^TK1/n, where 1 denotes a vector whose elements are all 1, and K the kernel matrix. Fisher vector Ф_Θ(x_i) is obtained as mentioned in Section 3.3.1. The function h(·) measures the squared fitting errors of the corresponding SGBNs for the data D₁ and D₂ from the two classes. It is defined as

$$h(\mathbf{D},\Theta )=\sum _{i=1}^m{\Vert {\mathbf{f}}_i-{\theta }_i^{⊺}\mathbf{Pa}\left({\mathrm{x}}_i\right))\Vert }_2,$$

where all the symbols are defined as in 1. The two user-defined parameters T₁ and T₂ explicitly control the degree of fitting during the learning process (Section 4.2). The DAG constraints here are the same to that used in 1. Please recall that the DAG constraint is ∣Θ_ji∣ × P_ij = 0, where P_ij = {0, 1}, reflecting the structure of Θ. Enforcing DAG in this way has somewhat enforced the graph sparcity (by constraining the $\mathcal{L}1$-norm of Θ_ij). Therefore, we do not impose additional sparseness constraints on Θ to keep our optimization simple.

One possible approach for solving Eqn. (6) is to alternately optimize the separating hyperplane w and the parameter Θ. That is,

$$\begin{array}{cc}\hfill & \underset{\theta }{\min }J\left(\Theta \right)\hfill \\ \hfill s.t.& h({\mathbf{D}}_1,{\Theta }_1)\le T_1,h({\mathbf{D}}_2,{\Theta }_2)\le T_2,\hfill \\ \hfill & {\Theta }_1\in \mathit{DAG},{\Theta }_2\in \mathit{DAG}.\hfill \end{array}$$ (7)

where

$$\begin{array}{cc}\hfill & J\left(\Theta \right)=\underset{\mathrm{w}}{\min }\frac{1}{2}\text{tr}\left({\mathbf{S}}_T\right){\Vert \mathrm{w}\Vert }_2^2\hfill \\ \hfill s.t.& y_i\left({\mathrm{w}}^{⊺}{\Phi }_{\Theta }\right({\mathrm{x}}_i)+b)\ge 1,\forall i.\hfill \end{array}$$ (8)

Note that for a given Θ, the term tr(S_T ) is constant to (8). For the term ${\Vert \mathrm{w}\Vert }_2^2$, due to the strong duality in SVM optimization, we solve it by

$$\begin{array}{cc}\hfill J_0\left(\Theta \right)& =\underset{\alpha }{\max }\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{y}_i{y}_j{\alpha }_i{\alpha }_j{K}_{\Theta }({\mathrm{x}}_i,{\mathrm{x}}_j)\hfill \\ \hfill s.t.& \sum _{i=1}^n{\alpha }_i{y}_i=0,{\alpha }_i\ge 0\forall i,\hfill \end{array}$$ (9)

where α_i is the lagrangian multiplier. Many quadratic programming package could be used to solve (7). We use fmincon-SQP (sequential quadratic programming) in matlab. Our learning process is summarized in Table 1.

Table 1.

Discriminatively Learning Θ

Input: Θ(0) estimated by A-SGBN
Output: Θ* learned by (7)
1. Let Θ(t–1) = Θ(0)
2. Compute ${\Phi }_{\Theta }^{(t-1)}$ and ${\mathbf{K}}_{\Theta }^{(t-1)}$ by (3)
3. Compute $\mathrm{t}r{\left({\mathbf{S}}_T\right)}^{(t-1)}=\mathrm{tr}\left({\mathbf{K}}_{\Theta }^{(t-1)}\right)-1^{⊺}{\mathbf{K}}_{\Theta }^{(t-1)}1∕n$
4. Solve J0(Θ(t–1)) and α* by (9)
5. J(Θ(t–1)) = J0(Θ(t–1)) × tr(ST)(t–1)
6. Compute ▿Θ(t–1)J by (10)
7. For a given α*, minimize (7) using J(Θ(t–1)) and  ▿(Θ(t–1)J; Obtain the optimal Θ(t)
8. Let Θ(t–1) = Θ(t)
9. Repeat Step 2-8 until convergence, let Θ* = Θ(t)

3.3.3 Discussion

Gradient of (7)

A simple form of gradient is favored by many optimization algorithms (including fmincon-SQP) to speed up the line search, which is true in our case. The gradient of the objective function in (7) can be computed as

$$\begin{array}{cc}\hfill {\nabla }_{\Theta }J=& -\frac{1}{2}\mathrm{tr}\left({\mathbf{S}}_T\right)\sum _{\mathit{ij}}{\alpha }_i^{\star }{\alpha }_j^{\star }{y}_i{y}_j{\nabla }_{\Theta }{K}_{\Theta }({\mathrm{x}}_i,{\mathrm{x}}_j)\hfill \\ \hfill & +J_0\left(\Theta \right)\left(\mathbf{I}+\frac{1}{n}{11}^{⊺}\right){\nabla }_{\Theta }{K}_{\Theta }({\mathrm{x}}_i,{\mathrm{x}}_j),\hfill \end{array}$$ (10)

where α* maximizes (9). The symbols I and 1 are defined as before. The terms tr(S_T) and J₀(Θ) have been computed when evaluating the objective function J(Θ) in 7, thus introduce no additional computational cost. ▿_ΘK_Θ(x_i, x_j) is simply a linear function of Θ:

$$\begin{array}{cc}\hfill \frac{\partial K_{\Theta }({\mathrm{x}}_i,{\mathrm{x}}_j)}{\partial {\theta }_l}=& \left[\mathbf{S}{\left(x_{\mathit{il}}\right)}^{⊺}\mathbf{S}\right(x_{\mathit{jl}})+\mathbf{S}{\left(x_{\mathit{jl}}\right)}^{⊺}\mathbf{S}(x_{\mathit{il}}\left)\right]{\theta }_l\hfill \\ \hfill & +\left(\mathbf{S}{\left(x_{\mathit{jl}}\right)}^{⊺}{\mathrm{s}}_0\right(x_{\mathit{il}})+\mathbf{S}{\left(x_{\mathit{il}}\right)}^{⊺}{\mathrm{s}}_0(x_{\mathit{jl}}\left)\right),\hfill \end{array}$$ (11)

where x_il denotes the l-th feature of the i-th sample, and S and s₀ are defined in (3).

Variable selection

Learning the whole set of SGBN parameters may encounter the “curse of dimensionality” when the training samples are insufficient. For example, we have less than 100 training samples, but 3600 parameters (from two classes) to learn. This may cause overfitting and make the estimation unstable. To handle this issue, we hypothesis that, learning only a selected subset of parameters may mitigate the overfitting and improve the discrimination. For this purpose, θ is partitioned into two parts: Θ = {Θ_sel, Θ_nosel}. We keep using the whole Θ for computing K_Θ, but optimize (7) only over Θ_sel. There are many options to determine Θ_sel. We initially compute the Pearson correlation between each component of Ф_Θ and the class labels on the training data, and select the top θ_i with the highest correlations. To keep our problem simple, only the parameters associated with edges present in the graph are optimized. In this way, the optimization may only eliminate but never add edges in the graph, which avoids the violation of DAG, as well as maintaining the sparcity of the initial A-SGBN. It is remarkable that even this simple selection process has been able to greatly improve the discrimination experimentally.

Extension

Although focusing on each node corresponding to a scalar ROI feature, our method is readily to be extended to handle multiple features (feature vector) of an ROI. In this case, the conditional distribution for node i becomes $p({\mathrm{x}}_i\mid \mathbf{Pa}({\mathrm{x}}_i\left)\right)=\mathcal{N}({\mathrm{x}}_i\mid {\sum }_{{\mathrm{x}}_j\in \mathbf{PA}\left({\mathrm{x}}_i\right)}{\mathbf{M}}_{\mathit{ij}}{\mathrm{x}}_j,{\Sigma }_i)$, where PA and M are all matrix. Our learning remains the same. In our future work, we will apply this extension to analyze fMRI where each ROI is associated with a vector of temporal signal.

4. Experiment

We test our proposed A-SGBN and DL-A-SGBN with the baseline SGBN (B-SGBN) from [2] (without normalizing the data) in three aspects: i) model fitting, ii) discrimination, and iii) connectivity. Three data sets are used in our experiment: the MRI and FDG-PET data mentioned in Section 3.1, and another MRI-II data that uses the MR images from the same subjects as MRI, but involves 40 different ROIs (see supplementary material). Although not as discriminative as that in MRI, the ROIs in MRI-II are more spread across the frontal, parietal, occipital and frontal lobes, thus specially used for a detailed lobe-to-lobe comparison on connectivity. We randomly partition each data set into 30 groups of training-test pairs. Each group includes 80 training and 40 test samples in MRI and MRI-II, or 60 training and 43 test samples in PET.

4.1. Comparison of Fitting

Our DL-A-SGBN targets to become discriminative without sacrificing too much power of data representation compared with B-SGBN. Since the change of data fitting from A-SGBN to DL-A-SGBN has been explicitly controlled by the user-defined parameters T₁ and T₂, we simply compare the model fitting between A-SGBN and B-SGBN. The fitting errors are tested on both training and test data for each class in all three data sets. The root of mean squared fitting errors (RMS) are summarized in Table 2. In order to test if the fittings of A-SGBN is statistically different from that of B-SGBN, a paired t-test (two-tailed) is conducted on the fitting errors over the 30 groups for each data set, respectively. The resulting p-value is also given in the last column in Table 2.

Table 2.

Fitting Error (RMS) Averaged over 30 Training-Test Groups

MRI		B-SGBN	A-SGBN	p-value
Training	MCI	0.6344	0.6192	0
	NC	0.5962	0.5896	0
Test	MCI	0.7385	0.7301	0
	NC	0.6801	0.6763	3.2e-4
PET		B-SGBN	A-SGBN	p-value
Training	NC	0.5466	0.5334	0
	AD	0.6291	0.6195	0
Test	NC	0.6171	0.6100	5e-8
	AD	0.7508	0.7467	2.2e-6
MRI-II		B-SGBN	A-SGBN	p-value
Training	MCI	0.6756	0.6675	0
	NC	0.6441	0.6382	0
Test	MCI	0.8047	0.8033	0.055
	NC	0.7381	0.7366	9.1e-4

As shown, on all three data sets, our A-SGBN fits the data consistently better than B-SGBN. Such improvement is significant as indicated by the small p-values (except for MCI group in MRI-II). This finding indicates that our A-SGBN might better reflect the underlying distribution of the data, which makes it perform well on both the training and the test data. Another interesting finding is that the generative models explain the NC better than the MCI (in MRI data set) or the AD (in PET data set) patients. This may reflect the common impression that compared with the healthy population, the AD population might be more heterogeneous and therefore have more difficulty to find a unified model for representation.

4.2. Comparison of Discrimination

Our proposed learning process results in two kinds of models: two DL-A-SGBN models with one for each class, and one SBN-induced SVM classifier that considers only the boundary of the two classes. We test whether our learning can improve the discrimination power on both kinds. The A-SGBN models estimated separately for each class are used as the initial solution. In order to keep reasonable interpretation, we allow maximal 1% additional squared fitting errors (that is, T_i = 1.01 × T_i0, (i = 1, 2), where T_i0 is the squared fitting error of the initial solution) to be introduced during the learning of DL-A-SGBN. We test both the SVM classifier and the DL-A-SGBNs. For the SVM classifier, to agree with (6), we use $\mathcal{L}2$-SVM with Fisher kernels. For DL-A-SGBNs, as mentioned before, we simply compare the values of the estimated likelihood, and assign the sample to the class with a larger likelihood. We also conduct a paired t-test (two-tailed) to examine the statistical significance of the improvement over the 30 groups for all three data sets. The results are summarized in Table 3.

Table 3.

Test Classification Accuracy (%) Averaged over 30 Training-Test Groups

	SGBN-induced SVM classifier
	A-SGBN (%)	DL-A-SGBN (%)	p-value
MRI	71.42	74.50	6.2e-5
PET	57.75	65.43	0
MRI-II	57.25	61.83	1.4e-6
	SGBN classifier
	A-SGBN (%)	DL-A-SGBN (%)	p-value
MRI	71.08	74.83	6.8e-5
PET	67.36	71.47	4.7e-7
MRI-II	59.75	65.42	1.2e-6

It can be seen that, as expected, optimizing (6) significantly improves the discrimination power of SVM classifiers by 3.08% for MRI, 7.68% for PET, and 4.58% for MRI-II. More importantly, by learning a discriminative SVM classifier, we also simultaneously improve the discrimination power of the generative models DL-A-SGBN by 3.75% for MRI, 4.11% for PET, and 5.67% for MRI-II. Such improvements are statistically significant as indicated by the small p-values. Moreover, when cross-referencing the third columns in Table 3, it is noticed that our SVM classifiers perform just comparably (for MRI) or even worse (for PET and MRI-II) than our generative DL-A-SGBNs. This may be because our Fisher vectors have very high dimensionality, which causes the serious overfitting of data in SVM classifiers. Such situation might be somewhat leveraged for DL-A-SGBN since the Gaussian model may regularize the fitting. Based on this assumption, we further select a number of leading features from Fisher vectors by computing the Pearson corrlation of the features and the labels, and use the selected features to construct the Fisher kernel for the SVM classifiers. As shown in the last column in Table 4, the simple feature selection step can further significantly improve the classification performance of the fisher-kernel based SVM: from 74.5% to 80.08% for MRI, from 65.43% to 77.83% for PET, and from 61.83% to 73.5% for MRI-II.

Table 4.

Test Classification Accuracy (%) Averaged over 30 Training-Test Groups

	B-SGBN	A-SGBN	DL-A-SBN	SVM (sel)
MRI	62.08	71.08	74.83	80.08
PET	61.32	67.36	71.47	77.83
MRI-II	53.08	59.75	65.42	73.50

In Table 4, the improvement from our proposed learning method is scrutinized at each processing step. Compared with the B-SGBN induced from [2], introducing a biased node (A-SGBN) better fits the population, therefore improves the prediction on test data by 9% for MRI, 6.04% for PET, and 6.67% for MRI-II. The discrimination power of A-SGBN is further improved by 3 ~ 6% via our discriminative parameter learning. This leads to generative models DL-A-SGBN achieving a classification accuracy above 70%, with no more than 1% increase of the squared fitting error. Morever, by selecting leading features in the SGBN-induced Fisher vectors, we can construct more discriminative SVM classifiers with additional 6% or more improvement from our DL-A-SGBN to differentiate both MCI vs NC groups in MRI or MRI-II and AD vs NC groups in PET.

In summary, compared with the baseline B-SGBN, our proposed method can increase the prediction accuracies as high as 18% for MRI, 16% for PET, and 20% for MRI-II by using Fisher kernel induced SVM classifiers with feature selection. Meanwhile, these SVM classifiers are linked to the learned generative model DL-A-SGBN whose discrimination powers have also been increased by about 10% from B-SGBN on all three data sets. Our DL-A-SGBN models are not only discriminative, but also descriptive with only a slight increase in the squared fitting errors (at most 1% increase, controlled by the optimization parameter).

4.3. Comparison of Connectivity

In order to gain more insight into the results, we also conduct a lobe-to-lobe comparison on the connectivity derived by our methods and B-SGBN. It is found that, although the 40 ROIs used in MRI and PET are individually discriminative, they do not necessarily cover the representative regions across the whole brain. For example, the 40 nodes used in the MRI data set are mostly located in the temporal lobe and the subcortical region. Therefore, we specially design the MRI-II data set by selecting 40 regions that cover the frontal, parietal, occipital and temporal (including the subcortical region) lobes from MR images of the same subjects involved in MRI data. Although MRI-II (with the best test accuracy of 73.5%) is less discriminative than MRI (with the best test accuracy of 80.08%) as shown in Table 4, we consistently observe significant improvements of our method over B-SGBN.

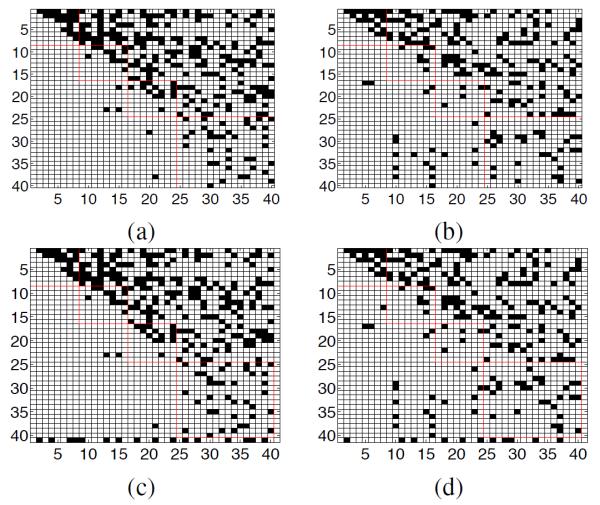
The structures of the brain networks recovered from NC and MCI groups are displayed in Fig. 2 by using B-SGBN and DL-A-SGBN, respectively. The network structure is obtained by binarizing the edges θ with a threshold of 0.01. Each row i represents the effective connections (dark dots) starting from the node i, and each column j representes the effective connections ending at the node j.

Figure 2.

Structure of Connectivity: (a) NC by B-SGBN, (b) MCI by B-SGBN, (c) NC by the proposed DL-A-SGBN, (d) MCI by the proposed DL-A-SGBN.

With similar parameter settings, the B-SGBN produces 273 edges for NC, and 224 edges for MCI, while our DLA-SGBN produces 285 edges for NC, and 236 edges for MCI. Please note that DL-A-SGBN has an additional bias node corresponding to the last row and column. Because the bias node has no parent node, the last column is all zero. We check the edge difference between the two methods lobe by lobe, and give the result in Table 5. As shown, the two methods produce similar network structures both visually and quantitatively in most brain regions. There are in total 36 different edges (less than 15%) for NC network, and 11 different edges (around 5%) for MCI network. About half different connections are identified within the temporal lobe (15 for NC, 5 for MCI), for which we also include subcortical structures such as hippocampus and amygdala. It is known that temporal lobe (and some subcortical structures) plays a very important role in the progression of AD. Such a structural difference in this lobe may potentially reflect the different capacity of prediction between our DL-A-SGBN and the B-SGBN.

Table 5.

Number of edge difference between the baseline B-SGBN and the proposed DL-A-SGBN in two groups, respectively: NC (MCI)

	Frontal [1:8]	Parietal [9:16]	Occipital [17:24]	Temporal [25:40]
Frontal	1 (0)	1 (1)	3 (0)	0 (0)
Parietal	0 (1)	0 (0)	3 (0)	4 (0)
Occipital	0 (0)	1 (0)	2 (1)	5 (1)
Temporal	0 (0)	0 (1)	1 (1)	15 (5)

Traditional brain connectivity analysis focuses on the analysis of brain structure which is a binarized connectivity. For example, the network structures from both the BSGBN and our DL-A-SGBN indicate the loss of effective connections (around 17%) in MCI group in almost all lobes (slightly in the frontal lobe), which agrees well with documented studies. However, binarizing connectivity depends on the selection of threshold. If some connection strength has been weakened by the disease but not reduced below the threshold, this change will be unnecessarily ignored when merely studying the brain structure. This observation is affirmed by our learning process that promotes the discrimination of A-SGBN. Simply optimizing the connection strength across a subset of selected nodes has already significantly improved the prediction with only a minimum (or mostly no) change of brain structure.

Moreover, using SGBN-induced fisher kernels, we are able to produce a new kind of features to analyze brain connectivity: the subject specific change of connection strength between nodes. We investigate the selected features of MRI-II used in our SBN-induced SVM classifier and visualize three most discriminative connection changes (Fig. 1 right) happening at “middle temporal gyrus left” (in brown) → “superior parietal lobe left” (in purple), “hippocampus right” (in blue) →“superior parietal lobe left”, and “inferior temporal gyrus left” (in green) →“middle occipital gyrus right” (in cyan). Also discriminative are the connections from the bias node to “middle occipital gyrus right” and to “precuneus left”.

Figure 1.

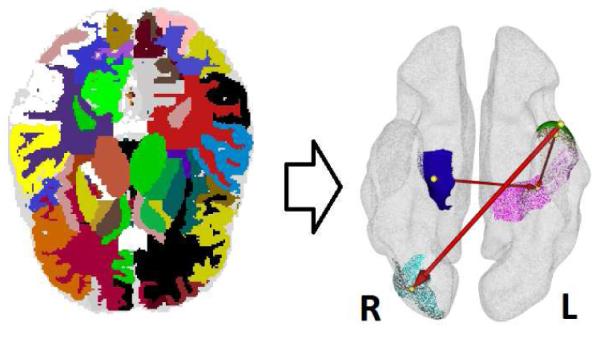
Left: ROI partitions on MRI. Right: Some identified directional relationships discriminative for AD. (Please refer to Section 4.3. The figure is best viewed on monitor.)

5. Conclusion

In this paper, we present a framework to model brain effective connectivity encoded with essential discrimination information. With the link of Fisher kernel, our proposed framework is able to simultaneously produces generative SGBN models and its associated SVM classifier that are sufficiently discriminative for brain network analysis for AD. In addition, by considering the changes rate of connection strength, our method also provides a new perspective for brain connectivity analysis.