Abstract
Classification of proteins into families is one of the main goals of functional analysis. Proteins are usually assigned to a family on the basis of the presence of family-specific patterns, domains, or structural elements. Whereas proteins belonging to the same family are generally similar to each other, the extent of similarity varies widely across families. Some families are characterized by short, well-defined motifs, whereas others contain longer, less-specific motifs. We present a simple method for visualizing such differences. We applied our method to the Arabidopsis thaliana families listed at The Arabidopsis Information Resource (TAIR) Web site and for 76% of the nontrivial families (families with more than one member), our method identifies simple similarity measures that are necessary and sufficient to cluster members of the family together. Our visualization method can be used as part of an annotation pipeline to identify potentially incorrectly defined families. We also describe how our method can be extended to identify novel families and to assign unclassified proteins into known families.
Genome projects (Bernal et al. 2001) are generating sequence data at a much faster rate than can be effectively analyzed. The goal of functional genomics is to determine the function of proteins predicted by these sequencing projects (Bork et al. 1998; Eisenberg et al. 2000; Tsoka and Ouzounis 2000). Because experimental evidence about individual proteins is difficult to obtain, a common strategy is to classify proteins into families on the basis of the presence of shared features or by clustering using some similarity measure. The underlying assumption is that members of the same family may possess similar or identical biochemical functions (Hegyi and Gerstein 1999) and that one can assign the functions of well-characterized members of a family to other members whose functions are not known or not well understood (Heger and Holm 2000).
The simplest methods for clustering proteins into families rely on sequence-similarity measures, such as those obtained by BLAST (Altschul et al. 1990). More sophisticated approaches detect domains using domain databases (Bateman et al. 2002; Servant et al. 2002; Mulder et al. 2003), optionally use the order of domains as a fingerprint for the protein, and classify proteins into families on the basis of the presence of shared domains or similar domain architecture (Geer et al. 2002). Classification of proteins into families using structural similarities (Holm and Sander 1996) is, at present, limited by the relatively small number of structures available in PDB (Berman et al. 2000)—only 22,874 as of Oct 16th, 2003.
Similarity-based clustering is a two-step process—one first needs to determine pairwise similarities between all pairs of proteins and then apply a clustering method that uses the similarity matrix to group proteins into clusters. However, methods that quantify similarity by using some attribute of the best BLAST hit and use single-linkage clustering are not always successful. One problem such methods face is the detection of the multidomain structure of many protein families. Ideally, proteins should be classified into a single family only if they exhibit highly similar domain architecture. Best hit-based approaches may group together different multidomain proteins that share a common domain (Smith and Zhang 1997) and are prone to mistakes in the presence of promiscuous domains (Doolittle 1995; Marcotte et al. 1999). Several graph-based clustering methods have been proposed to overcome some of the limitations of single-linkage clustering (Matsuda et al. 1999; Enright and Ouzounis 2000; Enright et al. 2002). We show that some of the shortcomings of single-linkage clustering can be overcome by post-processing (and, if possible, grouping) BLAST hits into matches.
In this study, we test our methods on the protein families of Arabidopsis thaliana. The Arabidopsis thaliana genome was fully sequenced in 2000 (Arabidopsis Genome Initiative 2000), and the predicted proteome contains 28,995 annotated proteins. However, as of Jan 7th, 2004, only 5473 proteins have been classified into 741 families. The gene family information page maintained at The Arabidopsis Information Resource (TAIR) (Rhee et al. 2003) lists the different research groups involved in Arabidopsis thaliana gene-family identification, and provides references to publications describing the properties and construction of the gene families. In several cases, the construction of the family is fairly complicated and is based on an in-depth understanding of the properties of similar well-characterized families in other sequenced genomes. The computational methods utilized include scanning the protein sequences for known domains or motifs, identifying transmembrane regions, analyzing hydropathy plots, detecting homologs of characterized proteins from other species, etc. Phylogenetic analysis or clustering based on domain architecture is usually used to further divide large clusters into smaller families.
In this work, we study whether Arabidopsis thaliana families constructed by such diverse methods can be characterized by a small set of biologically meaningful parameters. In other words, we do not attempt to discover families ab initio; rather, we show that most discovered families can be described by one or two parameters. We consider two different parameter schemes. In the first scheme, similarity between two proteins is measured in terms of the fraction of the proteins participating in a gapped alignment (cover) and the percentage identity of such an alignment. We also analyze a second scheme in which similarity is measured in terms of relative score, that is, the ratio of the score of the alignment to the self-similarity score (score of a protein with itself).
In either scheme, we say that a family is clusterable if carrying out single-linkage clustering with some particular threshold value for the parameter(s) groups members of that family into a single cluster. Carrying out the clustering operation with a lower threshold usually results in the cluster becoming corrupted by members of other families, whereas raising the threshold may split the family across multiple clusters. We describe a novel method for visualizing the variation in clusterability with choice of parameters. Our method identifies the parameter values that best characterize a family, and thereby provides ready answers to questions of the form “How similar are members of family X?”
One result of our work is the discovery that, despite the wide variety of methods used in the construction of protein families, 76% of all analyzed Arabidopsis thaliana families are fully clusterable by the proposed simple parameter schemes. Our results, available online at http://warta.bio.psu.edu/htt_doc/ArabCluster, also show relationships between families that share members, and help identify potentially incorrect family assignments. We also show how our results could be used to identify novel families and assign unclassified proteins to known families.
METHODS
Constructing Matches From Hits
Let A be the set of all protein sequences. We compare the proteins of A against each other by running BLASTp with e-value 0.0001. The result is a set of hits, in which each hit is a local alignment that aligns a region of one protein sequence with a region from another protein sequence with a particular score. By parsing the BLAST output, we can define, for each hit, location attributes that specify which regions of the proteins are participating in the local alignment and quality attributes that indicate how good the hit is. More formally, a hit h that aligns region [x1, x2] of protein x with region [y1, y2] of protein y has the following location attributes:
start(h, x) = x1, end(h, x) = x2, location(h, x) = [x1, x2]
start(h, y) = y1, end(h, y) = y2, location(h, y) = [y1, y2]
and the following quality attributes:
identity(h)—the percentage identity of the hit
aln_len(h)—the length of the alignment
cover(h, x)—the % of protein x participating in the hit
cover(h, y)—the % of protein y participating in the hit
score(h)—the bit score of the hit as reported by BLAST
We term the hit that aligns the entire length of a protein sequence p against itself as a self-hit and use the notation self-score(p) to refer to the score of such a hit. On the basis of these self scores, we can define two relative score (quality) attributes for any hit h involving distinct proteins x, y:
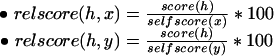 |
If there are multiple hits between a pair of proteins, the best hit alone may not represent the full extent of similarity between the proteins. At the same time, it may not be possible to take all of the hits into consideration, as a single domain in one protein can match multiple occurences of a repetitive motif in the other protein. A common strategy is to summarize the similarity using a compatible set of hits. We say that a set of hits between a pair of proteins is compatible if the regions participating in the alignments are nonoverlapping, and if the lines representing the hits do not intersect in a pictorial representation of the hits (see Fig. 1). More formally, hits h1, h2 between a pair of proteins x, y, are compatible if:
Figure 1.
Three hits between proteins p1, p2 are shown at left. Hits h1, h2 are incompatible, as the participating regions are in the opposite order. Thus, if score(h1) > score(h2), the best match will be constructed from h1, h3, otherwise, it will be constructed from h2, h3.
location(h1, x) ∩ location(h2, x) = φ and location(h1, y) ∩ location(h2, y) = φ
(end(h1, x) < start(h2, x)) and (end(h1, y) < start(h2, y)) or
(end(h2, x) < start (h1, x)) and (end(h2, y) < start(h1, y))
A set of hits H between a pair of proteins x, y is compatible if all pairs of hits in H are compatible by the above definition. Such a compatible set of hits can be grouped into a match, m. A match has the same quality attributes as a hit. Percentage identity is computed by taking the weighted percentage identity across the hits in H, that is,
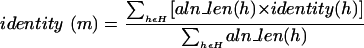 |
whereas all other quality attribute values can be obtained by adding up the corresponding values across the hits in H. Thus, a match can be thought of as a type of global alignment constructed from several local alignments. We define the best match, m(x, y), between distinct proteins x, y as the match with the highest score. A more formal treatment of compatible hits, matches, and simple methods for calculating the best match are available in Veeramachaneni (2002) and Zhang (2003). In the remainder of this work, we use the term “match” to refer to the best match between a pair of proteins.
Clustering
In this study, we consider two different similarity measures; the first measure, based on percentage identity (i) and percentage cover (c) is called the (i, c)-similarity measure, and the second measure, based on relative score (r) is termed the r-similarity measure. We describe in detail clustering based on the (i, c)-similarity measure only, as the actual clustering algorithm used is independent of the similarity measure.
We represent the similarity relationships in our protein data set by an undirected weighted graph, G. The nodes of G correspond to the set of all proteins A, and edges connect proteins x, y if, and only if, there is some hit with x as the query and y as the subject (or vice-versa). The weight of an edge represents the extent of similarity between the proteins connected by the edge. In the case of (i, c) clustering, the weight of the edge is given by a pair—the first element of the pair is the percentage identity of the best match between the proteins and the second element is the percentage of the proteins participating in the match (cover). More formally,
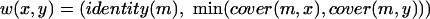 |
where m is the best match of proteins x, y. In a similar manner, the weight used in the case of r-clustering is given by
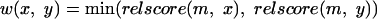 |
The graph representation of similarity data is amenable to several graph-based clustering algorithms including single-linkage clustering, k-means (Michalski et al. 1998) and MCL (Enright et al. 2002). We used single-linkage clustering, which is equivalent to finding connected components in the similarity graph, as it is the simplest of all clustering methods, and more importantly, because it has no hidden parameters.
To observe the effect of using different percentage identity and cover thresholds on the formation of clusters, we carried out (i, c)-clustering 100 times by varying percentage identity i and percentage cover c independently in increments of 10, from 0 to 90. For a particular choice of (i, c), we first construct a restricted graph Gi,c from G by retaining only those edges with weight at least (i, c). We then identify clusters by computing connected components of Gi,c (see Fig. 2). It is easy to see that G0,0, which is identical to G, will be a dense graph that yields a few large clusters, and that G90,90 will be a relatively sparse graph that yields several small clusters.
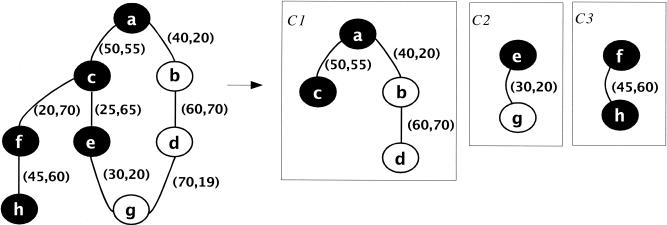
Figure 2.
A similarity graph G of eight proteins is shown at left. The weights on the edges show the percentage identity and cover of the best match between the pairs of proteins. When clustering with threshold (30, 20), G30, 20 is created from G by removing edges c—e, c—f, and d—g. G30,20 contains, three connected components that form the clusters C1, C2 C3 shown at right.
Relative score-based clustering is carried out in a similar manner by varying the threshold r from 0 to 90, in increments of 10.
Measuring Cluster Quality
Let P ⊆ A be the set of proteins that have been classified into a set of families F (some proteins may belong to more than one family). We are interested in checking whether the clusters produced by our method for a particular choice of (i, c) (or r) correspond to the protein families, F, defined by experts. In this respect, we are only interested in how well our method clusters know family members, not whether it accurately identifies unclassified proteins with similar properties. Therefore, we remove from our clusters all proteins that are unclassified (A–P). We are now left with a partition of P into clusters that we shall denote by Ci,c.
Ideally, each family of F will correspond to a single cluster of Ci,c. However, the more likely scenario is that some families will be spread across several clusters, or that several families will be grouped into a single cluster. Intuitively, we would consider the clustering parameters (i, c) to be “good” with respect to a family F if
the majority of the members of F are in a single cluster (concentration)
in each cluster that contains members of F, the majority of proteins belong to family F (purity)
Note that these two measures are orthogonal—if all of the classified proteins P are placed in a single cluster, then concentration is high, but purity is low. On the other hand, if each protein of P is placed in an individual cluster of size 1, then purity is high, but concentration is low. Concentration and purity reflect the sensitivity and specificity, respectively, of the clustering with respect to the family under consideration. Another method for measuring clustering quality that attempts to combine concentration, purity is matching rate (Kawaji et al. 2001).
We measure the concentration, purity, matching rate of family F in a particular cluster C ∈ Ci,c as follows:
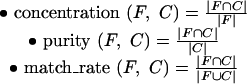 |
In other words, concentration measures the fraction of the family present in the cluster, whereas purity corresponds to the fraction of the cluster that belongs to the family. It is easy to see that the matching rate measure, which combines these two measures, satisfies the condition match_rate(F,C) ≤ min(concentration(F,C), purity(F,C)) and, therefore, cannot distinguish clusters with high concentration, low purity from clusters with low concentration, high purity.
We now extend these definitions to a set of clusters as:
concentration(F, Ci,c) = 100 × maxC∈Ci,c concentration(F,C)
purity(F,Ci,c) = 100 × ΣC∈Ci,c[purity(F,C) × concentration(F,C)]
match_rate(F,Ci,c) = 100 × maxC∈Ci,c match_rate(F,C)
When measuring quality in terms of concentration and purity, we say that a family F is (x, y) clusterable by parameters (i, c) if concentration(F,Ci,c) ≥ x and purity(F,Ci,c) ≥ y. Similarly, if matching rate is the measure of clustering quality, we say that a family F is x clusterable if match_rate(F,Ci,c) ≥ x.
In the example shown in Figure 2, the proteins belong to two families—the B family with five members is shown in black, and the W family with three members is shown in white. The computation of concentration, purity, and matching rate for the two families is summarized in the table below:
Table 1.
| C1 | C2 | C3 | overall | ||
|---|---|---|---|---|---|
| family B | concentration | 2/5 | 1/5 | 2/5 | 40 |
| purity | 2/4 | 1/2 | 2/2 | 70 | |
| match rate | 2/7 | 1/6 | 2/5 | 40 | |
| family W | concentration | 2/3 | 1/3 | 0/3 | 66 |
| purity | 2/4 | 1/2 | 0/2 | 50 | |
| match rate | 2/5 | 1/4 | 0/2 | 40 |
Although (30, 20) may not be the right clustering parameters for families B, W, this does not mean that the families are not clusterable. In fact, family B is (100, 100) clusterable by parameters (0, 50) and family W is (100, 100) clusterable by parameters (60, 0).
Displaying Clustering Quality
For a particular family, we display the variation in clustering quality as a function of the clustering parameters (i, c) in the form of a 10 × 10 grid (see Fig. 3). If the quality is measured in terms of concentration and purity, each grid element is shown in a rgb color triple, where the extent of red corresponds to the purity, and the extent of green corresponds to the concentration (blue is always set to 0.0). When matching rate is used as the quality measure, the grid element is shown in shades of gray, with white representing match rate 100, and black representing match rate 0. In the interest of conciseness, these Variation in Clustering Quality pictures will be referred to as VCQ pictures in the rest of this work.
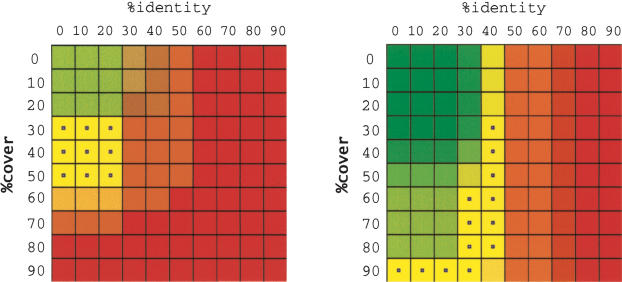
Figure 3.
Clustering quality of the B family from Figure 2 is shown at left. The quality picture for the MDR family of the ABC superfamily of Arabidopsis thaliana is shown at right.
The clustering quality of family B, which consists of the black nodes from Figure 2, is shown on the left hand side of Figure 3. In the top left corner, where i = 0, c = 0, all members of the B family are in the same cluster (high concentration or green), but the cluster also contains all members of the W family (low purity or red). This leads to a strong green color. At the opposite end of the picture, each member of the B family is in its own trivial cluster of size 1 (high purity, low concentration), leading to the red color. As indicated by the calculations shown in the table, the grid element corresponding to i = 30, c = 20 is filled with a color that is 40% green and 70% red, resulting in a slightly reddish color. Also note that because the B family is fully clusterable by parameters (0, 50), the grid element at that location is 100% red, 100% green, that is, yellow. A small blue dot is used to indicate such perfect concentration, purity.
The results for the MDR family of proteins (Sanchez-Fernandez et al. 2001), are also shown in Figure 3. This family clusters perfectly when percentage identity is chosen between 30 and 40 and percentage cover at least 60. The perfect clusterability at high cover indicates that members of the family are of approximately the same length, and that a low-percentage identity extends across almost the entire length of the proteins.
Notes on Clusterability
Because every protein matches itself with 100% identity and cover, it is easy to see that any family of size 1 is (100, 100) clusterable. We call such families trivial families.
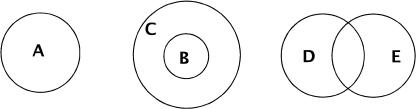
We classify nontrivial families into several categories on the basis of the extent of shared family members. The categories can be described without ambiguity in set theoretic terms; however, we choose to illustrate them with the help of Figure 4 due to space constraints.
Figure 4.
Possible relationships between families on the basis of shared members.
atomic family: no members are shared (A)
subset family: all members are shared with some family (B)
superset family: contains a subset family (C)
intersected family: some members are shared (D, E)
In reality, the picture can be more complicated, as a family can fall into more than one category, for example, a superset family can itself be a subset or intersected family, etc. However, even with this simple picture, one can see that our expectations regarding the clusterability of a family vary with the category in which the family falls. For instance, we would expect family A to be more clusterable than the other families.
RESULTS
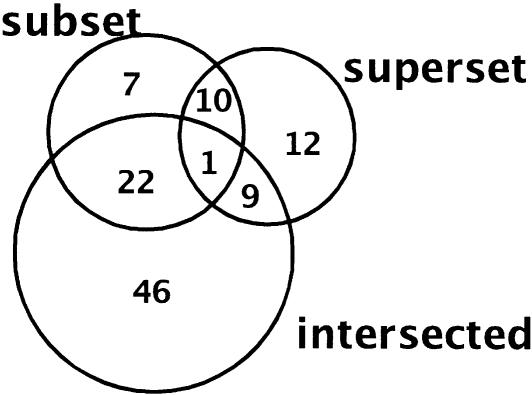
The complete set of 28,581 Arabidopsis thaliana protein sequences from TIGR formed the set A. Gene family information downloaded from http://www.arabidopsis.org on July 28, 2003 helped us classify 4241 of these proteins into 571 families. A total of 119 families are trivial and 345 are atomic. The classification of the remaining 107 families is shown in Figure 5.
Figure 5.
Venn diagram showing the classification of the nonatomic families as of July 28, 2003. A total of 22 families can be classified as subset and intersected, whereas one family falls into all of the three shown categories.
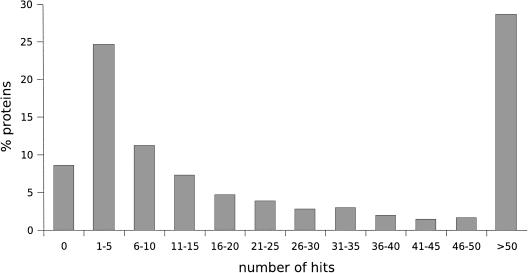
The entire set of proteins A was compared against itself using BLASTp with a e-value threshold of 0.0001. The distribution of the resulting 2,254,453 hits is shown in Figure 6. A total of 8.6% of proteins participate in no hits at all, whereas 1.3% participate in more than 1000 hits. A total of 19 nontrivial families defined by experts contain proteins that have no hits to any other proteins—clearly these families will not be (100, 100) clusterable for any choice of clustering parameters.
Figure 6.
Distribution of the number of BLAST hits per protein.
In 76% of the cases, there is exactly one hit between a pair of proteins, so the best match is identical to this hit. In the other cases, where there are multiple hits—due to repeated motifs or conserved domains separated by a distance—we compute the compatible set of hits with the maximum score and create the best match.
Clusters were determined using single linkage clustering. Graph G0,0, in which no edges are discarded, contains 238 connected components (clusters), whereas G90, 90, in which all edges with percentage identity and cover less than 90 are removed, yields 3961 clusters.
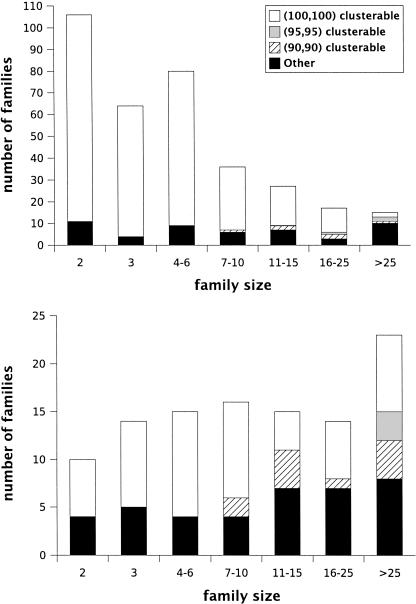
Finally, unclassified proteins were removed from the computed clusters, and the clustering quality for each family was computed for all choices of clustering parameters. Overall, 86% of atomic families are at least (90, 90) clusterable for some choice of clustering parameters, whereas only 64% of nonatomic families are similarly clusterable. The variation of clusterability, with family size and classification is shown in Figure 7. The results for r clustering are almost as good (within 2%).
Figure 7.
The graph at top shows the variation of clusterability with family size for atomic families. A similar graph for nonatomic families is shown at bottom. Please note that the scales used are different.
VCQ pictures similar to Figure 3 for each family and superfamily are available at http://warta.bio.psu.edu/htt_doc/ArabCluster. All of the pictures and the Web pages are constructed on-demand by perl scripts querying a MySQL database that stores the necessary information.
DISCUSSION
Match as Unit of Similarity
In this study, we use single-linkage clustering as the mechanism for grouping similar proteins. The potential drawbacks of using single-linkage clustering have been documented in several papers that propose more sophisticated clustering methods. However, our goal in this study was not to discover families, but rather to characterize existing families by meaningful attributes such as identity, cover, and relative score. We avoided the use of biologically unmeaningful parameters such as inflation value (Enright et al. 2002), connectivity ratio (Matsuda et al. 1999), z-score cutoff value (Enright and Ouzounis 2000), which are used in the automated detection of families by other similarity graph-based clustering methods. Another reason for using single-linkage clustering is that it was the most common clustering method used by researchers involved in the creation of Arabidopsis families listed at http://www.arabidopsis.org.
In an effort to overcome some of the problems associated with using single-linkage clustering for grouping members of multidomain families, we use the notion of a match that can be thought of as a form of gapped alignment composed of possibly multiple BLAST hits. Note that the concept of a match is not novel—it has been used implicitly by programs such as Sim4 (Florea et al. 1998), est_genome (Mott 1997) and Spidey (Wheelan et al. 2001) to align mRNA sequences to genomic sequences. In fact, even the construction of a gapped BLAST hit from ungapped hsps embodies this concept (although, of course, there are additional parameters like gap penalties at work in this case). It has also been used as a measure of similarity by programs such as XDOM (Gouzy et al. 1997), and in the creation of HOVERGEN (Duret et al. 1994), HOBACGEN (Perriere et al. 2000) databases.
Figure 8 shows an instance where our usage of match as the basic unit of similarity helps distinguish members of two different families in the ABC superfamily (Sanchez-Fernandez et al. 2001). In this particular case, all hits have very similar identities (≈30%), cover (≈40%) and score. Thus, single-linkage clustering based on the best hit alone would have grouped all three proteins together. However, when we compute the best match, the cover (and relative score) between the two MDR family proteins doubles, and this helps separate them from the ATH family. A similar process helps distinguish the MDR proteins from those of the PMP, ATM, and TAP families of the ABC superfamily (see http://warta.bio.psu.edu/htt_doc/ArabCluster/sfams/sf2.html).
Figure 8.
MDR family proteins contain two transmembrane domains, whereas ATH family proteins contain only one. All of the hits between the MDR proteins and the ATH protein are shown at left as lines connecting the transmembrane regions. The hits that form the best matches are shown at right.
Overall, only 2% of the matches computed are composed of multiple hits. One reason for this unexpectedly small number could be that our criteria for hits to be compatible is too stringent—we require hits not to overlap at all. It is possible that allowing for small overlaps between hits—as is done in XDOM (Gouzy et al. 1997)—will permit more nontrivial matches. A second reason for the small number of matches with multiple hits is that in many cases, multidomain proteins are connected by a single hit. For instance, proteins PHYB_ARATH, PHYD_ARATH of the Histidine Kinase family (Hwang et al. 2002) have identical domain architecture comprising of five full-length, nonoverlapping Pfam (Bateman et al. 2002) domains. However, the BLAST comparison results in a single hit between the proteins that encompasses all the five domains. Overall, the matches formed by a single hit are always likely to be a significant majority, as the number of multidomain proteins is exponentially smaller than the number of single domain proteins (Wolf et al. 1999).
Usefulness of VCQ Pictures
At present, the usual manner of describing the sequence level similarity of a family is by statements of the form “amino acid identity of family F ranges from 20%–80%”. However, such statements are not very helpful in understanding what distinguishes family F from other families at the sequence level, that is, it is possible for a protein to match a member of F with identity 30% and still not be a member F. Our VCQ pictures provide this information, as the underlying method takes into consideration all known protein families. Thus, if family F clusters perfectly for all (i, c) parameter combinations from, say, (30, 30) to (50, 80), then one can be confident that no (classified) protein not belonging to F matches any member of F with similarity (30, 30) or higher; (30, 30) is the parameter that distinguishes F from other families, whereas the overall yellow region in the picture gives an idea of the similarity within the family.
VCQ pictures (like Fig. 3), can give a rough idea of the nature and extent of conserved domains in a family. Families with small, unique domains are clusterable by a high identity, low-cover threshold that is visible as a yellow region in the top right-hand side of the (i, c)-clustering VCQ picture, whereas multidomain families are likely to be clusterable by low-identity, high-cover thresholds.
One can also use the pictures to identify families that have been defined too broadly (concentration is unusually low, even at low thresholds), or too narrowly (purity is unusually low, even at high thresholds).
Note that the VCQ picture of a family may change as more proteins are classified and novel families are created. However, updating the pictures is fairly simple, as the time-consuming steps of measuring similarities and carrying out the clustering with different thresholds are independent of the classification of proteins into families. When family definitions are added or modified, we simply have to filter the precomputed clusters to discard unclassified proteins and remeasure the quality.
Comparison of Clustering Schemes
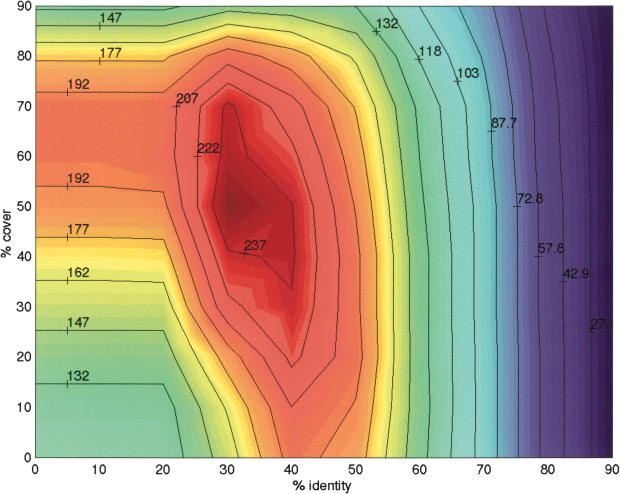
Our first clustering scheme uses percentage identity and cover as the similarity measure. We analyzed our (i, c)-clustering results to measure how effective these parameters were individually. The results summarized in Table 1 show that using these parameters in combination improves the clusterability results significantly. Figure 9 shows the number of families that are clusterable for different (i, c) parameter combinations. Because low values of threshold can decrease purity and high values can decrease concentration, it comes as no surprise that intermediate values of parameters i, c are most effective at clustering families – in particular, the parameter combination (i = 30, c = 50) alone is capable of clustering 252 (56%) of the nontrivial families.
Table 1.
Clustering Quality Results for the 452 Nontrivial Families
| (i, c) | i | c | r | |
|---|---|---|---|---|
| (100,100) | 340 (75%) | 274 (61%) | 229 (51%) | 332 (73%) |
| (90,90) | 369 (82%) | 290 (64%) | 256 (57%) | 362 (80%) |
The columns represent different clustering schemes — column labeled i refers to clustering using percentage identity alone, column labeled c refers to clustering using percentage cover alone, etc. The first row lists families that are (100,100) clusterable, whereas the second includes families that are at least (90,90) clusterable.
Figure 9.
Contour plot showing, for each choice of identity and cover, the number of nontrivial families that are (90, 90) clusterable.
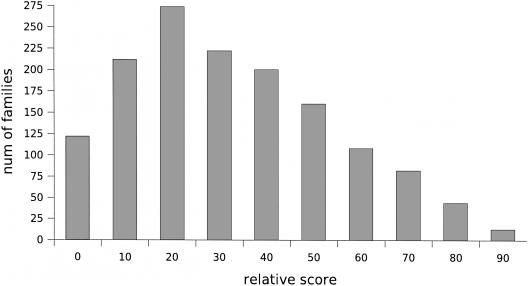
The second clustering scheme uses relative score as a measure of similarity. Relative score-based clustering is computationally simpler, as it needs to be carried out only 10 times as opposed to 100 times for (i, c)-clustering. The results shown in Table 1 indicate that it is almost as effective as (i, c)-clustering. However, as high-identity, low-cover matches and low-identity, high-cover matches can have the same relative score, it is harder to gain an understanding regarding the nature of similarity within a family by viewing the relative score-based clustering quality picture. Analogous to Figure 9, we show in Figure 10 the number of families that are clusterable at different relative score levels.
Figure 10.
Number of families that are (90, 90) clusterable at different levels of relative score thresholds.
Factors Affecting Clusterability
As can be inferred from the results presented in the previous section, small families have a higher chance of being clusterable. However, equally important is the type of the family—atomic families are much more likely to be clusterable than subset, superset, or intersected families. One should also keep in mind that the same family is sometimes independently listed by several groups. For instance, the PDR family appears three times—as a member of the ABC superfamily (Sanchez-Fernandez et al. 2001), as a member of the ABC Transporters superfamily, and yet again, independently as the ABC transporter PDR subfamily (van den Brule and Smart 2002). Only the final version, which is a superset of the other two is fully clusterable. Due to such inconsistencies, it is natural that some nonatomic families will not be clusterable. Our Web site displays for each family all other related families (families with which members are shared), and thus makes it easier to spot such inconsistencies.
We now list some of the reasons why an atomic family may not be clusterable in our analysis:
Idiosyncracies in the family: One example is the structure of the two members of the PMP family (ABC superfamily) shown in Figure 11. The PMP proteins are supposed to be half-molecule ABC transporters (Sanchez-Fernandez et al. 2001), however, Q94FB9 is a full-molecule transporter with each half being PMP like. This causes the cover of the match between the two proteins to reduce by 50%. Attempts to cluster them together by lowering the threshold for cover will only gather other ABC proteins with two transmembrane domains.
Very similar families: Two of the Eukaryotic Initiation Factors Gene superfamily are eIF4A eIF4A, and eIF4A-like (Metz et al. 1992). The former family is fully clusterable, but the latter consists of five members, that by all quantitative measures of similarity, are as similar to each other as they are to members of the eIF4A family. The main reason for the proteins to be in different families seems to be historical; the members of the eIF4A family were the first ones of the superfamily to be characterized and studied, whereas the members of the eIF4A-like family have not been studied completely. Note that the two families taken together are clusterable, so it is still possible that experimental validation will result in the families being merged at some later point in time. In that case, the resulting family will be fully clusterable.
Level of grouping: Proteins can be classified into groups that are variously labeled as classes, subfamilies, families, superfamilies, etc. In general, it is expected that members of the same family share significant sequence similarity, whereas members of a superfamily may share structural similarity. However, these criteria are not rigid and can be interpreted differently by different groups. For instance, the plant U-box proteins are classified into a single family with five different classes on the basis of their domain architecture (Azevedo et al. 2001). However, concentration(F, C0,0) is <100, that is, all proteins of the U-box family do not come into one cluster, even when none of the edges in the similarity graph are discarded! This indicates that the overall level of similarity is not very high.
Incorrect data at TAIR: We mined the tabular data at TAIR for information about protein families. Occasionally, the data is inconsistent with literature. For instance, the 67 members of the Core Cell Cycle gene superfamily that fall into seven families (Vandepoele et al. 2002) are listed in a single family. Again, due to the overall low level of similarity, the members fail to cluster together, even when no threshold is applied. We indicate such cases by drawing an X in the grid element corresponding to (i = 0, c = 0). Overall, there are 22 such atomic families.
Figure 11.
The domain structure of two PMP proteins is shown in the figure. The transmembrane domains are colored black, and the nucleotide-binding factors are shown in gray. The two hits between the proteins are shown by black lines.
The one nonbiological parameter that affects our results slightly is the e-value that was chosen for the initial BLAST run. All of the results described in this study were the result of running BLAST with an e-value threshold 0.0001. This somewhat stringent e-value is responsible for some low-similarity families not being clusterable. When we repeated our analysis with e-value set to 1, the number of no-trival families that had proteins with 0 hits reduced from 19 to 7. This resulted in a small increase in the overall number of families that were clusterable.
Identifying New Families
As indicated by Figure 9, the parameters at which a family forms a distinct cluster can vary widely. At one extreme, we have the MLO (Devoto et al. 2003), MRS2 (Li et al. 2001) families, which are so distinctive that they cluster perfectly at the (0, 0) level, and at the other extreme, we have the families of the ABC superfamily, that, because of the presence of common domains, form distinct clusters only when the threshold is raised to (50, 30). Clearly, there is no magic parameter combination at which the clusters are guaranteed to form a complete family.
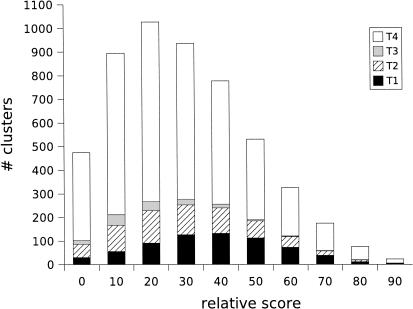
The only fact we can be sure of is that clusters that form at higher thresholds are purer than those that form at lower thresholds. For instance, consider Figure 12, which shows the distributions of the number of clusters (of size at least 5) with respect to relative score threshold. For the purpose of this figure, each cluster was classified into one of four categories:
Figure 12.
Distribution of the number of clusters of size at least five at different relative score thresholds. The clusters are further classified on the basis of their purity, etc.
T1: pure, fully classified (all members of the cluster belong to the same family)
T2: pure, partially classified (all of the classified members of the cluster belong to the same family)
T3: impure
T4: none of the members of the cluster have family annotations
The negligible number of clusters of type T3, when relative score threshold 50 (or greater) is used, indicates that, at this level, almost all clusters are likely to be pure. Thus, one can choose a cluster of type T4, align its member sequences, detect conserved blocks in the multiple alignment, and construct a new family by identifying all unclassified proteins that contain the blocks. Whereas T4 clusters formed with relative score threshold 90 are also going to be pure, they are not appropriate seeds for the discovery of new families, as the sequences in those clusters are likely to be almost identical, making it impossible to extract functionally relevant blocks from the alignment. In many cases, one can also predict the family of unclassified members of clusters of type T2 on the basis of the classified members.
However, any such predictions or new family definitions need to be followed with more comprehensive work to identify the functional role of the conserved regions. One should also note that the relative score threshold of 50 may not be appropriate in the case of other genomes—only after a significant number of protein families are defined, can we calibrate a suitable threshold that can aid in the detection of the remaining families.
Applicability to Other Species Data
The genomes of complex eukaryotes like human, mouse, and rat have recently been completed. The proteomes of these organisms differ in domain complexity from that of Arabidopsis thaliana. A preliminary analysis of InterPro (Mulder et al. 2003) domain matches to each of these proteomes indicates that, on an average, each Arabidopsis protein matches 4.5 InterPro domains, whereas the corresponding number for human proteins is 9. Given that protein families usually consist of proteins with similar domain architectures, we believe that the larger number of domains per protein actually improves the clusterability of the protein families. For instance, consider two families F1 defined by domain architecture Dx.Dy and F2 with domain architecture Dy.Dz. Under the simplistic assumption that the domains are distinct, but of equal length, one can see that F1, F2 will separate into different clusters only when the cover (or relative score) threshold is >50. On the other hand, if the domain architecture consisted of 10 distinct domains, and the two families shared only one of them, this separation of the families can be accomplished with any cover (or relative score) threshold >10. Note that because clusters may become pure at lower thresholds, the best choice of clustering parameters is likely to be different for these proteomes.
Conclusion
In this study, we describe a similarity measure that is more comprehensive than simply choosing an attribute of the best BLAST hit. We show that this similarity measure can help overcome some of the limitations of single-linkage clustering with regard to multidomain protein families. We present a novel method for visualizing the sequence similarity within protein families. This is accomplished by showing, in a color plot, how the clusterability of a family varies with choice of clustering parameters. Families that cluster with highly specific small domains display a different pattern in their clusterability plot from families with large, but variable domains. We applied our method to visualize the protein families of Arabidopsis thaliana and make the results available through a Web interface. Our display method provides answers to questions of the form—“What is the similarity of members of family X?”—thus helps reveal some of the parameters that might have been used in the creation of the family. We show how our method can be used to detect possibly incorrect family assignments. Finally, we describe how our method can be used to assign families to some unclassified proteins and how novel families can be discovered.
Acknowledgments
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.2079204. Article published online before print in May 2004.
References
- Altschul, S.F., Gish, W., Miller, W., Myers, E.W., and Lipman, D.J. 1990. Basic local alignment search tool. J. Mol. Biol. 215: 403–410. [DOI] [PubMed] [Google Scholar]
- Arabidopsis Genome Initiative. 2000. Analysis of the genome sequence of the flowering plant Arabidopsis thaliana. Nature 408: 796–815. [DOI] [PubMed] [Google Scholar]
- Azevedo, C., Santos-Rosa, M.J., and Shirasu, K. 2001. The U-box protein family in plants. Trends Plant Sci. 6: 354–358. [DOI] [PubMed] [Google Scholar]
- Bateman, A., Birney, E., Cerruti, L., Durbin, R., Etwiller, L., Eddy, S.R., Griffiths-Jones, S., Howe, K.L., Marshall, M., and Sonnhammer, E.L. 2002. The Pfam protein families database. Nucleic Acids Res. 30: 276–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman, H.M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T.N., Weissig, H., Shindyalov, I.N., and Bourne, P.E. 2000. The Protein Data Bank. Nucleic Acids Res. 28: 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernal, A., Ear, U., and Kyrpides, N. 2001. Genomes OnLine Database (GOLD): A monitor of genome projects world-wide. Nucleic Acids Res. 29: 126–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bork, P., Dandekar, T., Diaz-Lazcoz, Y., Eisenhaber, F., Huynen, M., and Yuan, Y. 1998. Predicting function: From genes to genomes and back. J. Mol. Biol. 283: 707–725. [DOI] [PubMed] [Google Scholar]
- Devoto, A., Hartmann, H.A., Piffanelli, P., Elliott, C., Simmons, C., Taramino, G., Goh, C.S., Cohen, F.E., Emerson, B.C., Schulze-Lefert, P., et al. 2003. Molecular phylogeny and evolution of the plant-specific seven-transmembrane MLO family. J. Mol. Evol. 56: 77–88. [DOI] [PubMed] [Google Scholar]
- Doolittle, R.F. 1995. The multiplicity of domains in proteins. Annu. Rev. Biochem. 64: 287–314. [DOI] [PubMed] [Google Scholar]
- Duret, L., Mouchiroud, D., and Gouy, M. 1994. HOVERGEN, database of homologous vertebrate genes. Nucleic Acids. Res. 22: 2360–2365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenberg, D., Marcotte, E.M., Xenarios, I., and Yeates, T.O. 2000. Protein function in the post-genomic era. Nature 405: 823–826. [DOI] [PubMed] [Google Scholar]
- Enright, A.J. and Ouzounis, C.A. 2000. Generage: A robust algorithm for sequence clustering and domain detection. Bioinformatics 16: 451–457. [DOI] [PubMed] [Google Scholar]
- Enright, A.J., Van Dongen, S., and Ouzounis, C.A. 2002. An efficient algorithm for large-scale detection of protein families. Nucleic Acids Res. 30: 1575–1584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Florea, L., Hartzell, G., Zhang, Z., Rubin, G.M., and Miller, W. 1998. A computer program for aligning a CDNA sequence with a genomic DNA sequence. Genome Res. 8: 967–974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geer, L.Y., Domrachev, M., Lipman, D.J., and Bryant, S.H. 2002. CDART: Protein homology by domain architecture. Genome Res. 12: 1619–1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouzy, J., Eugene, P., Greene, E.A., Kahn, D., and Corpet, F. 1997. XDOM, a graphical tool to analyze domain arrangements in any set of protein sequences. Comput. Appl. Biosci. 13: 601–608. [DOI] [PubMed] [Google Scholar]
- Heger, A. and Holm, L. 2000. Towards a covering set of protein family profiles. Prog. Biophys. Mol. Biol. 73: 321–337. [DOI] [PubMed] [Google Scholar]
- Hegyi, H. and Gerstein, M. 1999. The relationship between protein structure and function: A comprehensive survey with application to the yeast genome. J. Mol. Biol. 288: 147–164. [DOI] [PubMed] [Google Scholar]
- Holm, L. and Sander, S. 1996. Mapping the protein universe. Science 273: 595–602. [DOI] [PubMed] [Google Scholar]
- Hwang, I., Chen, H.C., and Sheen, J. 2002. Two-component signal transduction pathways in Arabidopsis. Plant Physiol. 129: 500–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawaji, H., Yamaguchi, Y., Matsuda, H., and Hashimoto, A. 2001. A graph-based clustering method for a large set of sequences using a graph partitioning algorithm. Genome Inform. Ser. Workshop Genome Inform. 12: 93–102. [PubMed] [Google Scholar]
- Li, L., Tutone, A.F., Drummond, R.S., Gardner, R.C., and Luan, S. 2001. A novel family of magnesium transport genes in Arabidopsis. Plant Cell 13: 2761–2775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcotte, E.M., Pellegrini, M., Ng, H.L., Rice, D.W., Yeates, T.O., and Eisenberg, D. 1999. Detecting protein function and protein–protein interactions from genome sequences. Science 285: 751–753. [DOI] [PubMed] [Google Scholar]
- Matsuda, H., Ishihara, T., and Hashimoto, A. 1999. Classifying molecular sequences using a linkage graph with their pairwise similarities. Theor. Comput. Sci. 210: 305–325. [Google Scholar]
- Metz, A.M., Timmer, R.T., and Browning, K.S. 1992. Sequences for two cDNAs encoding Arabidopsis thaliana eukaryotic protein synthesis initiation factor 4A. Gene 120: 313–314. [DOI] [PubMed] [Google Scholar]
- Michalski, R.S., Bratko, I., and Kubat, M. 1998. Machine learning and data mining. Wiley, New York.
- Mott, R. 1997. Estgenome: A program to align spliced DNA sequences to unspliced genomic DNA. Comput. Appl. Biosci. 13: 477–478. [DOI] [PubMed] [Google Scholar]
- Mulder, N.J., Apweiler, R., Attwood, T.K., Bairoch, A., Barrell, D., Bateman, A., Binns, D., Biswas, M., Bradley, P., Bork, P., et al. 2003. The InterPro Database, 2003 brings increased coverage and new features. Nucleic Acids Res. 31: 315–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perriere, G., Duret, L., and Gouy, M. 2000. HOBACGEN: Database system for comparative genomic in bacteria. Genome Res. 10: 379–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhee, S.Y., Beavis, W., Berardini, T.Z., Chen, G., Dixon, D., Doyle, A., Garcia-Hernandez, M., Huala, E., Lander, G., Montoya, M., et al. 2003. The Arabidopsis Information Resource (TAIR): A model organism database providing a centralized, curated gateway to Arabidopsis biology, research materials and community. Nucleic Acids Res. 31: 224–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Fernandez, R., Davies, T.G., Coleman, J.O., and Rea, P.A. 2001. The Arabidopsis thaliana ABC protein superfamily, a complete inventory. J. Biol. Chem. 276: 30231–30244. [DOI] [PubMed] [Google Scholar]
- Servant, F., Bru, C., Carrere, S., Courcelle, E., Gouzy, J., Peyruc, D., and Kahn, D. 2002. Prodom: Automated clustering of homologous domains. Brief Bioinform. 3: 246–251. [DOI] [PubMed] [Google Scholar]
- Smith, T.F. and Zhang, X. 1997. The challenges of genome sequence annotation or “the devil is in the details”. Nat. Biotechnol. 15: 1222–1223. [DOI] [PubMed] [Google Scholar]
- Tsoka, S. and Ouzounis, C.A. 2000. Recent developments and future directions in computational genomics. FEBS Lett. 480: 42–48. [DOI] [PubMed] [Google Scholar]
- van den Brule, S. and Smart, C.C. 2002. The plant PDR family of ABC transporters. Planta 216: 95–106. [DOI] [PubMed] [Google Scholar]
- Vandepoele, K., Raes, J., De Veylder, L., Rouze, P., Rombauts, S., and Inze, D. 2002. Genome-wide analysis of core cell cycle genes in Arabidopsis. Plant Cell 14: 903–916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veeramachaneni, V. 2002. “Aligning fragmented sequences.” Ph.D. thesis, The Pennsylvania State University, University Park, PA.
- Wheelan, S.J., Church, D.M., and Ostell, J.M. 2001. Spidey: A tool for mRNAto-genomic alignments. Genome Res. 11: 1952–1957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf, Y.I., Brenner, S.E., Bash, P.A., and Koonin, E.V. 1999. Distribution of protein folds in the three superkingdoms of life. Genome Res. 9: 17–26. [PubMed] [Google Scholar]
- Zhang, H. 2003. Alignment of BLAST high-scoring segment pairs based on the longest increasing subsequence algorithm. Bioinformatics 19: 1391–1396. [DOI] [PubMed] [Google Scholar]
WEB SITE REFERENCES
- http://www.arabidopsis.org/; The Arabidopsis Information Resource (TAIR).
- http://warta.bio.psu.edu/htt_doc/ArabCluster; Arabidopsis families similarity pictures.