Variance in Death and Its Implications for Modeling and Forecasting Mortality

Abstract

The slope and curvature of the survivorship function reflect the considerable amount of variance in length of life found in any human population. Part is due to the well-known variation in life expectancy between groups: large differences according to race, sex, socioeconomic status, or other covariates. But within-group variance is large even in narrowly defined groups, and changes substantially and inversely with the group average length of life. We show that variance in length of life is inversely related to the Gompertz slope of log mortality through age, and we reveal its relationship to variance in a multiplicative frailty index. Our findings bear a variety of implications for modeling and forecasting mortality. In particular, we examine how the assumption of proportional hazards fails to account adequately for differences in subgroup variance, and we discuss how several common forecasting models treat the variance along the temporal dimension.

1 Introduction

Length of life is a fundamental dimension of human prosperity. We measure this dimension either with period life expectancy at birth, e₀, the average length of life, or we measure its inverse either with age-specific mortality rates that underpin the life table, or with the log odds of death. Correctly modeling mortality is crucial for inference in both observational and experimental settings, and thus for forecasting. In this paper, we illustrate how patterns in the variance of length of life, whether measured across subgroups at a point in time or in human populations over long periods of time, bear strong implications for how we model mortality and test hypotheses in cross-sectional and longitudinal settings.

In the cross section and over short panels, the Cox (1972) proportional hazards model and the logit or logistic regression model are standard tools in epidemiological studies and in medical research. As they are typically specified, these models assume that subgroups experience proportionally higher or lower hazards relative to a baseline. We show that cross-sectional patterns in the variance in length of life across subgroups, where variance is inversely related to average life expectancy, are not at all adequately captured by proportional hazards. This is because variance in length of life is closely tied to the age slope of mortality; subgroup differences in the variance in length of life are equivalent to subgroup differences in the age slope of mortality. Regardless of the precise nature of baseline mortality, which may be modeled nonparametrically, proportional hazards impose the same age slope and thus the same variance in length of life on all subgroups.

Violations of the proportional hazards assumption have been extensively remarked and explored (Hess 1995, Lee and Go 1997, Therneau and Grambsch 2000), and researchers have suggested various methods to address them. One option is to augment standard models by injecting individual frailty (Vaupel et al. 1979, Hougaard 1995). As we discuss, frailty models are helpful because they add an additional parameter that directly impacts variance. But the concept of frailty does not help us intuitively understand cross-sectional or intertemporal patterns in variance; it simply improves the fit of models without increasing our understanding. One class of models designed to account for frailty, accelerated failure time (AFT) models, posits a proportional scaling of the distribution of survival time across subgroups, which inappropriately implies a positive rather than negative relationship between mean and variance. Approaches that relax the assumption of proportional scaling, such as the use of stratified Cox regression, time-dependent covariates, or the nonparametric method of Kaplan and Meier (1958) are preferable.

From an aggregate perspective, the expansion of human life in the past century (Preston 1975, Caldwell 1976) and its socioeconomic implications have stimulated efforts to analyze and forecast mortality trends (Tuljapurkar and Boe 1998), which are guided by insights gained from mortality models. A natural focus of these efforts is the period expectation of life at birth, e₀. Mortality change is commonly summarized in terms of trends in e₀, and mortality models are evaluated on their ability to match historical trends in life expectancy. These uses of e₀ gained considerable support from two recent findings: that e₀ has increased at a nearly constant rate in many industrial countries since 1955 (White 2002), and that since 1840 annual world record female e₀ has also increased at a nearly constant rate (Oeppen and Vaupel 2002). Some have argued that such constancy is fundamental in analyzing mortality change (Bongaarts and Feeney 2002, 2003), and one researcher (Bongaarts 2005) has extended a simple model (Vaupel 1986) to forecast mortality change. But e₀ is only the mean of the distribution of ages at death, and we show here that the variance of this distribution provides important additional information. As we reveal, temporal change in the variance in age at adult death is not necessarily captured by simple models, which may inappropriately constrain how we should conceptualize and analyze mortality change.

This paper is organized in four main parts. First, we discuss cross-sectional and temporal patterns in distributions of period life-table ages at death. We recount how historical increases in e₀ in the industrialized countries have been accompanied by equally striking decreases in the variance of the age of adult death (Edwards and Tuljapurkar 2005). These trends show clearly that mortality decline over time has compressed the variance between individuals at the same time as it has increased average life expectancy. Cross-sectional patterns reveal the same inverse relationship between subgroup variance and average. While overall variance has declined over time, very large differences in variance between subgroups remain. Less advantaged groups experience both lower average length of life and higher variance.

Second, we show how the variance in age of adult death can be approximately computed for any reasonable model of mortality rates, and illustrate this with three commonly used models, the Gompertz (1825), the logistic, and a Gompertz model with multiplicative frailty. In particular, we reveal the inverse relationship between the Gompertz slope and the variance in length of adult life. A particular age slope of mortality will reflect a particular variance, but while it can be consistent with different subgroup average lengths of life, it cannot accurately capture the large differences in subgroup variances. Adding frailty into the model can explain variance, but not in a satisfactory way in terms of any intuition.

Third, we explore the implications of these insights for common mortality models. As concerns forecasting, we show that any generalization of the Bongaarts-Vaupel translation argument yields an unchanging variance in the age at adult death over time, which may or may not be a preferable characteristic. Over long periods of time, trends in the variance have comprised a major qualitative aspect of mortality change in industrialized countries, and we suspect the same is true for developing countries. We recount world-record trends in the variance in age of adult death, and discuss their implications for understanding secular mortality change. In the setting of panel data on individuals, we illustrate how Gompertz slopes that vary systematically across subgroups violate the assumption of proportionality, and we discuss how various methods to address this either succeed or fail in modeling variance correctly.

Finally, we discuss how our results fit into ongoing research on aging more generally. Insights into the plasticity of the Gompertz slope and what may be driving it are particularly relevant for gauging the future of the human aging process. Results in the literature on genetic interventions in nonhuman species become particularly intriguing when combined with the insights we present here. Our results are related to work on the “rectangularization” of the survivorship schedule (Wilmoth and Horiuchi 1999, Kannisto 2000) and on its shape more generally (Cheung et al. 2005). They are also connected to research on the existence of a maximum age at death (Fries 1990, Olshansky et al. 1990, Wachter and Finch 1997). All these topics subsume questions as to the possible limiting forms of the distribution of age at death. Our analysis makes no assumptions or deductions about such a limit, but aims to illuminate the nature and significance of trends in the variability of age at death.

Other recent work in social science examines contributions of subgroup variance to overall inequality in other measures of well-being like income (Western and Bloom 2009). We believe such research shows much promise, and that applying similar techniques to the study of mortality would prove fruitful in future pursuits. Our focus here is primarily on aggregate inequality in length of life, which we show is linked to the Gompertz slope and the commonly used proportional hazards model.

2 Distributions of Age at Death Over Time, Space, and Characteristic

The age pattern of life table deaths in any period, which is also the distribution of period length of life, is found from mortality rates μ(a) by age a in that period. We define cumulative mortality as

$$M\left(a\right)={\int }_0^a\mu \left(s\right)ds,$$ (1)

and survivorship is given by

$$\ell \left(a\right)=\exp [-{\int }_0^a\mu (s\left)ds\right]=\ell \left(a\right)=\exp [-M(a\left)\right].$$ (2)

The probability density of death at age a is

$$\varphi \left(a\right)=\mu \left(a\right)\ell \left(a\right).$$ (3)

Even when it is small as in industrialized countries during the past half century, infant mortality produces some nonzero φ(0) at the extreme left end of the distribution. But φ(a) falls to very low levels thereafter and remains low until well into adult ages.

Figure 1 plots φ(a) for racial subgroups within the U.S. in 2004 based on life tables prepared by Arias (2007). In that year, e₀ among African Americans was 73.1 years, 5.2 fewer years than for whites. Part of this was due to a greater density of deaths in infancy, which approached 0.015% for blacks, more than twice the level for whites, but there were also differences in the much larger probability of death at older ages. Life expectancy conditional on reaching age 10, e₁₀, was 68.9 for whites but only 64.3 for blacks. The width of the distribution around older ages, which we measure by the standard deviation above age 10 or S₁₀, introduced by Edwards and Tuljapurkar (2005) and discussed shortly, is also visibly different across racial groups. For whites in 2004, S₁₀ = 14.9, while among blacks it was almost 2 years higher. Patterns of inequality in length of life through other dimensions of socioeconomic status (SES) such as income or education look essentially the same (Edwards and Tuljapurkar 2005), as do differences by sex.

Figure 1.

Distributions of age at death by race in the U.S. in 2004

Source: Arias (2007). Data are life-table deaths by race _nd_x for both sexes combined.

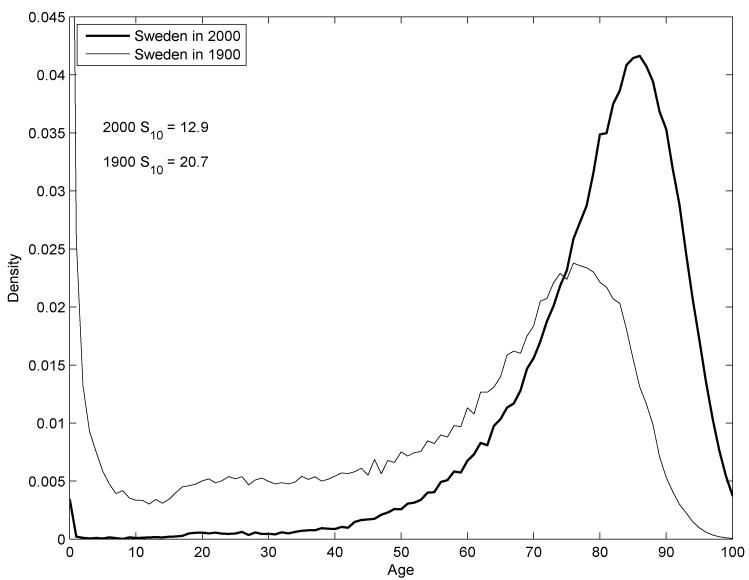
A similar picture emerges when we examine distributions of length of life over time instead of across characteristic. Figure 2 plots deaths for both sexes combined in Sweden in 1900 and 2000, revealing that long-term temporal variation looks a lot like cross-sectional variation. Higher status or more time is rewarded with less variance and higher mean. Dis-similarities include the much higher level of infant mortality in 1900 and the large “baseline” probability of death at practically any age. Both of these features reflected the prevalence of infectious disease before the completion of the epidemiological transition.

Figure 2.

Distributions of age at death in Sweden in 1900 and 2000

Source: Human Mortality Database (2009). Data are life-table deaths _nd_x for both sexes combined.

Comparing Figures 1 and 2 reveals another interesting pattern of differences in the distribution of length of life across geographic boundaries. The standard deviation in adult length of life among U.S. whites, is about 2 years higher than it is in Sweden. This is the point made by Wilmoth and Horiuchi (1999) and Edwards and Tuljapurkar (2005), and recently extended to developing countries by Edwards (2010). Cross-national trends conform to the pattern of higher status bringing higher mean and lower variance.

We measure variance in adult ages at death by choosing a cutoff age A at which probabilities of death are near their minimum and are relatively stable over time. Following Edwards and Tuljapurkar (2005), we focus on S₁₀, the standard deviation of length of life starting from age A = 10, but results are similar across various cutoffs. Infant and child deaths contribute strongly to total variation in length of life, but as we now explain, they do so in a relatively uninformative way that masks important trends. Consider the average age at death starting from birth in the period life table, also known as e₀. Write T for the random age of death of an individual in a hypothetical cohort following a period life table, where ℓ(A), the familiar survivorship probability at age A, is also the probability of adult death (T > A). Then period life expectancy at birth can be decomposed as

$$e_0=[1-\ell (A\left)\right]M_{-}+\ell \left(A\right)M_{+},$$ (4)

where M₋ and M₊ are (conditional) average ages of death for those who die young or die as adults, respectively. In the industrialized countries in the last five or six decades, M₋ is much below 1 year for all subgroups, and 1−ℓ(A) is well under 10%, so the main determinant of e₀ is the timing of adult death. We can also decompose total variance starting from birth as

$$\mathrm{Var}\left(T\right)=[1-\ell (A\left)\right]V_{-}+\ell \left(A\right)V_{+}+[1-\ell (A\left)\right]{(M_{-}-e_0)}^2+\ell \left(A\right){(M_{+}-e_0)}^2,$$ (5)

where V₋ and V₊ are (conditional) variances of age at death for those who die young or die as adults. For all subgroups in the industrialized countries, only the second and third of these four terms matter. The first term is small because both its components are small, and the last term is small because e₀ has become almost arbitrarily close to M₊. While the third term contributes substantially to Var(T), it does so only because M₋ is very small relative to e₀. This difference is not at all informative about substantive variation in the adult ages at which most deaths occur.

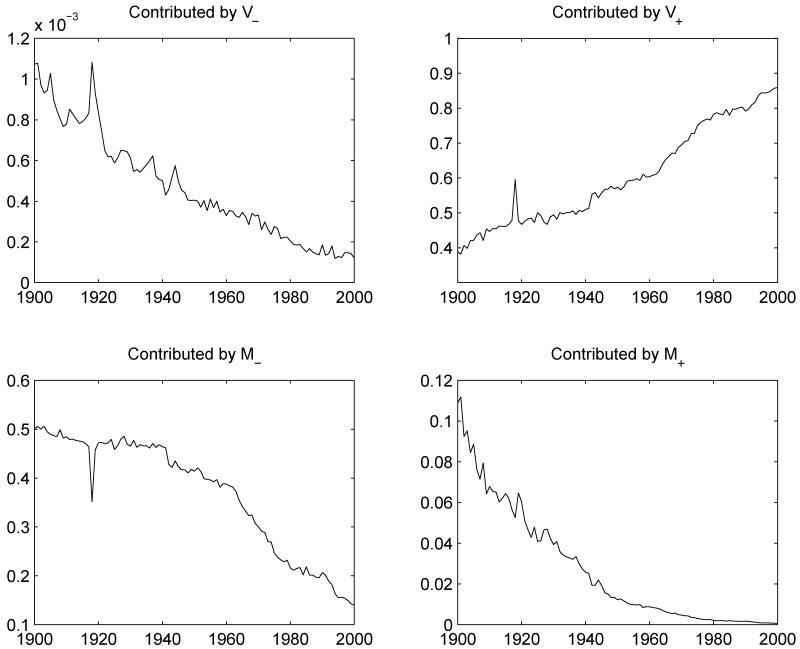
Figure 3 shows the four components in equation (5) using Swedish data over the period 1900 to 2003 and A = 10. Since about 1940, the element that matters most to understanding total variability in age at death is the second term in equation (5), ℓ(A) V₊, which is shown at upper-right. Today, variance in length of life above age 10 accounts for over 85% of total variability in Sweden, while variance below age 10 such as attributable to infant mortality is responsible for less than 15%. While we have not performed a formal analysis, we believe a similar bottom line ought to emerge were we to examine distributions of length of life among subgroups defined by SES or race, which is difficult owing to data constraints. We know it to be true for either sex, and we also find that sex differences in variance today are driven primarily by sex differences in adult variance rather than in infant mortality, a result that mirrors work by Glei and Horiuchi (2007) on the sex differential in life expectancy. Given that trends in variance are important and interesting, a vital question is whether we are capturing them correctly when we model mortality.

Figure 3.

Decomposing total variance in length of life in Sweden since 1900

Source: Human Mortality Database (2009) and authors’ calculations. Each panel shows a component’s proportion of total variance in period length of life, which is the weighted sum of squared differences between life expectancy at birth, e₀, and midpoints of single years of age up to 110, where the weights are life-table deaths _nd_x. See equation (5) in the text for the formulation of each component; V₋ is the variance of age at death below age 10 weighted by deaths below age 10, V₊ is the variance above age 10 weighted by deaths above 10, M₋ is the squared difference between e₀ and the mean age at death below age 10 weighted by deaths below 10, and M₊ is the squared difference between e₀ and the mean age at death above 10 weighted by deaths above 10.

3 Theoretical Models of Adult Mortality

The most celebrated model of adult age-specific mortality is that of Gompertz (1825), in which the force of mortality rises exponentially with age. But recent work by Vaupel et al. (1998), Thatcher et al. (1998) and others suggests that a logistic model with an asymptote describes old-age mortality more accurately. The logistic can also be seen as a result of a model in which Gompertz mortality is modified by a multiplicative frailty (Vaupel et al. 1979). Frailty, if it occurs in this form, should clearly contribute to the variability in age at death. While it can, we do not find this an entirely compelling account of historical or cross-sectional patterns in S₁₀. Overall, traditional models are not well-equipped to deal with or provide understanding about variance.

We next present analytical results showing how the variance in age at adult death depends on the parameters of mortality models. We consider first a general mortality model without frailty, and the special cases of Gompertz and logistic, then a general model with multiplicative frailty, with special cases of gamma frailty, and Gompertz with gamma frailty.

3.1 General Mortality Model

Suppose that adult mortality μ(a) is an increasing positive function of age a. Survivorship falls to zero as age increases because cumulative mortality M(a) is increasing. The probability distribution of age at death for adults, φ(a), increases at young adult ages, reaches a mode a₀ and then falls, ultimately reaching zero by very high ages.

To proceed, we take a Taylor expansion of the age-at-death distribution φ(a) around the mode a₀, and then we approximate the resulting quadratic with a normal distribution. The mathematical appendix presents detailed steps. The end result is the following relationship:

$$\varphi \left(a\right)\approx \varphi \left(a_0\right)\exp \left(-\frac{{(a-a_0)}^2}{2{\sigma }^2}\right),$$ (6)

where

$${\sigma }^2=\frac{\varphi \left(a_0\right)}{\mid {\varphi }^{″}\left(a_0\right)\mid }=\frac{\mu \left(a_0\right)}{\mid {\mu }^{″}\left(a_0\right)-2{\mu }^3\left(a_0\right)\mid }.$$ (7)

The variance term σ² depends on the curvature of the mortality function and roughly equals the variance in age at adult death. This approximation provides a useful and often accurate estimate of the moments of φ(a) — we use it here and also check its accuracy by numerical computation.

3.2 The Gompertz Model

We write the Gompertz mortality function as

$$\mu \left(a\right)={\mu }_0{e}^{\beta a},$$ (8)

where the parameter β is the familiar age-slope of log mortality, a constant in the Gompertz model. In the U.S. for both sexes combined, the age-slope is about 0.087 (Edwards 2009); that is, mortality rates increase 8.7% with each year of age. From equation (7) (see appendix) the variance in adult age at death is approximately given by

$${\sigma }^2\approx \frac{1}{{\beta }^2}.$$ (9)

Thus the Gompertz variance in age at death depends only on the slope parameter β and not on μ₀. It is possible to obtain an exact expression for the variance by analytical integration in terms of special functions, but the results are not especially illuminating. However, we have computed numerically the exact variance for a range of values of β and μ₀ that are appropriate for twentieth century human mortality. We find that the exact value of σ depends only weakly on μ₀ and that equation (9) is a very accurate approximation.

It follows that a Gompertz model can only describe differences in the variance of the adult age at death with differences in the Gompertz parameter β, the age-slope of log mortality. There is a one-to-one inverse relationship between the age-slope of mortality and the variance in length of life. Were equation (9) an exact relationship, β = 0.087 would be consistent with σ = 11.5.

3.3 The Logistic Model

When measured by S₁₀, U.S. levels of σ are higher than implied by β = 0.087, more in the range of 15.0 rather than 11.5. We know there are departures from linearity in log mortality rates at advanced ages; how does this affect σ as a function of β? We write the logistic model for mortality as

$$\mu \left(a\right)=\frac{e^{\beta a}}{C+e^{\beta a}},$$ (10)

where C is the asymptote, commonly set to equal unity. From equation (7) (see appendix) the approximate variance is

$${\sigma }^2=\frac{1+\beta }{{\beta }^2}.$$ (11)

Thus the logistic also displays the remarkable property that the variance in age at death depends only on the slope parameter β. It follows that a logistic model can only describe changes in the variance of the adult age at death if the slope parameter β changes with time.

Note that if we fit a Gompertz model and a logistic model to a particular data set, the value of β must be similar in both. To see why, compare the two models near a = 0 which here indicates the start of adult age. With the same β, the logistic model implies only a slightly larger variance in age at adult death than the Gompertz. We expect this difference because the density φ for the logistic model shallows as age increases; see the discussion after equation (6). For β = 0.087, equation (11) implies σ = 12.0, closer to reality than the Gompertz but not by much. Of course, when we measure σ with S₁₀, we are including variance due to traffic accidents, violence, and other causes that asymmetrically impact the young in a decidedly non-Gompertz way. For the U.S., this problem may be particularly acute. Edwards and Tuljapurkar (2005) find that removing external-cause mortality reduces S₁₀ by 1–1.5 years, leaving still perhaps 1.5 years in extra S₁₀ that cannot be well explained by logistic or decelerating log mortality, or by external causes.

A natural next step is to examine the connection between frailty in mortality and variance in length of life, two concepts that are related. A convenient way to proceed is by generalizing the Gompertz model. Next we discuss a model that incorporates frailty, including two special cases.

3.4 General Mortality, Multiplicative Frailty

Following Vaupel et al. (1979), suppose that every individual has a random frailty Z and that g(z) dz is the probability that Z takes values between z and z + dz. Then mortality $\stackrel{‒}{\mu }$ is given by the product of the frailty parameter Z and a baseline mortality function μ(a):

$$\stackrel{‒}{\mu }(a\mid Z)=Z\mu \left(a\right).$$ (12)

The usual specification of a frailty distribution assumes that average frailty is 1, and that the distribution of frailty has some variance. It is convenient to define the following averages with respect to frailty:

$$h_j\left(a\right)=\epsilon \left[Z^j{e}^{-ZM\left(a\right)}\right],\text{for}j=1,2,3.$$ (13)

Then the approximate variance in age at death is just a generalization of equation (7):

$${\sigma }^2=\frac{\varphi \left(a_0\right)}{\mid {\varphi }^{″}\left(a_0\right)\mid }=\frac{h_1\left(a_0\right)\mu \left(a_0\right)}{\mid {\varphi }^{″}\left(a_0\right)\mid }.$$ (14)

As shown in the appendix, φ″ depends on h₁, h₂, and h₃. But when every frailty is set equal to 1, these are all equal, and the variance reduces to the value in equation (7).

3.5 General Mortality, Gamma Multiplicative Frailty

To obtain a useful qualitative sense of the effect of frailty, we consider the special case when frailty Z follows a gamma distribution (Vaupel et al. 1979). Let the probability that Z lies between w and w + dw be given by g(w) dw, where

$$g\left(w\right)=\frac{k^k}{\Gamma \left(k\right)}{w}^{k-1}{e}^{-k}.$$ (15)

The average frailty is 1 and the variance of frailty is Var(Z) ≡ s² = 1/k.

As we show in the appendix, the magnitude of frailty selection depends on both the variance in frailty s² and the cumulative mortality hazard. Strong selection works to decrease the modal age at death. To examine the variance, we can find the second derivative φ″ at the modal age and use it in a Taylor approximation:

$${\sigma }^2=\frac{\mu \left(a_0\right)}{\mid {\mu }^{″}\left(a_0\right)-{\mu }^3\left(a_0\right)\left[\right(1+s^2\left)\right(2+s^2\left)\right]∕\left[\right(1+s^{2}M{\left(a_0\right)}^2\left)\right]\mid }.$$ (16)

The selection effect appears in the denominator, where s² multiplies by the cumulative mortality M(a₀) at ages below the mode. Strong selection via a large M(a₀) will combine with variance in frailty s² to reduce the denominator and thus inflate the variance σ² in age at death.

3.6 Gompertz Mortality, Gamma Multiplicative Frailty

We can learn more by combining the above multiplicative gamma-distributed frailty with the Gompertz baseline mortality from equation (8). In the appendix, we derive the modal age at death for such a model. We obtain the variance in age at death using equation (16), equation (33) from the appendix, and a little algebra, which yields the parsimonious result that

$${\sigma }^2=\frac{(1+s^2)}{{\beta }^2}.$$ (17)

Comparing this with equation (9) for the standard Gompertz, both shown along the bottom row in Table 1, shows that frailty amplifies the variance in age at death. A Gompertz model with gamma frailty can describe changes in the variance of the adult age at death with changes either in the Gompertz slope parameter β, or in the variance in frailty s², or in both.

Table 1.

Characteristics of the distribution of adult death in three models

Parameter	Gompertz	Logistic	Gompertz Gamma
Mortality at age a, μ(a)	μ0eβa	$\frac{e^{\beta a}}{C+e^{\beta a}}$	Zμ 0 eβa
Density of deaths at a,φ(a)	μ(a)e−(μ(a)-μ0)/β	${(C+1)}^{1∕\beta }\frac{e^{\beta a}}{{(C+e^{\beta a})}^{1+1∕\beta }}$	$\mu \left(a\right){\left(\frac{k}{k+M\left(a\right)}\right)}^{k+1}$
Mode age at death, a0	$\frac{1}{\beta }\log (\beta ∕{\mu }_0)$	$\frac{1}{\beta }\log \left(\beta C\right)$	$\frac{1}{\beta }\log (\beta ∕{\mu }_0-s^2)$
Variance in age at death, σ2	$\frac{1}{{\beta }^2}$	$\frac{1+\beta }{{\beta }^2}$	$\frac{1+s^2}{{\beta }^2}$

Notes: In the logistic model, C is the asymptote, commonly set to equal one. The cumulative force of mortality at age a is $M\left(a\right)={\int }_0^{a}ds\mu \left(s\right)$. In the Gompertz Gamma model, the multiplicative frailty index Z is distributed gamma with density equal to $g\left(w\right)=\frac{k^k}{\Gamma \left(k\right)}{w}^{k-1}{e}^{-k}$, an average ε(Z) = 1, and a variance Var(Z) ≡ s² = 1/k.

3.7 Summary

Our key finding is that the Gompertz slope of log mortality through age, often called the rate of aging, is inversely related to the variance in length of life. Differences across time, space, or SES in the latter can only be captured by differences in age-slopes of mortality. This insight is not greatly altered if mortality follows a logistic curve, flattening out at advanced ages. Injecting frailty into standard mortality models loosens the relationship between variance in life span and the Gompertz slope. A Gompertz model with Gamma multiplicative frailty allows us to model heterogeneity in variance as deriving from heterogeneity in either the Gompertz slope, in the variance in frailty, or in both.

Normative or etiological insights from our exploration of these models are more elusive. The basic result concerning variance in the Gompertz slope is important because some have viewed the Gompertz slope as a kind of species-specific parameter that is eternally fixed while the intercept may fluctuate (Finch et al. 1990). But we show it can only be constant if we add a free parameter like frailty and allow it to fluctuate arbitrarily in order to fit the data. A more straightforward reading of the evidence is that instead, both nature and nurture must affect the Gompertz slope, at least in human populations and potentially in other species.

The addition of multiplicative frailty to a Gompertz model only addresses changing variances in age at death if we assume that frailty distributions have been changing quite rapidly over time. Temporal change in frailty has not been a standard feature of mortality models, and it is not clear why the distribution of such frailties would have narrowed. From an evolutionary perspective, it is not clear why frailty should have persisted into modern humans at all. It is also unclear why in the cross section African Americans should have persistently higher frailty than whites, or why Americans in general should endure higher levels than Europeans or Japanese. Frailty models may allow us to model mortality better in a strictly mechanical sense, but they do not appreciably improve our understanding.

4 Models of Adult Mortality in Practice

These results concerning variance in length of life and the age-slope of mortality bear implications for modeling and forecasting. In this section we examine how variance is implicitly or explicitly treated in an array of common frameworks. We first examine forecasting models, including a recent technique that involves mortality “translation,” which we explain below, as well as the the popular Lee and Carter (1992) forecasting model, which can be seen as a generalized Gompertz model. Then we discuss several standard mortality models that are commonly used in short panels with microdata, where cross-sectional patterns in variance are more important. We examine the Cox (1972) model, the class of nonparametric models suggested by the methods of Kaplan and Meier (1958), and accelerated failure time (AFT) models, which some have associated with frailty models.

4.1 Aggregate Forecasting Models

4.1.1 Mortality Translation: Bongaarts-Feeney

The pioneering model of mortality translation due to Bongaarts and Feeney (2003) provides an appealingly simple description of mortality change, although it is controversial. A recent edited volume by Barbi et al. (2008) provides a thorough overview of the method, which is related to the concept of tempo effects in mortality (Bongaarts and Feeney 2002).

One can describe the Bongaarts-Feeney model in terms of a hypothetical cohort following a period life table. Let T₁ be the random age at death of an individual in this cohort in period t₁. In a later period t₂ > t₁, suppose that the effect of mortality change between the two periods is completely described by delaying each death by the same amount. We assume infant mortality is practically zero and thus can also be delayed in this fashion, which although unrealistic is consistent with our focus on adult mortality. Each random age at death T₁ in the first period is thus replaced in the later period by the random age at death T₁ + D, where D > 0 is fixed. We see at once that the average age at death increases from e₀(t₁) = ε[T₁] in period t₁ to e₀(t₂) = e₀(t₁) + D in the later period t₂. If we increase the mean age at death by some fixed annual amount, we have found a model of mortality change that describes a constant trend in e₀. We use the term mortality translation for any such model.

Notice that translation only affects the mean age at death and not its variance. Shifting every random age at death from T₁ to T₂ = T₁ + D results in a constant variance, Var(T₁) = Var(T₂), so long as D is fixed. In fact, translation leaves unchanged all the central moments of the random age at death. Put geometrically, translation necessarily implies that the shape of the distribution of age death does not change.

Mortality translation is appealing because it can be used with any mortality model. Bongaarts and Feeney (2003) and Bongaarts (2005) used translation for a Gompertz and a logistic model. Vaupel (1986) used a Gompertz model in essentially the same way, although he did not explicitly refer to translation.

It is obvious that mortality translation, by construction, cannot describe temporal changes in the variance in the probability distribution of age at death, or for that matter, of other central moments of φ related to the shape of the distribution, such as skewness or kurtosis. As revealed by Wilmoth and Horiuchi (1999), Cheung et al. (2005), and Edwards and Tuljapurkar (2005), trends in all of these moments have been and remain very interesting even in industrialized countries. Prior to 1960, S₁₀ was strongly declining in industrialized countries, a pattern that is repeating itself among many developing countries today (Edwards 2010). To be sure, Bongaarts and Feeney (2003) never intended their model to apply universally across historical periods; their aim was mortality forecasting for the U.S. and other industrialized countries. But while S₁₀ has remained roughly steady on average in the U.S. since 1960, it has also fluctuated up and down within a 1.5-year band over time (Edwards and Tuljapurkar 2005), or ±5%. Forecasting via translation makes a strong prediction about long-term trends in the variance.

4.1.2 Generalized Gompertz: Lee-Carter

Lee and Carter (Lee and Carter 1992) proposed a parsimonious three-parameter model that explains temporal trends in mortality well in industrialized countries (Lee and Miller 2001). Using the singular value decomposition, they estimate

$$\log \mu (x,t)=a\left(x\right)+b\left(x\right)k\left(t\right),$$ (18)

where μ(a, t) is the mortality at age a in period t, a, b are time-independent age profiles [[or vectors]], and k(t) is a random walk with negative drift.

The profile a(x) is an average of age-specific log mortality rates over the historical sample period, so it ends up being approximately Gompertz or logistic in shape. But b(x) is not necessarily constant with age, as it would have to be in a Gompertz model with a fixed age slope over time. Indeed, fits of b(x) typically reveal stark age differences in rates of mortality decline in industrialized countries (Tuljapurkar et al. 2000). By consequence, the slope and curvature of mortality in this model are free to evolve over time, which as our results show can easily lead to changes in the variance of age at death. The singular value decomposition of equation (18) produces optimal fits of age-specific mortality rates; the moments of the distribution of ages at death are backed out of the model rather than hard-wired as in the Bongaarts-Feeney translation model.

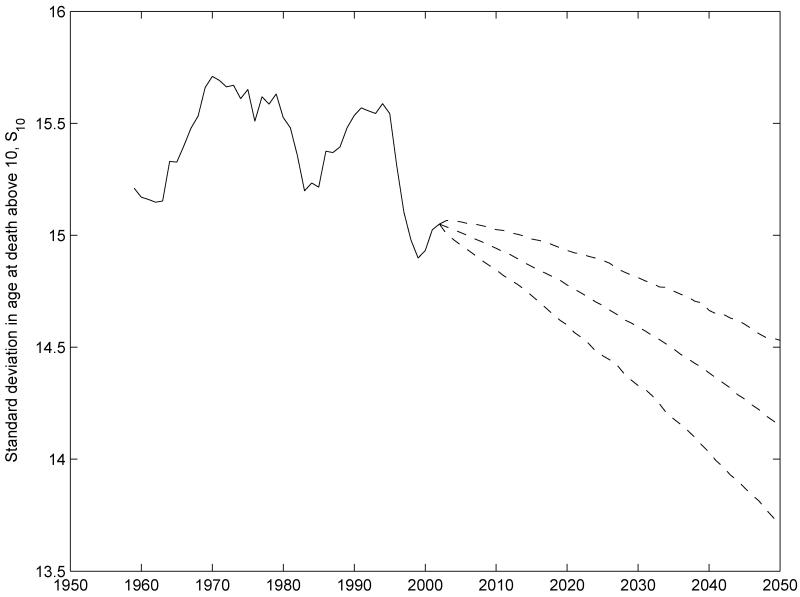
Figure 4 depicts historical data since 1959 and probabilistic forecasts of S₁₀ for U.S. out to 2050 using the Lee-Carter model applied to log mortality rates for both sexes combined from the Human Mortality Database (2009). The forecast is shown by three dashed lines that indicate the 2.5, 50, and 97.5 percentiles of the distribution. Several characteristics are informative. There is clearly a trend in S₁₀, which declines in the median forecast from 15 years around 2000 to just above 14 years by 2050. While this looks like a bold prediction given the figure, by comparison practically all other high-income countries except for France already enjoy levels of S₁₀ around 14 or below.

Figure 4.

Historical patterns and Lee-Carter forecasts of S₁₀ for both sexes combined in the U.S.

Source: Human Mortality Database (2009) and authors’ calculations. S₁₀ is the standard deviation in ages at death based on the period life table. The authors fit the Lee-Carter model as shown in equation (18) via singular value decomposition applied to log age-specific mortality rates for both sexes combined below age 100 from the HMD. Dashed lines represent the 2.5, 50, and 97.5 percentiles of the probabilistic forecast made assuming k(t) follows a random walk with drift.

4.1.3 Implications

Over the last two centuries, the variance in age at adult death as measured by the standard deviation S₁₀ has declined by almost 50%. Were we to use a Gompertz model to describe period mortality at ages over 10, then the slope of the Gompertz model would have to increase by about 40% in order to replicate observed trends in S₁₀. A logistic model for period mortality would require a larger increase, about 50%, in the slope. Over the past 50 years, the trend in S₁₀ has been toward much more gradual decline, perhaps 1% in the U.S., but temporary fluctuations in the variance around its slight downward trend have been much larger, more like 10%.

Because mortality translation models do not allow for any change in the variance of adult death, we urge some caution in applying their results to the age pattern of deaths, even though they may describe recent changes in e₀ perfectly well. A striking result about long run mortality change is the demonstration by Oeppen and Vaupel (2002) that world-record high e₀ has risen at a remarkable linear rate over the past 160 years. Such uniformity suggests that upper bounds on life span, prognosticated and then consistently broken throughout this period, are not as clear as some currently believe. The pace of human development and achievement measured in this way has been rapid and surprisingly steady across several distinct periods of socioeconomic and epidemiological transitions. But Edwards and Tuljapurkar (2005) describe how long-term trends in the record-low variance paint a very different picture regarding the gains in human well-being along the dimension of mortality. True, progress against the Gompertz slope has indeed been achieved, contrary to the opinions of those who may have viewed it as immutable. But long-term gains have come more in fits and starts rather than continuously, and this highlights the remaining challenges, as does the considerable heterogeneity across countries in progress against variance during the last century. We do not fully understand the sources of variance in life spans, nor the underlying health inequalities they presumably reflect, and this is a problem for policy as well as for modeling and forecasting mortality. Translation models provide a good statistical fit to mortality patterns in industrialized countries since 1950 (Bongaarts 2005). But the shape of the age distribution of deaths provides enough important insights that we should probably not assume it to be fixed over long periods of time. By contrast, the Lee and Carter (1992) forecasting model can and does predict changes in the variance in the age at death, but with caveats.

4.2 Short Panel Models

4.2.1 Cox Proportional Hazards

The semiparametric model of Cox (1972) is often said to be the gold standard for modeling survival in clinical settings and other relatively short panels. The model’s lone assumption is that hazards are proportional across groups identified by covariates. Meanwhile, the shape of the underlying mortality mortality is not parameterized.

Although the Cox model does not require background mortality to be Gompertz, the fact remains it often is, at least approximately, because mortality rates tend to increase exponentially until very advanced ages. Given this, our theoretical result that ties the Gompertz slope to the variance in length of life also implies that the Cox proportional hazards assumption is flatly inconsistent with cross-sectional patterns in variance. In addition to having lower mean length of life, low-status groups also have higher variance, which means they must have a smaller Gompertz slope or less steeply increasing mortality with age. Thus it is clear that hazards are not proportional across individuals of varying ages and statuses. By incorrectly assuming that they are, the standard Cox model will fail to model any differences in subgroup variance.

It is by no means a revelation that hazards are often not proportional across groups, of course. Researchers have developed a variety of tools to test for violations of proportionality and a set of alternative models when violations are found (Hess 1995, Lee and Go 1997, Therneau and Grambsch 2000). One solution is to use time-varying coefficients; another is to perform stratified Cox regression. In either case, the analyst must judge which characteristics on which to stratify or to allow to vary over time. Our results suggest that allowing the effect of race or SES to vary systematically over time should adequately capture the different subgroup variances and Gompertz slopes. Whether it is sufficient to use just one of these covariates rather than several to model differences in the age-slope is unknown.

4.2.2 Accelerated Failure Time Models

Another class of tools that researchers use when the proportional hazards assumption is violated are accelerated failure time (AFT) models (Therneau and Grambsch 2000). These are parametric models of survival time rather than of the hazard, which take the form

$$\log T=a+XB+∊$$ (19)

where X is a vector of covariates and ε is an error term. Interestingly, AFT models have been discussed in the context of modeling mortality with multiplicative frailty (Hougaard 1995), as well as in an alternative conceptualization of tempo effects in mortality (Rodríguez 2008).

But a proportional scaling of length of life between racial subgroups or across SES, as in the AFT model, is even more misspecified than a proportional scaling of hazards vis-à-vis the variance. While any scaling, additive or proportional, can provide adequate fit to the mean lengths of life across subgroups, a proportional scaling implies that the error in the level of length of life, namely the variance, becomes larger with longer mean length. This is precisely the opposite of what we see in data.

While it is tempting to suggest a linear modeling of survival time as an alternative, the error term in such a model would clearly be heteroscedastic. Without correction, the robustness of inference would suffer, and like the standard Cox, a linear AFT model would fail to model subgroup variances correctly.

4.2.3 Kaplan-Meier Estimation

Another alternative to the Cox model is the fully nonparametric estimator of the survivorship function due to Kaplan and Meier (1958). Given the difficulties that standard parametric models seem to face in capturing the variance in length of life, which is reflected in the slope of survivorship, a nonparametric approach would seem at first to be ideal. One challenge is that the Kaplan-Meier estimator may sacrifice efficiency when compared with parametric approaches (Miller, Jr. 1983). Another challenge is that identifying which covariates ought to matter and how is left entirely up to the researcher.

4.2.4 Implications

Subgroup differences in variance in length of life and the varying age-slopes in mortality rates they imply are a large problem for short panel models. Without correction, the Cox proportional hazards model will fail to capture subgroup differences in life-span variance. Modeling time-varying covariates, which are really age-varying and thus exactly what is needed, is one solution, and stratified Cox regression is another, but both will reduce power. While AFT models appear if anything to worsen the modeling problem, the Kaplan-Meier estimator would clearly improve it. The question is whether the efficiency cost exceeds the costs of misspecification or reduced power, and the exact tradeoff is likely to be application-specific. We intend this section merely as a renewed warning, with new theoretical underpinnings, about a known but important issue in micro-level modeling.

5 Summary and Discussion

Our primary message is that the Gompertz slope, the rate of increase in mortality through age, has not been particularly constant across time, space, or characteristic, because neither has the variance in length of life. The Gompertz slope, which is often conceptualized as the rate of aging, typically increases with higher status, although aggregate patterns across OECD countries do not neatly fit this simplified view. The result of a steeper Gompertz slope is a reduction in the variance around length of life, and it has often been accompanied by a reduction in the Gompertz intercept, which raises life expectancy. Future patterns can always diverge from historical experience, but recent developments in mortality in advanced countries have typically reflected the past (Lee and Miller 2001).

Variance in length of life is costly, whether viewed at the population level as aggregate health inequality or at the individual level as a mean-preserving spread in how long we live (Edwards 2008). When rephrased as a faster rate of aging, a steeper Gompertz slope may not sound like something good. But the compression of mortality around an ever-increasing adult mode age at death is a reduction in a very large uncertainty, and it is progress against arguably preventable premature death.

Historical data reveal a massive decrease in the uncertainty around adult length of life concomitant with revolutions in nutrition, public health, and the prevention of communicable disease. Although progress against variance in developing countries has continued (Edwards 2010), compression has largely stalled in industrialized countries since 1960 (Wilmoth and Horiuchi 1999, Edwards and Tuljapurkar 2005). As we discussed, a critical question for forecasting models is how future patterns in the variance of age at death will unfold.

Given the long-term nonstationarity of variance, and the rapidity of its decline prior to 1960, it is questionable how helpful extrapolative forecasts may be. This seems especially true given the pace of scientific advancement in the genetics of aging, an entirely new field with the potential to change the way we age. In a recent review, de Magalhães et al. (2005) discuss how an array of genetic interventions in lab mice affect the Gompertz slope. It is an unanswered but provocative question whether new knowledge about may be able to rectangularize human survivorship even further in some future gerontological revolution.

This is not to say that gains against the diseases of old age are the only possible source of gains against variance, which is almost certainly not true. That variance is higher among subgroups with lower SES is a fairly clear indication that we can make considerable progress against variance by addressing the disease of socioeconomic inequality. While there is no clear link between population S₁₀ and income or educational inequality, it is telling that we see racial differences in S₁₀, which could in principle be driven by genetic differences, that look almost identical to SES differences. This is a straightforward extension of the conclusion that racial differences in mortality seem to be a manifestation of racial differences in SES (Preston and Taubman 1994). But reducing inequality in SES is likely to be a function of political will, which few demographers and health economists would be comfortable forecasting.

A Mathematical appendix

A.1 General Mortality Model

Using an apostrophe to indicate a derivative with respect to age, we differentiate equation (3) to reveal

$$\frac{d\varphi }{da}={\varphi }^{\prime }={\mu }^{\prime }\ell +\mu {\ell }^{\prime }.$$ (20)

The change in the value of φ between age a₁ and a slightly larger age a₁ + x is the sum of two terms. The first, x μ′(a) _ℓ(a), represents an increase in the probability due to the increase with age of the death rate μ; the second, xμ(a) ℓ′(a) = −x²(a), represents a decrease in the probability due to the decrease with age of survivorship ℓ(a).

At the modal age at death, which we will denote a₀, density is maximized. Because φ′ = 0 at the mode, the two components in equation (20) must be perfectly balanced.

Combining that with the fact that ℓ′ = −μℓ and thus −μℓ′ = μ²ℓ reveals that

$${\mu }^{\prime }\left(a_0\right)=\frac{d\mu }{da}={\mu }^2\left(a_0\right).$$ (21)

If the mortality curve μ(a) were to steepen so that μ′ were higher at every age a, the mode would have to shift to a younger age in order to maintain equality.

A second-order Taylor series expansion of φ(a) around the mode a₀ is φ(a) = φ(a₀) + (1/2)φ″ (a − a₀)², where φ′ is d²φ/da² evaluated at a = a₀. There is no linear term because the first derivative is zero at a = a₀. We rewite this as

$$\varphi \left(a\right)\approx \varphi \left(a_0\right)\left(1-\frac{{(a-a_0)}^2}{2{\sigma }^2}\right),$$ (22)

where σ² is given by equation (7). Here φ″(a₀) is the (negative) second derivative of φ(a) evaluated at the mode a₀ and μ″(a₀) is second derivative of μ(a) at the mode a₀. When the distribution φ(a) is reasonably sharply peaked around the mode a₀, we can approximate it by the normal distribution given in equation (6).

The variance in age at adult death is approximately given by the σ² appearing in equation (7). This variance depends on the curvature of the mortality function, i.e., whether the slope of mortality steepens or shallows around the modal age. If the curve steepens, then μ″(a₀) > 0 and the variance is smaller than for a curve that shallows at the mode.

A.2 The Gompertz Model

The density of age at death for the Gompertz model is

$$\varphi \left(a\right)=\mu \left(a\right)e^{-\left(\mu \right(a)-{\mu }_0)∕\beta }.$$ (23)

Because the Gompertz mortality rises exponentially, the density φ falls steeply at very high ages. In addition, equation (21) shows that the mode satisfies

$$\mu \left(a_0\right)=\beta ,$$ (24)

so the modal age at death is

$$a_0=\frac{1}{\beta }\log (\beta ∕{\mu }_0).$$ (25)

These results and those following are summarized in Table 1. We expect a₀ to decrease if β increases, a property that holds for (25) so long as a₀ > 1/β which is true for any plausible human mortality pattern.

Applying equation (7) to the Gompertz case reveals a key result of this paper: the variance in adult age at death for the Gompertz model is approximately given by equation (9).

A.3 The Logistic Model

Integration of equation (10) shows that the probability density of deaths in the logistic model is given by

$$\varphi \left(a\right)={(C+1)}^{1∕\beta }\frac{e^{\beta a}}{{(C+e^{\beta a})}^{(1+1∕\beta )}}.$$ (26)

This density falls as a simple exponential e^−a for high ages, much more slowly than for the Gompertz model. For the logistic, the modal age at death is

$$a_0=\frac{1}{\beta }\log \left(\beta C\right).$$ (27)

Equation (7) reveals that the approximate variance is given by equation (11).

A.4 General Mortality, Multiplicative Frailty

Given the mortality function in equation (12), the probability distribution of age at death is

$$\varphi (a\mid Z)=Z\mu \left(a\right)\exp (-ZM(a\left)\right),$$ (28)

with cumulative mortality M(a) defined as in equation (1). The population probability distribution of age at death is the expectation over frailty,

$$\varphi \left(a\right)=\epsilon \left[\varphi \right(a\mid Z\left)\right]=\int g\left(z\right)\varphi (a\mid z)dz.$$ (29)

Given equation (13), the modal age at death in the population must satisfy

$${\mu }^{\prime }\left(a\right)={\mu }^2\left(a\right)\frac{h_2}{h_1}.$$ (30)

Note that if every frailty were equal to 1, we would have h₂ = h₁ and this equation would reduce to our earlier equation (21). Also, we have

$${\varphi }^{″}\left(a_0\right)=h_1{\mu }^{″}+{\mu }^3\left\{h_3-3\left(\frac{h_2^2}{h_1}\right)\right\},$$ (31)

where the h_i are evaluated at the mode a₀.

A.5 General Mortality, Gamma Multiplicative Frailty

The gamma distribution in equation (15) is convenient, as Vaupel et al. pointed out, because we can use it with any baseline mortality μ(a) to find an explicit expression for the population average distribution of age at death, whose general form was given by equation (29):

$$\varphi \left(a\right)=\mu \left(a\right){\left(\frac{k}{(k+M(a\left)\right)}\right)}^{k+1}.$$ (32)

We can differentiate to find that the modal age at death is defined by the condition

$${\mu }^{\prime }\left(a_0\right)=\left(\frac{1+s^2}{1+s^{2}M\left(a_0\right)}\right){\mu }^2\left(a_0\right).$$ (33)

Notice that if all individuals had the same frailty, s² = 0 and equation (33) would reduce to the simpler equation (21). Qualitatively, the denominator on the right describes how frailty alters the rate of change of average mortality and survival depending on how much selection acts against more frail individuals. The magnitude of selection depends on both the variance s² in frailty, and the cumulative mortality hazard M(a). Strong selection will act to decrease the modal age at death.

A.6 Gompertz Mortality, Gamma Multiplicative Frailty

The modal age at death for this model is found using equation (33) with Gompertz mortality as given by equation (8), which yields the condition

$$\mu \left(a_0\right)=(\beta -s^2{\mu }_0).$$ (34)

This reveals an equation for the mode:

$$a_0=\frac{1}{\beta }\log (\beta ∕{\mu }_0-s^2).$$ (35)

Compared with equation (25) for the standard Gompertz, which is shown in the first column of the third row of Table 1, this equation reveals how frailty acts to reduce the modal age at death.