Systematic Shifts in the Balance of Excitation and Inhibition Coordinate the Activity of Axial Motor Pools at Different Speeds of Locomotion

Abstract

An emerging consensus from studies of axial and limb networks is that different premotor populations are required for different speeds of locomotion. An important but unresolved issue is why this occurs. Here, we perform voltage-clamp recordings from axial motoneurons in larval zebrafish during “fictive” swimming to test the idea that systematic differences in the biophysical properties of axial motoneurons are associated with differential tuning in the weight and timing of synaptic drive, which would help explain premotor population shifts. We find that increases in swimming speed are accompanied by increases in excitation preferentially to lower input resistance (Rin) motoneurons, whereas inhibition uniformly increases with speed to all motoneurons regardless of Rin. Additionally, while the timing of rhythmic excitatory drive sharpens within the pool as speed increases, there are shifts in the dominant source of inhibition related to Rin. At slow speeds, anti-phase inhibition is larger throughout the pool. However, as swimming speeds up, inhibition arriving in-phase with local motor activity increases, particularly in higher Rin motoneurons. Thus, in addition to systematic differences in the weight and timing of excitation related to Rin and speed, there are also speed-dependent shifts in the balance of different sources of inhibition, which is most obvious in more excitable motor pools. We conclude that synaptic drive is differentially tuned to the biophysical properties of motoneurons and argue that differences in premotor circuits exist to simplify the coordination of activity within spinal motor pools during changes in locomotor speed.

Introduction

All animals locomote over a range of speeds. In limbed creatures, increases in speed are associated with changes in gait (Grillner, 1975; Pearson, 1976). A growing body of work in mice is beginning to reveal the spinal mechanisms responsible for gait transitions, which involve differences in the contribution of genetically identifiable excitatory and inhibitory premotor populations (Gosgnach et al., 2006; Crone et al., 2009; Zhong et al., 2011; Talpalar et al., 2013). However, one of the first demonstrations of switches in spinal circuits during increases in locomotor speed was provided by studies of swimming in larval zebrafish (McLean et al., 2008). In particular, subsets of premotor excitatory neurons originating from the P0 progenitor domain, called V0-eD neurons (Satou et al., 2012), are active at slow speeds, but these cells are then inhibited at faster speeds as a new excitatory population arising from the P2 progenitor domain, called V2a neurons (Kimura et al., 2006), is engaged. At the fastest speeds, cells within the V2a population are in turn silenced, as others are activated. While speed-dependent differences in appendicular premotor populations are relatively intuitive, given requisite differences in interlimb coordination (Berkowitz et al., 2010), it is unclear why this occurs during axially based locomotion, where smooth gradations in tail beat amplitudes and frequencies generate faster speeds of swimming (McLean et al., 2008; Green et al., 2011).

One possible explanation is that different sets of premotor interneurons are required to coordinate the recruitment patterns of heterogeneous axial motor pools. Our recent work studying the biophysical properties of axial motoneurons in larval zebrafish has revealed remarkable diversity related to recruitment order. Motoneurons are recruited from the bottom of spinal cord up, with progressively larger, lower Rin motoneurons added to the active pool as swimming frequency increases (McLean et al., 2007). The recruitment order of motoneurons is associated with systematic differences in nonlinear membrane properties that match Rin. Higher Rin ventral motoneurons exhibit intrinsic bursting responses to current steps, while lower Rin dorsal motoneurons respond with either phasic or tonic firing patterns (Menelaou and McLean, 2012). Given that lower Rin motoneurons likely require more current to get them to threshold, these findings raise the following questions related to speed control: (1) How does the relative distribution of excitatory and inhibitory synaptic input lead to the orderly recruitment of axial motoneurons? (2) How does the timing of synaptic drive accommodate differences in the biophysical properties of motoneurons to maintain left–right alternation during speeds of swimming that engage the entire axial pool?

Here, we have measured the synaptic input to identified axial motoneurons by performing whole-cell voltage-clamp recordings in larval zebrafish during “fictive” swimming to address these issues. We reveal that systematic differences in the weight of excitation and the timing of excitation and inhibition are in fact tuned to the biophysical properties of axial motoneurons. Our findings suggest that differences in premotor circuit architecture act to simplify the coordination of heterogeneous axial motor pools during changes in swimming speed, which could reflect a generalizable principle for speed control in spinal locomotor networks.

Materials and Methods

Fish care.

All experiments were performed on wild-type 4- to 5-d-old zebrafish obtained from an in-house breeding facility (Aquatic Habitats). At this age, the fish are freely swimming, but are still nourished by their yolk. Since secondary sexual characteristics are not evident in larvae, sex could not be easily determined and so experiments were performed on larvae of either sex. Fish were raised and maintained at 28.5°C, but recordings were performed at room temperature (∼22°C). All procedures described below conform to NIH guidelines regarding animal experimentation and were approved by the Northwestern University Institutional Animal Care and Use Committee.

Electrophysiology.

To examine premotor synaptic drive at different speeds of locomotion, we performed whole-cell voltage-clamp recordings from axial motoneurons in chemically immobilized larvae, while simultaneously monitoring fictive swimming output from superficial peripheral motor nerves (Fig. 1A,B). Whole-cell patch and peripheral motor nerve recordings were performed as described previously (Drapeau et al., 1999; Masino and Fetcho, 2005), using a modified patch solution to perform voltage-clamp recordings (see below). Briefly, larvae were first anesthetized in MS-222 and then immobilized in α-bungarotoxin (Sigma-Aldrich), both of which were dissolved in extracellular solution (1 mg/ml). The composition of extracellular solution was as follows (in mm): 134 NaCl, 2.9 KCl, 1.2 MgCl₂, 10 HEPES, 10 glucose, and 2.1 CaCl₂, adjusted to pH 7.8 with NaOH. After fish were immobilized (5–10 min), they were secured on their right side to the bottom of a Sylgard-coated, glass-bottom dish containing anesthetic solution using custom-etched tungsten pins inserted through the notochord (Fig. 1A). To record motoneuron activity from peripheral nerves, skin was removed from just behind the swim bladder to just past the anus using fine forceps. To access spinal motoneurons, a single muscle segment was dissected away carefully under a dissecting microscope with a sharpened tungsten dissecting pin.

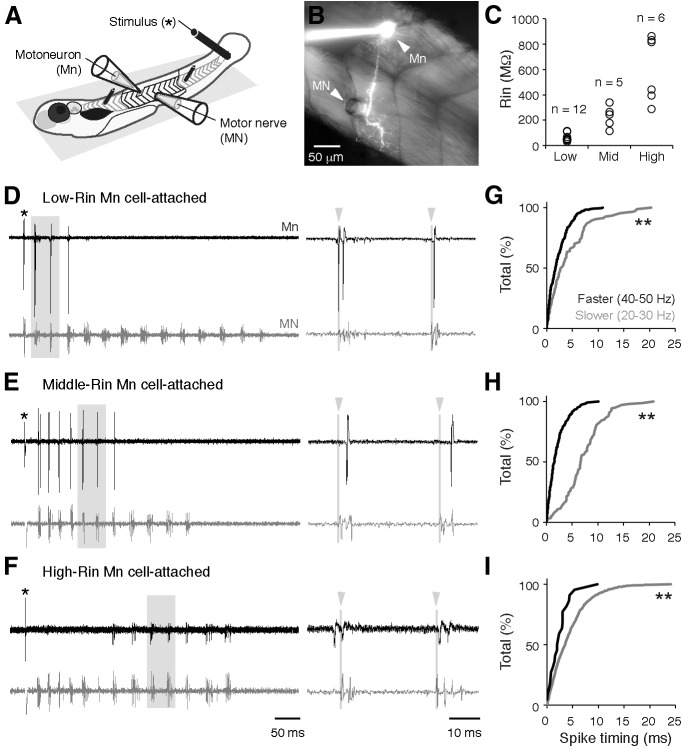
Figure 1.

Patterns of motoneuron activity and spike timing. A, Chemically immobilized zebrafish larvae are pinned down to a Sylgard platform and recordings from a spinal motoneuron (Mn) and peripheral motor nerve (MN) are performed following dissection (see Materials and Methods for details). B, Image of a fluorescently filled Mn and its projection into the segmented axial musculature. Note the suction electrode for the MN recording placed in close proximity to the Mn recording site. C, Distribution of input resistance (Rin) values for low-, middle- (mid), and high-Rin pools of motoneurons. D–F, Cell-attached recordings from Mns with progressively greater Rin and simultaneous MN recordings. Expanded traces on the right are taken from regions boxed in gray. Gray lines and arrowheads mark the start of the motor burst cycle, used to quantify spike timing. G–I, Cumulative distributions of the absolute values of spike timing relative to the onset of the MN bursts (at time 0) at slower speeds (gray) and faster speeds (black) for low-Rin (G), middle-Rin (H), and high-Rin Mns (I). Double asterisks indicate a significant difference. See Results for statistical data.

After the dissection, the preparation was rinsed and covered in anesthetic-free extracellular solution, and then moved to the physiological recording apparatus. Cells were targeted using a 40×/1.0 NA water-immersion objective (W Plan-Apochromat; Zeiss) on a compound microscope equipped with DIC optics (Axio Examiner; Zeiss) and a CCD camera (Rolera-XR; QImaging). Cell-attached and whole-cell recordings were made using standard-wall 1 mm outer diameter borosilicate capillaries (Sutter Instrument), pulled to 0.5–1 μm tip diameters (resistance, 5–14 MΩ) using a micropipette puller (Flaming/Brown; Sutter Instrument). Peripheral motor nerve activity was recorded with suction electrodes placed over the muscle clefts at a consistent location close to the whole-cell recording site (Fig. 1B). Suction electrodes were made by first pulling patch electrodes as described above and then breaking the tips to diameters of 20–50 μm. A microforge (MF-830; Narishige) was used to simultaneously heat polish and bend the tip to compensate for the approach angle (∼20°) to improve the contact between the opening of the electrode and the muscle cleft. Patch electrodes were backfilled with intracellular solution (122 mm CsMeSO₃, 0.1–1 mm QX314-Cl, 1 mm TEA-Cl, 3 mm MgCl₂, 10 mm HEPES, 1 mm EGTA, 4 mm Na₂-ATP, and 50 μm Alexa Fluor hydrazide) and then advanced into the exposed portion of the spinal cord using a motorized micromanipulator (MP-225; Sutter Instrument or Patchstar, Scientifica) while maintaining positive pressure (∼25–50 mmHg) via a pneumatic transducer (Model DPM-1B; Bio-Tek Instruments) to prevent the tip from clogging. A cesium-based solution containing QX314 was used to disambiguate synaptic currents from Na- and K-channel-dependent processing. Alexa Fluor hydrazide was included in the patch solution to confirm the morphology of motoneurons and also to confirm the axon was not severed after the recordings, by switching to an epifluorescent light source (Fig. 1B). Sequential DIC and epifluorescent images at different focal planes were captured using a CCD camera and QCapture Suite imaging software (QImaging). Images were processed for illustrative purposes using Photoshop (Adobe).

A holding potential of –65 mV was maintained during the course of achieving a GΩ cell-attached seal. At this stage, we acquired the firing pattern of cells during fictive swimming. Subsequently whole-cell recordings were obtained by penetrating the membrane using gentle suction pulses or a very brief electric pulse. After breaking in, the input resistance (Rin) of the motoneuron was measured using 5 mV hyperpolarizing steps at a holding potential of approximately –75 mV. To obtain Rin values, we first calculated the membrane time constant (τ) and total charge (Qt) from the capacitance transients of the voltage steps according to the pClamp10 User Guide, using custom-written MATLAB code. The time constant and total charge were then used to calculate the access resistance (Ra) according to Ra = τ × ΔV/Qt. Finally, Rin was calculated from the steady-state current in response to the voltage steps according to ΔI = ΔV/(Ra + Rin). The values obtained using this method overlap with those measured in current-clamp mode from the same morphological classes of motoneurons (Menelaou and McLean, 2012). Motoneurons were voltage clamped at approximately –75 mV to isolate EPSCs. IPSCs were recorded by holding at approximately +10 mV. These values represent the calculated chloride ion and cation reversal potentials, respectively. Values were corrected for a calculated junction potential of –11 mV (pClamp 10; Molecular Devices). For all recordings standard correction for capacitance was applied. Recordings were performed both with and without series compensation (50–60%). Only data where compensated series resistance did not exceed 60 MΩ were included for analysis. In addition, we monitored series resistance during the course of the experiments and cells displaying any deviation >5% were excluded from analysis. Whole-cell and peripheral motor nerve recordings were acquired using a Multiclamp 700A amplifier (Molecular Devices), a Digidata series 1322A digitizer (Molecular Devices), and pClamp 10 software (Molecular Devices).

Analysis.

Data were analyzed off-line using DataView (Heitler, 2009), MATLAB (MathWorks), and Excel (Microsoft). DataView was used to identify cyclical motor bursts and the onset times of motor bursts were imported into MATLAB. DataView was also used to identify spikes in cell-attached recordings, and the onset times of spikes were also imported into MATLAB. Custom MATLAB programs were written to analyze cell-attached data as well as excitatory and inhibitory currents. Swim frequency was calculated as the inverse of the time difference between two successive motor bursts. To more reliably evoke a broader range of swim frequencies than those observed spontaneously, we delivered a brief electrical stimulus to the skin to mimic tactile input (Clarke and Roberts, 1984). The highest frequencies within a bout tend to occur immediately following the stimulus (McLean et al., 2008); however, increases in frequency within this period could be achieved by increasing the intensity of the electrical stimulus (2–10 V, 0.1 ms). Recruitment patterns during evoked decelerations in swimming frequency and spontaneous accelerations are virtually indistinguishable (McLean et al., 2008). To avoid the potential confounding influence of direct sensory inputs to motoneurons following the electrical stimulus, we did not analyze the first motor burst. To compare spiking activity or synaptic input across different speeds, we normalized time between successive motor bursts. This was done by dividing the time between the onset of a motor burst (0) and onset of the next burst (1) in 100 equal segments, which allowed us to analyze events in relation to the motor burst cycle and compare motor burst cycles at different frequencies. Since inhibition peaks between consecutive motor bursts, we analyzed inhibition arriving from phase 0 to 1. However, excitatory drive for any given swim burst begins midway through the previous motor burst cycle. Thus, the analysis of excitatory input was performed from phase –0.5 to 0.5. EPSCs and IPSCs arriving from –0.05 to 0.45 were defined as “in-phase,” while those arriving from 0.45 to 0.95 were defined as “anti-phase.” The values for anti-phase EPSCs were subtracted from in-phase values to isolate the in-phase contribution.

To analyze different swim speeds, synaptic currents were binned at 10 Hz intervals. For any given speed bin, at least three events had to take place in that frequency range for the data to be included in the analysis. Peak excitatory current and peak inhibitory current were the averaged excitatory or inhibitory maximum of three or more events in a given frequency bin. Excitatory and inhibitory gains were calculated as the slope of changes in peak current at swim speeds ranging from 20 to 50 Hz. For analysis of temporal dynamics of excitation and inhibition at different speeds for different cells, we analyzed synaptic currents from phase −0.5 to 0.5, divided into 100 equal segments. The averaged excitatory and inhibitory currents across cells for any given speed bin were then normalized to the peak value of the current.

Statistics.

Before statistical analysis, all data were tested for normality to determine whether parametric versus nonparametric examinations were appropriate. Consequently, statistical comparisons of cumulative distributions were made using a Kolmogorov–Smirnov (K-S) test, comparisons between independent groups were performed using Mann–Whitney U tests with a Bonferroni correction for multiple comparisons, and comparisons between related groups were performed using either a paired two-sample t test or a Wilcoxon matched-pairs test, again with corrections for multiple comparisons. The significance of correlations was determined using either a Pearson or a Spearman rank R correlation test. Degrees of freedom (df) are reported parenthetically with the respective D, U, t, Z, R, or Rs values of these tests, according to convention (K-S and Mann–Whitney U, df = n1 + n2 − 2; paired two-sample t test and Wilcoxon matched-pairs test, df = n − 1; Pearson correlation test and Spearman rank R correlation test, df = n − 2). Statistical analysis was performed using StatPlus Professional (AnalystSoft) in conjunction with Microsoft Excel. All data are reported as means ± SE, unless stated otherwise. Significance was set at p < 0.05.

Results

Previous work has identified at least three morphologically distinguishable classes of axial motoneurons in larvae (Menelaou and McLean, 2012; Asakawa et al., 2013). The “primary” motoneurons, so named due to their early differentiation (Myers et al., 1986), appear to preferentially innervate deeper, fast-twitch muscles. Among the “secondary” motoneurons, which develop later (Myers et al., 1986), there are cells that have deep innervation patterns comparable to primaries, and cells that appear to preferentially innervate more superficial, slow-twitch muscles. Following assessments of recruitment order in cell-attached mode (Fig. 1D–F), and measurements of Rin immediately after breaking into the cell, we confirmed the morphology of all recorded cells by switching to an epifluorescent light source (Fig. 1B). Using post hoc morphology information, we divided our dataset into three groups based on these anatomical distinctions. Consistent with our prior work (McLean et al., 2007, 2008; Menelaou and McLean, 2012), primaries had the lowest Rin values, secondaries that preferentially innervate superficial slow-twitch muscle fibers had the highest Rin values, and secondaries that likely innervate both fast- and slow-twitch muscles had Rin values distributed in between (Fig. 1C). Given that Rin covaries with other factors contributing to intrinsic excitability (e.g., size, resting membrane potential, rheobase, spike threshold, and after-hyperpolarization amplitude) at this stage (Menelaou and McLean, 2012), for the purposes of this study, we will refer to these groups as low-Rin, high-Rin, and middle-Rin motoneurons, respectively.

To begin to examine the synaptic basis for the rhythmic activation of heterogeneous motoneurons at different speeds, we first assessed the firing patterns of these three groups during fictive swimming, where the frequency of successive motor bursts recorded from peripheral motor nerves can be used as an indication of swim speed. Figure 1, D–F, illustrates swim responses to a brief electrical stimulus, which generates a broad range of swimming frequencies, with the fastest frequencies typically occurring immediately after the stimulus (McLean et al., 2008). Consistent with prior work (Menelaou and McLean, 2012), the low-Rin motoneurons were more reliably active during this initial period of high-frequency swim activity (Fig. 1D). Of the 404 spikes recorded, 95 were observed between 20 and 30 Hz, while 309 were observed between 40 and 50 Hz. High-Rin motoneurons were more consistently active later in the swim response when frequency had declined (Fig. 1F). Of the 1446 spikes recorded, 1424 were observed between 20 and 30 Hz, with only 22 found between 40 and 50 Hz, consistent with the silencing of subsets of secondary motoneurons at fast speeds (Menelaou and McLean, 2012). Middle-Rin motoneurons bridged the two populations (Fig. 1E). Of a total 287 spikes, 103 were observed between 20 and 30 Hz and 184 between 40 and 50 Hz. Notably, however, we observed cycles of fictive motor bursts occurring at the same frequency in which low-, middle-, and high-Rin motoneurons were all concurrently spiking (Fig. 1D–F, right), meaning that synaptic drive must coordinate simultaneous activation of motoneurons with heterogeneous Rin. A closer examination of the timing of spikes at slower (20–30 Hz) versus faster (40–50 Hz) frequencies revealed significantly reduced spike jitter at fast speeds among motoneurons active at both ranges of speed, as manifested by a compression of the cumulative distribution of values in time (Fig. 1G–I; K-S tests for G, D(402) = 0.26, p < 0.001; for H, D(285) = 0.67, p < 0.001; for I, D(1444) = 0.27, p < 0.05. Note, degrees of freedom reflect the number of spikes, not the number of motoneurons). Consequently, in addition to activating heterogeneous motoneurons at different speeds, synaptic drive must ensure stricter temporal control of spiking across the axial motor pool at speeds of fictive swimming in which the entire motor pool is active.

Because the firing behavior measured with cell-attached recordings in our dataset was consistent with previous data performed in the current-clamp configuration, this set the stage for an examination of the synaptic drive that could explain the observed features of motoneuron activity, namely: (1) preferential activation of high-Rin motoneurons at slower locomotor speeds, (2) increased participation of lower Rin motoneurons at higher speeds, (3) reduced reliability of firing of the highest Rin motoneurons at higher speeds, and (4) sharpening of spike timing in all motoneurons at increased locomotor speeds.

Excitatory drive to motoneurons

There are two forms of excitation to axial motoneurons during undulatory swimming (Roberts et al., 1998; Grillner, 2006): rhythmic excitation arriving in-phase, which drives the cyclical bursts of motor activity, and tonic excitation evident in anti-phase, which provides a background source of depolarizing drive. For the purposes of this study, we will use the terms in-phase and anti-phase to categorize these different forms of excitation. How does excitation vary with speed and Rin across the axial motor pool? Figure 2, A–C, illustrates EPSCs in response to a brief electrical stimulus in low-, middle-, and high-Rin motoneurons. In all three groups we observed rhythmic EPSCs in-phase with ipsilateral motor bursts and a more tonic, anti-phase excitatory drive (Fig. 2A–C). This pattern was present in all motoneurons across the entire range of locomotor speeds, as demonstrated in waterfall plots averaging the excitatory drive in each group at different frequency bins (Fig. 2D–F). As expected from biophysical principles and earlier observations (Menelaou and McLean, 2012), lower Rin motoneurons are recipients of stronger (larger amplitude) excitatory synaptic drive (Fig. 2A–C, right). Notably, these differences were speed and phase dependent. At slow speeds, all three groups received comparable amplitude in-phase EPSCs, while the low-Rin motoneurons received more tonic, anti-phase excitatory drive than mid- and high-Rin motoneurons (Fig. 2G; Mann–Whitney U tests for in-phase values: “low-mid,” U(15) = 42, p > 0.05; “low-high,” U(16) = 33, p > 0.05; “mid-high,” U(9) = 24, p > 0.05; for anti-phase values: low-mid, U(15) = 54, p < 0.05; low-high, U(16) = 69, p < 0.01; mid-high, U(9) = 9, p > 0.05). At faster speeds excitatory input diverges dramatically, with low-Rin motoneurons exhibiting significantly more of both in-phase and anti-phase excitatory drive than middle- and high-Rin motoneurons (Fig. 2H; Mann–Whitney U tests for in-phase values: low-mid, U(15) = 56, p < 0.05; low-high, U(16) = 72, p < 0.01; mid-high, U(9) = 2, p < 0.05. For anti-phase values: low-mid, U(15) = 59, p < 0.01; low-high, U(16) = 72, p < 0.01; mid-high, U(9) = 2, p < 0.05). Analysis of the peak synaptic excitation at fast swimming speeds reveals an inverse relationship between maximal excitatory input and motoneuron Rin, with strongest synaptic drive to the lowest Rin motoneurons (Fig. 2I; Spearman rank R correlation test, Rs(21) = –0.87, p < 0.001).

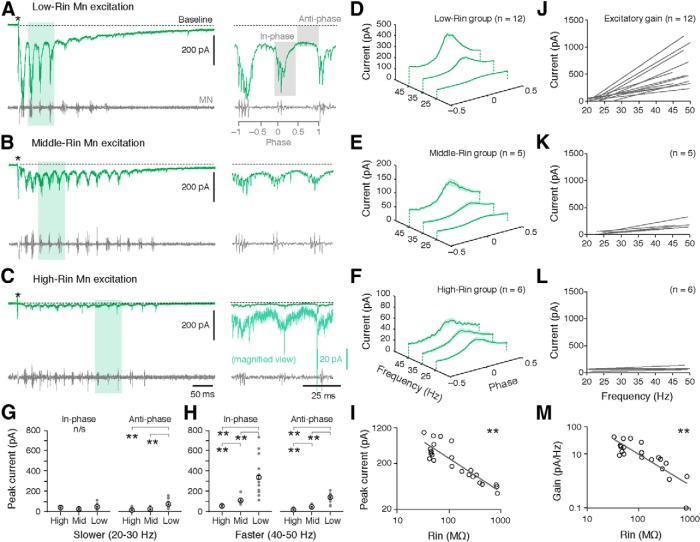
Figure 2.

Changes in excitatory drive to motoneurons as a function of speed and input resistance. A–C, Voltage-clamp recordings of excitatory currents during a bout of fictive swimming (stimulus artifact at asterisk) from motoneurons (Mns) with progressively higher input resistance (Rin). Expanded traces on the right are taken from regions shaded in green. A, Right, the regions assessed for in-phase and anti-phase excitation are shaded in gray. C, The expanded trace has been magnified vertically to more clearly observe rhythmic excitatory current (light green, note color-matched scale bar). D–F, Excitatory currents normalized to phase and averaged in 10 Hz speed bins for low- (D), middle- (E), and high-Rin pools of motoneurons (F). The shaded area represents the SE. G, Comparison of excitation arriving in-phase or anti-phase between the different motor pools at 20–30 Hz (slower swimming). H, As in G, but at 40–50 Hz (faster swimming). I, Log-log plot of peak excitatory current as a function of Mn Rin. Each data point represents an individual preparation. J–L, Regression lines of excitatory current as a function of speed (gain) for Mns within the groups shown to the left in D–F. M, Log-log plot of excitatory gain as a function of Mn Rin. Each data point represents an individual preparation.

This preferential excitatory input to lower Rin motoneurons at higher swim speeds is reflected in systematic differences in the excitatory gain for motoneurons within each group as a function of Rin (Fig. 2J–L). When calculated on a cell-by-cell basis for motoneurons, excitatory synaptic gain is also inversely correlated with Rin, with highest synaptic gains in the lowest Rin motoneurons (Fig. 2M; Spearman rank R correlation test, Rs(21) = –0.80, p < 0.001). Consequently, both peak current and excitatory gain across speeds in motoneurons are inversely correlated with Rin, consistent with systematic differences in the distribution of excitatory drive to different motoneurons based on their excitability.

Inhibitory drive to motoneurons

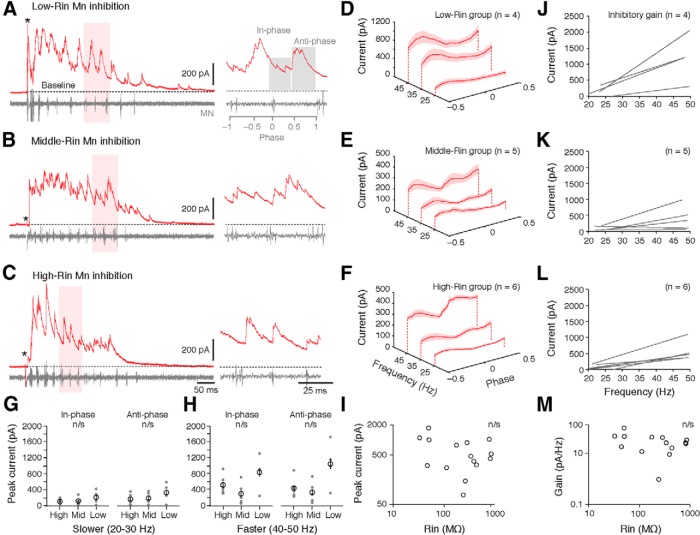
Does inhibitory input to motoneurons follow the same pattern as excitation? There are two sources of inhibition responsible for patterning rhythmic motoneuron activity in axial networks (Grillner, 2006; Roberts et al., 2008): in-phase inhibition arrives close to the start of the motor burst cycle, and contributes to ipsilateral motor burst termination; whereas anti-phase inhibition arrives in the middle of the motor burst cycle and maintains left–right alternation. Figure 3, A–C, illustrates IPSCs in response to a brief electrical stimulus in low-, middle-, and high-Rin motoneurons. In all three groups, IPSCs arrived throughout the motor burst cycle. Averaged values of IPSCs normalized to phase in waterfall plots demonstrate a clear peak in inhibition at anti-phase and a dip in inhibition around the motor burst (phase 0) in all groups and at all speeds (Fig. 3D–F). In contrast to excitation, however, the levels of inhibitory drive to the three groups were uncorrelated to Rin (Fig. 3, A–C, right). There were no significant differences in either form of inhibition at slower (Fig. 3G; Mann–Whitney U tests for in-phase values: low-mid, U(7) = 6, p > 0.05; low-high, U(8) = 7, p > 0.05; mid-high, U(9) = 15, p > 0.05; for anti-phase values: low-mid, U(7) = 7, p > 0.05; low-high, U(8) = 8, p > 0.05; mid-high, U(9) = 13, p > 0.05) or faster speeds (Fig. 3H; Mann–Whitney U tests for in-phase values: low-mid, U(7) = 2, p > 0.05; low-high, U(8) = 8, p > 0.05; mid-high, U(9) = 22, p > 0.05; for anti-phase values: low-mid, U(7) = 2, p > 0.05; low-high, U(8) = 4, p > 0.05; mid-high, U(9) = 18, p > 0.05). The absence of any speed-dependent relationship with Rin was also apparent when inhibitory gain was calculated for motoneurons within each group (Fig. 3J–L). As a result, there was no significant correlation for peak levels (Fig. 3I; Pearson correlation test, R(13) = –0.04, p > 0.05) or gain of inhibitory current based on motoneuron Rin (Fig. 3M; Spearman rank R correlation test, Rs(13) = –0.16, p > 0.05). This held true even when the in-phase and anti-phase components were analyzed separately (in-phase peak, Spearman Rs(13) = –0.11, p > 0.05; in-phase gain, Pearson R(13) = –0.21, p > 0.05; anti-phase peak, Spearman Rs(13) = –0.4, p > 0.05; anti-phase gain, Pearson R(13) = –0.43, p > 0.05). These data suggest that, unlike excitation, inhibition is uniformly distributed across the motor pool, with global increases in inhibitory current during faster swimming.

Figure 3.

Changes in inhibitory drive to motoneurons (Mns) as a function of speed and input resistance. A–C, Voltage-clamp recordings of inhibitory currents during a bout of fictive swimming (stimulus artifact at asterisk) from Mns with progressively higher input resistance (Rin). Expanded traces on the right are taken from regions shaded in red. A, Right, the regions assessed for in-phase and anti-phase inhibition are shaded in gray. D–F, Inhibitory currents normalized to phase and averaged in 10 Hz speed bins for low- (D), middle- (E), and high-Rin pools of motoneurons (F). G, Comparison of inhibition arriving in-phase or anti-phase between the different motor pools at 20–30 Hz (slower swimming). H, As in G, but at 40–50 Hz (faster swimming). I, Log-log plot of peak inhibitory current as a function of Mn Rin. Each data point represents an individual preparation. J–L, Regression lines of inhibitory current as a function of speed (gain) for Mns within the groups shown to the left in D–F. Note, for low-Rin motoneurons, we were only able to obtain IPSC data from 4 of the 12 cells. M, Log-log plot of inhibitory gain as a function of Mn Rin. Each data point represents an individual preparation.

Timing of excitation and inhibition

Our findings thus far indicate that increases in excitation are inversely proportional to Rin at faster swimming speeds, whereas inhibition broadly increases as a function of swim speed, regardless of Rin. Because rhythmic activity of motoneurons relies not only on the levels, but also the timing of synaptic drive, we next investigated how the temporal profile of excitation and inhibition corresponded to the spiking patterns of the same motoneurons at different speeds of swimming. To facilitate comparisons of the timing of peak synaptic drive across conditions, we normalized excitatory and inhibitory currents to their peak values (see Materials and Methods). At slow speeds, excitation and inhibition peaked largely out of phase with each other regardless of motoneuron identity (Fig. 4A–C, left). Critically, the peak of excitation arrived during a clear ebb in inhibition, which matches the distribution of spikes at this speed (Fig. 4A–C, gray histograms). At faster speeds the distribution of spikes was also well aligned with the distribution of excitation in all three groups (Fig. 4A–C, right). However, in contrast to slow speeds, the timing of excitation was sharper and appeared to be more synchronous. There were also clear differences in the temporal patterning of inhibitory drive related to motoneuron Rin. At slow speeds, inhibition predominated anti-phase for all three groups of motoneurons (Fig. 4A–C, left). At faster speeds there was a shift in the dominance of in-phase inhibition: only in the high-Rin motoneurons did in-phase inhibition appear to exceed anti-phase inhibition (Fig. 4C, right).

Figure 4.

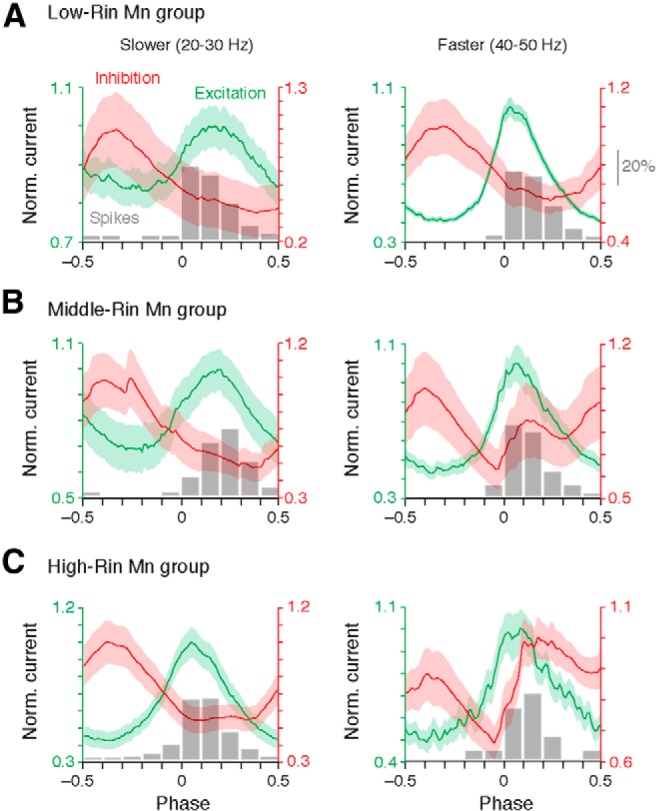
Differences in the timing of excitation and inhibition with an increase in speed related to motor group. A–C, Averaged and normalized (to peak) traces of excitation and inhibition overlaid on normalized histograms of spike timing (shown in gray) from low- (A), middle- (B), and high-Rin motoneuron (Mn) groups (C) at slow speeds (left) and fast speeds (right). The shaded area represents the SE. Note histograms of spike timing are normalized as percentages of the total number of spikes recorded in cell-attached mode at that speed range (scale bar in A, right). Values were originally presented in Figure 1, G–I, and are reported in the Results.

To see if these patterns were systematically related to motoneuron Rin, we first compared the half-width of excitation to motoneuron Rin at slower and faster speeds (Fig. 5A). Consistent with the observation that rhythmic excitation occupies a consistent fraction of the motor burst cycle when normalized to phase (Fig. 4A–C), excitatory half-widths were longer at slower speeds than faster ones (18.8 ± 0.8 ms vs 8.1 ± 0.2 ms, respectively; paired two-sample t test, t(22) = 2.1, p < 0.001). This temporal compression of excitation occurred uniformly throughout the motor pool, as half-widths bore no relation to Rin at slow (Fig. 5A, left; Pearson correlation test, R(21) = –0.25, p > 0.05) or fast speeds (Fig. 5A, right; Pearson correlation test, R(21) = 0.36, p > 0.05). However, when we examined the timing of peak excitatory current, we found that at slow speeds, excitation peaked systematically earlier in the phase of the swim cycle in higher Rin motoneurons (Fig. 5B, left; Spearman Rank test, Rs(21) = –0.43, p < 0.05). At faster speeds, this pattern was no longer obvious, with peak excitation arriving uniformly early in the swim phase throughout the pool (Fig. 5B, right; Spearman Rank test, Rs(21) = 0.11, p > 0.05). Collectively, these observations suggest that excitatory drive to the entire pool originates from the same premotor population at faster speeds.

Figure 5.

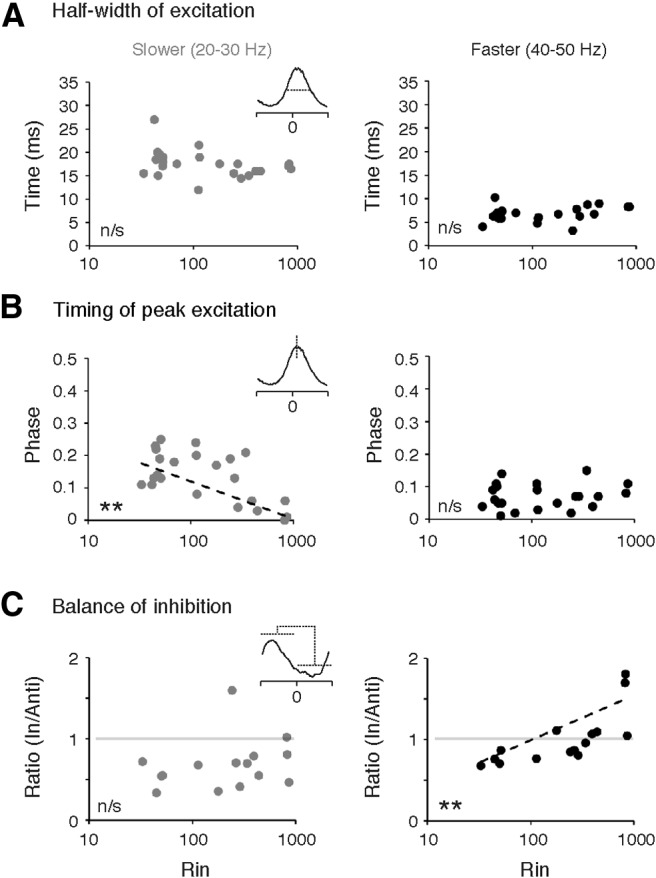
Changes in the timing of excitation and inhibition related to input resistance. A, Half-width of excitation as a function of motoneuron input resistance (Rin) at slow (left) and fast (right) speeds. B, Timing of peak excitation as a function of motoneuron Rin at slow (left) and fast (right) speeds. C, Ratio of in-phase to anti-phase inhibition expressed as a function of Mn Rin at slow (left) and fast (right) speeds. Ratio is calculated from the average level of total current between phase −0.05 to 0.45 (in-phase) and 0.45 to 0.95 (anti-phase).

The temporal dispersal of inhibition precluded any analysis of half-widths for in- or anti-phase inhibition; however, to examine speed-related differences in the timing of inhibition, we calculated the average ratio of in-phase to anti-phase inhibition as a function of Rin at slower and faster speeds (Fig. 5C). Consistent with the pooled data, at slower speeds anti-phase inhibition dominated regardless of Rin, with most ratios falling below 1 (Fig. 5C, left). Consequently, there was no correlation between the balance of inhibition and Rin (Pearson correlation test, R(13) = 0.21, p > 0.05). However, at faster speeds there was a shift in the ratio such that values approached and even exceeded 1 (Fig. 5C, right). This shift was most obvious in the higher Rin motoneurons, yielding a significant positive correlation (Pearson correlation test, R(13) = 0.84, p < 0.001). These data are consistent with the idea that the dominance of in- versus anti-phase inhibition shifts from the lowest to the highest Rin motoneurons at faster speeds of swimming.

Discussion

Our experiments were designed to examine whether synaptic drive to motoneurons is tuned to accommodate the biophysically heterogeneous properties of axial motoneurons, allowing for coordinated patterns of activity during changes in swimming speed. By performing voltage-clamp recordings from axial motoneurons of larval zebrafish, we found that the amplitude and timing of excitatory and inhibitory drive to the motor pool varies systematically with speed and Rin. As swim frequency increases and larger, lower Rin motoneurons are recruited, there is a preferential increase in excitatory drive to these cells. In all motoneurons, rhythmic excitatory drive temporally sharpens at faster swimming speeds. Inhibition, however, follows different rules. Unlike excitation, inhibition increases relatively uniformly to all motoneurons, but its temporal profile shifts in a speed- and Rin-dependent manner. While in-phase inhibition increases relative to anti-phase inhibition in all motoneurons at faster swimming speeds, this phenomenon is most pronounced in high-Rin motoneurons where in-phase inhibition dominates anti-phase inhibition.

How do these variations in the patterns of excitation and inhibition play a role in rhythmically activating motoneurons at different speeds? In larger, low-Rin motoneurons, excitatory synaptic drive is well below threshold at slow speeds when smaller, high-Rin motoneurons are activated. This observation is consistent with the cell-autonomous aspect of the “size principle,” arising from studies of hindlimb motoneuron recruitment during reflexive movements (Henneman, 1985). In addition, smaller, higher Rin motoneurons exhibit nonlinear bursting responses, which would act synergistically with excitatory drive and systematically increase their firing reliability (Menelaou and McLean, 2012). However, at faster speeds of swimming, increases in rhythmic excitatory input biased to less excitable cells drives lower Rin motoneurons to threshold. This observation is more compatible with ideas originating from network-based models explaining hindlimb motoneuron recruitment, where synaptic input is differentially distributed (Burke, 1979). Thus, our results support a hybrid model of motoneuron recruitment during locomotion: intrinsic properties of motoneurons are most important in determining population recruitment at slow speeds, but at faster speeds, the amplitude of synaptic excitation is selectively larger in motoneurons that support more powerful movements.

Are these observations consistent with switches in excitatory premotor circuitry? Paired patch-clamp recordings, neuronal ablations, and optogenetic activation experiments have demonstrated a major role for two classes of excitatory spinal interneurons in directly driving motoneuron activity during locomotion in zebrafish larvae, called V0-eD cells (McLean et al., 2007, 2008) and V2a cells (Kimura et al., 2006; Bhatt et al., 2007; Eklöf-Ljunggren et al., 2012; Bagnall and McLean, 2014; Ljunggren et al., 2014). At slow speeds, all motoneurons receive broader rhythmic excitatory drive, but it is systematically phase delayed in lower Rin motoneurons (Fig. 5B). These differences in timing are incompatible with identical shared premotor input to all motoneurons. One possibility is that the V0-eD cells and/or V2a cells engaged at slow speeds have shorter latency input to higher Rin motoneurons, which generates the phase-advanced oscillations compared with lower Rin motoneurons. A similar phenomenon has been observed at slow speeds in adult zebrafish, which argues for the persistence of this manifestation of synaptic heterogeneity (Ausborn et al., 2012). At faster speeds, however, peak excitation sharpens and is more synchronous throughout the pool. It is unlikely that this pattern is a function of the incremental addition of premotor drive biased to less excitable motoneurons, given that in zebrafish larvae the premotor V0-eD and V2a neurons active at slow speeds are turned off at speeds exceeding 40 Hz (McLean et al., 2008). Thus, the synaptic drive to higher Rin motoneurons between 40 and 50 Hz must arise from interneurons that are active at these speeds. This is most easily explained by a shift to a single population with short-latency inputs to the entire motor pool. Thus, one argument for switches in premotor drive is to provide a more homogeneous source of drive at faster speeds, where firing patterns within the axial motor pool can be more strictly regulated.

At least for the V2a population, our recent anatomical study provides some potential clues to the patterns of connectivity underlying this observation (Menelaou et al., 2014). V2a cells engaged at fast speeds have more extensive local axon collaterals that ramify throughout the dorsoventral extent of spinal cord, compared with V2a cells active at slow speeds whose axons remain ventral. Thus, when fast V2a neurons are engaged, cells throughout the axial motor pool could receive more synchronous drive. When combined with our demonstrations of speed-related differences in the weight and timing of phasic excitation, the implication is that increases in speed are accompanied by shifts from a more heterogeneous circuit with uniform drive to the motor pool, to a more homogeneous circuit with drive preferentially weighted to lower Rin motoneurons. In this sense, the inhibition of premotor interneurons during faster speeds would help remove conflicting sources of excitatory drive that might interfere with appropriately patterned activity at faster speeds.

Our explanations of differences in drive argue for differences in direct synaptic input; however, an alternative explanation, not mutually exclusive, is that electrical coupling within the axial motor pools helps distribute oscillator drive during locomotion (Perrins and Roberts, 1995; Bagnall and McLean, 2014). This could also explain the significantly higher level of tonic excitatory drive to lower Rin motoneurons at slow swim speeds (Fig. 2G). In this scenario, V2a-motoneuron connections would strictly adhere to their recruitment order (i.e., slow to slow, fast to fast). Indeed, recent work has demonstrated that such patterns of connectivity exist in older zebrafish (Ampatzis et al., 2014). Future work examining the extent of electrical coupling between axial motoneurons and the patterns of connectivity between V2a neurons and motoneurons in larvae should help distinguish between these two possibilities.

While prior work has defined switches in sets of premotor excitatory networks across speeds (McLean et al., 2008), to date there is no evidence that inhibitory networks also undergo such switching. Because inhibition increases uniformly throughout the motor pool at faster speeds (Fig. 3I,M), our data do not rule out the possibility that more inhibitory interneurons are added incrementally to the active pool (McLean et al., 2007). Instead, the best evidence that inhibitory wiring is not simply incremental is the shifts in timing, with in-phase inhibition dominating at fast speeds preferentially in higher Rin motoneurons. While we cannot disambiguate the sources of in-phase or anti-phase inhibition based on our data, it is generally accepted that in axial networks ipsilateral inhibitory neurons provide in-phase inhibition and commissural inhibitory neurons provide anti-phase inhibition (Grillner, 2006; Roberts et al., 2008). Our finding that in-phase inhibition increases with speed has also been seen in Xenopus tadpoles, where inhibitory synaptic potentials are more evident at faster speeds in spinal motoneurons and a number of premotor interneurons (Li et al., 2004). Critically, the sharper peaks we observe for in-phase inhibition in higher Rin motoneurons (Fig. 4A–C) argue for a switch to a population that can provide more synchronous drive to these cells.

At least two plausible wiring diagrams could explain the preferential increase of in-phase inhibition relative to anti-phase inhibition in higher Rin motoneurons at faster speeds. Recurrent inhibition of high-Rin motoneurons by low-Rin motoneurons via Renshaw cells occurs in limb circuits (Ryall et al., 1972; Friedman et al., 1981). A similar mechanism might mediate recurrent inhibition in axial circuits where inhibition of high-Rin motoneurons is driven by low-Rin motoneurons. In support, intraspinal axon collaterals from zebrafish axial motoneurons (Menelaou and McLean, 2012) could provide direct excitation to Renshaw-like cells in axial networks (Higashijima et al., 2004; Li et al., 2004). Alternatively, V2a neurons recruited to drive locomotion at faster speeds could recruit inhibitory interneurons in a feedforward manner, placing the locus of control in premotor excitatory circuits rather than in motoneurons. Experiments testing the connectivity of motoneurons and V2a neurons to Renshaw-like cells in fish should help distinguish between these possible scenarios.

It is likely that the frequency-dependent increase in in-phase inhibition to higher Rin cells in the absence of increases in excitation explains why smaller motoneurons are sometimes silenced at faster speeds (Menelaou and McLean, 2012). This observation is consistent with computational simulations of mammalian limb motoneurons predicting that differences in the relative weight and distribution of inhibition could result in motoneurons being activated out of sequence (Heckman and Binder, 1993). In endogenously rhythmogenic higher Rin neurons that continue to fire at faster speeds (Menelaou and McLean, 2012), on-cycle inhibition could curtail or even reset intrinsic bursting, as recently demonstrated in Xenopus tadpoles (Li and Moult, 2012; Moult et al., 2013). Collectively, the sharpening of excitation coupled with differences in the relative timing of inhibition help explains the stricter temporal control of spiking at faster speeds, which acts to synchronize rhythmic activity within the axial motor pool. In this sense, our data are also consistent with the proposal that both balanced and alternating modes of synaptic drive are at work within rhythmic spinal networks (Berg et al., 2007; Stein, 2010), and we extend this idea to suggest that these modes are specifically used in a speed and cell type-dependent manner.

Prior work in juvenile/adult zebrafish suggests that Rin plays no role in motoneuron recruitment (Gabriel et al., 2011). However, these experiments measured synaptic currents at swim frequencies ranging from 1 to 8 Hz, whereas adult zebrafish are capable of swimming up to 60 Hz (Liu and Westerfield, 1988; Kyriakatos et al., 2011; Ampatzis et al., 2013). Over this more narrow speed range, the lower Rin motoneurons are not consistently driven to threshold, and the amount of synaptic drive measured does not reflect how much input these cells might receive at faster speeds. While the cellular and synaptic properties of rhythmogenic spinal networks will undoubtedly be modified as animals mature, future work examining excitatory and inhibitory currents over a broader functional range in juvenile/adult zebrafish should determine whether the synergistic cellular and synaptic mechanisms of motoneuron recruitment in larval fish described here apply to older fish as well. Notably, current-clamp analyses of motoneuron recruitment over the entire speed range in juvenile/adults (Ampatzis et al., 2013) are consistent with the results seen in larvae (Menelaou and McLean, 2012), suggesting that shared principles governing recruitment of axial motoneurons during swimming in zebrafish may be at work.