Latent variable modeling

A latent variable model, as the name suggests, is a statistical model that contains latent, that is, unobserved, variables. Their roots go back to Spearman's 1904 seminal work[1] on factor analysis, which is arguably the first well-articulated latent variable model to be widely used in psychology, mental health research, and allied disciplines. Because of the association of factor analysis with early studies of human intelligence, the fact that key variables in a statistical model are, on occasion, unobserved has been a point of lingering contention and controversy. The reader is assured, however, that a latent variable, defined in the broadest manner, is no more mysterious than an error term in a normal theory linear regression model or a random effect in a mixed model.

Modern latent variable modeling comprises a large collection of useful models and strategies for mental health research. Indeed, one may argue that the notion of the latent variable is perhaps the single most important concept exported from the psychological sciences to the statistical sciences. As computing technology and software tools continue to improve, researchers will be able to specify and test more complex latent variable models that better reflect the complex realities of data collected in psychiatry and mental health research.

In the parlance of latent variable modeling, observed (or manifest) variables are those variables in the model for which direct, observable scores are available. For example, in a latent variable model for measuring level of depression (the latent variable of interest), the full range of clinician ratings or self-reported symptoms of mood disturbance, anhedonia, sleep disturbance, weight problems, psychomotor problems, worthlessness or guilt, and so forth, may serve as the observed variables. These observed variables can be discrete or continuous.

Just as observed variables, latent variables can be continuous or discrete. This, together with the types of observed variables, helps define broad classifications of latent variable models. The classification in Table 1 is largely based on descriptions in Bartholomew and Knott.[2] Traditionally, the different classes of latent variable models have been regarded as disparate entities and each flourished in a different disciplinary home. For example, research on educational testing has historically relied heavily on item response theory, whereas modeling in psychology has witnessed the popularity of factor analysis and structural equation modeling. A contemporary perspective maintains that irrespective of the types of observed or latent variables, a latent variable model can be properly constructed and estimated as long as the modeler fully specifies the relationship between the observed and the latent variables (the measurement model) and the relationship among the latent variables (the structural model). For example, suppose a researcher has obtained a set of categorical (discrete) ratings on symptoms of major depressive disorder (MDD) and post-traumatic stress disorder (PTSD) for a sample of patients. A potential latent variable model for this data set could contain two latent variables, one for MDD and another for PTSD. Each latent variable is defined (measured) by the corresponding set of discrete ratings, but the latent variables themselves are continuous, reflecting the potentially dimensional nature of the disorders. Albeit simple, the structural model could be specified such that the two latent variables are correlated, with a correlation coefficient to be estimated from data, indicating the degree to which there is shared variance.

Table 1. Classes of Latent Variable Models.

Observed Variable	Latent Variable
	Continuous	Discrete
Continuous	Factor Analysis/Structural Equation Modeling	Latent Profile Analysis/Mixture Modeling
Discrete	Item Response Theory/Latent Trait Analysis	Latent Class Analysis

It is instructive to consider some concrete examples of latent variable models. Take the linear factor analysis model with a single latent variable as a case-in-point. Jöreskog[3] referred to this model as the congeneric test model when the observed variables are educational or psychological test scores. The relation between observed and latent variables is fully specified according to a simple linear regression model:

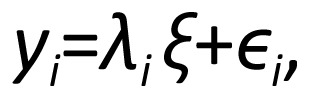(1)

where the outcome variable y_i is an observed variable and there may be i = 1, …, m of them in any factor analysis. The predictor ξ is a latent variable (a common factor), and ϵ_i may be regarded as a disturbance term (a unique factor). The regression coefficient λ_i is called the factor loading of variable y_i on common factor ξ, representing the strength of association between the observed variable and the latent common factor. There is one unique factor per observed variable, and typically they are assumed to be normally distributed with zero means, uncorrelated with ξ, and with unique variance σ_i². Thus, the conditional distribution of y_i given ξ is normal with mean λ_i ξ and variance σ_i², just as in a linear regression model. This conditional distribution is a measurement model in the sense that it provides the necessary linkage between the observed variables and the latent variables. It directly incorporates the component of measurement error into the observed variable. As such, the latent variables in a properly specified measurement model can be thought of as having been purged of measurement error.

In factor analysis, because the common factor is unobserved, a (prior) distribution is imposed on ξ, which is typically taken to be standard normal. This simple distribution of ξ is a structural model for the latent variable. When there are more than one ξ in the model, the structural model can describe the relationship among the latent variables. This will subsequently be important for structural equation modeling. In general, the prior distribution of latent variables typically stems not from statistical considerations, but from the substantive needs of the research questions that the latent variable modeling is attempting to address, on a case-by-case basis. Is the question a taxometric one? Or might there be a continuum of underlying dimensions? Or both? Should the structural model only include latent variables? Or perhaps observed exogenous covariates are required to explain the heterogeneity? Or both? Often the right answer is the more complex one since phenomena studied in mental health research are usually quite complex.

Suppose the number of observed variables m is equal to 4. There exists another equivalent way of representing the factor analysis model, using a path diagram. Figure 1 is largely based on Jöreskog's[3] example for sets of congeneric tests. The directional arrows represent regression paths. The rectangular nodes are observed variables and circles are latent variables. The bidirectional curved arrows represent variances (when the arrow heads point to the same variable) or covariances (when the arrow heads point to two different variables). The path diagram makes it clear that the factor loadings and the unique variances are the key parameters to estimate. Once their values are known, one can use the model to provide optimal predictions of the latent variable scores based on observed variable values.

Figure 1. A Path Diagram Example.

Furthermore, the path diagram representation opens the door to more complex latent variable structural modeling along the lines of path analysis.[4] Indeed, with Jöreskog's[5] factor analytic simultaneous equations model and the advent of the LISREL software program, one may specify simultaneous regression equations for the latent variables, and use maximum likelihood or other methods to fit the model directly to a sample of data. For example, one may consider simultaneous regression equations of the type

(2)

where η is a vector of endogenous latent variables, ξ is a vector of exogenous latent variables, B and Γ contain the regression coefficients, and ζ is a vector of equation disturbance terms. The simultaneous regression equations permit the direct estimation and testing of substantively important conceptual models containing mediation effects, that is, variable X causing Z, which in turn causes Y. Bollen[6] contains an authoritative treatment of the main topics in structural equation modeling.

Equation (1) connects the observed and latent variables using a linear model. This is possible because the outcome (observed) variable is assumed to be continuous. The application of concepts developed in generalized linear models[7] to latent variable modeling (e.g., link functions) has led to a unified treatment of latent variable models for categorical observed variables.[8] The so-called two-parameter logistic item response theory model[9] is arguably the most widely recognized member of the family of models for discrete observed data. Mathematically, this model relates the probability of endorsing a dichotomously scored variable to the underlying latent variable using a logistic function:

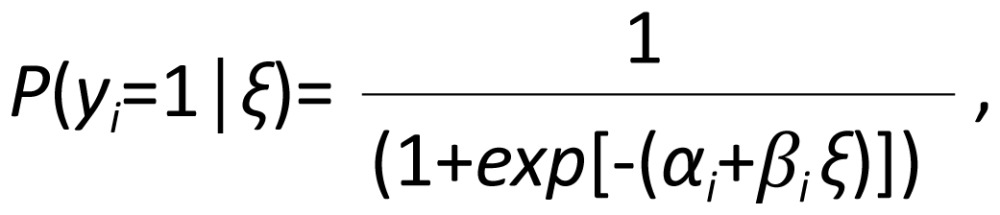(3)

where ξ is still the latent variable, y_i the observed variable, and α_i and β_i are the intercept and slope parameters of this logistic model. Using the language of generalized linear models, equation (3) differs from equation (2) in that a logit link function is used instead of an identity link function. With the availability of modern item response modeling frameworks and software,[10] item response theory has become a standard tool in psychological assessment and health-related outcomes research.[11]

More recently, general frameworks implemented in software packages such as Mplus[12] allow the structural modeling of mixtures of discrete and continuous latent variables, for example, regressing a latent classification variable on a set of continuous latent variable predictors, further extending the flexibility of structural equation modeling. Nonlinear relationships among latent variables (e.g., moderation or interaction effects) can also be assessed with the advent of Bayesian computational methods.[13],[14] Finally, structural equation modeling provides a comprehensive set of tools for the analysis of longitudinal or repeated measures data, through the latent curve modeling framework.[15] Here the connection between latent variable models and multilevel (random coefficient) models becomes transparent. For large subclasses of latent curve models, one can find equivalent multilevel formulations.[16] In sum, after more than a century of development, latent variable modeling encompasses a broad range of statistical techniques that may be useful for modeling mental health data.

Biography

Li Cai is an associate professor of education and psychology at the University of California at Los Angeles (UCLA), where he also serves as Co-Director of the National Center for Research on Evaluation, Standards, and Student Testing (CRESST). His methodological research agenda involves the development, integration, and evaluation of innovative latent variable models that have wide-ranging applications in educational, psychological, and health-related domains of study. A key component on this agenda is statistical computing, particularly as related to multidimensional item response theory (IRT) and multilevel modeling. He has also collaborated with researchers at UCLA and elsewhere on projects examining measurement issues in mental health, substance abuse treatment, and patientreported outcomes research.