TASK-SPECIFIC STABILITY IN MUSCLE ACTIVATION SPACE DURING UNINTENTIONAL MOVEMENTS

Abstract

We used robot-generated perturbations applied during position-holding tasks to explore stability of induced unintentional movements in a multi-dimensional space of muscle activations. Healthy subjects held the handle of a robot against a constant bias force and were instructed not to interfere with hand movements produced by changes in the external force. Transient force changes were applied leading to handle displacement away from the initial position and then back towards the initial position. Inter-trial variance in the space of muscle modes (eigenvectors in the muscle activations space) was quantified within two sub-spaces, corresponding to unchanged handle coordinate and to changes in the handle coordinate. Most variance was confined to the former sub-space in each of the three phases of movement, the initial steady state, the intermediate position, and the final steady state. The same result was found when the changes in muscle activation were analyzed between the initial and final steady states. Changes in the dwell time between the perturbation force application and removal led to different final hand locations undershooting the initial position. The magnitude of the undershot scaled with the dwell time, while the structure of variance in the muscle activation space did not depend on the dwell time. We conclude that stability of the hand coordinate is ensured during both intentional and unintentional actions via similar mechanisms. Relative equifinality in the external space after transient perturbations may be associated with varying states in the redundant space of muscle activations. The results fit a hierarchical scheme for the control of voluntary movements with referent configurations and redundant mapping between the levels of the hierarchy.

Introduction

Stability of motor action is crucial for successful performance, particularly given the unpredictable changes in both external and muscle forces. Over the past years, the idea of organizing task-specific stability in redundant spaces of elemental variables has been developed (Schöner 1995; Scholz and Schöner 1999). This approach is readily compatible with the principle of abundance (Gelfand and Latash 1998; Latash 2012), which suggests that the famous problem of motor redundancy (Bernstein 1967) has been inadequately formulated: The central nervous system (CNS) is not trying to find unique solutions for this problem but uses all elemental variables within redundant systems to ensure stability of salient performance variables. For example, during a task of occupying a hand position in space, joint angles of the arm (elemental variables) can vary across trials while keeping the hand position (salient performance variable) relatively invariant. This strategy results in variable time patterns of elemental variables when a person performs the same action again and again.

Among the numerous methods of exploring stability during natural human motor actions performed by redundant systems, two methods have been used lately in studies that specifically focused on the issues of redundancy and abundance. One of them is based on analysis of variance within the space of elemental variables (for example, individual joint rotations) across repetitive trials at a task (for example, reaching). Natural variation in the initial conditions is expected to lead to larger variance in directions of lower stability. Within the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999), inter-trial variance is estimated in two sub-spaces. One of the sub-spaces (UCM) corresponds to no changes in a selected performance variable (for example, coordinate of the end-effector), to which all elemental variables contribute. The other sub-space is orthogonal to the UCM; variance in that sub-space leads to variance in the selected performance variable. If the former (V_UCM) is larger than the latter (V_ORT), both quantified per degree-of-freedom in the corresponding sub-spaces, a conclusion is drawn that a synergy in the space of elemental variables stabilizes the performance variable (reviewed in Latash et al. 2007).

The second method uses smooth perturbations to the system of interest while subjects are instructed not to react to such perturbations (“do not interfere voluntarily”, cf. Feldman 1966; Latash 1994). Recently, two studies used transient perturbations during steady-state tasks. In one of the studies (Wilhelm et al. 2013), the subjects produced constant total force with four fingers, and then one of the sensors moved up and down leading to changes in all four finger forces. After the perturbation was over, the subjects showed total force values similar to those in trials without sensor motion. This phenomenon is related to equifinality, a property of a motor system to attain the same final state despite possible transient changes in external conditions (cf. Bizzi et al. 1976; Kelso and Holt 1980; Schmidt and McGown 1980; Latash and Gottlieb 1990). Individual finger forces, however, differed between the initial and final states. Inter-trial variance of finger force changes was mostly compatible with unchanged total force (V_UCM> V_ORT). In the second study (Zhou et al. 2014a), the subjects grasped a handle and occupied an initial position against a bias force produced by a robot. Then, the robot produced transient changes in the force leading to handle motion. After the force changes were over, analysis of variance in the joint configuration space showed that most variance between the initial and final states was compatible with both unchanged handle position and orientation. Both results confirm the main postulate that a voluntary action is associated with different task-specific stability in directions spanning the UCM and orthogonal to the UCM sub-spaces within the redundant spaces of elemental variables.

Within this study, we accept the framework of the referent configuration (RC) hypothesis (Feldman 2009), which is a development of the classical equilibrium-point hypothesis (Feldman 1966, 1986) for natural multi-muscle actions. According to the RC hypothesis, at the highest hierarchical level, neural signals specify referent values for salient, task-specific variables, the RC at that level, given the external force field. Deviations between actual values of those variables and the RC lead to muscle activations that move the variables towards the RC. A sequence of few-to-many transformations lead to signals to alpha-motoneuronal pools, which play the role of RC at that level, interact with the afferent feedback, and result in muscle activations according to the equilibrium-point hypothesis. The RC hypothesis combined with the principle of motor abundance (Latash 2010) predicts, in particular, lower stability (reflected in higher inter-trial variance) in the muscle activation space in directions compatible with the RC defined at the highest level (task level).

In this study we explored this predictions in the space of muscle activations during position-holding by the dominant arm against an external force. The experiment involved transient smooth perturbations applied by the robot to the handle held by the subject (similarly to Zhou et al. 2014a; however, the arm posture and perturbation characteristics were different). The subjects occupied an initial arm posture against a standard bias force produced by the robot. Further, they were always instructed not to interfere with arm motion produced by the robot force changes; as a result, all movements were unintentional. A change in the robot force led to motion to a new equilibrium state where the arm stayed until the robot force returned back to the bias value. We assumed that elemental variables corresponded to parallel changes in activation within a few muscle groups (muscle modes, M-modes, Krishnamoorthy et al. 2003; Danna-dos-Santos et al. 2008). Two predictions were tested. Hypothesis-1 was that inter-trial variance in the M-mode space at any steady state would show structure stabilizing handle position in a sense V_UCM> V_ORT. This prediction follows some of the earlier studies of multi-muscle arm synergies (Krishnamoorthy et al. 2007; Mattos et al. 2013) with an important difference: All earlier studies explored postures after intentional movements, while in the current study movements to new postures were produced by changes in the external force. Hypothesis-2 was that the transient perturbation would produce larger deviations in the M-mode space along directions corresponding to no changes in the handle coordinate (within the corresponding UCM). This prediction follows the mentioned studies by Wilhelm et al. (2013) and Zhou et al. (2014a), which were performed, however, in different spaces of elemental variables, kinetic and kinematic, and also the general idea that redundant systems are less stable in directions spanning the UCM. We tested this prediction using the differences in muscle activations observed prior to and after the perturbation when the robot force was the same.

This study represents the next natural step following an earlier study of joint configuration variance during unintentional movements produced by external force changes (Zhou et al. 2014a). In both studies, the method of analysis of inter-trial variance based on the UCM hypothesis was used to explore potential performance variables that could be stabilized during actions induced by changes in the external bias force, despite the fact that subjects were not asked to “control” any of the analyzed performance variables. There are a few important differences between the two studies. Note that the space of muscle activation signals is higher-dimensional as compared to the space of joint rotations. An additional step in the UCM-based analysis involved identification of potential velemental variables (M-modes) in this study. Besides, changes in potential performance variables cannot be easily mapped on changes in M-modes because of the lack of a geometric model. So, the Jacobian of this mapping had to be discovered experimentally as in earlier studies (Krishnamoorthy et al. 2007; Mattos et al. 2013).

Methods

Subjects

Seven subjects (6 males) with the mean weight 72 ± 11.9 kg (mean ± standard deviation), mean height 1.75 ± 0.08 m, and mean age 27.4 ±4.8 years participated in this experiment. All the subjects were self-declared right-handers and were free of any known neurological or motor disorder. While this study follows an earlier experiment with analysis of joint configuration variance (Zhou et al. 2014a), we would like to emphasize that this is a completely different study with different subjects, procedures, analyses, and goals. All the procedures of the experiment were approved by the Office for Research Protection of the Pennsylvania State University.

Apparatus

Subjects were required to occupy a specific arm posture while holding the handle of a three degrees-of-freedom (DOFs) robotic arm (HapticMaster). HapticMaster (Moog, The Netherlands), which is an admittance-controlled robot, was used to record displacement of the end-effector of the robotic arm and to exert forces on the subject’s right arm. First, the robot produced a constant baseline force (F_BASE). Further, the robot produced transient perturbation force (F_PERT), which represented deviations from F_BASE (see later).

The handle of the manipulandum had three kinematic DOFs—roll, pitch, and yaw. A customized visual studio program (Visual studio2010-Microsoft Corp., WA, USA) was used to control the HapticMaster robot. Kinematic data were sampled at 60 Hz. According to the company specifications, the resolution was defined by the encoder, which has 2000 counts per rotation. This comes down to not more than 8.5•10⁻⁶ rad per count.

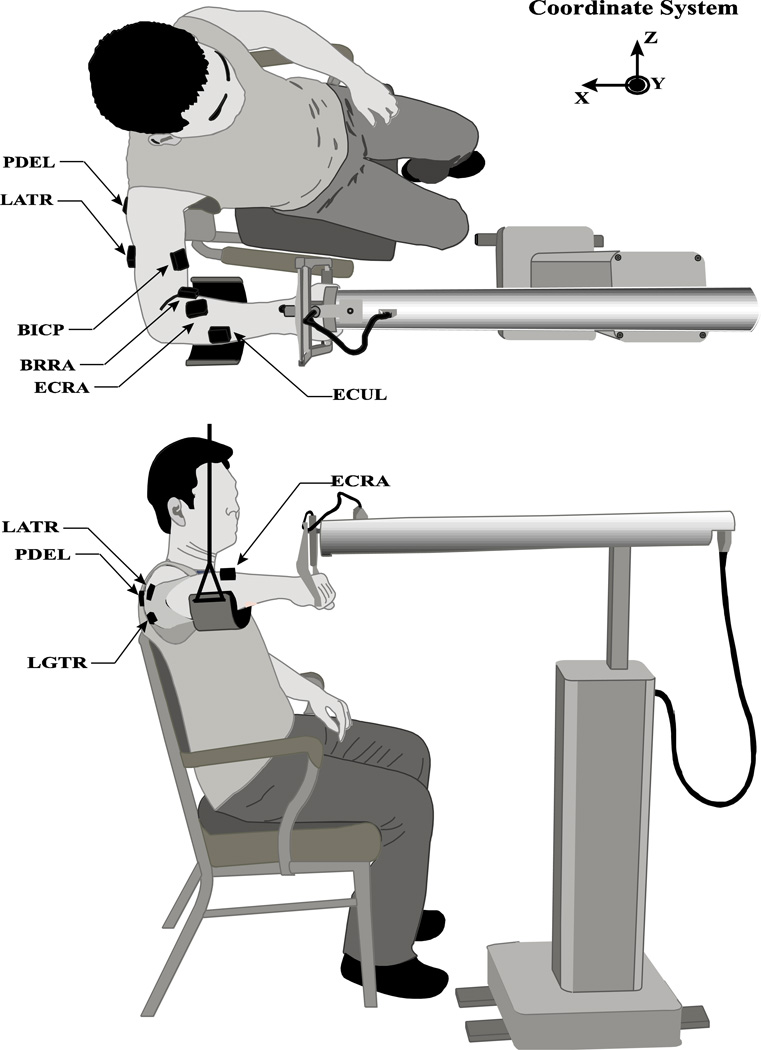
Subjects sat on a chair and held the handle in a comfortable position with the right hand while the right arm was supported against the gravity using a sling hanging from the ceiling 5 m above. The shoulder was abducted 90° such that the arm segments were in a horizontal plane. The shoulder angle was about 10° and the angle at the elbow was about 90° relative to the frontal plane (see Figure 1). The robot coordinate system was used, in which the X-axis was a horizontal axis pointing toward the posterior direction and Y-axis was a horizontal axis pointing toward the right side of the subject. The Z-axis pointed vertically upward .The initial three-dimensional position of the robot’s end-effector (handle) was set as the origin of the coordinate space.

Figure 1.

The experimental setup, top view (top) and side view (bottom). The subject sat on a chair and grasped comfortably the handle of the robotic arm with the right hand. A sling supported the arm against the gravity. The robotic arm was aligned in such a way that the subject’s hand could move over 10 cm freely, mainly in a parasagittal plane along the negative X direction. Wireless active electrodes were used to record EMG signals from 10 muscles. The placement of a few electrodes is shown. LATR – lateral triceps; PDEL – posterior deltoid; LGTR – long head of triceps; ECRA – extensor carpi radialis.

A 20″ computer monitor was placed next to the robotic arm in front of the subjects to provide visual feedback. A 10-mm yellow circle in the middle of the screen indicated the location of the hand. A target location (used in the Voluntary-movement task, see later) was shown by a 10-mm white circle. The visual gain was 0.5: 1 cm of handle displacement corresponded to 0.5 cm cursor motion on the screen.

Surface muscle activity (EMG) signals were recorded using a 16-channel Trigno Wireless System (Delsys Inc., MA, USA) at 1080 Hz with a 16-bit resolution. Active electrodes with built-in amplifiers (rectangular shape, 37mm × 26mm × 15mm dimensions) were attached with adhesive tape to the skin over the bellies of the following muscles on the right side of the body: brachioradialis (BRRA), extensor carpi radialis (ECRA), extensor carpi ulnaris (ECUL), flexor carpi radialis (FCRA), flexor carpi ulnaris (FCUL), biceps (BICP), triceps long head (LGTR), triceps lateral head (LATR), Posterior deltoid (PDEL), and latissimusdorsi (LATD). For each muscle, the electrode placement was selected using the published guidelines (Perotto et al. 2011). The correct placement of the electrode was then confirmed by observing EMG patterns when the subjects performed a set of isometric contraction and related free movements (Kendall et al. 2005). The signals were pre-amplified, band-pass filtered (20–450 Hz), and transmitted to a receiver unit attached to a desktop computer (Dell, Xeon3.6 GHz). A customized LabVIEW-based software (LabVIEW2010–National Instruments, Austin, TX, USA) synchronized with the controller software of HapticMaster was used to collect EMG data.

Procedures

Prior to the experiments, the subjects went through a familiarization session. During this session, the subjects performed each of the involved tasks. They were trained “not to intervene” when changes in the robot force produced arm displacements. During that session, the experimenter adjusted the magnitude of force change produced by the robot, so that the subject’s hand moved away from the initial position by about 10 cm.

At the beginning of each experiment, the subject sat in the chair and occupied the initial configuration, i.e., holding the handle of the robotic arm by the right hand with the specified angles in the elbow and shoulder joints. In this position, the length of the sling was adjusted to ensure comfortable support at 90° abduction of the shoulder joint. The subjects were instructed to keep this position and not to move the trunk. The experiment consisted of three tasks: The Voluntary-movement task, the Position-holding task, and the Perturbation task.

The goal of the Voluntary-movement task was to identify a low-dimensional set of elemental variables (M-modes, Krishnamoorthy et al. 2003) in the high-dimensional space of muscle activations. In this task, subjects were asked to perform continuous movements against five different baseline forces—10, 15, 20, 25, and 30 N. In each movement, subjects performed six cycles moving the handle in the X direction between the initial position and the target placed 10-cm away. The initial and target positions were shown on the screen. The movement was paced by a metronome at 1.3 Hz. A 30-s rest was provided for subjects at the end of each trial. These particular task characteristics were selected based on pilot observations in the familiarization session to cover the whole range of coordinates, robot-generated forces, and velocities that were observed in the Perturbation task.

The purpose of the Position-holding task was to record EMG signals that were later used to normalize the EMG signals from the other two tasks in order to facilitate the between-subjects comparison of data. In this task, subjects performed two trials in which they were supposed to maintain the handle at the initial position for 4 s against +40N and −40N F_BASE. Participants were given a 30-s rest between these two trials. The EMG signals recorded in the middle of this time interval were then rectified and filtered with a customized MATLAB program (MATLAB 7.11, Mathworks Inc., USA).

The Perturbation task included 66 trials. Each trial had three phases (Preparation, Perturbation, and Recovery), which are shown in Figure 2. During Preparation, the subjects were supposed to maintain the initial position of the handle against F_BASE for 2–4 s (Preparation in Figure 2). Based on pilot trials, we used F_BASE=10 N for the male and F_BASE=7 N for the female participants.

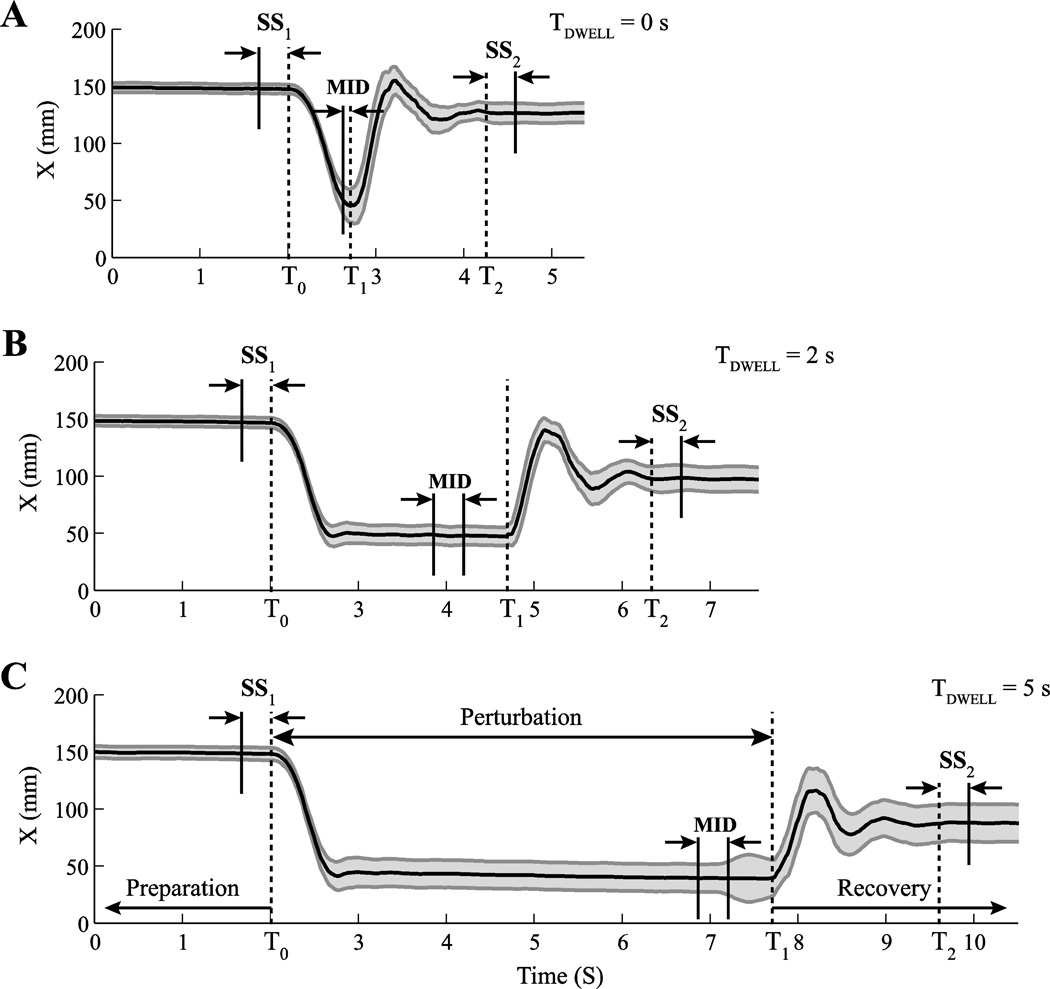
Figure 2.

Hand trajectories along the X-axis for a typical subject (Subject #3). The solid lines are the mean hand displacement along the X-axis across trials for the dwell times T_DWELL = 0 s (A), T_DWELL = 2 s (B), and T_DWELL = 5 s (C). The shaded areas show one standard error. Trials are aligned based on F_PERT onset (T₀). Preparation (before T₀) was the time period in which the subject held the handle in the initial position. During Perturbation (T₀ to T1), a change in the applied force took place (F_PERT≠ 0). Recovery (after T₁) represents the time interval following the removal of F_PERT. The dashed line at T₂ shows the end of the hand movement. SS₁, MID, and SS₂ are the time intervals selected for statistical analysis.

The second phase (Perturbation in Figure 2) started at an unpredictable time. A change in F_BASE (F_PERT) was applied along the same direction. The amplitude of F_PERT was selected based on a few practice trials before the beginning of this task. During those trials, subjects were instructed not to interfere voluntarily in any manner with arm motion produced by F_PERT. As illustrated in Figure 2, F_PERT led to an unintentional arm motion to a new equilibrium state, where the arm remained nearly motionless until F_PERT was removed. Note that the subjects were not instructed to control arm trajectory or position in any sense after they had occupied the initial position in the Preparation phase. The magnitude of F_PERT was selected to move the subject’s hand over about 10 cm away from the initial position. The handle velocity was calculated during the movement by the customized visual studio program, and its peak value (V_PEAK) was updated online. F_PERT changed from zero to its maximum magnitude during a time period of 400 ms and was kept at that magnitude until the handle velocity dropped below 10% of V_PEAK during that trial. At this point, the robot either removed F_PERT immediately (dwell time, T_DWELL = 0), maintained F_PERT for 2 s (T_DWELL = 2), or for 5 s (T_DWELL = 5) before removing F_PERT and returning to F_BASE. This led to arm motion towards the initial position but with variable undershoots that scaled with T_DWELL. The time when the robot removed F_PERT is shown in Fig. 2 as T₁.

The third phase (Recovery in Figure 2) started right after the Perturbation phase. During that phase, the subject’s hand went back toward the initial position. The subjects were instructed to keep holding the handle at the final position for about 3 s before releasing the handle. The instruction to the subjects was: “Allow the robot to move your arm. Do not interfere voluntarily with those movements.”

The onset (T₀, Figure 2) and the end (T₂, Figure 2) of the movement were defined as the times when the speed of the handle went above and below 5% of V_PEAK in that particular trial, respectively. Each subject performed 66 trials, 22 trials in a row per each of the three T_DWELL values presented in a random order. There were 5-s rest intervals after each trial and a longer, 60-s rest interval after each 22 trials. There was also a 1-min rest interval between the Voluntary-movement and Position-holding tasks, and a 3-min rest interval between the Position-holding and Perturbation tasks. Participants were allowed to request a break whenever they wanted, though none of them reported fatigue (assessed only based on subjects’ verbal reports). We did not expect considerable learning effects because the explicit task was very simple: Occupy the initial arm position and then “do nothing”.

Data Processing

The recorded data were analyzed offline using a customized MATLAB 7.11 program. The raw EMGs were first band-passed filtered (60–350 Hz, fourth-order, zero-lag Butterworth filter), full-wave rectified, and low-pass filtered by applying a 100-ms duration moving average filter. The main reason for the relatively heavy filtering was the episodes of vibration that could occur at the interface between the subject’s hand and the robot. These episodes occurred in some, but not all, subjects, possibly due to specific co-contraction patterns and limb mechanics. To avoid effects of these vibrations on the EMG signals, we increased the low frequency of the band-pass. This frequency range is also the same as in some earlier studies that explored EMGs of arm muscles (e.g., Mattos et al. 2013). In two subjects, no vibrations were seen. We re-analyzed the data for those two subjects with the more traditional 20–450 Hz filtering and with the 60–350 Hz filtering; the main outcome variables (see below) were nearly identical. For consistency, we decided to use the same filtering parameters across all subjects.

EMG signals recorded during two Position-holding trials were averaged within 1-s intervals in the middle of each trial; then for each muscle, the maximal value across the two trials was used to normalize the muscle activity during Voluntary-movement and Perturbation tasks. Note that arm movements were relatively low-amplitude and not very fast. In particular, in the main experimental series, the initial task was a steady state. Then, the robot imposed a relatively low-amplitude motion leading to low-amplitude, slow changes in muscle activations (as illustrated in Figure 3). Analysis was performed mainly using steady states (see later). Hence we view using a positional task for EMG normalization as acceptable. The filtered and normalized EMGs were integrated over 18 samples (IEMG_NORM) to match the sampling rate of the kinematic data. The kinematic data (position and velocity of the handle gripped by the subjects) were low-pass filtered at 20 Hz with a fourth-order, zero-lag Butterworth filter.

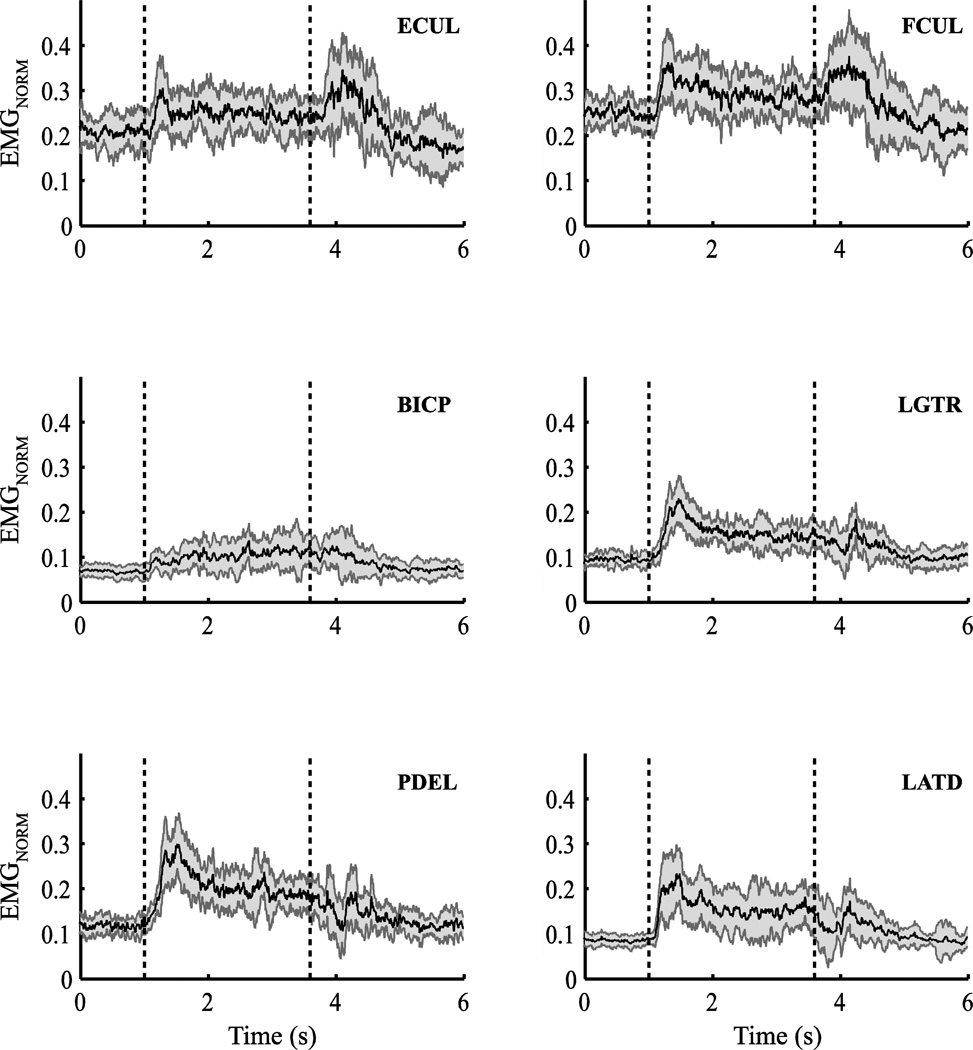
Figure 3.

EMG traces for a subset of muscles, extensor carpi ulnaris (ECUL), flexor carpi ulnaris (FCUL), biceps (BICP), triceps long head (LGTR), posterior deltoid (PDEL), and latissimus dorsi (LATD) for a representative subject (Subject #2) with T_DWELL = 2 s. Averages across repetitive trials are presented; the shaded areas represent standard errors computed across trials. Muscle activations for each subject were normalized according to the averaged activity of the respective muscle during Position-holding trials (see Methods for details). The vertical dashed lines mark the start and the end of the perturbation force application.

Defining Muscle modes

EMGs from the Voluntary-movement trials were used to analyze the correlation structure of the integrated, normalized EMG data (IEMG_NORM). To avoid edge effects, the first and last cycles were omitted from each of those trials, and only the data during the remaining four cycles were analyzed. The IEMG_NORM data from the trials against different baseline forces (F_BASE) were concatenated to form a 10-column matrix in which each column represented one of the muscles under study. The number of rows reflected the number of samples analyzed across all cycles and trials (1491 ± 113). Although the movement was paced by the metronome (at 1.3 Hz), the number of samples per cycle differed across cycles within a subject and across subjects. On average, there were about 74 samples per cycle. Since the first and last cycles were omitted from each trial, four cycles per condition were analyzed (20 cycles across all of the baseline forces).

This matrix was subjected to Principal Component Analysis (PCA) based on the correlation matrix. In this study PCA was used instead of non-negative matrix factorization (NMF; cf. Ting and McKay 2007) because PCs are orthogonal to each other. Further analysis of variance in the Perturbation trials requires an orthogonal coordinate system (see later).

Based on the Kaiser criterion (Kaiser 1960), three PCs were accepted, later confirmed by the scree plot examination. We also imposed an additional criterion that at least one muscle had to be significantly loaded in all the accepted PCs. Later, Varimax rotation procedure was applied with factor extraction. This procedure resulted in the identification of three elemental variables (M-modes) for each subject.

Defining the Jacobian matrix (J matrix)

The Jacobian matrix was computed using multiple linear regression analysis to determine the relations between small changes in M-modes between consecutive samples (ΔM-modes) and associated changes in the X-coordinate of the handle (ΔX) for each subject separately:

$$\Delta \mathrm{X}=k_1\mathrm{\Delta }{\text{M-mode}}_1+k_2\mathrm{\Delta }{\text{M-mode}}_{2+}{k}_3\mathrm{\Delta }{\text{M-mode}}_3$$ (1)

Before applying the multiple regression analysis, ΔM-modes and ΔX were low-pass filtered at 5 Hz with a second-order, zero-phase lag Butterworth filter. The low-pass filtering was performed to avoid effects of high-frequency signal changes unrelated to the Voluntary-movement task. The analysis was run over ΔM-mode and ΔX values computed for each subject over all the cycles. The coefficients of the regression yielded the Jacobian matrix: J = [k₁ k₂ k₃].

Analysis of variance within the uncontrolled manifold hypothesis

The uncontrolled manifold (UCM) hypothesis assumes that a neural controller acts within a set of elemental variables (in this study, M-modes) and facilitates their co-variation to ensure stability of a particular performance variable (in this study, X-position of the handle). In particular, this is expected to lead to a task-specific structure of variance across trials, which is quantified as the sum of two components. One of the components does not have an effect on the performance variable (variance within the UCM, V_UCM), while the other does (variance orthogonal to the UCM, V_ORT). After both V_UCM and V_ORT are quantified per dimension in the corresponding spaces, V_UCM> V_ORT signifies presence of a synergy stabilizing the performance variable (Scholz and Schoner 1999, Latash et al. 2007).

While arm motion in the Perturbation task was produced by robot force changes and, hence, could be considered unintentional, we hypothesized that hand position could be a potential performance variable stabilized by co-varied changes in the M-mode space. Analysis of variance in the M-mode space was performed on the data collected in the Perturbation task. For each subject and each condition, the trials were aligned by T₀. The two steady states prior to and after the application of F_PERT were characterized by 300-ms time intervals, 300 ms prior to T₀ (SS1, Figure 2) and 300 ms after T₂ (SS₂, Figure 2). We also analyzed the data in-between the application and removal of F_PERT (MID, Figure 2). For T_DWELL = 0 s, 100-ms intervals prior to T1 were selected to represent this phase, while for T_DWELL = 2 s and T_DWELL = 5 s, 300-ms time intervals were selected prior to (T₁– 500) ms. The shorter time for the MID interval in the trials with T_DWELL = 0 was selected because the data did not show a long enough steady state.

Analysis of the structure of variance in the M-mode space was performed in each of the three mentioned intervals, SS1, SS₂, and MID. In addition, the difference in the M-mode magnitudes between the SS1 and SS₂ intervals was analyzed (ΔSS).

For each analysis, the mean magnitude of M-mode changes over each time interval across trials (ΔM̅) was computed for each subject. For each trial, ΔM̅ was then subtracted from changes in M-mode magnitudes (ΔM) of respective time interval:

$$\mathrm{\Delta }{M}_{\mathit{\text{demean}}}=\mathrm{\Delta }M-\overline{\mathrm{\Delta }M}$$ (2)

The null-space of the J matrix was used as a linear approximation of the UCM. The null-space of J is a set of solutions to the equation Jx = 0 in which x is a column vector. In this study, the dimension of ΔM (M-mode) space is three (n = 3). The UCM is two-dimensional, and the orthogonal subspace is one-dimensional (d = 1). The vectors of demeaned ΔM were then projected onto the null-space of J (f_UCM), which was spanned by a set of basis vectors, ε_i, and onto the orthogonal subspace (f_ORT)

(3)

$$f_{ORT}=\mathrm{\Delta }{M}_{\mathit{\text{demean}}}-{(f_{UCM})}^T$$

The across-trials variance within the UCM and ORT subspaces as well as the total amount of variance, per dimension in respective spaces, were calculated as:

$$V_{UCM}={\sigma }_{UCM}^2=\frac{1}{(n-d)(N_{\mathit{\text{trials}}})}\sum _{i=1}^N{\left|f_{UCM}\right|}^2$$ (4)

$$V_{ORT}={\sigma }_{ORT}^2=\frac{1}{(d)(N_{\mathit{\text{trials}}})}\sum _{i=1}^N{\left|f_{ORT}\right|}^2$$

$$V_{TOT}={\sigma }_{TOT}^2\frac{1}{(n)(N_{\mathit{\text{trials}}})}\sum _{i=1}^N{(M_{\mathit{\text{demean}}})}^2$$

Where N_trials represents the number of trials for different dwell times.

An index of synergy was computed as the relative amount of V_UCM within V_TOT:

$$\mathrm{\Delta }V=\frac{V_{UCM}-V_{ORT}}{V_{TOT}}$$ (5)

The range of ΔV was between 1.5 (ΔV_upper) when all variance was within the UCM and −3 (ΔVl_ower) when all variance was within the orthogonal subspace. For further analyses, ΔV values were log-transformed using a modified Fisher’s z-transform (Solnik et al. 2013):

$$\mathrm{\Delta }{V}_z=\frac{1}{2}\cdot \mathit{\text{log}}\left[\frac{\left|\mathrm{\Delta }{V}_{\mathit{\text{lower}}}\right|+\mathrm{\Delta }V}{\mathrm{\Delta }{V}_{\mathit{\text{upper}}}-\mathrm{\Delta }V}\right]-\frac{1}{2}\cdot \mathit{\text{log}}\left[\frac{\left|\mathrm{\Delta }{V}_{\mathit{\text{lower}}}\right|}{\mathrm{\Delta }{V}_{\mathit{\text{upper}}}}\right]$$ (6)

Statistics

SPSS 20.0 (IBM Corp. USA) was used to perform all statistical analyses. The data are presented in the text and figures as means and standard errors (SE). Three-way ANOVA with repeated-measures was used to evaluate the effects of Phase (three levels: SS1, SS₂, and MID) and T_DWELL (three levels: 0 s, 2 s, and 5 s) on the two variance components, factor Variance (two levels: V_UCM and V_ORT). Two-way repeated-measures ANOVA was performed on the z-transformed index of synergy (ΔV_Z) with the factors Phase and T_DWELL. Two-way ANOVA with repeated-measures was used to test the effect of T_DWELL on the V_UCM and V_ORT variance components (factor Variance) in the differences between the two steady states (ΔSS data). In addition, two-way ANOVA with repeated-measures and one-way ANOVA with repeated-measures were performed to analyze the effect of Phase (three levels: SS1, SS₂, and ΔSS) on Variance (V_UCM and V_ORT) and on ΔV_Z, respectively.

For all analysis p < 0.05 was considered as statistically significant. All comparisons were performed using Greenhouse-Geisser corrections and significant effects were examined using pairwise comparisons with Bonferroni corrections.

As in similar earlier studies of synergies in the muscle mode space (Krishnamoorthy et al. 2003; Danna-dos-Santos et al. 2007, 2008; Klous et al. 2010), we were looking for large effect sizes, on the order of 1–1.5. While the number of subjects was low, it was expected to be sufficient to reach statistical significance for the expected large effect sizes. Indeed, analyses of the main outcome variables (see Results) showed significant effects of the main factors such as Phase, Variance, and T_DWELL.

Results

Movement Kinematics

The application of F_PERT resulted in a displacement of the handle, primarily along the X-axis over about 10 cm. After F_PERT was removed, the handle moved towards the initial position. It stopped, however, consistently short of the initial handle X coordinate. The magnitude of the difference between the initial and final handle positions (ΔX) was relatively small (about 10% of the total hand displacement) for the shortest dwell time (T_DWELL = 0), and it increased with an increase in T_DWELL. For T_DWELL = 5 s, the magnitude of ΔX approached 50% of the total hand displacement.

The mean across trials (±SE) of the hand displacement along the X-axis for a typical subject (Subject #3) for different dwell times (T_DWELL) is presented in Figure 2. Note the larger ΔX for the longer T_DWELL. The deviations along the Y-axis and Z-axis were much smaller (on the order of a few mm) and were not analyzed.

One-way repeated-measures ANOVA on ΔX showed a significant effect of T_DWELL (F_(2,6) = 41.701; p < 0.01). Pairwise comparisons confirmed larger ΔX for T_DWELL = 5 s (41.04 ± 5.22 mm) as compared to ΔX for T_DWELL = 2 s (31.27 ± 4.38 mm), which were significantly larger than ΔX for T_DWELL = 0 s (15.87 ± 3.46 mm).

Defining M-modes

Figure 3 illustrates time profiles of the normalized EMGs for a few selected muscles acting at the wrist, elbow, and shoulder joints for a typical trial with T_DWELL=2 s performed by a representative subject (Subject #2). The first and second vertical dashed lines in Figure 3 indicate the application and removal of F_PERT, respectively. The EMG patterns of most muscles showed significant modulation during the trial; other muscles, however, showed poorly reproducible, low-amplitude EMG modulation. Right after the perturbation, there was a substantial increase in the activity of the muscles related to the unintentional movement of the hand. EMG patterns were rather consistent within-a-subject (see the error shades in Figure 3), but highly variable across subjects, making presentation of averaged across subjects data meaningless. Note that most analyses were performed on a within-a-subject basis until the comparison of normalized variance indices.

M-modes were identified using principal component analysis with rotation and factor extraction applied to the indices of integrated muscle activities (IEMG_NORM) during Voluntary-movement trials for each subject separately (see Methods). On average the first three PCs (M-modes) accounted for 73.2 ± 1.9% (ranging from 66.2% to 79.7%) of the total variance. The first three M-modes explained 40 ± 2.9%, 21.4 ± 2.1%, and 11.7 ± 0.6% of the total variance, respectively. An example of the M-mode structure (loadings of the muscles on the first three factors) for a typical subject is shown in Table 1; the significant loadings (with the absolute magnitude > 0.4) are shown in bold.

Table 1.

Muscle loadings for the first three M-modes

Muscle	M1-mode	M2-mode	M3-mode
BRRA	−0.0208	0.6487	−0.0195
ECRA	−0.0789	0.6598	0.0283
ECUL	−0.0517	−0.0762	0.8056
FCRA	0.2254	0.3269	0.0088
FCUL	−0.0036	0.1135	0.5805
BICP	0.4080	0.0603	−0.0030
LGTR	0.4566	−0.0127	0.0091
LATR	0.4462	−0.0840	0.0971
PDEL	0.4512	−0.0482	0.0347
LATD	0.4029	0.0713	−0.0454

Results of the PCA after Varimax rotation and factor extraction for a representative subject. The columns show the loading factors for the three M-modes with the significant values shown in bold. BRRA - brachioradialis, ECRA - extensor carpi radialis, ECUL - extensor carpi ulnaris, FCRA - flexor carpi radialis, FCUL - flexor carpi ulnaris, BICP - biceps, LGTR - triceps long head, LATR - triceps lateral head, PDEL - posterior deltoid, LATD – latissimus dorsi.

The pattern in which the significant loadings for agonist and antagonist muscles around a joint were observed within a single PC, and the loadings had the same sign (either positive or negative) was defined as a co-contraction pattern. Co-contractions were common across subjects (ranging from 0 to 3 per a set of 3 M-modes, with the median = 2).

Multiple linear regressions were used to define the coefficients in a linear equation that linked small changes in the three M-modes magnitude (ΔM-modes) and small changes in the hand position along the X-axis (ΔX, performance variable) for each subject. The resulted set of coefficients (the J matrix) yielded, on average, adjusted R-squared values of 0.49 ± 0.05 (ranging from 0.35 to 0.68). All ΔM-modes were significant predictors of ΔX (p < 0.001 for each of the ΔM-modes and for each subject).

Analysis of Variance Components

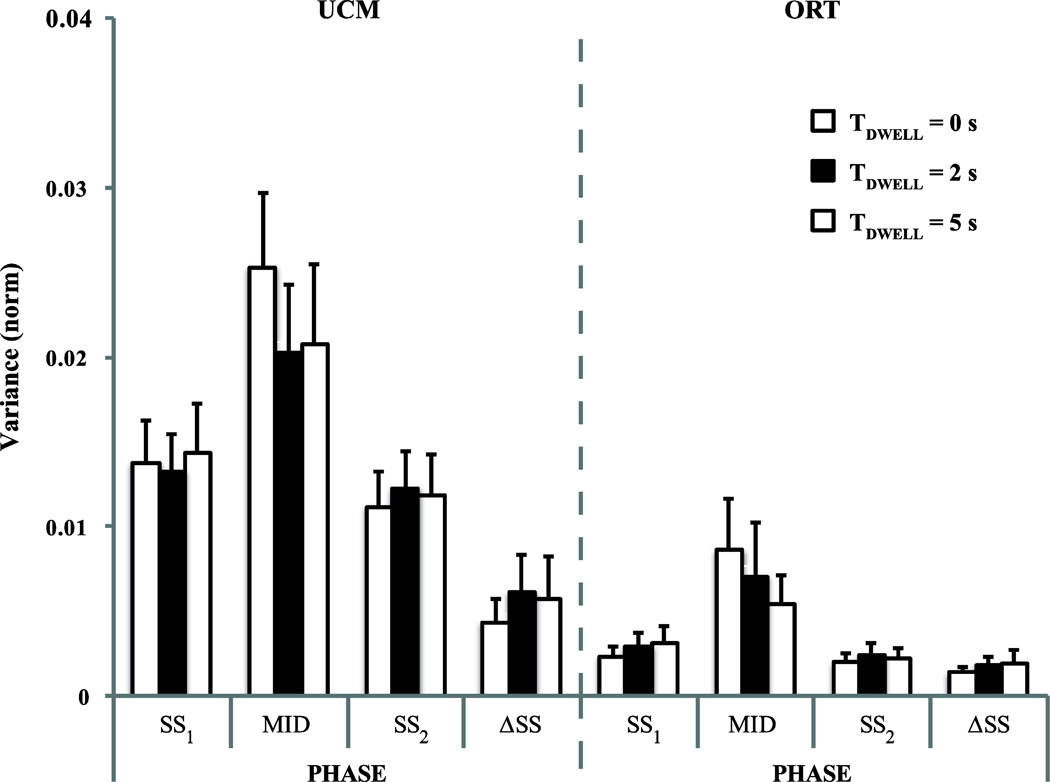
The analysis of two variance components, V_UCM and V_ORT, quantified within the UCM hypothesis framework, was carried out on the data from the Perturbation trials for each subject separately (see Methods for details). Overall, V_UCM was consistently larger than V_ORT across all the comparisons. Both variance indices were much larger in the middle of the trial (MID) across all T_DWELL values. Overall, T_DWELL had only minor effects on the magnitudes of both V_UCM and V_ORT in contrast to its significant effects on the final hand position (as in Figure 2). Figure 4 illustrates the mean ± SE values of V_UCM and V_ORT across subjects for each phase of the movement, normalized per DOF.

Figure 4.

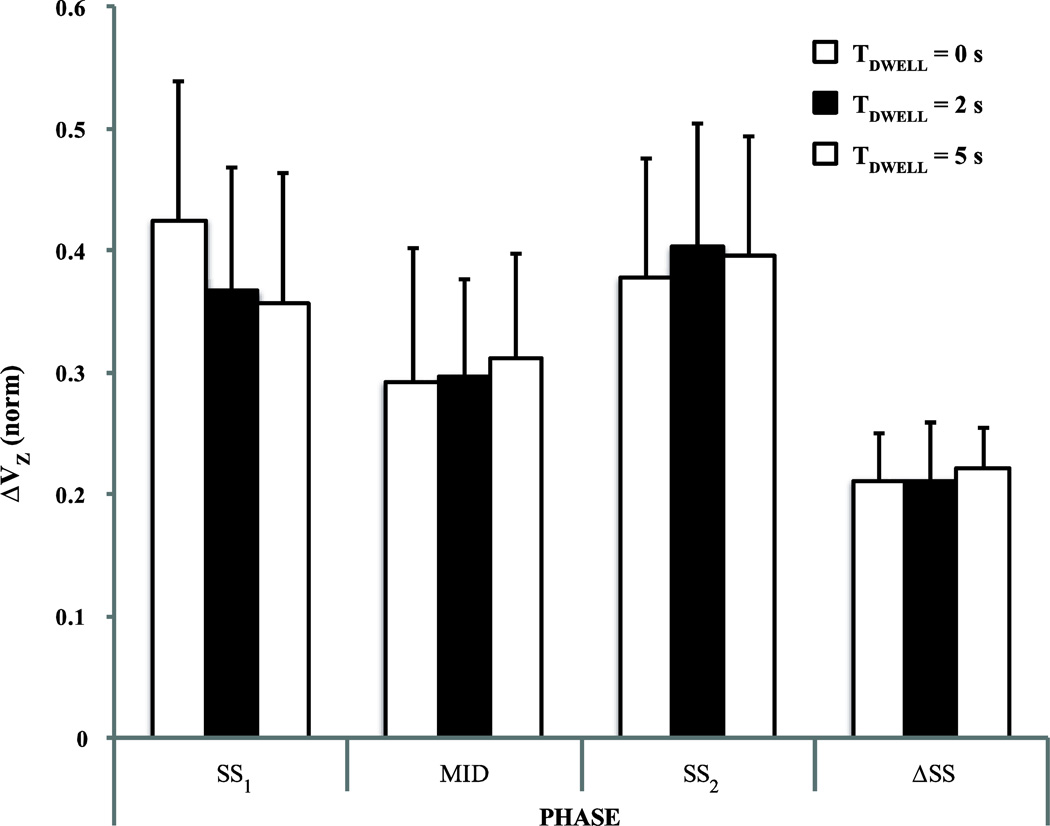
Variance within the uncontrolled manifold, UCM (V_UCM) and within the orthogonal space (V_ORT) for the SS1, MID, and SS₂ phases and for the difference between the two steady states, ΔSS. Means ± SE across subjects are presented. The white, black, and striped bars show the data for T_DWELL = 0 s, 2 s, and 5 s conditions, respectively.

These effects were supported by a three-way ANOVA, with the factors Phase, T_DWELL, and Variance, which showed main effects of Variance (F₍1_,6) = 19.239, p < 0.01) and Phase (F₍1.25,7.5) = 14.90, p < 0.005). Across all conditions, on average, V_UCM = 0.0159 ± 0.0026 was higher than V_ORT = 0.004 ± 0.0012. Pairwise comparisons have confirmed that both V_UCM (0.0221 ± 0.0036) and V_ORT (0.007 ± 0.0026) in phase MID were significantly greater than their respective values in phases SS1 (V_UCM: 0.0138 ± 0.0025; V_ORT: 0.0028 ± 0.0008) and SS₂ (V_UCM: 0.0117 ± 0.002; V_ORT: 0.0022 ± 0.0006). There was no main effect of T_DWELL and no significant interactions.

The index of synergy (ΔV) was consistently positive across all the comparisons reflecting the mentioned inequality V_UCM> V_ORT. The mean ± SE values of the z-transformed ΔV (ΔV_Z) values over the subjects are shown in Figure 5. Positive values for ΔV_Z were observed over all subjects and conditions, and there were no significant differences across the three conditions, SS1, SS₂, and MID.

Figure 5.

Fisher’s z-transformed synergy indices (ΔV_Z) for the SS1, MID, and SS₂ phases and for the difference between the two steady states, ΔSS. The bar plots show the mean values across subjects with standard error bars. The white, black, and striped bars show the data for T_DWELL = 0 s, 2 s, and 5 s conditions, respectively.

The difference in the M values observed in the two steady-state phases (ΔSS in Fig. 4 and Fig. 5) was also subjected to the analysis of variance. This analysis confirmed main effect of Variance (F_(1,6) = 7.18, p < 0.05) with V_UCM (0.0056 ± 0.0019) significantly greater than V_ORT (0.0017 ± 0.0005) (the rightmost sets of columns in Fig. 4). Fig. 4 shows that the values of both V_UCM and V_ORT for ΔSS condition are smaller than their respective values in other phases. The two-way ANOVA, Phase × Variance, confirmed main effects of Variance (F₍1_,6) = 24.686, p < 0.005) and Phase (F₍1.₃4,8.06) = 7.686, p < 0.05) while the interaction Variance × Phase was just under the significance level (F₍1.₃1,7.₈7) = 4.855, p = 0.053). Across all conditions, on average, V_UCM = 0.0103 ± 0.0017 was higher than V_ORT = 0.0022 ± 0.0006. This was reflected in consistently positive values of ΔV (the right columns in Fig. 5). Pairwise comparisons confirmed smaller V_UCM (0.0054 ± 0.0019) and V_ORT (0.0017 ± 0.0005) for ΔSS as compared to their values in phases SS₂ (V_UCM: 0.0117 ± 0.002; V_ORT: 0.0022 ± 0.0006) and SS1 (V_UCM: 0.0138 ± 0.0025; V_ORT: 0.0028 ± 0.0008).

Discussion

Both hypotheses formulated in the Introduction have been confirmed. Indeed, inter-trial M-mode variance at all three states, initial (SS₁), intermediate (MID), and final (SS₂) was mostly confined to the UCM computed for the handle coordinate in support of the first hypothesis. When M-mode variance was computed using the differences in the muscle activations between the initial and final phases within each trial, most of this difference was compatible with unchanged final handle position in support of the second hypothesis. So, the transient perturbations used in the study resulted in relatively low variance in the space of performance variables (cf. equifinality, Bizzi et al. 1976; Kelso and Holt 1980; Schmidt and McGown 1980; Latash and Gottlieb 1990), and relatively large variance in the muscle activation space. We would like to emphasize that this structure of variance was observed despite the fact that the subjects were not instructed to “control” hand position beyond the initial state. Further, we discuss implications of the results for the neural control of voluntary actions.

Multi-muscle synergies and the control with referent configurations

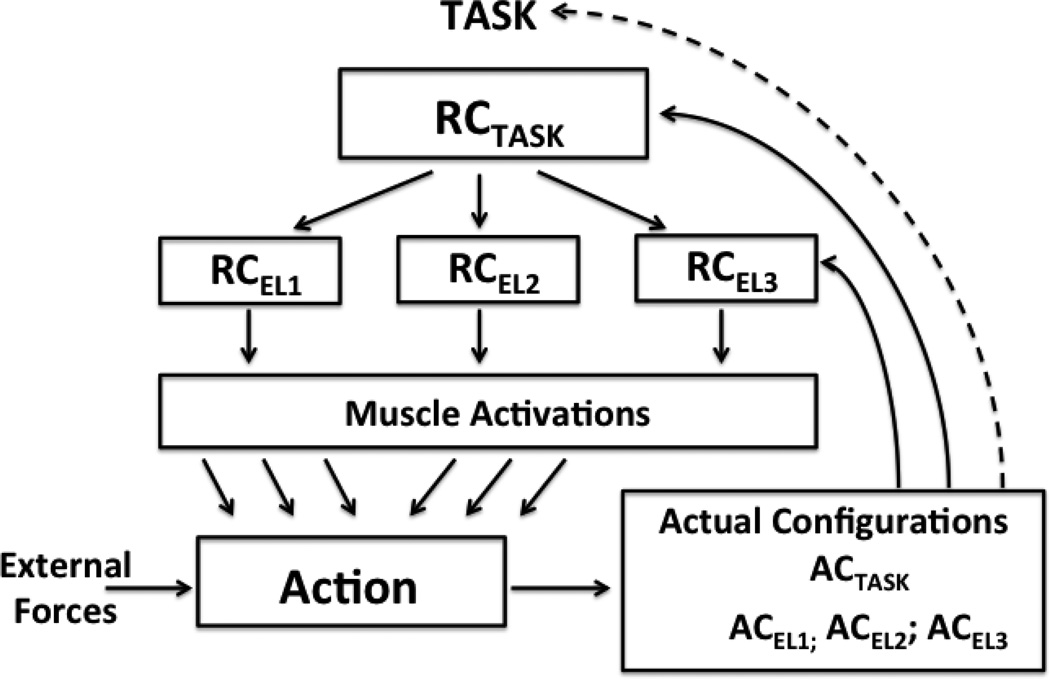
Recently, a scheme for the control of redundant motor systems has been developed based on several ideas including those of hierarchical control with a sequence of few-to-many mappings, control with referent body configurations, and feedback loops stabilizing task-specific variables (Latash 2010, 2012). For the purposes of our study, this scheme may be illustrated as a sequence of two steps (Figure 6). First, referent values for salient performance variables, such as the handle location and orientation (defined by the task in the initial posture but free to change in other phases of our experiment) are reflected in RC_TASK. Further, RC_TASK is projected on a higher-dimensional set of elemental variables (RC_EL). We assume that the subject can scale RC_EL one at a time; so, RC_EL are related to the notion of primitives (reviewed in Flash and Hochner 2005; Hogan and Sternad 2012). Muscle activations reflect deviations of the actual values of elemental variables from the corresponding RC_EL. In an earlier study (Robert et al. 2008), changes in muscle activations during a whole-body task were directly linked to changes in the body RC in support of this general scheme.

Figure 6.

Within the suggested scheme, the task results in the creation of a referent configuration (RC_TASK) reflecting referent values for salient task-specific variables. RC_TASK projects on a redundant set of elemental referent configurations (RC_EL1; RC_E12; and RC_EL3) reflected in the structure of M-modes. Muscle activations in combination with the external forces result in changes in the actual body configurations, both AC_TASK and AC_EL. The difference between the RC and AC pairs drives changes in muscle activations until the system reaches an equilibrium state. The dashed line shows a hypothetical back-coupling process leading to drifts at the task level when the actual configuration is kept away from the corresponding RC for a relatively long time interval. Central back-coupling loops are not illustrated (see the text).

While RC_EL are not directly observable, their effects on muscle activations are. As in earlier studies (Krishnamoorthy et al. 2003, 2004; Danna-dos-Santos et al. 2007; Robert et al. 2008), we used PCA with rotation and factor extraction in the space of muscle activations to identify groups of muscles that show activations with parallel scaling and viewed those muscle modes (M-modes) as reflections of shifts in individual RC_EL. Further we assumed that a back-coupling mechanism, for example involving feedback loops on the outputs of neurons reflecting RC_EL (qualitatively similar to the classical Renshaw cell system, see Latash et al. 2005) or on sensory signals reflecting effects of RC_EL on behavior induced co-variation of RC_EL stabilizing the salient performance variables related to RC_TASK. This co-variation was estimated using the analysis in the space of M-modes based on the framework of the UCM hypothesis (Scholz and Schöner 1999).

Matrix factorization methods have been used broadly over the past 10 years or so for analysis of activation patterns in large muscle groups (D’Avela et al. 2003; Ivanenko et al. 2004, 2005; Ting and Macpherson 2005; Ting and McKay 2007). Most of those studies used the term “muscle synergies” for muscle groups identified with such methods and emphasized stability of muscle composition in such groups over task variations (Ivanenko et al. 2005; Torres-Oviedo and Ting 2010). Within the scheme illustrated in Fig. 6, we would prefer to address such muscle groups as elemental variables or M-modes that reflect the basis (RC_EL), on which synergies stabilizing behavior are built. Note that several studies documented changes in the composition of M-modes when the task becomes challenging (Krishnamoorthy et al. 2004; Danna-dos-Santos et al. 2009) and with practice (Asaka et al. 2008). As implied by the scheme in Fig. 6, M-modes can indeed be viewed as synergies with individual muscle activations as elemental variables. The purpose of these synergies may be ensuring stable elemental shifts in the body RC (RC_EL) with variable muscle contributions.

While many M-modes corresponded to activation patterns without co-contraction of agonist-antagonist muscle pairs, M-modes with co-contractions were also common (see also earlier studies documenting such M-modes, Krishnamoorthy et al. 2004; Danna-dos-Santos et al. 2008). Within the equilibrium-point hypothesis, muscle co-contraction can be produced by the so-called c-command (Feldman 1980, 1986; Latash 1992). Indeed, in one of the studies, direct relations between co-contractions within large muscle groups in whole-body tasks were associated with the c-command (Slijper and Latash 2000). It is possible that some of the RC_EL included components related to both reciprocal activation and co-activation within agonist-antagonist muscle pairs.

Task-specific stability in muscle activation space

Stability of natural actions is paramount for successful motor behavior in the environment characterized by unpredictable forces and changing goals. Within the suggested scheme, stability is ensured by short-latency central back-coupling loops (Latash et al. 2005) and also longer-latency loops from sensory receptors that ensure that actual body configuration is ultimately reaching the task-related RC. The stationary or moving RC plays the role of an attractor, to which the actual body configuration moves. RC_EL at hierarchically lower levels and all biomechanical variables are constrained only in directions that move the body away from the RC and not so much in directions that are compatible with the body configuration staying at the RC.

Since RC, by definition, reflects the task, this general scheme is a particular realization of the idea of task-specific stability in different directions within a multi-dimensional, redundant space (Schöner 1995). It has been tested with two main approaches. First, application of an unexpected perturbation leads to deviations of the redundant system from its preferred trajectory primarily in directions that do not affect important performance variables (within the UCM for the task, Mattos et al. 2010, 2013). Second, analysis of inter-trial variance during repetitive tasks shows more variance within the UCM computed for important performance variables as compared to variance orthogonal to the UCM (reviewed in Latash et al. 2007). The latter method has been applied to analysis of activation patterns in multi-muscle systems in both whole-body tasks such as swaying and stepping (Danna-dos-Santos et al. 2006; Wang et al. 2006; Robert et al. 2008; Klous et al. 2010) and in arm tasks such as force production and reaching tasks (Krishnamoorthy et al. 2007; Mattos et al. 2013). All these studies have shown that inter-trial variance in the redundant M-mode space during intentional movements was mostly compatible with such performance variables as center of pressure coordinate, shear force, force applied by the hand, and hand trajectory.

Our study shows that movements produced by changes in the external force field are also characterized by a similar structure of variance (V_UCM > V_ORT), even when the subject tries not to react to the external force changes. The instruction did not require the subject to pay particular attention to any performance variables that changed under F_PERT. The fact that the EMG signals showed a structure of variance suggesting a synergy stabilizing hand position even when the subjects tried not to interfere with hand movements produced by external force changes is one of the most important (and unexpected) findings of the study. During such unintentional movements (MID and SS₂ phases), variance in the M-mode space was mostly confined to the UCM computed for the endpoint position as the performance variable (Figs. 4 and 5). Note that the subjects were instructed not to react to hand motion induced by the robot (“let the robot move your arm”). We view these observations as natural consequences of the general scheme for the production of voluntary movements. In particular, this scheme predicts that most variance at lower levels of the assumed hierarchy would be compatible with the RC specified at the task level. If the subjects in our experiments were indeed not changing the task RC, as required by the instruction, similar task-specific stability in response to both external forces (perturbations leading to unintentional movements) and intrinsically generated changes in the neural input (intentional movements) could be expected. Within the scheme in Fig. 6, these changes are produced by action of the feedback loops from receptors sensitive to the robot-induced changes in mechanical variables, such as muscle spindle endings, Golgi tendon organs, cutaneous and subcutaneous receptors. The similar structure of the M-mode variance across all the phases justifies the scheme in Fig. 6 with the feedback loop from the peripheral receptors projecting on the highest level of the hierarchy.

Following a transient perturbation, the scheme in Fig. 6 is expected to show relatively small, consistent deviations in the task-specific variables and less constrained, larger deviations in directions within the UCM. Data supporting with this prediction have recently been observed in multi-finger force production and multi-joint positional tasks in response to transient perturbations (Wilhelm et al. 2013; Zhou et al. 2014a). In both cited studies both performance and elemental variables were mechanical, digit forces and joint rotations. The current study is the first to show that following a transient perturbation relatively low variance in performance (handle coordinate) is associated with relatively large variance in the M-mode space (compare V_ORT and V_UCM for ΔSS in Fig. 4). In other words, even if a redundant motor system seems to come to a similar state following a transient perturbation, the state of its elements may change substantially in directions that do not affect task-specific aspects of behavior. This may be expected in response to such factors as spontaneous changes in activation levels of neurons (sometimes referred to as “neural noise”), and the well-known hysteresis properties of sensory and motor elements and reflex loops.

Unintentional shifts of the referent configuration

Within the scheme in Fig. 6, RC at the hierarchically highest level is defined exclusively by the task. Transient perturbation are expected to lead to transient deviations of the endpoint from its position, but when the external force returns to its baseline value, return of the endpoint to the same coordinate is expected (cf. equifinality, Bizzi et al. 1976; Kelso and Holt 1980; Schmidt and McGown 1980; Latash and Gottlieb 1990). A few recent papers have reported that a dwell time within a transient perturbation may lead to violations of equifinality (Wilhelm et al. 2013; Ambike et al. 2014; Zhou et al. 2014b). Related observations include a drop in force during isometric force production tasks after turning the visual feedback off (Slifkin et al. 2000; Vaillancourt and Russell 2002; Shapkova et al. 2008). These observations suggest that when actual configuration of the body is kept away from its RC for a relatively long time, unintentional drift of RC towards the actual configuration can take place. This effect is illustrated in Fig. 6 with a dashed feedback arrow.

We explored this phenomenon by using different dwell times (T_DWELL) between the application and removal of F_PERT. Longer T_DWELL were associated with larger deviations of the final hand position from the initial one (ΔSS) in support for the relatively slow feedback causing shifts of RC. Note that these shifts were associated with a similar structure of variance (no effect of T_DWELL on any variance index), which can be expected from the scheme in Fig. 6. We can conclude, therefore, that three types of movements, one intentional (the initial steady-state) and two unintentional (produced by changes in the external force and by the RC drift), are characterized by a similar structure of variance in the muscle activation space. So far, these results provide the strongest support for the general theoretical view that voluntary movements are based on control with referent configurations organized in a hierarchical scheme that ensures synergies stabilizing important performance variables. Note that, while there was substantial variability in the patterns of muscle activation across subjects, the patterns were consistent within-a-subject. Since we analyzed the data within each subject separately before pooling outcome variables, such as variance indices, across subjects, the large across-subjects variability in the EMG patterns was not a major issue.

Concluding comments

We would like to acknowledge a few limitation of this study. The steps of identifying M-modes and the Jacobian can be criticized as accounting for relatively small amounts of variance in the original muscle activation data (typically, 60%-70%). While these values may seem low, they are similar to those reported in earlier studies with multi-muscle data processing (Krishnamoorthy et al. 2003, 2007; Danna-dos-Santos et al. 2006; Mattos et al. 2013). Indeed, surface EMG signals are typically noisy and, in studies with relatively low modulation of muscle activation (rather slow movements, as in the current study), one cannot expect much more variance to be linked to global mechanical variables.

The relatively heavy filtering of the EMG data may be seen as another drawback. It was used to filter out mechanical vibrations that were present in some subjects during the changes in the robot force. As mentioned in Methods, our analysis of the data of two subjects who showed no such vibrations with different filtering parameters suggests that the filtering had only very small effects on the main outcome variables. So, we do not view the filtering parameters as potentially leading to invalid conclusions based on the inter-trial analysis of variance.

We tested a relatively small number of subjects. However, the data set was of sufficient power to reach statistical significance in the main comparisons, and none of the other main comparisons were close to the significance level. As in earlier studies of multi-muscle synergies (Krishnamoorthy et al. 2003; Danna-dos-Santos et al. 2007, 2008; Klous et al. 2010), we looked for large effect sizes on the order of 1 – 1.5, and 7 subjects are sufficient to detect such effects. We have to admit, however, that the unbalanced number of male and female subjects is a drawback of the study.

We also relied on compliance of our subjects with the “do not intervene” instruction. There is no objective method that would allow proving non-intervention because all measurable variables are expected to show changes with perturbations due to reflex effects, the length- and velocity-dependence of muscle forces, and straightforward mechanics. We trained the subjects to ignore the arm motion induced by the perturbation, but this point remains a weakness. An earlier study compared behaviors under the “intervene” and “do not intervene” instructions and showed more consistent behavior in subjects under the latter instruction (Latash 1994).

The experimental design involved only one direction of perturbation. We view this limitation as reasonable for the first steps in exploring how multi-muscle systems react to transient perturbations. The inter-trials analysis of variance requires multiple repetitions at each condition, which naturally limits the number of conditions one can explore without the subjects getting bored and fatigued.