On Achieving Experimental Accuracy from Molecular Dynamics Simulations of Flexible Molecules: Aqueous Glycerol

Abstract

The rotational isomeric states (RIS) of glycerol at infinite dilution have been characterized in the aqueous phase via a 1 μs conventional molecular dynamics (MD) simulation, a 40 ns enhanced sampling replica exchange molecular dynamics (REMD) simulation, and a reevaluation of the experimental NMR data. The MD and REMD simulations employed the GLYCAM06/AMBER force field with explicit treatment of solvation. The shorter time scale of the REMD sampling method gave rise to RIS and theoretical scalar ³J_HH coupling constants that were comparable to those from the much longer traditional MD simulation. The ³J_HH coupling constants computed from the MD methods were in excellent agreement with those observed experimentally. Despite the agreement between the computed and the experimental J-values, there were variations between the rotamer populations computed directly from the MD data and those derived from the experimental NMR data. The experimentally derived populations were determined utilizing limiting J-values from an analysis of NMR data from substituted ethane molecules and may not be completely appropriate for application in more complex molecules, such as glycerol. Here, new limiting J-values have been derived via a combined MD and quantum mechanical approach and were used to decompose the experimental ³J_HH coupling constants into population distributions for the glycerol RIS.

Introduction

Glycerol has a complex conformational space because of its high flexibility and because of the presence of vicinal hydroxyl groups that are capable of stabilizing various rotamers through intramolecular hydrogen bonds (H-bonds), Figure 1. The physical properties of glycerol exhibit a peculiar dependence on variations in either temperature or pressure.^1,2 The number of H-bonds increases with pressure,¹ while the intermolecular distribution of pure liquid glycerol shows little temperature dependence from 193 K to 296 K.² Glycerol may also exist as a supercooled liquid, a property that makes its crystallization possible only through special techniques.² Decreases in temperature generally lead to the formation of a glass phase at 185 K.³ The resistance to crystallization has been exploited by nature, wherein glycerol is utilized alone⁴ or in mixtures with trehalose as a cryoprotectant.⁵ In vitro glycerol helps preserve biomolecular structure⁶ as well as enhances the self-assembly of biomolecules.⁷ These properties have stimulated extensive characterizations of the conformational equilibria of glycerol in different phases employing either experimental^2,3,8–12 or theoretical methods.^1,9,13–20

Figure 1.

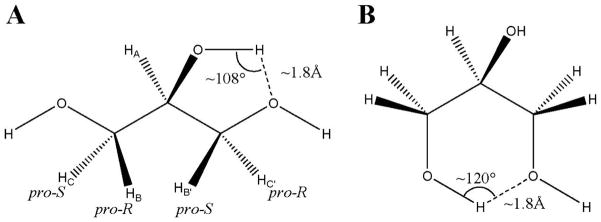
Schematic representations of glycerol indicating the atoms utilized to form potential five-membered (A) and six-membered (B) ring hydrogen bonds. The hydrogen atoms involved in scalar ³J-couplings are also indicated (A).

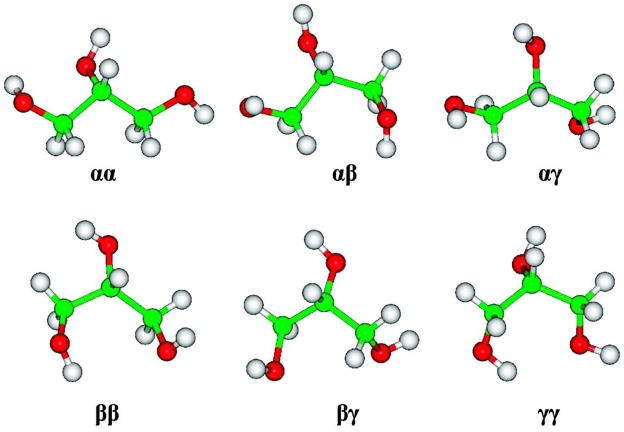
In glycerol, the dihedral angles defining rotations about the CC bonds are generally utilized to characterize the backbone rotamers. Employing Bastiansen’s nomenclature,⁸ α denotes a gauche torsion angle for the O₁C₁C₂O₂ sequence and a trans orientation for the O₁C₁C₂C₃ sequence, β corresponds to a trans O₁C₁C₂O₂ conformation, and γ is ascribed to a gauche and trans orientation for the O₁C₁C₂O₂ and O₁C₁C₂H₂ sequences, respectively, Figure 1. An unambiguous definition of all of the rotational isomeric states (RIS) of the backbone leads to six unique states: αα, αβ, αγ, ββ, βγ, and γγ. Each backbone rotamer in turn displays different hydroxyl rotamers giving rise to a total of 27 H–O–C–C torsion angle RIS.

The exclusive presence of the αα backbone structure in the crystalline phase has been reported from neutron scattering experiments¹¹ and is seen in short molecular dynamics (MD) simulations of neat crystalline glycerol.¹³ For all the other phases, there is some disagreement between theoretical and experimental results as well as between independent experimental studies particularly in the gas phase. Electron-diffraction gas-phase studies indicate a mixture of the αα and αγ rotamers,⁸ while later experimental analysis from the microwave data identified γγ as the main rotamer with a secondary presence of the αγ rotamer.¹⁴ From a theoretical perspective, ab initio quantum mechanical (QM) calculations^15–17 of isolated rotamers of glycerol were in general agreement with the observations from the electron-diffraction experiment. Gas-phase QM calculations^9,18,19 were generally consistent with gas-phase MD simulations,²⁰ which all indicated that αα and αγ were the major rotamers. The experimental conformational properties of glycerol in aqueous solution have been determined principally by NMR spectroscopy,^9,12 which indicated that the αγ rotamer was the most abundant followed by αβ, αα, and βγ, in approximately comparable populations, while the γγ and ββ rotamers were the least populated. In contrast, in the pure liquid phase, X-ray²¹ and neutron diffraction experiments^2,10 indicated the presence of only the αα rotamer. In addition to the αα rotamer, a combined QM and experimental approach that involved fitting the density functional theory (DFT) calculated IR-spectra of selected monomers of glycerol to the experimental spectra,¹⁸ and MD simulation^13,20 studies, showed that the αγ rotamer was also a significant contributor in the neat liquid phase. MD simulations^13,20 have indicated that the αα and αγ rotamers are predominant in the glass phase, a conclusion that contrasts with neutron diffraction data that showed the presence of only the βγ rotamer.³

Several empirical potential energy models for glycerol have been proposed and have been applied to the gas, liquid, and crystalline phases.^1,13,20,22 Also, a few MD simulations have been reported for glycerol, which seek to address mechanisms that occur under physiological conditions, such as the transportation of glycerol across cell membranes of microorganisms.^23,24 In those MD studies, the conformational properties of glycerol in aqueous solution were not examined despite the fact that a full understanding of the thermodynamics of initial binding would require inclusion of the dynamics of glycerol in the periplasm.²⁵ A model that is capable of reproducing the experimental aqueous phase conformational properties of glycerol would lend some confidence to the predictions of free energies of binding from more elaborate simulational studies. In a recent MD simulation investigation utilizing different concentrations of glycerol in the aqueous phase,²⁶ the rotamer populations were found to be insensitive to the composition of the mixtures. However, the very short MD time scale (500 ps) employed in that work²⁶ may limit the significance of the results. Here, we present a model, employing the recently reported GLYCAM06 force field,²⁷ for studying the conformational properties of glycerol in aqueous solutions at infinite dilution.^25,28 To the best of our knowledge, this study is the first attempt to characterize the conformational properties of dilute glycerol via MD simulations on the physiologically relevant microsecond time scale.

Methods

Conventional MD Simulations

The GLYCAM06 parameter set²⁷ was employed with the SANDER module of the AM-BER8²⁹ software suite for all molecular mechanics (MM) and MD simulations. Ensemble-averaged partial atomic charges for glycerol were generated by restrained fitting (restraint weight = 0.01) to the QM molecular electrostatic potentials (HF/6-31G*) of 100 rotamers, following the procedure described previously,^30,31 giving rise to the following values (in atomic units): Q_O1 = Q_O3 = −0.674, Q_O2 = −0.663, Q_C1 = Q_C3 = 0.249, Q_C2 = 0.302, Q_HO1 = Q_HO3 = 0.409, and Q_OH2 = 0.393. Aliphatic protons carry zero net charge in GLYCAM06. A molecule of glycerol was immersed in a box of 235 pre-equilibrated TIP3P³² water molecules, and the initial solvent configurations were subjected to energy minimization via 50 cycles of steepest descent followed by 950 cycles of conjugate gradient optimization. The entire system was then minimized via the same protocol. This was followed by a short simulated annealing of the system in which it was heated from 5 to 300 K over 50 ps and then was cooled to 5 K over another 50 ps. Initial atomic velocities were allocated from a Boltzmann distribution at 5 K. Prior to the production MD run, the entire system was heated from 5 to 300 K over 70 ps and was maintained at that temperature for a further 80 ps. Production dynamics simulations were performed for 1 μs under isobaric–isothermal (nPT) conditions with a 2 fs time step used to integrate the equations of motion. Long-range electrostatic interactions were treated using particle mesh Ewald summation.³³ To avoid potential imbalances in the internal energies of five- and six-membered intramolecular hydrogen bonds,³⁴ a unit scale factor was employed for all 1–4 nonbonded electrostatic and van der Waals interactions (SCEE = SCNB = 1.0). The SHAKE algorithm³⁵ was employed to constrain bonds containing hydrogen atoms to their equilibrium values.

Replica Exchange MD Simulations

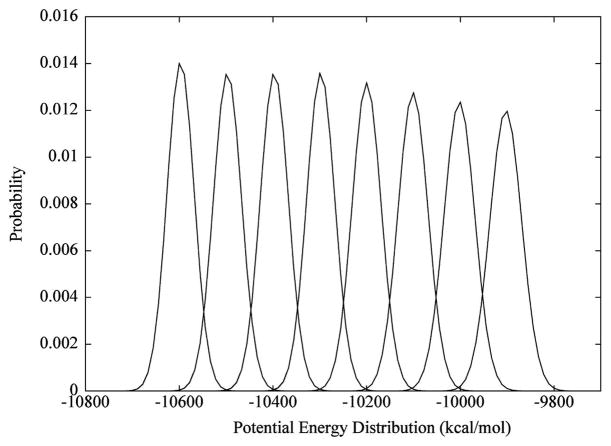
The replica exchange MD (REMD) simulations were performed using the SANDER module of the AMBER9³⁶ software package. An exponential equation was fit to a range of sample temperatures available in the replica exchange section of the AMBER9 users’ manual. An interpolation between the given temperatures was performed to obtain eight successive approximate target temperatures (299.9, 308.0, 316.4, 324.9, 333.7, 342.8, 352.1, and 361.6 K). A molecule of glycerol was submersed in a pre-equilibrated octahedral water box of 1114 water molecules, and the system was equilibrated via the same protocol outlined in the conventional MD simulation section. During the simulation, long-range electrostatic interactions were treated using the particle mesh Ewald summation, and scaling of 1–4 nonbonded electrostatic and van der Waals interactions was turned off. From this single equilibrated system, eight simulations were generated by heating to the eight approximate target temperatures noted above. A 10 ns production dynamics ensued under the constant temperature–volume ensemble. Gaussian distributions³⁷ of the potential energies from these simulations were plotted to determine whether energy overlaps occurred within the temperature range, Figure 2. Utilizing the lowest target temperature (300 K) from the simulations, and a swap acceptance probability of 0.2, the final target temperatures (300, 303, 306, 309, 312, 315, 318, and 322 K) were obtained through an iterative process described previously.³⁷ Prior to the exchange dynamics, the systems were heated to their respective target temperatures. The hybrid solvent REMD approach was employed,³⁸ retaining 100 closest water molecules during each replica exchange process. A 2 fs time step was employed to integrate the equations of motion. An exchange was attempted every 250th step for a total of 250 × 80 000 steps, resulting in an overall simulation time of 8 × 40 ns for the replicas.

Figure 2.

Gaussian potential energy distributions indicating the feasibility of temperatures employed in the replica exchange simulation.

Coordinates were collected at 5 ps, or 20 ps, intervals from the REMD and conventional MD simulations, respectively, for subsequent analysis, which was performed with either the CARNAL or PTRAJ modules of AMBER8.

Results and Discussion

In the present study, the relative abundance of each of the backbone RIS was computed from a 1 μs explicit solvent MD simulation and was compared to available aqueous phase experimental NMR J-couplings and populations.^9,12 The MD data could be clustered into nine RIS, Figure 3A, which were subsequently grouped into six unique backbone RIS according to internal rotational symmetry. To determine whether the simulation had reached statistical equilibrium within the 1 μs time scale, the populations of the six unique backbone RIS were monitored as a function of simulation time, Figure 3B. During the initial equilibration stage (0–150 ps), only the αα and βγ rotamers were present with average populations of 42 and 58%, respectively. Throughout the first 200 ns, the rotamer populations showed wide fluctuations that equilibrated only after approximately 300 ns and continued to display minor fluctuations in the population distribution up to 600 ns. The long simulational time required in the traditional MD simulation to achieve rotamer sampling equilibration raises the question as to whether similar results might not be achieved in a much shorter time via the utilization of enhanced sampling methods. To this end, the REMD simulation approach described in the Methods section was employed. During the first 15 ns of the REMD simulations, the populations of the RIS varied significantly, showed less variation between the 15–30 ns interval, and became more stable during the last 10 ns of the simulation, Figure 3C.

Figure 3.

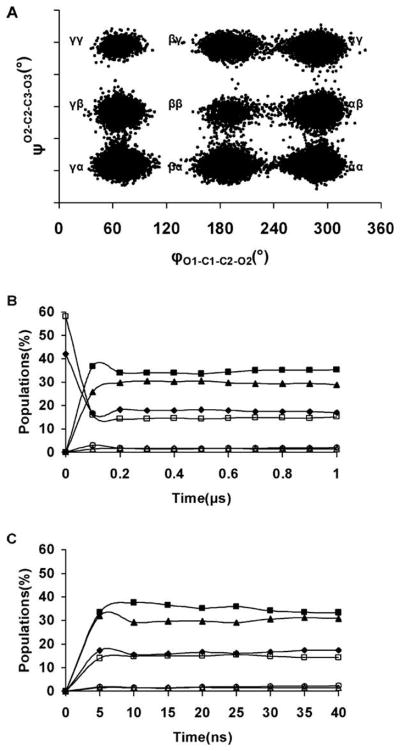
A scatter plot of two backbone dihedral angles, φ(O₁–C₁–C₂–O₂) and ψ(O₂–C₂–C₃–O₃), during the 1 μs MD simulation (A). Evolution of the six RIS of glycerol vs simulation time. Traditional MD (B) and REMD (C). αγ(■), αβ (▲), αα(◆), βγ(□), γγ(○), and ββ(△).

Relative Energies from a Boltzmann Population Analysis

The relative energies of the six backbone RIS, computed from a Boltzmann analysis of the experimental¹² and theoretical populations, are presented in Table 1. In the course of the MD and REMD simulations, each hydroxyl torsion angle displayed frequent transitions between all three staggered rotamers (data not shown). As such, the relative energies computed here are averages over the staggered rotamers of the hydroxyl hydrogen atoms in the respective six unique backbone RIS, Figure 4. The most unstable rotameric state (ββ) was within 2 kcal/mol of the most stable (αγ). The relative energies of some backbone conformers of glycerol have also been reported at the QM SM5.42/HF/6-31G* and B3LYP/6-31+G**//SM5.42/HF/6-31G* levels of theory⁹ and as expected depend on the hydroxyl hydrogen torsion angles. The relative energies of each of the backbone RIS from the QM study⁹ were calculated by averaging the relative energies of the hydroxyl rotamers and are shown in Table 1. The trends of the relative energies in decreasing order of stability are αβ ≈ βγ < αα ≈ αγ < ββ ≈ γγ and αα < αγ ≈ αβ < βγ < γγ< ββ at the SM5.42/HF/6-31G* and B3LYP/6-31+G**//SM5.42/HF/6-31G* levels of theory, respectively. These trends in relative energies are at variance with those computed from the MD simulation, namely, αγ < αβ < αα ≈ βγ < γγ < ββ, and are disordered with respect to the relative energies derived from the experimental populations. However, with the exception of the ββ state, all of the relative energies computed from the NMR-derived populations are under 1 kcal/mol, placing extreme demands on any computational method.

TABLE 1.

Relative Energies^a for Glycerol RIS

rotamer	NMR12,b	1 μs MDb	SM5.42 HF/6-31G*9,c	B3LYP/6-31+G**//SM5.42/HF/6-31G*9,c
αγ	0	0	0.22	0.47
αβ	0.20–0.21	0.13	0.00	0.53
αα	0.21–0.26	0.43	0.21	0.00
βγ	0.26–0.37	0.50	0.02	1.00
γγ	0.34–0.61	1.46	1.09	1.20
ββ	1.03	1.70	1.06	1.97

^aIn kcal/mol.

^bFrom a Boltzmann analysis of the RIS populations.

^cDetermined from the reported QM data⁹ by averaging the relative energies of all the hydroxyl group rotamers of each of the backbone RIS.

Figure 4.

The six unique backbone RIS of glycerol extracted from the MD trajectory.

Comparison with NMR Data

To compare directly with the experimental NMR data, a generalized Karplus equation³⁹ was employed to compute the scalar ³J_HH-coupling constants of each terminal methylene hydrogen atom (H_B, H_B′, H_C, and H_C′) to the central hydrogen atom (H_A), Figure 1A. These couplings were calculated for each snapshot, extracted at 5 ps, or 20 ps, intervals from the REMD and conventional MD trajectories, respectively, and then averaged, Table 2. In terms of the NMR spectrum, the coupling of each pair of prochiral methylene protons to the central proton is indistinguishable. As such, only two instead of four independent coupling constants are observed. To make a direct comparison with the experimental data, the MD-computed average coupling constants between each methylene proton and the central proton were further averaged with those of its magnetically equivalent pair to afford the final scalar ³J_HH-couplings, Table 2. Notably, the coupling constants computed from the 1 μs MD and 40 ns REMD simulation methods were essentially identical with each other and were indistinguishable from the experimental data. This agreement suggested that the variations among the relative energies might be related more to the approximations imposed in the decomposition of the NMR J-values into rotamer populations than to inaccurate MD data. To examine this possibility further, a detailed examination of rotamer populations was undertaken.

TABLE 2.

Computed^a and Experimental Scalar ³J_HH-Couplings

	1 μs MD	40 ns REMD	symmetry averaged		experimental12
			1 μs MD	40 ns REMD
3JAB	6.3 ± 1.0	6.4 ± 1.0	6.3 ± 1.0	6.3 ± 1.0	6.3 ± 0.2
3JAB′	6.3 ± 1.0	6.2 ± 1.0
3JAC	4.0 ± 0.8	4.1 ± 0.8	4.0 ± 0.8	4.1 ± 0.8	4.4 ± 0.1
3JAC′	4.0 ± 0.8	4.1 ± 0.8

^aIn Hz, computed using an empirical Karplus equation³⁹ and averaged over all structures extracted at 5 and 20 ps intervals for the REMD and conventional MD, respectively.

Rotamer Populations

The rotamer populations computed from the traditional MD and REMD simulations are presented in Table 3. To quantify simulational convergence, as well as to judge the statistical significance of the results of the MD simulations, error estimates were computed by considering each rotamer population as a binomial random variable. That is, the population of each of the RIS (αα, αβ, etc.) within the simulation was incremented if any observed set of torsion angles occurred within the limits of the values employed to define the state. Employing the central limit theorem, which is appropriate given the large number of data points, the statistical properties of the RIS could then be readily characterized⁴⁰ and are summarized here. The proportion, P, of the occurrence of a given state (X) in n trials is

TABLE 3.

Rotamer Populations for Glycerol from MD and REMD Simulations and Derived from NMR Data

rotamer	1 μs MD	40 ns REMD	NMR-derived
			QM limiting J-valuesa	empirical limiting J-valuesb	empirical limiting J-valuesc	experimental limiting J-values12
αγ	35 ± 0.2	33 ± 0.2	23	23	23	28–30
αβ	28 ± 0.2	31 ± 0.2	27	27	27	20–21
αα	17 ± 0.2	17 ± 0.1	27	28	26	18–21
βγ	15 ± 0.2	14 ± 0.1	11	11	12	15–17
γγ	3 ± 0.1	3 ± 0.1	5	5	5	10–12
ββ	2 ± 0.1	2 ± 0.0	7	7	7	5

^aLimiting J-values computed at the B3LYP/HIIIsu3//B3LYP/6-31G** level, averaging over representative geometries for each of the RIS.

^bLimiting J-values computed from a Karplus curve,³⁹ averaging over representative geometries for each of the RIS.

^cLimiting J-values computed from a Karplus curve,³⁹ averaging over all conformers in each of the RIS.

$$P=\frac{\mathrm{X}}{n}$$ (1)

Since the relative population proportions are well established in the simulation (see Figure 3), we can estimate the standard deviation of P(σ_P) by

$${\sigma }_P\approx \sqrt{\frac{P(1-P)}{n}}$$ (2)

For example, for the αα state, the observed P from the MD simulation is 0.17 and for the 1 μs simulation n = 50 000 (snapshots extracted at 20 ps intervals). Therefore, the standard deviation can be estimated as 0.0016 or approximately 0.2%.

The populations obtained from the much shorter REMD simulation were comparable with those determined from the 1 μs MD simulation. From the data in Table 3, the theoretical populations were in qualitative agreement with those derived from NMR experimental data.^9,12 Recent simulations of different compositions of the aqueous phase²⁶ indicated the following trend in rotamer abundance: αα (40%), αγ (30%), αβ (20%), γγ (5%), βγ (5%), and ββ (0%) over all the concentrations examined. However, when compared to the present results, it appears probable that statistical equilibration was not achieved in that 500 ps study. In the present work, the model predicted that rotamers that could form internal H-bonds were the least populated, namely, γγ (3 ± 0.1%) and ββ (2 ± 0.1%). These rotamers would be expected to be destabilized in solution primarily because of the breaking of internal H-bonds by solvent as has been predicted to occur in carbohydrates in aqueous solution.³⁴

The excellent agreement between the MD-derived coupling constants from this work and those determined experimentally suggested that there should be a corresponding agreement between the observed theoretical and experimentally derived rotamer populations; however, this was not the case. For example, the 1 μs MD populations of the αβ (28 ± 0.2%) and γγ (3 ± 0.1%) RIS were higher and lower, respectively, compared to the experimental values of 20–21% and 10–12%, respectively. The experimental rotamer populations were derived by utilizing the limiting ³J_HH-values determined from disubstituted ethane molecules.¹² The derivation of the populations of RIS from experimental J-coupling constants typically invokes a linear combination of states weighted by associated state (or limiting) J-values. The final populations are therefore heavily dependent on these limiting J-values, which can rarely be determined directly from experimental data without invoking further approximations. The present results suggested a need to reevaluate the RIS populations from the experimental J-values.

Therefore, a combined MD–QM approach was utilized to compute limiting J-values for the gauche (J_G) and trans (J_T) coupling constants, Table 4. Additionally, by employing the states identified in the MD simulations, it was possible to take into consideration the effects of hydroxyl group rotations on the limiting J-values. Thus, MD simulation was employed to identify the RIS, while QM methods, employing the Gaussian 03 software package,⁴¹ were utilized to compute the J_G and J_T values for representative structures from each of the RIS. The 1 μs trajectory was clustered into the nine symmetry-related backbone RIS identified during the MD simulation. On the basis of the staggered rotamers of the H–O–C–C dihedral angles, each of the RIS was further subdivided giving rise to 27 clusters for the single-weighted (αβ, αγ, and βγ) or 15 clusters for the double-weighted (αα, ββ, and γγ) backbone rotamers. An average structure was computed for each cluster, and a single structure that was the closest match to this average, on the basis of root-mean-squared deviation in the atomic positions, was extracted from the MD trajectory and was subjected to direct QM J-coupling calculations. Thus, a single “real” structure was employed to approximate the average “virtual” geometry of each RIS. Prior to the J-coupling calculations, each structure was optimized at the QM B3LYP/6-31G** level, while the backbone and hydroxyl torsion angles were frozen at their solution-preferred conformations. The J-couplings were computed with the B3LYP functional employing the HIIIsu3 basis set as implemented recently for J-calculations.^42,43 For comparison, limiting J_G- and J_T-values were also derived from the average RIS geometries employing a generalized Karplus equation.³⁹ To compute the J_G and J_T-values for each of the backbone RIS, a population-weighted average of the QM J-values was computed taking into consideration the population of each hydroxyl rotamer and the population of its symmetry-related cluster in the corresponding backbone cluster. Employing the QM-computed J_G and J_T-values computed in this work, the experimental NMR coupling constants¹² were decomposed into the populations of the individual RIS as described previously,¹² Table 3. The populations computed from these new J_G and J_T-values were comparable among the QM and MD simulation methods, and all suggested that the αα, αβ, and αγ states account for approximately 75% of the conformational distribution of the aqueous phase, while the βγ, ββ, and γγ states account for the remainder. However, the populations obtained using the QM-computed J_G and J_T-values (derived using average geometries) differed significantly from both the MD RIS populations and the experimentally derived RIS populations. These results indicate the significant influences that the choice of limiting J-value and model geometry may have when converting experimentally observable J-values into rotamer populations. Moreover, in decomposing the J-values into the populations of the experimental RIS, it was assumed that the J_G and J_T-values for all the RIS were identical,12 suggesting that the OCCO atoms adopted ideal staggered conformations (±60°, 180°). Here, the J_G and J_T-values computed at the B3LYP/HIIIsu3//B3LYP/6-31G** level of theory, Table 5, are different for the symmetry-related proton as well as for proton on the same carbon atom indicating that the aforementioned assumption may not be accurate.

TABLE 4.

Limiting J_G and J_T-Values Computed from the 1 μs MD Simulation Data

	JG	JT
QM J-valuesa averaged over representative geometries for each of the RIS	2.46	9.86
empirical J-valuesb averaged over representative geometries for each of the RIS	2.35	10.04
empirical J-valuesb averaged over all conformers in the RIS	2.57	9.67

^aComputed at the B3LYP/HIIIsu3//B3LYP/6-31G** level.

^bComputed using an empirical Karplus equation in Hz.³⁹

TABLE 5.

Limiting J-Values Computed^a Level for the Coupled Aliphatic Protons in Each RIS

rotamer	JAB	JAB	JAC	JAC	〈JG〉	〈JT〉
αγ	8.88	1.69	1.29	2.35	1.77	8.88
αβ	9.01	4.61	1.49	11.21	3.05	10.11
αα	9.48	9.42	1.44	1.28	1.36	9.45
βγ	4.50	1.85	10.82	2.09	2.81	10.82
γγ	1.65	2.11	3.01	2.39	2.29
ββ	3.47	3.49	10.10	10.01	3.48	10.05

^aB3LYP/HIIIsu3//B3LYP/6-31G**.

Conclusion

The conformational properties of glycerol in the aqueous phase were examined through traditional MD and REMD simulation methods. Scalar ³J_HH coupling constants computed from both simulation methods were essentially identical and were in excellent agreement with the available experimental data. That the explicit solvent MD simulations of glycerol with the GLYCAM06 force field reproduced the NMR J-couplings indicates that the force field together with the TIP3P water model can effectively compute the subtle balance between the intraglycerol and glycerol–water nonbonded interactions.

The rotamer populations of the RIS from the MD and REMD simulations were in qualitative agreement with those derived from the NMR J-values; however, the approximations associated with deriving the experimental populations can be problematic. Employing QM-computed limiting J-values for state geometries derived from MD simulations resulted in an internally consistent set of populations. However, these populations differed from both the MD populations and from the experimentally derived values. The resulting rotamer populations suggest that the approximations employed in the experimental determination of these populations, which involved limiting J-values taken from substituted ethane molecules, may not be the most accurate approach. In this light, the J_G and J_T-values derived via the combined MD–QM approach may represent more consistent values to be employed in determining the solution conformational properties of glycerol. Ultimately, however, it is more accurate to compute and compare theoretical J-values with experimentally observable J-values than to include the additional approximations necessary to decompose the experimental J-values into RIS populations. This problem is exacerbated in the case of glycerol in which molecular symmetry reduces the number of experimental J-values.

In terms of the length of the simulations, it was shown that the use of an enhanced sampling method, such as REMD, gave rise to rotamer populations that were comparable to those from a 1 μs MD simulation in a significantly shorter time. This fact is extremely significant for larger flexible molecules for which 1 μs MD simulations with explicit solvent are presently unattainable.