A Multiresolution Method for Parameter Estimation of Diffusion Processes

Abstract

Diffusion process models are widely used in science, engineering and finance. Most diffusion processes are described by stochastic differential equations in continuous time. In practice, however, data is typically only observed at discrete time points. Except for a few very special cases, no analytic form exists for the likelihood of such discretely observed data. For this reason, parametric inference is often achieved by using discrete-time approximations, with accuracy controlled through the introduction of missing data. We present a new multiresolution Bayesian framework to address the inference difficulty. The methodology relies on the use of multiple approximations and extrapolation, and is significantly faster and more accurate than known strategies based on Gibbs sampling. We apply the multiresolution approach to three data-driven inference problems – one in biophysics and two in finance – one of which features a multivariate diffusion model with an entirely unobserved component.

1 Introduction

Diffusion processes are commonly used in many applications and disciplines. For example, they have served to model price fluctuations in financial markets (Heston, 1993), particle movement in physics (McCann, Dykman, and Golding, 1999), and the dynamics of biomolecules in cell biology and chemistry (Golightly and Wilkinson, 2008). Most diffusion processes are specified in terms of stochastic differential equations (SDEs). The general form of a one-dimensional SDE is

$$\mathrm{d}{Y}_t=\mu (Y_t,\mathit{\theta })\mathrm{d}t+\sigma (Y_t,\mathit{\theta })\mathrm{d}{B}_t,$$

where t is continuous time, Y_t is the underlying stochastic process, μ(·) is the drift function, a function of both Y_t and a set of parameters θ, σ(·) is the diffusion function, and B_t is Brownian motion.

While an SDE model is specified in continuous time, in most applications data can only be observed at discrete time points. For example, measurements of physical phenomena are recorded at discrete intervals — in chemistry and biology, molecular dynamics are often inferred from the successive images of camera frames. The price information in many financial markets is recorded at intervals of days, weeks, or even months. Inferring the parameters θ of an SDE model from discretely observed data is often challenging because it is almost never possible to analytically specify the likelihood of these data (the list of special cases of SDEs that do admit an analytic solution is surprisingly brief). Inferring the parameters from a discretely observed SDE model is the focus of this paper.

One intuitive approach to the problem is to replace the continuous-time model with a discrete-time approximation. In order to have the desirable accuracy, one often has to use a highly dense discretization. Dense discretization, however, leads to two challenging issues: (i) accurate discrete-time approximations often require the discretization time length to be shorter than the time lag between real observations, creating a missing data problem; (ii) highly dense discretization often imposes an unbearable computation burden. In this paper, we propose a new multiresolution Monte Carlo inference framework, which operates on different resolution (discretization) levels simultaneously. In letting the different resolutions communicate with each other, the multiresolution framework allows us to significantly increase both computational efficiency and accuracy of estimation.

1.1 Background

With direct inference of SDE parameters typically being infeasible, researchers have experimented with a wide number of approximation schemes. The methods range from using analytic approximations (Aït-Sahalia, 2002) to utilizing approaches that rely heavily on simulation (see Sørensen, 2004, for a survey of various techniques). An alternate strategy to approximating the likelihood directly is to first approximate the equation itself, and subsequently find the likelihood of the approximated equation. Among possible discretizations of SDEs (see Pardoux and Talay, 1985, for a review), the Euler-Maruyama approach (Maruyama, 1955; Pedersen, 1995) is perhaps the simplest. It replaces the SDE with a stochastic difference equation:

$$\mathrm{\Delta }{Y}_t=\mu (Y_{t-1},\mathit{\theta })\mathrm{\Delta }t+\sigma (Y_{t-1},\mathit{\theta })\sqrt{\mathrm{\Delta }t}{Z}_t,$$

where ΔY_t = Y_t − Y_t−1, Δt is the time lag between observations Y_t−1 and Y_t, and Z_t are i.i.d. normal (0, 1) random variables. In most cases, one cannot choose the rate at which data is generated – observation rate is typically dictated by equipment limitations or by historical convention – and applying the discretization scheme directly to the observed data may yield very inaccurate estimates.

More accurate inference is made possible, however, by incorporating the idea of missing data into the approximation approach. In this framework, the Δt of the discretization scheme can be reduced to below the rate at which data is actually gathered. The complete data Y_t of the specified model then becomes either missing or observed. Simulation could be used to integrate out the missing data and compute maximum likelihood estimates of the parameters (Pedersen, 1995). The difficulty of this simulated maximum likelihood estimation method lies in the difficulty of finding an efficient simulation method. See Durham and Gallant (2002) for an overview.

The same methodology – combining the Euler-Maruyama approximation with the concept of missing data – can also be used to estimate posterior distributions in the context of Bayesian inference. For example, one can use the Markov chain Monte Carlo (MCMC) strategy of a Gibbs sampler to conditionally draw samples of parameters and missing data, and form posterior estimates from these samples (Jones, 1998; Eraker, 2001; Elerian, Chib, and Shephard, 2001). While the approximation can be made more accurate by reducing the discretization step size Δt, this will generally cause the Gibbs sampler to converge at a very slow rate. Not only does the reduction in discretization step size lead to more missing data - requiring more simulation time per iteration – but adjacent missing data values become much more correlated, leading to substantially slower convergence.

For more efficient computation, Elerian, Chib, and Shephard (2001) suggested conditionally drawing missing data using random block sizes. Along similar lines but from a general perspective, Liu and Sabatti (2000) adapted group Monte Carlo methodology to this problem: changing the block size and using group Monte Carlo to update the blocks. Another possible approach to drawing missing data is to attempt to update all values in a single step. Roberts and Stramer (2001) proposed first transforming the missing data so that the variance is fixed and constant; then a proposal for all transformed missing data between two observations is drawn from either a Brownian bridge or an Ornstein-Uhlenbeck process, and accepted using the Metropolis algorithm. Chib, Pitt, and Shephard (2004) proposed a different transformation method, avoiding the use of variance-stabilizing transformations. Golightly and Wilkinson (2008) extended this approach, proposing a global Gibbs sampling scheme that can be applied to a large class of diffusions (where reducibility is no longer required). Stuart, Voss, and Wilberg (2004) also investigated conditional path sampling of SDEs, but employed a stochastic PDE-based approach instead. Beskos, Papaspiliopoulos, Roberts, and Fearnhead (2006) proposed a method which not only draws all the missing data at once, as these other researchers have suggested, but does so using the actual SDE, rather than an Euler-Maruyama discretization. This is accomplished using exact retrospective sampling of the actual diffusion paths. For further details on this inference approach, see Beskos and Roberts (2005) and Beskos, Papaspiliopoulos, and Roberts (2009).

1.2 The multiresolution approach

While there has been much investigation on how to update missing data values in an Euler-Maruyama approximation scheme, all such schemes rely on a single discretization level for approximating the true likelihood. This leads to a delicate balance: on one hand, low resolution (large Δt) approximations require less computation effort, but the results are inaccurate; on the other hand, high resolution (small Δt) approximations are more accurate, but they require very intense computation. We propose a multiresolution framework, which simultaneously considers a collection of discrete approximations to estimate the posterior distributions of the parameters, such that different levels of approximations are allowed to communicate with one another. There are three critical advantages to this approach over using only one approximation level. First, the convergence rate of the MCMC simulation can be substantially improved; coarser approximations help finer approximations converge more quickly. Second, a more accurate approximation to the diffusion model can be constructed using multiple discretization schemes: each level’s estimates of the posterior distribution can be combined and improved through extrapolation. Third, the overall accuracy of the posterior estimates can be augmented incrementally. If a smaller value of Δt is later determined necessary, the computational burden is considerably lower relative to starting a brand new sampler at the new value of Δt. This last feature allows the multiresolution framework to be most useful in practice, as the appropriate value of Δt is typically unknown at the outset of analysis. Allowing its value to be decreased incrementally over the course of analysis can be of great practical service.

Taken in combination, these three features of the multiresolution method allow for more computationally efficient, more accurate, and more convenient inference of the parameters. The remainder of this paper is organized as follows: Section 2 introduces the general notation used in this paper. Section 3 introduces the multiresolution sampler, a cross-chain MCMC algorithm between Euler-Maruyama approximations at different resolution levels. Section 4 describes how samples from these levels can be combined through extrapolation to form more accurate estimates of the true posterior distribution. Practical implementations the multiresolution approach – combining multiresolution sampling with extrapolation – are presented in Section 5. The performance of the proposed method is illustrated with three different SDE applications where no analytic form of the likelihood is presently known. The paper concludes with a discussion in Section 6.

2 Notation and two illustrative examples

It is instructive to examine simple examples of diffusions to better understand the details of different inference strategies. One of the simplest SDEs is the Ornstein-Uhlenbeck (OU) process:

$$\mathrm{d}{Y}_t=\gamma (\mu -Y_t)\mathrm{d}t+\sigma \mathrm{d}{B}_t.$$

It is fortunate that the exact solution to this equation is known, thus allowing us to directly examine the error introduced by approximate inference strategies.

Let Y = (Y₀, Y₁, ···, Y_n) denote the n + 1 values of observed data, beginning with an initial value Y₀. For simplicity, it is assumed that the observations Y have been observed at regular time intervals of ΔT. The exact likelihood of Y under the OU process is:

$$f_{\text{exact}}(\mathit{Y}\mid \mu ,\gamma ,\sigma )=\prod _{t=1}^n\frac{1}{\sqrt{\pi g}\sigma }exp\left\{-\frac{1}{g{\sigma }^2}{\left((\mu -Y_t)-\sqrt{1-\gamma g}(\mu -Y_{t-1})\right)}^2\right\},$$

where g = (1 − exp(−2γΔT))/γ, and for simplicity we ignore the initial distribution of Y₀ and treat it as a fixed value. In order to contrast this exact likelihood with Euler-Maruyama approximations to the likelihood, we introduce notation to describe the complete data – the union of the observations Y with the intermediate values of missing data. Let Y^(k) be the vector of complete data, where we put 2^k − 1 regularly spaced values of missing data between two successive observations, such that the complete data interobservation time in Y^(k) is Δt = ΔT/2^k. For example, Y⁽⁰⁾ = Y, and ${\mathit{Y}}^{(1)}=\left(Y_0^{(1)},Y_1^{(1)},\cdots ,Y_{2n-1}^{(1)},Y_{2n}^{(1)}\right)$. In this example with k = 1, the even indices correspond to observed values, and the odd indices to missing values. Generally, the elements of the vector Y^(k) are labeled from 0 to 2^kn, with every 2^k th element corresponding to an actual observation. The likelihood of the complete data under the Euler-Maruyama approximation is

$$f_k\left({\mathit{Y}}^{(k)}\mid \mu ,\gamma ,\sigma \right)=\prod _{j=1}^{2^{k}n}\frac{1}{\sqrt{2\pi \mathrm{\Delta }t}\sigma }exp\left\{-\frac{1}{2\mathrm{\Delta }t{\sigma }^2}{\left(Y_j^{(k)}-Y_{j-1}^{(k)}-\gamma \mathrm{\Delta }t(\mu -Y_{j-1}^{(k)})\right)}^2\right\}.$$

Note that two different choices of k correspond to two different Euler-Maruyama approximations. The observed data will be the same, yet correspond to differently indexed elements. For instance, if $Y_j^{(k)}$ is an observed value of the process, then $Y_{2j}^{(k+1)}$ will be the identical value. For convenience, we use Y^{k} to denote all the missing data in the kth approximation scheme, Y^{k} = Y^(k)\Y.

The exact posterior distribution of the parameters in the OU process can be found by specifying a prior p(μ, γ, σ): f_exact (μ, γ, σ | Y) ∝ p(μ, γ, σ) f_exact (Y | μ, γ, σ, Y₀). The Euler-Maruyama approximation is found by integrating out the missing data:

$$f_k(\mu ,\gamma ,\sigma \mid \mathit{Y})\propto {\int }_{{\mathit{Y}}^{\{k\}}}p(\mu ,\gamma ,\sigma )f_k\left({\mathit{Y}}^{(k)}\mid \mu ,\gamma ,\sigma \right)\mathrm{d}{\mathit{Y}}^{\{k\}}.$$

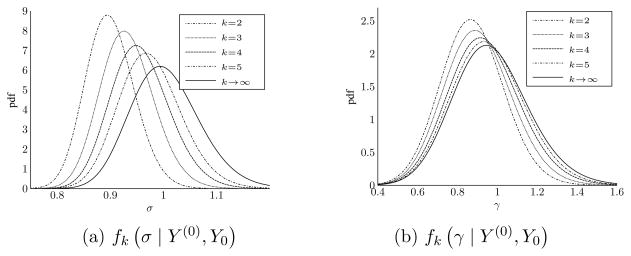
For the OU process, the posterior density f_k(μ, γ, σ | Y) can be calculated analytically. As k → ∞, f_k (μ, γ, σ | Y) will approach the true posterior f_exact (μ, γ, σ | Y). This is illustrated in Figure 1, which plots the posteriors of f_k (σ | Y) and f_k (γ | Y) for several values of k, along with the respective true posteriors. These posteriors are based on 200 observations of a simulated OU process with ΔT = 0.5, μ = 0, γ = 1, and σ = 1. The noninformative (improper) prior p (μ, γ, σ) ∝ γ/σ was used, replicating the example of Liu and Sabatti (2000).

Figure 1.

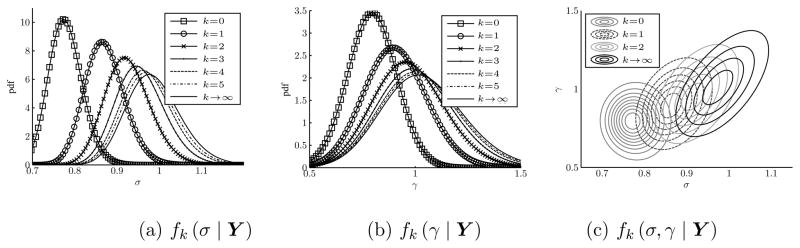
Euler-Maruyama approximation of the posterior of σ and γ in the OU process. Posteriors are based on 200 points of simulated data with ΔT = 0.5, μ = 0, and σ = γ = 1. The prior is p (μ, γ, σ) ∝ γ/σ. The third panel is a contour plot showing the joint parameter space.

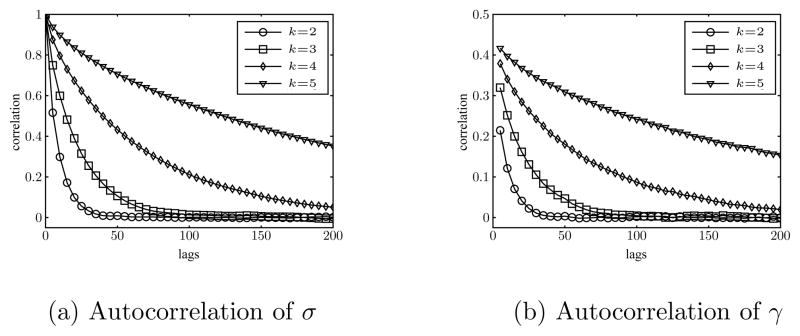
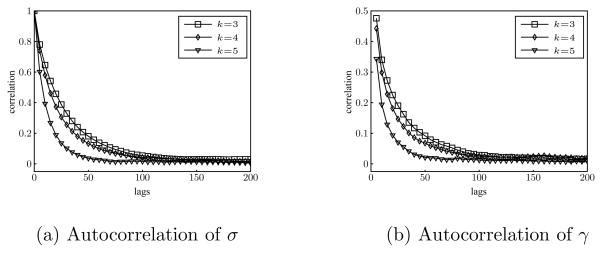
As described in the introduction, the difficulty with this approximation scheme lies in the integration of the missing data. Unlike the OU process, most SDE applications require sampling of both the parameters and the missing data, and these are all strongly dependent on one another. Consider the common solution of using a Gibbs sampler to integrate out the missing data: the joint posterior of both parameters and missing data is sampled conditionally, one parameter or missing data value at a time. As k increases, not only does it take longer to iterate the sampler – as there is more missing data – but each sequential draw is increasingly correlated. With all other values held constant, the conditional draws are almost deterministic: the sampler becomes nearly trapped. To illustrate this difficulty, a Gibbs sampler was run to generate samples from the posterior distributions of the parameters, using the same set of simulated data of the OU process as in Figure 1. The autocorrelations of sampled σ and γ are shown in Figure 2, both increasing substantially with k. This highlights the trade-off in using the Euler-Maruyama approximation approach. While it allows for numerical tractability, it can be very computationally expensive to achieve a high degree of accuracy relative to the true posterior specified by the original diffusion.

Figure 2.

Autocorrelation of the posterior samples of σ and γ of the OU process from a Gibbs sampler output. Convergence slows as k increases.

With its constant diffusion function, the OU process is a very special example of an SDE. A more complex SDE can help demonstrate some of the practical difficulties in working with these types of models. A good example of this is the Feller process – frequently referred to as CIR model in the economics literature (Cox, Ingersoll, and Ross, 1985) – as the diffusion function is not constant. The Feller process is

$$\mathrm{d}{Y}_t=\gamma (\mu -Y_t)\mathrm{d}t+\sigma \sqrt{Y_t}\mathrm{d}{B}_t.$$ (2.1)

The support of Y_t is 0 to ∞, and the parameters γ, μ, and σ are also constrained to be non-negative. A closed-form solution to the joint posterior of parameters of the Feller process can be written using the special function I_a (·), the modified Bessel function of order a (Kou and Kou, 2004):

$$\begin{array}{l}{f}_{\text{exact}}(\mu ,\gamma ,\sigma \mid \mathit{Y})\propto p(\mu ,\gamma ,\sigma ){\left(\frac{2\gamma e^{\gamma \mathrm{\Delta }T(\frac{\mu \gamma }{{\sigma }^2}-\frac{1}{2})}}{{\sigma }^2(1-e^{-\gamma \mathrm{\Delta }T})}\right)}^{n-1}\times \\ \prod _{i=1}^{n-1}{(Y_i/Y_{i-1})}^{\frac{\mu \gamma }{{\sigma }^2}-\frac{1}{2}}exp\left[-\frac{2\gamma (Y_i+e^{-\gamma \mathrm{\Delta }T}{Y}_{i-1})}{{\sigma }^2(1-e^{-\gamma \mathrm{\Delta }T})}\right]I_{\frac{2\mu \gamma }{{\sigma }^2}-1}\left(\frac{4\gamma \sqrt{Y_{i-1}{Y}_i{e}^{-\gamma \mathrm{\Delta }T}}}{{\sigma }^2(1-e^{-\gamma \mathrm{\Delta }T})}\right).\end{array}$$ (2.2)

This expression allows the error resulting from using the Euler-Maruyama approximation to be examined directly. Figure 3 shows an example of different approximate posteriors using one simulated dataset from the Feller process. A total of 200 data points were drawn using ΔT = 0.5, and μ, γ, and σ all equal to 1. We use the same prior p (μ, γ, σ) ∝ γ/σ as before.

Figure 3.

Posterior distributions of σ and γ in the Feller process based on Euler-Maruyama approximations. Posteriors are based on 200 points of simulated data with ΔT = 0.5, and μ = σ = γ = 1. p (μ, γ, σ) ∝ γ/σ.

Here, the approximate Euler-Maruyama parameter posterior f_k(μ, γ, σ | Y) cannot be obtained analytically; a Gibbs sampler is used to integrate out the missing data instead. Using the prior above, the conditional distributions of each parameter γ, κ = γμ, and σ² are standard distributions: either a (truncated) normal or an inverse-Gamma. The conditional distribution of each value of missing data, however, is not a traditional one:

$$f_k(Y_j^{(k)}\mid \mu ,\sigma ,\gamma ,Y_{j-1}^{(k)},Y_{j+1}^{(k)})\propto {(Y_j^{(k)})}^{-1/2}exp\left[-\frac{1}{2{\sigma }^2\mathrm{\Delta }t}\left(\frac{{(Y_j^{(k)})}^2}{Y_{j-1}^{(k)}}-(1-{\gamma }^2\mathrm{\Delta }{t}^2+\frac{2\gamma \mu \mathrm{\Delta }t}{Y_{j-1}^{(k)}})Y_j^{(k)}+\frac{1}{Y_j^{(k)}}{(Y_{j+1}^{(k)}-\gamma \mu \mathrm{\Delta }t)}^2\right)\right].$$ (2.3)

For most SDEs, the conditional distribution of missing data will not be a familiar one that can be easily sampled from. One possibility is to use a Metropolized-Gibbs step: first draw a new value of the missing data from a proposal distribution; then accept or reject the proposed draw according to the Metropolis-Hastings rule. Among many possible proposal distributions, a convenient one is:

$${\pi }_k\left(Y_j^{(k)}\mid \mathit{\theta },Y_{j-1}^{(k)},Y_{j+1}^{(k)}\right)~\mathcal{N}\left((Y_{j+1}^{(k)}+Y_{j-1}^{(k)})/2,{\sigma }^2\left(Y_{j-1}^{(k)},\mathit{\theta }\right)\mathrm{\Delta }t/2\right).$$

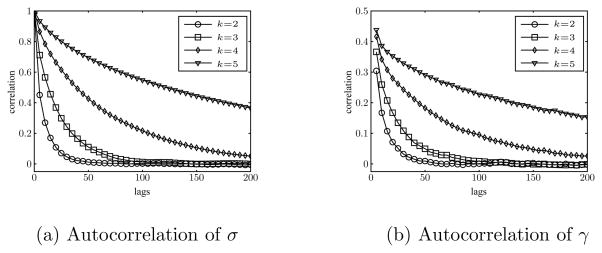
This normal proposal has the advantage of being readily drawn from and asymptotically correct: as Δt → 0, the acceptance rate approaches 1 (Eraker, 2001). Note that when the support of the process is strictly positive, we can simply use a truncated normal distribution. Using this proposal, we applied the (Metropolized) Gibbs sampler to the Feller process. The results serve as a second illustration of the difficulty of using the Gibbs approach to integrate out the missing data as k becomes large. Figure 4 shows how the autocorrelations of σ and γ substantially increase with k.

Figure 4.

Autocorrelation of Feller process posterior samples σ and γ from the output of a Gibbs sampler. Convergence slows as k increases.

The OU and Feller process examples highlight the problems associated with applying a Gibbs sampler to computing posteriors under Euler-Maruyama approximations. While it may be theoretically possible to achieve arbitrary accuracy by selecting the appropriate value of k, it may not be practically feasible to wait for the Gibbs sampler to converge. Furthermore, the OU process and the Feller process are the rare cases where the difference between the approximated and true posteriors can be observed. In practice, the accuracy of a selected Euler-Maruyama approximation is unknown; one only knows that it converges to the correct distribution as k → ∞.

3 Multiresolution sampling

3.1 The sampler

Traditionally, the use of an Euler-Maruyama approximation requires a single resolution choice (corresponding to a single choice of Δt). The selection of a low resolution (large Δt) will result in a quickly-converging sampling chain, which is, unfortunately, inaccurate. A high resolution choice (small Δt) can result in a highly accurate estimate, yet will be slow – many samples will be required both for convergence and to build up an estimate of the posterior distribution.

In contrast, our proposed multiresolution sampler employs a collection of Euler-Maruyama discretization at different resolutions. “Rough” approximations are used to locate the important regions of the parameter space, while “fine” approximations fill in and explore the local details. Low-resolution approximations quickly explore the global (parameter) space without getting stuck in one particular region; high-resolution approximations utilize the information obtained at the low-resolution explorations to yield accurate estimates in a relatively short time. By combining the strength of low and high resolutions (and mixing global and local explorations), this approach provides an inference method that is both fast and accurate. The key ingredient of the multiresolution sampler is to link different resolution approximations, using the empirical distribution of the samples collected at low resolutions to leap between states during high resolution exploration.

In the multiresolution sampler, Euler-Maruyama approximations at m consecutive resolutions k, k + 1, …, k + m − 1 are considered together. A sampling chain associated with each resolution is constructed. The multiresolution sampler starts from the lowest resolution chain k. This initial chain is sampled using any combination of local updates. For example, one may use the simple Gibbs algorithm to update the missing data Y^{k} and the parameters θ. Alternatively, one could combine the Gibbs algorithm with the block-update strategy of Elerian, Chib, and Shephard (2001) or the group-update algorithm of Liu and Sabatti (2000) to evolve (Y^{k}, θ).

After an initial burn-in period, an empirical distribution of (Y^{k}, θ) is constructed from the Monte Carlo samples. The multiresolution sampler then moves to the second lowest resolution chain, at level k +1. At each step of the multiresolution sampler, the state of (Y^{k+1}, θ) is updated using one of two operations. With probability 1 − p, say 70%, the previous sample ( ${\mathit{Y}}_{\mathit{old}}^{\{k+1\}}$, θ_old) undergoes a local update step to yield the next sample. For example, in the case of Gibbs, this involves conditionally updating each element of θ_old and each missing data value in ${\mathit{Y}}_{\mathit{old}}^{\{k+1\}}$. With probability p, say 30%, a global, cross-resolution move is performed to leap ( ${\mathit{Y}}_{\mathit{old}}^{\{k+1\}}$, θ_old) to a new state.

The cross-resolution move is accomplished in three stages. First, a state ( ${\mathit{Y}}_{\mathit{trial}}^{\{k\}}$, θ_trial) is drawn uniformly from the empirical distribution formed by the earlier chain at resolution k. Second, ( ${\mathit{Y}}_{\mathit{trial}}^{\{k\}}$, θ_trial) is augmented to ( ${\mathit{Y}}_{\mathit{trial}}^{\{k+1\}}$, θ_trial) by generating the necessary additional missing data values (as missing data in the Euler approximations at levels k and (k+1) have different dimensions). Third, ( ${\mathit{Y}}_{\mathit{trial}}^{\{k+1\}}$, θ_trial) is accepted to be the new sample with a Metropolis-Hastings type probability. As this cross-resolution step plays a pivotal role in the multiresolution sampler’s effectiveness, we shall describe it in full detail in Section 3.2.

After running the (k+1)-resolution chain for a burn-in period, an empirical distribution of (Y^{k+1}, θ) is constructed from the posterior samples; this empirical distribution will in turn help the (k+2)-resolution chain to move. The multiresolution sampler on the (k+2)-resolution chain is then started and updated by the local move and the global cross-resolution move with probabilities 1 − p and p. In the cross-resolution move, the old sample ( ${\mathit{Y}}_{\mathit{trial}}^{\{k+2\}}$, θ_trial) leaps to a new state with the help of the empirical distribution constructed by the (k+1)-resolution chain. In this way, the multiresolution sampler successively increases the resolution level until the Euler-Maruyama approximation with the finest resolution k+m is reached. Each sampling chain (other than the one at the lowest resolution) is updated by two operations: the local move and the cross-resolution move. The basic structure of the multiresolution sampler is summarized in Algorithm 1

Algorithm 1.

The Multiresolution Sampler

Let i = 0. Start from the k-resolution chain. Collect samples from fk (θ, Y{k} | Y) using any combination of local updating algorithms. Discard some initial samples as burn-in, and retain the remaining samples as the empirical distribution of (Y{k}, θ) from fk (θ, Y{k} | Y). Let i ← i + 1. Start the (k+i)-resolution chain. Initialize the chain to a state ( ${\mathit{Y}}_{\mathit{old}}^{\{k+i\}}$, θold). With probability 1 − p, perform a local update step to generate a new sample from fk+i (θ, Y{k+i} | Y), using any combination of local updates. With probability p, perform a cross-resolution move: Randomly select a state ( ${\mathit{Y}}_{\mathit{trial}}^{\{k+i-1\}}$, θtrial) from the empirical distribution of the (k+i-1)-chain. Augment ( ${\mathit{Y}}_{\mathit{trial}}^{\{k+i-1\}}$, θtrial) to ( ${\mathit{Y}}_{\mathit{trial}}^{\{k+i\}}$, θtrial) by generating additional missing data values. With a Metropolis-Hasting type probability r, accept ( ${\mathit{Y}}_{\mathit{trial}}^{\{k+i\}}$, θtrial) as the next sample in the chain; with probability 1 − r, keep the previous values of ( ${\mathit{Y}}_{\mathit{old}}^{\{k+i\}}$, θold) as the next sample in the chain. Rename the most recent draw as ( ${\mathit{Y}}_{\mathit{old}}^{\{k+i\}}$, θold), and repeat from Step 4 until a desired number of samples are achieved (typically determined in part by monitoring the chain for sufficient evidence of convergence). Discard some initial samples of the chain as burn-in, and retain the remaining samples to form an empirical distribution of (Y{k+i}, θ) from fk+i (θ, Y{k+i} | Y). If a finer approximation to the SDE is desired, repeat from Step 3.

3.2 The cross-resolution move

The cross-resolution move provides the means for successive resolution approximations to communicate with each other, allowing a rapidly mixing low resolution approximation to speed up the convergence of a higher resolution chain. There are two key insights behind the move: (i) As the amount of missing data increases, the posterior distributions of the parameters under different resolutions become closer; an example of this can be seen in Figures 1 and 3, which illustrate how the posterior distributions of θ overlap to an increasing degree as k, the resolution level, increases. Notably, the high resolution cases are where help is most needed because of the slow convergence of the local update. This suggests that in the sampling of a high resolution chain (say k = 5), generating proposals (independently) from a lower resolution chain (say k = 4) will have a high chance of being accepted, and will significantly speed up the high resolution chain’s convergence. (ii) Although it is not feasible to directly draw from an Euler-Maruyama distribution, we can employ the empirical distribution to resolve this difficulty. With a sufficient number of samples, the empirical distribution built on them will be nearly identical to the analytic one. Furthermore, it is trivial to draw from an empirical distribution: simply select uniformly from the existing samples.

Based on these two insights, the cross-resolution move is implemented in the multiresolution sampler by using the empirical distribution of a low resolution chain to generate a new sample for the high resolution chain. To carry this move out, it is important to note that different resolution levels do not share the same dimensionality. Thus, once a sample is drawn from the empirical distribution of a lower resolution scheme, we must augment it with additional missing data values. A natural way of doing this is to divide the missing data at resolution (k+1) into two groups, Y^{k+1} = Y^{k} ∪ Z^{k+1}, where Z^{k+1} are the additional missing data at resolution (k+1). Figure 5 illustrates how such successive approximations line up relative to one another. Thus, the lower resolution chain k generates the missing Y^{k}, and we are free to propose the remaining Z^{k+1} from any distribution

Figure 5.

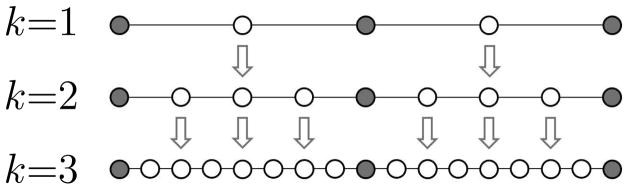
Graphic depicting three Euler-Maruyama approximations. Shaded circles represent observed data, while empty circles represent missing data. The arrows show how a draw from one approximation can be partially used as a proposal in the next.

$$T_{k+1}({\mathit{Z}}^{\{k+1\}}\mid \mathit{\theta },{\mathit{Y}}^{\{k\}},\mathit{Y}).$$

Typically, the dimensionality of Z^{k+1} is high, but each of its components are independent of each other, conditioned on θ, Y^{k}, and Y, such that T_k+1 boils down to independent draws from univariate distributions (or d-dimensional distributions for a d-dimensional SDE), which are much easier to construct.

Algorithm 2.

Cross-resolution Move of Multiresolution Sampler

Let (θold, ${\mathit{Y}}_{\mathit{old}}^{\{k+1\}}$) be the current set of parameters and missing data. Draw (θtrial, ${\mathit{Y}}_{\mathit{trial}}^{\{k\}}$) from the empirical distribution of fk(θ, Y{k}|Y). Let ${\pi }_k^{\mathit{trial}}=f_k({\mathit{\theta }}_{\mathit{trial}},{\mathit{Y}}_{\mathit{trial}}^{\{k\}}\mid \mathit{Y})$. Draw ${\mathit{Z}}_{\mathit{trial}}^{\{k+1\}}$ from a distribution $T_{k+1}({\mathit{Z}}^{\{k+1\}}\mid {\mathit{\theta }}_{\mathit{trial}},{\mathit{Y}}_{\mathit{trial}}^{\{k\}},\mathit{Y})$. Let ${\tau }_{k+1}^{\mathit{trial}}=T_{k+1}({\mathit{Z}}_{\mathit{trial}}^{\{k+1\}}\mid {\mathit{\theta }}_{\mathit{trial}},{\mathit{Y}}_{\mathit{trial}}^{\{k\}},\mathit{Y})$. Recall that ${\mathit{Y}}_{\mathit{trial}}^{\{k+1\}}={\mathit{Y}}_{\mathit{trial}}^{\{k\}}\cup {\mathit{Z}}_{\mathit{trial}}^{\{k+1\}}$. Let ${\pi }_{k+1}^{\mathit{trial}}=f_{k+1}({\mathit{\theta }}_{\mathit{trial}},{\mathit{Y}}_{\mathit{trial}}^{\{k+1\}}\mid \mathit{Y})$. Similarly, let ${\pi }_k^{\mathit{old}}=f_k\left({\mathit{\theta }}_{\mathit{old}},{\mathit{Y}}_{\mathit{old}}^{\{k\}}\mid \mathit{Y}\right),{\tau }_{k+1}^{\mathit{old}}=T_{k+1}\left({\mathit{Z}}_{\mathit{old}}^{\{k+1\}}\mid {\mathit{\theta }}_{\mathit{old}},{\mathit{Y}}_{\mathit{old}}^{\{k\}},\mathit{Y}\right)$ and ${\pi }_{k+1}^{\mathit{old}}=f_{k+1}\left({\mathit{\theta }}_{\mathit{old}},{\mathit{Y}}_{\mathit{old}}^{\{k+1\}}\mid \mathit{Y}\right)$. Accept $\left({\mathit{\theta }}_{\mathit{trial}},{\mathit{Y}}_{\mathit{trial}}^{\{k+1\}}\right)$) as the next sample from fk+1(θ, Y{k+1} | Y) with probability $$r=min\left\{1,\frac{{\pi }_{k+1}^{\mathit{trial}}/({\pi }_k^{\mathit{trial}}{\tau }_{k+1}^{\mathit{trial}})}{{\pi }_{k+1}^{\mathit{old}}/({\pi }_k^{\mathit{old}}{\tau }_{k+1}^{\mathit{old}})}\right\}.$$ Otherwise, with probability 1 − r, keep $\left({\mathit{\theta }}_{\mathit{old}},{\mathit{Y}}_{\mathit{old}}^{\{k+1\}}\right)$ as the next sample.

Algorithm 2 summarizes the cross-resolution move from the kth approximation to the (k+1)th approximation. A reader familiar with the equi-energy sampler (Kou, Zhou, and Wong, 2006) might note that the idea of letting different resolutions communicate with each other echoes the main operation of the equi-energy sampler, in which a sequence of distributions indexed by a temperature ladder is simultaneously studied: the flattened distributions help the rough ones to be sampled faster. Indeed, it was the equi-energy sampler’s noted efficiency that motivated our idea of the cross-resolution move. We conclude this section by giving practical guidelines for how to choose the proposal distribution T_k+1, and how to determine the appropriate probability p of a cross-resolution move.

3.2.1 Choosing T_k+1

We are free to choose the distribution T_k+1 to conditionally augment the additional missing data (Step 2). A good choice, however, will make the acceptance rate of the independence move approach 1 as k increases. To see how the cross-resolution move improves the Monte Carlo convergence, let us turn to the OU example process introduced in Section 2. A simple proposal in this case is

$$T_{k+1}(Y_j^{(k+1)}\mid \mathit{\theta },Y_{j-1}^{(k+1)},Y_{j+1}^{(k+1)})~\mathcal{N}\left((Y_{j+1}^{(k+1)}+Y_{j-1}^{(k+1)})/2,{\sigma }^2(Y_{j-1}^{(k+1)},\mathit{\theta })\mathrm{\Delta }t/2\right)$$

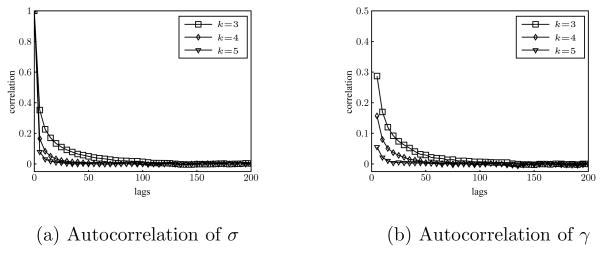
independently for each $Y_j^{(k+1)}\in {\mathit{Z}}^{\{k+1\}}$, where Δt = ΔT/2^k+1. This is the proposal used to update the missing data in the Gibbs sampler of Section 2. The autocorrelations of the OU process parameters σ and γ under the cross-resolution move are shown in Figure 6. These can be directly contrasted with the Gibbs sampler autocorrelations shown in Figure 2, as the identical data set was used in both samplers. In addition to the evident improvement of the autocorrelation, we note that in the cross-resolution move – in contrast to the local update move – the autocorrelation decreases as k increases. This reflects the fact that the acceptance rate is increasing as the successive Euler-Maruyama approximations increasingly overlap with one another.

Figure 6.

Autocorrelation of OU process parameters σ and γ from the output of a multiresolution sampler. Convergence improves as k increases.

A good choice of T_k+1 can make the multiresolution sampler very efficient. On the other hand, a poor choice of T_k+1 can result in a low acceptance rate of the cross-resolution proposal. There does not appear to be, however, a foolproof recipe that guarantees a good distribution T_k+1 for any arbitrary SDE. One useful technique that can make T_k+1 easier to choose is to transform some aspect of the SDE to stabilize the variance (Roberts and Stramer, 2001). For instance, if Y_t is a Feller process (2.1) and we let $Z_t=f(Y_t)=2\sqrt{Y_t}$, then by Itō’s formula $\mathrm{d}{Z}_t=(\frac{2\mu }{Z_t}-\frac{Z_t}{2}-\frac{{\sigma }^2}{2Z_t\gamma })\gamma \mathrm{d}t+\sigma \mathrm{d}{B}_t$. The distribution of missing data under Z_t, with its constant variance function, is much closer to a normal than the original Y_t. Figure 7 shows the autocorrelation of σ and γ from the output of the multiresolution sampler on Z_t. As k increases, the convergence rate of the multiresolution sampler improves. This stands in contrast to Figure 4 of the Gibbs sampler.

Figure 7.

Autocorrelation of variance-stabilized Feller process parameters σ and γ from the output of a multiresolution sampler. Convergence improves as k increases.

3.2.2 Choosing p

The probability p of making a cross-chain move in the multiresolution sampler (or the fraction of moves on a deterministic schedule) can be chosen as follows. Consider a local-update MCMC algorithm (for example, the Gibbs sampler or the block update algorithm). For a given quantity of interest τ = h(θ), we may approximate the effective sample size E_G of N iterations of these local updates up to first order by

$$E_G\approx N\frac{1-\eta }{1+\eta },$$

where η is the lag-1 autocorrelation of τ: η = cor(τ^(t), τ^(t+1)) (see for instance Liu, 2001, Section 5.8). Now suppose that at each cycle of the local updates, a cross-resolution move targeting p(θ, Y^{k+1} | Y) with acceptance rate a is made with probability p. Then τ^(t) and τ^(t+1) are independent with probability ap and have correlation η with probability 1−ap, such that the lag-1 autocorrelation of τ using these cross-resolution moves decreases to (1−ap)η. If E_M denotes the effective sample size of the multiresolution sampler combining local updates with cross-resolution proposals, the efficiency of this algorithm relative to the local updates alone can be measured as

$$\frac{E_M}{E_G}=\frac{(1-\eta +ap\eta )(1+\eta )}{(1+\eta -ap\eta )(1-\eta )}.$$ (3.1)

The value of p can then be adjusted if a and η are known, or estimated after an initial pilot run. For instance, if the basic Gibbs sampler has lag-1 autocorrelation η = .75 for a parameter of interest, it takes ap = .25 to double the effective sample size. For η = .9, we only need ap = .1, which helps quantify the great potential of multiresolution sampling when the autocorrelations of the local updates are high.

4 Multiresolution inference

The multiresolution sampler uses the rapid convergence of low resolution chains to in turn speed up the high resolution chains. At the completion of sampling, the multiresolution sampler has samples from several approximation levels. For the subsequent statistical inference, a naive approach might be to simply focus on the highest resolution approximation – since it is the most accurate – and ignore the low resolution samples, treating them just as a computational byproduct of the procedure. This approach, however, does not use all the samples effectively, wasting a great deal of both information and computation. In fact, the different approximations can be combined by extrapolation to significantly reduce the estimation error.

4.1 Multiresolution extrapolation

Extrapolation is a technique often used in numerical analysis. It is a series acceleration method used to combine successive approximations to reduce error. Richardson extrapolation (Richardson, 1927) is a general statement of the approach, which can be applied whenever a function F(h) converges to a value F₀ = lim_h→0 F(h). Consider the expansion of such a limit:

$$F_0=F(h)+a_m{h}^m+O(h^{m^{\prime }}),$$ (4.1)

where m′ > m and a_m ≠ 0. Taking the view that F(h) is an approximation to the limit F₀, two successive approximations F(h) and $F(\frac{h}{s})$ can be combined to form a more accurate estimate of F₀ by eliminating the a_mh^m term in the expansion:

$$R(h)=\frac{s^{m}F(\frac{h}{s})-F(h)}{s^m-1}=F_0+O(h^{m^{\prime }}).$$

Compared to F(h), the error in R(h) is at least an order smaller. Additional extrapolation can be applied recursively to R(h) to eliminate even higher order terms in the expansion. The Romberg method of integration is an example of Richardson extrapolation applied to numerical integration (Romberg, 1955). Richardson extrapolation has also been applied to simulating and numerically solving SDEs (Talay and Tubaro, 1990; Kloeden, Platen, and Hofmann, 1995; Durham and Gallant, 2002).

In our Bayesian inference of diffusions, the multiresolution sampler gives us samples from several Euler-Maruyama approximations of the posterior distribution. Our goal is to combine them in order to have a more accurate estimate of the true posterior. To do so, we perform extrapolation. This multiresolution extrapolation allows us to reduce the discretization error by an order or more. For example, suppose a function g(θ) of the parameters is of scientific interest. An extrapolated point estimate can be obtained by first calculating the posterior mean or median of g(θ) based on the samples from each Euler-Maruyama approximation and then performing an extrapolation. Similarly, a 1 − α credible interval of g(θ) can be obtained by calculating its α/2 and 1 − α/2 quantiles from each Euler-Maruyama approximation and then performing an extrapolation on these quantiles. For most inference problems, point and interval estimation suffices. Occasionally, one might want to look at the marginal posterior density of a particular parameter θ_j. In this case, we can perform extrapolation on a kernel density estimate f̂(θ_j) at each value of θ_j on a grid. By piecing together these extrapolated values we obtain an extrapolated estimate for the marginal posterior density of θ_j.

A key ingredient of successful extrapolation is establishing the exponent m in equation (4.1). We will show in Appendix A that the Euler-Maruyama approximation for the posterior distribution has the exponent m = 1 for the posterior mean, quantiles, and kernel density estimates.

As an example of the method, consider combining the k = 2 and k = 3 approximations of a given quantile α of θ_j. Let us designate this extrapolated quantile estimate as $R_{\alpha }^{-1}(2\cup 3)$. With m = 1, and with the k = 3 approximation having twice the discretization rate as the k = 2 approximation, we have the formula

$$R_{\alpha }^{-1}(2\cup 3)=2F_{\alpha }^{-1}(k=3)-F_{\alpha }^{-1}(k=2).$$

Combining k = 3 and k = 4 is similar:

$$R_{\alpha }^{-1}(3\cup 4)=2F_{\alpha }^{-1}(k=4)-F_{\alpha }^{-1}(k=3).$$

Combining k = 2, k = 3, and k = 4, however, is different. Rather than combine the quantiles directly, we (recursively) combine the extrapolated estimates $R_{\alpha }^{-1}(2\cup 3)$ and $R_{\alpha }^{-1}(3\cup 4)$ together:

$$R_{\alpha }^{-1}(2\cup 3\cup 4)=\frac{1}{3}(4R_{\alpha }^{-1}(3\cup 4)-R_{\alpha }^{-1}(2\cup 3)).$$

Note that here this combination is to eliminate the next higher-order term; thus, in this formula, m = 2.

4.2 Illustration of multiresolution extrapolation

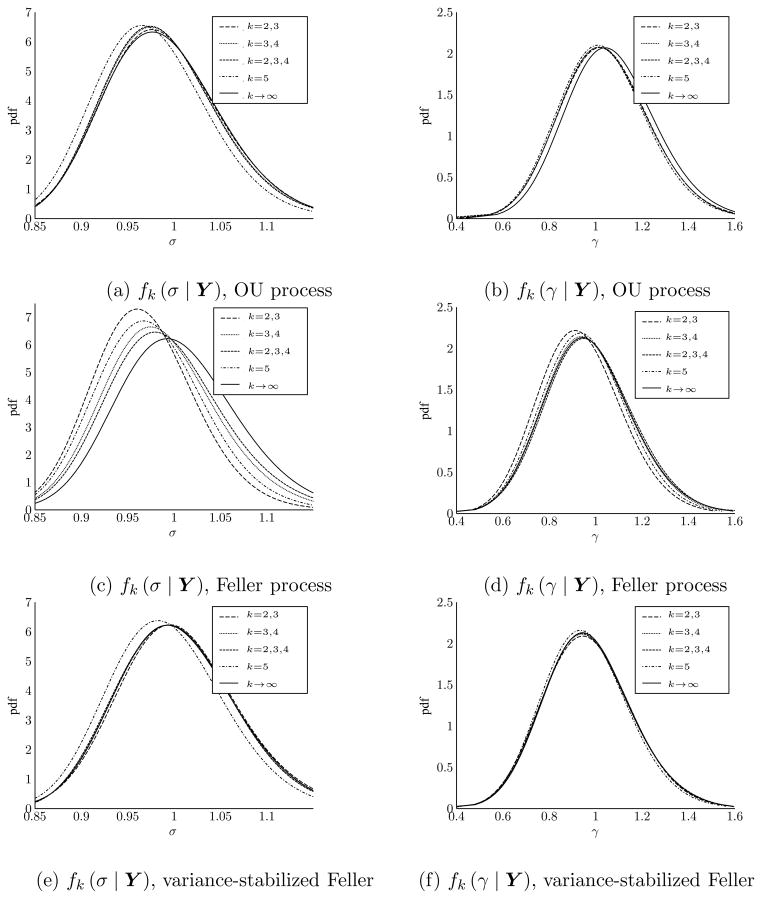
To provide an illustrative example, extrapolated density approximations for the OU, Feller, and variance-stabilized Feller processes are displayed in Figure 8. Several observations immediately follow from this Figure:

Figure 8.

Posterior distribution estimates of σ and γ for different diffusions. Posterior estimates are created by combining two or more Euler-Maruyama estimates of the posterior quantiles and reconstructing the estimate of the distribution.

1. Combining two posterior estimates through extrapolation significantly reduces the error. Combining the approximations using only 3 and 7 interpolated missing data points between observations (k = 2 and k = 3), for example, generally produces an estimate that is as accurate or even more accurate than the corresponding estimate based on a single approximation using 31 values of missing data (k = 5). This illustrates a major advantage of the multiresolution approach: using the combined strength of the multiresolution sampler and extrapolation, one does not always require a highly dense discretization rate for an accurate result; proper combination of low resolution approximations can often lead to a better result than a single high resolution approximation.

2. A comparison between the Feller and variance-stabilized Feller results again highlights the advantage of using a variance-stabilizing transformation wherever possible.

3. Combining three Euler-Maruyama approximation schemes (in this example, k = 2, 3, and 4), can be effective at reducing the overall error, as this eliminates both the first- and second-order errors. Thus, even in cases where the discretization error is largely in higher-order terms, the benefit derived from using extrapolation has the potential to be quite significant.

These observations suggest that whenever the computational challenge of sampling from a high-dimensional Euler-Maruyama approximation is substantial, it can be more efficient to sample from several lower-dimensional approximations and combine the resulting estimates with a final extrapolation step.

5 Multiresolution method in practice

In this Section, we shall apply the multiresolution approach to three realistic SDE models, one in biophysics and two in finance. Comparisons were made to chains that used only the simple Gibbs-type local updates. However, it is worth emphasizing that any strategy that increases the efficiency of the Gibbs sampler can be incorporated into the multiresolution sampler’s local updates. This includes the block-update strategies of Elerian, Chib, and Shephard (2001) or the group moves of Liu and Sabatti (2000). The metric we use for comparison is the relative mean squared error (MSE) R̂, the ratio of the mean squared error of the Gibbs approach to the mean squared error of the multiresolution approach, both relative to the true posterior parameter distribution in each example. Since the true posterior in these nontrivial examples cannot be obtained analytically, we performed an exhaustive search. Higher and higher resolution chains were run to full convergence (many millions of iterations), until the last chain matched the extrapolated estimate of the two chains directly below it to within 0.1 standard deviations on 50 equally spaced quantiles of each parameter’s marginal density. This last chain was then retained as a proxy for the ground truth.

5.1 Double-well potential model for optical trap

The following general potential model is used to model a wide number of natural phenomena:

$$\mathrm{d}{Y}_t=-U^{\prime }(Y_t)\mathrm{d}t+\sigma \mathrm{d}{B}_t,$$

where U(x) is a potential function, and U′(x) is the first derivative of U(x) with respect to x. In a variety of circumstances, such as enzymatic reactions and electron transfer, the potential function is characterized as having a double well. In such cases, the following potential is often used as a model:

$$U(x)\propto \gamma {(x^2-{\beta }^2)}^2+\gamma c(x^3/3-{\beta }^{2}x)$$

The SDE model corresponding to data Y_t observed in this potential is thus:

$$\mathrm{d}{Y}_t=-(4Y_t^3+c{Y}_t^2-4{\beta }^2{Y}_t-c{\beta }^2)\gamma \mathrm{d}t+\sigma \mathrm{d}{B}_t$$

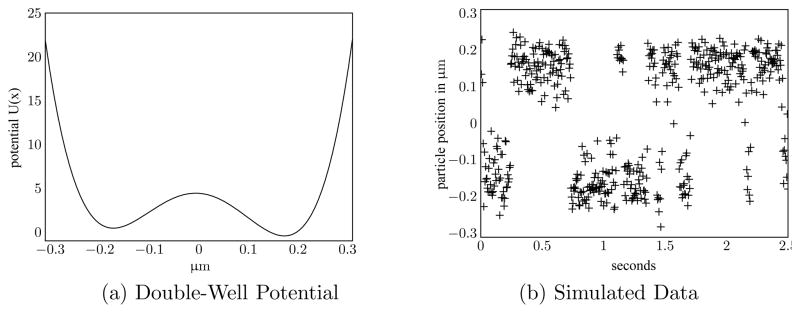
Note that U(x) has local minima at ±β and a local maximum at −c/4, provided c < 4|β|. Figure 9(a) plots the double-well potential U(x).

Figure 9.

Example of simulated data from a double-well potential model. β = 0.1725, c = 0.0259, γ= 5000, and σ = 3.

We apply this model to an example from biophysics. In this case, Y_t describes the location of a particle when placed in an optical trap. McCann, Dykman, and Golding (1999) studied the behavior of a submicrometer-sized dielectric particle in a double-well optical trap. They acquired the location of the particle in time using a high-speed camera. While McCann et al. have not made their data publicly available, they have published their estimates of the double-well potential itself, as well as some of the inferred particle positions over time. We fit the double-well potential model to these results and found values of β = 0.1725, c = 0.0259, γ = 5000, and σ = 3. Using these parameters, we simulated this process and sampled observations at a rate of ΔT = 1 ms to record a total of 500 data points. An example of simulated observations from the process are plotted in Figure 9(b).

Using an exhaustive numerical search, we determined that resolution level k = 5 was indistinguishable from our proxy for the ground truth. We compare the ratio of the MSE of the Gibbs approach to that of the multiresolution method as follows. After a burn-in period of 10,000 iterations, we ran the Gibbs sampler for 1000 iterations at resolution k = 5, i.e. with 31 values of missing data between observations. A prior p(γ, β², c, σ) ∝ γ/σ ·1{c < 4|β|} is used to obtain the parameter posteriors, where 1{·} denotes the indicator function. With this prior the conditional parameter draws of γ, κ = γc, β², and σ² are truncated normals or inverse-Gamma. We recorded the time it took to draw these 1000 samples, then gave the same time budget to the multiresolution sampler on levels k = 3 and k = 4; that is, with 7 and 15 values of missing data between observations. At level k = 4, the lag-1 parameter autocorrelations were around .85 and the cross-resolution proposals from k = 3 had a 30% acceptance rate. We set the cross-resolution proposal rate to p = 0.5, such that the multiresolution sampler at k = 4 is expected to have twice the effective sample size of the Gibbs sampler at k = 4 according to the rule-of-thumb in (3.1).

Each sampler (Gibbs and multiresolution) was run many times starting from different initial values, to produce the ratio of MSE between the Gibbs and multiresolution estimates displayed in Table 1. Here, the multiresolution sampler is roughly two to three times as efficient as a single Gibbs sampler. This is roughly the value we expect, assuming that (3.1) holds and that the computation time for Gibbs samplers doubles with each k.

Table 1.

Ratios of MSE. Estimates of posterior quantiles from a Gibbs sampler versus those from the multiresolution method for the double-well potential model over the same amount of computer time.

γ MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	2.4 ± 0.65
Q0.25	2.3 ± 0.64
Q0.5	2.2 ± 0.59
Q0.75	2.1 ± 0.54
Q0.95	1.8 ± 0.45

c MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	1.6 ± 0.34
Q0.25	2.2 ± 0.45
Q0.5	3.1 ± 0.66
Q0.75	3.0 ± 0.59
Q0.95	2.8 ± 0.59

5.2 Generalized CIR model for US treasury bill rate

Diffusions are often used as models for short-term interest rates in the field of mathematical finance. Chan et al. (1992) have suggested using the generalized Cox, Ingersoll and Ross (gCIR) model:

$$\mathrm{d}{Y}_t=\gamma (\mu -Y_t)\mathrm{d}t+\sigma Y_t^{\psi }\mathrm{d}{B}_t,$$

where γ, σ, ψ, and Y_t are all positive. Both the OU and Feller processes are special cases of this generalized process: ψ = 0 is the OU process and ψ = 1/2 is the Feller process.

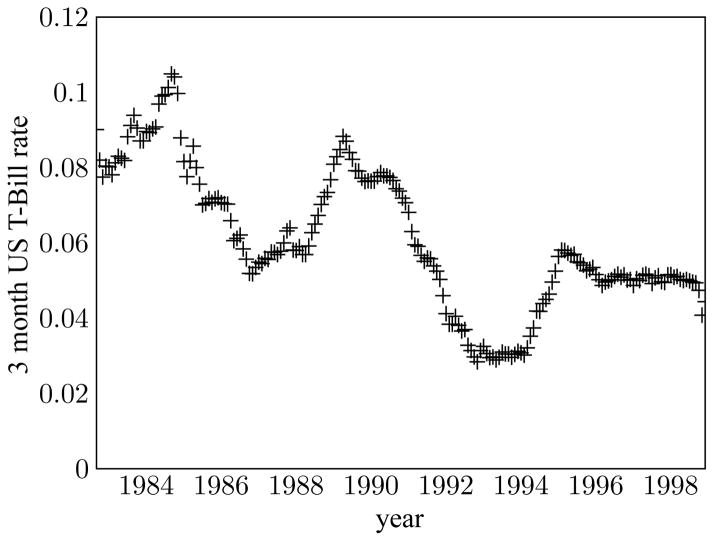
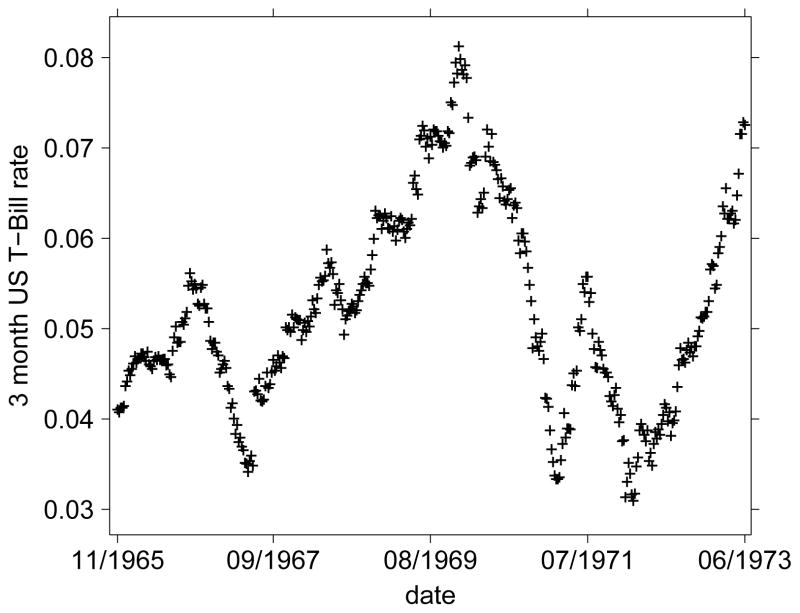
We apply the gCIR model to interest rate data consisting of 16 years of monthly records, from 8/1982 to 11/1998, of the 3-month U.S. Treasury Bill rate, as compiled by the Federal Reserve Board. This data, shown in Figure 10, is available for download at http://research.stlouisfed.org/fred2/series/TB3MA/downloaddata?cid=116. The data has been converted into a fraction by dividing by 100 (thus 0.1 is a rate of 10%). There are 196 observations in total.

Figure 10.

Sixteen years of monthly 3-month U.S. Treasury Bill rate data, as compiled by the Federal Reserve Board.

The prior used in our investigations is p(γ, μ, σ, ψ) ∝ γ/σ, with the prior on ψ additionally being uniform on the interval [0, 1]. This is the same prior on ψ used by Roberts and Stramer (2001). We used ΔT = 1/12 to reflect that the data was recorded monthly. Our exhaustive numerical evaluation of the ground truth yielded posterior means of μ, γ, σ and ψ equal to 0.0471, 0.1923, 0.0628, and 0.6851 respectively.

Following burn-in (10,000 iterations), we ran the Gibbs sampler for 10, 000 iterations at the appropriate level k = 5 (as determined by the exhaustive numerical search). We ran the multiresolution sampler on k = 2 and k = 3 for the same amount of time alocated to the Gibbs sampler. In this case, the lag-1 autocorrelations for k = 3 were around 0.95 while the multiresolution acceptance rate was again around 30%. Setting the cross-resolution move probability to p = 0.5 was expected to increase efficiency by a factor of 4. The resulting posteriors of the two chains k = 2 and k = 3 were combined using multiresolution extrapolation into final estimates of posterior quantiles. The simulation was independently repeated multiple times for both the Gibbs sampler and the multiresolution method.

Table 2 shows the ratio of the MSE of the Gibbs estimate to the MSE of the multiresolution approach, for a range of posterior quantiles of σ and ψ, two parameters of particular interest to researchers studying short term interest rate. For this particular model and data set, extrapolation allows us to skip two resolution levels k = 4 and k = 5, such that the multiresolution approach is seen to be 10 to 30 times more efficient than a standard Gibbs sampler.

Table 2.

Ratios of MSE. Estimates of posterior quantiles from a Gibbs sampler versus those from the multiresolution method for the gCIR process over the same amount of computer time.

σ MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	32 ± 6.2
Q0.25	17 ± 3.8
Q0.5	11 ± 2.0
Q0.75	11 ± 1.8
Q0.95	18 ± 2.4

ψ MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	13 ± 2.0
Q0.25	10 ± 1.7
Q0.5	10 ± 1.5
Q0.75	16 ± 2.7
Q0.95	38 ± 6.0

5.3 Stochastic volatility model

So far, we have benchmarked the multiresolution approach against a single Gibbs sampler of an Euler-Maruyama approximation. The added cost of obtaining multiresolution samples is well offset by the increasing autocorrelation as the resolution k increases. It should be pointed out, however, that for univariate SDEs there exists an alternative data augmentation scheme which does not use Euler-Maruyama discretization, or any direct discretization of the complete diffusion path Y_t itself. Instead, it is based on a factorization of Y_t with respect to a parameter-free Brownian measure, made possible by the Girsanov change-of-measure theorem. This approach was first considered by Roberts and Stramer (2001) and has been developed, for instance, in Beskos, Papaspiliopoulos, Roberts, and Fearnhead (2006).

Borrowing from the terminology employed by these authors, we have implemented one such “exact-path” scheme on the double-well and gCIR models presented above. Although the conditional parameter draws are more difficult than with the Euler-Maruyama approximation, the autocorrelations of θ were much lower, both discretization schemes having the same level of accuracy for a given resolution k. While it is possible to implement a multiresolution sampler on the exact-path scheme, the benefit of reducing small parameter autocorrelations even further is rather modest, and generally does not make up for the cost of obtaining multiresolution samples in the first place.

An important step of the exact-path scheme above was to transform the given diffusion process Y_t to a different diffusion process Z_t = η(Y_t, θ) with unit diffusion:

$$\mathrm{d}{Z}_t=\alpha (Z_t,\mathit{\theta })\mathrm{d}t+\mathrm{d}{B}_t.$$

It is easy to show that η(y, θ) = ∫ σ⁻¹(y, θ)dy satisfies this requirement in the univariate case. However, for multidimensional diffusion processes such a transformation generally does not exist. A simple example is Heston’s (1993) stochastic volatility model for a financial asset S_t,

$$\begin{array}{l}\mathrm{d}{S}_t=\alpha S_t\mathrm{d}t+V_t^{1/2}{S}_t\mathrm{d}{B}_{St}\\ \mathrm{d}{V}_t=-\gamma (V_t-\mu )\mathrm{d}t+\sigma V_t^{1/2}\mathrm{d}{B}_{Vt},\end{array}$$ (5.1)

where the two Brownian motions B_St and B_Vt have correlation cor(B_St, B_Vt) = ρ. In typical applications, only discrete observations S = (S₀, …, S_n) of the financial asset are recorded. The “instantaneous variance” or volatility process V_t is completely unobserved.

Implementation of the exact-path scheme for Heston’s model is not as simple as in the univariate case, but can be achieved by using simultaneous time-scale transformations t ↦ ϑ_V(t) and t ↦ ϑ_S(t) (Kalogeropoulos, Roberts, and Dellaporta, 2010). Even then, the transformations are only possible because the volatility V_t itself is a diffusion process: $\mathrm{d}{V}_t=-\gamma (V_t-\mu )\mathrm{d}t+\sigma V_t^{1/2}\mathrm{d}{B}_{Vt}$. While extending the exact-path approach to the more general setting appears to pose a considerable technical challenge, the Euler-Maruyama Gibbs-type scheme can easily be adapted to multiple dimensions. This simple scheme does, however, suffer from a heavy computational burden, which stands to be greatly reduced by the multiresolution approach.

We have fit Heston’s stochastic volatility model to 400 weekly 3-month U.S. Treasury Bill rates from 5/11/1965 to 29/6/1973, displayed in Figure 11. Inference was performed using Euler-Maruyama posterior approximations on the transformed process X_t = log(S_t) and $Z_t=2V_t^{1/2}$. Since there are 252 trading days in a year, the financial convention for weekly data is to set ΔT = 5/252. We used the prior p(α, γ, μ, σ, ρ) ∝ γσ²; a variety of noninformative priors were found to give very similar answers.

Figure 11.

Weekly observations of 3-month U.S. Treasury Bill rates.

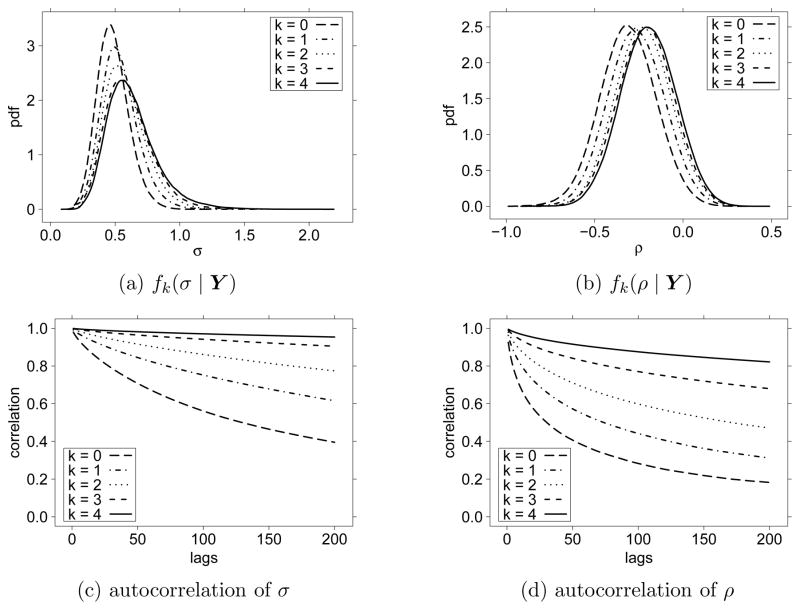
Posterior densities and autocorrelations for σ and ρ are displayed in Figure 12, for Gibbs samplers at resolution levels k = 0 to k = 4. Since the volatility process V_t is unobserved, the n + 1 = 400 volatility points V = (V₀, …, V_n) corresponding to the observed data S must also be integrated out, which has a considerable impact on the mixing time of the Gibbs samplers. Even at the lowest level k = 0, the lag-1 autocorrelation of σ is 0.98, the highest of any autocorrelation encountered in the previous examples. At level k = 4, over 20 million Gibbs samples were required to give the posterior densities their full convergence shape.

Figure 12.

Densities and autocorrelations for Heston’s model parameters σ and ρ.

In the following evaluation, we compare the multiresolution approach not only to a single k = 4 Gibbs sampler, but also to parallel Gibbs samplers running at k = 2 and k = 3. This accounts for the widespread availability of simultaneous computing resources, allowing researchers to run several Euler-Maruyama approximations at once and later combine them to produce estimates by extrapolation.

In total, three Gibbs samplers were run for 200,000 iterations each, at k = 2, 3, and 4. The first two Gibbs samplers k = 2 and k = 3 were combined to form extrapolated parameter estimates. To benefit from available technology, a parallelized version of the multiresolution sampler was implemented as follows. First, a Gibbs sampler is started at k = 0 and run for some burn-in period. Then, another Gibbs sampler is started at k = 1, and both samplers are run simultaneously; the cross-resolution proposals linking these samplers can now be drawn uniformly from an ever-increasing pool of samples. After another burn-in period, a third Gibbs sampler is started at k = 2 and run alongside the two others. It is linked to the k = 1 sampler by cross-resolution proposals, which continue to link k = 1 to k = 0. Finally, the k = 3 Gibbs sampler is added to the ensemble, with cross-resolution proposals connecting all four samplers. Multiresolution extrapolation is then performed using the last two levels k = 2 and k = 3.

A direct time comparison between the Gibbs samplers and the multiresolution sampler is difficult and perhaps uninformative in this setting. Instead, we assume that computation time scales as O(2^k) for the same number of samples. We also assume that the cost of computing one cross-resolution proposal and acceptance rate, when correctly implemented, is negligible compared to the cost of computing one full cycle of missing data and parameter updates in the Gibbs sampler. In our experience, this tends to be the case when the complete data themselves are the parameters’ sufficient statistics. Thus, each step of the multiresolution sampler consists of both a local update cycle and a cross-resolution move. Now, suppose that the multiresolution sampler is given M iterations at k = 0, then spends M iterations running k = 0 and k = 1 together, M iterations at k = 0, 1, 2, and M iterations at k = 0, 1, 2, 3. This is equivalent to M(1 + 1/2 + 1/4 + 1/8) ≈ 2M iterations of the Gibbs sampler at k = 3, and M iterations of the Gibbs sampler at k = 4.

Extrapolated quantiles using multiresolution samplers with M = 100, 000 iterations are compared to the extrapolated quantiles of the Gibbs samplers at k = 2 and k = 3 in Table 3. Even though the cross-resolution acceptance rate is only around 15%, the MSE of the extrapolated Gibbs samplers is generally three to ten times higher than for the multiresolution sampler. Moreover, this assumes that the user running the Gibbs samplers either knows that extrapolation between k = 2 and k = 3 is sufficient, or happens to run them in parallel at the first step of the analysis. With the multiresolution sampler, it is not as crucial to know or guess the “correct” resolution (or combination of resolution levels) in advance, as higher resolution levels can be sampled incrementally at a substantially lower cost.

Table 3.

Ratio of MSEs for extrapolated Gibbs samplers (k = 2, 3) to multiresolution sampler.

α MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	9.6 ± 2.3
Q0.25	1.4 ± 0.39
Q0.5	1.1 ± 0.34
Q0.75	1.6 ± 0.5
Q0.95	9.6 ± 2.9

γ MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	10 ± 2.8
Q0.25	7.4 ± 1.8
Q0.5	5.1 ± 1.1
Q0.75	4.2 ± 0.85
Q0.95	3.3 ± 0.4

β MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	12 ± 3.4
Q0.25	6.6 ± 1.6
Q0.5	4.6 ±1
Q0.75	3.9 ± 0.85
Q0.95	2.6 ± 0.4

σ MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	11 ± 2.8
Q0.25	5.6 ± 1.2
Q0.5	3.9 ± 0.75
Q0.75	3.3 ± 0.6
Q0.95	2.2 ± 0.3

ρ MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	18 ± 2.5
Q0.25	14 ± 2.2
Q0.5	10 ± 1.5
Q0.75	8.3 ± 1.3
Q0.95	7.9 ± 1.2

We next give M = 200, 000 iterations to each step of the parallelized multiresolution sampler – M iterations for k = {0}, {0, 1}, {0, 1, 2}, {0, 1, 2, 3} – to compare to the 200,000 iterations of the single Gibbs sampler at k = 4. Both samplers require about the same amount of computation as discussed in the previous paragraph. Ratios of MSEs comparing the single Gibbs sampler to the multiresolution sampler with extrapolation are computed in Table 4. In this case, the multiresolution approach is five to twenty times more efficient than a single Gibbs sampler.

Table 4.

Ratio of MSEs for single Gibbs sampler (k = 4) to multiresolution sampler.

α MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	120 ± 26
Q0.25	22 ± 5
Q0.5	8.8 ± 2.2
Q0.75	9.1 ± 2.3
Q0.95	87 ± 19

γ MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	17 ± 4.4
Q0.25	5.8 ± 1.4
Q0.5	5.4 ± 1.2
Q0.75	6 ± 1.2
Q0.95	8.5 ± 1.6

β MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	17 ± 4.6
Q0.25	4.2 ± 1.2
Q0.5	4.8 ± 1.2
Q0.75	7.2 ± 1.6
Q0.95	27 ± 4

σ MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	26 ± 7
Q0.25	6.3 ± 1.3
Q0.5	3.2 ± 0.65
Q0.75	2.9 ± 0.55
Q0.95	3.3 ± 0.6

ρ MSE Ratio
	$\widehat{R}\pm \widehat{\text{sd}}(\widehat{R})$
Q0.05	60 ± 10
Q0.25	41 ± 8
Q0.5	21 ± 5
Q0.75	16 ± 3.8
Q0.95	14 ± 2.8

6 Conclusion

We have proposed a multiresolution Bayesian inference approach for estimating the parameter posterior of diffusion models. The method calls for samples to be drawn not just from one but multiple Euler-Maruyama approximations that communicate with each other. The fast but rough approximations help speed up the fine ones using cross-resolution moves. Moreover, combining the samples using multiresolution extrapolation can improve accuracy by an order or more, allowing the overall discretization level to be much lower than if a single chain had been used.

In our illustrations of the multiresolution sampler, we used the Gibbs-type move for local updating. In practice, any strategy that increases the sampling efficiency at a fixed resolution can be incorporated into the multiresolution sampler as well. This includes, for example, the block-update strategy of Elerian, Chib, and Shephard (2001) or the group-update strategy of Liu and Sabatti (2000). Our multiresolution approach thus complements these existing methods by allowing them to be accelerated by cross-resolution moves.

Another practical advantage of the multiresolution method is how the precision of its estimates can be improved incrementally. Rarely does one know ahead of time what the correct value of (2^k − 1) – the number of missing data values between observations – will actually be. The idea of running a computationaly intensive sampler at some level k only to find out that an even higher level approximation must be started from scratch is certainly unappealing. In contrast, the additional computation time for each level of the multiresolution sampler is considerably smaller. Proceeding incrementally allows the appropriate level k to be naturally determined over the course of the analysis.

We have implemented the multiresolution approach in one- and two-dimensional settings. The same methodology can be applied to general multidimensional diffusions, and even to jump diffusions (for example, Kou, 2002), and infinite-activity processes such as the variance-gamma process (Madan, Carr, and Chang, 1998) as well. It is likely that in these more complicated settings, a fully parallel version of the multiresolution sampler as in Section 5.3 will be most desirable. This version of the sampler is referred to as an interacting MCMC algorithm by Fort, Moulines, and Priouret (2011), evoking the one-way relation between the “target” chain at level k+1 and the “auxiliary” chain at level k. While convergence results therein and elsewhere (Hua and Kou, 2011) have been established for a similar implementation of the equi-energy sampler, the main theorems of Fort et al. hold under more general conditions. It would be very interesting to see whether they apply to the multiresolution sampler as well. More complicated inferential settings may also call for more creative cross-resolution missing data proposals T_k+1. With the absence of a variance-stabilizing transformation in multiple dimensions, the multiresolution sampler could potentially be combined with dynamic importance weighting (Wong and Liang, 1997) in order to achieve higher cross-resolution acceptance rates. Further investigation of these ideas is currently under way.

A Appendix: The expansion order of posterior estimates

In this section, we show that the posterior mean, quantiles, and kernel density estimates of parameters under the Euler-Maruyama discretization scheme have exponent m = 1 in the expansion (4.1). Let us restate the general form of the SDE as:

$${dY}_t=\mu (Y_t,t,\mathit{\theta })dt+\sigma (Y_t,t,\mathit{\theta }){dB}_t.$$

We assume the discrete observations Y = Y⁽⁰⁾ occur at times t = {t₀, …, t_n}. For notational ease, we rewrite Y as y = (y₀, …, y_n), and denote Y(t) = {Y(t₁), …, Y(t_n)}.

Without loss of generality, let us assume t₀ = 0. Then the Euler approximation Y^(k)(t), with time discretization Δt = ΔT/2^k, is given by

$$Y^{(k)}((j+1)\mathrm{\Delta }t)=Y^{(k)}(j\mathrm{\Delta }t)+\mu (Y^{(k)}(j\mathrm{\Delta }t),j\mathrm{\Delta }t,\mathit{\theta })\mathrm{\Delta }t+\sigma \left(Y^{(k)}(j\mathrm{\Delta }t),j\mathrm{\Delta }t,\mathit{\theta }\right)(B_{(j+1)\mathrm{\Delta }t}-B_{j\mathrm{\Delta }t}),$$

where j = 0, 1, 2, …. Using the notation established in Section 2, p(θ) is the prior distribution of θ, f is the density function of Y, and f_k is the density function of the Euler-Maruyama approximation Y^(k). We assume Y^(k)(0) and Y(0) are drawn from the same distribution.

In examining weak convergence, we are interested in determining how the posterior expectation E(g(θ)|Y^(k)(t) = y) under the Euler-Maruyama discretization approximates the true posterior expectation E(g(θ)|Y(t) = y) as a function of k. In real applications, however, owing to measurement, equipment, and rounding errors, as well as numerical precision, the realistic posterior expectation accessible to us is best stated as E(g(θ)|Y(t) ∈ (y − ε, y + ε)), where ε is a small number corresponding to the precision level. This posterior expectation

$$E(g(\mathit{\theta })\mid Y(\mathit{t})\in (\mathit{y}-\epsilon ,\mathit{y}+\epsilon ))=\frac{\int d\mathit{\theta }{\int }_{y_0-\epsilon }^{y_0+\epsilon }\cdots {\int }_{y_n-\epsilon }^{y_n+\epsilon }g(\mathit{\theta })p(\mathit{\theta })f(Y(\mathit{t})\mid \mathit{\theta })dY(\mathit{t})}{\int d\mathit{\theta }{\int }_{y_0-\epsilon }^{y_0+\epsilon }\cdots {\int }_{y_n-\epsilon }^{y_n+\epsilon }p(\mathit{\theta })f(Y(\mathit{t})\mid \mathit{\theta })dY(\mathit{t})}$$

involves many step functions 1_{[yi−ε,yi+ε]}(z) which are not mathematically convenient. Thus, we replace the step function by a smooth kernel w and focus instead on how E_ε,w(g(θ)|Y^(k)(t) ≃ y), our shorthand notation for

$$E_{\epsilon ,w}(g(\mathit{\theta })\mid Y^{(k)}(\mathit{t})\simeq \mathit{y})=\frac{\int d\mathit{\theta }\int \cdots \int g(\mathit{\theta })p(\mathit{\theta })f_k(Y^{(k)}(\mathit{t})\mid \mathit{\theta }){\prod }_i[\frac{1}{\epsilon }w(\frac{Y^{(k)}(t_i)-y_i}{\epsilon })]d{Y}^{(k)}(\mathit{t})}{\int d\mathit{\theta }\int \cdots \int p(\mathit{\theta })f_k(Y^{(k)}(\mathit{t})\mid \mathit{\theta }){\prod }_i[\frac{1}{\epsilon }w(\frac{Y^{(k)}(t_i)-y_i}{\epsilon })]d{Y}^{(k)}(\mathit{t})},$$

where w is a smooth (four times continuously differentiable) density function, approximates

$$E_{\epsilon ,w}(g(\mathit{\theta })\mid Y(\mathit{t})\simeq \mathit{y})=\frac{\int d\mathit{\theta }\int \cdots \int g(\mathit{\theta })p(\mathit{\theta })f(Y(\mathit{t})\mid \mathit{\theta }){\prod }_i[\frac{1}{\epsilon }w(\frac{Y(t_i)-y_i}{\epsilon })]dY(\mathit{t})}{\int d\mathit{\theta }\int \cdots \int p(\mathit{\theta })f(Y(\mathit{t})\mid \mathit{\theta }){\prod }_i[\frac{1}{\epsilon }w(\frac{Y(t_i)-y_i}{\epsilon })]dY(\mathit{t})}.$$

Theorem A.1

Suppose the following three conditions hold for an SDE:

1. μ(x, t, θ) and σ²(x, t, θ) have linear growth; i.e., μ²(x, t, θ) + σ²(x, t, θ) ≤ K(θ)(1 + x²) for every θ

2. μ(x, t, θ) and σ²(x, t, θ) are twice continuously differentiable with bounded derivatives for every θ; i.e., $\mid \frac{\partial }{\partial t}\mu (x,t,\mathit{\theta })\mid ,\mid \frac{\partial }{\partial x}\mu (x,t,\mathit{\theta })\mid ,\left|\frac{{\partial }^2}{\partial x^2}\mu (x,t,\mathit{\theta })\right|,\mid \frac{\partial }{\partial t}{\sigma }^2(x,t,\mathit{\theta })\mid ,\mid \frac{\partial }{\partial x}{\sigma }^2(x,t,\mathit{\theta })\mid$, and $\left|\frac{{\partial }^2}{\partial x^2}{\sigma }^2(x,t,\mathit{\theta })\right|$ are all bounded by N(θ);

3. σ²(x, t, θ) is bounded from below for every θ; i.e., σ²(x, t, θ) ≥ λ(θ) > 0.

Then, for any integrable function g,

$$E_{\epsilon ,w}(g(\mathit{\theta })\mid Y^{(k)}(\mathit{t})\simeq \mathit{y})-E_{\epsilon ,w}(g(\mathit{\theta })\mid Y(\mathit{t})\simeq \mathit{y})=\frac{C_g}{2^k}+o(2^{-k}),$$

where C_g is a constant which does not depend on k.

Proof

We note

$$E_{\epsilon ,w}(g(\mathit{\theta })\mid Y^{(k)}(\mathit{t})\simeq \mathit{y})=\frac{\int p(\mathit{\theta })g(\mathit{\theta })E\{{\prod }_{i=1}^n[\frac{1}{\epsilon }w(\frac{Y^{(k)}(t_i)-y_i}{\epsilon })]\mid \mathit{\theta }\}d\mathit{\theta }}{\int p(\mathit{\theta })E\{{\prod }_{i=1}^n[\frac{1}{\epsilon }w(\frac{Y^{(k)}(t_i)-y_i}{\epsilon })]\mid \mathit{\theta }\}d\mathit{\theta }}.$$ (A.1)

Denote $v_j(Y^{(k)}(t_j),\mathit{\theta })=E\{{\prod }_{i=j+1}^n[\frac{1}{\epsilon }w(\frac{Y^{(k)}(t_i)-y_i}{\epsilon })]\mid Y^{(k)}(t_j),\mathit{\theta }\}$, and $u_j(Y(t_j),\mathit{\theta })=E\{{\prod }_{i=j+1}^n[\frac{1}{\epsilon }w(\frac{Y(t_i)-y_i}{\epsilon })]\mid Y(t_j),\mathit{\theta }\}$. Then, we have the recursion

$$\begin{array}{l}{v}_l(Y^{(k)}(t_l),\mathit{\theta })=E\left\{\frac{1}{\epsilon }w\left(\frac{Y^{(k)}(t_{l+1})-y_{l+1}}{\epsilon }\right)v_{l+1}(Y^{(k)}(t_{l+1}),\mathit{\theta })|Y^{(k)}(t_l),\mathit{\theta }\right\}\\ u_l(Y(t_l),\mathit{\theta })=E\left\{\frac{1}{\epsilon }w\left(\frac{Y(t_{l+1})-y_{l+1}}{\epsilon }\right)u_{l+1}(Y(t_{l+1}),\mathit{\theta })|Y(t_l),\mathit{\theta }\right\}\end{array}$$

from the Markov property. By Theorem 14.1.5 of Kloeden and Platen (1992), for any smooth (fourth continuously) differentiable function q,

$$E\{q(Y^{(k)}(t_{l+1}),\theta )\mid Y^{(k)}(t_l)=y,\mathit{\theta }\}-E\{q(Y(t_{l+1}),\mathit{\theta })\mid Y(t_l)=y,\mathit{\theta }\}=\frac{A_q}{2^k}+o(2^{-k}),$$

where the constant A_q does not depend on k, y, or l. It follows that if we assume v_l+1(y, θ) − u_l+1(y, θ) = B_l+1/2^k + o(2^−k), then

$$\begin{array}{l}{v}_l(y,\mathit{\theta })=E\left\{\frac{1}{\epsilon }w\left(\frac{Y^{(k)}(t_{l+1})-y_{l+1}}{\epsilon }\right)v_{l+1}(Y^{(k)}(t_{l+1}),\mathit{\theta })|Y^{(k)}(t_l)=y,\mathit{\theta }\right\}\\ =E\left\{\frac{1}{\epsilon }w\left(\frac{Y^{(k)}(t_{l+1})-y_{l+1}}{\epsilon }\right)[u_{l+1}(Y^{(k)}(t_{l+1}),\mathit{\theta })+\frac{B_{l+1}}{2^k}+o(2^{-k})]|Y^{(k)}(t_l)=y,\mathit{\theta }\right\}\\ =E\left\{\frac{1}{\epsilon }w\left(\frac{Y^{(k)}(t_{l+1})-y_{l+1}}{\epsilon }\right)u_{l+1}(Y^{(k)}(t_{l+1}),\mathit{\theta })|Y^{(k)}(t_l)=y,\mathit{\theta }\right\}+\frac{B_{l+1}}{2^k}+o(2^{-k})\\ =E\left\{\frac{1}{\epsilon }w\left(\frac{Y(t_{l+1})-y_{l+1}}{\epsilon }\right)u_{l+1}(Y(t_{l+1}),\mathit{\theta })|Y(t_l)=y,\mathit{\theta }\right\}+\frac{A}{2^k}+\frac{B_{l+1}}{2^k}+o(2^{-k})\\ =u_l(y,\mathit{\theta })+\frac{A+B_{l+1}}{2^k}+o(2^{-k}).\end{array}$$

Therefore, using backward induction, we obtain that v₀(x, θ) − u₀(x, θ) = B₀/2^k + o(2^−k), which, combined with the assumption that Y^(k)(t₀) and Y(t₀) have the same distribution, implies that

$$E\left\{\prod _{i=1}^n\left[\frac{1}{\epsilon }w\left(\frac{Y^{(k)}(t_i)-y_i}{\epsilon }\right)\right]|\mathit{\theta }\right\}-E\left\{\prod _{i=1}^n\left[\frac{1}{\epsilon }w\left(\frac{Y(t_i)-y_i}{\epsilon }\right)\right]|\mathit{\theta }\right\}=\frac{C(\mathit{\theta })}{2^k}+o(2^{-k}),$$

for some constant C(θ) depending on θ. Taking this result back to (A.1), we obtain

$$\begin{array}{l}{E}_{\epsilon ,w}(g(\mathit{\theta })\mid Y^{(k)}(\mathit{t})\simeq \mathit{y})=\frac{\int p(\mathit{\theta })g(\mathit{\theta })E\{{\prod }_{i=1}^n[\frac{1}{\epsilon }w\left(\frac{Y(t_i)-y_i}{\epsilon }\right)]\mid \mathit{\theta }\}d\mathit{\theta }+\frac{\mathrm{\Delta }T}{2^k}\int p(\mathit{\theta })g(\mathit{\theta })C(\mathit{\theta })d\mathit{\theta }+o(2^{-k})}{\int p(\mathit{\theta })E\{{\prod }_{i=1}^n[\frac{1}{\epsilon }w\left(\frac{Y(t_i)-y_i}{\epsilon }\right)]\mid \mathit{\theta }\}d\mathit{\theta }+\frac{\mathrm{\Delta }T}{2^k}\int p(\mathit{\theta })C(\mathit{\theta })d\mathit{\theta }+o(2^{-k})}\\ =\frac{\int p(\mathit{\theta })g(\mathit{\theta })E\{{\prod }_{i=1}^n[\frac{1}{\epsilon }w\left(\frac{Y(t_i)-y_i}{\epsilon }\right)]\mid \mathit{\theta }\}d\mathit{\theta }}{\int p(\mathit{\theta })E\{{\prod }_{i=1}^n[\frac{1}{\epsilon }w\left(\frac{Y(t_i)-y_i}{\epsilon }\right)]\mid \mathit{\theta }\}d\mathit{\theta }}+\frac{C_g}{2^k}+o(2^{-k})\\ =E_{\epsilon ,w}(g(\mathit{\theta })\mid Y(\mathit{t})\simeq \mathit{y})+\frac{C_g}{2^k}+o(2^{-k}).\end{array}$$

We make explicit use of this theorem by noting the following corollary on the posterior cdf and quantiles:

Corollary A.2

The posterior cdf $F_{\epsilon ,w}^j$ of the jth parameter θ_j satisfies

$$F_{\epsilon ,w}^j(z\mid Y^{(k)}(\mathit{t})\simeq \mathit{y}):=E_{\epsilon ,w}(1({\theta }_j\le z)\mid Y^{(k)}(\mathit{t})\simeq \mathit{y})=F_{\epsilon ,w}^j(z\mid Y(\mathit{t})\simeq \mathit{y})+\frac{C}{2^k}+o(2^{-k}).$$

If the posterior cdf $F_{\epsilon ,w}^j$ has non-zero derivative, then the quantile $F_{\epsilon ,w,j}^{-1}$ of θ_j satisfies

$$F_{\epsilon ,w,j}^{-1}(\alpha \mid Y^{(k)}(\mathit{t})\simeq \mathit{y})=F_{\epsilon ,w,j}^{-1}(\alpha \mid Y(\mathit{t})\simeq \mathit{y})+\frac{C^{\prime }}{2^k}+o(2^{-k}),$$

for fixed 0 < α < 1.

Proof

Taking g(θ) of Theorem A.1 to be the indicator function 1(θ_j ≤ z) immediately yields the first equation. The assumption that $F_{\epsilon ,w}^j$ has non-zero derivative enable us to invert it to obtain the second equation.

We can make the connection between Corollary A.2 and equation (4.1) explicit by noting h = ΔT/2^k. Therefore, to apply extrapolation to the quantiles of a parameter posterior, we should use the exponent m = 1.

Similarly, suppose that we wish to estimate the density f(θ_j) of parameter j at a specific value θ_j = x. Suppose that a kernel density estimate f̂(x) is of the form

$$\widehat{f}(x)=\frac{1}{Mh}\sum _{i=1}^{M}K\left(\frac{x-{\theta }_j^{(i)}}{h}\right),$$

where K is a (symmetric) kernel, h is a bandwidth parameter and ${\theta }_j^{(1)},\dots ,{\theta }_j^{(M)}$ is a collection of M samples from f(θ_j). In this case, for fixed h, f̂(x) can be seen as a sample estimate of

$$E\left\{\frac{1}{h}K\left(\frac{x-{\theta }_j}{h}\right)|\mathit{Y}(\mathit{t})\simeq \mathit{y}\right\},$$

such that g(θ) = K((x − θ_j)/h)/h. As long as the kernel K is integrable, Theorem A.1 also applies. Moreover, if the kernel density estimate f̂(x) at each resolution level is normalized, then so is the density estimate obtained by extrapolation.