Abstract
A goal of many health studies is to determine the causal effect of a treatment or intervention on health outcomes. Often, it is not ethically or practically possible to conduct a perfectly randomized experiment and instead an observational study must be used. A major challenge to the validity of observational studies is the possibility of unmeasured confounding (i.e., unmeasured ways in which the treatment and control groups differ before treatment administration which also affect the outcome). Instrumental variables analysis is a method for controlling for unmeasured confounding. This type of analysis requires the measurement of a valid instrumental variable, which is a variable that (i) is independent of the unmeasured confounding; (ii) affects the treatment; and (iii) affects the outcome only indirectly through its effect on the treatment. This tutorial discusses the types of causal effects that can be estimated by instrumental variables analysis; the assumptions needed for instrumental variables analysis to provide valid estimates of causal effects and sensitivity analysis for those assumptions; methods of estimation of causal effects using instrumental variables; and sources of instrumental variables in health studies.
Keywords: instrumental variables, observational study, confounding, comparative effectiveness
1. Introduction
The goal of many medical studies is to estimate the causal effect of one treatment vs. another, i.e., to compare the effectiveness of giving patients one treatment vs. another. To compare the effects of treatments, randomized controlled studies are the gold standard in medicine. Unfortunately, randomized controlled studies cannot answer many comparative effectiveness questions because of cost or ethical constraints. Observational studies offer an alternative source of data for developing evidence regarding the comparative effectiveness of different treatments. However, a major challenge for observational studies is confounders – pre-treatment variables that affect the outcome and differ in distribution between the group of patients who receive one treatment vs. the group of patients who receive another treatment.
The impact of confounders on the estimation of a causal treatment effect can be mitigated by methods such as propensity scores, regression and matching[1–3]. However, these methods only control for measured confounders and do not control for unmeasured confounders.
The instrumental variable (IV) method was developed to control for unmeasured confounders. The basic idea of the IV method is 1) find a variable that influences which treatment subjects receive but is independent of unmeasured confounders and has no direct effect on the outcome except through its effect on treatment; 2) use this variable to extract variation in the treatment that is free of the unmeasured confounders; and 3) use this confounder-free variation in the treatment to estimate the causal effect of the treatment. The IV method seeks to find a randomized experiment embedded in an observational study and use this embedded randomized experiment to estimate the treatment effect.
1.1. Tutorial Aims and Outline
IV methods have long been used in economics and are being increasingly used to compare treatments in health studies. There have been many important contributions to IV methods in recent years. The goal of this tutorial is to bring together this literature to provide a practical guide on how to use IV methods to compare treatments in a health study. We focus on several important practical issues in using IVs: (1) when is an IV analysis needed and when is it feasible? (2) what are sources of IVs for health studies; (3) how to use the IV method to estimate treatment effects, including how to use currently available software; (4) for what population does the IV estimate the treatment effect; (5) how to assess whether a proposed IV satisfies the assumptions for an IV to be valid; (6) how to carry out sensitivity analysis for violations of IV assumptions and (7) how does the strength of a potential IV affect its usefulness for a study.
In the rest of this section, we will present an example of using the IV method that we will use throughout the paper. In Section 2, we discuss situations when one should consider using the IV method. In Section 3, we discuss common sources of IVs for health studies. In Section 4, we discuss IV assumptions and estimation for a binary IV and binary treatment. In Section 5, we discuss the treatment effect that the IV method estimates. In Section 6, we provide a framework for assessing IV assumptions and sensitivity analysis for violations of assumptions. In Section 7, we demonstrate the consequences of weak instruments. In Section 8, we discuss power and sample size calculations for IV studies. In Section 9, we present techniques for analyzing outcomes that are not continuous outcomes, such as binary, survival, multinomial and continuous outcomes. In Section 10, we discuss multi-valued and continuous IVs. In Section 11, we discuss using multiple IVs. In Section 12, we present IV methods for multi-valued and continuously valued treatments. In Section 13, we suggest a framework for reporting IV analyses. In Section 14, we provide examples of using software for IV analysis.
If you are just beginning to familiarize yourself with IVs we recommend focussing on Sections 1-4, 5.1-5.2, 6-8 and 13-14, while skipping Sections 5.3-5.5 and 9-12. Sections 5.3-5.5 and 9-12 contain interesting, cutting-edge, and more specialized applications of IVs that the beginner may want to return to at a later point. We include these sections for advanced readers, or those interested in more specialized applications.
Table 1 is a table of notation that will be used throughout the paper.
Table 1.
Table of notation.
| Notation | Meaning |
|---|---|
| Y | observed outcome |
| Y1, Y0 | potential outcome if treatment is 1, potential outcome if treatment is 0 |
| D | observed treatment |
| D1, D0 | potential treatment if instrumental variable (IV) is 1, potential treatment if IV is 0 |
| Z | observed IV |
| X | measured confounders |
| C | compliance class |
| U | unmeasured confounder |
| CACE | Complier Average Causal Effect, the average effect of treatment for the compliers (C = co) |
1.2. Example: Effectiveness of high level neonatal intensive care units
As an example where the IV method is useful, consider comparing the effectiveness of premature babies being delivered in high volume, high technology neonatal intensive care units (high level NICUs) vs. local hospitals (low level NICUs), where a high level NICU is defined as a NICU that has the capacity for sustained mechanical assisted ventilation and delivers at least 50 premature infants per year. [4] used data from birth and death certificates and the UB-92 form that hospitals use for billing purposes to study premature babies delivered in Pennsylvania. The data set covered the years 1995-2005 (192,078 premature babies). For evaluating the effect of NICU level on baby outcomes, a baby's health status before delivery is an important confounder. Table 2 shows that babies delivered at high level NICUs tend to have smaller birthweight, be more premature, and the babies’ mothers tend to have more problems during the pregnancy. Although the available confounders, which include those in Table 2 and several other variables that are given in [4], describe certain aspects of a baby's health prior to delivery, the data set is missing several important confounding variables such as fetal heart tracing results, the severity of maternal problems during pregnancy (e.g., we only know whether the mother had pregnancy induced hypertension but not the severity) and the mother's adherence to prenatal care guidelines.
Table 2.
Imbalance of measured covariates between babies delivered at high level NICUs vs. low level NICUs. The standardized difference is the difference in means between the two groups in units of the pooled within group standard deviation, i.e., for a binary characteristic X, where D = 1 or 0 according to whether the baby was delivered at a high or low level NICU, the standardized difference is .
| Characteristic X | P(X|High Level NICU) | P(X|Low Level NICU) | Standardized Difference |
|---|---|---|---|
| Birthweight < 1500g | 0.12 | 0.05 | 0.28 |
| Gestational Age <= 32 weeks | 0.18 | 0.07 | 0.34 |
| Mother College Graduate | 0.28 | 0.23 | 0.12 |
| African American | 0.22 | 0.09 | 0.36 |
| Gestational Diabetes | 0.05 | 0.05 | 0.03 |
| Diabetes Mellitus | 0.02 | 0.01 | 0.06 |
| Pregnancy Induced Hypertension | 0.12 | 0.08 | 0.13 |
| Chronic Hypertension | 0.02 | 0.01 | 0.07 |
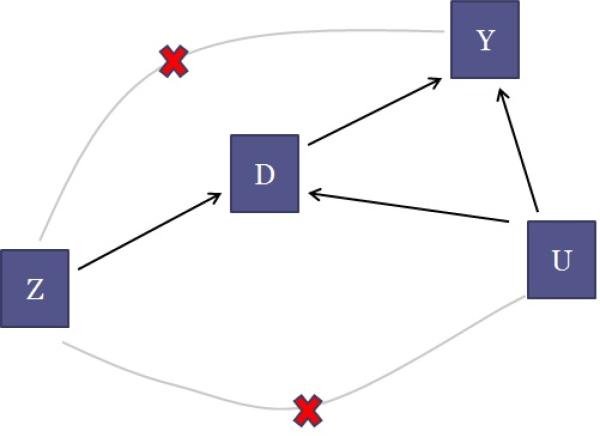
Figure 1, which is an example of a directed acyclic graph [5], illustrates the difficulty with estimating a causal effect in this situation. The arrows denote causal relationships. Read the arrow between the treatment D and outcome Y like so: Changing the value of D causes Y to change. In our example, Y represents in-hospital mortality, and D indicates whether or not a baby attended a high level NICU. Our goal is to understand the arrow connecting D to Y , that is, the effect of attending a high level NICU on in-hospital mortality compared to attending a low level NICU. Assume that Figure 1 shows relationships within a strata of the observed covariates X, e.g., Figure 1 represents the relationships for only babies with gestational age 33 weeks and mother had pregnancy induced hypertension. The U variable causes concern as it represents the unobserved level of severity of the preemie and it is causally linked to both mortality (sicker babies are more likely to die) and to which treatment the preemie receives (sicker babies are more likely to be delivered in high level NICUs). Because U is not recorded in the data set, it cannot be precisely adjusted for using statistical methods such as propensity scores or regression. If the story stopped with just D, Y and U, then the effect of D on Y could not be estimated.
Figure 1.
Directed acyclic graph for the relationship between an instrumental variable Z, a treatment D, unmeasured confounders U and an outcome Y.
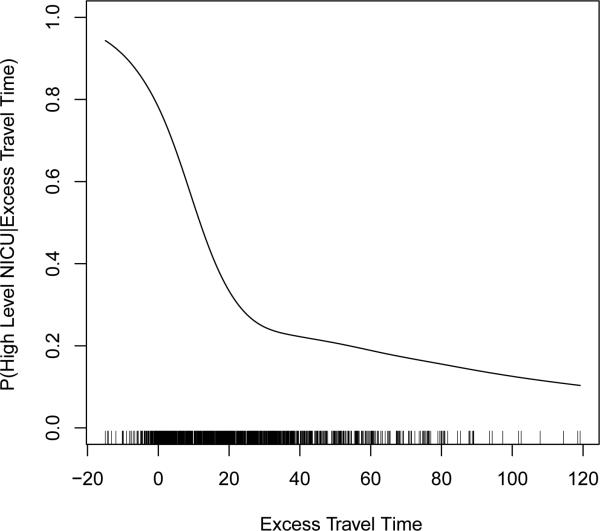
IV estimation makes use of a form of variation in the system that is free of the unmeasured confounding. What is needed is a variable, called an IV (represented by Z in Figure 1), that has very special characteristics. In this example we consider excess travel time as a possible IV. Excess travel time is defined as the time it takes to travel from the mother's residence to the nearest high level NICU minus the time it takes to travel to the nearest low level NICU. We write Z = 1 if the excess travel time is less than or equal to 10 minutes (so that the mother is encouraged by the IV to go to a high level NICU) and Z = 0 if the excess travel time is greater than 10 minutes. (We dichotomize the instrument here for simplicity of discussion.)
There are three key features a variable must have in order to qualify as an IV (see Section 4 for mathematical details on these features and additional assumptions for IV methods). The first feature (represented by the directed arrow from Z to D in Figure 1) is that the IV causes a change in the treatment assignment. When a woman becomes pregnant, she has a high probability of establishing a relationship with the proximal NICU, regardless of the level, because she is not anticipating having a preemie. Proximity as a leading determinant in choosing a facility has been discussed in [6]. By selecting where to live, mothers assign themselves to be more or less likely to deliver in a high level NICU. The fact that changes in the IV are associated with changes in the treatment is verifiable from the data.
The second feature (represented by the crossed out arrow from Z to U) is that the IV is not associated with variation in unobserved variables U that also affect the outcome. That is, Z is not connected to the unobserved confounding that was a worry to begin with. In our example, this would mean unobserved severity is not associated with variation in geography. Since high level NICUs tend to be in urban areas and low level NICUs tend to be the only type in rural areas, this assumption would be dubious if there were high level of pollutants in urban areas (think of Manchester, England circa the Industrial Revolution) or if there were more pollutants in the drinking water in rural areas than in urban areas. These hypothetical pollutants may have an impact on the unobserved levels of severity. The assumption that the IV is not associated with variation in the unobserved variables, while certainly an assumption, can at least be corroborated by examining the values of variables that are perhaps related to the unobserved variables of concern (see Section 6.1).
The third feature (represented by the crossed out line from Z to Y in Figure 1) is that the IV does not cause the outcome variable to change directly. That is, it is only through its impact on the treatment that the IV affects the outcome. This is often referred to as the exclusion restriction assumption. In our case, the exclusion restriction assumption seems reasonable as presumably a nearby hospital with a high level NICU affects a baby's mortality only if the baby receives care at that hospital. That is, proximity to a high level NICU in and of itself does not change the probability of death for a preemie, except through the increased probability of the preemie being delivered at the high level NICU. See Section 6.2.2 for further discussion about the exclusion restriction in the NICU study.
2. Evaluating the Need for and Feasibility of an IV Analysis
As discussed above, IV methods provide a way to control for unmeasured confounding in comparative effectiveness studies. Although this is a valuable feature of IV methods relative to regression, matching and propensity score methods which do not control for unmeasured confounding, IV methods have some less attractive features such as increased variance. When considering whether or not to include an IV analysis in an evaluation of a treatment effect, the first question one should ask is whether or not an IV analysis is needed. The second question one should ask is whether or not an IV analysis is feasible in the sense of there being an IV that is close enough to being valid and has a strong enough effect on the treatment to provide useful information about the treatment effect. In this section, we will discuss how to think about these two questions.
2.1 Is an IV analysis needed?
The key consideration in whether an IV analysis is needed is how much unmeasured confounding there is. It is useful to evaluate this using both scientific considerations and statistical considerations.
Scientific Consideration
Whether or not there is any unmeasured confounding should be first thought of from a scientific point of view. In the NICU example discussed in Section 1.2, mothers (as advised by doctors) who choose to deliver in a far away high level NICU rather than a nearby low level NICU often do so because they think their baby may be at a high risk of having a problem and that delivery at a high level NICU will reduce this risk. Investigators know that a lot of variables can be confounders (i.e., associated with delivery at a high level NICU and associated with in hospital mortality) such as variables indicating a baby's health prior to delivery. They know that the data set available for analyses is missing several important confounding variables such as fetal heart tracing results, the severity of maternal problems during pregnancy and the mother's adherence to prenatal care guidelines. When unmeasured confounding is a big concern in a study like in the NICU study, analyses with IV methods are desired and helpful to better understand the treatment effect.
Unmeasured confounders are particularly likely to be present when the treatment is intended to help the patient (as compared to unintended exposures)[7]. When two patients who have the same measured covariates are given different treatments, there are often rational but unrecorded reasons. In particular, administrative data often does not contain measurements of important prognostic variables that affect both treatment decisions and outcomes such as lab values (e.g., serum cholesterol levels), clinical variables (e.g., blood pressure and fetal heart tracing results), aspects of lifestyle (e.g., smoking status, eating habits) and measures of cognitive and physical functioning[8, 9].
Common sources of IVs for health studies are discussed in Section 3. When using IV analyses, the assumptions that are required for a variable to be a valid IV are usually at best plausible, but not certain. If the assumptions are merely plausible, but not certain, are IV analyses still useful? Imbens and Rosenbaum [10] provide a nice discussion of two settings in which IV analyses with plausible but not certain IVs are useful: 1) When one is concerned about unmeasured confounding in any way, it's helpful to replace the implausible assumption of no unmeasured confounding by a plausible assumption, although not a certain assumption, with IV methods; 2) When there is concern about unmeasured confounding, IV analyses play an important role in replicating an observational study. Consider two sequences of studies, the first sequence in which each study involves only adjusting for measured confounders and the other sequence in which each study involves using a different IV (one of the studies in this second sequence could also involve only adjusting for measured confounders). Throughout the first sequence of studies, the comparison is likely to be biased in the same way. For example, a repeated finding that people with more education are more healthy from different survey data sets that do not contain information about genetic endowments or early life experiences does little to address the concern of unmeasured confounding from these two variables. However, if different IVs are used for education, e.g., a lottery that affects education[11], a regional discontinuity in educational policy[12], a temporal discontinuity in educational policy[13] and distance lived from a college when growing up[14], and if each IV is plausibly, but not certainly, valid, then there may be no reason why these different IVs should provide estimates that are biased in the same direction. If studies with these different IVs all provide evidence that education affects health in the same direction, this would strengthen the evidence for this finding[15] (when different IVs are used, each IV identifies the average treatment effect for a different subgroup, so that we would only expect that findings from the different IVs would agree in direction if the average treatment effects for the different subgroups have the same direction; see Section 5.5 and 11 for discussion).
In summary, when unmeasured confounding is a big concern in a study based on one's understanding of the problem and data, investigators should consider IV methods in their analyses. At the same time, if investigators only expect a small amount of unmeasured confounding in their study, [16] suggest that investigators may not want to use IV methods for the primary analysis but may want to consider IV methods for a secondary analysis.
Statistical Tests
Under some situations in practice, especially for exploratory studies, investigators may not have enough scientific information to determine whether or not there is unmeasured confounding. Then statistical tests can be helpful to provide additional insight. The Durbin-Wu-Hausman test is widely used to test whether there is unmeasured confounding[17–19]. The test requires the availability of a valid IV. The test compares the ordinary least squares estimate and IV estimate of the treatment effect; a large difference between the two estimates indicates the potential presence of unmeasured confounding.
The Durbin-Wu-Hausman test assumes homogeneous treatment effects, meaning that the treatment effect is the same at different levels of covariates. The test cannot distinguish between unmeasured confounding and treatment effect heterogeneity[16, 20]. As an alternative approach, [20] developed a test that can detect unmeasured confounding as distinct from treatment effect heterogeneity in the context of the model described below in Section 4.1.
2.2. Valid IVs
As discussed in Section 1, a variable must have three key features to qualify as an IV: 1) Relevance: the IV causes a change in the treatment received; 2) Effective random assignment: the IV is independent of unmeasured confounding conditional on covariates as if it was randomly assigned conditional on covariates; 3) Exclusion restriction: the IV does not have a direct effect on outcomes, i.e., it only affects outcomes through the treatment. Section 4 includes mathematical details on these features and assumptions. To use IV methods in a real study, investigators need to evaluate if there is any variable which satisfies the three features and qualifies as a good IV based on both scientific understanding and statistical evidence. Please see Section 3 below for sources of IVs in health studies. Note that not all of the features/assumptions can be completely tested, but methods have been proposed to test certain parts of the assumptions. Please see Section 6 for a discussion about how to evaluate if a variable satisfies those features/assumptions needed to be a valid IV.
We would also like to point out that even if there is no variable which is a perfectly valid IV, an IV analysis may still provide helpful information about the treatment effect. As discussed above, when there is unmeasured confounding, a repeated finding from a sequence of analyses with different IVs (even though none of the IVs is perfect) will provide very helpful evidence on the treatment effect [10]. Also, sensitivity analyses can be performed to assess the evidence provided by an IV analysis allowing for the IV not being perfectly valid; see Section 6.2.
2.3. Strength of IVs
An IV is considered to be a strong IV if it has a strong impact on the choice of different treatments and a weak IV if it only has a slight impact. When the IV is weak, even if it is a valid IV, treatment effect estimates based on IV methods have some limitations, such as large variance even with large samples. Then investigators face a trade-off between an IV estimate with a large variance and a conventional estimate with possible bias [16]. Additionally, the estimate with a weak IV will be sensitive to a slight departure from being a valid IV. Please see Section 7 for more detailed discussion on the problems when only weak IVs are available in a study.
In summary, whether or not an IV analysis will be helpful for a study depends on if unmeasured confounding is a major concern, if there is any plausibly close to valid IV, and if the IV is strong enough for a study. For studies with treatments that are intentionally chosen by physicians and patients, there is often substantial unmeasured confounding from unmeasured indications or severity[7, 10, 16]. Therefore, an IV analysis can be most helpful for those studies. When an IV is available, even if it is not perfectly valid, an IV analysis or a sequence of IV analyses with different IVs can provide very helpful information about the treatment effect. For studies in which unmeasured confounding is not a big concern and no strong IV is available, we suggest investigators to consider IV analyses as secondary or sensitivity analyses.
3. Sources of Instruments in Health Studies
The biggest challenge in using IV methods is finding a good IV. There are several common sources of IVs for health studies.
Randomized Encouragement Trials
One way to study the effect of a treatment when that treatment cannot be controlled is to conduct a randomized encouragement trial. In such a trial, some subjects are randomly chosen to get extra encouragement to take the treatment and the rest of the subjects receive no extra encouragement[21]. For example, [22] studied the effect of maternal smoking during pregnancy on an infant's birthweight using a randomized encouragement trial in which some mothers received extra encouragement to stop smoking through a master's level staff person providing information, support, practical guidance and behavioral strategies [23]. For a randomized encouragement trial, the randomized encouragement assignment (1 if encouraged, 0 if not encouraged) is a potential IV. The randomized encouragement is independent of unmeasured confounders because it is randomly assigned by the investigators and will be associated with the treatment if the encouragement is effective. The only potential concern with the randomized encouragement being a valid IV is that the randomized encouragement might have a direct effect on the outcome not through the treatment. For example, in the smoking example above, the encouragement could have a direct effect if the staff person providing the encouragement also encouraged expectant mothers to stop drinking alcohol during pregnancy. To minimize a potential direct effect of the encouragement, [23] asked the staff person providing encouragement to avoid recommendations or information concerning other habits that might affect birthweight such as alcohol or caffeine consumption and also prohibited discussion of maternal nutrition or weight gain. A special case of a randomized encouragement trial is a usual randomized trial in which the intent is for everybody to take their assigned treatment, but in fact some people do not adhere to their assigned treatment so that assignment to treatment is in fact just an encouragement to treatment. For such randomized trials with non-adherence, random assignment can be used as an IV to estimate the effect of receiving the treatment vs. receiving the control provided that random assignment does not have a direct effect (not through the treatment); see Section 4.7 for further discussion and an example.
Distance to Specialty Care Provider
When comparing two treatments, one of which is only provided by specialty care providers and one of which is provided by more general providers, the distance a person lives from the nearest specialty care provider has often been used as an IV. For emergent conditions, proximity to a specialty care provider particularly enhances the chance of being treated by the specialty care provider. For less acute conditions, patients/providers have more time to decide and plan where to be treated, and proximity may have less of an influence on treatment selection, while for treatments that are stigmatized (e.g., substance abuse treatment), proximity could have a negative effect on the chance of being treated. A classic example of using distance as an IV in studying treatment of an emergent condition is McClellan et al.'s study of the effect of cardiac catheterization for patients suffering a heart attack[24]. The IV used in the study was the differential distance the patient lives from the nearest hospital that performs cardiac catheterization to the nearest hospital that does not perform cardiac catheterization. Another examples is the study of the effect of high level vs. low level NICUs [4] that was discussed in Section 1.2. Because distance to a specialty care provider is often associated with socioeconomic characteristics, it will typically be necessary to control for socioeconomic characteristics in order for distance to potentially be independent of unmeasured confounders. The possibility that distance might have a direct effect because the time it takes to receive treatment affects outcomes needs to be considered in assessing whether distance is a valid IV.
Preference-Based IVs
A general strategy for finding an IV for comparing two treatments A and B is to look for naturally occurring variation in medical practice patterns at the level of geographic region, hospital or individual physician, and then use whether the region/hospital/individual physician has a high or low use of treatment A (compared to treatment B) as the IV. [9] termed these IVs “preference-based instruments” because they assume that different providers or groups of providers have different preferences or treatment algorithms dictating how medications or medical procedures are used. Examples of studies using preference-based IVs are [25] that studied the effect of surgery plus irradiation vs. mastectomy for breast cancer patients using geographic region as the IV, [26] that studied the effect of surgery vs endovascular therapy for patients with a ruptured cerebral aneurysm using hospital as the IV and [27] that studied the benefits and risks of selective cyclooxygenase 2 inhibitors vs. nonselective nonsteroidal antiinflammatory drugs for treating gastrointenstinal problems using individual physician as the IV. For proposed preference-based IVs, it is important to consider that the patient mix may differ between the different groups of providers with different preferences, which would make the preference-based IV invalid unless patient mix is fully controlled for. It is useful to look at whether measured patient risk factors differ between groups of providers with different preferences. If there are measured differences, there are likely to be unmeasured differences as well; see Section 6.1 for further discussion. Also, for proposed preference-based IVs, it is important to consider whether the IV has a direct effect (not through the treatment); a direct effect could arise if the group of providers that prefers treatment A treats patients differently in ways other than the treatment under study compared to the providers who prefer treatment B. For example, [28] studied the efficacy of phototherapy for newborns with hyperbilirubinemia and considered the frequency of phototherapy use at the newborn's birth hospital as an IV. However, chart reviews revealed that hospitals that use more phototherapy also have a greater use of infant formula; use of infant formula is also thought to be an effective treatment for hyperbilirubinemia. Consequently, the proposed preference-based IV has a direct effect (going to a hospital with higher use of phototherapy also means a newborn is more likely to receive infant formula even if the newborn does not receive phototherapy) and is not valid. The issue of whether a proposed preference-based IV has a direct effect can be studied by looking at whether the IV is associated with concomitant treatments like use of infant formula [9]. A related way in which a proposed preference-based IV can have a direct effect is that the group of providers who prefer treatment A may have more skill than the group of providers who prefer treatment B. Also, providers who prefer treatment A may deliver treatment A better than those providers who prefer treatment B because they have more practice with it, e.g., doctors who perform surgery more often may perform better surgeries. [29] discuss a way to assess whether there are provider skill effects by collecting data from providers on whether or not they would have treated a different provider's patient with treatment A or B based on the patient's pretreatment records.
Calendar Time
Variations in the use of one treatment vs. another over time could result from changes in guidelines; changes in formularies or reimbursement policies; changes in physician preference (e.g., due to marketing activities by drug makers); release of new effectiveness or safety information; or the arrival of new treatments to the market [16]. For example, [30] studied the effect of hormone replacement therapy (HRT) on cardiovascular health among postmenopausal women using calendar time as an IV. HRT was widely used among postmenopausal women until 2002; observational studies had suggested that HRT reduced cardiovascular risk, but the Womens’ Health Initiative randomized trial reported opposite results in 2002, which caused HRT use to drop sharply. A proposed IV based on calendar time could violate the assumption of being independent of unmeasured confounders by being associated with unmeasured confounders that change in time such as the characteristics of patients who enter the cohort, changes in other medical practices and changes in medical coding systems [16]. The most compelling type of IV based on calendar time is one where a dramatic change in practice occurs in a relatively short period of time [16].
Genes as IVs
Another general source for potential IVs is genetic variants which affect treatment variables. For example, [31] studied the effect of HDL cholesterol on myocardial infarction using as an IV the genetic variant LIPG 396Ser allele for which carriers have higher levels of HDL cholesterol but similar levels of other lipid and non-lipid risk factors compared with noncarriers. Another example is that [32] studied the effect of maternal smoking on orofacial clefts in babies using genetic variants that increase the probability that a mother smokes as IVs. The approach of using genetic variants as an IV is called Mendelian randomization because it makes use of the random assignment of genetic variants conditional on parents’ genes discovered by Mendel. Although genetic variants are randomly assigned conditional on a parent's genes, genetic variants need to satisfy additional assumptions to be valid IVs that include the following:
Not associated with unmeasured confounders through population stratification. Most Mendelian randomization analyses do not condition on parents’ genes, creating the potential of the proposed genetic variant IV being associated with unmeasured confounders through population stratification. Population stratification is a condition where there are subpopulations, some of which are more likely to have the genetic variant, and some of which are more likely to have the outcome through mechanisms other than the treatment being studied. For example, consider studying the effect of alcohol consumption on hypertension. Consider using the ALDH2 null variant, which is associated with alcohol consumption, as an IV (individuals who are homozygous for the ALDH2 null variant have severe adverse reactions to alcohol consumption and tend to drink very little [33]). The ALDH2 null variant is much more common in people with Asian ancestry than other types of ancestry [34]. Suppose ancestry was not fully measured. If ancestry is associated with hypertension through mechanisms other than differences in the ALDH2 null variant (e.g., through different ancestries tending to have different diets), then ALDH2 would not be a valid IV because it would be associated with an unmeasured confounder.
Not associated with unmeasured confounders through genetic linkage. Genetic linkage is the tendency of genes that are located near to each other on a chromosome to be inherited together because the genes are unlikely to be separated during the crossing over of the mother's and father's DNA [35]. Consider using a gene A as an IV where gene A is genetically linked to a gene B that has a causal effect on the outcome through a pathway other than the treatment being studied. If gene B is not measured and controlled for, then gene A is not a valid IV because it is associated with the unmeasured confounder gene B.
No direct effect through pleiotropy. Pleiotropy refers to a gene having multiple functions. If the genetic variant being used as an IV affects the outcome through a function other than affecting the treatment being studied, this would mean the genetic variant has a direct effect. For example, consider the use of the APOE genotype as an IV for studying the causal effect of low-density lipoprotein cholesterol (LDLc) on myocardial infarction (MI) risk. The ∊2 variant of the APOE gene is associated with lower levels of LDLc but is also associated with higher levels of high-density lipoprotein cholesterol, less efficient transfer of very low density lipoproteins and chylomicrons from the blood to the liver, greater postprandial lipaemia and an increased risk of Type III hyperlipoproteinaemia (the last three of which are thought to increase MI risk)[33]. Thus, the gene APOE is pleiotropic, affecting myocardial infarction risk through different pathways, making it unsuitable as an IV to examine the causal effect of any one of these pathways on MI risk.
[36] and [33] provide good reviews of Mendelian randomization methods.
Timing of Admission
Another source of IVs for health studies is timing of admission variables. For example, [37] used day of the week of hospital admission as an IV for waiting time for surgery to study the effects of waiting time on length of stay and inpatient mortality among patients admitted to the hospital with a hip fracture. Day of the week of admission is associated with waiting time for surgery because many surgeons only do non-emergency operations on weekdays, and therefore patients admitted on weekends may have to wait longer for surgery. In order for weekday vs. weekend admission to be a valid IV, patients admitted on weekdays vs. weekends must not differ on unmeasured characteristics (i.e., the IV must be independent of unmeasured confounders) and other aspects of hospital care that affect the patients’ outcomes besides surgery must be comparable on weekdays vs. weekends (i.e., the IV has no direct effect). Another example of a timing of admission variable used as an IV is hour of birth as an IV for a newborn's length of stay in the hospital [38, 39].
Insurance Plan
Insurance plans vary in the amount of reimbursement they provide for different treatments. For example, [40] used drug co-payment amount as an IV to study the effect of β-blocker adherence on clinical outcomes and health care expenditures after a hospitalization for heart failure. In order for variations in insurance plan like drug co-payment amount to be a valid IV, insurance plans must have comparable patients after controlling for measured confounders (i.e., the IV is independent of unmeasured confounders) and insurance plans must not have an effect on the outcome of interest other than through influencing the treatment being studied (i.e., the IV has no direct effect).
We have discussed several common sources of IVs for health studies and considerations to think about in deciding whether potential IVs from these sources satisfy the assumptions to be a valid IV. A detailed understanding of how treatments are chosen in a particular setting may yield additional, creative ideas for potential IVs. In Section 4, we will formally state the assumptions for an IV to be valid and discuss how to use a valid IV to estimate the causal effects of a treatment.
4. IV Assumptions and Estimation for Binary IV and Binary Treatment
In this section, we consider the simplest setting for an instrumental variable design, when both the instrument and treatment are binary. The main ideas in IV methods are most easily understood in this setting and the ideas will be expanded to more complicated settings in later sections.
4.1 Framework and Notation
The Neyman-Rubin potential outcomes framework[41, 42] will be used to describe causal effects and formulate IV assumptions. The classic econometric formulation of instrumental variables is in terms of structural equations and assumptions about the IV being uncorrelated with structural error terms; the formulation in terms of potential outcomes that is described here provides clarity about what effects are being estimated when there are heterogeneous treatment effects and provides a firm foundation for nonlinear as well as linear outcome models[21, 43]. Suppose there are N subjects. Let Z denote the N-dimensional vector of IV assignments with individual elements Zi, i = 1,..., N, where Zi = 0 or 1. Level 1 of the IV is assumed to mean the subject was encouraged to take level 1 of the treatment, where the treatment has levels 0 and 1. Let Dz be the N-dimensional vector of potential treatment under IV assignment z with elements , i = 1, . . . , N, or 0 according to whether person i would receive treatment level 1 or 0 under IV assignment z. Let Yz,d be the N-dimensional vector of potential outcomes under IV assignment z and treatment assignment d where is the outcome subject i would have under IV assignment z and treatment assignment d. The observed treatment for subject i is and the observed outcome for subject i is . Let Xi denote observed covariates for subject i. When we write expressions like E(Y), we mean the expected value of Y for a randomly sampled subject from the population.
[43] considered an IV to be a variable satisfying five assumptions – the stable unit treatment value assumption, the IV is positively correlated with treatment assumption, the IV is independent of unmeasured confounders assumption, the exclusion restriction assumption and the monotonicity assumption. We will describe the first four of these assumptions and then describe the need for the fifth assumption or some substitute to obtain point identification. The first four assumptions are
IV-A1 Stable Unit Treatment Value Assumption (SUTVA). If then and if and , then . In words, this assumption says that the treatment affects only the subject taking the treatment and that there are not different versions of the treatment which have different effects (see [43, 44] for details). The stable unit treatment value assumption allows us to write as where z here denotes subject i having IV assignment z and as where z and d here denote subject i having IV assignment z and treatment d.
IV-A2 IV is positively correlated with treatment received. E(D1|X) > E(D0|X) (Note that we have assumed that level 1 of the IV means that the subject was encouraged to take level 1 of the treatment).
- IV-A3 IV is independent of unmeasured confounders (conditional on covariates X).
IV-A4 Exclusion restriction (ER). This assumption says that the IV affects outcomes only through its effect on treatment received: for all i. Under the ER, we can write for any z, i.e., is the potential outcome for subject i if she were to receive level 1 of the treatment (regardless of her level of the IV) and is the potential outcome if she were to receive level 0 of the treatment. The exclusion restriction assumption is also called the no direct effect assumption.
Assumptions IV-A2, IV-A3 and IV-A4 are the assumptions depicted in Figure 1. These assumptions are the “core” IV assumptions that basically all IV approaches make; assumption IV-A1 is typically implicitly made as well. The core IV assumptions enable bounds on treatment effects to be identified but do not point identify a treatment effect[45].
To see why the core IV assumptions alone do not point identify a treatment effect and to understand what additional assumptions would identify a treatment effect, it is helpful to introduce the idea of compliance classes[43]. A subject in a study with binary IV and treatment can be classified into one of four latent compliance classes based on the joint values of potential treatment received [43]. The four compliance classes are referred to as never-takers, always-takers, defiers and compliers. We denote subject i's compliance class as Ci, which are defined like so: Ci = never-taker (nt) if ; complier (co) if ; always-taker (at) if and defier (de) if . Note that there being four compliance classes is not an assumption but an exhaustive list of the possible types of compliance. Note also that a subject' compliance class is relative to a particular IV, e.g., in studying the effect of regular exercise on the lung function of patients with chronic pulmonary obstructive disease, a person might be a complier if the IV is Z = 1 means the person will receive $1000 if she regularly exercises vs. Z = 0 means the person will receive no extra payment if she regularly exercises but the person might be a never taker if Z = 1 means the person will receive only $100 if she regularly exercises. Table 3 shows the relationship between the latent compliance classes and the observed groups.
Table 3.
The relation between observed groups and latent compliance classes
| Zi | Di | Ci |
|---|---|---|
| 1 | 1 | Complier or Always-taker |
| 1 | 0 | Never-taker or Defier |
| 0 | 0 | Never-taker or Complier |
| 0 | 1 | Always-taker or Defier |
Suppose the outcome is binary so that the observed data (Y, D, Z) is a multinomial random variable with 2 × 2 × 2 = 8 categories. Under Assumptions (IV-A1)-(IV-A4), there are ten free unknown parameters: P(Z = 1), P(Y1 = 1|C = at), P(Y1 = 1|C = co), P(Y0 = 1|C = co), P(Y0 = 1|C = nt), P(Y1 = 1|C = de), P(Y0 = 1|C = de), P(C = at), P(C = co) and P(C = nt) (note that P(C = de) is determined by P(C = co) + P(C = at) + P(C = nt) + P(C = de) = 1). Since there are ten free parameters but the observed data multinomial random variable has only 8 categories (so 7 free probabilities), the model is not identified. Two types of additional assumptions have been considered that reduce the number of free parameters: (i) an assumption about the process of selecting a treatment based on the IV that restricts the number of compliance classes by ruling out defiers; (ii) assumptions that restrict the heterogeneity of treatment effects among the different compliance classes.
We first consider the approach (i) to point identification of restricting the number of compliance classes. The assumption made by [43] rules out defiers:
IV-A5 Monotonicity assumption. This assumption says that there are no subjects who are “defiers,” who would only take level 1 of the treatment if not encouraged to do so, i.e., there is no subject i with .
Monotonicity is automatically satisfied for single-consent randomized encouragement designs in which only the subjects encouraged to receive the treatment are able to receive it[46] (for this design, there are only compliers and never takers). Monotonicity is also plausible in many applications in which the encouragement (Z = 1) provides a clear incentive and no disincentive to take the treatment. For the setting of a binary outcome, (IV-A5) reduces the number of free parameters to seven, enabling identification since there are seven free probabilities for the observed data. However, the model only identifies the average treatment effect for compliers. The never-takers and always-takers do not change their treatment status when the instrument changes, so under the ER assumption, the potential treatment and potential outcome under either level of the IV (Zi = 1 or 0) is the same. Consequently, the IV is not helpful for learning about the treatment effect for always-takers or never-takers. Compliers are subjects who change their treatment status with the IV, that is, the subjects would take the treatment if they were encouraged to take it by the IV but would not otherwise take the treatment. Because these subjects change their treatment with the level of the IV, the IV is helpful for learning about their treatment effects. The average causal effect for this subgroup, , is called the complier average causal effect (CACE) or the local average treatment effect (LATE). It provides the information on the average causal effect of receiving the treatment for compliers.
Approach (ii) to making assumptions about IVs to enable point identification of a treatment effect keeps Assumptions (IV-A1)-(IV-A4) but does not make Assumption (IV-A5) (Monotonicity); instead, it makes an assumption that restricts the heterogeneity of treatment effects among the compliance classes. The strongest such assumption is that the average effect of the treatment is the same for all the compliance classes, E(Y1 – Y0|C = co) = E(Y1 – Y0|C = at) = E(Y1 – Y0|C = nt) = E(Y1 – Y0|C = de). This assumption identifies the average treatment effect for the whole population (this can be derived by using the same reasoning as in the derivation of (2)). A weaker restriction on the heterogeneity of treatment effects among the compliance classes is the no current treatment value interaction assumption[47]:
| (1) |
Assumption (1) combined with (IV-A1)-(IV-A4) identifies the average effect of treatment among the treated, E(Y1 – Y0|D = 1). Under Assumptions (IV-A1)-(IV-A5), Assumption (1) says that the average treatment effect is the same among always takers and compliers conditional on X, since the left hand side of (1) is the average effect of treatment among compliers and always takers and the right hand side is the average effect among always takers (all conditional on X). For further information on approach (ii), see [48, 49].
We are going to focus on approach (i) to the IV assumptions (i.e., Assumptions (IV-A1)-(IV-A5)) for the rest of this tutorial. An attractive feature of this approach is that the monotonicity assumption (IV-A5) is reasonable in many applications (e.g., when the encouragement level of the IV provides a clear incentive to take treatment and no disincentive); see also Section 5.3 for discussion of a weaker assumption than monotonicity which has similar consequences. Although the effect identified by (IV-A1)-(IV-A5), the CACE, is only the effect for the subpopulation of compliers, the data is in general not informative about average effects for other subpopulations without extrapolation, just as a randomized experiment conducted on men is not informative about average effects for women without extrapolation[50]. By focusing on estimating the CACE, the researcher sharply separates exploration of the information in the data from extrapolation to the (sub)-population of interest[50]. See Section 5.1-5.2 for discussion of extrapolation of the CACE to other (sub)-populations.
[51] showed that Assumptions (IV-A1)-(IV-A5) are equivalent to a version of common approach to IV assumptions in economics. In economics, selection of treatment A vs. B is often modeled by a latent index crossing a threshold, where the latent index is interpreted as the expected net utility of choosing treatment A vs. B. For example,
where
Zi independent of εi1, εi2
[51] showed that a nonparametric version of the latent index model is equivalent to the Assumptions (IV-A1)-(IVA5) above that [43] use to define an IV.
4.2 Two stage least squares (Wald) estimator
Let us first consider IV estimation when there are no observed covariates X. For binary IV and treatment variable, [43] show that under Assumptions (IV-A1)-(IV-A5), the CACE is nonparametrically identified by
| (2) |
where the second equality follows from the monotonicity assumption (Assumption IV-A5), the third equality follows from the IV is independent of unmeasured confounders assumption (Assumption IV-A3), the fourth equality follows from the exclusion restriction assumption (Assumption IV-A4) and the fifth equality follows from the IV is correlated with treatment received assumption (Assumption IV-A2).
The standard IV estimator for a binary IV and a binary treatment is the sample analogue of the first expression in (2),
| (3) |
where Ê denotes the sample mean. The standard IV estimator is called the Wald estimator after [52].
The standard IV estimator is also called the two stage least squares (2SLS) estimator because it can be obtained from the following two stage least squares procedure: (i) regress D on Z by least square to obtain Ê(D|Z); (ii) regress Y on Ê(D|Z). The coefficient on Ê(D|Z) from the regression (ii) equals (3). Since (3) can be obtained by the two stage least squares procedures, we denote (3) by CÂCE2SLS,
| (4) |
To see why two stage least squares provides a consistent estimate of the CACE, write Y = α + CACE × D + u, where α is chosen so that E(u) = 0. Then, under the monotonicity and exclusion restriction assumption,
Thus, under the IV independent of unmeasured confounders assumption, E(Y|Z) = α + CACE × E(D|Z) and an unbiased estimate of the CACE can be obtained from regressing Y on E(D|Z). We do not know E(D|Z) but can replace it by the consistent estimate Ê(D|Z) from regressing D on Z, and then regress Y on Ê(D|Z); this is the two stage least squares procedure. The standard error for CÂCE2SLS is not the standard error from the second stage regression but needs to account for the sampling uncertainty in using Ê(D|Z) as an estimate of E(D|Z); see [53–55] and [56], Chapter 9.8 Specifically, the asymptotic standard error for CÂCE2SLS is given in [55], Theorem 3. The 2SLS estimator CÂCE2SLS can also be written as [54].
The 2SLS estimator does not take into full account the structure in Table 3 that the observed outcomes are mixtures of outcomes from different compliance classes. [57–60] develop approaches to estimating the CACE that use the mixture structure to improve efficiency. For example, [59] develops an empirical likelihood approach that is consistent under the same assumptions as 2SLS but that provides substantial efficiency gains in some finite sample settings.
4.3 Estimation with Observed Covariates
As discussed above, various methods have been proposed to use IVs to overcome the problem of unmeasured confounders in estimating the effect of a treatment on outcomes without covariates. However, in practice, IVs may be valid only after conditioning on covariates. For example, in the NICU study of Section 1.2, race is associated with the proposed IV excess travel time and race is also thought to be associated with infant complications through mechanisms other than level of NICU delivery such as maternal age, previous Caesarean section, inadequate prenatal care and chronic maternal medical conditions [61]. Consequently, in order for excess travel time to be independent of unmeasured confounders conditional on measured covariates, it is important that race be included as a measured covariate. To incorporate covariates into the two-stage least squares estimator, regress Di on Xi and Zi in the first stage to obtain D̂i and then regress Yi on D̂i and Xi in the second stage. Denote the coefficient D̂i in the second stage regression by . The estimator estimates a covariate-averaged CACE as we shall discuss [62]. Let (λ, ϕ) be the minimum mean squared error linear approximation to the average response function for compliers E(Y|X D, C = co), i.e., (λ, ϕ) = arg minλ*,ϕ* E[Y – ϕ*T X – λ*D)2|C = co] (where X is assumed to contain the intercept). Specifically, if the complier average causal effect given X is the same for all X and the effect of X on the outcomes for compliers is linear (i.e., E(Y|X D, C = co) = ϕT X + λD), then λ equals the CACE. The estimator is a consistent (i.e., asymptotically unbiased) estimator of λ. Thus, if the complier average causal effect given X is the same for all X and the effect of X on the outcomes for compliers is linear, is a consistent estimator of the CACE. As discussed in Section 4.2, the standard error for is not the standard error from the second stage regression but needs to account for the sampling uncertainty in using D̂i as an estimate of E(Di|Xi, Zi); see [53–55] and [56], Chapter 9.8. Other methods besides two-stage least squares for incorporating measured covariates into the IV model are discussed in [59, 63–69] among others. [63] and [64] introduce covariates in the IV model of [55] with distributional assumptions and functional form restrictions. [65] consider settings under fully saturated specifications with discrete covariates. Without distributional assumptions or functional form restrictions, [66] develops closed forms for average potential outcomes for compliers under treatment and control with covariates. [59] discuss incorporating covariates with an empirical likelihood approach.
4.4. Robust Standard Errors for 2SLS
When there is clustering in the data, standard errors that are robust to clustering should be computed. For 2SLS, this can be done by using robust Huber-White standard errors[70]. Code for computing robust Huber-White standard errors for IV analysis with clustering in R is given in Section 14. For the NICU study, there is clustering by hospital.
Even when there is no clustering, we recommend always using the robust Huber-White standard errors for 2SLS as the non-robust standard error's correctness requires additional strong assumptions about the relationships between the different compliance classes’ outcome distributions and homoskedasticity while the robust standard error's correctness does not require these assumptions; see Theorem 3 in [55] and Section 4.2.1 of [62]. Code for computing robust Huber-White standard errors without clustering in R is given in Section 14.
4.5. Two Sample IV
The 2SLS estimator (4) can be used when information on Y, Z, D and X are not available in a single data set, but one data set has Y, Z and X and the other data set has D, Z and X. One can estimate the regression function Ê(D|Z, X) from the first data set and then compute Ê(D|Zi, Xi) for the subjects i in the second data set and regress Yi on Ê(D|Zi, Xi) and Xi for the second data set. This is called two-sample two stage least squares[71, 72]; see [72] for how to compute standard errors. An example of using two-sample two-stage least squares is [73] that studied the effect of food stamps on body mass index (BMI) in immigrant families using differences in state responses to a change in federal laws on immigrant eligibility for the food stamp program as an IV. The National Health Interview Study was used to estimate the effect of state lived in on BMI and the Current Population Survey was used to estimate the effect of state lived in on food stamp program participation because neither data set contained all three variables.
4.6. Example 1: Analysis of NICU study
For the NICU study, Table 4 shows the two stage least squares estimate for the effect of high level NICUs using excess travel time as an IV and compares the 2SLS estimate to the estimate that does not adjust for any confounders and the multiple regression estimate that only adjusts for the measured confounders (those in Table 4 plus several other variables described in [4]) The unadjusted estimate is that high level NICUs increase the death rate, causing 10.9 more deaths per 1000 deliveries; this estimate is probably strongly biased by the selection bias that doctors and mothers are more likely to insist on babies being delivered at a high level NICU if the baby is at high risk of mortality. The regression estimate that adjusts for measured confounders is that high level NICUs save 4.2 babies per 1000 deliveries. The two stage least squares estimate that adjusts for measured and unmeasured confounders is that high level NICUs save even more babies, 5.2 babies per 1000 deliveries.
Table 4.
Risk Difference Estimates for Mortality Per 1000 Premature Births in High Level NICUs vs. Low Level NICUs. The confidence intervals account for clustering by hospital through the use of Huber-White robust standard errors.
| Estimator | Risk Difference | Confidence Interval |
|---|---|---|
| Unadjusted | 10.9 | (6.6, 15.3) |
| Multiple Regression, Adjusted for Measured Confounders | −4.2 | (−6.8, −1.5) |
| Two Stage Least Squares, Adjusted for Measured and Unmeasured Confounders | −5.9 | (−9.6, −2.2) |
As illustrated by Table 4, the multiple regression estimate of the causal effect will generally have a smaller confidence interval than the 2SLS estimate. However, when the IV is valid and there is unmeasured confounding, the multiple regression estimate will be asymptotically biased whereas the 2SLS estimate will be asymptotically unbiased. Thus, there is a bias-variance tradeoff between multiple regression vs. 2SLS (IV estimation). When the IV is not perfectly valid, the 2SLS estimator will be asymptotically biased, but the bias-variance tradeoff may still favor 2SLS. [74] develops a diagnostic tool for deciding whether to use multiple regression vs. 2SLS.
4.7. Example 2: The Effect of Receiving Treatment in a Randomized Trial with Nonadherence
An important application of IV methods is to estimating the effect of receiving treatment in randomized trials with nonadherence. When some subjects do not adhere to their assigned treatments in a randomized trial, the intention to treat (ITT) effect is often estimated, IT̂T = Ê(Y|Z = 1) – Ê(Y|Z = 0); ITT is estimating the effect of being assigned the active treatment compared to being assigned the control (e.g., a placebo or usual care). When there is nonadherence, the ITT effect is different from the effect of receiving the treatment vs. the control. Both of these effects are valuable to know. One situation when knowing the effect of receiving the treatment vs. the control is particularly valuable is when the treatment non-adherence pattern is expected to differ between the study sample and the target population[75–77]. In this situation, the ITT estimate may be biased for estimating the effect of offering the treatment to the target population[75, 76] and a key quantity that needs to be known to accurately predict the effect of offering the treatment to the target population is the effect of actually receiving the treatment[76, 77]. For example, [75] discuss a trial of vitamin A supplementation to reduce child mortality. In the trial, the Vitamin A supplementation was implemented by having children take pills and some children who were randomized to treatment did not take the pills. The ITT effect is the effect of making Vitamin A pills available to children. However, if the the trial showed that taking the pills was efficacious, Vitamin A supplementation would not likely be implemented by providing pills but instead by fortifying a daily food item such as monosodium glutamate or salt[75]. By knowing the effect of receiving Vitamin A supplementation (the biologic efficacy) and the rate at which Vitamin A supplementation would be successfully delivered under a fortification program, we can estimate the effectiveness of a fortification program. A second situation in which knowing the effect of receiving treatment vs. control is particularly valuable is when patients who are interested in fully adhering to a treatment are making decisions about whether to take the treatment[76, 78]. For example, [78] mention the setting that to decide whether to use a certain contraception method, a couple may want to know the failure rate if they use the method as indicated, rather than the failure rate in a population that included a substantial proportion of non-adherers.
A standard estimate of the effect of receiving the treatment vs. the control is the as treated estimate, E(Y|D = 1) – Ê(Y|D = 0), which compares the outcomes of subjects who received the treatment vs. the control regardless of the subjects’ assigned treatment. The as-treated estimate may be biased for estimating the effect of receiving the treatment because of unmeasured confounding, e.g., individuals with better diet may be more likely to adhere to treatment and to have better outcomes regardless of treatment. Another standard estimate is the per protocol estimate, Ê(Y|Z = 1, D = 1) – Ê(Y|Z = 0. D = 0), which compares the outcomes of subjects who were assigned to the treatment and followed the treatment protocol to subjects who were assigned the control and followed the control protocol; similar to the as treated estimate, the per protocol estimate may be biased for estimating the effect of receiving the treatment because of unmeasured confounding, e.g., individual with better diet may be more likely to adhere to treatment but all subjects may adhere with the control if the control is usual care. The IV method has the potential of overcoming bias from unmeasured confounding in estimating the effect of receiving the treatment. Consider as a possible IV, the randomly assigned treatment Z. The randomly assigned treatment satisfies the IV is independent of unmeasured confounders assumption (IV-A3) because of the randomization and the randomly assigned treatment will usually make receiving treatment more likely, thus satisfying (IV-A2) that the IV is positively correlated with treatment received. It needs to be considered whether the randomly assigned treatment satisfies the exclusion restriction (IV-A4) and monotonicity assumptions (IV-A5) for specific trials. In the Vitamin A pill trial mentioned above, the treatment was only available to those assigned to treatment so that monotonicity was automatically satisfied. [75] argue that the exclusion restriction is also likely satisfied for the Vitamin A trial because for never takers, being assigned to the treatment group vs. the control group is unlikely to affect mortality (there was no placebo in the trial). In contrast, [79] raise concern about the exclusion restriction holding in certain mental health randomized trials. If the randomly assigned treatment does satisfy all the IV assumptions (IV-A1)-(IV-A5) for a trial, then the two stage least squares (Wald) estimator (4) is a consistent estimate of the effect of actually receiving treatment for compliers. The numerator of (4) is equal to the intent to treat estimate and the denominator of (4) is an estimate of the proportion of compliers.
Table 5 shows the mortality rates in the Vitamin A trial, stratified by assigned treatment and received treatment[75]. The ITT estimate for the effect on the mortality rate per 1000 children is 3.8 – 6.4 = -2.6, the as treated estimate is 1.2 – 7.7 = -6.5, the per protocol estimate is 1.2 – 6.4 = -5.2 and the IV estimate is . As discussed above, the assumptions for randomization assignment to be a valid IV are plausible for the Vitamin A trial and the IV estimate says that taking the Vitamin A pills saves an estimated 3.3 per 1000 children among those children who would take the Vitamin A pills if offered them (the compliers in this trial – note that there are no always takers in this trial).
Table 5.
Mortality rates in Vitamin A trial, stratified by assigned treatment and received treatment. The top part of the table shows all three strata and the bottom part shows certain collapsed strata
| Randomization Assignment | Treatment Received | # of Children | Deaths (per 1000) | Mortality Rate |
|---|---|---|---|---|
| Control | Control | 11,588 | 74 | 6.4 |
| Treatment | Control | 2,419 | 34 | 14.1 |
| Treatment | Treatment | 9,675 | 12 | 1.2 |
| Treatment | Control or Treatment | 2,419+9,675=12,094 | 34+12 | 3.8 |
| Control or Treatment | Control | 11,588+2,419 | 74+34 | 7.7 |
5. Understanding the Treatment Effect that IV Estimates
As discussed in Section 4, the IV method estimates the CACE, the average treatment effect for the compliers (i.e. E[Y1 – Y0|C = co]), which might not equal the average treatment effect for the whole population. Although we might ideally want to know the average treatment effect for the whole population, the average treatment effect for compliers often provides useful information about the average treatment for the whole population and the average treatment effect for compliers may be of interest in its own right. In Section 5.1, we discuss how to relate the average treatment for compliers to the average treatment effect for the whole population and in Section 5.2, we discuss how to understand more about who the compliers are, which is helpful for interpreting the average treatment effect for compliers in its own right. In Sections 5.3-5.5, we discuss additional issues related to understanding the treatment effect that IV estimates. In particular, in Section 5.3, we discuss interpreting the treatment effect when the compliance class is not deterministic; in Section 5.4, we discuss interpreting the treatment effect when there are different versions of the treatment; and in Section 5.5, we discuss interpretation issues when there is heterogeneity in response.
5.1 Relationship between Average Treatment Effect for Compliers and Average Treatment Effect for the Whole Population
As discussed in Section 4, the IV method estimates the CACE, the average treatment effect for the compliers (i.e. E[Y1 – Y0|C = co]). The average treatment effect in the population is, under the monotonicity assumption, a weighted average of the average treatment effect for the compliers, the average treatment effect for the never-takers and the average treatment effect for the always-takers:
The IV method provides no direct information on the average treatment effect for always-takers (i.e., E[Y1 – Y0|C = at]) or the average treatment effect for never-takers (i.e., E[Y1 – Y0|C = nt]). However, the IV method can provide useful bounds on the average treatment effect for the whole population if a researcher is able to put bounds on the difference between the average treatment effect for compliers and the average treatment effects for never-takers and always-takers based on subject matter knowledge. For example, suppose a researcher is willing to assume that this difference is no more than b. Then
| (5) |
where the quantities on the left and right hand sides of (5) other than b can be estimated as discussed in Section 4 and [58, 60, 64]. For binary or other bounded outcomes, the boundedness of the outcomes can be used to tighten bounds on the average treatment effect for the whole population or other treatment effects [45, 80]. Qualititative assumptions, such as that the average treatment effect is larger for always-takers than compliers, can also be used to tighten the bounds, e.g., [80–82].
In thinking about extrapolating the CACE to the full population, it is useful to think about how compliers’ outcomes compare to always takers and never takers’ outcomes[50]. The data provide some information about this. Specifically, we can compare
| (6) |
Under (IV-A1)-(IV-A5), [83] shows that the following are consistent estimates of the quantities in (1) when there are no covariates: Ê(Y0|C = nt) = Ê(Y|D = 0, Z = 1), , Ê(Y1|C = at) = Ê(Y|D = 1, Z = 0) and ; when there are covariates, the methods of [66] or [64] can be used to estimate the quantities in (1). If compliers never takers and always takers are found to be substantially different in levels by evidence of a substantial difference between E(Y0|C = nt) and E(Y0|C = co) and/or between E(Y1|C = at) and E(Y1|C = co), then it appears much less plausible that the average effect for compliers is indicative of average effects for other compliance types. On the other hand, if one finds that potential outcomes given the control for never takers and compliers are similar, and potential outcomes given the treatment are similar for compliers and always takers, it is more plausible that average treatment effects for the groups are also comparable[50]. For example, in the Vitamin A trial described in Table 5, the mortality rate for never takers is estimated to be 14.1 (per 1000 children) and for compliers under control is estimated to be 4.8 (note that there are no always takers in the Vitamin A trial). This substantial difference in estimated mortality rates between the compliance classes suggests that we should be cautious in extrapolating the CACE to the full population.
5.2 Characterizing the Compliers
The IV method estimates the average treatment effect for the subpopulation of compliers. In most situations, it is impossible to identify which subjects in the data set are “compliers” because we only observe a subject's treatment selection under either Z = 1 or Z = 0 which means we cannot identify if the subject would have complied under the unobserved level of the instrument. So who are these compliers and how do they compare to noncompliers? To understand this better, it is useful to characterize the compliers in terms of their distribution of observed covariates [9, 62]. The mean of a covariate Xi among the compliers is the following under the IV assumptions 1-5 from Section 4.1, where f represents the probability mass function or probability density function,
| (7) |
where
| (8) |
where X denotes the vector of measured covariates that need to be condition on for (IV-A3) to hold and X denotes the covariate for which we are examining its distribution among the compliers (note that X need not be included in X). An alternate representation for E(X|C=co) from [66] is E(X|C=co)=E[κi*Xi]/E[κi] where κi=1-Di*(1-Zi)/[1-P(Zi=1|Xi)]-(1-Di)/P(Zi=1|Xi). We can estimate E(X|C=co) by usign logistic regression to estimate P(Zi=1|Xi) and using these estimates to estimate κi and then estimating E(X|C=co) by the sample mean of *X divided by the sample mean of . The prevalence ratio of a binary characteristic X among compliers compared to the full population is
Table 6 shows the mean of various characteristics X among compliers vs. the full population, and also shows the prevalance ratio. Babies whose mothers are college graduates are slightly underrepresented (prevalence ratio = 0.87) and African Americans are slightly overrepresented (prevalence ratio = 1.14) among compliers. Very low birthweight (< 1500 g) and very premature babies (gestational age ≤ 32 weeks) are substantially underrepresented among compliers, with prevalence ratios around one-third; these babies are more likely to be always-takers, i.e., delivered at high level NICUs regardless of mother's travel time. Babies whose mothers’ have comorbidities such as diabetes or hypertension are slightly underrepresented among compliers. Overall, Table 6 suggests that higher risk babies are underrepresented among the compliers. If the effect of high level NICUs is greater for higher risk babies, then the IV estimate will underestimate the average effect of high level NICUs for the whole population.
Table 6.
Complier characteristics for NICU study. The second column shows the estimated proportion of compliers with a characteristic X, the third column shows the estimated proportion of the full population with the characteristic X and the fourth column shows the estimated ratio of compliers with X compared to the full population with X.
| Characteristic X | Prevalence of X among compliers | Prevalence of X in full population | Prevalence Ratio of X among compliers to full population |
|---|---|---|---|
| Birthweight < 1500g | 0.03 | 0.09 | 0.33 |
| Gestational Age <= 32 weeks | 0.04 | 0.13 | 0.34 |
| Mother College Graduate | 0.23 | 0.26 | 0.87 |
| African American | 0.17 | 0.15 | 1.14 |
| Gestational Diabetes | 0.05 | 0.05 | 0.91 |
| Diabetes Mellitus | 0.02 | 0.02 | 0.77 |
| Pregnancy Induced Hypertension | 0.08 | 0.10 | 0.82 |
| Chronic Hypertension | 0.02 | 0.02 | 0.89 |
5.3 Understanding the IV Estimate When Compliance Status Is Not Deterministic
For an encouragement that is uniformly delivered, such as patients who made an appointment at a psychiatric outpatient clinic are sent a letter encouraging them to attend the appointment [84], it is clear that a subject is either a complier, always taker, never taker or defier with respect to the encouragement. However, sometimes encouragements that are not uniformly delivered are used as IVs. For example, in the NICU study, consider the IV of whether the mother's excess travel time to the nearest high level NICU is more than 10 minutes. If a mother whose excess travel time to the nearest high level NICU was more than 10 minutes moved to a new home with an excess travel time less than 10 minutes, whether the mother would deliver her baby at a high level NICU might depend on additional aspects of the move, such as the location and availability of public transportation at her new home [85] and the exact travel time to the nearest high level NICU at her new home. Consequently, a mother may not be able to be deterministically classified as a complier or not a complier – she may be a complier with respect to certain moves but not others. Another example of nondeterministic compliance is that when physician preference for one drug vs. another is used as the IV (e.g., Z = 1 if a patient's physician prescribes drug A more often drug B), whether a patient receives drug A may depend on how strongly the physician prefers drug A [9, 86]. Another situation in which nondeterministic compliance status can arise is that the IV may not itself be an encouragement intervention but a proxy for an encouragement intervention. Consider the case of Mendelian randomization, in which the IV is often a single nucleotide polymorphism (SNP). Changes in the SNP itself may not affect the exposure D. Instead, genetic variation at another location on the same chromosome as the SNP, call it L, might affect D. The SNP might just be a marker for the subject's genetic code at location L. The encouragement intervention is having a certain genetic code at L and the SNP is just a proxy for this encouragement. Consequently, even if a subject's exposure level would change as a result of a change in the genetic code at location L, whether the subject is a complier with respect to a change in the SNP depends on whether the change in the SNP leads to a change in the genetic code at location L, which is randomly determined through the process of recombination[85].
Brookhart and Schneeweiss [9] provide a framework for understanding how to interpret the IV estimate when compliance status is not deterministic. Suppose that the study population can be decomposed into a set of κ + 1 mutually exclusive groups of patients based on clinical, lifestyle and other characteristics such that within each group of patients, whether a subject receives treatment is independent of the effect of the treatment. All of the common causes of the potential treatment receiveds D1, D0 and the potential outcomes Y1, Y0 should be included in the characteristics used to define these groups. For example, if there are L binary common causes of (D1, D0, Y1, Y0), then the subgroups can be the κ + 1 = 2L possible values of these common causes. Denote patient membership in these groups by the set of indicators S = {S1, S2, . . ., Sκ}. Consider the following model for the expected potential outcome:
The average effect of treatment in the population is and the average effect of treatment in subgroup j is α1 + α3,j. Under the IV assumptions (IV-A1)-(IV-A4) in Section 4.1, i.e., all the assumptions except monotonicity, the 2SLS estimator (4) converges in probability to the following quantity:
| (9) |
where
The IV estimator (9) is a “weighted average” of treatment effects in different subgroups, where the subgroups in which the instrument has a stronger effect on the treatment get more weight. Note that when the compliance class is deterministic, then the subgroups can be defined as the compliance classes and (9) just says that the IV estimator is the average treatment effect for compliers. In the NICU study, where compliance class may not be deterministic, Table 6 suggests that babies in lower risk groups, e.g., not very low birthweight or not very low gestational age, are weighted more heavily in the IV estimator. If there are subgroups for which the instrument has no effect on their treatment level, then that subgroup gets zero weight. For example, mothers or babies with severe preexisting conditions may virtually always be delivered at a high level NICU, so that the IV of excess travel time has no effect on their treatment level [4]. If there are subgroups for which the encouraging level of the instrument makes them less likely to receive the treatment, then this subgroup would get “negative weight” and (9) is not a true weighted average, potentially leading the IV estimator to have the opposite sign of the effect of the treatment. For example, [9] discussed studying the safety of metformin for treating Type II diabetes vs. other antihyperglycemic drugs among patients with liver disease using physician preference as the IV (Z = 1 if a physician is more likely to prescribe metformin than other antihyperglycemic drugs). Metformin is contraindicated in patients with decreased renal function or liver disease, as it can cause lactic acidosis, a potentially fatal side effect. [9] speculated that physicians who infrequently use metformin (Z = 0) will be less likely to understand its contraindications and would therefore be more likely to misuse it. If this hypothesis is true, then for estimating the effect of metformin on lactic acidosis, the IV estimator could mistakenly make metformin appear to prevent lactic acidosis because the subgroup(s) of patients with decreased renal function or liver disease, for which metformin causes lactic acidosis, would have a negative weight wj. When the compliance class is deterministic, a subgroup getting negative weight means that there are defiers, violating the monotonicity assumption.
5.4. Understanding the Treatment Effect Estimated by IV When SUTVA is Violated
Consider the (IV-A1) assumption from Section 4.1, SUTVA. Two ways in which SUTVA could be violated are (i) there are different versions of the treatment that have different effects, i.e., Yi1 depends on which version of the treatment was received or (ii) there is interference between units, i.e., Yi1 depends on whether unit i′ received the treatment or control[87]. When one of these violations occur, the IV estimate (4) may still be interpretable as long as (IV-A2)-(IV-A5) hold.
Consider first the no different versions of the treatment part of SUTVA. This would be violated if there are different ways of implementing the treatment that have different effects. For example, consider the effect of lowering one's body mass index on one's mental health. There are different ways that a lower body mass index might be achieved, e.g., by eating less or by exercising more, and these different ways of lowering body mass index might have different effects on mental health. The version of the treatment effect estimated by IV is the one that implements the treatment in the same way as the IV. For example, consider estimating the effect of body mass index on mental health using the FTO gene as an IV for body mass index[88]. It has been hypothesized that FTO affects body mass index through affecting appetite and there is some support for this hypothesis[89]. If this hypothesis is correct, then the treatment effect of lowering body mass index on mental health that is estimated by using the FTO gene as an IV is the version that involves lowering body mass index by reducing food intake. An intervention that lowered body mass index by increasing exercise might have different effects on mental health than an analysis that uses FTO as an IV suggests[90].
Consider next the no interference assumption part of SUTVA that subject A receiving the treatment affects only subject A and not other subjects. In the NICU study, the no interference assumption is reasonable – if preemie A is treated at a high level NICU, this does not affect preemie B's outcome. However, if there were crowding effects (e.g., treating additional babies at a hospital decreases the quality of care for babies already under care at that hospital), this assumption might not be true. The no interference assumption is also not appropriate for situations like estimating the effect of a vaccine on an individual because a non-vaccinated individual A may benefit from individual B receiving the vaccine because A can no longer become infected from contact with person B[91]. When no interference fails to hold, the IV method is roughly estimating the difference between the effect of the treatment and the spillover effect of some units being treated on those units left untreated (see [92] for a precise formulation and details).
5.5. Interpreting the Treatment Effect Estimated by IV When There Are Heterogeneous Responses
As discussed in section 4.1, the treatment effect estimated by the IV applies to only a subset of the subjects, namely the subjects whose treatment level is modified by the level of the IV. In a binary setting, we refer to the subjects that respond to the IV as the compliers, in constrast to the never-takers and always-takers. If there is heterogeneity in the response to the treatment (i.e., for some i, i′), then the IV estimate is only valid for the compliers and may not generalize to the entire population. In fact, in many medical situations it is almost certain that there is heterogeneity in response to treatment. Further, it is often the case that the always-takers always take the treatment because it is believed their response to the treatment is quite large, whereas the never-takers either have minimal or even a negative response to the treatment. If only one instrument is available, the treatment effect is not identifiable for the never-takers and always-takers. Careful thought is needed to state for which populations the IV estimate is valid.
In the NICU example, the compliers are those preemies whose NICU level would change due to travel time to the different facilities. The “always-taker” preemies tended to be more difficult to treat (e.g., younger, lower birthweight; see Table 4) and thus more obviously in need of care at a high-level NICU. It is quite possible that the treatment effect for the “always-takers” subgroup is larger than the effect estimated by the IV analysis.
Continuing with this logic, if the compliance groups are determined by how their treatment level changes due to the IV, then it follows that different IVs may estimate different treatment effects because the effects are being estimated on different subgroups. That is, if two different analyses are run on the same population, using two different but completely valid IVs, it is entirely possible for the effect estimates to differ because the composition of the compliers changes. For example, the preemies who have their NICU level changed by relative proximity to treatment facilities may have a different risk profile than preemies who would have their NICU level changed by a modification to hospital contracts with insurance providers, wherein a large percentage of the population would have to pay “out-of-network” fees in order to receive care at a high-level facility.
The issue of multiple IVs is discussed in more detail in section 11.
6. Assessing the IV Assumptions and Sensitivity Analysis for Violations of Assumptions
For most proposed IVs, there is some uncertainty about whether the proposed IV actually satisfies the IV assumptions. Consequently, it is important to empirically assess whether a proposed IV satisfies the IV assumptions. Although not all of the assumptions can be completely tested, there are methods that test certain parts of the assumptions; we discuss these methods in Section 6.1. Even if a proposed IV is not perfectly valid, it may still provide useful inferences about treatment effects as long as it does not violate the assumptions for being a valid IV too badly. In Section 6.2, we discuss sensitivity analysis methods that characterize how much inferences are affected by a proposed IV violating the assumptions by specified magnitudes.
6.1. Assessing the IV Assumptions
The assumption (IV-A2) that the IV is correlated with the treatment received can be straightforwardly assessed by looking at the association between the IV and the treatment; see Section 7 for discussion of measures of this association. This section will discuss assessing the other two core IV assumptions, (IV-A3) that the IV is independent of unmeasured confounders and (IV-A4) that the IV affects the outcome only through treatment received (the exclusion restriction).
Assessing whether the IV is independent of unmeasured confounders
The association between the (proposed) IV and the measured confounders may provide insight into whether there is any association between the IV and the unmeasured confounders conditional on the measured confounders. Although the measured confounders can be controlled for and an association between the IV and a measured confounder does not necessarily imply that there will be an association between the IV and unmeasured confounders, if a measured confounder(s) is only a proxy for a true confounder, then an association between the IV and this measured confounder(s) suggests that there will be an association between the IV and the unmeasured part of the true confounder. If there are two or more sources of confounding, then it is useful to examine if the observable part of one source of confounding is associated with the IV after controlling for the other sources of confounding. These ideas will be illustrated using the NICU study described in Section 1.2. Table 7 shows the imbalance of measured covariates across levels of the IV. The standardized difference (fourth column) compares the difference in means between the encouraged (Z = 1) and unencouraged (Z = 0) groups in units of the pooled standard deviation. The racial composition is very different between the near (Z = 1) and far (Z = 0) babies, with near babies being much more likely to be African American. Since race has a substantial association with neonatal outcomes [61, 93], it is sensible to examine the association of other measured confounders with the IV after controlling for race. Tables 8 and 9 show the association of the IV with measured confounders for whites and African Americans. After stratifying on race, the clinical measured confounders such as low birthweight, gestational age < = 32 weeks and maternal comorbidities (diabetes and hypertension) are generally similar between babies whose mother lives near to a high level NICU vs. babies whose mother lives farther away, although there are some significant associations. This similarity between the clinical status of near vs. far babies after controlling for race provides some support that the IV is approximately valid. However, whether the mother is a college graduate differs substantially between white near vs. far mothers, suggesting that there may be residual confounding due to socioeconomic status.
Table 7.
Imbalance of measured covariates between babies living near vs. far from a high level NICU (relative to the nearest low level NICU). The standardized difference (fourth column) is the difference in means between the two groups in units of the pooled within group standard deviation, i.e., for a binary characteristic X, where Z = 1 or 0 according to whether the baby lives near or far, the standardized difference is . The bias ratio is the ratio of the bias from failing to adjust for X from the IV method compared to the bias from ordinary least squares (OLS); a bias ratio of less than 1 indicates that the IV method would be less biased than OLS from failing to adjust for X.
| Characteristic X | P(X|Near) | P(X|Far) | p-value | Standardized Difference | Bias Ratio |
|---|---|---|---|---|---|
| Birthweight < 1500g | 9.4% | 7.7% | < 0.01 | 0.06 | 0.52 |
| Gestational Age <= 32 weeks | 14.3% | 11.7% | < 0.01 | 0.07 | 0.52 |
| Mother College Graduate | 25.9% | 26.1% | 0.26 | 0.00 | 0.08 |
| African American | 25.6% | 4.6% | < 0.01 | 0.61 | 3.66 |
| Gestational Diabetes | 5.2% | 5.2% | 0.47 | 0.00 | 0.27 |
| Diabetes Mellitus | 1.8% | 1.9% | 0.07 | −0.01 | 0.35 |
| Pregnancy Induced Hypertension | 10.6% | 10.1% | < 0.01 | 0.02 | 0.30 |
| Chronic Hypertension | 1.9% | 1.3% | < 0.01 | 0.04 | 1.37 |
Table 8.
Imbalance of measured covariates between babies born to white mothers living near vs. far from a high level NICU (relative to the nearest low level NICU). The standardized difference (fourth column) is the difference in means between the two groups in units of the pooled within group standard deviation. The bias ratio is the ratio of the bias from failing to adjust for X from the IV method compared to the bias from ordinary least squares (OLS); a bias ratio of less than 1 indicates that the IV method would be less biased than OLS from failing to adjust for X.
| Characteristic X | P(X|Near) | P(X|Far) | p-value | Standardized Difference | Bias Ratio |
|---|---|---|---|---|---|
| Birthweight < 1500g | 7.5% | 7.2% | 0.07 | 0.01 | 0.08 |
| Gestational Age <= 32 weeks | 11.8% | 11.1% | < 0.01 | 0.02 | 0.16 |
| Mother College Graduate | 34.4% | 26.8% | < 0.01 | 0.17 | 1.72 |
| Gestational Diabetes | 5.6% | 5.3% | 0.02 | 0.01 | 0.80 |
| Diabetes Mellitus | 1.8% | 1.9% | 0.08 | −0.01 | 0.40 |
| Pregnancy Induced Hypertension | 10.6% | 10.1% | < 0.01 | 0.01 | 0.11 |
| Chronic Hypertension | 1.6% | 1.3% | < 0.01 | 0.02 | 1.04 |
Table 9.
Imbalance of measured covariates between babies born to African American mothers living near vs. far from a high level NICU (relative to the nearest low level NICU). The standardized difference (fourth column) is the difference in means between the two groups in units of the pooled within group standard deviation. The bias ratio is the ratio of the bias from failing to adjust for X from the IV method compared to the bias from ordinary least squares (OLS); a bias ratio of less than 1 indicates that the IV method would be less biased than OLS from failing to adjust for X.
| Characteristic X | P(X|Near) | P(X|Far) | p-value | Standardized Difference | Bias Ratio |
|---|---|---|---|---|---|
| Birthweight < 1500g | 13.5% | 11.9% | < 0.01 | 0.05 | 0.82 |
| Gestational Age <= 32 weeks | 19.3% | 16.6% | < 0.01 | 0.07 | 0.95 |
| Mother College Graduate | 8.0% | 10.7% | < 0.01 | −0.09 | 3.15 |
| Gestational Diabetes | 4.2% | 4.3% | 0.67 | −0.01 | 1.39 |
| Diabetes Mellitus | 1.9% | 2.6% | < 0.01 | −0.05 | 2.66 |
| Pregnancy Induced Hypertension | 11.8% | 10.0% | < 0.01 | 0.06 | 1.35 |
| Chronic Hypertension | 2.8% | 2.4% | 0.12 | 0.03 | 0.68 |
Comparing the standardized differences in measured covariates between babies delivered at high vs. low level NICUs (fourth column of Table 2) to the standardized differences between babies living near vs. far from a high level NICU (fifth column of Table 7), we see that the standardized differences are generally smaller for the near/far groups (the IV) than the high level NICU/low level NICUs (the treatment). This suggests that the proposed IV, living near vs. far from a high level NICU, is “more randomly assigned” than the treatment of delivering at a high level NICU vs. a low level NICU. However, even though a proposed IV may be more randomly assigned than a treatment, an IV analysis based on the proposed IV may still be more biased than a regression/propensity score analysis that assumes the treatment is randomly assigned conditional on the measured covariates, because IV analyses are more sensitive to bias[94].
The bias ratio, shown in the last column of Tables 7-9, is a measure of how biased an IV analysis would be from failing to adjust from the confounder as compared to an ordinary least squares analysis[9] The below discussion of the bias ratio is drawn from [9] (the bias ratio is the prevalence difference ratio of [9] divided by the strength of the IV). Denote the confounder by U. Consider the following model for the potential outcome:
| (10) |
where E(∊d|U) = 0. The average treatment effect is E[Y1 – Y0] = α1. The observed data is
Assume that E(∊d|D, U) = 0 for d = 0 or 1. This assumption means that if U were controlled for, the parameters of (10) could be consistently estimated by least squares. By iterated expectations, E[∊0 + D(∊1 – ∊0)|D] = 0. Therefore,
so that an ordinary least squares analysis that did not adjust for U would be biased by
To evaluate the 2SLS estimator (4) using Z as an IV, consider the further assumption that E[∊0|Z] = 0 so that the proposed IV Z can be related to the observed outcome only through its effect on D or association with U; also assume that E(∊1 – ∊0|C) is the same for all compliance classes C so that the complier average causal effect is equal to the overall average causal effect α1. These assumptions together say that if U were controlled for, the 2SLS estimator would consistently estimate the average treatment effect α1. Under these assumptions, the probability limit of the 2SLS estimator that does not control for U can be written as
The asymptotic bias of the 2SLS estimator is thus
| (11) |
The ratio of the absolute bias of the 2SLS estimator to the absolute bias of the OLS estimator from failing to control for U is
| (12) |
We estimate the bias ratio for each measured confounder by plugging in sample means for the expectations in (12). In order for us to think that the IV analysis is less biased than OLS, the bias ratios should be less than 1, particularly for those variables clearly related to the outcome. Table 8 shows that for whites, the bias ratios are generally less than 1, particularly for the clinical variables gestational age and birthweight that are important to the outcome (mortality). On the other hand, Table 9 shows that for African Americans, the bias ratios are often greater than 1. The bias ratios suggest that IV analysis reduces bias for whites compared to OLS but maybe not for African Americans.
Assessing whether the IV satisfies the exclusion restriction
In order for the IV to satisfy the exclusion restriction, it must only influence the outcome through its influence on the treatment under study. For many clinical problems, there may be other treatments that could be used alongside the treatment under study[16]. If a proposed IV is associated with these concomitant treatments, then it would violate the exclusion restriction if these concomitant treatments affect the outcome. Thus, exploring the association between the proposed IV and concomitant treatments can help determine whether the exclusion restriction is violated because of associations between the treatment under study and co-interventions. For example, [28] studied the efficacy of phototherapy for newborns with hyperbilirubinemia and considered the frequency of phototherapy use at the newborn's birth hospital as an IV. Besides phototherapy, another treatment that is given for infants suffering from hyperbilirubinemia is to supplement breastfeeding with infant formula. [28] found that hospitals that use more phototherapy also have a greater use of infant formula. Consequently, the proposed preference-based IV has a direct effect (going to a hospital with higher use of phototherapy also means a newborn is more likely to receive infant formula even if the newborn does not receive phototherapy) and violates the exclusion restriction if use of infant formula influences outcomes. For the NICU study, the treatment of a high level NICU vs. a low level NICU encompasses all aspects of care at the NICU and so there are not concomitant treatments to consider.
Joint test of whether IV is independent of unmeasured confounders and satisfies the exclusion restriction
A way of testing whether a proposed IV is both independent of measured confounders and satisfies the exclusion restriction is to find a subpopulation for whom the link between the IV and treatment received is thought to be broken and then test whether the IV is associated with the outcome in this subpopulation. The only way in which the IV could be associated with the outcome in such a subpopulation is if the IV was associated with unmeasured confounders or directly affected the outcome through a pathway other than treatment received. Figure 2 shows an example. [95] study the effect of children in Africa getting malaria on their becoming stunted (having a height that is two standard deviations below the expected height for the child's age) and consider the sickle cell trait as a possible IV. The sickle cell trait is that a person inherits a copy of the hemoglobin variant HbS from one parent and normal hemoglobin from the other. While inheriting two copies of HbS results in sickle cell disease and substantially shortened life expectancy, inheriting only one copy (the sickle cell trait) is protective against malaria and is thought to have little detrimental effect on health[96]. To test whether the sickle cell trait indeed does not affect stunting in ways other than reducing malaria and is not associated with unmeasured confounders, [95] considered whether the sickle cell trait is associated with stunting among African-American children; the sickle cell trait has high prevalence among African-Americans but does not affect rates of malaria because malaria is not present in the United States. [97] and [98] found no evidence that sickle cell trait is associated with growth and development in African-American children. This absence of association supports that the dashed lines in Figure 2 are indeed absent, which would mean that the proposed IV of the sickle cell trait does indeed satisfy the core IV assumptions (IV-A3) of being independent of unmeasured confounders and (IV-A4) of affecting outcomes only through treatment received. Although this test supports that the sickle cell trait is a valid IV, the test does not have power to detect certain ways in which the IV could be invalid, e.g., the sickle cell trait might be associated with an unmeasured genetic variant that interacts with environment in such such a way that the unmeasured genetic variant only affects height in African children but not African-American children.
Figure 2.
Causal diagrams for the effect of the sickle cell trait (the IV) and malaria episodes (the treatment) on stunting (the outcome) in African children and African-American children. If the sickle cell trait is a valid IV, then the dashed lines should be absent and the sickle cell trait will have no effect on stunting among African-American children.
A related way of testing whether a proposed IV is both independent of unmeasured confounders and satisfies the exclusion restriction is to find a “treatment- unaffected outcome” that the treatment is thought not to affect and test whether the IV is associated with the treatment-unaffected outcome after controlling for measured confounders. Because the treatment does not affect the treatment-unaffected outcome, if the IV is associated with the outcome after controlling for measured confounders, this suggests that the IV might either be associated with unmeasured confounders or violate the exclusion restriction. Figure 3 explains the motivation behind the test and under what situations does the test have power to detect that the proposed IV is invalid. Let Y 2 denote the treatment unaffected outcome and Y the outcome of interest. There are four ways in which the IV could be associated with the treatment unaffected outcome Y 2: (i) the IV could be associated with unmeasured confounders for Y 2 that are also unmeasured confounders for the outcome of interest Y (common unmeasured confounders); (ii) the IV could have a direct effect on Y 2 through a pathway that also results in a direct effect on Y (common pathway of direct effect); (iii) the IV could be associated with unmeasured confounders for Y 2 that are not unmeasured confounders for Y (Y 2 specific unmeasured confounders); (iv) the IV could have a direct effect on Y 2 through a pathway that is specific to Y 2 and does not result in a direct effect on Y . For cases (i) and (ii), an association between the proposed IV Z and the treatment unaffected outcome Y 2 implies that the IV is invalid. For cases (iii) and (iv), an association between the proposed IV and the treatment unaffected outcome does not imply that the IV is invalid. In order for the test using a treatment-unaffected outcome to have high power to detect a proposed IV as being invalid, the unmeasured confounder that the invalid proposed IV is related to must also be strongly related to the treatment-unaffected outcome or the proposed IV must have a strong direct effect on the treatment-unaffected outcome[99]. For example, in Figure 3, the test has no power if the proposed IV is invalid, but only related to Y specific unmeasured confounders or only has a direct effect through a Y specific pathway. [100] use a treatment-unaffected outcome to test the validity of a proposed IV in a study of the effect of C-section vs. normal delivery for babies born between 23-24 weeks on mortality using hospital C-section rate (on babies born at any age) as a proposed IV. C-section is thought not to affect mortality for babies who are not very premature, e.g., babies born between 30-34 weeks. To test the validity of the proposed hospital C-section rate IV, [100] used mortality for babies born between 30-34 weeks as a treatment-unaffected outcome and tested whether hospital C-section rate was associated with mortality for babies born between 30-34 weeks.
Figure 3.
Causal diagram explaining the motivation behind the treatment-unaffected outcome test for the validity of an IV. The IV is Z, the treatment is D, the outcome of interest is Y and the treatment unaffected outcome is Y 2.
Newcomers to IV methods often think that the validity of the IV can be tested by regressing the outcome on treatment received, the IV and measured confounders, and testing whether the coefficient on the IV is significant. However, this is not a valid test as even if the IV assumptions hold, the coefficient on the IV would typically be nonzero. One way to see this is that if there are no measured confounders, the test amounts to testing whether (i) E[Y|Z = 1, D = 1] – E[Y|Z = 0, D = 1] = 0 and (ii) E[Y|Z = 1, D = 0] – E[Y|Z = 0, D = 0] = 0. These are the differences between (i) the average potential outcome of the group of always-takers and compliers together when these subjects are encouraged to receive treatment and receive treatment vs. those of always-takers alone when they are not encouraged to receive treatment but do receive treatment and (ii) the average potential outcome of never-takers when encouraged to receive treatment but do not receive treatment vs. those of the group of never-takers and compliers when they are not encouraged to receive treatment and do not receive treatment. If the IV assumptions (IV-A1)-(IV-A5) hold, then (i) is equal to zero if and only if the average potential outcome of compliers and always-takers are the same when both groups receive treatment and (ii) is equal to zero if and only if the average potential outcomes of compliers and never-takers are the same when both groups do not receive treatment. Typically, the average potential outcome of compliers and always-takers (compliers and never-takers) will not be the same when both groups receive (do not receive) treatment even if the IV assumptions hold.
6.2. Sensitivity Analysis
A sensitivity analysis seeks to quantify how sensitive conclusions from an IV analysis are to plausible violations of key assumptions. Sensitivity analysis methods for IV analyses have been developed by [9, 43, 94, 101, 102] among others. Here we will present approaches to sensitivity analysis for violations of IV Assumptions (IV-A3)-(IV-A5).
6.2.1. Sensitivity Analysis for Violations of the IV Independent of Unmeasured Confounders Assumption.
Assume that the concern is that the IV may be related to an unmeasured confounder U which has mean 0 and variance 1 and is independent of the measured confounders X (U can always be taken to be the residual of the unmeasured confounder given the measured confounders to make this assumption plausible). Consider the following model:
| (13) |
Note that since Z is binary, we can always write Ui = ρ + ηZi + vi, E(vi|Zi) = 0, but the condition E(vi|Xi, Zi) = 0 in model (13) requires an additional assumption such as that the relationship between Z and the unmeasured confounder U is the same across strata of X; this assumption could be relaxed by allowing η to depend on X at the cost of making the sensitivity parameters harder to interpret. The parameter β in (13) is the causal effect of increasing D by one unit. The sensitivity parameters are δ, the effect of a one standard deviation increase in the unmeasured confounder on the mean of the potential outcome under no treatment, and η, how much higher the mean of the unmeasured confounder Ui is in standard deviation units for Zi = 1 vs. Zi = 0. Model (13) says that Zi would be a valid IV if both the measured confounders Xi and the unmeasured confounder Ui were controlled for. Under model (13), the following holds:
Consequently, a consistent estimate of and inferences for β can be obtained by carrying out a two stage least squares analysis with Yi – δηZi as the outcome variable, Di as the treatment variable, Xi as the measured confounders and Zi as the IV. Table 10 shows a sensitivity analysis for the NICU study. If there was an unmeasured confounder U that decreased the death rate in low level NICUs by 1 death per 1000 deliveries for a one standard deviation increase in U and was 0.5 standard deviations higher on average in subjects with Z = 1 vs. Z = 0 (Sensitivity Parameter Vector II in Table 10), then there would still be strong evidence that high level NICUs reduce mortality substantially (95% CI: 1.0 to 8.3 deaths prevented per 1000 deliveries). However, if instead the unmeasured confounder U had a stronger effect on the death rate, decreasing the death rate by 5 per 1000 deliveries for a one standard deviation increase in U, and was 0.5 standard deviations higher in subjects with Z = 1 vs. Z = 0 (Sensitivity Parameter Vector III in Table 10), then there would no longer be strong evidence that high level NICUs reduce mortality substantially (95% CI: 3.3 deaths prevented to 4.0 deaths caused by high level NICUs per 1000 deliveries). It can be useful to calibrate the effect of a potential unmeasured confounder U to that of a measured confounder. For example, an increase in gestational age from 30 to 33 weeks, which is a one standard deviation increase in gestational age, is associated with a reduction in the death rate of 22 per 1000 deliveries and the mean gestational age is 0.093 standard deviations smaller among near (Z = 1) vs. far (Z = 0) babies. For a comparable U that reduced the death rate by 22 per 1000 deliveries for a one standard deviation increase in U and was 0.093 standard deviations smaller in babies with Z = 1 vs. Z = 0 (Sensitivity Parameter Vector VI in Table 10), there would still be strong evidence that high level NICUs reduce mortality substantially (95% CI: 6.8 to 15.2 deaths prevented per 1000 deliveries).
Table 10.
Estimates and 95% confidence intervals for the risk difference in mortality per 1000 premature births in high level NICUs vs. low level NICUs (i.e., 1000β) for different values of the sensitivity parameters in (13). The sensitivity parameters are 1000δ, the effect of a one standard deviation increase in the unmeasured confounder on the number of deaths per 1000 premature babies if all babies delivered in low level NICUs and η, how much higher the mean of the unmeasured confounder Ui is in standard deviations for babies who live near to the high level NICU, Zi = 1, vs. those who live far, Zi = 0.
| Sensitivity Parameter Vector # | 1000δ | η | Risk Difference () | 95% CI for Risk Difference |
|---|---|---|---|---|
| I | 0 | 0 | −5.9 | (−9.6, −2.2) |
| II | −1 | 0.5 | −4.6 | (−8.3, −1.0) |
| III | −5 | 0.5 | .4 | (−3.3, 4.0) |
| IV | 1 | 0.5 | −7.1 | (−11.0 −3.3) |
| V | 5 | 0.5 | −12.1 | (−16.5, −7.7) |
| VI | −22 | −0.093 | −11.0 | (−15.2, −6.8) |
6.2.2. Sensitivity Analysis for Violation of the Exclusion Restriction Assumption
A sensitivity analysis for violations of the exclusion restriction can be carried out in a similar manner as above. For example, for the NICU study, a way in which the exclusion restriction could be violated is that travel time to the hospital could have a direct effect on the outcome. This would occur when it is important that the mother reaches the hospital very quickly such as during an umbilical cord prolapse. Such need for reaching the hospital very quickly is relatively uncommon but does occasionally occur in perinatal care [6]. A model for this direct effect is
| (14) |
Model (14) assumes that babies who deliver at a low level NICU never have to travel far, but babies who deliver at a high level NICU might have to travel far and λ is the effect of having to travel far on the death rate. Under model (14), a consistent estimate of and inferences for β can be obtained by carrying out a two stage least squares analysis with Yi – λ(1 – Zi)Di as the outcome variable, Di as the treatment variable, Xi as the measured confounders and Zi as the IV. For the NICU study, if λ = .001 so that having to travel far to a high level NICU increases the death rate by 1 per 1000 deliveries, then there is still strong evidence that high level NICUs prevent deaths; we estimate that high level NICUs prevent 5.1 deaths per 1000 deliveries with a 95% confidence interval of preventing 1.5 to 8.7 deaths per 1000 deliveries. If λ = .005 so that having to travel far to a high level NICU increases the death rate by 5 per 1000 deliveries, then there is no longer strong evidence that high level NICUs prevent deaths; we estimate that high level NICUs prevent 1.9 deaths per 1000 deliveries but the upper end of the 95% confidence interval is that high level NICUs cause 1.9 extra deaths per 1000 deliveries. However, having to travel far to a high level NICU increasing the death rate by 5 per 1000 deliveries would be a large direct effect given that the overall death rate is only 18.5 per 1000 deliveries.
When a proposed IV Z is thought to be independent of unmeasured confounders but there is concern that Z might have a direct effect on the outcome, [103] proposed an extended instrumental variables strategy for obtaining an unbiased estimate of the causal effect of treatment. The strategy involves using Z × W as an instrumental variable, where W is a covariate, and the required assumptions are that the covariate W interacts with Z in affecting treatment but the direct effect of Z does not depend on W.
6.2.3. Sensitivity Analysis for Violation of the Monotonicity Assumption
Suppose that (IV-A1)-(IV-A4) hold but (IV-A5), the monotonicity assumption, is violated. Then, the 2SLS estimate (4) converges to the CACE plus a bias term[43]:
| (15) |
(this can be proved by considering the effect of violations of monotonicity in the derivation of (2)). The bias due to violations of monotonicity is composed of two factors. The first factor, is related to the proportion of defiers and is equal to zero under the monotonicity assumption. The smaller the proportion of defiers, the smaller the bias will be from violations of the monotonicity assumption. However, if the IV is weak in the sense that the average effect of the IV Z on D is small, then even a few defiers could generate a large bias; the stronger the IV, the less sensitive the IV estimate is to violations of the monotonicity assumption[43]. The second factor, E[Y1 – Y0|C = de] – E[Y1 – Y0|C = co], is the difference in the average treatment effect between defiers and compliers. If the average treatment effect is identical for defiers and compliers, violations of the monotonicity assumption generate no bias. The less variation there is in the average treatment effect among defiers and compliers, the smaller the bias from violations of the monotonicity assumption.
7. Weak Instruments
The strength of an IV refers to how strongly the IV is associated with the treatment after controlling for the measured confounders X. An IV is weak if this association is weak. When the IV is encouragement (vs. no such encouragement) to accept a treatment, the IV is weak if the encouragement only has a slight impact on acceptance of the treatment. The strength of the IV can be measured by the proportion of compliers. The proportion of compliers can be estimated by
| (16) |
Another measure of the strength of the IV is the partial r2 when adding the IV to the first stage model for the treatment after already including the measured confounders X [104, 105].
Studies that use weak IVs face three problems:
- High Variance. The IV method is estimating the complier average causal effect (CACE) and the only subjects that are contributing information about the CACE are the compliers. Thus, the weaker the IV is (i.e., the smaller the proportion of compliers), the larger is the variance of the IV estimate. One might think that for a sample of size N, the variance of the IV estimate would be equivalent to the variance from having a sample of N × P (C = co) known compliers. However, the situation is actually worse because additional variability is contributed from the always-takers and never-takers having different sample means in the encouraged and unencouraged groups, even though the population means are the same. For example, suppose that the never-takers and compliers under Z = 0 have the same population mean, the always-takers and compliers under Z = 1 have the same population mean and all groups have the same population variance, i.e.,
Then, the asymptotic variance of the two stage least squares estimator of the CACE is(17)
[55]. The asymptotic variance for the treatment effect estimate from a sample of N known compliers, i.e., CÂCEknown complier sample = Ê(Y|Z = 1) – Ê(Y|Z = 0), is(18)
Therefore, for a sample of size N, under assumption (17), the variance of the IV estimate is equivalent to the variance from having a sample of NP(C = co)2 known compliers. For example, for a sample size of 10,000 with 20% compliers, the variance of the IV estimate is equivalent to that from a sample of 400 known compliers as could be obtained from a randomized trial of size 400 with perfect compliance. Thus, weak IVs can drastically reduce the effective sample size, resulting in high variance and potentially low power. For settings in which assumption (17) does not apply, it is still generally true that the variance of the IV estimate from a sample of size N is more than the variance from having a sample of N × P (C = co) known compliers due to the extra variability contributed from the always-takers and never-takers (this follows from [55], Theorem 3). If V ar(Y|C = nt) > V ar(Y|C = co, Z = 0) and V ar(Y|C = at) > V ar(Y|C = co, Z = 1), then the variance of the IV estimate is greater than that from having a sample of NP(C = co)2 known compliers. See Section 8 for discussion of power and sample size calculations for IV studies. Misleading inferences from two stage least squares. When the IV is weak enough, confidence intervals formed using the asymptotic distribution for two stage least squares may be misleading even when the IV is perfectly valid[104, 106]. When the IV is weak, the two-stage least squares estimate can have substantial finite sample bias towards the ordinary least squares estimate and the asymptotic variance understates the actual variance. To see the source of the finite sample bias, consider using a randomly generated number for each subject as an IV; the random number should provide no useful information about the treatment effect because it is unrelated to the treatment. Although the random number is unrelated to the unmeasured confounding variables in the population, it will have some chance association with the unmeasured confounders in a sample and thus, some confounding will get transferred to the predicted value of the treatment. This will result in some unmeasured confounding getting transferred to the second stage estimate of the treatment effect, resulting in bias[104, 106, 107]. [108] studied what strength of IV is needed to ensure that two-stage least squares provides reliable inferences. They suggested looking at the first stage partial F statistic for testing that the coefficient on the IV(s) is zero (where the first stage is the regression of treatment on IVs and measured confounders). For one IV, if this first stage partial F statistic is less than about 10, the two stage least squares inferences are misleading in the sense that the Type I error rate of a nominal 0.05 level test is actually greater than 0.15. If more than one IV is used, then the first stage partial F statistic needs to be larger to avoid misleading inferences, greater than 12 for two IVs, greater than 16 for five IVs and greater than 21 for ten IVs. A number of methods have been developed that provide accurate inferences when the IV is weak. One approach is to use the Anderson-Rubin test statistic to test H0 : CACE = β0 by testing whether the coefficient of Z is 0 in the linear regression of Y – β0D on Z and X using an F test[109]. If there is a constant treatment effect (i.e., is the same for all i), is linear in X and is homoskedastic and normally distributed, then this is an exact test regardless of the strength of the IV. A related permutation inference method that is less reliant on assumptions is developed in [10] and illustrated in [94]. A conditional likelihood ratio method is developed in [110], where the approach involves considering the conditional distribution of the likelihood ratio statistic, conditioning on the value of nuisance parameters. This conditional likelihood method and the Anderson-Rubin test are implemented in a Stata program CLRv2. The R package ivpack, that is is discussed in Section 14, implements the Anderson-Rubin test using the function anderson.rubin.ci.
Highly sensitive to bias from unmeasured confounders. Recall formula (11) for the bias in the IV estimator when the proposed IV is associated with an unmeasured confounder U. The numerator measures the association between the IV and the unmeasured confounder (multiplied by how much the unmeasured confounder affects the outcome). The denominator is the proportion of compliers and reflects the strength of the IV. Thus, when the IV is weak (i.e., the proportion of compliers is small), the effect of the IV being invalid from being associated with an unmeasured confounder is greatly exacerbated and even a minor association between the IV and an unmeasured confounder can lead to substantial bias. [94, 104].
In summary, when the IV is weak, the IV estimate may have high variance and if it is weak enough (i.e., partial first stage F statistic less than 10), it is important to use inference methods other than two stage least squares to provide accurate inferences. These inference methods may inform us that the confidence interval for the treatment effect is very wide, but it is possible that even when the IV is weak, if the treatment effect is large enough and the sample size is big enough, there may still be a statistically significant treatment effect assuming the IV is valid. The third problem with weak IVs is that they are very sensitive to bias from being slightly invalid, i.e., being slightly correlated with unmeasured confounders. This problem does not go away with a larger sample size. A slightly biased but strong IV may be preferable to a less biased but weak IV [94].
8. Power and Sample Size Calculations for IV studies
Power calculations are an important part of designing a study. As discussed in Section 7, under (17), the variance of the 2SLS estimator is (18) and the sample size needed for an IV study is approximately equal to that needed for a conventional observational study to detect the same magnitude of effect divided by the proportion of compliers squared. More generally, when (17) does not hold, power and sample size formulas for an IV study to be analyzed by 2SLS are given by [111, 112]. When the IV might be weak, we recommend computing the power under an analysis that is appropriate for weak IVs such as the Anderson-Rubin test. [113] provide a formula for computing the power for the Anderson-Rubin test and the function power.iv in the R package ivpack that is discussed in Section 14 computes this power.
9. Binary, Survival, Multinomial and Distributional Outcomes
Most of the early development of instrumental variable methods in econometrics was for continuous, uncensored outcomes. In this section, we consider special issues that arise in applying IV methods to other types of outcomes such as binary, survival, multinomial and distributional outcomes.
9.1. Binary Outcomes
For binary outcomes without measured confounders, two stage least squares estimates the risk difference for compliers. When there are measured confounders, two stage least squares (2SLS) still seeks to estimate the risk difference for compliers but the second stage model that 2SLS uses, E(Yi|D̂i, Xi) = α + βD̂i + γTXi, does not constrain the probability of the binary outcome Y to be between 0 and 1. [62] argues that, in spite of not accounting for the constraints imposed by a binary outcome, the 2SLS estimate of β is still often close to methods such as [66] that account for the constraints and that “2SLS approximates the causal relation of interest.” An approach to estimating the risk difference for binary outcomes that respects the nature of binary outcomes is the matching approach of Baiocchi et al.[102]. In this approach, units with Z = 1 are matched to units with Z = 0 with similar values of measured confounders and permutation inference is used to make inferences about the effect ratio. We applied this approach to the NICU study in [4] and estimated that high level NICUs save 7.8 babies per 1000 deliveries, fairly similar to the two stage least squares estimate in Table 4.
Another approach for binary outcomes is to specify a functional form for that is constrained between 0 and 1, such as a logistic model
| (19) |
The causal parameter of interest in (19) that we can hope to identify with an IV is β, the log odds ratio for the effect of treatment for compliers; this is an odds ratio analogue of the CACE. In analogy with two stage least squares, the two-stage predictor substitution (2SPS) approach to estimating β is to fit a logistic regression of the treatment D on the IV Z and the covariates Xi, obtaining D̂ and then fit a logistic regression of Y on D̂ and X. However, because of the noncollapsibility of logistic regression, 2SPS is generally asymptotically biased. See [114] for an analytical expression for this bias and simulation studies. Another approach to estimating β in (19) is two-stage residual inclusion (2SRI) [115, 116]. The first stage of 2SRI is the same as that of 2SPS (i.e., fit a logistic regression of D on Z and X), but in 2SRI, the second stage is to fit a logistic regression of Y on D, X and the residual from the first stage regression; the coefficient on D in the second stage regression is the estimate of β. 2SRI is asymptotically biased for β in (19) except when there is no unmeasured confounding [114]. There are several approaches that provide consistent estimates of model (19) under certain additional assumptions. [64] develops a parametric approach; [66] and [67] develop semiparametric approaches. Relatedly, [49] develops a semiparametric approach to estimating the parameter
| (20) |
which is the log odds ratio for the effect of treatment among those who receive treatment. The quantity (20) is similar to β in (19) but expresses the effect of treatment for those who receive treatment instead of the compliers. Under IV assumptions (IV-A1)-(IV-A5), to consistently estimate (20), the method in [49] requires the assumption that the effect of treatment is the same for always-takers and compliers (see (9) in [49]).
Another approach for binary outcomes is the bivariate probit model that specifies a probit functional form for and assumes an explicit functional form of the bivariate distribution of the error term from the model relating treatment to the covariates and IV and the error term from the outcome model [117, 118]. This model leans on the parametric assumptions of the error terms, leaving the conclusions sensitive to violations of these assumptions. Additionally, these models suffer from difficulty in maximizing the likelihood functions and trouble with calculating appropriate standard errors [119].
For good general reviews of IV estimation of causal effects in the binary outcome case, see [49, 120].
9.2. Multinomial Outcomes
[121] considered IV estimation for multinomial outcomes (i.e., nominal or ordinal outcomes). For ordinal outcomes, one approach is to choose coding scores Wj for the categories j = 1, . . ., J; then the CACE is
where tj, vj and sj are the probabilities for the jth category for compliers under treatment and control, and never-takers respectively; and qj is the probability for observed group Zi = 0, Di = 0 for the jth category. The coding score needs to be chosen. Among the options are equally spaced scores (or linear transformations of them), midranks and ridit scores. A sensitivity analysis can be performed with different choices of scores to see how the results differ. Another approach for ordinal outcomes is to use a measure of stochastic superiority of treatment over control for compliers:
| (21) |
SSC = 0.5 indicates no causal effect and SSC > 0.5 indicates beneficial effect of the treatment for compliers if a higher value of the outcome is a better result. Compared to the CACE, SSC is easy to interpret and avoids the problem of choosing scores Wj, but without use of weighting scores, it may not describe the strength of the effect well when some specific categories are known to be more important than other categories in measuring the treatment effect.
For nominal outcomes, it is difficult to get a summary measure of the causal effect such as the CACE or SSC for ordinal outcomes. Instead, the treatment effect on the entire outcome distributions of compliers with and without treatment can be evaluated, i.e., compare tj to vj, j = 1, ..., J and test the equality of tj and vj, j = 1, ..., J. [121] estimated those causal effects with the likelihood method and proposed a bootstrap/double bootstrap version of a likelihood ratio test for the inference when the true values of parameters are on the boundary of the parameter space under the null.
9.3. Survival Outcomes
For survival outcomes, a common complication is censoring. For example, one type of censoring is administrative censoring, which means that a subject survived until the end of the time window of the study. For estimating the effect of a treatment on a survival outcome using an IV, [122] considered a structural accelerated failure time model and developed semiparametric estimators for this model. [123] provided a good discussion of their approach and comparisons with other survival analysis methods. [124] and [125] considered a structural proportional hazards model in which the hazard of the potential failure time under treatment for a certain group of subjects is proportional to the hazard of the potential failure time under control for these same subjects. Both the structural accelerated failure time model and the structural proportional hazards model are semiparametric models, where the effect of the treatment on the distribution of failure times is modeled parametrically.
Baker [126] extended the models and assumptions for discrete-time survival data and derived closed form expressions for estimating the difference in the hazards at a specific time between compliers under treatment and control based on maximum likelihood. [126]'s estimator is analogous to the standard IV estimator for a survival outcome. [127] discussed this standard IV approach and parametric maximum likelihood methods for the difference in survival at a specific time between compliers under treatment and control.
Here, the standard IV approach of [126] will be reviewed. Let Sc1(V), Sc0(V), Sat(V) and Snt(V) be the potential survival functions at time V of compliers in the treatment and control groups and of always-takers and never-takers respectively, Sz(V) be the survival probabilities at time V for the group with assignment Z = z, and Szd(V) be the survival probabilities at time V for the group with assignment Z = z and treatment received D = d. By Table 3 and the monotonicity assumption (IV-A5) that rules out defiers, the following holds:
Similar to the standard IV estimator for the CACE (4), the standard IV estimator for the compliers difference in survival probabilities at time V under treatment vs. control is the following, where Ŝz(V) is the Kaplan-Meier estimator of the survival probability at time V for the group with assignment Z = z,
| (22) |
In addition to (IV-A1)-(IV-A5), an additional assumptions is needed to ensure that the estimator (22) is consistent for the compliers difference in survival probabilities at time V:
Independence assumption of failure times and censoring times: The distributions of potential failure times T and censoring times C are independent of each other. Type I censoring (i.e., censoring times are the same for all subjects) and random censoring are two special cases.
Although the standard IV estimator (22) is very useful, it may give negative estimates for hazards and be inefficient because it does not make full use of the mixture structure implied by the latent compliance model. When the survival functions follow some parametric distributions, [127] used the EM algorithm to obtain the MLE on the difference in survival probabilities for compliers. However, the MLEs could be biased when the parametric assumptions are not valid. To address this concern, [127] developed a nonparametric estimator based on empirical likelihood that makes use of the mixture structure to gain efficiency over the standard IV method while not depending on parametric assumptions to be consistent.
9.4. Effect of treatment on distribution of outcomes
As discussed in previous sections, a large literature on methods of analysis for treatment effects focuses on estimating the effect of treatment on average outcomes, e.g., the CACE [43, 55]. However, in addition to the average effect, knowledge of the causal effect of a treatment on the outcome distribution and its general functions can often provide additional insights into the impact of the treatment and therefore be of significant interest in many situations [128]. For example, in a study of the effect of school subsidized meal programs on children's weight, both low weight and high weight are adverse outcomes; therefore, knowing the effect of the program on the entire distribution of outcomes rather than just average weight is important for understanding the impact of the program. For an individual patient deciding which treatment to take, the patient must weigh the effects of the possible treatments on the distribution of outcomes, the costs of the treatments and the potential side effects of the treatments [129]. Therefore, making the best decision requires information on the treatment's effect on the entire distribution of outcomes rather than just the average effect because a patient's utility over outcomes may be nonlinear over the outcome scale. [130], [131]. [132], [133] and [134] provide examples in HIV care, neonatal care and cancer care respectively.
For distributional treatment effects on nondegenerate outcome variables with bounded support, without any parametric assumption, [83] used the standard IV approach to estimate the counterfactual cumulative distribution functions (cdfs) of the outcome of compliers with and without the treatment:
| (23) |
However, [83] and [58] pointed out that these standard IV estimates of the potential cdfs for compliers may not be nondecreasing functions as cdfs should be. Furthermore, as discussed in Section 4.2, the standard IV approach does not make full use of the mixture structure [58] implied by the latent compliance class model (see Table 3) and hence could be inefficient. Instead, [58] proposed a normal approximation and two multinomial approximations to the outcome distributions. However, the estimator based on a normal approximation could be biased when the outcomes are not normal, and for the approach based on multinomial approximations, a systematic approach for choosing the multinomial approximations is needed. [60] developed a semiparametric instrumental variable method based on the empirical likelihood approach. Their approach makes full use of the mixture structure implied by the latent compliance class model without parametric assumptions on the outcome distributions, takes into account the nondecreasing property of cdfs and can be easily computed from the data. Their method can be applied to general outcomes and general functions of outcome distributions. [60] showed that their estimator has good properties and is substantially more efficient than the standard IV estimator (23).
10. Multi-valued IVs
In some settings, the IV has multiple values or is continuous. For example, in the NICU study example from Section 1.2, the mother's excess travel time from the nearest high level NICU compared to the nearest low level NICU is continuous. Clinicians often find it easier to think about the validity of the IV assumptions and the interpretation of the IV estimate in terms of a binary IV. For this reason, we have dichotomized excess travel time in terms of being less than or equal to 10 minutes or greater than 10 minutes. We could instead use the excess travel time itself as the IV and estimate the effect of a high level NICU by two stage least squares, i.e., regress high level NICU on excess travel time and the measured covariates to get predicted high level NICU attendance and then regress death on predicted high level NICU attendance and the measured covariates. This results in an estimate that high level NICUs save 7.6 babies per 1000 deliveries with a 95% confidence interval of saving 4.3 to 11.0 babies per 1000 deliveries, a similar inference to that from Table 4 in which we dichotomized the IV.
Theorem 2 of [55] shows that both the dichotomized IV estimate and the continuous IV estimate converge to weighted averages of treatment effects, where the more “compliant” subjects get greater weight. Specifically, suppose Z is discrete but has multiple-values z0, . . ., zK such that an extended monotonicity assumption holds:
| (24) |
i.e., a higher level of the IV always leads to at least as high a level of the treatment. For the NICU study example, we round excess travel time to the nearest integer so that the range of excess travel times is -15 to 120 and let the IV Z be 120-excess travel time so that z0 = 0, z1 = 1 . . ., z136 = 135 and high values of a Z make a baby more likely to be delivered at a high level NICU. Now, consider using g(Z) as an IV where g is an increasing function, e.g., for dichotomizing the IV at zj, g(z) = 1 if Z ≥ zj, g(z) = 0 if Z < zj or for treating Z as a continuous IV, g(z) = z. For simplicity, suppose there are no covariates X. Then, the two stage least squares estimate using the IV g(Z), i.e., Ĉov(Y, g(Z))Ĉov(D, g(Z)) converges to
where αzk,zk-1 is the average causal effect for subjects who are “compliers at zk,” i.e., subjects who would take the treatment if the IV Z was ≥ zk but would not take the treatment if the IV was < zk, and λ1, . . ., λK are nonnegative weights that add up to 1 where
[55]. Figure 4 shows the estimated weights λk for the dichotomized IV of excess travel time ≥ 10 and the continuous IV where we used the gam function in R to estimate P(D = 1|Z) nonparametrically and the density function in R to estimate P(Z = z) nonparametrically. The dichotomized IV and continuous IV have similar weights but the dichotomized IV puts greater weight on subjects who would change whether or not they would take the treatment right around 10 minutes of excess travel time.
Figure 4.
The two stage least squares estimate for the NICU study using an IV is a weighted average of the average causal effects for subjects who are “compliers at level z” (subjects who would go to a high level NICU if the excess travel time was at most z but otherwise go to a low level NICU), where the weighting depends on the coding of the IV. The figure shows these weights for two IVs, (i) the dichotomized IV of excess travel time ≤ 10 minutes or excess travel time > 10 minutes and (ii) the continuous IV of excess travel time.
Multiple values of the IV provides us with the opportunity to identify a richer set of causal effects [135]. Suppose the IV is continuous and the extended monotonicity assumption (24) holds. The limit of the treatment effect for subjects who would the take treatment if the IV was equal to z but not take the treatment if the IV was a little less than z is ; [136] refer to this as the marginal treatment effect at z. Treatment effects of interest can all be expressed as a weighted average of these marginal treatment effects [136]. Identification of the average treatment effect over the whole population requires identification of all the marginal treatment effects. In order for all the marginal treatment effects to be identified using the IV (and thus the average treatment effect identified), it is required that for large values of Z, P(D = 1|Z) approaches 1 and for small values of Z, P(D = 1|Z) approaches 0[136]; [137] shows how to estimate marginal treatment effects and the average treatment effect when this condition is satisfied. For the NICU study, P(D = 1|Z) do not approach 1 or 0 over the range of excess travel times in the data; see Figure 5.
Figure 5.
Scatterplot smooth estimate of P(D = 1|Z) where D = 1 is attending a high level NICU and Z is excess travel time. The estimate was obtained using the gam function in R. The observed values of excess travel time are shown at the bottom of the plot.
When the IV is multi-valued, one might want to consider “strengthening the IV” by focusing only on subjects with high levels of the IV vs. low levels of the IV and removing subjects with middle levels of the IV. [94] showed that under certain conditions, studies with stronger IVs are less sensitive to bias. [102] developed a method for strengthening an IV based on near-far matching. In near-far matching, optimal nonbipartite matching is used to construct pairs that are far apart on their levels of the IV (e.g., excess travel time in the NICU example) but near on their levels of the measured covariates[138]. Permutation inference or two stage least squares, with dummy variables for each matched pair included as measured covariates, can be used to estimate the treatment effect using the constructed matched pairs. Practical aspects of near-far matching are discussed in [139].
11. Multiple IVs
In some settings, there may be multiple IVs available. For example, [38] used IV methods to estimate the effect of longer postpartum stays on newborn readmissions. [38] used two IVs, (1) hour of birth and (2) method of delivery (normal vs. C-section). Hour of birth influences length of stay because it affects whether a newborn will spend an extra night in the hospital; for example, [38] found that newborns born in the a.m. have longer lengths of stay than newborns born in the p.m. Method of delivery influences length of stay because mothers need more time to recuperate after a C-section than following a normal delivery, and newborns are rarely discharged before their mothers. The compliers with respect to each IV are different – the compliers with respect to the hour of birth IV are newborns who would only stay an extra day if born in the a.m. compared to the p.m. while the compliers with respect to the method of delivery IV are newborns who would only stay an extra day if delivered by C-section compared to normal delivery. Each IV identifies the average treatment effect for its group of compliers, so that each IV is identifying the average treatment effect for a different subgroup.
Two stage least squares can be used to combine the IVs – in the first stage, regress D on both Z1 and Z2 (as well as X) and then use the predicted D as usual in the second stage. Under the assumption of homogeneous treatment effects (i.e., treatment effects are the same for all subjects or more weakly, average treatment effects are the same for all the κ + 1 subgroups defined in Section 5.3), for each IV, the complier average causal effect for the compliers with respect to that IV is the same and equal to the average treatment effect for the whole population, and the two stage least squares estimate is the optimal way to combine the IVs to estimate this average treatment e ffect under an additional assumption of constant variance (i.e., the variance of potential outcomes under the control given the measured covariates X is the same for all X)[53]. When treatment effects are heterogeneous, the complier average causal effect for the compliers with respect to each IV may be different, and two stage least squares estimates a weighted average of the complier average causal effects for the different IVs with the complier average causal effects for the stronger IVs getting greater weight [55, 65]. When there are two or more distinct IVs, it is useful to report the estimates from the individual IVs in addition to the combined IVs since the IVs are estimating the average treatment effects for different subgroups (see Section 5.5)
When there are multiple IVs and treatment effects are homogeneous, the overidentifying restrictions test can be used to test the validity of the IVs [54, 140]. The overidentifying restrictions test tests whether the estimates from the different IVs are the same. When treatment effects are homogeneous, if the estimates from two different IVs converge to different limits, this would show that at least one of the IVs is invalid. There are two problems with using the overidentifying restrictions test to test the validity of IVs. First, if treatment effects are heterogeneous, then the complier average causal effects for the two IVs may be different even though both IVs are valid; in this case, the overidentifying restrictions test would falsely indicate that at least one of the IVs is invalid. Second, even if treatment effects are homogeneous, two IVs A and B may both be biased but in the same way so that the asymptotic limit of the estimators based on IV A and B respectively are the same; in this case, the overidentifying restrictions test would give false assurance that the IVs are valid[101].
12. Multi-valued and Continuously Valued Treatments
The treatment under study may take on multiple or continuous values, for example, the dose of a medication. Two stage least squares can still be applied. [65] present the following formula that shows that the two stage least squares estimator converges to a weighted average of the effect of one unit changes in the treatment level. Suppose the treatment can take on levels 0, 1, . . ., d̄ and that monotonicity holds in the sense that . Assume there are no covariates. Then, the two stage least squares estimator converges to
| (25) |
where . The numerator of ωd is the proportion of compliers at point d, that is the proportion of individuals driven by the encouraging level of the IV from a treatment intensity less than d to at least d. The ωd's are nonnegative and sum to one. The quantity E[Yd – Yd–1|Dz=1 ≥ d > Dz=0] in (25) is the causal effect of a one unit increase in the treatment from d – 1 to d for compliers at point d. (25) shows that the two stage least squares estimator converges to a weighted average of the causal effects of one unit increases in the treatment from d – 1 to d for compliers at point d, where the points d at which there are more compliers get greater weight. The weights ωd can be estimated because under the assumption (IV-A5) of monotonicity and (IV-A3) that the IV is independent of the potential treatment receiveds, we have P(Dz=1 ≥ d > Dz=0) = P(Dz=1 ≥ d) – P(Dz=0 ≥ d) = P(D ≥ d|Z = 1) – P(D ≥ d|Z = 0). See [65] for an extension of these formulas to the setting where there are covariates X that are controlled for.
Researchers often times dichotomize multi-valued or continuous treatments. However, using IV methods with a dichotomized continuous treatment can lead to an overestimate of the treatment effect. Let β denote the average causal effect (25) that the two stage least squares estimator for a multi-valued treatment converges to. [65] show that if this treatment is dichotomized as B = 1 if D ≥ l, B = 0 if D < l for some 1 ≤ l ≤ l=d_, then the two stage least squares estimator using the binary treatment B converges to ϕ× (25) where (25) is the probability limit of the 2SLS estimator using the continuous treatment D and
The only situation when ϕ = 1 is when the IV has no effect other than to cause people to switch from D = l – 1 to D = l. Otherwise, when a multi-valued treatment is incorrectly parameterized as binary, the resulting estimate tends to be too large relative to the average per-unit effect of the treatment (25). The problem with dichotomizing a multi-valued treatment is that the IV has a direct effect because the encouraging level of the IV can push a person to a higher level of treatment even if B would be 1 under both the non-encouraging and encouraging levels of the IV. Although dichotomizing a continuous treatment results in a biased estimate of the treatment effect (25), the sign of the treatment effect is still consistently estimated.
If the treatment effect for compliers is linear, i.e., the causal effect of a one unit increase in the treatment from d – 1 to d for compliers at point d is the same for all d, then the two stage least squares estimator estimates this linear treatment effect. If the treatment effect is nonlinear, then with a binary IV, it is not possible to estimate anything other than the weighted treatment effect (25). If the IV is continuous, then the IV can be used to form multiple IVs (e.g., Z, Z2, Z3, etc.) and a nonlinear treatment effect can be estimated [141]. For example, suppose YD=d = Y0 + β1d + β2d2. Then, β1 and β2 can be consistently estimated with a continuous IV Z by using two least squares where D̂ is estimated by regressing D on Z and Z2, D̂2 is estimated by regressing D2 on Z and Z2, and β1 and β2 are estimated by regressing Y on D̂ and D̂2. [48] discusses other estimation approaches for estimating nonlinear treatment effects.
Multi-valued treatments may not be strictly ordered by dose. [80] consider the setting of a treatment with three levels – control (0) and two active levels A and B, where A and B are not ordered by dose and some subjects may prefer A to B and some may prefer B to A. [80] develop bounds on causal effects for this setting.
13. Reporting an IV analysis
[16] and [142] proposes useful reporting standards for an IV analysis to help readers properly interpret and evaluate the validity of an IV analysis. Here we propose related reporting standards that use the methodologies in our tutorial.
Describe theoretical basis for choice of IV. Discuss why the IV is expected to affect the treatment, be approximately independent of unmeasured confounders and not have a direct effect on the outcome other than through influencing the treatment. Section 3 discusses common sources of IVs for health studies and issues in thinking about their validity. The most compelling IVs often come from settings that can be thought of as natural experiments, settings in which the assignment of the IV to subjects, though not randomized, seem to resemble a randomized experiment in that it is haphazard rather than the result of deliberation or considered judgement[143].
Report strength of IV and results from first-stage model. The authors should report the first stage model relating the treatment to the IV and the measured confounders, and report measures of the strength of the IV such as the proportion of compliers and the first stage partial F statistic for testing that the coefficient on the IV(s) is zero.
Report distribution of measured confounders across levels of the IV and treatment. As discussed in Section 6, ideally, an IV should be unrelated to the measured confounders (e.g., characteristics of the patient) as it would be if it were randomly assigned. To evaluate this, it is useful to construct a table like Table 7. If the IV is associated with a measured confounder but it can plausibly be argued that the IV is approximately independent of other confounders after conditioning on a measured confounder, then it is useful to construct tables like Tables 8 and 9 that condition on the measured confounder. It is also helpful to report the means and frequencies of the measured confounders across levels of the treatment as in Table 2 and to calculate the bias ratios as in Tables 7-9. This allows the reader to assess the potential for confounding in the IV relative to the confounding in the treatment[16].
Explore concomitant treatments. As discussed in Section 6, the proposed IV would violate the exclusion restriction and be invalid if it is associated with concomitant treatments (other than the one under study) which also influence the outcome. Such possible violations of the exclusion restriction can be assessed by examining whether the IV is associated with concomitant treatments.
Discuss the interpretation of the treatment effect estimated by the IV. The IV method estimates the average causal effect of the treatment for compliers or, more generally, when compliance status is not deterministic, a weighted average of causal effects where subgroups in which the instrument has a stronger effect on the treatment get more weight. To understand what subgroups are getting more weight in the IV estimate, it is useful to construct a table like Table 6 that shows the relative weight different subgroups are getting in the IV estimate.
Report a sensitivity analysis. The IV assumptions are unlikely to hold perfectly. It is useful to report a sensitivity analysis like Table 10 to show how sensitive inference are to various violations of the IV assumptions so that readers can assess how inferences would change under plausible violations of the IV assumptions.
14. Software
Software for implementing IV analyses is available in R, SAS and Stata. Here we illustrate analyzing the NICU study using the ivpack package, freely downloadable from CRAN, in the freely available software R.
library(ivpack) # y is the nx1 vector of the outcome (mortality) # d is the nx1 vector of the treatment (1 if high level NICU, 0 if low level NICU) # xmat is the nxp matrix of observed covariates (e.g., birthweight, gestational age, etc.) # z is the IV # (1 if excess travel time <=10 minutes, 0 if excess travel time greater than 10 minutes) # Fit first stage model first.stage.model=lm(d~ z+xmat) # Calculate Partial F statistic for testing whether instrument has an effect # in the first stage model first.stage.model.without.z=lm(d~ xmat) anova(first.stage.model.without.z,first.stage.model) Analysis of Variance Table Model 1: d ~ xmat Model 2: d ~ z + xmat Res.Df RSS Df Sum of Sq F Pr(>F) 1 192017 40737 2 192016 34964 1 5772.6 31702 < 2.2e-16 *** # The partial F statistic is 31702, which is much greater than 10, # so that IV is strong enough for two stage least squares inference to be reliable. # Estimate proportion of compliers first.stage.model.logistic=glm(d~ z+xmat,family=binomial) newdata.z1=data.frame(z=rep(1,length(z)),xmat); expected.treatment.zequal1=predict(first.stage.model.logistic, newdata=newdata.z1,"response"); newdata.z0=data.frame(z=rep(0,length(z)),xmat) expected.treatment.zequal0=predict(first.stage.model.logistic, newdata=newdata.z0,"response"); proportion.compliers=mean(expected.treatment.zequal1-expected.treatment.zequal0); proportion.compliers [1] 0.3953096 # We estimate that 39.53% of the subjects are compliers # Proportion of compliers that are low birth weight (<1500g), see Table 6 low.birth.weight=bthwght<1500 Z.given.X.model=glm(z~xmat,family=binomial) prob.z.equal.1.given.X=predict(z.given.X.model,type="response") kappa=1-d*(1-z)/(1-prob.z.equal.1.given.X)-(1-d)/prob.z.equal.1.given.X prob.compliers.low.birth.weight=mean(low.birth.weight.kappa)/mean(kappa) prop.compliers.low.birth.weight [1] 0.02898901 # Bias ratio for low birth weight, see Table 7 bias.ratio.low.birth.weight= abs(((mean(low.birth.weight[z==1])-mean(low.birth.weight[z==0]))/ (mean(d[z==1])-mean(d[z==0])))/ (mean(low.birth.weight[d==1])-mean(low.birth.weight[d==0]))); bias.ratio.low.birth.weight [1] 0.5157605 # Two stage least squares analysis ivmodel=ivreg(y~ d+xmat|z+xmat) # This summary gives the non-robust standard errors summary(ivmodel) Coefficients: Estimate Std. Errort value Pr(>|t|) (Intercept) 5.183e-01 1.019e-02 50.845 < 2e-16*** d −5.888e-03 1.644e-03 −3.581 0.000342*** xmatbthwght −6.298e-06 6.698e-07 −9.403 < 2e-16*** ... # We estimate that the effect of going to a high level NICU is to # reduce the mortality rate for compliers by .005888 or 5.9 babies # per 1000 deliveries # Standard errors that are robust for heteroskedasticity but not clustering robust.se(ivmodel) # Huber-White standard errors that account for clustering due to hospital # and are also robust to heteroskedasticity # hospid is an identifier of the hospital the baby was delivered at cluster.robust.se(ivmodel,hospid) t test of coefficients: EstimateStd. Errort value Pr(>|t|) (Intercept) 5.1830e-01 2.7084e-02 19.1369 < 2.2e-16*** d −5.8879e-03 1.9021e-03 −3.0955 0.0019653** xmatbthwght −6.2983e-06 1.3268e-06 −4.7471 2.065e-06*** ... # Sensitivity Analysis for IV being associated with unmeasured confounders # Second row of Table 10 delta=-1/1000 eta=.5; adjusted.y=y-delta*eta*z; sens.est=ivreg(adjusted.y~ d+xmat|z+xmat) cluster.robust.se(sens.est,hospid) t test of coefficients: EstimateStd. Error t value Pr(>|t|) (Intercept) 5.1780e-01 2.6995e-02 19.1818 < 2.2e-16*** d −4.6396e-03 1.8678e-03 −2.4840 0.0129941* ... # Sensitivity Analysis for violation of exclusion restriction lambda=.001 # having to travel far to a high level NICU increases the # death rate by 1 per 1000 deliveries adjusted.y=y-lambda*(1-z)*d sens.est=ivreg(adjusted.y~ d+xmat|z+xmat) cluster.robust.se(sens.est,hospid) t test of coefficients: EstimateStd. Error t value Pr(>|t|) (Intercept) 5.1733e-01 2.6922e-02 19.2159 < 2.2e-16*** d −5.0945e-03 1.8550e-03 −2.7464 0.0060260** ... # Compute the power for an IV study. # Consider the model Y^(d=0)=beta0+u, Y^d=Y^(d=0)+beta1, D=gamma0+gamma*z+v. # Power for a study with in which the null hypothesis causal effect is 0, # the true causal effect is 1, the sample size is 250, the instrument is # binary with probability .5 (so variance = .25), the standard deviation # of potential outcome under control is 1, the effect of the instrument # is to increase the probability of a binary treatment being 1 from .25 to # .75. The correlation between u and v is assumed to be .5. The # significance level for the study will be alpha = .05 # The function sigmav.func computes the SD of v for a binary instrument, # binary treatment. sigmav.func(prob.d1.given.z1=.75,prob.d1.given.z0=.25,prob.z1=.5) # The sigmav.func finds sigmav=.4330127 # Power of the study power.iv(n=250, lambda=1, gamma=.5, var.z=.25, sigmau=1, sigmav=.4330127, rho=.5, alpha = 0.05) $power [1] 0.8714241
Acknowledgements
Jing Cheng and Dylan Small were supported by grant RC4MH092722 from the National Institute of Mental Health. Jing Cheng was also supported by grant NIH/NIDCR U54DE019285 and Dylan Small by grant NSF SES-1260782. The authors thank Scott Lorch for the use of the data from the NICU study.
References
- 1.Rosenbaum P, Rubin D. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70(1):41–55. [Google Scholar]
- 2.D'Agostino R., Jr Tutorial in biostatistics: propensity score methods for bias reduction in the comparison of a treatment to a non-randomized control group. Statistics in Medicine. 1998;17:2265–2281. doi: 10.1002/(sici)1097-0258(19981015)17:19<2265::aid-sim918>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 3.Stuart E. Matching methods for causal inference: a review and a look forward. Statistical Science. 2010;25:1–21. doi: 10.1214/09-STS313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lorch S, Baiocchi M, Ahlberg C, Small D. The differential impact of delivery hospital on the outcomes of premature infants. Pediatrics. 2012 doi: 10.1542/peds.2011-2820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pearl J. Causality. Cambridge University Press; 2009. [Google Scholar]
- 6.Phibbs C, Mark D, Luft H, Peltzman-Rennie D, Garnick D, Lichtenberg E, McPhee S. Choice of hospital for delivery: a comparison of high-risk and low-risk women. Health Services Research. 1993;28(2):201. [PMC free article] [PubMed] [Google Scholar]
- 7.Miettinen O. The need for randomization in the study of intended effects. Statistics in Medicine. 1983;2:267–271. doi: 10.1002/sim.4780020222. [DOI] [PubMed] [Google Scholar]
- 8.Walker A. Confounding by indication. Epidemiology. 1996;7:335–336. [PubMed] [Google Scholar]
- 9.Brookhart M, Schneeweiss S. Preference-based instrumental variable methods for the estimation of treatment effects: assessing validity and interpreting results. The International journal of biostatistics. 2007;3(1):14. doi: 10.2202/1557-4679.1072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Imbens G, Rosenbaum P. Robust, accurate confidence intervals with weak instruments: quarter of birth and education. Journal of the Royal Statistical Society, Series A. 2005;168:109–126. [Google Scholar]
- 11.Buckles K, Malamud O, Morrill M, Wozniak A. The effect of college education on health. IZA Discussion Paper. 2012:6659. doi: 10.1016/j.jhealeco.2016.08.002. [DOI] [PubMed] [Google Scholar]
- 12.Angrist J, Krueger A. Does compulsory school attendance affect schooling and earnings? Quarterly Journal of Economics. 1991;106:979–1014. [Google Scholar]
- 13.Harmon C, Walker I. Estimates of the economic return to schooling for the united kingdom. American Economic Review. 1995;85:1278–1286. [Google Scholar]
- 14.Card D. Using geographic variation in college proximity to estimate the return to schooling. In: Christofides L, Grant E, Swidinsky R, editors. Aspects of Labor Market Behaviour. University of Toronto Press; Toronto: 1995. pp. 201–222. [Google Scholar]
- 15.Rosenbaum P. Replication effects and biases. The American Statistician. 2001;55:223–227. [Google Scholar]
- 16.Brookhart M, Rassen J, Schneeweiss S. Instrumental variable methods in comparative safety and effectiveness research. Pharmacoepidemiology and drug safety. 2010;19(6):537–554. doi: 10.1002/pds.1908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Durbin J. Errors in variables. Revue de l'institut International de Statistique. 1954;22:23–32. [Google Scholar]
- 18.Wu D. Alternative tests of independence between stochastic regressors and disturbances. Econometrica: Journal of the Econometric Society. 1973;41:733–750. [Google Scholar]
- 19.Hausman J. Specification tests in econometrics. Econometrica. 1978;46:1251–1271. [Google Scholar]
- 20.Guo Z, Cheng J, Lorch S, Small D. Using an instrumental variable to test for unmeasured confounding. doi: 10.1002/sim.6227. Working Paper. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Holland P. Causal inference, path analysis, and recursive structural equations models. Sociological Methodology. 1988;18:449–484. [Google Scholar]
- 22.Permutt T, Hebel J. Simultaneous-equation estimation in a clinical trial of the effect of smoking on birth weight. Biometrics. 1989;45:619–622. [PubMed] [Google Scholar]
- 23.Sexton M, Hebel J. A clinical trial of change in maternal smoking and its effect on birth weight. Journal of the American Medical Association. 1984;251:911–915. [PubMed] [Google Scholar]
- 24.McClellan M, McNeil B, Newhouse J. Does more intensive treatment of acute myocardial infarction in the elderly reduce mortality? analysis using instrumental variables. Journal of the American Medical Association. 1994;272(11):859. [PubMed] [Google Scholar]
- 25.Brooks J, Chrischilles E, Scott S, Chen-Hardee S. Was breast conserving surgery underutilized for early stage breast cancer? Instrumental variables evidence for stage II patients from Iowa. Health Services Research. 2004:38. doi: 10.1111/j.1475-6773.2003.00184.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Johnston S. Combining ecological and individual variables to reduce confounding by indication: case studysubarachnoid hemorrhage treatment. Journal of Clinical Epidemiology. 2000;53:1236–1241. doi: 10.1016/s0895-4356(00)00251-1. [DOI] [PubMed] [Google Scholar]
- 27.Brookhart M, Wang P, Solomon D, Schneeweiss S. Evaluating short-term drug effects using a physician-specific prescribing preference as an instrumental variable. Epidemiology. 2006;17:268–275. doi: 10.1097/01.ede.0000193606.58671.c5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Newman T, Vittinghoff E, McCulloch C. Efficacy of phototherapy for newborns with hyperbilirubinemia: a cautionary example of an instrumental variable analysis. Medical Decision Making. 2012;32:83–92. doi: 10.1177/0272989X11416512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Korn E, Baumrind S. Clinician preferences and the estimation of causal treatment differences. Statistical Science. 1998;13:209–235. [Google Scholar]
- 30.Shetty K, Vogt W, Bhattacharya J. Hormone replacement therapy and cardiovascular health in the United States. Medical Care. 2009;47:600–606. doi: 10.1097/MLR.0b013e31818bfe9b. [DOI] [PubMed] [Google Scholar]
- 31.Voight B, Peloso G, Orho-Melander M, Frikke-Schmidt R, Barbalic M, Jensen M, Hindy G, Hólm H, Ding E, Johnson T, et al. Plasma HDL cholesterol and risk of myocardial infarction: a mendelian randomisation study. Lancet. 2012;380:572–580. doi: 10.1016/S0140-6736(12)60312-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wehby G, Jugessur A, Moreno L, Murray J, Wilcox A, Lie R. Genetic instrumental variable studies of the impacts of risk behaviors: an application to maternal smoking and orofacial clefts. Health Services and Outcomes Research Methodology. 2011;11:54–78. doi: 10.1007/s10742-011-0071-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lawlor D, Harbord R, Sterne J, Timpson N, Smith G. Mendelian randomization: Using genes as instruments for making causal inferences in epidemiology. Statistics in Medicine. 2008;27:1133–1163. doi: 10.1002/sim.3034. [DOI] [PubMed] [Google Scholar]
- 34.Goedde H, Agarwal D, Fritze G, Meier-Tackmann D, Singh S, Beckmann G, Bhatia K, Chen L, Fang B, Lisker R. Distribution of ADH2 and ALDH2 genotypes in different populations. Human Genetics. 1992;88:344–346. doi: 10.1007/BF00197271. [DOI] [PubMed] [Google Scholar]
- 35.Sham P. Statistics in Human Genetics. Arnold; London: 1998. [Google Scholar]
- 36.Didelez V, Sheehan N. Mendelian randomization as an instrumental variable approach to causal inference. Statistical Methods in Medical Research. 2007:16. doi: 10.1177/0962280206077743. [DOI] [PubMed] [Google Scholar]
- 37.Ho V, Hamilton B, Roos L. Multiple approaches to assessing the effects of delays for hip fracture patients in the United States and Canada. Health Services Research. 2000;34:1499–1518. [PMC free article] [PubMed] [Google Scholar]
- 38.Malkin J, Broder M, Keeler E. Do longer postpartum stays reduce newborn readmissions? Analysis using instrumental variables. Health Services Research. 2000;35:1071–1091. [PMC free article] [PubMed] [Google Scholar]
- 39.Goyal N, Zubizarreta J, Small D, Lorch S. Hospital Pediatrics. Length of stay and readmission among late preterm infants: an instrumental variable approach. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cole J, Norman H, Weatherby L, Walker A. Drug copayment and adherence in chronic heart failure: effect on costs and outcomes. Pharmacotherapy. 2006;26:1157–1164. doi: 10.1592/phco.26.8.1157. [DOI] [PubMed] [Google Scholar]
- 41.Neyman J. On the application of probability theory to agricultural experiments. Statistical Science. 1990;5:463–480. [Google Scholar]
- 42.Rubin D. Estimating causal effects of treatments in randomized and non-randomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- 43.Angrist J, Imbens G, Rubin D. Identification of causal effects using instrumental variables. Journal of the American Statistical Association. 1996;91(434):444–455. [Google Scholar]
- 44.Rubin D. Formal modes of statistical inference for causal effects. Journal of Statistical Planning and Inference. 1990;25:279–292. [Google Scholar]
- 45.Balke A, Pearl J. Bounds on treatment effects for studies with imperfect compliance. Journal of the American Statistical Association. 1997;92(439):1171–1176. [Google Scholar]
- 46.Zelen M. A new design for randomized clinical trials. The New England Journal of Medicine. 1979:1242–1245. doi: 10.1056/NEJM197905313002203. [DOI] [PubMed] [Google Scholar]
- 47.Robins J. Correcting for non-compliance in randomized trials using structural nested mean models. Communications in Statistics – Theory and Methods. 1994;23:2379–2412. [Google Scholar]
- 48.Tan Z. Marginal and nested structural models using instrumental variables. Journal of the American Statistical Association. 2010;105(489):157–169. [Google Scholar]
- 49.Vansteelandt S, Bowden J, Babnezhad M, Goetghebeur E. On instrumental variables estimation of causal odds ratios. Statisitcal Science. 2011;26(3):403–422. [Google Scholar]
- 50.Imbens G, Wooldridge J. Lecture notes 5, Instrumental variables with treatment effect heterogeneity: Local average treatment effects. What's New in Econometrics, National Bureau of Economic Research. 2007 Summer. [Google Scholar]
- 51.Vytlacil E. Independence, monotonicity, and latent index models: An equivalence result. Econometrica. 2002;70:331–341. [Google Scholar]
- 52.Wald A. The fitting of straight lines if both variables are subject to error. Annals of Mathematical Statistics. 1940;11:284–300. [Google Scholar]
- 53.White H. Asymptotic Theory for Econometricians. Academic Press; New York: 1984. [Google Scholar]
- 54.Davidson R, MacKinnon J. Estimation and Inference in Econometrics. Oxford University Press; New York: 1993. [Google Scholar]
- 55.Imbens G, Angrist J. Identification and estimation of local average treatment effects. Econometrica. 1994:62. [Google Scholar]
- 56.Freedman D. Statistical Models: Theory and Practice. Cambridge University Press; Cambridge: 2009. [Google Scholar]
- 57.Imbens G, Rubin D. Estimating outcome distributions for compliers in instrumental variables models. The Review of Economic Studies. 1997;64(4):555–574. [Google Scholar]
- 58.Imbens G, Rubin D. Bayesian inference for causal effects in randomized experiments with noncompliance. The Annals of Statistics. 1997:305–327. [Google Scholar]
- 59.Cheng J, Small D, Tan Z, Ten Have T. Efficient nonparametric estimation of causal effects in randomized trials with noncompliance. Biometrika. 2009;96(1):19–36. [Google Scholar]
- 60.Cheng J, Qin J, Zhang B. Semiparametric estimation and inference for distributional and general treatment effects. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2009;71(4):881–904. [Google Scholar]
- 61.Lorch S, Kroelinger C, Ahlberg C, Barfield W. Factors that mediate racial/ethnic disparities in US fetal death rates. American Journal of Public Health. 2012;102:1902–1910. doi: 10.2105/AJPH.2012.300852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Angrist J, Pischke JS. Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press; Princeton: 2009. [Google Scholar]
- 63.Little R, Yau L. Statistical techniques for analyzing data from prevention trials: treatment of no-shows using Rubin's causal model. Psychological Methods. 1998;3:147–159. [Google Scholar]
- 64.Hirano K, Imbens G, Rubin D, Zhou X. Assessing the effect of an influenza vaccine in an encouragement design. Biostatistics. 2000;1(1):69–88. doi: 10.1093/biostatistics/1.1.69. [DOI] [PubMed] [Google Scholar]
- 65.Angrist J, Imbens G. Two-stage least squares estimation of average causal effects in models with variable treatment intensity. Journal of the American Statistical Association. 1995;90:430–442. [Google Scholar]
- 66.Abadie A. Semiparametric instrumental variable estimation of treatment response models. Journal of Econometrics. 2003;113:231–263. [Google Scholar]
- 67.Tan Z. Regression and weighting methods for causal inference using instrumental variables. Journal of the American Statistical Association. 2006;101:1607–1618. [Google Scholar]
- 68.O'Malley A, Frank R, Normand S. Estimating cost-offsets of new medications: use of new antipsychotics and mental health costs for schizophrenia. Statistics in Medicine. 2011;30:1971–1988. doi: 10.1002/sim.4245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Okui R, Small D, Tan Z, Robins J. Doubly robust instrumental variables regression. Statistica Sinica. 2012;22:173–=205. [Google Scholar]
- 70.White H. Instrumental variables regression with independent observations. Econometrica. 1982;50:483–499. [Google Scholar]
- 71.Angrist J, Krueger A. The effect of age at school entry on educational attainment: an application of instrumental variables with moments from two samples. Journal of the American Statistical Association. 1992;87:328–336. [Google Scholar]
- 72.Inoue A, Solon G. Two-sample instrumental variables estimators. The Review of Economics and Statistics. 2010;92:557–561. [Google Scholar]
- 73.Kaushal N. Do food stamps cause obesity? Evidence from immigrant experience. Journal of Health Economics. 2007;26:968–991. doi: 10.1016/j.jhealeco.2007.01.006. [DOI] [PubMed] [Google Scholar]
- 74.Basu A, Chan K. Can we make smart choices between OLS and contaminated IV methods? Health Economics. 2013 doi: 10.1002/hec.2926. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Sommer A, Zeger S. On estimating efficacy from clinical trials. Statistics in Medicine. 1991;10:45–52. doi: 10.1002/sim.4780100110. [DOI] [PubMed] [Google Scholar]
- 76.Sheiner L, Rubin D. Intention-to-treat analysis and the goal of clinical trials. Clinical Pharmacology & Therapeutics. 1995;56:6–10. doi: 10.1016/0009-9236(95)90260-0. [DOI] [PubMed] [Google Scholar]
- 77.Small D, Ten Have T, Joffe M, Cheng J. Random effects logistic models for analysing efficacy of a longitudinal randomized treatment with non-adherence. Statistics in Medicine. 2006;25:1981–2007. doi: 10.1002/sim.2313. [DOI] [PubMed] [Google Scholar]
- 78.Hernán M, Hernández-Díaz S. Beyond the intention to treat in comparative effectiveness research. Clinical Trials. 2012;9:48–55. doi: 10.1177/1740774511420743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Ten Have T, Normand SL, Marcus S, Brown C, Lavori P, Duan N. Intent-to-treat vs. non-intent-to-treat analyses under treatment non-adherence in mental health randomized trials. Psychiatric Annals. 2008;38:772–783. doi: 10.3928/00485713-20081201-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Cheng J, Small D. Bounds on causal effects in three-arm trials with noncompliance. Journal of the Royal Statistical Society, Series B. 2006;68(5):815–836. [Google Scholar]
- 81.Bhattacharya J, Shaikh A, Vytlacil E. Treatment effect bounds under monotonicity assumptions: an application to swan-ganz catherization. American Economic Review. 2008;98(2):351–356. [Google Scholar]
- 82.Siddique Z. Partially identified treatment effects under imperfect compliance: the case of domestic violence. Journal of the American Statistical Association. in press. [Google Scholar]
- 83.Abadie A. Bootstrap tests for distributional treatment effects in instrumental variable models. Journal of the American Statistical Association. 2002;97:284–292. [Google Scholar]
- 84.Kitcheman J, Adams C, Prevaiz A, Kader I, Mohandas D, Brookes G. Does an encouraging letter encourage attendance at psychiatric outpatient clinics? The Leeds Prompts randomized study. Psychological Medicine. 2008;38:717–723. doi: 10.1017/S0033291707001766. [DOI] [PubMed] [Google Scholar]
- 85.Joffe M. Principal stratification and attribution prohibition: good ideas taken too far. International Journal of Biostatistics. 2011;7(1):1–22. doi: 10.2202/1557-4679.1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Hernán M, Robins J. Instruments for causal inference: an epidemiologist's dream? Epidemiology. 2006;17(4):360. doi: 10.1097/01.ede.0000222409.00878.37. [DOI] [PubMed] [Google Scholar]
- 87.Rubin D. Statistics and causal inference: Comment: Which ifs have causal answers. Journal of the American Statistical Association. 1986;81(396):961–962. [Google Scholar]
- 88.Kivimaki M, Jokela M, Hamer M, Geddes J, Ebmeier K, Kumari M, Singh-Manoux A, Hingorani A, Batty G. Examining overweight and obesity as risk factors for common mental disorders using fat mass and obesity-associated (FTO) genotype-instrumented analysis: The whitehall II study, 19852004. American Journal of Epidemiology. 2011;173:421–429. doi: 10.1093/aje/kwq444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Wardle J, Carnell S, Haworth C, Farooqi I, O'Rahilly S, Plomin R. Obesity associated genetic variation in FTO is associated with diminished satiety. Journal of Clinical Endocrinology and Metabolism. 2008;90:3640–3643. doi: 10.1210/jc.2008-0472. [DOI] [PubMed] [Google Scholar]
- 90.Burgess S, Butterworth A, Malarstig A, Thompson S. Use of mendelian randomisation to assess potential benefits of clinical intervention. British Medical Journal. 2012;345:e7325. doi: 10.1136/bmj.e7325. [DOI] [PubMed] [Google Scholar]
- 91.Hudgens M, Halloran M. Towards causal inference with interference. Journal of the American Statistical Association. 2008;103:832–842. doi: 10.1198/016214508000000292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Sobel M. What do randomized studies of housing mobility demonstrate? Causal inference in the face of interference. Journal of the American Statistical Association. 2006;101:1398–1407. [Google Scholar]
- 93.Demissie K, Rhoads G, Ananth C, Alexander G, Kramer M, Kogan M, Joseph K. Trends in preterm birth and neonatal mortality among blacks and whites in the United States from 1989 to 1997. American Journal of Epidemiology. 2001;154:307–315. doi: 10.1093/aje/154.4.307. [DOI] [PubMed] [Google Scholar]
- 94.Small D, Rosenbaum P. War and wages: The strength of instrumental variables and their sensitivity to unobserved biases. Journal of the American Statistical Association. 2008;103:924–933. [Google Scholar]
- 95.Kang H, Kreuels B, Adjei O, May J, Small D. The causal effect of malaria on stunting: A mendelian randomization and matching approach. International Journal of Epidemiology. doi: 10.1093/ije/dyt116. in press. [DOI] [PubMed] [Google Scholar]
- 96.Aidoo M, Terlouw D, Kolczak M, McElroy P, ter Kuile F, Kariuki S, Nahlen B, Lal A, Udhayakumar V. Protective effects of the sickle cell gene against malaria morbidity and mortality. Lancet. 2002;359:1311–1312. doi: 10.1016/S0140-6736(02)08273-9. [DOI] [PubMed] [Google Scholar]
- 97.Rehan N. Growth status of children with and without sickle cell trait. Clinical Pediatrics. 1981;20:705–709. doi: 10.1177/000992288102001103. [DOI] [PubMed] [Google Scholar]
- 98.Kramer M, Rooks Y, Pearson H. Growth and development in children with sickle-cell trait. New England Journal of Medicine. 1978;299:686–689. doi: 10.1056/NEJM197809282991303. [DOI] [PubMed] [Google Scholar]
- 99.Rosenbaum P. Observational Studies. Springer Verlag; 2002. [Google Scholar]
- 100.Yang F, Zubizarreta J, Small D, Lorch S, Rosenbaum P. Aporetic conclusions when testing the validity of an instrumental variable. Working paper. [Google Scholar]
- 101.Small D. Sensitivity analysis for instrumental variables regression with overidentifying restrictions. Journal of the American Statistical Association. 2007;102:1049–1058. [Google Scholar]
- 102.Baiocchi M, Small D, Lorch S, Rosenbaum P. Building a stronger instrument in an observational study of perinatal care for premature infants. Journal of the American Statistical Association. 2010;105(492):1285–1296. [Google Scholar]
- 103.Joffe M, Small D, Brunelli S, Ten Have T, Feldman H. Extended instrumental variables estimation for overall effects. International Journal of Biostatistics. 2008:4. doi: 10.2202/1557-4679.1082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Bound J, Jaeger D, Baker R. Problems with instrumental variables estimation when the correlation between the instruments and the endogenous explanatory variables is weak. Journal of the American Statistical Association. 1995;90:443–450. [Google Scholar]
- 105.Shea J. Instrument relevance in multivariate linear models: a simple measure. Review of Economics and Statistics. 1997;79:348–352. [Google Scholar]
- 106.Nelson CR, Startz R. Some further results on the exact small sample properties of the instrumental variable estimator. Econometrica. 1990;58:967–976. [Google Scholar]
- 107.Han C, Schmidt P. The asymptotic distribution of the instrumental variable estimators when the instruments are not correlated with the regressors. Economics Letters. 2001;74:61–66. [Google Scholar]
- 108.Stock J, Wright J, Yogo M. A survey of weak instruments and weak identification in generalized method of moments. Journal of Business and Economic Statistics. 2002;20:518–529. [Google Scholar]
- 109.Anderson T, Rubin H. Estimation of the parameters of a single equation in a complete system of stochastic equations. Annals of Mathematical Statistics. 1949;20:46–63. [Google Scholar]
- 110.Moreira M. A conditional likelihood ratio test for structural models. Econometrica. 1990;71:463–480. [Google Scholar]
- 111.Freeman G, Cowling B, Schooling C. Power and sample size calculations for mendelian randomization studies using one genetic instrument. International Journal of Epidemiology. 2013;42:1157–1163. doi: 10.1093/ije/dyt110. [DOI] [PubMed] [Google Scholar]
- 112.Brion MJ, Shakhbazov K, Visscher P. Calculating power for mendelian randomization studies. International Journal of Epidemiology. 2013;42:1497–1501. doi: 10.1093/ije/dyt179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Jiang Y, Small D, Zhang N. Sensitivity analysis and power for instrumental variable studies 2013. doi: 10.1111/biom.12873. Working Paper. [DOI] [PubMed] [Google Scholar]
- 114.Cai B, Small D, Ten Have T. Two-stage instrumental variable methods for estimating the causal odds ratio: analysis of bias. Statistics in Medicine. 2011;30:1809–1824. doi: 10.1002/sim.4241. [DOI] [PubMed] [Google Scholar]
- 115.Nagelkerke N, Fidler V, Bernsen R, Borgdorff M. Estimating treatment effects in randomized clinical trials in the presence of non-compliance. Statistics in Medicine. 2000;19:1849–1864. doi: 10.1002/1097-0258(20000730)19:14<1849::aid-sim506>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- 116.Terza J, Basu A, Rathouz P. Two-stage residual inclusion estimation: addressing endogeneity in health econometric modeling. Health Economics. 2008;27:527–543. doi: 10.1016/j.jhealeco.2007.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Muthen B. A structural probit model with latent variables. Journal of the American Statistical Association. 1979;74:807–811. [Google Scholar]
- 118.Bhattacharya J, Goldman D, McCaffrey D. Estimating probit models with self-selected treatments. Statistics in Medicine. 2006;25:389–413. doi: 10.1002/sim.2226. [DOI] [PubMed] [Google Scholar]
- 119.Freedman D, Sekhon J. Endogeneity in probit response models. Political Analysis. 2010;18:138–150. [Google Scholar]
- 120.Clarke P, Windmeijer F. Instrumental variable estimators for binary outcomes. Journal of the American Statistical Association. 2012;107:1638–1652. [Google Scholar]
- 121.Cheng J. Estimation and inference for the causal effect of receiving treatment on a multinomial outcome. Biometrics. 2009;65(1):96–103. doi: 10.1111/j.1541-0420.2008.01020.x. [DOI] [PubMed] [Google Scholar]
- 122.Robins J, Tsiatis A. Correcting for non-compliance in randomized trials using rank preserving structural failure time models. Communications in Statistics, Theory and Methods. 1991;20:2609–2631. [Google Scholar]
- 123.Joffe M. Administrative and artificial censoring in censored regression models. Statistics in Medicine. 2001;20:2287–2304. doi: 10.1002/sim.850. [DOI] [PubMed] [Google Scholar]
- 124.Loeys T, Goetghebeur E. A causal proportional hazards estimator for the effect of treatment actually received in a randomized trial with all-or-nothing compliance. Biometrics. 2003;59:100–105. doi: 10.1111/1541-0420.00012. [DOI] [PubMed] [Google Scholar]
- 125.Cuzick J, Sasieni P, Myles J, Tyler J. Estimating the effect of treatment in a proportional hazards model in the presence of non-compliance and contamination. Journal of the Royal Statistical Society, Series B (Methodological) 2007;69:565–588. [Google Scholar]
- 126.Baker S. Analysis of survival data from a randomized trial with all-or-none compliance: estimating the cost-effectiveness of a cancer screening program. Journal of the American Statistical Association. 1998;93:929–934. [Google Scholar]
- 127.Nie H, Cheng J, Small D. Inference for the effect of treatment on survival probability in randomized trials with noncompliance and administrative censoring. Biometrics. 2011;67:1397–1405. doi: 10.1111/j.1541-0420.2011.01575.x. [DOI] [PubMed] [Google Scholar]
- 128.Poulson R, Gadbury G, Allison D. Treatment heterogeneity and individual qualitative interaction. The American Statistician. 2012;66:16–24. doi: 10.1080/00031305.2012.671724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Hunink M, Glasziou P, Siegel J, Weeks J, Pliskin J, Elstein A, Weinstein M. Decision Making in Health and Medicine: Integrating Evidence and Values. Cambridge University Press; 2001. [Google Scholar]
- 130.Karni E. A theory of medical decision making under uncertainty. Journal of Risk and Uncertainty. 2009;39:1–16. [Google Scholar]
- 131.Pliskin J, Shepard D, Weinstein M. Utility functions for life years and health status. Operations Research. 1980;28:206–224. [Google Scholar]
- 132.Hogan J, Lee J. Marginal structural quantile models for longitudinal observational studies with time-varying treatment. Statistica Sinica. 2004;14:927–944. [Google Scholar]
- 133.Saigal S, Stoskopf B, Feeny D, Furlong W, Burrows E, Rosenbaum P, Hoult L. Differences in preferences for neonatal outcomes among health care professionals, parents, and adolescents. Journal of the American Medical Association. 1999;281:1991–1997. doi: 10.1001/jama.281.21.1991. [DOI] [PubMed] [Google Scholar]
- 134.Sommers BD, Beard CJ, Dahl D, D'Amico AV, Kaplan IP, Richie J, Zeckhauser RJ. Decision analysis using individual patient preferences to determine optimal treatment for localized prostate cancer. Cancer. 2007;110:2210–2217. doi: 10.1002/cncr.23028. [DOI] [PubMed] [Google Scholar]
- 135.Imbens G. Nonadditive models with endogenous regressors. In: Blundell R, Newey W, Persson T, editors. Advances in Economics and Econometrics, Ninth World Congress of the Econometric Society. Cambridge University Press; New York: 2007. [Google Scholar]
- 136.Heckman J, Vytlacil E. Local instrumental variables and latent variable models for identifying and bounding treatment effects. Proceedings of the National Academy of Sciences. 1999;96:4730–4734. doi: 10.1073/pnas.96.8.4730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Basu A, Heckman J, Navarro-Lozano S, Urzua S. Use of instrumental variables in the presence of heterogeneity and self-selection: an application to treatments of breast cancer patients. Health Economics. 2007;16(11):1133–1157. doi: 10.1002/hec.1291. [DOI] [PubMed] [Google Scholar]
- 138.Lu B, Greevy R, Xu X, Beck C. Optimal nonbipartite matching and its statistical application. The American Statistician. 2011;65:21–30. doi: 10.1198/tast.2011.08294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Baiocchi M, Small D, Yang L, Polsky D, Groeneveld P. Near/far matching: a study design approach to instrumental variables. Health Services and Outcomes Research Methodology. 2012;12:237–253. doi: 10.1007/s10742-012-0091-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Sargan J. The estimation of economic relationships using instrumental variables. Econometrica. 1958;26:393–415. [Google Scholar]
- 141.Kelejian H. Two-stage least squares and econometric systems linear in parameters but nonlinear in the endogenous variables. Journal of the American Statistical Association. 1971;66:373–374. [Google Scholar]
- 142.Davies N, Smith G, Windmeijer F, Martin R. Issues in the reporting and conduct of instrumental variable studies: a systematic review. Epidemiology. 2013:24. doi: 10.1097/EDE.0b013e31828abafb. [DOI] [PubMed] [Google Scholar]
- 143.Angrist J, Krueger A. Instrumental variables and the search for identification: from supply and demand to natural experiments. Journal of Economic Perspectives. 2001;15:69–85. [Google Scholar]