On the Mechanics of Functional Asymmetry in Bipedal Walking

Abstract

This paper uses two symmetrical models, the passive compass-gait biped and a five-link 3D biped, to computationally investigate the cause and function of gait asymmetry. We show that for a range of slope angles during passive 2D walking and mass distributions during controlled 3D walking, these models have asymmetric walking patterns between the left and right legs due to the phenomenon of spontaneous symmetry-breaking. In both cases a stable asymmetric family of gaits emerges from a symmetric family of gaits as the total energy increases (e.g., fast speeds). The ground reaction forces of each leg reflect different roles, roughly corresponding to support, propulsion, and motion control as proposed by the hypothesis of functional asymmetry in able-bodied human walking. These results suggest that body mechanics, independent of neurophysiological mechanisms such as leg dominance, may contribute to able-bodied gait asymmetry.

I. Introduction

Gait asymmetry is commonly observed in quadrupeds [1] and impaired humans [2], but evidence suggests that able-bodied humans sometimes exhibit this behavior as well [3]-[7]. Understanding when and why this phenomenon occurs is important to gait research, where symmetry is commonly assumed in order to simplify data collection and analysis. Many methods exist for quantifying asymmetric motion between the right and left legs, using variables such as step length, joint range of motion, velocity profiles, and ground reaction forces (GRF) [8]. However, the underlying causes are still the subject of debate (see [3] for a review).

The hypothesis of functional asymmetry in able-bodied walking proposes that each leg serves different roles, such as vertical support, medio-lateral (ML) control, and/or anterior-posterior (AP) propulsion [3]. Differences between leg roles were observed during fast walking trials in [5], [6], suggesting that challenging locomotor tasks require asymmetric strategies. This is exemplified by reports of asymmetry in athletic race walking [7], running, and cycling [9], which were attributed to ground irregularities, shoes, and conditioning on curved tracks. The most common explanation for functional asymmetry is leg dominance, but conflicting reports exist for this theory [10].

We propose that body mechanics may be responsible for functional asymmetry. Gait asymmetries have been reported in computational simulations of planar “passive” walkers that use only momentum and gravity to propel forward motion down a shallow slope [11], [12]. These passive models reflect certain characteristics of human walking, such as ballistic motion during swing phase [13] and energetic efficiency down shallow slopes [14], and therefore act as simple surrogate models for the study of biped mechanics (see [15] for a review of other quantitative approaches). Although the dynamical equations of motion may yield a stable solution corresponding to a symmetric gait, small changes in model parameters can cause qualitatively different behavior at a bifurcation point, after which a new (stable) asymmetric solution emerges from the (unstable) symmetric solution. The symmetrical mechanics of these walkers admit two families of solutions, one symmetric and one asymmetric. However, the functions of these asymmetries have not been studied, and the period-doubling phenomenon has not been shown to extend to more realistic 3D models that walk on level ground.

This paper examines the cause and function of gait asymmetry using two physically symmetrical models. The passive 2D compass-gait biped is studied to show that gait can exhibit functional asymmetry due solely to passive mechanics, independent of control mechanisms. We then consider a 3D five-link model to show that functional asymmetry also occurs in more complex, controlled bipeds that walk in 3D environments. We show that small symmetric changes in model parameters, the slope angle for the 2D biped and leg mass distribution for the 3D biped, cause the emergence and growth of asymmetry in kinematic and kinetic variables. We find that these very different models have a common property: the symmetric family of gaits is stable for walking with low energy and the asymmetric family is stable with high energy. We study reaction forces from the asymmetric gaits and find distinct leg functions roughly corresponding to support, motion control, and propulsion. These results show that under certain conditions gait asymmetry is beneficial for dynamical stability, suggesting two important implications for human walking:

• Mechanics alone might explain functional asymmetry in able-bodied humans.

• Asymmetry does not imply instability as is often assumed clinically for stroke, cerebral palsy, and amputee gait.

We begin in Section II by analyzing previously unaddressed kinetic and stability variables in the passive biped from [11]. In Section III we extend these results to the 3D biped from [16]. We compare gait energetics and leg functions between these models in Section IV and conclude in Section V.

II. Passive Compass-Gait Biped

Passive walking gaits arise on inclined surfaces when the potential energy converted into kinetic energy is lost at impact events. We start by modeling these walking dynamics for the compass-gait biped and defining gait asymmetry.

A. Dynamical Model

The planar compass-gait biped of Fig. 1 has point feet that coincide with the ankle joints. This simple model’s two degreeof-freedom (DOF) configuration is given by the vector θ = (θ_s, θ_ns) in the configuration space Q = S¹ × S¹ (two copies of the unit circle), representing the stance angle at the ankle and the non-stance/swing angle at the hip. The system state is given by vector x = (θ^T, θ̇^T)^T in state space TQ, where θ̇ ∈ ℝ² contains the joint velocities. The single-support phase dynamics are represented by a differential equation of the form

$$M\left(\theta \right)\ddot{\theta }+C\left(\theta ,\dot{\theta }\right)\dot{\theta }+N\left(\theta \right)=0,$$ (1)

where M ∈ ℝ^2×2 is the inertia/mass matrix, C ∈ ℝ^2×2 contains the Coriolis/centrifugal terms, and N ∈ ℝ² is the vector of gravitational torques (see Appendix for expressions).

Fig. 1.

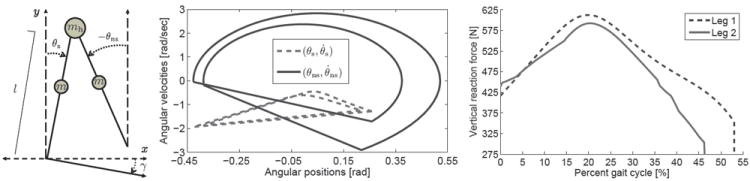
The passive, planar compass-gait biped (left). Phase portrait (center) and vertical ground reaction forces (right) of the period-two passive gait on slope angle 0.0838 rad. Note that the second step cycle is shifted to coincide with the first step cycle in the reaction force figure for visual comparison.

The continuous single-support phase is constrained by h_γ (θ) ≥ 0, where the scalar function h_γ gives the height of the swing foot above ground with slope angle γ. The instantaneous impact event from ground strike occurs when the state trajectory intersects the switching set¹

$$G=\{\left(\theta ,\dot{\theta }\right)\mid h_{\gamma }\left(\theta \right)=0,{\dot{h}}_{\gamma }=({\nabla }_{\theta }{h}_{\gamma })\dot{\theta }<0\}\subset T\mathrm{Q}.$$

We model these impulsive events as perfectly plastic (inelastic) collisions [11], so any solution trajectory intersecting the ground plane is subjected to the discontinuous impact map Δ : G → TQ (which also relabels θ_s and θ_ns, see Appendix). We then have the hybrid dynamical system

$$\begin{array}{ll}\hfill M\left(\theta \right)\ddot{\theta }+C\left(\theta ,\dot{\theta }\right)\dot{\theta }+N\left(\theta \right)=0& \mathrm{for}\left(\theta ,\dot{\theta }\right)\notin G\\ \hfill ({\theta }^{+},{\dot{\theta }}^{+})=\mathrm{\Delta }\left({\theta }^{-},{\dot{\theta }}^{-}\right)& \mathrm{for}\left({\theta }^{-},{\dot{\theta }}^{-}\right)\in G.\end{array}$$

Walking gaits correspond to solutions x(t) = (θ(t), θ̇(t)) of the above system that are periodic, i.e., x(t) = x(t + T) for some minimal T > 0 and all t. These solutions define isolated orbits in state space known as hybrid limit cycles, which correspond to equilibria of the return map P : G → G. This map represents the hybrid system as a discrete system between impact events, sending state x_j ∈ G ahead one step to x_j+1 = P(x_j). A symmetric periodic solution x(t) has a fixed point x* = P(x*). A periodic solution that is asymmetric has a period greater than one, requiring multiple compositions of the return map to find a fixed point x* = P^k(x*), for k > 1.

We say that a fixed point x* of the discrete system

$$x_{j+k}=P^k(x_j),k\ge 1,$$ (2)

is stable if for each ε > 0, there exists a constant γ > 0 such that for all sequences {x_j} with |x₀−x*| ≤ γ, |x_kj −x*| ≤ ε for all j ≥ 0. A fixed point is (locally) asymptotically stable if it is stable and |x_kj−x*| → 0 as j → ∞. Exponential stability is yet stronger with exponential convergence to x*. The set of states around x* that converge to this locally stable fixed point is known as the region of attraction.

We verify local exponential stability in system (2) by numerically computing the linearized map ∇_xP^k about x* (see Appendix). This yields a discrete linear system that is exponentially stable if and only if the magnitudes of the eigenvalues of ∇_xP^k(x*) are strictly less than one. If any absolute eigenvalue is greater than one, x* is an unstable solution of (2). This also corresponds to cyclic walking, but small perturbations will eventually cause large deviations from the solution trajectory (e.g., falling). Able-bodied human gaits are known to be stable in this orbital sense [17].

B. Varying the Slope Angle

This biped’s mechanics admit symmetric and asymmetric families of gaits depending on certain model parameters [11], [18]. We will examine how gait kinetics change between the families of solutions parameterized by the ground slope. We choose the model parameters in Table I based on adult (male) means reported in [19], grouping the trunk masses at the hip.

TABLE I.

Compass-Gait Biped Parameters

Parameter	Variable	Value
Hip mass	mh	31.73 [kg]
Leg mass	m	13.5 [kg]
Leg length	ℓ	0.856 [m]
Slope angle	γ	0.06 – 0.0853 [rad]

For a range of slopes the steady-state gait is symmetric and (locally exponentially) stable. This family of gaits becomes unstable on large slopes beyond a bifurcation point at γ = 0.073 rad, splitting into a stable asymmetric family. These gaits are cyclic every two steps with one long and one short step (depicted in Fig. 1). We observe 4-step asymmetric gaits after the second bifurcation at γ = 0.0843 rad. Our simulations no longer exhibit cyclic behavior beyond 0.0853 rad.

These evolving gaits are visualized in bifurcation diagrams, which show changes in “gait descriptors” (variables of the steady gait) over a range of slopes around bifurcation points, where the most interesting behavior occurs. Gait descriptors of stable solutions are given in solid lines and (approximate) unstable solutions in dashed lines in Fig. 2, where asymmetric solutions have two or more branches showing the descriptor for each step cycle in the gait. We see that step length, velocity, and impact energy dissipation of the symmetric gait evolve monotonically with slope, and the same holds for the asymmetric descriptors averaged over the gait cycle. This trend is also true of total mechanical energy at each impact event (Fig. 3). Integrating the GRF vector for each step cycle, we find in Fig. 4 that the AP impulse (midstance to foot strike) of the symmetric solution follows a monotonic trend whereas the vertical impulse remains close to constant. Additional kinematic and temporal descriptors are given in [11].

Fig. 2.

Steady-state passive biped: step length (left), step velocity (step length divided by time period; center), and impact energy dissipation (right) over slope angles between 0.06 and 0.0853 rad (3.44 and 4.89 degrees). Solution is solid if stable and dashed if unstable.

Fig. 3.

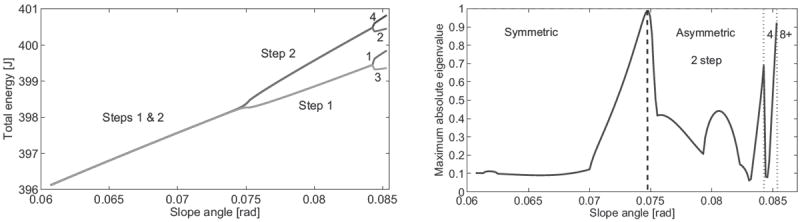
Steady-state passive biped: gait energy (left) and maximum absolute eigenvalue (right) over slope angle.

Fig. 4.

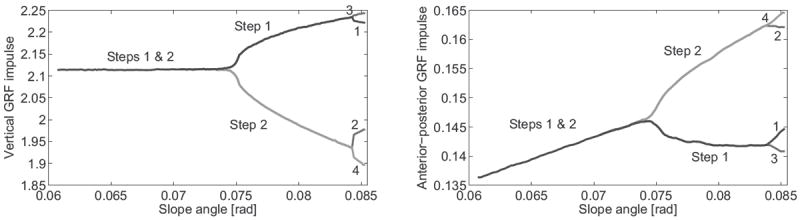
Steady-state passive biped: vertical (left) and AP (right) GRF impulse over slope angle. Step cycle impulses are calculated by integrating the GRF vector (over the entire step period for vertical, after midstance for AP) and normalizing by $M_{\mathrm{tot}}g\sqrt{\ell /g}$ to be dimensionless.

The eigenvalues of the return map P between steps offer a mathematically meaningful definition of local stability. The maximum absolute eigenvalue (MAE) is an inverse scale for stability between zero and one: a smaller value implies faster attenuation of perturbations in some local region around the nominal joint trajectory. For the sake of comparison between families of solutions, eigenvalues are calculated with the period-4 return map. We find in Fig. 3 (right) that some asymmetric gaits after the bifurcation point are more stable than any symmetric gait before the bifurcation point (e.g., MAE of 0.061 at 0.083 rad versus 0.09 at 0.066 rad). The MAE of the 4-step gait also drops significantly after the 2-step gait becomes unstable at the second bifurcation point.

Fig. 3 (right) shows multiple local stability minima within the range of walking gaits, where the global minima resides in the 2-step asymmetric family. This can be explained by the fact that high-speed (asymmetric) gaits dissipate more energy at impacts than low-speed (symmetric) gaits. Energy dissipation can attenuate perturbations, which is reflected in the smaller eigenvalues of the asymmetric family. Similar behavior for passive hopping models was observed in [20], where some asymmetric gaits also appeared to have larger regions of attraction than symmetric gaits. This phenomenon can be explained by the presence of multiple orbital branches in the asymmetric solution, by which these gaits can occupy greater volume in the state space. In the current study we do not investigate this distinctly different metric for stability.

III. Five-Link 3D Biped with Knees

The 3D model in Fig. 5 has two phases during single support: knee-swing with six DOFs and knee-lock with five DOFs. The stance knee remains locked through each step cycle. The biped walks on a flat surface with sufficient static friction to prevent slipping at the foot contact point. We model internal/external rotation about the stance leg as an unactuated DOF with passive viscous damping (e.g., from soft/hard tissue). This reflects the fact that the human ankle provides actuation for flexion/extension and inversion/eversion, but internal/external rotation (i.e., yaw) is passive [21].

Fig. 5.

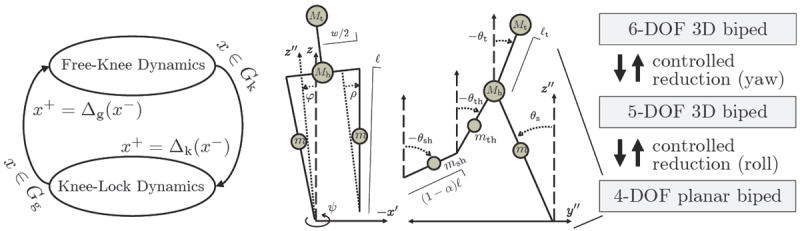
Diagrams of the 3D biped’s hybrid system (left), frontal and sagittal planes (center), and controlled reduction (right). The control strategy dynamically decouples the 4-DOF dynamics of the sagittal plane by reducing the yaw DOF of the transverse plane and the lean DOF of the frontal plane.

A. Dynamical Model

This biped has coordinates q = (ψ, φ, θ^T)^T in Q = T⁶ (six unit circles), where ψ, φ ∈ S¹ are respectively the yaw and lean variables at the stance foot, and vector θ = (θ_s, θ_t, θ_th, θ_sh)^T contains the sagittal-plane variables for the stance leg, torso, swing thigh, and swing shank, respectively. Knee-lock phase provides θ_th ≡ θ_sh. Hip abduction/adduction are fixed at a constant angle ρ to simplify the control problem.

The system state is x = (q^T, q̇^T)^T ∈ TQ. We model knee- and ground-strike events with instantaneous and perfectly plastic impacts, resulting in transitions between six and five DOF dynamics according to the hybrid system of Fig. 5 (assuming a steady walking gait). The ground-strike switching set G_g is the subset of states where the swing foot height is zero, and its reset map is Δ_g. The knee-strike set G_k contains the states where θ_th − θ_sh = 0, and its reset map is Δ_k. The dynamics for each single-support phase have the form

$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+N(q)=\mathit{Bu},$$ (3)

where M ∈ ℝ^n×n, C ∈ ℝ^n×n, and N ∈ ℝⁿ are defined as before, n ∈ {5, 6}. Control input u ∈ ℝⁿ⁻¹ and torque map B ∈ ℝ^n×n−1 model actuation at every DOF except ankle yaw.

The control strategy from [22], depicted in Fig. 5, produces 3D walking by effectively decoupling the sagittal plane and inheriting its naturally stable passive mechanics. This decomposition of the biped dynamics into lower-dimensional control problems is achieved by enforcing momentum conservation laws, expressed as nonholonomic constraints J_c(q)q̇ = λ(q), that stabilize the yaw and lean dynamics. The feedback control law injects energy-shaping terms that provide this behavior:

$$\begin{array}{lll}\hfill u& =& {(B^{T}B)}^{-1}{B}^T[C(q,\dot{q})\dot{q}+N(q)+M(q)({\ddot{q}}_{\mathrm{des}}+\upsilon )]\\ \hfill {\ddot{q}}_{\mathrm{des}}& =& M_{\lambda }^{-1}(q)[C_{\lambda }(q,\dot{q})\dot{q}+N_{\lambda }(q)],\end{array}$$

where M_λ ∈ ℝ^n×n contains shaped inertia/mass terms, C_λ ∈ ℝ^n×n contains shaped Coriolis/centrifugal/gyroscopic terms, N_λ ∈ ℝⁿ contains shaped potential torques, and input υ ∈ ℝⁿ enforces J_c(q)q̇ = λ(q). These terms are provided in supplemental Mathematica files at http://ieeexplore.ieee.org.

This control law depends explicitly on the biped’s model parameters, so when parameters are varied the torques resulting from the same input state vector will change. The closed-loop hybrid dynamics during left stance exactly mirror that of right stance (with opposite signs for hip width w and angle ρ) due to bilateral symmetry across the sagittal plane. We model a step cycle by defining the return map P : G_g → G_g between ground-strike events, which implicitly accounts for bilateral symmetry by flipping the signs of out-of-plane variables (ψ, φ, ψ̇, φ̇) and parameters w, ρ. As was the case in Section II, symmetric gaits will correspond to period-one fixed points and asymmetric gaits will correspond to higher-period fixed points of this return map.

In the following simulations we adopt the human-like parameters in Table II, assuming point masses at the locations shown in Fig. 5. The bilateral mass ratio μ = m_th/(m_th + m_sh), for thigh mass m_th and shank mass m_sh, is the parameter we will vary with m = m_th + m_sh held constant.

TABLE II.

Five-Link 3D Biped Parameters

Parameter	Variable	Value
Hip mass	Mh	14.11 [kg]
Torso mass	Mt	17.61 [kg]
Leg mass (thigh + shank)	m	13.5 [kg]
Torso length	lt	0.55 [m]
Leg length (thigh + shank)	ℓ	1 [m]
Hip length	w	0.2 [m]
Hip abduction/adduction angle	ρ	0.0564 [rad]
Thigh/shank length ratio	α	0.5
Thigh/shank mass ratio	μ	0.74 – 0.764
Slope angle	γ	0 [rad]

B. Varying the Leg Mass Distribution

Similar to the 2D case, the mechanics of our 3D biped admit a symmetric and asymmetric family of gaits based on mass ratio μ. We examine values within the range of adult human ratios reported in [19], where the female mean is 0.7545 and male mean is 0.7658. For our model the steady-state gait is symmetric and stable over a wide range (we only show μ ≥ 0.75 in Figs. 6-8), but becomes unstable and splits into a stable asymmetric gait beyond 0.76. Stable 4-step gaits are found after the second bifurcation at 0.763, where the 2-step family becomes unstable. We observe non-cyclic motions and eventual falls for μ > 0.764, which are excluded in Figs. 6-8. Bilateral symmetry in the physical model allows the asymmetric gaits² to be reflected across the sagittal plane (i.e., the legs swap roles) depending on initial conditions.

Fig. 6.

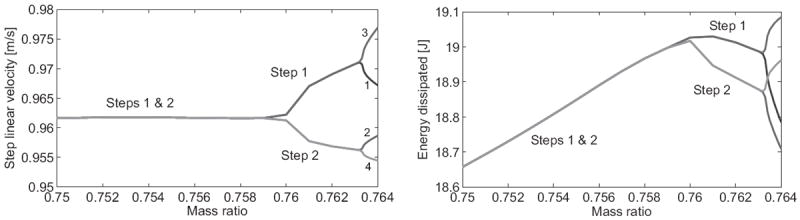
Steady-state five-link biped: step velocity (left) and impact energy dissipation (right) over mass ratio.

Fig. 8.

Steady-state five-link biped: vertical (left), AP (center), and absolute ML (right) GRF impulse over mass ratio. Impulses are calculated by integrating the GRF vector (over the entire step period for vertical, after midstance for AP and ML) and normalizing by $M_{\mathrm{total}}g\sqrt{\ell /g}$ to be dimensionless.

The symmetric solution’s velocity is nearly constant over the relevant range of mass ratios in Fig. 6, whereas the impact dissipation monotonically increases until the first bifurcation reverses this trend. The total energy at each impact event increases monotonically over the entire range in Fig. 7 (left). The AP and vertical impulses in Fig. 8 follow a monotonic decreasing trend whereas the ML impulse varies in an approximately sinusoidal fashion. Fig. 7 (right) shows multiple local stability minima, where the MAE drops significantly after each bifurcation point. However, in this case the global minimum for the period-4 return map resides in the symmetric family.

Fig. 7.

Steady-state five-link biped: gait energy (left) and maximum absolute eigenvalue (right) over mass ratio.

These simulations show a symmetric change in physiology causing asymmetry to emerge from complex biped mechanics. We used a control strategy that embraces the passive dynamics of the sagittal plane, so we argue that these mechanics are primarily responsible for the asymmetry as in Section II.

IV. Discussion

Spontaneous symmetry-breaking is a common manifestation of parametric perturbations in nonlinear systems [23]. We offered two models of different complexity to show that functional asymmetry is an intrinsic property of biped mechanics. Although these models do not have an ankle-foot complex that allows non-instantaneous double-support phase, bifurcations have been observed in passive bipeds with rolling feet and compliant feet [24]. We therefore argue that including feet and double support will not qualitatively change our findings.

A. Interpretations for Able-Bodied Gait

Total energy is the only gait descriptor that has a monotonically increasing relationship with the bifurcation parameter in both the planar and 3D cases (Figs. 3 and 7), suggesting that energy (influenced by walking speed) plays a fundamental role in the emergence of asymmetry. Period-doubling behavior may be a natural way for the body mechanics to compensate for extra energy in the walking gait. This observation is experimentally supported by tests of the functional asymmetry hypothesis [5], [6], where asymmetry was observed in AP impulses only during fast walking (Fig. 10). However, a causal relationship is difficult to prove in nonlinear hybrid dynamics.

Fig. 10.

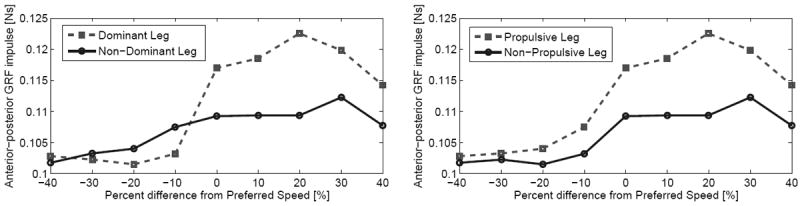
Mean values of normalized AP (propulsive) impulse for twenty human subjects walking at nine speeds during experiments reported in [6]. Data points from [6] are grouped by leg dominance (left) and leg function (right).

The hypothesis of functional asymmetry proposes distinct biomechanical functions of the legs, where one contributes more to propulsion and the other to body-weight support/transfer and motion control [3]-[6]. This is supported by the asymmetric family of 2D solutions in Figs. 2-4, where each leg contributes different impulses per step cycle and dissipates different energy at step-to-step transitions. These functions are manifested in the reaction forces seen in Fig. 1. The first stance phase provides support with a vertical impulse 15% greater than the second, whereas the second performs propulsion with an AP impulse 14.3% greater than the first.

In the 3D asymmetric case of Figs. 8-9, the first stance phase provides lean control with a ML impulse 106% greater than the second. We see less distinction in the support and propulsion roles – the vertical and AP impulses of the second leg are both 1% greater than the first leg (these roles are more distinct in the period-4 gait of Fig. 8). This shows that ML control can be primarily performed by a distinct leg.

Fig. 9.

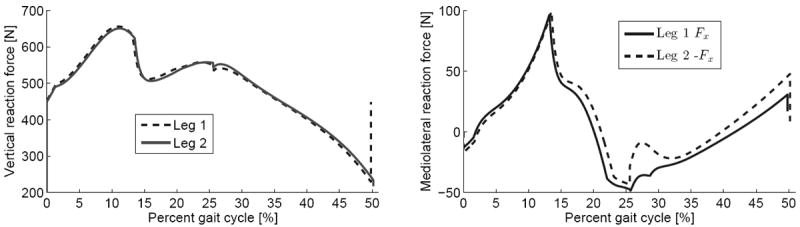
Vertical (left) and mediolateral (right) ground reaction forces for the period-two 3D gait of μ = 0.763, where the second step cycle is shifted to coincide with the first step cycle for visual comparison. The first leg’s F_x curve has the opposite sign of the second leg’s F_x curve, so the latter is negated for comparison (right).

Passive walking requires no energy contribution from the biped, so the existence of passive asymmetric gaits shows that asymmetry can be very energetically efficient. For walking speeds beyond the first bifurcation point (Fig. 3), the asymmetric solution is stable and the symmetric solution is not. Both correspond to cyclic walking motion, but the biped can employ the asymmetric gait at no cost, allowing the lower extremity mechanics to naturally attenuate perturbations. Walking symmetrically at the same speeds requires active stabilization from the motor control system, which must apply torques at some cost to attenuate destabilizing perturbations. We observed similar behavior in the controlled 3D model beyond the first bifurcation point (Fig. 7), where walking symmetrically requires a different control strategy for stability.

The 3D case study suggests that normal human mass ratios between the thigh and shank could promote asymmetric gait. If these results are indeed characteristic of human walking, asymmetries observed in able-bodied studies might be explained in part by humans attempting to maximize stability and/or efficiency. The leg corresponding to each biomechanical function may relate to limb dominance, but in the human trials of Fig. 10 the propulsive function appears to flip between legs at different speeds (the right side of Fig. 10 is a better match with the simulated bifurcation of Fig. 4). This swapping of roles could be the result of differing initial conditions for each trial (e.g., starting with a different leg, step length, or velocity).

Asymmetries in kinetic variables may be more apparent than in kinematic and temporal variables, where no noticeable changes were observed as a function of walking speed in ablebodied children and young adults [25]. The motor control system may actively suppress asymmetry in non-challenging tasks for more than aesthetic reasons – unbalanced joint strain over time can lead to musculoskeletal deterioration [8].

B. Interpretations for Pathological Gait

Gait symmetry and speed are common outcome metrics in clinical rehabilitation, but symmetry has not been shown to enable faster walking for stroke subjects [2]. In fact, variables for asymmetry are highly correlated with speed in hemiparetic stroke gait, where asymmetric leg motion accompanies increases in step length/velocity [2]. Attempts at enforcing symmetry using an orthosis to induce knee flexion have resulted in new asymmetries such as exaggerated frontalplane motion from hip adductor coupling [26]. Gait asymmetry also results from apparent bilateral neurological impairments, a common example being cerebral palsy [27].

The basic mechanics of walking may also play a role in these asymmetries. The range of biomechanical parameters examined in Section III-B can be interpreted as a range of bilateral³ impairments (e.g., abnormal mass distributions from prosthetic legs). These simulations suggest that impairment can alter biomechanics in such a way that abnormal asymmetry improves stability and efficiency and enables faster walking. This scenario would render the asymmetric family optimal (e.g., Fig. 3), pushing the biomechanics toward asymmetric behavior. If the healthy nervous system prevents the growth of asymmetry, a deficit might instead render the control system unable to compensate for the natural tendency of biped mechanics to admit asymmetric gaits. Studies are needed of these underlying mechanisms behind abnormal gait asymmetry.

V. Conclusions

We observed functional gait asymmetry in simulations of increasingly complex biped models after small changes in environmental and biomechanical parameters. In both cases the symmetric family of gaits is stable for walking with low energy and the asymmetric family is stable with high energy. Reaction forces showed asymmetric leg functions roughly corresponding to support, ML control, and propulsion. These asymmetric behaviors could be swapped between legs depending on the biped’s initial conditions.

This work serves to inform studies of functional asymmetry about possible divisions of leg function: one leg can perform more ML control even when the support and propulsion functions are shared by both legs. The form of functional asymmetry depends on the walking conditions, as seen from the differences between Sections II and III. We argue that perioddoubling bifurcation, also known as spontaneous symmetrybreaking, might explain in part the phenomenon of functional asymmetry and why it only appears in certain tasks.

These results motivate a new line of inquiry into the origin of able-bodied gait asymmetry, which may challenge the neurophysiological hypothesis of limb dominance. This may also have significant implications on clinical practices concerning pathological asymmetry, such as gait retraining after stroke and prosthesis fitting after lower-limb amputation.

Biographies

Robert D. Gregg IV (S’08-M’10) received the B.S. degree in electrical engineering and computer sciences from the University of California, Berkeley in 2006 and the M.S. and Ph.D. degrees in electrical and computer engineering from the University of Illinois at Urbana-Champaign in 2007 and 2010, respectively.

He is a Postdoctoral Fellow in the Department of Mechanical Engineering, Northwestern University and the Center for Bionic Medicine, Rehabilitation Institute of Chicago. His research is in the control mechanisms of bipedal locomotion with application to both autonomous and wearable robots.

Dr. Gregg is a recipient of the Engineering into Medicine Postdoctoral Fellowship from the Northwestern University Clinical and Translational Sciences Institute. He also received the Best Technical Paper Award of the 2011 International Conference on Climbing and Walking Robots, the 2009 O. Hugo Schuck Award from the IFAC American Automatic Control Council, and the Best Student Paper Award of the 2008 American Control Conference.

Yasin Y. Dhaher (SM’08) received the B.S. and M.Sc. degrees in mechanical engineering from Yarmouk and Jordan University of Science and Technology, Irbid, Jordan, in 1987 and 1990, respectively, and the Ph.D. degree in theoretical mechanics from Michigan State University, East Lansing, in 1997.

He holds faculty appointments in the Physical Medicine and Rehabilitation Department and the Biomedical Engineering Department of Northwestern University, Evanston, IL, and a Senior Research Scientist position at the Sensory Motor Performance Program (SMPP) at The Rehabilitations Institute of Chicago, Chicago, IL. He is the Director of the Joint Neuromechanics, and the Neuromechanics of Impaired Locomotion Laboratories at SMPP. He chairs the Biomechanics Core Curriculum Committee at the Biomedical Engineering Department, Northwestern University. His research is focused on two related topics: biomechanics and motor control. Using computational and experimental approaches, the primary goal of his investigations is to evaluate and improve rehabilitations interventions after neurological and musculoskeletal disabilities.

Dr. Dhaher serves on the Editorial Board of the IEEE TRANSACTIONS ON BIOMEDICAL ENGINEERING and the International Journal of Experimental and Computational Biomechanics.

Amir Degani (S’06-M’11) received the B.Sc. degree in mechanical engineering from the Technion - Israel Institute of Technology, Israel in 2002, and the M.S. and Ph.D. degrees in robotics from Carnegie Mellon University, Pittsburgh, PA in 2006 and 2010, respectively.

He is currently a senior lecturer at the Faculty of Civil and Environmental Engineering at the Technion - Israel Institute of Technology, Israel. His research program includes mechanism analysis, synthesis and design with emphasis on minimalistic concepts and the study of non-linear dynamic hybrid systems.

Dr. Degani received the best paper award in the IEEE BioRob Conference in 2006, and the best video award in IEEE ICRA Conference in 2010. He has five pending patents in the medical robotics field.

Kevin Lynch (M’96-SM’05-F’10) received a BSE in electrical engineering from Princeton in 1989 and a PhD in robotics from Carnegie Mellon in 1996. After a year as a postdoctoral fellow at the Mechanical Engineering Laboratory in Tsukuba, Japan, he joined Northwestern University, where he is currently a Professor in Mechanical Engineering. He is also codirector of the Northwestern Institute on Complex Systems (NICO). His research interests include robot manipulation, dynamic locomotion, self-organizing multi-agent systems, and human-robot interaction.

Prof. Lynch has received the NSF CAREER Award, the IEEE Early Career Award in Robotics and Automation, the SAE Teetor Educational Award, Northwestern’s McCormick School of Engineering and Applied Science Teacher of the Year Award, and Northwestern’s Charles Deering McCormick Professorship of Teaching Excellence. He is a Senior Editor of the IEEE Transactions on Automation Science and Engineering and an IEEE Fellow.

Appendix

We derive the rigid-body inertia matrix M, potential energy V, and swing foot height function h in Mathematica using the method of exponential twists described in [30]. We then perform a coordinate transformation from relative to static coordinates, so the sagittal-plane DOFs are all measured with respect to vertical. The gravitational torque vector is given by N = ∇_qV and the Coriolis matrix C can be written in components from matrix M as (see [31])

$$c_{\mathit{ij}}=\frac{1}{2}{\dot{m}}_{\mathit{ij}}+\frac{1}{2}\sum _{k=1}^n\left(\frac{\partial m_{\mathit{ik}}}{\partial q_j}-\frac{\partial m_{\mathit{jk}}}{\partial q_i}\right){\dot{q}}_k.$$ (4)

All simulations are computed in MATLAB using ode113 with event detection (based on the switching sets). After finding a k-fixed point x* = P^k (x*), the Taylor series expansion about x* gives P^k (x* + Δx*) ≈ P^k (x*) + (∇P^k)Δx* for a perturbation vector Δx* ∈ ℝ²ⁿ. The linearized map ∇P^k can be numerically computed by separately perturbing each dimension in the state vector and computing the output of the k^th return map. This results in two 2n × 2n matrices: ΔX, a diagonal matrix containing 2n perturbation vectors $\mathrm{\Delta }{x}_i^{\ast }$, and E, containing 2n return state errors $P^k\left(x^{\ast }+\mathrm{\Delta }{x}_i^{\ast }\right)-x^{\ast }$ in response to each state perturbation $\mathrm{\Delta }{x}_i^{\ast }$. The linearized return map ∇P^k = E(ΔX)⁻¹ then yields the eigenvalues [11].

The symbolic terms in dynamical equation (1) of the planar compass-gait biped are given by

$$\begin{array}{c}M(\theta )=\left(\begin{array}{cc}\frac{{\ell }^2}{4}(5m+4m_{\mathrm{h}})& -\frac{{\ell }^{2}m}{2}\cos \left({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}}\right)\\ -\frac{{\ell }^{2}m}{2}\cos \left({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}}\right)& \frac{{\ell }^{2}m}{4}\end{array}\right)\\ C(\theta ,\dot{\theta })=\frac{{\ell }^{2}m}{2}\left(\begin{array}{cc}0& -{\dot{\theta }}_{\mathrm{ns}}\sin ({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})\\ {\dot{\theta }}_{\mathrm{s}}\sin ({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})& 0\end{array}\right)\\ N(\theta )={\nabla }_{\theta }V(\theta )=\left(\begin{array}{c}-g\ell (3m+2m_{\mathrm{h}})\sin ({\theta }_{\mathrm{s}})/2\\ \mathit{g\ell m}\sin ({\theta }_{\mathrm{ns}})/2\end{array}\right),\end{array}$$

where V (θ) = gℓ((3m + 2m_h) cos(θ_s) − m cos(θ_ns))/2. The swing foot height function is given by

$$h_{\gamma }(\theta )=l((\cos ({\theta }_{\mathrm{s}})-\cos ({\theta }_{\mathrm{ns}}))+(\sin ({\theta }_{\mathrm{s}})-\sin ({\theta }_{\mathrm{ns}}))\tan (\gamma )).$$

Swapping coordinate labels between the stance and swing legs and conserving angular momentum through impact (see [11]) yields the impact map Δ(θ, θ̇) = ((θ_ns, θ_s)^T, P(θ) θ̇), where

$$\begin{array}{lll}\hfill P_{11}(\theta )& =& -2(m+2m_{\mathrm{h}})\cos ({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})/K(\theta )\\ \hfill P_{12}(\theta )& =& m/K(\theta )\\ \hfill P_{21}(\theta )& =& (m-4(m+m_{\mathrm{h}})\cos (2({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})))/K(\theta )\\ \hfill P_{22}(\theta )& =& 2m\cos ({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})/K(\theta ),\\ \hfill K(\theta )& =& -3m-4m_{\mathrm{h}}+2m\cos (2({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{ns}})).\end{array}$$

The fixed points at the initial slope γ = 0.06, first bifurcation point γ = 0.073, and second bifurcation point γ = 0.0843 are

$$\begin{array}{lll}\hfill x_{\gamma }^{\ast }=0.06& =& {(-0.3499,0.2299,-1.6795,-2.0600)}^T\\ \hfill x_{\gamma }^{\ast }=0.073& =& {(-0.3829,0.2369,-1.8113,-2.2712)}^T\\ x_{\gamma }^{\ast }=0.0843& =& {(-\mathrm{0.42810.2596}-1.9420-1.6874)}^T.\end{array}$$

The symbolic terms of matrix M for the 3D biped are too large to express in this appendix but are derived in the same manner as above. The knee-lock (5-DOF) dynamics can be derived separately or with the knee-free (6-DOF) dynamics plus a constraint force A^T Λ in the left-hand side of equation (3), where A = ∇_q(θ_th − θ_sh) is a constraint matrix and Λ is a Lagrange multiplier [30]. We derive the impact maps using the procedure in [32, Section II.B]. The modeling terms for both the 5-DOF and 6-DOF dynamics are provided in supplementary Mathematica files at http://ieeexplore.ieee.org.