Dosimetric effect of tissue heterogeneity for ¹²⁵I prostate implants

Abstract

Aim

To use Monte Carlo (MC) together with voxel phantoms to analyze the tissue heterogeneity effect in the dose distributions and equivalent uniform dose (EUD) for ¹²⁵I prostate implants.

Background

Dose distribution calculations in low dose-rate brachytherapy are based on the dose deposition around a single source in a water phantom. This formalism does not take into account tissue heterogeneities, interseed attenuation, or finite patient dimensions effects. Tissue composition is especially important due to the photoelectric effect.

Materials and methods

The computed tomographies (CT) of two patients with prostate cancer were used to create voxel phantoms for the MC simulations. An elemental composition and density were assigned to each structure. Densities of the prostate, vesicles, rectum and bladder were determined through the CT electronic densities of 100 patients. The same simulations were performed considering the same phantom as pure water. Results were compared via dose–volume histograms and EUD for the prostate and rectum.

Results

The mean absorbed doses presented deviations of 3.3–4.0% for the prostate and of 2.3–4.9% for the rectum, when comparing calculations in water with calculations in the heterogeneous phantom. In the calculations in water, the prostate D₉₀ was overestimated by 2.8–3.9% and the rectum D_0.1cc resulted in dose differences of 6–8%. The EUD resulted in an overestimation of 3.5–3.7% for the prostate and of 7.7–8.3% for the rectum.

Conclusions

The deposited dose was consistently overestimated for the simulation in water. In order to increase the accuracy in the determination of dose distributions, especially around the rectum, the introduction of the model-based algorithms is recommended.

1. Background

Low dose-rate brachytherapy (LDRBT), using ¹²⁵I and ¹⁰³Pd permanent implants, has become very popular in the treatment of early stage prostate cancer. The American Association of Physicists in Medicine (AAPM) Task Group No. 43 (TG-43)¹ and the updated report (TG-43U1)² recommended a water-based dose calculation formalism for this low-energy emitting sources. The dose deposition is described around a single source in a spherical water phantom and then interpolated in order to obtain tables of absorbed dose to be used in the planning systems (PS). However, the influence of tissue and applicator heterogeneities, interseed attenuation, or finite patient dimensions can significantly change the absorbed dose values in the PS.³ Moreover, for low-energy sources, the photoelectric effect predominates and differences in the mass-energy absorption coefficients between water and other tissues may result in significant differences in dose distributions.

Chibani et al.⁴ investigated the effects of seed anisotropy and interseed attenuation for ¹⁰³Pd and ¹²⁵I prostate implants using Monte Carlo (MC) methods for two idealized and two real prostate implants. Absolute total dose differences between full MC simulations and point-source dose-kernel superposition were as high as 7.4% for the idealized model and 6.1% for the clinical model for the ¹⁰³Pd implants and 4.4% for the idealized and 4.6% for the clinical for the ¹²⁵I. Carrier et al.⁵ found deviations of 6.8% for the prostate D₉₀ parameter (dose achieving 90% of the target volume) when comparing a clinical technique to a full MC simulation, of which 4.3% were due to the interseed attenuation and 2.5% to the tissue composition. Hanada et al.⁶ compared the TG-43U1 parameters, Λ and gL(r), using MC simulations, for water and prostate tissue. The comparison of the D₉₀ prostate parameter showed a dose underestimation of 1.7% for the prostate tissue relative to water. CT-based studies comparing homogeneous water phantom with a heterogeneous phantom revealed a dose underestimation of 2.8 Gy in D₉₀⁷ and a decrease of 5.6% in the tissue irradiated volume.⁸

In order to overcome these issues, new model-based dose calculation algorithms (MBDCA) are now available for brachytherapy. These algorithms account for heterogeneity corrections. The recently released AAPM report TG-186³ provides guidance for the use of these algorithms in terms of the dose-specification medium, voxel-by-voxel interaction correction cross sections, and a commissioning process.

2. Aim

The purpose of this work was to understand the importance of these MDCAs in terms of the tissue heterogeneity correction. Dose distributions of LDRBT treatments of prostate cancer with ¹²⁵I permanent implants using Monte Carlo methods were performed in a water medium and in a heterogeneous medium with the density and tissue composition of the prostate and surrounding tissues, and the values compared. For the simulations, we used two anthropomorphic voxel phantoms extracted from the computed tomography (CT) of two patients with prostate cancer. Dose deposition was evaluated on a voxel-by-voxel basis for the prostate and the rectum and compared via dose–volume histograms (DVH), equivalent uniform dose (EUD), tumor control probability (TCP) and normal tissues complication probability (NTCP).

3. Materials and methods

3.1. Monte Carlo dose calculations

The simulations were performed using the MCNPX code version 27a⁹ and the default photon scattering cross section tables from the National Nuclear Data Center's ENDF/B-VI.8 library¹⁰ based on EPDL97.¹¹ CT DICOM images of two patients with prostate cancer were segmented using the ImageJ version 1.44p¹² software and converted into the MCNPX code in order to create two voxel phantoms. A CT of a patient with a small prostate (prostate A: 31 cm³) and a big prostate (prostate B: 109 cm³) were chosen. The size of each voxel is the same as the CT voxel: 0.94 mm × 0.94 mm × 5 mm. To each structure of interest, a given density and elemental composition (Table 1) were assigned. The elemental composition of the skin, bladder, rectum, prostate, spinal cord, bones and muscle, as well as skin density, were taken from the ICRP publication 89.¹³ Elemental compositions of the spinal cord and residual tissue, as well as the respective densities, and muscle and bone densities were taken from the ICRU 44 report.¹⁴ Finally, the densities of the prostate, vesicles, rectum and bladder were determined through the CT electronic densities of 100 patients with prostate cancer. These patients had a median age of 68 years old, median of prostate volume of 58.2 cm³, and a median Gleason score of 7. In order to evaluate the tissue heterogeneity influence in the dose distributions, a comparison was performed by considering all the mentioned structures as pure water in the simulations.

Table 1.

Elemental composition and density assigned to each segmented structure in the voxel phantoms.

Medium/tissue	Elemental composition (% by mass)											Density (g/cm3)
	H	C	N	O	Na	Mg	P	S	Cl	K	Ca
Water2	11.2			88.8								0.9982
Skin13	10.0	20.4	4.2	64.5	0.2		0.1	0.2	0.3	0.1		1.10013
Bladder13	10.5	9.6	2.6	76.1	0.2		0.2	0.2	0.3	0.3		1.014a
Rectum13,b	10.6	11.5	2.2	75.1	0.1		0.1	0.1	0.2	0.1		0.932a
Prostate13	10.5	25.6	2.7	60.2	0.1		0.2	0.3	0.2	0.2		1.027a
Vesicles13,c	10.5	25.6	2.7	60.2	0.1		0.2	0.3	0.2	0.2		0.989a
Spinal cord14,d	10.7	14.5	2.2	71.2	0.2		0.4	0.2	0.3	0.3		1.04014
Bone13,e	3.5	16.0	4.2	44.5	0.3	0.2	9.5	0.3			21.5	1.92014
Muscle13	10.2	14.3	3.4	71.0	0.1		0.2	0.3	0.1	0.4		1.05014
Residual tissue14,f	11.4	59.8	0.7	27.8	0.1		0.1	0.1				0.95014

^aThis study.

^bConsidered alimentary tract stomach and intestine elemental composition.

^cConsidered prostate tissue elemental composition.

^dConsidered brain elemental composition and density.

^eAdult mineral bone.

^fAdipose tissue.

The geometry description in the MC simulations of seeds were based on the Amersham model 6711seed manufactured by General Electric Health Care, taken from Dolan et al.¹⁵ Seeds were placed in a modified peripheral loading, first they were positioned in the periphery of the prostate and then some seeds were added in the central portion to compensate the low absorbed doses in the center. A dose prescription of 145 Gy was considered, with an initial source activity of 0.7 mCi. A total of 93 seeds were used for prostate A and of 204 for prostate B. The MCNPX F6 tally, a track-length estimator, was used to determinate the energy deposition in each voxel in units of MeV g⁻¹ photon⁻¹ after the simulation of 1E8 particles.

3.2. EUD evaluation

Dose distributions were evaluated by isodose visualization, DVH and the AAPM TG-137¹⁶ dose reporting parameters for the prostate (V₁₀₀, V₁₅₀ and D₉₀) and rectum (V₁₀₀ and D_0.1cc). Comparison between heterogeneous and water calculations was also performed via the EUD.

The EUD concept was first developed by Niemierko¹⁷ for External Beam Radiotherapy (EBRT). It provides a method for evaluating non-uniform dose distributions based on models of clonogen survival. The EUD was later generalized for the evaluation of normal tissues.^18,19 It is defined as a radiobiological effective dose that, if delivered uniformly, would result in the same biological effect as a non-uniform dose distribution or, for normal tissues, would lead to the same NTCP. Here, the NTCP is calculated based on the Lyman's model²⁰ along with the method of effective volume by Kutcher and Burman.²¹

Using the differential dose–volume histogram (dDVH) of a given dose distribution, the generalized EUD to compute the rectum EUD is given by:

$$\text{gEUD}={\left(\sum _{i=1}^N{v}_i{D}_i^a\right)}^{1/a}$$ (1)

where N is the number of elements in the dDVH, v_i is the fractional organ volume receiving a dose D_i and a is a tissue-specific parameter that describes the volume effect. The parameter a is negative for tumors and approaches a minimum for a → −∞, and is positive for normal tissues, approaching a maximum dose for a → +∞ (serial organs).

For brachytherapy treatments, dose distributions are highly non-uniform and the mean dose does not reflect the biological effectiveness. As such, changes in dose distributions occurring above or below the mean dose lead to changes in the treatment outcome. Moreover, the brachytherapy treatment is highly influenced by the dose-rate, repair of sublethal damage and clonogen proliferation effects. Wang and Li²² described the EUD as a numerical value for any delivery scheme with respect to that for EBRT delivered in 2 Gy fractions, allowing for the comparison of different radiotherapy modalities, as EBRT and LDRBT. For tumors, EUD that results in the surviving fraction S is calculated by:

$$\text{EUD}=-\frac{\ln (S)}{\alpha +\beta \cdot d-1.4\cdot (\gamma /d)}$$ (2)

where α and β characterize intrinsic radiosensitivity, γ is the effective tumor cell repopulation rate (γ = ln(2)/T_pot); T_pot is the tumor-cell potential doubling time, and d is the dose per fraction (d = 2 Gy).

The LQ formalism and survival for LDRBT treatments have been abundantly discussed.^23–25 The surviving fraction for LDRBT is calculated as follows:

$$S=e^{-(\alpha \cdot D-\beta \cdot G\cdot D^2-\gamma \cdot T_{eff})}$$ (3)

where D is the total dose delivered, G is a protraction factor to account for the repair of sublethal damage, and T_eff is the effective treatment time at which the cell killing rate is too low to compete with cell repopulation.

In order to account for dose distributions heterogeneity, the overall surviving fraction, S, was calculated through the dDVH for each dose distribution^17,22:

$$S=\sum _{i=1}^N{v}_i\cdot S(D_i)$$ (4)

where S is the weighted average of the survival fractions taken over all N near-homogeneously irradiated sub-volumes of the target, and v_i is the fractional dose bin D_i in the dDVH.To compute the tumor control probability (TCP) from S, the Poisson statistics is used:

$$\text{TCP}=e^{-K\cdot S}$$ (5)

where K is the tumor clonogen cell number.

For normal tissues, Luxton et al.²⁶ derived an analytical approximation to the phenomenological LKB model^20,21 in order to calculate the EUD for a given NTCP. The expression to determinate rectum NTCP is as follows:

$$\text{NTCP}=\frac{1}{2}{e}^{k\cdot u-(k^2\cdot u^2/2)}$$ (6)

the parameter k was derived by Luxton et al.²⁶ in order to fit the Lyman equation, and u is a variable from the Lyman model,²⁰ given by:

$$u=\frac{D-T{D}_{50}}{m\cdot T{D}_{50}}\text{,}$$ (7)

where m is a dimensionless ‘scaling’ parameter, and TD₅₀ is the whole organ dose for which NTCP is 50%.

The parameter values used to compute the EUD, TCP and NTCP in this work are shown in Table 2.

Table 2.

Radiobiological parameters values used for the EUD, TCP and NTCP calculation for prostate and rectum.

Parameter	Value
λ (125I)	0.00048 h−1
Prostate
a19	−10
α27	0.15 Gy−1
Tpot 28,29	42 days, 1008 h
μ27	2.6 h−1
α/β30	2.7 Gy
K27	3.0 × 106 cells (intermediate-risk patient group)
k26	0.8154
Rectum
α/β31	5.5 Gy
μ32	0.6 h−1
a33	4.3
m33	0.19
TD50 33	81.9 Gy

4. Results

4.1. Dose–volume histograms (DVH) results

The DVHs obtained when comparing the results in the heterogeneous phantom (HT) and in water (W) in the two considered prostates are shown in Figs. 1–4. For prostate A, the results are shown in Fig. 1 for the prostate target volume and Fig. 2 for the rectum A as an organ at risk (OAR). For prostate B, Fig. 3 shows the prostate DVHs and Fig. 4, the rectum B. Maximum statistical errors were under 1% for prostates A and B, and around 7% for rectum A and 5% for rectum B. Statistical errors for the rectum are higher due to the lower doses (less particles) traversing this structure.

Fig. 1.

DVH obtained for the prostate A with the Monte Carlo simulation of 1E8 particles. Straight line: calculations in the heterogeneous phantom (HT); dashed line: calculations in water (W).

Fig. 2.

DVH obtained for the rectum A with the Monte Carlo simulation of 1E8 particles. Straight line: calculations in the heterogeneous phantom (HT); dashed line: calculations in water (W).

Fig. 3.

DVH obtained for the prostate B with the Monte Carlo simulation of 1E8 particles. Straight line: calculations in the heterogeneous phantom (HT); dashed line: calculations in water (W).

Fig. 4.

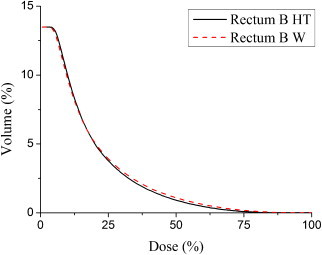
DVH obtained for the rectum B with the Monte Carlo simulation of 1E8 particles. Straight line: calculations in the heterogeneous phantom (HT); dashed line: calculations in water (W).

The results show that in the calculations where tissue heterogeneities are not taken into account, the absorbed dose is overestimated. A mean absorbed dose overestimation of 3.96% was obtained for prostate A and of 3.30% for prostate B. For the rectum, the same differences in the mean absorbed dose were of 4.86% for rectum A and of 2.28% for rectum B. Clinical endpoints regarding the AAPM TG-137¹⁶ dose reporting parameters, both for the prostate and the rectum, obtained with the simulations, are shown in Tables 3 and 4.

Table 3.

AAPM TG-137¹⁶ dose reporting parameters obtained for the prostates A and B with the simulations in the heterogeneous phantom (HT) and in water (W).

Dose parameter endpoint	Prostate A		Prostate B
	W	HT	W	HT
V100 > 95%	97%	97%	97%	97%
V150 ≤ 50%	46%	37%	44%	36%
D90 > 90 Gy	186 Gy	179 Gy	184 Gy	179 Gy

Table 4.

AAPM TG-137¹⁶ dose reporting parameters obtained for the rectums A and B with the simulations in the heterogeneous phantom (HT) and in water (W).

Dose parameter endpoint	Rectum A		Rectum B
	W	HT	W	HT
V100 < 2 cc	0.06 cc	0.00 cc	0.00 cc	0.00 cc
D0.1 < 150%	101%	93%	92%	86%

Regarding the prostate results, the D₉₀ parameter overestimation was of 3.91% for prostate A and of 2.79% for prostate B, when comparing the heterogeneous (HT) and water (W) results. Concerning the rectum D_0.1 parameter, a dose difference of 8% was found in rectum A and of 6% in rectum B.

4.2. Equivalent uniform dose (EUD) results

The overestimation of the clinical dose parameters in the calculations in water relative to the heterogeneous medium is reflected in the EUD determined through the DVHs shown in Figs. 1–4 and Eq. (1) for the rectum and Eqs. (2)–(4) for the prostate. Results for the EUD, TCP and NTCP are shown in Tables 5 and 6 for the prostate and rectum, respectively.

Table 5.

EUD and TCP obtained for prostates A and B with the simulations in the heterogeneous phantom (HT) and in water (W).

	Prostate A		Prostate B
	W	HT	W	HT
EUD (Gy)	88	85	84	81
TCP (%)	100.0	99.9	99.9	99.8

Table 6.

EUD and NTCP obtained for rectums A and B with the simulations in the heterogeneous phantom (HT) and in water (W).

	Rectum A		Rectum B
	W	HT	W	HT
EUD (Gy)	28	26	26	24
NTCP (%)	0.06	0.04	0.04	0.03

Comparing the results obtained in water and in the heterogeneous phantom, an equivalent dose overestimation of 3.53% was obtained for prostate A and of 3.70% for prostate B. These EUD values are reflected in a difference of 1% in the TCP. For rectal lower doses, differences are more significant, with the equivalent dose overestimated by 7.69% in rectum A and by 8.33% in rectum B. NTCP are very low for the rectum structure and a difference of 0.02% was obtained for rectum A and of 0.01% for rectum B.

5. Discussion

For LDRBT, the photoelectric effect plays a significant role, as the dose distributions are highly dependent on the atomic number of the irradiated tissue. Regarding, as an example, the prostate D₉₀ parameter, a dose overestimation between 2.8 and 3.9% was found, when comparing with the results in water.

Landry et al.³⁴ obtained an overestimation of 2.0% in D₉₀ when comparing the dose transported in a prostate tissue with elemental composition equivalent to ours but scored in water with simulations in water. Chibani et al.⁴ found a dose overestimation of 2.5% for the effects of anisotropy and interseed attenuation for the same D₉₀ parameter comparing a full MC simulation with a line-source kernel superposition method for the ¹²⁵I sources. Considering these two effects, a water-based calculation with the dose deposition described around a single source can lead to a dose overestimation above 6% for D₉₀. On the other hand, Carrier et al.⁵ when taking into account both tissue heterogeneity and interseed attenuation found a dose overestimation of 7.0% for D₉₀, when comparing a clinical technique with a MC simulation.

In addition to the tissue heterogeneity and interseed attenuation effects, there are other sources of uncertainty related to a water dose deposition formalism. For example, prostatic calcifications are present to some degree in many cases and tend to increase with advancing age.³⁵ The calcium content, due to its high cross section, increases the absorption of the ¹²⁵I X-rays. Meigooni et al.³⁶ had shown that changing the calcium content from 1.7% to 2.3% in a solid water phantom will change the conversion factors of a water equivalent material to water for ¹²⁵I sources up to 5%.

This study showed that taking into account the tissue heterogeneity instead of considering the whole body as pure water may change the dose deposition recorded in the LDRBT treatments with ¹²⁵I sources. All together, the combination of the tissue composition with other factors as the interseed attenuation and presence of calcification in the prostate may considerably change the clinical dosimetry parameters. It is proven, for example, that the D₉₀ correlates with the clinical outcome, and it is specially sensitive if it is near 140 Gy.³⁷ The implementation of the MBDCA in the clinical dosimetry of the LDRBT will allow to overcome most of these uncertainties, enabling greater accuracy in its dose recording. However, the recommendation of the AAPM report TG-186,³ should be carefully followed and changes in dose prescription would require more clinical trials.

6. Conclusions

MC simulations were performed in voxelized pelvic phantoms based on the TC pelvic DICOM images of two patients with prostate cancer. A specific elemental composition and density were assigned to each different structure in order to create anthropomorphic phantoms. Simulations in these phantoms were compared to simulations considering a simple water phantom with the same body contour to estimate differences in dose distributions due to the tissue heterogeneity effect. Considering either a physical DVH analysis or a biological EUD evaluation, simulations in water overestimate the actual absorbed dose distributions. Mean adsorbed dose overestimations between 3.3 and 4.0% were found for the prostate and between 2.3 and 4.9% for the rectum. Regarding the EUD evaluation, an overestimation between 3.5 and 3.7% for the prostate and between 7.7 and 8.3% for the rectum was obtained. It is expected that the new MBDCAs that are being introduced in the LDRBT PS could reduce these deviations allowing for more precise dose distribution evaluations in patients with prostate cancer.

Conflict of interest

None declared.

Financial disclosure

None declared.