NoFold: RNA structure clustering without folding or alignment

Abstract

Structures that recur across multiple different transcripts, called structure motifs, often perform a similar function—for example, recruiting a specific RNA-binding protein that then regulates translation, splicing, or subcellular localization. Identifying common motifs between coregulated transcripts may therefore yield significant insight into their binding partners and mechanism of regulation. However, as most methods for clustering structures are based on folding individual sequences or doing many pairwise alignments, this results in a tradeoff between speed and accuracy that can be problematic for large-scale data sets. Here we describe a novel method for comparing and characterizing RNA secondary structures that does not require folding or pairwise alignment of the input sequences. Our method uses the idea of constructing a distance function between two objects by their respective distances to a collection of empirical examples or models, which in our case consists of 1973 Rfam family covariance models. Using this as a basis for measuring structural similarity, we developed a clustering pipeline called NoFold to automatically identify and annotate structure motifs within large sequence data sets. We demonstrate that NoFold can simultaneously identify multiple structure motifs with an average sensitivity of 0.80 and precision of 0.98 and generally exceeds the performance of existing methods. We also perform a cross-validation analysis of the entire set of Rfam families, achieving an average sensitivity of 0.57. We apply NoFold to identify motifs enriched in dendritically localized transcripts and report 213 enriched motifs, including both known and novel structures.

INTRODUCTION

RNA structures play an important role in the function and regulation of almost all known classes of RNA. In coding transcripts, conserved secondary structures have been found in the untranslated regions (UTRs) that operate in cis to regulate processes such as alternative splicing, translation, and subcellular localization (for review, see Wan et al. 2011). Several of these cis-structures have been found to be motifs—modular elements that occur across multiple different transcripts and provide a similar function or regulatory signal. Examples include the selenocysteine insertion sequence (Walczak et al. 1996), the iron response element (Casey et al. 1988), and some localization signals (Martin and Ephrussi 2009). Structure motifs also play a well-documented role in noncoding RNA function, such as the cloverleaf structure of tRNAs and the long hairpin structure of premicroRNAs. The Rfam database (Burge et al. 2012) has organized many of these known motifs into structure “families” and provides a covariance model (CM) (Eddy and Durbin 1994) for each family, which can be used to quickly scan new sequences to infer instances of known motifs. However, the identification of novel motifs that are not already modeled by Rfam remains a challenging problem.

Existing algorithms for finding novel secondary structure motifs differ widely in their approaches, but almost all begin with some form of structure prediction. Structure prediction can be done for single sequences individually by maximizing thermodynamic stability, as in MFOLD (Zuker 1989, 2003) and RNAfold (Hofacker et al. 1994; Hofacker 2003), or can be done using covariance information of stem nucleotide pairs from a multiple alignment. Although alignment-based methods generally result in more reliable predictions than thermodynamic stability alone, building a multiple alignment of RNAs can be difficult when the primary sequences are highly diverged. For most traditional sequence aligners, performance drops off dramatically when aligning families with <60% sequence identity (Gardner et al. 2005). Given that many highly conserved structure families have an average sequence identity lower than this threshold (e.g., the tRNA family with 46% sequence identity), such aligners are often not sufficient for identifying RNA structure families. To address this issue, methods such as FoldalignM (Torarinsson et al. 2007), Dynalign (Mathews and Turner 2002), and LocARNA (Will et al. 2007) attempt to align RNAs by both sequence and structure simultaneously, using approximations of the Sankoff align-and-fold algorithm (Sankoff 1985). Although these methods generally perform better than traditional aligners on structural RNAs, they are computationally intensive and require time-saving heuristics when used to align a large number of sequences.

In order to identify structures that occur multiple times in a given data set, an additional step of clustering is needed. The choice of distance metric and clustering algorithm depend largely on the method used for structure prediction. Individually predicted structures can be compared by computing a distance metric over the base-pair probability matrices (Ding et al. 2005; Liu et al. 2008) or the dot-bracket structure representations (Moulton et al. 2000). A popular approach is to first reduce each individual structure to a tree representation, where stems and loops are reduced to a graph-theoretic representation, before computing a tree alignment or edit-distance (Hofacker 2003; Höchsmann et al. 2004; Liu et al. 2005; Steffen et al. 2006; Yao et al. 2006). A recent algorithm in this vein is GraphClust (Heyne et al. 2012), which uses the RNAshapes software (Steffen et al. 2006) to sample several low-energy structures that are then encoded as graphs and compared using a graph kernel. Alternatively, instead of predicting each individual structure and then comparing pairs of structures, the structural similarity between two RNAs can be derived directly from their pairwise alignment using an align-and-fold algorithm. This is the strategy used by RNAclust (Will et al. 2007) and FoldalignM. Once a distance matrix has been created for the sequences of interest, common clustering methods can be used to identify recurring structures. However, as these algorithms all use as their basis some form of folding or pairwise sequence alignment, they are limited by the tradeoff between speed and accuracy.

Here we describe a novel approach to RNA structure clustering which does not require folding or pairwise alignment of the input sequences. Our approach is inspired by the idea of an “empirical kernel,” where the distance between any two objects is computed within an observation-spanned subspace by comparing each object to a set of empirical examples or models (Scholkopf and Mika 1999). Using Rfam CMs as our empirical models, we thus measure the structural distance between two RNA sequences based on their respective scores against each CM. In this way, we represent each input sequence as a superposition of known structures. Part of the motivation for this approach comes from known examples of such superposition in nature, such as the presence of tRNA-like motifs in transfer-messenger RNA (tmRNA) (Moore and Sauer 2007) and in some internal ribosome entry sites (Jan et al. 2003). However, as we will show here, this approach can identify motifs even in the absence of trivial similarity between the motif and the reference models. Using this folding- and alignment-free distance measure as a basis, we developed a pipeline called NoFold for clustering and automatically extracting cohesive clusters, which can be used to find structure motifs in any set of RNA sequences. In a benchmark containing 20 Rfam structure families, we demonstrate that NoFold can simultaneously recapitulate almost all of the families with high sensitivity and precision and that this performance is robust to the presence of unrelated sequences within the data set or extraneous flanking sequence on the structural sequences. Using NoFold, we identify 213 motifs that are enriched in the 3′ UTRs and retained introns of dendritically localized transcripts, including a previously identified localization-mediating motif and several potentially novel structures with similarity to the Drosophila K10 localization element.

RESULTS

Construction and normalization of the structural feature space

Our approach is akin to measuring the distance between two locations not by direct measurement but by using their respective distance to a set of landmarks. For example, the distance between two street corners A and B might be measured by measuring the distance between A and three tall buildings, X, Y, and Z and also measuring the distance between B and the same X, Y, and Z buildings. The accuracy of such triangulation will depend on the relative location and the number of such landmark buildings. The advantage is that we do not have to make direct measurements between A and B, which might be difficult (e.g., because the streets are blocked).

Here, we used Rfam CMs as our landmarks to triangulate RNAs of unknown secondary structure, which enabled us to identify groups of similarly structured RNAs (motifs) without explicitly predicting the structures of those RNAs. CMs are a form of stochastic context-free grammar used by the Rfam database to model the consensus sequence and secondary structure of RNA structure families (Eddy and Durbin 1994; Burge et al. 2012). We used all 1973 CMs in Rfam v.10.1 to create an empirical feature space for triangulation and clustering of RNAs. The raw feature space consisted of 1973 dimensions, each corresponding to one CM. The coordinates of an arbitrary RNA sequence within this space was determined by scoring it against each CM using the cmscore module of Infernal (v.1.0.2) (Nawrocki et al. 2009) and using the resulting bitscores as the coordinates along each axis. These bitscores indicate how well a sequence matches each CM, taking into account compensatory base changes that maintain conserved pairing interactions. Thus, the feature space can map RNA sequences according to their similarity to known structures. We note that although scoring an RNA sequence against a CM can be considered a form of alignment, there was distinctly no pairwise sequence alignment of the RNA sequences to each other during this stage of the algorithm. Therefore, in contrast to existing alignment-based clustering algorithms, our algorithm had linear growth in the number of “alignments” with increasing data set size, rather than quadratic growth. Although the subsequent clustering step in our method was quadratic (Müllner 2011), in practice this part of the process was much faster than in alignment-based algorithms because only a simple distance measure needed to be calculated for each comparison, rather than an alignment (that will typically add another quadratic factor in terms of sequence length).

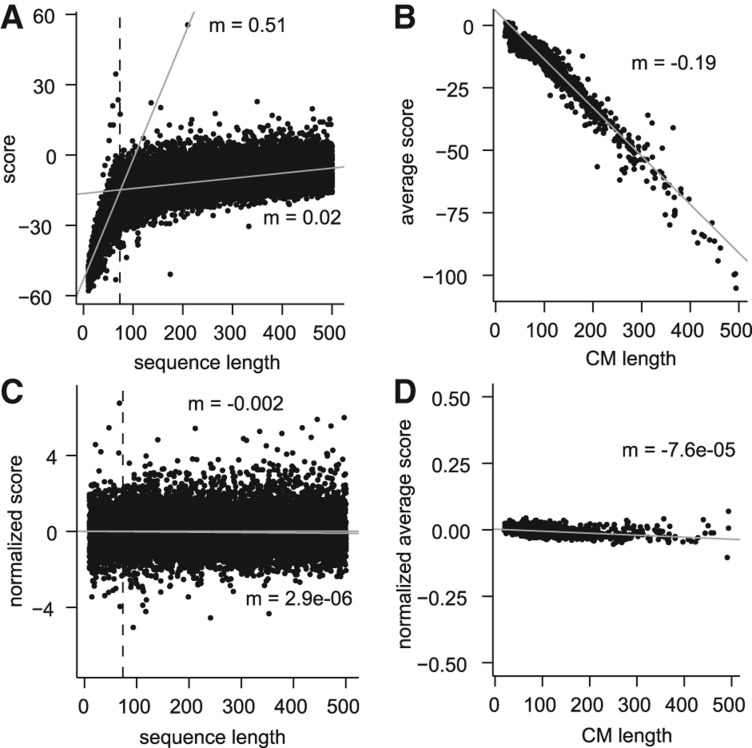
Initial analysis of the raw feature space using randomly selected transcript sequences revealed a relationship between the length of an RNA sequence and the score it received against a CM (Fig. 1A). For a given CM, this relationship was strongest for sequences that were shorter than the length of the CM itself and indicated that shorter sequences were being penalized in a manner proportional to their deficiency in length. We also observed that larger CMs tended to produce lower scores on average, even when only considering sequences longer than the length of the CM (Fig. 1B). To normalize for these two length effects, we separately estimated the mean and standard deviation of scores for each combination of sequence length (between 10 and 500 nt) and CM, and used these parameters to produce Z-standardized scores (Z-scores) according to the length of the original sequence and the particular CM. Specifically, the Z-score Z for a sequence of length l against CM c is calculated as Z = (x − µ_lc)/σ_lc, where x is the raw score and µ_lc and σ_lc are the mean and standard deviation, respectively, of the scores of sequences of length l against CM c. We applied this normalization to an independent data set and found that this procedure greatly reduced the relationship between sequence length and score (Fig. 1C) and zero-centered the range of scores produced by each CM (Fig. 1D).

FIGURE 1.

Normalization of the empirical feature space. Examples of CM score characteristics before (A,B) and after (C,D) normalization, for sequences and CMs of length ≤500 nt. (A) A representative example of the scores given to sequences of various lengths against a single CM, in this case tRNA. We consistently observe a relationship between sequence length and score that is most pronounced for sequences that are smaller than the size of the CM (73 nt in this case, indicated by the dashed line). Gray lines show separate linear regression fits to the scores of sequences shorter or longer than 73 nt, with slopes (m) indicated. (B) We additionally observed a relationship between the length of a CM and the average score that it produces. Average score was calculated based only on sequences with a length longer than the CM. (C) The length- and CM-specific procedure to calculate Z-scores greatly reduced the relationship between sequence length and score on an independent data set. Linear regression fit lines and slopes are indicated as in A. (D) Using Z-scores greatly reduced the relationship between CM length and the average score produced by the CM, and the average score for all CMs was close to zero.

Although Rfam CMs model a wide variety of structures, there are several subgroups of CMs that are structurally related (e.g., microRNAs) that may therefore produce very similar scores for a given RNA sequence even if the sequence does not belong to the CM model families. In agreement with this, we observed correlation in the scores produced by several groups of CMs; for example, mir-70 (RF00833) and mir-355 (RF00797) had a Spearman correlation of 0.72 in their scores against random sequences. These kinds of correlation over random sequences imply structural correlation of the models rather than biological correlation of the sequences and as such the model correlations are likely to distort the biological information from the ensemble of the CMs. To reduce our feature space to a set of independent axes, we first assessed the structural correlation of the CM models by measuring their length-normalized scores (Z-scores) over a randomly sampled set of 24,550 subsequences from the mouse and human transcriptome (see “Normalization of feature space” in Materials and Methods). We then performed principle components analysis (PCA) on the Z-scores, which resulted in an orthogonal set of axes (i.e., uncorrelated) ordered by the total variance explained by each coordinate. We selected the first 100 principle component axes as representing informative variation (see “Normalization of feature space” in Materials and Methods) and used the loadings of these axes directions to construct our final feature space for subsequent measurements. Another view is to think of the loadings as a set of weights on the CM Z-scores that results in a 100-dimensional RNA structure feature space. We refer to this space here as the RNA Empirical Structure Space (RESS). Each RESS coordinate is a weighted linear combination of the CM Z-scores; therefore, the RESS feature scores of a given sequence can be back transformed into individual CM Z-scores and analyzed in terms of Rfam models as demonstrated later in Results. The contributions of each CM to each RESS axis, as well as the correlations of each axis with GC content, CM length, and number of hairpins, are available on our supplementary website (kim.bio.upenn.edu/software/nofold.shtml).

Suitability of the RESS for structure similarity analysis

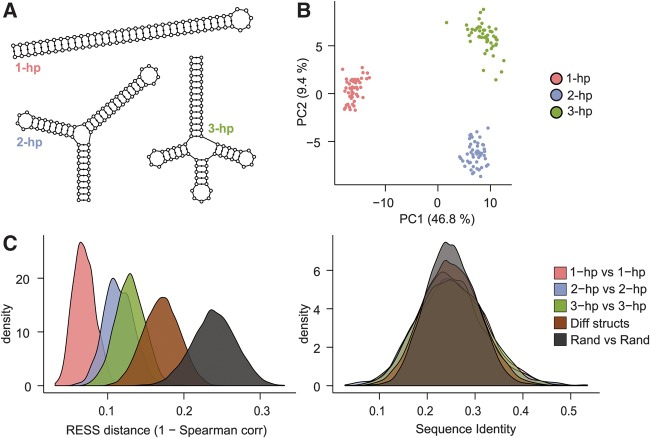
We first asked whether structurally similar sequences become grouped together when mapped to the RESS. As an initial test, we created three synthetic structures of the same length but with different numbers of hairpins (Fig. 2A) and generated sequences that had the appropriate base complementarity to form each of these structures. These sequences were generated randomly (but respecting pairing constraints; see “Synthetic structures” in Materials and Methods) to ensure that the members of each structure group were not trivially similar on the primary sequence level. We created 50 sequences for each structure and verified that, as expected, the sequences appeared random on the primary sequence level (25% average pairwise sequence identity). We scored the sequences against the Rfam CMs and projected them into the RESS. As an initial assessment of the relative positioning of the sequences within the RESS, we visualized the sequences using PCA ordination of the 100-dimensional RESS coordinates (Fig. 2B). The different structural sequences formed three well-separated clusters along the first and second PC axes, indicating that the RESS mapped the sequences with similar structure closer together than sequences of different structure.

FIGURE 2.

Structurally similar sequences are clustered together in the RESS. (A) Three synthetic structures designed for this analysis. (B) PCA of the structure sequences after projection to the RESS separates the sequences based on structure. (C) Distributions of the distances between pairs of related structure (“1-hp versus 1-hp,” “2-hp versus 2-hp,” and “3-hp versus 3-hp”), pairs of different structure (“Diff structs”), and pairs of random sequences (“Rand versus Rand”). Distance between pairs was calculated by Spearman distance (left panel) or sequence identity (right panel). Related structure pairs were closer, on average, than different or random pairs in the RESS.

We next sought to define a distance measure that could be used within the RESS to identify structurally related sequences. An appropriate distance measure should assign a small distance between pairs of related structures and a larger distance between pairs of unrelated structure. To test this, we used our data set of synthetic structure sequences to calculate distance measures on (1) pairs of sequences with the same structure, (2) pairs with different structure, and (3) pairs of completely random sequence. We found that Spearman distance (defined as one minus the Spearman correlation across RESS coordinates) worked well to distinguish the pairs of related structure from other types of pairs, and was a marked improvement over sequence identity alone (Fig. 2C) or Euclidean distance (see supplementary website). We therefore used this measure as the basis for identifying similar structures and clustering.

Automated structural clustering for motif identification

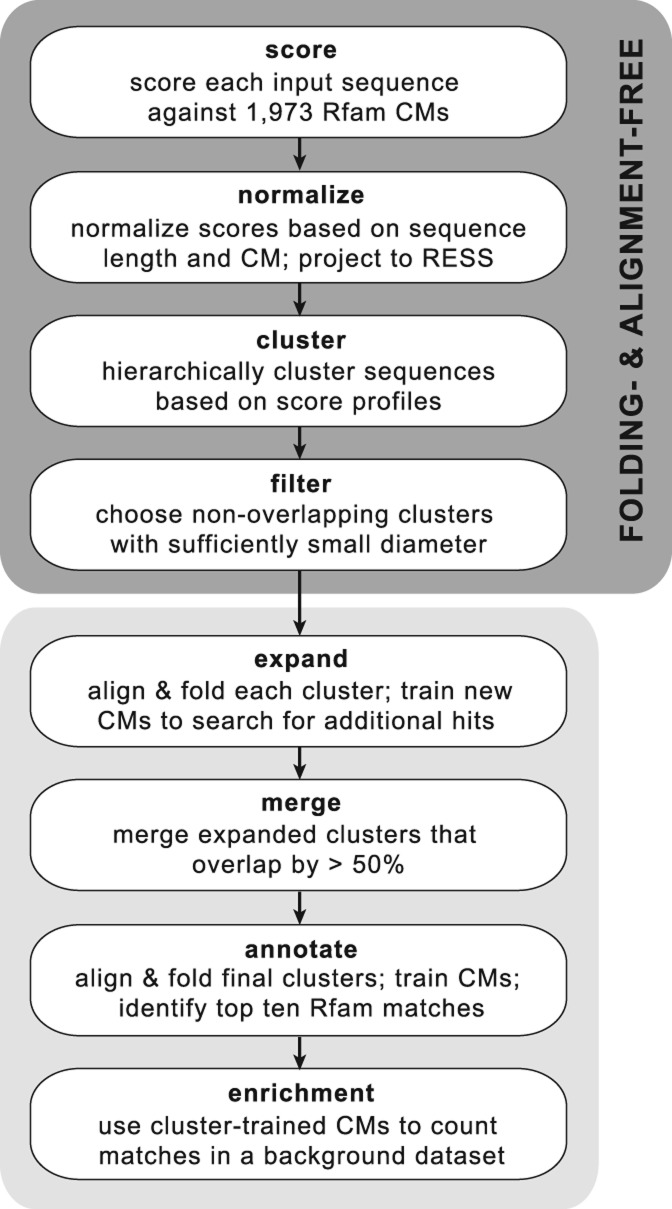
Toward the goal of identifying secondary structure motifs in large sequence data sets, we developed a pipeline for clustering sequences within the RESS and automatically extracting clusters with a sufficiently small diameter (calculated as the average pairwise Spearman distance among the cluster members). We call this pipeline “NoFold” to highlight the fact that it does not use folding or alignment in the initial steps of sequence comparison and clustering. The overall steps of the pipeline are illustrated in Figure 3 and explained in detail in the Materials and Methods. Briefly, input sequences were scored against the 1973 Rfam CMs, normalized and mapped to the RESS, and clustered by average-linkage hierarchical clustering using Spearman distance as the distance measure. The resulting hierarchical tree was cut into all possible clusters with three or more members, and all nonoverlapping clusters with a diameter below a certain threshold were extracted. The threshold was designed to control the false positive rate (FPR) and was derived from the distribution of cluster diameters that we observed when clustering randomly generated sequences. The threshold was set such that only ∼5% of nonstructural clusters will have a small enough diameter to pass this filter. To improve the sensitivity of the method, we aligned and folded the sequences within each passing cluster using LocARNA and used this to train a new CM for each cluster (“cluster-CMs”). We then used each cluster-CM to search the original sequence data set for additional instances of the modeled structure, similar to what has been done in GraphClust (Heyne et al. 2012) and CMfinder (Yao et al. 2006). When searching the data set, sequences were allowed to match to multiple cluster-CMs, which can occasionally lead to substantial overlap between the final clusters. We therefore merged any clusters that overlapped by >50% of their members.

FIGURE 3.

Outline of the NoFold approach for identification of structure motifs in unaligned RNA sequence data sets. The method does not require structure prediction or pairwise alignment of the input sequences for clustering, in contrast to existing methods.

To test the ability of NoFold to identify multiple structure motifs simultaneously, we created a data set consisting of sequences from the seed alignments of 20 Rfam structure families that varied widely in size and structure (Table 1). The sequences of each family were filtered such that no pair of sequences shared >75% sequence identity (after alignment), which resulted in an average sequence identity of 32%–54% per family and a total of 978 sequences. We used this data set to test NoFold under three conditions: (1) a basic test using the exact sequences reported by Rfam (“plain sequences”), (2) a test where 10–50 nt of random sequence was added to both ends of every sequence (“embedded sequences”), and (3) a repeat of the first test but with the addition of 3000 random, unrelated sequences matched to the dinucleotide frequency and length distribution of the Rfam sequences (“plain sequences with background”). These last two tests were designed to emulate common, yet challenging situations in RNA structure analysis where the exact boundaries of the RNA structures are not known (test 2) or a large proportion of the sequences in the data set do not contain an instance of a motif (test 3).

TABLE 1.

Clustering sensitivity of NoFold and GraphClust for three test conditions on the Rfam benchmark data set

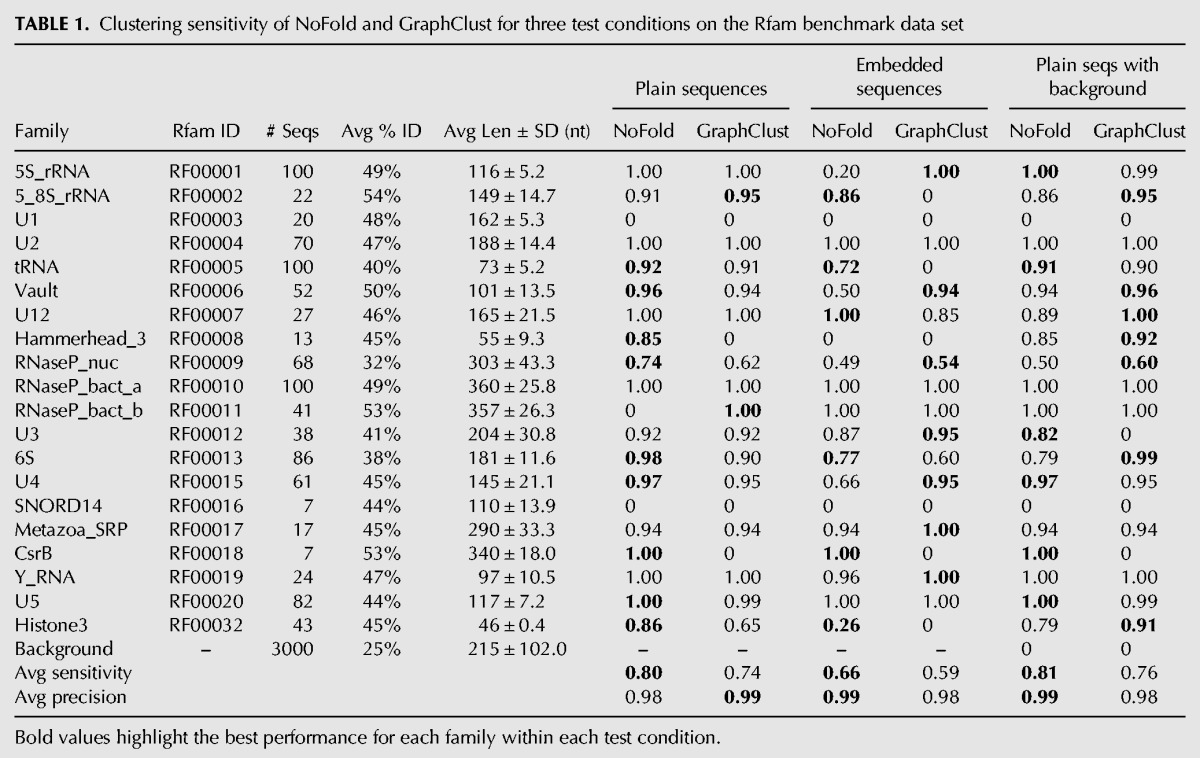
We note that because the Rfam families used in these test data sets are also represented directly by CMs that form the basis of the RESS, this potentially makes clustering of these sequences easier for NoFold. To reduce this effect, we removed from the feature space the test family CMs and any CMs that appeared to be very similar to one of the test families. We did this by examining the Z-scores (before projection into the RESS) of each test family against all CMs and removing CMs with an average Z-score >3 for any family. As the parameters used to calculate Z-scores are derived from a large sample of transcript sequences, a high Z-score for a given CM indicates that a sequence is more similar to that CM than what is typically observed. This procedure resulted in the removal of 44 CMs (see “Rfam benchmark tests” in Materials and Methods for full list). We verified through linear discriminant analysis that the top discriminating CMs for this data set were not related to the data set families after this removal process. All Rfam tests were carried out using this modified feature space.

We compared the performance of NoFold with GraphClust on the three test sets described previously (Table 1). Default parameters were used for both methods, with the exception that sliding window generation was turned off for GraphClust so that full-length structures would be clustered (we note that this may negatively affect the performance of GraphClust). We measured performance based on how well each family was reconstructed in the final set of clusters. In this context, we defined family “sensitivity” as the fraction of sequences from that family that were present in any cluster dominated by that family, and family “precision” as the fraction of sequences in clusters dominated by that family that actually belonged to that family. Both NoFold and GraphClust performed very well, but NoFold consistently detected more of the families and had a higher average sensitivity than GraphClust in all three tests. NoFold also had a slightly higher proportion of families that were detected in a single cluster rather than being split into multiple separate clusters (Fig. 4). Family sensitivity was not significantly correlated with the standard deviation of family sequence length (NoFold: r = −0.005, P = 0.98; GraphClust: r = 0.18, P = 0.45), indicating that the good clustering performance was not simply due to length similarity within families. Notably, both methods had very high precision (0.98–0.99) across all tests and did not return any clusters dominated by background sequences in the third test, indicating that these methods can appropriately distinguish between clusters of related and unrelated structure. The test set where sequences were embedded in random flanking sequence proved to be the most difficult, resulting in an average sensitivity drop of ∼0.15 for both methods. The performance drop for each family was significantly correlated with the length of the sequences in the family (Spearman correlation −0.53, P < 2.2 × 10⁻¹⁶), indicating that detection of smaller structures was impacted the most. We note that although some of the test families were related to each other (e.g., RF00009, RF00010, and RF00011), both NoFold and GraphClust were generally able to separate these families into separate clusters. Overall, these results demonstrate that NoFold can simultaneously detect multiple structural motifs of different sizes with very high sensitivity and precision and is comparable to or exceeds the performance of the current state-of-the-art software.

FIGURE 4.

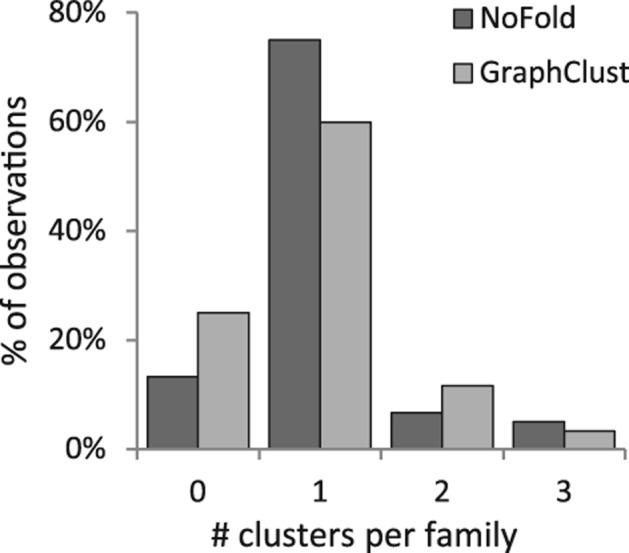
Distribution of the number of separate clusters assigned to each Rfam family for a given test. Clusters were assigned to a family only if it was the dominant family within that cluster. The observations for all 20 families across all three tests are displayed. Most families were assigned to only one cluster per test, and the maximum number of clusters per family in any test was three.

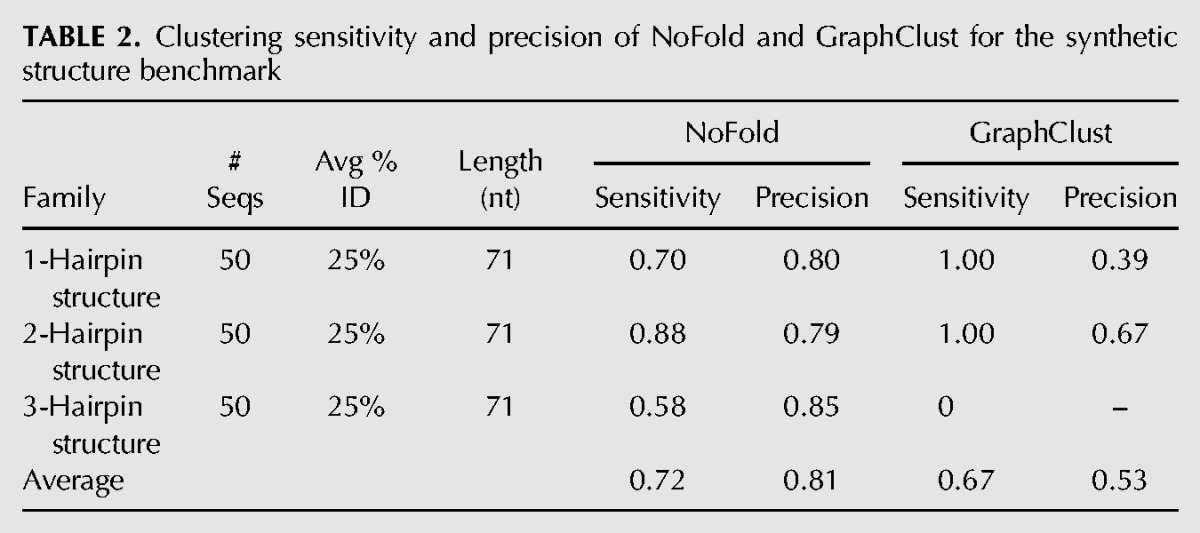
To verify that NoFold can perform well on structures that bear absolutely no evolutionary homology with CMs in the feature space, we additionally performed clustering on the sequences derived from the three synthetic structures described in the previous section. The results of this test for NoFold and GraphClust are summarized in Table 2. GraphClust detected all members of the 1-hairpin and 2-hairpin families, but did not detect the 3-hairpin structure. In contrast, NoFold detected all three structures with reasonable sensitivity. Most notably, the average precision of the NoFold clusters was much higher than the GraphClust clusters (0.81 versus 0.53, respectively), suggesting that the use of information from Rfam CMs by NoFold improved clustering even though the synthetic structures were not members of any Rfam family. Upon individual inspection of the clusters, we found that the GraphClust clusters each contained a substantial mix of all three structures, with a high degree of overlap between each cluster. For example, the largest cluster contained all 50 of the 1-hairpin sequences, but also contained 38 of the 2-hairpin sequences and 18 of the 3-hairpin sequences. The NoFold clusters, in contrast, were generally much more specific to a single family, as is reflected in its higher precision. Although it is possible that fine-tuning some of the GraphClust parameters (such as the number of clustering iterations) may improve its performance in these tests, these results are meant to represent the “out-of-the-box” performance of each method. Altogether, these results demonstrate that NoFold can reliably detect structure motifs in the complete absence of sequence conservation or homology with the feature space.

TABLE 2.

Clustering sensitivity and precision of NoFold and GraphClust for the synthetic structure benchmark

Finally, we performed clustering on the entire Rfam database using a setup similar to a cross-validation analysis. Specifically, we grouped all 1973 Rfam families into 10 subsets such that similar families were put into the same subset. This grouping was done by hierarchically clustering the CMs based on their scores against random sequences and then cutting the dendrogram to create exactly 10 clusters. The CMs in each cluster then determined which families were grouped together for the analysis (see “Rfam benchmark tests” in Materials and Methods). For each subset, we extracted up to 15 sequences per family such that no pairwise sequence identity exceeded 75%. We removed any families with <3 sequences, resulting in a total of 937 families (6085 sequences) included across all subsets. We ran each subset separately through NoFold, removing any CMs from the feature space that had an average Z-score >3 for any family, as described previously. GraphClust was run for 25 iterations (10 clusters/iteration) on each subset. The average family sensitivity across the 10 subsets was 0.57 for NoFold and 0.55 for GraphClust (0.51 and 0.55, respectively, when averaging directly across the families rather than the subsets). The lower sensitivity of both methods in this test reflects the inherent difficulty of this test compared with the 20-family test, as it requires the methods to separate many more families simultaneously, and each subset may contain several related families with similar structure. In addition, the performance of NoFold was likely impacted by the need to remove large portions of the feature space for each subset. The specificity of both methods remained high at 0.99. Full results of this analysis are available on our supplementary website.

Application of NoFold to novel motif discovery

An important process in neurons is the localization of specific transcripts to the dendrites, which allows for local translation and spatially restricted synaptic remodeling (Job and Eberwine 2001; Sutton and Schuman 2006; Bramham and Wells 2007). Targeting of transcripts to the dendrites is thought to be mediated primarily by RNA-binding proteins, which recognize cis-elements on the transcripts called dendritic targeting elements (DTEs). Under the assumption that some DTEs may be motifs that appear across multiple different transcripts, it should be possible to identify these motifs computationally. However, despite much work over the last 25 yr to pinpoint such motifs, only a few have so far been found (Eberwine et al. 2002; Holt and Schuman 2013). Given that almost all previous searches for DTEs have focused on primary sequence motifs, we asked whether it might instead be secondary structures that provide the common recognition element between transcripts. We decided to apply NoFold to a data set of known dendritically localized transcripts from rat to see if we could identify any structural motifs enriched in these sequences, which might explain their localization.

To aid in the functional interpretation of novel motifs, we added several types of automatic annotations to NoFold. First, as we had already scored each sequence against all Rfam CMs in the first step of NoFold, we made use of this rich source of information in order to annotate each cluster with the Rfam families it most resembles. To do this, we calculated the average Z-score of the sequences in the novel cluster for each CM and reported the 10 CMs with the highest average Z-score. As mentioned previously, the parameters for calculating the Z-scores were derived from an independent sampling of transcript sequences, so a high Z-score (>3) for a CM indicates that a sequence scored unusually well against that CM compared with the general transcriptome. Averaging Z-scores across a whole cluster tends to highlight the CMs that scored highly for multiple sequences in the cluster, suggesting a structural resemblance to the family modeled by these CMs. Although a high Z-score does not necessarily indicate functional homology, we have found it to be a useful first-pass annotation to guide deeper analysis. For additional annotation, we also created a multiple alignment and predicted a consensus structure for each final cluster using LocARNA. Using this alignment, we ran RNAz (Washietl et al. 2005) with default parameters to obtain several statistics such as the structure conservation index (SCI). We note, however, that these statistics should be interpreted with caution because RNAz was trained on different window sizes and different types of alignments. Finally, we automatically trained a new CM for each final cluster which can be used in the future to search additional databases for instances of the motifs.

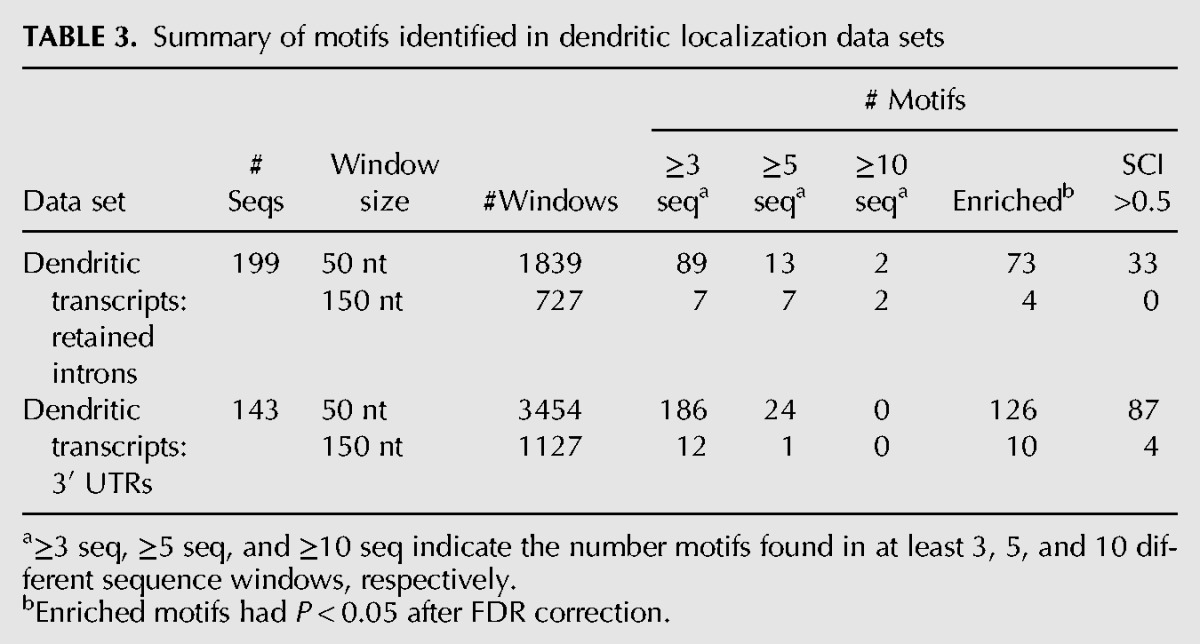
As a first step toward identifying structural DTEs, we compiled a list of 211 transcripts with experimental evidence for dendritic localization in rat neurons. From each transcript, we obtained from RefSeq (rn4) the 3′ UTR sequence as well as the sequence of any cytoplasmically retained introns (Khaladkar et al. 2013), which have previously been shown to harbor DTEs (Buckley et al. 2011). To focus our search on smaller structure elements, we used a sliding window approach to split each 3′ UTR and intron sequence into several smaller segments. We have validated that the use of a sliding window still allows for good sensitivity of motif detection (see supplementary website). We created 50- and 150-nt sliding window sets for the retained intron and 3′ UTR sequences of the dendritically localized transcripts and searched these regions for motifs using NoFold (Table 3). NoFold identified a total of 290 clusters (“motifs”) that contained three or more sequences. To test whether these motifs were enriched within dendritic transcripts, we created a background data sets consisting of introns or 3′ UTRs (RefSeq, rn4) from nondendritically localized transcripts and scanned this set for matches to the NoFold motifs (see “Dendritic localization data set” in Materials and Methods). This was done using the cluster-CM for each motif in conjunction with the cmsearch program (Nawrocki et al. 2009). We compared the number of motif matches between the dendritic sequences and nondendritic sequences and found a total of 213 of the motifs were significantly enriched in the dendritic transcripts (Fisher's exact test, FDR-adjusted P < 0.05).

TABLE 3.

Summary of motifs identified in dendritic localization data sets

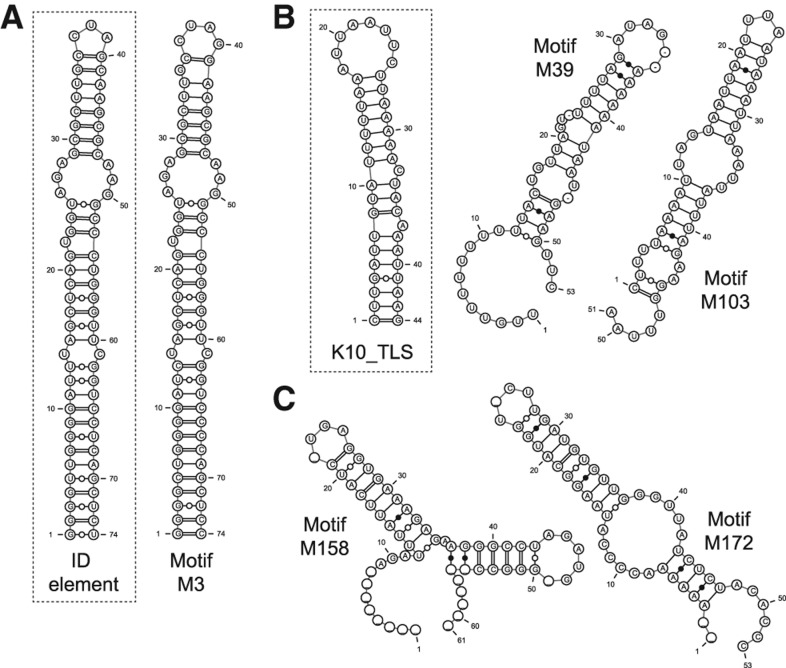
Previously, Buckley et al. (2011) found that a ∼74-nt hairpin structure within the retained introns of several dendritic transcripts was sufficient to confer dendritic localization in rat hippocampal neurons. These structures were instances of the ID element, a type of rodent SINE retrotransposon element that likely arose from the dendritically localized BC1 gene (Kim et al. 1994). We asked whether the ID element structure was among the motifs found by NoFold in our intron sequences. We found two motifs in the 50-nt set (M28 and M51) and one motif in the 150-nt set (M3) that had high sequence identity with the ID element, all of which were significantly enriched in the dendritic introns (Fisher's exact test, FDR-adjusted P < 0.05). M3 was additionally predicted to form a highly similar structure to the ID hairpin (Fig. 5A). This cluster contained sequences overlapping 10 of the 12 BLAST hits for the ID element within the intron sequences (see “Dendritic localization data set” in Materials and Methods), and additionally contained one extra instance of the ID element not found by BLAST. Although this extra sequence had low sequence identity with the ID hairpin sequence (59%), it was structurally conserved (SCI = 0.83) and was predicted to form a similar hairpin structure. Using the top 10 CM list annotation generated by NoFold, we found that the tRNA CM was the top CM for M3 by average Z-score (Z = 4.87), which is not surprising given that the ID element and BC1 RNA are evolutionarily related to alanine tRNA. We note that despite this similarity, scanning the full-length intron sequences with the tRNA CM using the traditional Rfam cmsearch only identified four instances of the ID element, highlighting the improved sensitivity that NoFold provides for motifs that are not directly modeled in Rfam.

FIGURE 5.

Consensus structures of motifs that are enriched in dendritically localized transcripts. (A) A motif (M3) found within dendritic introns with high sequence and structure similarity to the ID element hairpin (inset). (B) Two motifs (M39 and M103) with high average Z-scores for the K10 localization element (K10_TLS, inset) (M39, Z = 5.80; M103, Z = 5.47). Although sequence homology with K10_TLS was low, these motifs share the high AU content characteristic of K10_TLS. (C) Two examples of potentially novel structure motifs (M158, M172) found in dendritic 3′ UTRs.

In addition to the ID element, we also identified several motifs with similarity to known localization elements from Drosophila. Most strikingly, we found that 37 motifs were annotated as having the K10 transport/localization element CM (K10_TLS; RF00207) among their top 10 best CMs, with five of these motifs having an average Z-score >5 and 28 having a Z-score >3 for this CM. The K10_TLS is a 44-nt hairpin structure that mediates localization of the fs(1)K10 mRNA during Drosophila oocyte development (Serano and Cohen 1995). The majority of our K10_TLS-like motifs were predicted to have a stem–loop consensus structure enriched with AU base pairs (72% AU-content on average), similar to K10_TLS (Fig. 5B), although primary sequence identity was low. Overall, these 37 clusters encompassed a total of 60 unique genes, which is 28% of the total genes in the data sets, and 28 of the clusters were significantly enriched in dendritic transcripts (Fisher's exact test, FDR-adjusted P < 0.05). We also found nine motifs with another Drosophila localization structure, the Wingless localization element 3 (WLE3; RF01046), within their top 10 CMs, although only one had an average Z > 3. To our knowledge, a role for these motifs has not yet been described in mammals. Additionally, we identified several potentially novel motifs with stable and conserved structure, such as hairpin motif M172, which is found in six dendritic transcripts, and double-hairpin motif M158, which is found in four transcripts (Fig. 5C). Full data on all identified motifs are available on our supplementary website. Altogether, these results suggest that NoFold is useful as a first-pass high-throughput screen to identify the locations of recurring structural motifs in a data set, which can then be used to prioritize sequences for lower-throughput experimental analyses.

DISCUSSION

We have described here a novel approach for clustering RNA secondary structures that uses comparison to empirical models to map RNA sequences to a structural feature space (the RESS). By scoring primary RNA sequences across a large number of Rfam CMs and treating the scores as geometric coordinates, the RESS allows interpolation and extrapolation across existing models to identify novel combinations of structural features modeled by the original Rfam CMs. We find that sequences from the same structure family tend to cluster within the RESS and that these clusters can be extracted from unrelated sequences using unsupervised methods with very high sensitivity and precision. We use our approach to identify 213 motifs enriched in dendritically localized transcripts in rat. We hypothesize that some of these motifs may play a functionally important role in dendritic localization given their enrichment within dendritic transcripts and, for several motifs, high scores for CMs related to localization.

Within the dendritic RNAs we identified a large number of clusters that scored highly against the K10_TLS CM. It is unclear whether these clusters represent distinct structure families or are subgroups of one larger structure family that might include K10_TLS. Early studies of the K10_TLS indicated that the size and shape of the structure were most important for localization and that most nucleotides in the stem and loop regions can be changed as long as they do not disrupt base-pairing (Serano and Cohen 1995). More recently, a tertiary structure analysis of K10_TLS by NMR spectroscopy revealed that extensive purine stacking within the AU-rich stem region causes K10_TLS to take on an A′-form helix conformation with a widened major groove, and that this geometry is important for localization (Bullock et al. 2010). Although tertiary features such as this are not directly modeled by CMs and therefore may not be captured by our method, it is possible that the high AU content found in most of our K10_TLS-like motifs could allow them take on an A′-form helix and therefore be localized by a similar mechanism. As these results are still preliminary, additional experiments will be needed to verify these motifs and identify which proteins recognize them.

Beyond the experimental data set considered here, there are many possible applications of NoFold. For example, to identify structures bound by a particular RNA-binding protein, one could analyze sequences that are known to be bound by that protein to see if any common motifs emerge. A similar tactic could be applied to find motifs involved in splicing, RNA stability, and translational efficiency. On our supplementary website, we provide the initial results of an analysis of structures involved in noncanonical translation initiation as an additional example. The RESS itself could also be used directly as a feature space for supervised classification of RNAs, e.g., classification of unannotated noncoding RNAs into broad functional categories, as has been attempted using other types of features (Leung et al. 2013).

We note that because the scoring process scales linearly with increasing data set size, this approach is feasible for data sets up to several thousand sequences. Specifically, on one CPU core, a single 50 nt sequence was scored in an average of 0.012 sec per CM, or ∼24 sec for the entire Rfam CM set. As the scaling for increasing sequence lengths is quadratic, we generally recommend using sequences or sliding windows of <300 nt. We have implemented an option to parallelize the scoring process and several of the downstream steps of NoFold, which can greatly decrease runtime when the appropriate hardware is available. Runtime for the downstream steps of the NoFold process generally depended on the number of clusters that passed the thresholds, but usually took substantially less time than scoring. Although the overall runtime of GraphClust was generally shorter than NoFold on a single core (3 min for GraphClust versus 39 min for NoFold on a 100-sequence data set), NoFold was sped up considerably when parallelized (4.2 min on 16 cores for the same data set). In contrast, we observed that GraphClust did not always make use of all available cores (2.2 min on 16 cores for the same data set). This appears to be dependent on the number of clusters that were actually found.

An important limitation of our approach can arise from the use of empirical models to construct the feature space. An ideal set of empirical models should comprise all of the major structures of RNA such that any RNA structure can be placed “inside” the coordinates. By using all available models, we hoped to create such a feature space, but we do not have any guarantee. Another remaining limitation of our method is the detection of structures embedded in larger sequences. Here we used a sliding window to segment larger sequences to aid in detecting such structures, at the expense of some sensitivity. More sophisticated methods that might optimize for subsequence structures will yield improvements in this area. The development of alternate methods for segmenting large sequences will likely continue to improve the sensitivity of NoFold and other existing motif finders. Another avenue for improvement is in cluster delineation. Here we developed several data-driven criteria for cluster identification, but many other machine learning approaches may be applied to the basic concept of RESS.

An interesting future consideration will be the tailoring of different collections of empirical models to suit specific applications. Although here we used the entire set of Rfam v.10.1 CMs to define our feature space, different utility might be found using different subsets of CMs (or other models). As discussed in the Introduction and Results, the coordinate space established by the RESS using the CMs may be seen as a set of canonical models against which novel sequences are compared with assess their interrelationships. We hypothesize that if the models are at large scale (e.g., a sparse set of very different secondary structures), this is akin to having very coarse-grained models and such a subset of models (i.e., CMs) may be useful for large-scale structure discrimination but not for fine-scaled differences. Alternatively, we hypothesize that a set of closely related CMs may help discriminate fine-scaled differences. Thus, future work may entail using different subsets of CMs and resulting RESS coordinates for different subgroups of structures.

MATERIALS AND METHODS

Data and software

NoFold is available on our supplementary website (kim.bio.upenn.edu/software/nofold.shtml). Full clustering results and input data sets used in this study are also available on the site.

Scoring of RNA sequences

Sequences were scored against each of the 1973 Rfam CMs (v.10.1) using the cmscore module of Infernal (v.1.0.2) with options “--search --a” (Nawrocki et al. 2009).

Normalization of feature space

To obtain normalization parameters, a data set was generated by extracting sequences of varying length from random locations within transcripts sampled from the whole mouse (UCSC, mm9) and human (RefSeq, hg19) transcriptomes. Any exactly identical sequences were removed. We included 50 sequences of each length in the range of 10–500 nt in the data set, for a total of 24,550 sequences. We used this data set to obtain the parameters for normalization and standardization of the feature space that were used for all other data sets. First, for each CM, we estimated the mean and standard deviation of scores obtained by sequences of each length. We used these parameters to Z-score sequences in a length- and CM-dependent manner, as described in the text. Next, after normalizing the scores of the 24,550 sequences in this manner, we performed PCA (using prcomp in R) on the data set to obtain a set of independent axes. We retained only the axes with an eigenvalue >1.0 (Kaiser criterion), which yielded 124 axes. We rounded this down to the top 100 axes and recorded the loadings for these axes to use for future data sets. Finally, we recorded a set of parameters to re-standardize the 100 PC axes. All subsequent data sets were mapped to this normalized feature space (the RESS) using the parameters estimated here.

Synthetic structures

We designed the following synthetic structures, which we show below in dot-bracket notation (where matching parentheses represent paired bases and periods represent unpaired bases):

• 1-hp: (((((((((((((((((((((((((((((((((.....)))))))))))))))))))))))))))))))))

• 2-hp: (((((((((((((((((((((((.....)))))))))))))((((((((....))))))))))))))))))

• 3-hp: (((((((((((((((((((....)))))(((((.....)))))(((((....)))))))))))))))))))

Two-dimensional representations of these structures are also shown in Figure 2A. We randomly generated 50 sequences for each structure by generating complementary base pairs simultaneously (but randomly) as defined in the dot-bracket string. This ensured that each sequence had at least the potential to form the exact intended structure. Only Watson–Crick base pairs (A–U and G–C) were used. G–U wobble pairs were not used for simplicity. We did not require that the MFE structure be equivalent to the intended structure, although we note that the majority of the sequences did form the intended structure when folded by RNAFold.

To test distance measures, we generated all possible pairs of sequences from the same structure, different structures, or random sequences (which may or may not have stable structure). For each pair of sequences, we measured their percent sequence identity and their Spearman distance within the RESS, where Spearman distance is defined as one minus the Spearman correlation of the coordinates of the two sequences in the RESS. The random sequences were generated to have the same average dinucleotide frequency as the structural sequences but had no particular structure. Average dinucleotide frequency was matched by generating sequences according to a first-order Markov process where the transition probability between each pair of nucleotides was estimated from the sequences of the original data set.

NoFold structure clustering pipeline

A procedure to delineate robust RNA sequence clusters in the structural feature space was implemented as follows. Scored sequences were clustered by hierarchical clustering (average linkage using Spearman distance) using the fastcluster package (Müllner 2011) in R. Using a procedure similar to that described in Khaladkar et al. (2008), the resulting dendrogram was cut into all possible clusters of size three or greater and the average pairwise Spearman distance between cluster members was calculated for each cluster (cluster “diameter”); then any clusters with a diameter larger than an empirically derived threshold were removed (see Threshold Determination, below). As cutting the dendrogram into all possible clusters results in many clusters that contain almost the same sequences, we implemented two filters for choosing nonoverlapping clusters: a “sensitive” filter (optimized for picking larger clusters) and a “specific” filter (optimized for picking tighter clusters). In the sensitive filter, clusters are first ranked by their size (large to small) and then by their diameter (small to large). Clusters were then chosen in a greedy manner from first to last, throwing out any clusters that overlap with a previously chosen cluster. In the specific filter, clusters with three or more members were simply ranked by diameter (small to large) and then chosen greedily as previously. We tested these two filters using sequences from the BRAliBase II benchmark data set (Gardner et al. 2005) and found that the specific filter produced fewer false positives but sometimes missed positive examples. To improve the sensitivity of this mode without sacrificing specificity, we implemented an additional cluster-expansion step, where a new CM was trained for each cluster (“cluster-CM”) based on the multiple alignment of the cluster sequences by LocARNA. These cluster-CMs were then used to pick up additional matches to the structure within the original sequence database using the cmsearch module of Infernal with options “--toponly --glocal.” A sequence was counted as a hit for a given cluster-CM if it obtained a bitscore of at least log₂(size of search database), or in the case of the dendritic and noncanonical translation data sets, a bitscore of at least 10. If any two expanded clusters overlapped by >50%, they were merged into one cluster. After cluster expansion and merging, each cluster was automatically annotated in several ways to help give insight into potential functions, as described in the text. RNAz was run using default parameters.

Threshold determination

An empirical threshold for filtering clusters based on diameter (average pairwise Spearman distance) was calculated based on the distribution of cluster diameters that result from clustering random, unrelated sequences. As the expected cluster diameter is dependent on the total number of sequences in the data set being clustered, we separately calculated this threshold for different database sizes (usually rounding the database size to the nearest 100). For a given data set size, we also calculated a separate threshold for each cluster size (where size refers to the number of cluster members), as clusters with more members tend to have larger diameters.

We created a data set of 10,000 random 50 nt sequences with the same average dinucleotide frequency as the mouse and human transcriptomes using a first-order Markov model as described in the “Synthetic Structures.” As these sequences were randomly generated, we do not expect them to share substantial structure. Sequences were scored and mapped to the RESS. To obtain the distribution of cluster diameters for a given data set size, we used the following procedure: (1) A subset of the 10,000 sequences was picked at random to create a data set of the desired size; (2) the subset was hierarchically clustered using Spearman distances and average linkage and all possible clusters were extracted from the resulting dendrogram; (3) the diameter of each cluster was calculated and recorded in separate lists based on the number of sequences in the cluster; (4) steps 1–3 were repeated enough times to obtain >10,000 observations of clusters of size three (this required more iterations for small data sets and fewer for large data sets). The result of this procedure was a distribution of cluster diameters for each size cluster. A “high-confidence” threshold for each cluster size was then defined as the distance at which 99% of the clusters of that size had a larger diameter than the threshold, and a “good-confidence” threshold was set at the 95% mark. At these thresholds, we would expect ∼1% and 5% of structurally unrelated clusters to pass the thresholds, respectively. The 95% threshold was used for choosing clusters in all analyses described here.

Rfam benchmark tests

RNA sequences were taken from the Rfam.seed file available on the Rfam FTP (v.10.1). This file contains sequences from the seed alignments of 1973 Rfam families. We extracted the sequences for the first 20 Rfam families (RF00001-RF00020) and filtered each family so that no pair of sequences had >75% sequence identity. Sequence identity was calculated using the alignments specified in the Rfam.seed file, which is a multiple alignment of the whole family. Insertion characters (e.g., “.”) were therefore ignored if they were present in both sequences being compared. After the sequence identity filtering, all remaining sequences in the family were used as part of the benchmark, up to a maximum of 100 sequences per family. Family RF00014 (DsrA) had only one sequence left after filtering (of the original five) and was therefore replaced by RF00032 (Histone3), which was chosen because it is often used in the literature as a structure analysis benchmark family and is a particularly small structure. Altogether, this yielded a data set of 978 sequences. All information about alignment was removed, including all nonnucleotide characters. We referred to this data set as the “plain sequences.” We additionally generated an “embedded sequence” data set and a “plain sequences with background” data set. The embedded data set was created by adding 10–50 nt (amount randomly chosen) of additional flanking sequence to both the 5′- and 3′-ends of each sequence in the plain data set. The flanking sequence was matched to the average mono-nucleotide frequency of the plain sequence data set. The background-containing data set consisted of the plain data set with an additional 3000 random sequences mixed in, such that the random sequences outnumbered the Rfam sequences ∼3:1. These sequences were generated to have the same average dinucleotide frequency as the plain data set to ensure that dinucleotide frequency alone was not sufficient to cause clustering of random sequences. Matching of the average dinucleotide frequency was performed using a first-order Markov process, as described in the “Synthetic structures.”

After scoring but before clustering, we examined the sequences of each family for particularly high scores against the feature space CMs. We identified all CMs that had an average Z-score >3 (as calculated using the Z-score parameters described in the “Normalization of feature space”) and removed these CMs from the RESS. This also required us to reestimate the RESS PCA projection without these CMs. The full list of CMs that were removed is as follows: 5S_rRNA, 5_8S_rRNA, U1, U2, tRNA, tRNA-Sec, Tymo_tRNA-like, mascRNA-menRNA, tmRNA, Vault, U12, Bacteria_large_SRP, Hammerhead_1, Hammerhead_3, RNaseP_nuc, RNase_MRP, RNaseP_arch, RNaseP_bact_a, RNaseP_bact_b, ACEA_U3, Fungi_U3, Plant_U3, U3, 6S, U4, U4atac, SNORD14, SNORD53_SNORD92, Archaea_SRP, Bacteria_small_SRP, DdR20, Fungi_SRP, Metazoa_SRP, Plant_SRP, Protozoa_SRP, CsrB, CsrC, PrrB_RsmZ, RsmY, mir-299, Y_RNA, ceN72-3, U5, Histone3. Linear discriminant analysis was performed using the MASS package in R, and the top loaded CM for each axis was examined manually. A list of the loadings obtained in this analysis is available on the supplementary website.

NoFold and GraphClust were run on each of the three data sets using default parameters, with the exception that sliding window generation was turned off for GraphClust to make the results more easily compared. It is possible that the use of a sliding window with both approaches could improve performance. Although GraphClust has many parameters that could potentially be tuned to produce better results, we felt that the default parameters were reasonable for the purposes of this test. In particular, the default specifies that GraphClust will be run for two iterations and find up to 10 clusters per iteration, which is theoretically sufficient to identify the 20 expected clusters in this particular data set. Our results should be interpreted as how each method performs “out-of-the-box,” without tuning of parameters or use of a priori knowledge of the size or number of motifs.

Rfam families were grouped for the cross-validation analysis by clustering all of the 1973 CMs based on their scores against a large set of random transcripts (same data set as described in “Normalization of feature space” previously). Hierarchical clustering using Spearman distance and Ward linkage was used. The dendrogram was cut at a height such that exactly 10 clusters were created by the cut. The CMs in each cluster then determined which families were grouped together for the analysis. The reason for clustering the families in this way was to reduce the number of CM features that had to be removed for each analysis. GraphClust was set to run for 25 iterations (10 clusters per iteration) for this analysis to ensure enough clusters could be detected in each subset. NoFold was run using default parameters.

Dendritic localization data set

Dendritic transcripts in rat hippocampal neurons were identified by in situ hybridization and soma-/dendrite-specific microarrays (C Francis and J Kim, unpubl.). A transcript was called “dendritically localized” if it had high expression in the dendrites relative to the soma in either the in situ or microarray analysis, yielding 182 dendritically localized transcripts. An additional 29 known dendritically localized transcripts in rodents were obtained from Subramanian et al. (2011). Sequences from the 3′ UTR of these transcripts were obtained from RefSeq annotations (rn4) using the UCSC genome browser. If more than one 3′ UTR was available for a given gene, only the longest sequence was used. Cytoplasmically retained intron sequence was identified in rat using RNA-seq (Khaladkar et al. 2013) and those belonging to a dendritically localized transcript were used for the data set. These sequences consisted only of the regions of the intron that were supported by reads, as described in Khaladkar et al. (2013). As intron and 3′ UTR sequences are long and may contain multiple structures, we generated sliding window data sets for each using a 50-nt window with a 35-nt slide or a 150-nt window with a 105-nt slide. Instances of the ID element within the intron data set were identified by a BLASTN search of the full length retained intron sequences using the default parameters on the BLAST website (Altschul et al. 1990).

As a background data set, we identified a set of nondendritically targeted transcripts based on their very low expression in dendrites relative to the soma from the microarray analysis. Introns and 3′ UTR sequences were extracted for a random subset of the top 1000 nondendritic transcripts and processed as above to create background data sets of 10,000–30,000 windows for each analysis. The GC content of the background data sets was 44%–48%, which was similar to the test sequences (43%–45% GC). To test a motif for enrichment within the dendritically localized set, we generated a cluster-CM for each final motif using cmbuild (Nawrocki et al. 2009) and used this to search the background data set as well as the original data set. The number of hits in each data set was used in a one-sided Fisher's exact test for enrichment of hits in the dendritic set, and Benjamini–Hochberg multiple testing correction was applied using R.

Figure generation

Plots were generated in R (www.r-project.org) using the ggplot2 package (ggplot2.org). Structure depictions were created using VARNA (Darty et al. 2009) based on consensus structure and sequence predictions from LocARNA.