Fast T₂ Mapping with Multiple Echo, Caesar Cipher Acquisition and Model-Based Reconstruction

Abstract

Purpose

Fast, quantitative T₂ mapping is of value to both clinical and research environments. However, many protocols utilizing fast spin-echo (FSE) pulse sequences contain acceleration-induced artifacts which compound when fitting parameter maps, especially in the presence of imperfect refocusing. This work presents a B₁-corrected, model-based reconstruction and associated Cartesian FSE phase-encode ordering that provides enhanced accuracy in T₂ estimates compared to other common accelerated protocols.

Theory and Methods

The method, called “Multiple echo, Caesar cipher Acquisition and Model-Based REConstruction” (ME-CAMBREC), directly fitted T₂, flip angle, and proton density maps on a row-by-row basis to k-space data using the extended phase graph model. Regularization was enforced in order to minimize noise amplification effects. ME-CAMBREC was evaluated in computational and physical phantoms, as well as human brain, and compared to other FSE-based T₂ mapping protocols, DESPOT2, and parallel imaging acceleration.

Results

In computational, phantom, and human experiments, ME-CAMBREC provided T₂ maps with fewer artifacts and less or similar error compared to other methods tested at moderate-to-high acceleration factors. In vivo, ME-CAMBREC provided error rates approximately one-half those of other methods.

Conclusion

Directly fitting multi-echo data to k-space using the extended phase graph can increase fidelity of T₂ maps significantly, especially when using an appropriate phase-encode ordering.

INTRODUCTION

The fast spin echo (FSE, also TSE, RARE) pulse sequence is widely used in MRI due to its ability to quickly acquire high-resolution T₂ weighted images which are relatively insensitive to spatial magnetic field variations (1). However, when FSE is used for quantitative T₂ mapping, image artifacts caused by amplitude modulation in the phase-encoded direction of k-space, particularly in the presence of B₁ field variations, can induce significant errors in estimated relaxation time values. The sensitivity to B₁ field variation can be addressed through use of the extended phase graph (EPG) algorithm (2), and model-based reconstruction of parametric images such as T₂ maps from k-space data can inherently eliminate acceleration-induced artifacts in FSE images (3,4). This work integrates these ideas into a fast and B₁-insensitive method for T₂ and proton density mapping.

The EPG algorithm for calculating echo amplitudes (2) has received attention recently for its ability to compensate for indirect- or stimulated-echo pathways in multiple spin-echo acquisitions, such as those used for FSE (5–7), T₂ mapping (8,9), or multi-exponential T₂ analysis (10,11). These coherence pathways occur as a result of refocusing flip angles that deviate from 180°, which may be by design (5–7) or due to in-plane field variations or slice profile effects. Prasloski et al. have also used the EPG algorithm for analysis of combined gradient and spin-echo imaging (12), which provided accelerated T₂ mapping at a predictable signal-to-noise ratio cost (13), but the EPG analysis remained decoupled from the reconstruction problem.

In most Fourier-reconstructed fast T₂ mapping methods, two general approaches are used to provide both acceleration and sensitivity to T₂. In the first, multiple acquisitions are made using a single (usually center-out) k-space trajectory prepared by a spin echo period to provide T₂ image contrast. In the second method, the k-space trajectory is altered (14) (or data is reordered, such as in view-shared protocols (15,16)) from one image to the next in order to weight the center of k-space differently without extending the echo train. Here the former is referred to as an echo-prepared (EP) acquisition and the latter as a variable trajectory (VT) acquisition. While EP techniques waste information before or after the echo trains, each VT image will have a unique set of artifacts which will compound when fitting T₂ maps. As both of these acquisition strategies are tailored to the requirements of Fourier-reconstructed images, a novel “Caesar cipher” acquisition strategy—named after the famed emperor’s method of encoding text by wrapping the alphabet modulo its length—which is more suited to the proposed model-based reconstruction algorithm was developed. The proposed method is referred to as “Multiple Echo, Caesar cipher Acquisition and Model-Based REConstruction” (ME-CAMBREC).

THEORY

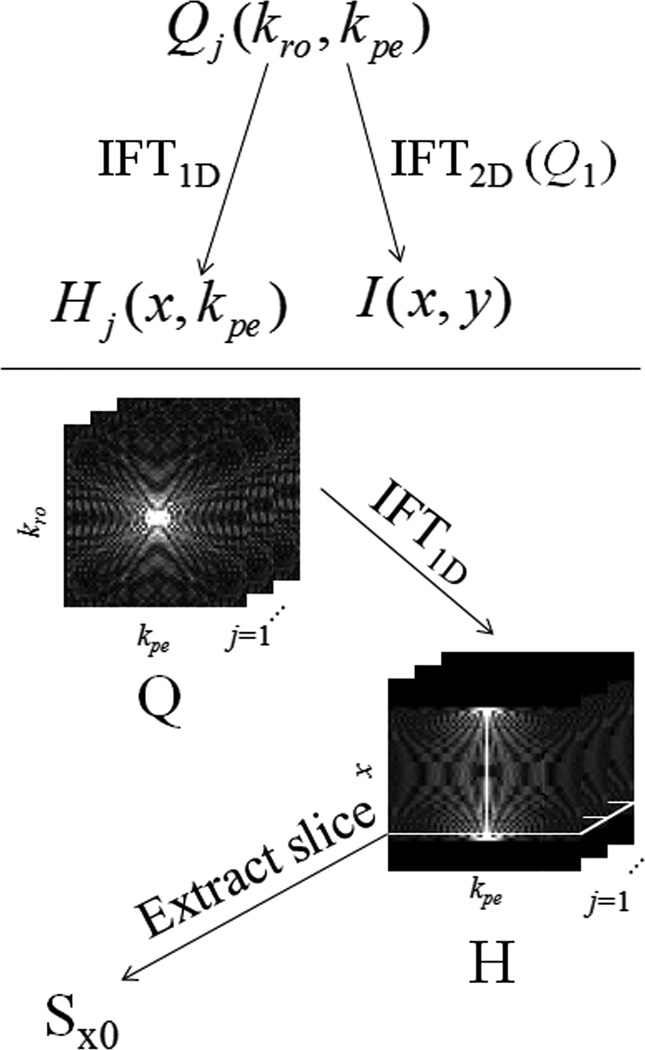
ME-CAMBREC simultaneously fits three parameters on a voxelwise basis—the relaxation time constant T₂, refocusing pulse flip angle θ, and the complex transverse magnetization immediately after excitation, M₊. First, N_Q fast spin echo k-space pseudo images Q_j (k_ro, k_pe) (with unique effective echo time indexed by j, j = 1 to N_Q) are acquired in a number of echo trains, N_T, less than the number of phase-encoded lines in Q, depending on the desired acceleration factor. (Note than when N_T = N_pe, the number of points in the phase encoded direction, the acquisition requires the same scan time as a non-accelerated multiple spin-echo pulse sequence.) Since all points along the readout direction of a given line occur in the same echo and are therefore assumed to have the same T₂ weighting, Q can be Fourier transformed in one dimension to create hybrid-space images H_j (x, k_pe). The ensemble of points corresponding to a certain spatial position, x₀, in the read direction—i.e., all phase encoded points k_pe across all N_Q pseudo images for a given x = x₀—are collected in a vector S_x0 (indexed by n) and paired with vectors t and k_pe, the echo times and phase encode k-values at which S_x0 were collected, respectively. Figure 1 demonstrates this data transformation in graphical form. Additionally, a reference image, I, is generated by inverse 2D Fourier transform of the Q₁ image, i.e. the k-space image with the shortest effective echo time, I = F_2D⁻¹{Q₁} = F_pe⁻¹{H₁}. This reference image is used in the model-based reconstruction as an initial guess, as part of a regularization penalty, and to threshold the parameter maps a priori. For each row of data (i.e., each value of x₀), voxels with magnitude < z % of the maximum of |I (x₀, y)| are not fitted and constrained to zero.

Fig 1. Data sorting and preparation.

Fast spin echo k-space images Q are transformed into a hybrid space H, from which parameter map reconstruction occurs row-by-row. A reference image I is also generated through simple Fourier reconstruction of the earliest effective echo time data.

Once the vector S_x0 has been constructed for a given image row, M₊, T₂, and θ are fitted simultaneously using the following cost function

$$\mathit{\text{cost}}=\sum _{n=1}^{N_Q{N}_{pe}}\sum _{c=1}^{N_C}{\left|\sum _{l=1}^L{C}_{c,l}{M}_{+,l}EPG\right(t_n,T_1=1\mathrm{s},T_{2,l},{\theta }_l\left)\text{exp}\right(-\frac{i2\pi l{k}_{pe,n}}{L})-S_{n,c}|}^2+\lambda ·p(M_{+},I),$$ [1]

where EPG(·) represents the extended phase graph calculation, m is an index corresponding to y position (l = 1 to L), and p is the regularization function, defined below, which is weighted in the cost by λ. The parameter C_c,l is the complex coil sensitivity at position l of the c^th receive coil element of an N_C coil array.

The regularization is a fractional variation constraint designed to penalize added sharpness in the fitted M₊ over the reference image I:

$$p=\sum _l{(\frac{\text{Re}[M_{+,l+1}-M_{+,l}]}{\text{Re}[M_{+,l+1}+M_{+,l}]}-\frac{\text{Re}[I_{l+1}-I_l]}{\text{Re}[I_{l+1}+I_l]})}^2+\sum _m{(\frac{\text{Im}[M_{+,l+1}-M_{+,l}]}{\text{Im}[M_{+,l+1}+M_{+,l}]}-\frac{\text{Im}[I_{l+1}-I_l]}{\text{Im}[I_{l+1}+I_l]})}^2.$$ [2]

The spatial difference taken in the penalty function makes this regularization similar in spirit to total variation constraint, but with the following important distinctions: 1) the use of a blurred reference image, I, which will reduce the penalty burden in regions of genuine spatial variation of M₊, 2) the normalization by the sum of the values of M₊ or I, which is required due to the different scaling of the reference image caused by signal decay before the first echo, and 3) the usage of a 2-norm rather than a 1-norm, for ease of computation. The behavior of this regularization is intuitively straightforward. When the penalty weighting factor λ is close to zero, noise amplification from phase encoded lines acquired near the end of the echo train causes significant image degradation. As the weighting factor increases, the M₊ image becomes increasingly similar to a scaled version of I. The regularization used here is not intended to be optimal, but rather as an intuitive use of a priori knowledge regarding the M₊ map. Further study may find alternate regularization strategies that provide better performance, such as a sparsity constraint over some transform of the data.

Optimal tuning of λ is a nontrivial process. Here, a nonlinear L-curve approach was used, where the optimal λ is selected as the point where a marginal increase in penalty weighting begins to induce a notable increase in solution residuals. Mathematically speaking, the value of λ chosen is the value that maximizes the curvature, κ, of a log-residual vs. log-penalty graph parameterized by λ:

$$\kappa =\frac{\left(\frac{r}{\lambda p}\right)}{{(1+\frac{r^2}{{\lambda }^2{p}^2})}^{3/2}}(\frac{r}{{\lambda }^2\left({\nabla }_{\beta }{p}^T{H}^{-1}{\nabla }_{\beta }p\right)}-(\frac{r}{\lambda p}+1\left)\right)$$ [3]

This equation was adapted from (18), correcting for typographical errors. Here r is the sum-squared residual term and p is the scalar penalty term from Eq [1] and [2]. The gradient vector with respect to model parameters β is defined as Δ_βp, and H is the Hessian (second derivative) matrix of the entire cost function. By plotting κ against λ, an optimal value for λ can be estimated; in the following, a single value of λ was selected for each image using a small sample of the image rows.

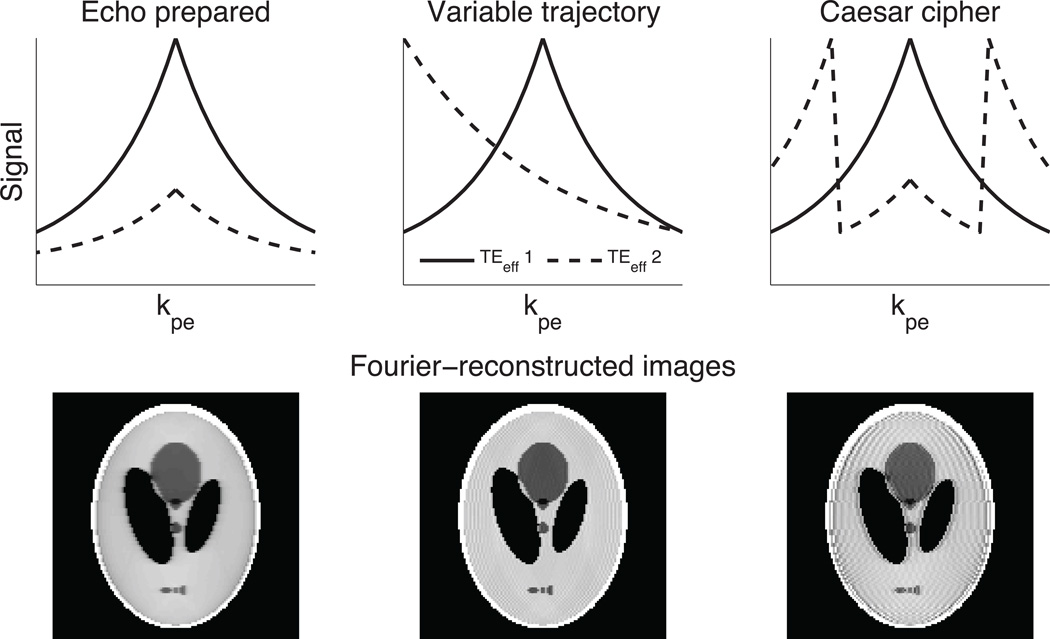
ME-CAMBREC also uses a novel acquisition scheme to further reduce noise amplification. Unlike Fourier reconstruction, which introduces artifacts related to the properties of a k-space amplitude modulation function, image noise in model-based reconstructions will be amplified at any spatial frequencies not sampled at early echo times. It is, therefore, disadvantageous to acquire the high spatial frequency lines of Cartesian k-space at the end of every echo train. Instead of using either the EP or VT methods to provide T₂ contrast, ME-CAMBREC provides T₂ contrast by sampling phase encoded lines in a Caesar cipher-like (CC) pattern. This trajectory can be considered an application of the rotated rapid acquisition relaxation enhanced (19) methodology to a center-out framework. In this acquisition strategy, the first echo train(s) acquire a center-out image (Q₁). The next pseudo images (Q_j, j = 2, 3, …) are acquired by pushing the entire trajectory down the echo train and moving the last phase encode lines—those which would require the echo train to be extended if they were acquired in center-out order—to the beginning of the echo train. For example, given the first trajectory k_pe=0,−1,1,−2,2 the second trajectory is k_pe=2,0,−1,1,−2, the third is k_pe=−2,2,0,−1,1, and so on, as shown in Figure 2. Acquiring fewer pseudo-images than the echo train length provides accelerated acquisition compared to conventional multiple spin echo imaging.

Fig 2. Artifact and k-space trajectory.

The upper portion of the figure represents the acquired echo train from shot to shot as effective echo time increases; the solid line is a center-out acquisition common to most FSE schemes, while the dashed line demonstrates a later TE_eff using the given acquisition strategy. In the echo-prepared image, blurring (but not ghosting) is present. Both types of artifact exist in other sampling schemes, with the proposed Caesar cipher acquisition clearly being unsuited to Fourier-based reconstruction.

METHODS

Computational Studies

The ME-CAMBREC method was compared to analysis of Fourier-reconstructed images using previously established trajectories, namely the EP and VT methods. The computational phantom used for each experiment was as follows. A 128 (N_ro) × 128 (N_pe) Shepp-Logan phantom with intensity values ranging from 0.8 to 1 was used as a proton density map; each compartment of that map had its own uniform T₂, ranging from 60–500 ms; a flip angle map varying smoothly across the image over 110–130° was used for all EPG-based analysis, and a similar map varying from 170–190° was used for exponential model fitting. A four-shot (N_T = 4N_Q) mock acquisition using each trajectory was performed with the following parameters: echo spacing (ESP) = 10 ms, echo train length (ETL) = 32 echoes, effective echo time (TE_eff) = 10, 90, 170, 240 ms for CC and EP, TE_eff = 10, 40, 90, 160 ms for VT. (The VT acquisition scheme used lower effective echo times because it is not suited to acquiring the k_pe = 0 line after the halfway point of the echo train; doing so would require an outside-in type trajectory.) Since N_T = 4N_Q = 16 = N_pe/8, the acceleration rate, R, for all mock acquisitions was equal to 8. Noise was added to the data at a magnitude image signal to noise ratio (SNR) of 15 for the median intensity voxels of the Shepp-Logan phantom, which represents about the lowest SNR permissible for quantitative imaging. The ME-CAMBREC reconstructions were regularized using optimal weighting levels (see the Fitting Algorithm section). The resultant parameter maps were compared to the actual underlying parameters as were reconstructed maps using data with median SNR = 30, 60, and 120. Additionally, parameter maps from Fourier-reconstructed voxel-wise fitting to the extended phase graph and exponential models were created for comparison using both EP and VT trajectories. Error metrics were calculated root-mean-square (RMS) errors relative to known values, reflecting parameter estimate variance more than bias error at low SNR and the opposite at high SNR.

In order to compare the proposed method to a more disparate fast T₂ mapping protocol, DESPOT2 (20), the Cramer-Rao lower bound of the variance of T₂ was calculated for both ME-CAMBREC and a sample implementation of DESPOT2 (21) using the same Shepp-Logan phantom. The mean coefficient of variation of T₂ estimates (defined as the Cramer-Rao bound divided by the true value) across an image row was calculated. Additionally, since each method will have unique noise characteristics and scan times, these were accommodated in an overall calculation of SNR efficiency (i.e., T₂ SNR per unit root scan time). The DESPOT2 acquisitions simulated the following parameters: spoiled gradient-recalled echo: TR = 11.7 ms, flip angles = 4° and 15°, receiver bandwidth = 15.6 kHz; steady-state free precession: TR = 3.7 ms, flip angles = 15° and 55°, receiver bandwidth = 62.5 kHz. Both methods assumed a 256 × 256 in-plane matrix, with DESPOT2 acquiring 128 points in the third dimension and ME-CAMBREC acquiring this many 2D slices. Scan parameters for ME-CAMBREC were adapted from the human imaging protocol (see Human Experiments), with the receiver bandwidth adjusted to 36.6 kHz to acquire the new matrix size in the same echo spacing. Simplifying assumptions for DESPOT2 included instantaneous approach to steady state, no compressed sensing/partial Fourier acceleration, and a priori knowledge of confounding factors such as off-resonance/flip angle maps which are often measured in practice.

Phantom Studies

An eight-tube phantom containing copper sulfate and manganese chloride solutions (T₂ range: approximately 15ms–150ms) was imaged on a 4.7 T/31 cm Agilent/Varian (Santa Clara, CA) DirectDrive MRI system equipped with single element volume coil (N_C = 1, Eq [1]) using CC, EP, and VT k-space sampling methods. A multiple spin echo pulse sequence with constant gradient dephasing in every inter-echo period was used with the following parameters: matrix size = 64 (N_ro) × 64 (N_pe), ETL = 16 echoes; TE_eff = 5, 25, 45, and 60 ms for CC and EP and 5, 15, 25, and 30 ms for VT; refocusing flip angle = 120°; N_Q = 4; N_T = 16; ESP/TR = 5/2500 ms; slice thickness = 2 mm; refocusing pulse width = 5 mm. It should be noted that this wide refocusing pulse width would require a 1.5 mm gap between slices if the acquisition were performed in multi-slice mode, although only one slice was acquired here. These data were subjected to ME-CAMBREC (CC) and Fourier-reconstructed EPG analysis (EP, VT). The T₂ maps resulting from these protocols were compared to EPG analysis of a fully-sampled multiple spin-echo dataset acquired using the same scan parameters and double the echo train length. The errors were calculated as relative errors of the mean of each sample tube, reflecting systematic bias and artifact more than noise characteristics.

Human Studies

The brain of a healthy volunteer was imaged on a 3.0-T Philips (Best, NL) Achieva MRI system using an 8-element head coil (N_C = 8, in Eq [1]) and a multiple spin-echo pulse sequence with uniform echo spacing and constant gradient dephasing in every inter-echo period. The following sequence parameters were used: ETL = 32, ESP/TR = 10/2500 ms, slice thickness = 5 mm (excitation)/15 mm (refocusing), in-plane resolution = 2 × 2 mm², number of averaged acquisitions = 1, SENSE acceleration factor = 1, and image matrix = 105 (N_ro) × 105 (N_pe). This resulted in a scan time of 4m 23s. (The slice gap required if a user wished to perform this scan in multi-slice mode would be 5 mm.) Coil sensitivity maps (C_c in Eq [1]) were estimated from the first echo image using a cubic polynomial basis. Two fully sampled multi-echo image sets were acquired, one using refocusing pulse flip angles prescribed at 120° and the other at 180°, in order to compare EPG methods to exponential decay fitting. These data were sub-sampled into datasets emulating CC, EP, and VT acquisition schemes, each with N_Q = 4, N_T = 16 (≈ N_pe/6.6) and ETL = 26 (to roughly match the matrix size of 105). The CC ordered sub-sample used TE_eff = 10, 80, 150, and 210 ms; for VT, TE_eff = 10, 40, 60, and 110 ms; for EP, TE_eff = 10, 20, 30, and 50. The EP TE_effs were low in order to prevent extending the echo train and substantially changing the total scan time between protocols. These sub-sampled data represented an R = 6.6 acceleration compared with the fully sampled data. These data were analyzed in a similar manner to the phantom studies, specifically focusing on a heterogeneous rectangular region of interest (ROI) containing both white matter and deep gray matter, but excluding cerebrospinal fluid due to its long T₂. For all accelerated methods, error was defined as the difference between estimated T₂ values and those estimated from fully sampled data. Error metrics were tabulated as RMS errors over a heterogeneous region, reflecting both noise and artifact. For comparison, previously published (22) T₂ values of the dominant signal component of various brain regions have also been presented.

ME-CAMBREC was also compared to the sensitivity encoding (SENSE) method of parallel imaging acceleration (23). The same coil sensitivity maps were used for ME-CAMBREC and SENSE. ME-CAMBREC was performed using fully-sampled data reduced by a factor R ≈ 2 (N_Q = 13, N_T = 52 ≈ N_pe/2). The ME-CAMBREC T₂ map was compared to one resulting from voxelwise EPG fitting of 32 SENSE-reconstructed images with acceleration factor R = 2. In turn, ME-CAMBREC was performed on a data subset which was both undersampled in k-space (R = 2, i.e. all odd k_pe lines were excluded) and undersampled in the echo dimension (N_Q = 13, N_T = 26) for a total acceleration factor of roughly R = 4. This “sub-Nyquist” ME-CAMBREC reconstruction was compared to purely accelerating in the k-spatial dimension (SENSE, R = 4) and purely accelerating in the echo dimension with R ≈ 4 (ME-CAMBREC, N_Q = 7, N_T = 28 ≈ N_pe/4).

Fitting Algorithm

For fitted voxels, initial guesses for M₊ (real and imaginary values) were taken from the image I, T₂ was initialized to a linearized least-square estimate for all points in S where k_pe = 0, and θ was initialized to the prescribed value. For all cases, T₁ was constrained to 1 s, and the intensity threshold, z, was set to 5 %.

An iterative nonlinear least-squares solver (lsqnonlin in MATLAB (The MathWorks, Natick, MA)) was used to minimize the cost function. In order to accelerate the computation of each iteration, the gradient of the cost-function with respect to model parameters was calculated using a direct analytical formulation of the penalty gradient and a computational shortcut for the gradient of the sum squared residual:

$$\frac{\partial c}{\partial \beta }=2\text{Re}\left[\sum _n\frac{\partial M_{+,a}EPG(t_n,T_1=1\mathrm{s},T_{2,a},{\theta }_a)}{\partial \beta }\text{exp}\right(-\frac{2\pi ia{k}_{\text{pe},n}}{M}\left){r_n}^{*}\right]+\lambda \frac{\partial p}{\partial \beta },$$ [4]

where r_n^* is the complex conjugate of the residual at index n, and β represents any of the fitted parameters. This shortcut is enabled through the knowledge that each reconstruction parameter β only appears in the equations of a single spatial point a. An extension of this equation into a second differential order can be used to expedite calculation of the cost function’s Hessian matrix as well, for use in determining the optimal regularization level. The entire algorithm allows for fitting one image row in 15–30 seconds on standard personal computer hardware, but this should not be considered an optimized reconstruction time.

RESULTS

Computational experiments

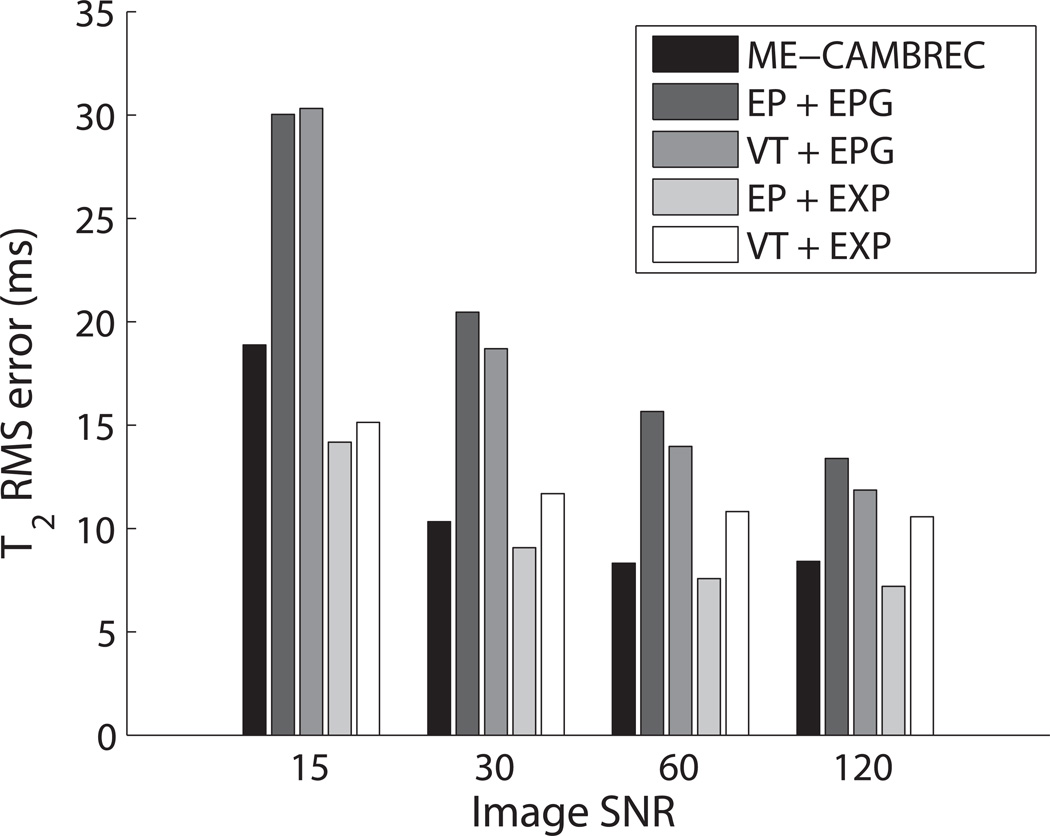
Table 1 summarizes the root-mean-squared error (ε_rms) of all three reconstructed parameter maps from simulated data, excluding cerebrospinal fluid-like regions with very long T₂ (500ms) which would otherwise dominate error calculations. The errors presented were for data with median SNR = 60. Propagation of error laws dictate that parameter estimate variance should decrease at least linearly with the standard deviation of the image noise, but Fig 3 shows a diminishing return in total RMS error due to inherent bias in the estimators. Model-based reconstruction of CC k-space encoded data (i.e., ME-CAMBREC) performed well relative to Fourier-reconstructed protocols. Perhaps unsurprisingly, the simple echo-prepared, exponential fit FSE protocol demonstrated high sensitivity to T₂ and the lowest error when near-perfect refocusing was simulated.

Table 1. RMS error of reconstruction in a computational phantom.

Results from the computational study utilizing four FSE images (at SNR = 60) for each method. The labels, such as Fourier-EPG + EP, denote the method of reconstruction (Fourier transform or model-based fitting), the decay model used in the fit (EPG or exponential, EXP), and the k-space view ordering (CC, EP, or VT). ME-CAMBREC provided lower RMS errors in T₂ estimates than any other method except echo prepared FSE fit to an exponential decay curve.

Recon. + Acq.	εrms, M+ (a.u.)	εrms, T2 (ms)	εrms, θ (°)
Model-Based + CC (ME-CAMBREC)	0.21	8.3	22.0
Fourier-EPG + EP	0.15	15.7	21.7
Fourier-EPG + VT	0.16	14.0	17.4
Fourier-EXP + EP	0.05	7.6	-
Fourier-EXP + VT	0.05	10.8	-

Fig 3. RMS Errors in estimated T₂ vs SNR for various FSE methods.

Legend keys refer to the acquisition trajectory (EP or VT) and the fitting model (EPG or exponential, EXP). EXP fits were applied to data refocused using 170–190° pulses; all others were applied to 110–130° refocused data. As SNR increases, ME-CAMBREC and other accelerated protocols approach a lower error limit due to estimate bias. In practice, ME-CAMBREC demonstrates better T₂ accuracy than most Fourier-reconstructed methods at both high and low SNR.

ME-CAMBREC was discovered to have an SNR efficiency (i.e., T₂ SNR per unit root scan time) 2.4 times higher than that of a previously published four-angle implementation of DESPOT2. This was primarily due to the sensitivity of multiple spin-echo sequences compared to steady-state sequences.

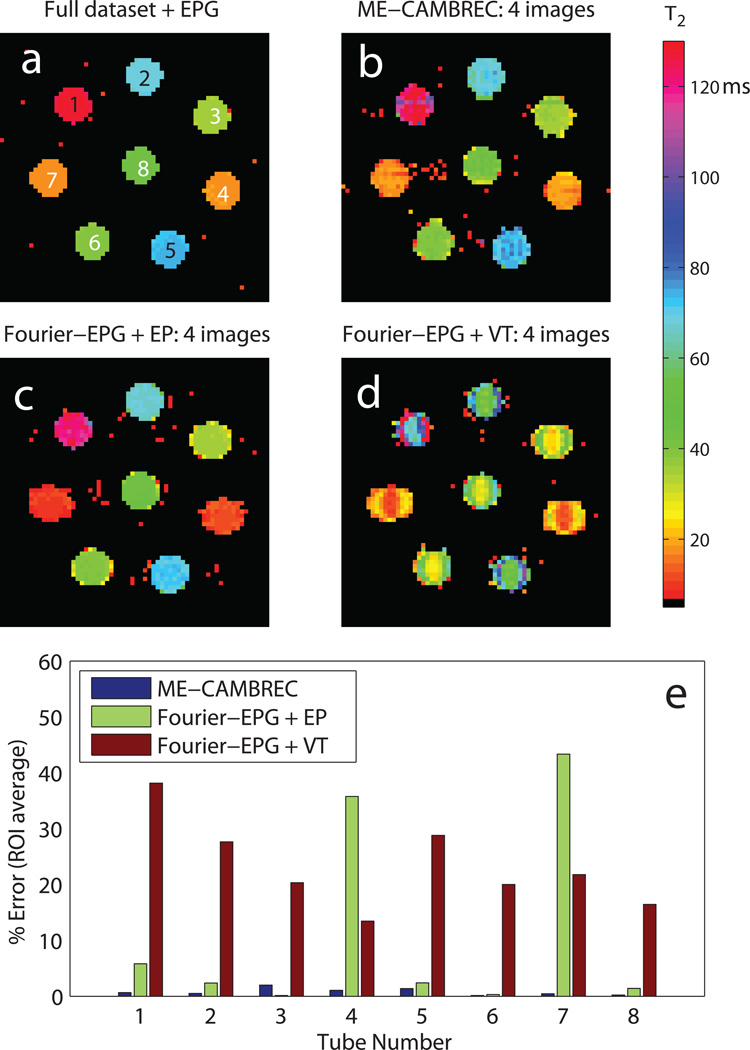
Phantom experiments

Figure 4 shows T₂ maps (top) and relative errors (bottom) from the phantom experiments for different acquisition and analysis protocols. ME-CAMBREC method performed well across the range of T₂s, with relative errors of less than 5%. Although any EPG analysis of the CuSO₄ solutions (T₁ ≈ T₂) in the presence of imperfect refocusing will result in a small bias in the T₂ estimates (8), Fig 4 shows that the unknown T₁ does not result in additional error or artifact in ME-CAMBREC maps. As was the case in the computational study, accelerated Fourier-reconstructed EPG analysis performed poorly for certain T₂s, especially short ones such as those of tubes 4 and 7. T₂ was underestimated by both Fourier FSE methods, in some cases by more than 30%. Severe artifact was also present in both Fourier-based T₂ maps.

Fig 4. Reconstructed T₂ maps in a physical phantom.

In short T₂ regions such as tubes 4 and 7, Fourier-based fast T₂ mapping methods either underestimate (c) or overestimate (d) high spatial frequency signal, resulting in blurring and edge enhancement respectively. While the proposed nonlinear reconstruction method has decreased stability for short T₂s relative to long T₂s, as visible in tube 7 of (b), the overall error remains consistently low (e). All accelerated methods used 1/4^th of the full dataset.

Human experiments

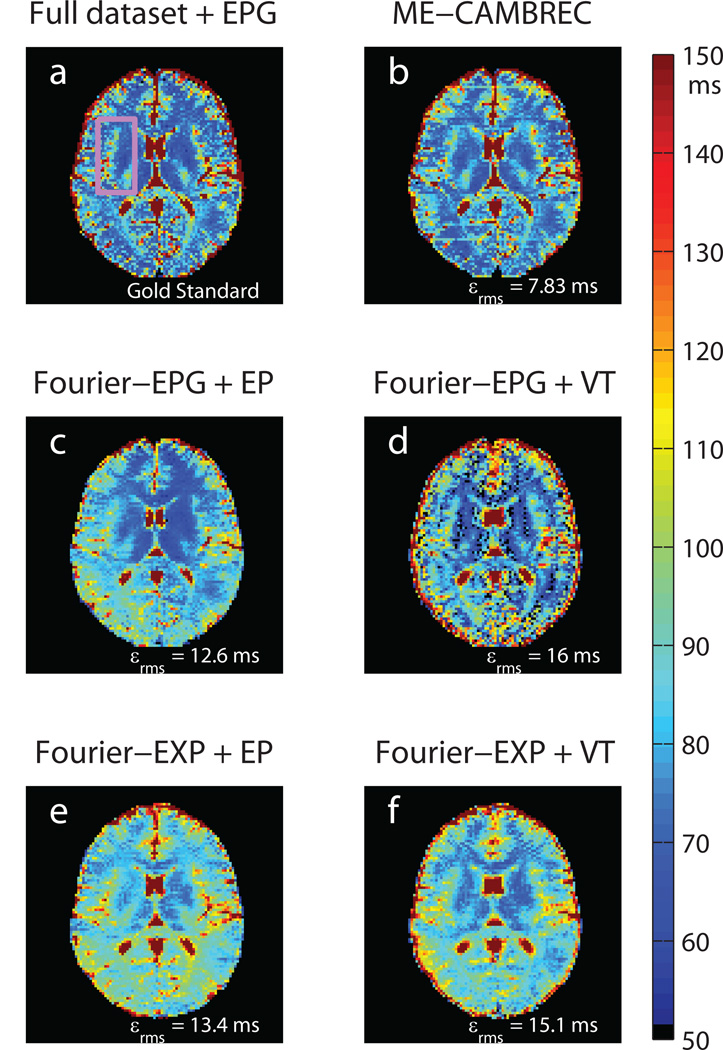
Figure 5 shows T₂ maps from the in vivo human brain imaging. The upper left frame shows a T₂ map generated from the fully sampled 120° refocused multiple spin echo sequence. Each of the other frames shows a T₂ map derived from a sub-set of the data which could be acquired in less than 1/6^th the time; panels b-d were taken from the 120° refocused scan and panels e-f used data refocused by 180° pulses. As in the phantom experiments, ME-CAMBREC generated a T₂ map most closely resembling that of the fully sampled dataset. The middle and lower panels of Fig 5, those corresponding to Fourier-reconstructed images, show enhanced artifact such as blurring and asymmetry compared to the maps from fully sampled data and ME-CAMBREC. Unlike in the computational experiment (Table 1), fitting in vivo high-refocusing flip angle data to the exponential model (Fig 5e–f) did not provide better error rates than the proposed method; these error rates were similar to those of maps fitted to the EPG model.

Fig 5. Reconstructed T₂ maps in healthy human brain.

The pink rectangle in the top-left fully sampled image (a) denotes the ROI used to measure RMS error. Note the asymmetry and systematic overestimation of T₂ in Fourier-reconstructed EP protocols (c, e) as well as the edge enhancement and ghosting artifacts visible in the Fourier-reconstructed VT protocols (d,f). All accelerated methods used 1/6.6^th of the full dataset (N_T = 16); data fit to the exponential model was acquired with a prescribed refocusing flip angle of 180° and was compared to a fully sampled dataset at that flip angle. All other images were derived from data acquired using a prescribed flip angle of 120°.

Table 2 quantitatively compares the T₂ estimates of various cerebral structures made using accelerated Fourier-based T₂ mapping methods, ME-CAMBREC, fully-sampled data and values from literature. Fully sampled data from the present study agreed well with literature values, showing no systematic bias. ME-CAMBREC accelerated at R = 6.6 underestimated T₂ relative to the fully sampled data, but differences were comparable in absolute value to those between the fully sampled data and literature. Similar absolute differences in estimated T₂ resulted from Fourier-reconstruction of R = 6.6 EP-trajectory data. The R = 6.6 VT-trajectory data underestimated T₂ with somewhat greater absolute differences to fully sampled data. In all cases, voxelwise paired t-tests indicated that differences between fully sampled data from the present study and all accelerated acquisitions were statistically significant.

Table 2. Mean T₂ values of various brain regions from literature, fully sampled data, and accelerated methods.

All results shown used the EPG model in the T₂ estimation. In all cases, voxelwise paired t-tests indicated that differences between fully sampled data from the present study and all accelerated acquisitions were statistically significant. Values from literature were estimated from Fig 6 in Ref 22.

	ROI mean T2 (ms)
	Fully Sampled		Accelerated, R = 6.6
	Literature (22)	Present Study	ME-CAMBREC (R = 6.6)	Fourier-EP (R = 6.6)	Fourier-VT (R = 6.6)
Corpus Callosum, Genu	68.2	68.7	66.7	72.3	67.7
Corpus Callosum, Splenium	80.4	84.7	80.4	84.2	77.7
Cortical Grey Matter	80.0	84.1	81.3	86.5	74.1
Insular cortex	85.6	83.8	82.0	81.2	74.4
Thalamus	65.6	68.0	66.3	70.6	60.2

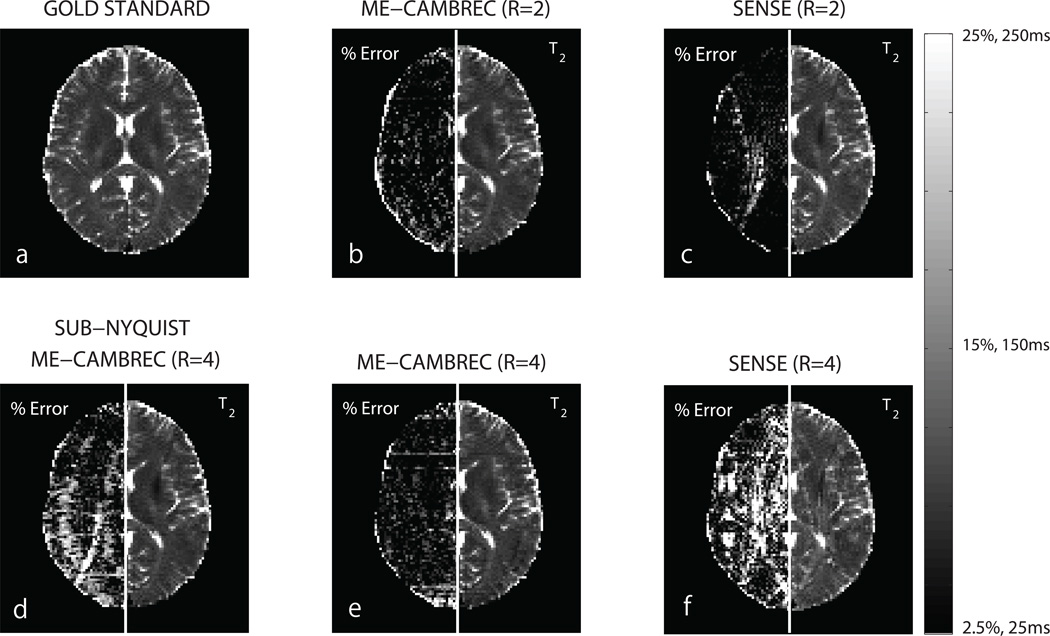
The comparison between ME-CAMBREC and SENSE acceleration/EPG fitting is presented in Fig 6. At acceleration factor R = 2, the methods are comparable, with SENSE performing better in regions with little aliasing and worse in regions with more intense aliasing. At higher acceleration rates (R = 4), ME-CAMBREC outperformed SENSE as visible in the left halves of panels e-f. Panel d shows reaching R = 4 acceleration by combining sub-sampling in k-space and the echo dimension by a factor of 2 each provided a poorer result than ME-CAMBREC with R = 4. That is, one can in principle combine traditional parallel acceleration with ME-CAMBREC, but for this case at least, acceleration by ME-CAMBREC alone was superior.

Fig 6. T₂ maps from ME-CAMBREC and EPG fitting to SENSE images.

The left side of each panel is a relative difference between the given T₂ map and the EPG-fit, fully-sampled, 180° refocused T₂ map. Panels b, d, and e are ME-CAMBREC reconstructions, while panels c and f are T₂ maps from EPG fitting to SENSE-reconstructed images. At acceleration factor 2, SENSE provides better T₂ maps than ME-CAMBREC in regions with little aliasing and worse maps in regions with more severe aliasing (b,c). ME-CAMBREC scales better to higher acceleration factors than SENSE (e,f). Acceleration by the sub-Nyquist sampling of k-space combined with sub-sampling the echo dimension (d) showed a poorer result than acceleration by sub-sampling the echo dimension alone (e).

DISCUSSION

In experimental environments designed to test noise propagation (computational), artifact and systemic error (phantom), and a combination of the two (human), ME-CAMBREC performed at least comparably to the best conventional FSE methods tested. Noise propagation was kept similar to Fourier-reconstructed exponential fitting (Table 1 and Fig 3), despite significant artifact reduction (Fig 4). The in vivo implementation, where both noise and artifact can contribute to significant errors, gave the greatest advantage over the other accelerated T₂ mapping methods tested. Visually, all ME-CAMBREC images presented here contain smearing artifacts in the phase encode direction which are not smooth in the readout direction, apparently caused by the row-by-row nature of the reconstruction. It is possible that extending the algorithm to jointly fit multiple rows with 2D regularization could alleviate this shortcoming at the cost of computational complexity. There is also an apparent underestimation of T₂ when averaged across regions of interest (Table 2) which can be seen in VT Fourier reconstruction fitted to the EPG model as well. This may imply that the artifact is caused by noise amplification at moderate spatial frequencies interacting with the EPG fitting. However, the quantitative errors of these artifacts and underestimation remain lower than those of Fourier-reconstructed fitted T₂ values. While ME-CAMBREC bias, like that of Fourier-based accelerated methods, limits accuracy at high SNR (Fig 3), deeper control over regularization-induced bias as compared to image artifact permits T₂ bias to be a somewhat tunable parameter, able to be traded off for estimate precision.

For high acceleration factors, each of the studies presented demonstrated that Fourier-reconstructed EPG fitting induces high errors in T₂ maps. This is not surprising, since the EPG model is a three-parameter model involving oscillating signal behavior: when fitting to a small subset of effective echo times, sensitivity to oscillations (θ) and decay (T₂) must be traded off through the selection of a proximate or disparate set of time points. However, the disagreement between the computational and human studies regarding the expected error of EP-FSE when fit to the exponential model is less parsimonious. The computational study suggests that EP-FSE may be a better option than model-based reconstruction when near ideal refocusing pulses are realized. As this is a Fourier reconstructed approach, though, the results of EP-FSE will be heavily dependent on the imaging subject’s sensitivity to artifact, which has been shown to rely on many additional factors such as feature size and echo train length (24). The large feature size of elements of the Shepp-Logan phantom, combined with the slowly varying underlying T₂ distribution, likely contributed in large part to the apparent superiority of the EP-FSE protocol.

In all experiments, ME-CAMBREC performed at or above the standards of conventional FSE T₂ mapping at a given acceleration factor (from 4 in the phantom experiments to 8 in the computational experiments). However, a wide variety of other fast T₂ mapping methods exist. The proposed method was directly compared to DESPOT2 by way of SNR efficiency, but no experiments were performed to test other aspects of the method which may or may not be limiting factors. For example, DESPOT2 can provide single-slice parameter maps at a slightly faster rate than ME-CAMBREC, although at lower precision due to differences in sensitivity. It should also be noted that DESPOT2 is typically run as a 3D protocol while extending ME-CAMBREC to 3D would be nontrivial. The model-based reconstruction would have to be applied simultaneously in multiple dimensions, both enabling acceleration in a second spatial dimension and creating new challenges in computational stability.

Accelerating using parallel imaging provided excellent results in the case of small acceleration factors (R = 2), as Fig 6c shows, but at higher acceleration factors (R = 4) generally provided poor results compared to ME-CAMBREC. Using ME-CAMBREC itself as a parallel imaging reconstruction method by sampling k-space in the same sub-Nyquist pattern across all pseudo-images provided lower quality results than purely undersampling in the echo dimension (Fig 6d–e). This is somewhat intuitive, since the number of echoes acquired is typically many times larger than the number of elements in a receive array, allowing more degrees of freedom in that dimension. Readers should note that undersampling k-space in a unique sub-Nyquist pattern between pseudo images (e.g., all even k-space lines for one image and all odd lines the next) is essentially equivalent to Nyquist-sampled ME-CAMBREC, since all data are fitted simultaneously.

Another accelerated T₂ mapping method which should be considered is view-shared projection-reconstruction (15,16), such as k-space weighted image contrast (KWIC). One primary advantage KWIC maintains over the ME-CAMBREC is motion insensitivity due to the repeated sampling of the center of k-space. Otherwise, however, KWIC is still somewhat vulnerable to high-spatial frequency image artifact and requires more scan time: the typical KWIC scan requires 32 echo trains, while the highest-accelerated method proposed here used only 16 excitations. Variations on PR-FSE have included a model-based reconstruction (3), which shares certain benefits of ME-CAMBREC with the motion insensitivity and data redundancy of KWIC. While this is certainly advantageous from a problem conditioning perspective, the Cartesian approach used by ME-CAMBREC and at least one other model-based T₂ mapping technique (25) can be used to separate reconstruction into N_ro independent inverse problems, simplifying the computation considerably. Ultimately, this trade-off allows ME-CAMBREC easier implementation and quicker reconstruction at the cost of parameter SNR relative to radial methods.

One other fast T₂ mapping protocol, curve reconstruction via principal component-based linearization with indirect echo compensation (CURLIE), uses PR-FSE, a model-based reconstruction, and the extended phase graph model (4). Although appearing at first glance to be very similar to ME-CAMBREC, CURLIE uses training data to effectively remove artifact from images using linear decompositions, then performs a voxelwise fitting to the EPG model. Thus, compared to the proposed method, CURLIE has major computational advantages, but applies an intermediate principal component-space rather than attempt to directly fit k-space signal to an underlying model. In the same vein, compressed sensing-based protocols which utilize sparse spaces in the parametric (TE) dimension (26) or a similar “model dictionary” dimension (27) can theoretically be used with the EPG model for accelerated T₂ mapping, especially when combined with a pseudo-random acquisition scheme.

Implementing ME-CAMBREC for volumetric coverage will present challenges for two reasons. As presented here, ME-CAMBREC used wider refocusing pulses compared to the excitation pulse, thereby requiring a slice gap if one wanted to implement a multi-slice acquisition. In principle, this limitation can be overcome by incorporating the known RF profiles into the reconstruction model, similarly to prior work (8). Also, under certain circumstances, multi-slice multiple spin echo acquisitions may be limited by specific absorption rate (SAR). However, ME-CAMBREC does offer the ability to use low-angle refocusing pulses without sacrificing image quality or quantitative accuracy, and this feature may be exploited to reduce the stringency of SAR limits or accelerate further by extending echo trains at the cost of added T₁ bias.

Finally, it should be noted that ME-CAMBREC as does not accommodate or account for non-mono-exponential transverse relaxation, as is known to occur in cerebral white matter due to the presence of myelin (28) and will occur whenever individual voxels include partial volume averages of two or more tissues with widely different T₂. One would expect this to be a particular problem in brain regions neighboring cerebral spinal fluid, although Figs 5 & 6 and a cursory analysis of data therein did not indicate any widespread problem. Extension of ME-CAMBREC to account for multi-exponential transverse relaxation would likely be SNR-limited and non-trivial to make effective. ME-CAMBREC will face similar challenges/limitations when motion or physiological noise sources significantly alter the signal from the model, although further study is necessary to assess such challenges.

CONCLUSIONS

The work presented here has demonstrated a novel regularized model-based reconstruction algorithm for generating T₂ maps from undersampled multi-echo data, such as those acquired via FSE sequences. A Cartesian acquisition scheme which is better tailored to its advantages than previously established k-space trajectories was also proposed and evaluated. The proposed method, dubbed Multiple Echo, Caesar cipher Acquisition and Model-Based REConstruction (ME-CAMBREC) generated T₂ maps with low error in computational, phantom, and human studies, and was demonstrated to be more efficient than a comparably accelerated non-FSE relaxometry protocol (DESPOT2). While other accelerated methods may have particular advantages, such as motion insensitivity, the ease of implementation of ME-CAMBREC combined with its demonstrated accuracy and precision, make it a potentially valuable tool in both research and clinical environments.