Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Oct 20;4:6675. doi: 10.1038/srep06675

Musical Interfaces: Visualization and Reconstruction of Music with a Microfluidic Two-Phase Flow

Sze Yi Mak 1,2, Zida Li 2, Arnaud Frere 2, Tat Chuen Chan 2, Ho Cheung Shum 1,2,a
PMCID: PMC4202207  PMID: 25327509

Abstract

Detection of sound wave in fluids can hardly be realized because of the lack of approaches to visualize the very minute sound-induced fluid motion. In this paper, we demonstrate the first direct visualization of music in the form of ripples at a microfluidic aqueous-aqueous interface with an ultra-low interfacial tension. The interfaces respond to sound of different frequency and amplitude robustly with sufficiently precise time resolution for the recording of musical notes and even subsequent reconstruction with high fidelity. Our work shows the possibility of sensing and transmitting vibrations as tiny as those induced by sound. This robust control of the interfacial dynamics enables a platform for investigating the mechanical properties of microstructures and for studying frequency-dependent phenomena, for example, in biological systems.

As a mechanical wave, sound can contain complicated information. In nature, animals, such as bats, whales, dolphins and elephants, use sound waves with different frequencies to find preys, navigate and communicate1. The prerequisite of these uses of sound is the ability to accurately detect sound for subsequent processing by the brain. Transmission of sound is therefore critical; it can take place in the form of a compressible wave within any medium, such as solid, liquid or gas, in descending speed of transmission and increasing spatial attenuation. Sound can also be transmitted along interfaces such as liquid-gas or liquid-liquid interfaces. Audible sound consists of vibration with a frequency ranging from 20 Hz to 20,000 Hz and an energy density on the order of 10−5 W/m2 2. Owing to the lower efficiency of sound wave transmission as compared to solid media, liquid is less commonly used for detecting and transmitting sound in artificial hearing devices. In human ears, the fluid motion in the cochlea sets the basilar membrane into vibrations; these vibrations are subsequently detected by the inner hair cell stereocilia bundle3,4,5,6 (Fig. 1a). Despite the relatively larger degree of attenuation of sound waves in the fluid-filled cochlea, the high sensitivity of the stereocilia bundle enables human hearing. This suggests that hearing with artificial fluid-based devices can potentially be realized if a highly sensitive detection mechanism is developed. At present, detection of sound wave in fluids can hardly be realized because of the lack of approaches to visualize the sound-induced fluid motion with sufficiently high sensitivity and resolution.

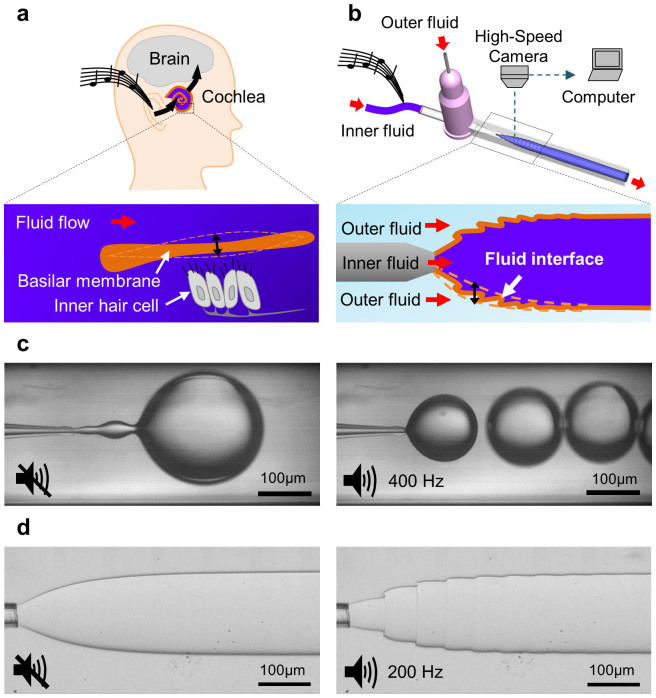
Figure 1. Schematics of hearing and the optical microscope images comparing jets with different interfacial tensions inside microcapillary devices.

Figure 1

Open in a new tab

(a) Schematic of hearing by human ear. (b) Schematic of hearing by the proposed “interfacial ear”. The inner and outer phases are driven by hydrostatic pressure. The tubing that directs the inner phase is attached on the membrane of a loudspeaker to introduce the vibration into the flow. (c) Optical microscope images of a co-flow of water-in-oil system in the jetting regime. Interfacial tension = 0.06 N/m. Left: No music is applied. Right: A musical note of 400 Hz is applied by a loudspeaker. (d) Visualization of the deformation of the passive interfaces in response to the applied vibration. Optical microscope images of a co-flowing jet with tripotassium phosphate and PEG constituting the inner and outer phase. Left: No external vibration is applied. Right: A musical note of 200 Hz is applied by a loudspeaker.

Despite the difficulty to detect sound waves in fluids, acoustics has been used in fluid manipulation. For instance, ultrasound can be applied to microfluidic systems to facilitate mixing of fluids7 and sorting of particles8. Surface acoustic waves (SAW) can be applied to microfluidic systems9,10 for pumping, mixing, droplet-generation10,11 and sensing12. While ultrasonic and SAW-based microfluidics involve high frequency acoustic waves, low frequency acousto-microfluidics is often overlooked and has thus been limited to applications in fluid control13,14,15. While microfluidic droplets have been used to generate electronic music16, to the best of our knowledge, no one has successfully retrieved sound waves by means of fluids. The development of acousto-microfluidics suggests a possibility for detection and visualization of sound in a fluid. Recently, all-aqueous systems have been applied to detect minute fluctuations induced by the stepper motor of syringe pumps17. Such passive interfaces may enable the retrieval of the minute vibration caused by sound wave in the form of interfacial ripples.

In this work, we demonstrate, for the first time, the visualization and reconstruction of music with a microfluidic two-phase flow with an ultra-low interfacial tension. In particular, we apply a sound-induced vibration to the inlet tubing, which transmits the vibration to the inlet fluid and causes the flow to fluctuate at the same frequency as the sound (Fig. 1b). The range of this “interfacial ear” is even wider than human ears, extending to the frequencies of infrasound. Our work shows the possibility of sensing and measuring tiny vibrations in fluidic flows. The aqueous-aqueous interface can serve as a versatile tool to detect any minute vibration as sophisticated as musical phrases in fluids. We demonstrate a robust way to apply and transmit sound-induced vibrations in fluids, with great potential as a platform for studying frequency-dependent phenomena, for example, the response of cells to vibration18.

Results

Music-induced interfacial ripple is uniquely observed in a liquid-liquid system with an ultra-low interfacial tension

We use a capillary microfluidic approach to visualize sound in an interface between two immiscible aqueous solutions (Fig. 1b, Supplementary Movie S1). A loudspeaker is connected to the tubing which directs the inner fluid. Sound resulting from the vibration of the membrane of the loudspeaker with vibration amplitude of about 1 μm causes the flexible tubing to vibrate, and the consequent vibration changes the driving pressure and the fluid flow rate periodically17,19.

Classical water-in-oil system has a high interfacial tension, typically in the order of tens of mN/m 20; thus the jet is highly susceptible to breakup due to Rayleigh-Plateau instability (Fig. 1c). When perturbed by tiny sound-induced vibrations, the jet often breaks up into droplets. Moreover, the water-oil interface does not display the waveform of the applied vibration. In contrast, by using two immiscible aqueous phases as the inner jet and outer continuous phases, the interfacial tension can be drastically reduced, making the aqueous jet less susceptible to break up and the interface more easily deformed17,21,22 (Fig. 1d). As a result, the aqueous jet becomes corrugated without breaking up into droplets. This unique property of the jet formed by an aqueous two-phase system (ATPS) provides the opportunity to demonstrate the vibration by the deformation of the interface. In our work, we tune the interfacial tension of the system to the order of 10−2 mN/m for visualization of interfacial ripple in a jetting regime. In addition to interfacial tension, viscosity of the fluids also affects the responses of the interface. High viscosity will lead to a high shear force, resulting in the suppression of the deformation of the interface and reduction of its responsiveness. The range of flow rate of the outer flow is 5 ml/h to 10 ml/h. The capillary number (Caout = μoutVout/γ) of the outer phase used in our experiment is on the order of O(0) to O(1), where μout and Vout are the viscosity and the mean velocity of the outer phase whereas γ is the interfacial tension. In this range of Ca values, viscous stress dominates interfacial tension effects. Under all operating conditions in our experiments, Caout + Wein ≥ O(1), where Wein is the Weber number of the inner jet. Therefore, the two-phase flow always stays in the jetting regime rather than the dripping regime23,24. An ideal fluid system for detection of sound should possess a low viscosity and a low interfacial tension. This observation explains why sound-induced responses can only be observed in an ATPS rather than a water-in-oil system, of which the interfacial tension is typically at least two orders of magnitude higher than that of ATPS. Although all the results are based on direct vibration of the tubing by the cone membrane of the loudspeaker, similar results are observed when the sound waves are amplified by focusing onto the tubing with a concave antenna.

Cymatics: Visualization of music with interfacial ripples

Due to the low interfacial tension, the aqueous-aqueous interface is sensitive to fluidic disturbances and can be easily deformed by them. For instance, fluctuation with a certain frequency can cause periodic ripples to form; this occurs even for fluctuations with amplitude as minute as those induced by sound. We demonstrate the responsiveness of the aqueous-aqueous interface to musical signals of different frequency, amplitude and waveform (see Supplementary Movie S2). In general, the frequency and the amplitude of ripples are expected to reflect the pitch and volume of the sound signals. At first glance, the frequency and the amplitude of ripples do increase with those of the applied musical signals (Fig. 2a).

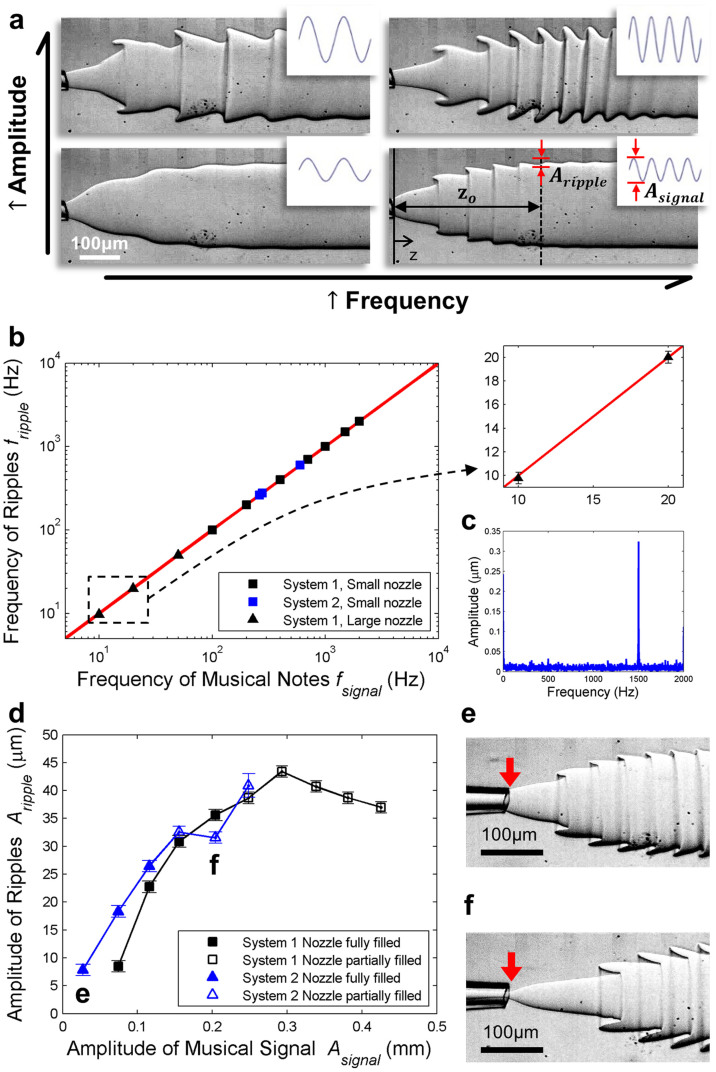
Figure 2. Visualization of the deformation of the passive interfaces in response to the applied vibration.

Figure 2

Open in a new tab

(a) Optical microscope images of the aqueous jet as the frequency and the amplitude of the musical signal increase from fsignal = 100 Hz to 200 Hz and from Asignal = 0.07 mm to 0.34 mm respectively. Corresponding input sound wave is displayed on the top right of each microscope image. Definition of Aripple and Asignal are illustrated in the bottom right images. The amplitude of ripple is defined as Aripple (z = z0), where z = 0 is at the tip of nozzle and z = z0 is at the minimum distance downstream where the jet no longer expands. The amplitude of musical signal refers to the vibration amplitude of the loudspeaker membrane. (b) Left: A log-log plot of frequency of ripples fripple as a function of the frequency of musical signal applied fsignal. The range of frequency tested is between 10 Hz and 2000 Hz. The straight line has a slope of one. Right: The magnified view showing two successive data points (fsignal, fripple): (10.00, 9.77 ± 0.5) and (20.00, 20.02 ± 0.5) in the range of infrasound. Each data point is obtained by averaging the results from three to six measurements. (c) A frequency spectrum obtained by analyzing a series of high-speed microscope images of an aqueous jet under the perturbation of a musical note of 1500 Hz, taken at 4000 fps. (d) Plot of amplitude of ripple Aripple against amplitude of musical signal Asignal. System 1 is composed of two immiscible aqueous solutions of sodium citrate and PEG while System 2 is composed of two immiscible aqueous solutions of tripotassium phosphate and PEG. In both systems, the PEG-rich phase constitutes the outer phase. System 1 has a lower viscosity ratio (μout/μin) than System 2. Each data point is obtained by averaging the results from ten measurements. Microscope images of the (e) fully-filled-nozzle regime and (f) partially-filled-nozzle regime.

To quantify the frequency response of the “interfacial ear”, different musical notes are applied to it and the resultant corrugated interface is captured using a high-speed camera. The radial vibration of the interface is traced by the vertical displacement of the interface in the two-dimensional microscope images. To characterize the operating frequency range and precision of the “interfacial ear”, we apply Fast Fourier Transform (FFT) to the displacement data and obtain the frequencies of the ripples induced by musical notes of frequencies ranging from 10 Hz to 2,000 Hz, which covers the frequency range of most notes of a standard piano and also the range of infrasound (<20 Hz). Within the operable amplitudes, the frequency of ripples matches that of the applied sound, as shown in Fig. 2b. The detectable frequency range is limited by the frame rate of the high-speed camera, the flow rates of fluids and the geometric dimensions of the microfluidic device. For our experiments, we pick a configuration that enables the capture of sound with audible pitch and volume. In the current microfluidic system, when the frequency of the sound goes beyond 2,000 Hz, the wavelength of ripples becomes very small and can hardly be measured. Technically, this problem can be solved by increasing the flow rate and frame rate of the camera. A microfluidic device with a larger nozzle diameter (>100 μm) is capable of detecting inaudible sound of frequency below 20 Hz. The expanded view on the right of Fig. 2b shows the data points, which are collected in the frequency range corresponding to infrasound using a device with a nozzle diameter of 125 μm. To demonstrate the system capability to differentiate sounds with different pitches with high accuracy, we compare the ripple frequency of two consecutive notes while progressively reducing their difference in frequency. An octave is the interval between two musical notes in which one has twice the frequency of the other. The pitch of modern music can be tuned based on twelve-tone equal temperament, where the frequency ratio between two adjacent notes equals to 21/12 25. Hence the base pitches are of smaller frequency differences. A#0 (29.1 Hz) is a semitone (the smallest interval) up from the base note A0 (27.5 Hz); these two notes have the smallest difference in frequency (Δf ~ 1.6 Hz). This is used as a minimum requirement for the frequency resolution in designing the “interfacial ear”. The frequency of ripples follows the frequency of the signal with an error bound of 0.5 Hz, as shown in the expanded view of Fig. 2b, which is significantly finer than the frequency resolution requirement of 1.6 Hz. Therefore, our method provides sufficient precision for recording musical signals.

The movement of the interface is caused by the fluctuations in the fluid flow. Intuitively, the degree of deformation increases with the amplitude of the fluctuation. Here, the amplitude of musical signal Asignal refers to the amplitude of the vibration of the loudspeaker membrane. As illustrated in the bottom right set of images in Fig. 2a, we define the amplitude of ripple (Aripple(z)) as the radial displacement of the interface measured at an axial distance z downstream from the nozzle. As the fluid moves downstream, the amplitude of ripples grows due to the expansion of the jet but decays due to the viscous stress from the surrounding fluids. To compare the jets subjected to different musical perturbations, we define a minimum axial distance, zo, downstream from the nozzle where the jet no longer expands and measure the amplitude of all ripples at z = zo for all jets obtained under different conditions. This effectively eliminates any effect due to jet expansion and decay due to viscous stresses. For small-amplitude ripples, the inner phase fully fills the nozzle, and thus the inner jet diameter at the nozzle is the same as the nozzle diameter (fully-filled-nozzle regime, Fig. 2e). In this regime, the amplitude of ripples increases with the amplitude of the musical signal applied (as shown by the filled symbols in Fig. 2d). However, if the amplitude of the ripple is so large that the inner phase does not fully fill the nozzle at all times (partially-filled-nozzle regime, Fig. 2f), the amplitude of ripples becomes uncontrolled. In addition, as the amplitude increases, the ripples adopt arrow-like shapes and the tips of the arrows approach the microchannel wall, resulting in the formation of a folded interface. Hence, the apparent Aripple(z) does not increase proportionately with the amplitude of the musical signal in the partially-filled-nozzle regime. Indeed, the frequency of ripples fripple increases linearly with the frequency of the musical signal fsignal while the amplitude of ripples Aripple increases with the amplitude of musical signal Asignal only when the inner phase fully fills the nozzle.

Visualization of sound signals of different waveforms

An effective sound visualization approach should be able to differentiate music with different timber. The timber of music is reflected by the difference in waveform of sound waves. Moreover, homophonic and polyphonic music have special quality of sound as a result of superposition of multiple waves. To characterize the detection limit of our proposed system, we subject the all-aqueous interface to sounds with different waveforms and homophonic music. The ripples are expected to evolve into different shapes with different applied waveforms. Clearly, a square wave provides a more abrupt change in pressure than a sinusoidal wave of the same frequency and amplitude. As a result, the interface is less smooth in shape when a square wave is applied (Fig. 3a, b). The waveform of harmonics, which is a superposition of two or more sinusoidal waves in which their frequencies are of simple ratios, is more complex; however, it can also be visualized in the form of ripples (Fig. 3c).

Figure 3. Visualization of sound signals of different waveforms.

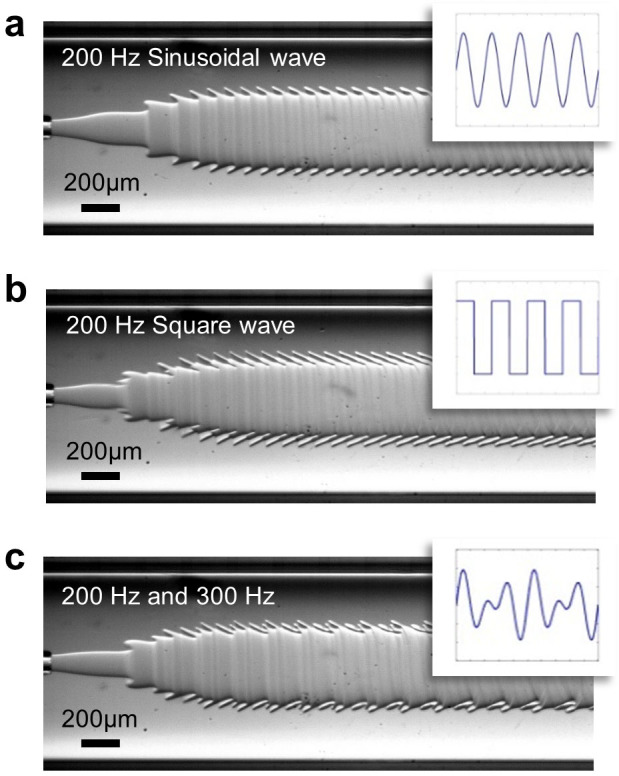
Figure 3

Open in a new tab

Varying the waveform of the musical signal from (a) a sinusoidal signal of 200 Hz to (b) a square signal of 200 Hz to (c) a composite signal (a superposition of 200 Hz and 300 Hz sinusoidal signals), while the amplitude is fixed at Asignal = 1 mm. Corresponding input sound wave is displayed on the top right of each microscope image.

Reverse cymatics: Reconstruction of music from all-aqueous interfacial ripples

After confirmation of the precise frequency response of our “interfacial ear”, we extend the recording of one single musical note to a piece of monotonic music with a single musical note playing at each instant. In Supplementary Movie S3, we perturb the fluids with a short phrase of Für Elise by Ludwig van Beethoven and analyze the resultant ripples. This piece is chosen because it is monotonic, simple in rhythm, covers a wide range of pitches, and contains musical notes with small frequency difference that requires a high frequency resolution.

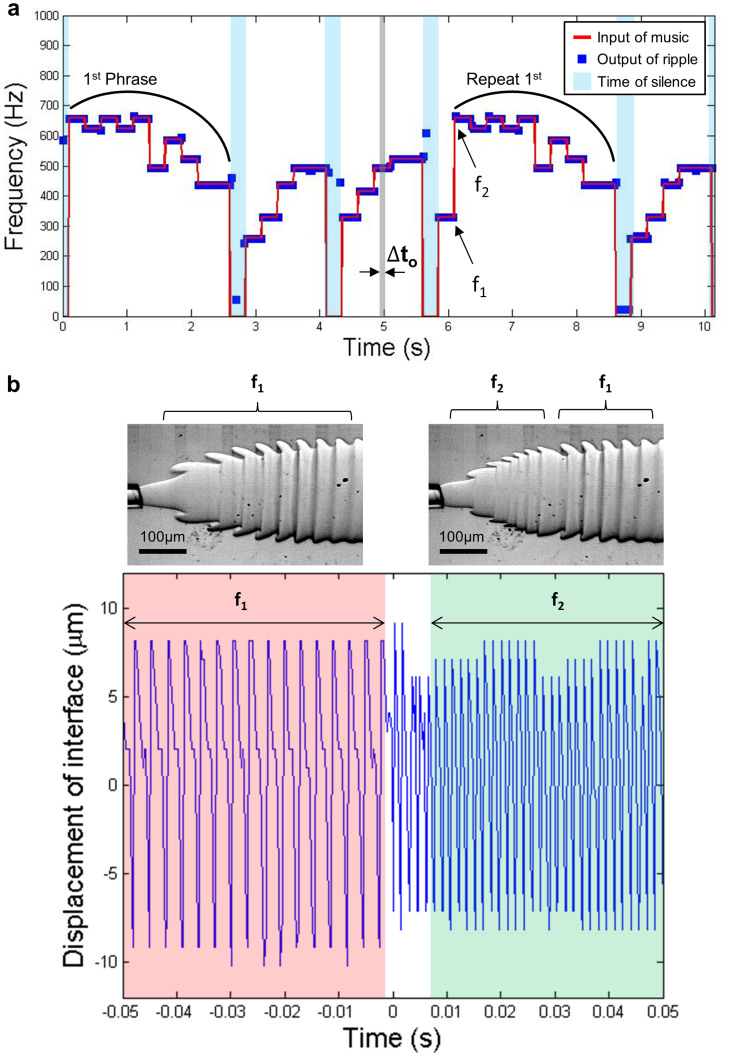
The resultant frequencies at different time periods are mostly the same as the corresponding pitch of the music for the ten seconds of recording displayed in Fig. 4a. The precision of frequency recording is tested with the two consecutive notes (D#2 = 622.3 Hz and E5 = 659.3 Hz) played in the first second. The output frequencies of the two consecutive notes are 625.0 ± 2.2 Hz and 656.3 ± 2.2 Hz respectively. The error bound of the frequency is ten-fold smaller than the required precision. Besides high accuracy, the output frequency mostly captures the frequency of the music correctly over the frequency range of 200 Hz to 700 Hz. The output frequency occasionally deviates from the frequency of the musical notes. These deviations can be discerned upon carefully listening to the output music. This is more likely to occur when the pitch of the note changes, for instance at t = 2.8 s and t = 5.6 s, due to the arbitrary selection of sampling data points for processing. The fluid interface actually responds with a higher temporal resolution (<10 ms) than the data processing allows, as shown by the displacement-time plot of interface and the high-speed images taken during the time interval when the frequency changes in Fig. 4b. The honest capture of this short music pieces confirms the reliability of the “interfacial ear”.

Figure 4. Reconstruction of frequency for Für Elise.

Figure 4

Open in a new tab

(a) Frequency-time plot of the musical notes played and the musical notes reconstructed by image analysis. The time interval (Δto = 33 ms) shaded in gray is the time interval between successive data points. The blue squares and the red lines denote the frequencies of ripples and of the musical notes played respectively. The time shaded in blue indicates the time of silence during which no music is played. The frequency range of this graph is confined to be between 0 Hz and 1000 Hz. The first phrase which begins at t = 0.1 s is repeated at t = 6.1 s. The procedure for recording music with our “interfacial ear” is demonstrated in Supplementary Movie S3. (b) The displacement-time plot of the interface with an abrupt change in the applied musical signal at t = 0 s (Bottom). Microscope images showing the shape of ripples before and after an abrupt change in the applied music (Top).

Discussion

In this paper, we demonstrate the visualization and reconstruction of music with a jet formed by an aqueous two-phase system. Sound wave, which is essentially a mechanical compressive wave, is directly displayed, for the first time, without converting the variation in pressure into signals of other forms, such as electrical ones, as in the case of traditional microphones. The response of ripples to sound with respect to frequency, amplitude, and time resolution has shown excellent robustness for reconstructing simple musical phrases.

The visualization of the frequency of sound in the form of ripples at the interface is enabled by tuning the flow rates of the fluids and the length scale of the micro-capillary device. These conditions define the range of sound frequencies our “interfacial ears” are sensitive to. At a higher interfacial velocity the ripples have a larger wavelength and are spaced further apart for easier visualization. In particular, a fast moving interface with an interfacial velocity on the order of tens of millimeter per second is essential for visualization and subsequent interpretation of sound waves with frequencies of over a thousand hertz. For instance, to visualize a 2000 Hz sound wave, an interfacial velocity of 0.03 m/s is achieved by increasing the flow rate of the fluids to around 10 ml/h and reducing the diameter of the nozzle to around 40 μm.

The amplitude response to sound is determined largely by the viscosities of the two phases. The two ATPSs (System 1 and 2) in our experiments have similar interfacial tensions, 0.03 and 0.06 mN/m, but different viscosity ratios, (μout/μin)|1 = 2.8 and (μout/μin)|2 = 23.1. For now we confine our discussion to the fully-filled-nozzle regime in which the amplitude of the ripples is more controlled. In this regime, System 1 shows a larger sensitivity of Aripple to Asignal than System 2, as it has a larger difference in Aripple per increment of Asignal (Fig. 2d). This confirms that a system with a lower viscosity difference between the two phases performs better in reflecting the amplitude of sound.

Our work shows the possibility of visualizing sound in a liquid-liquid system with low viscosity and low interfacial tension. It also suggests a way to sense tiny vibrations arising from other sources. Infrasound, which may cast potential hazards to health due to the sensitivity of human inner ear and other parts, despite being inaudible, can also be detected with our approach26. Cells are sensitive to minute vibrations at specific frequencies18. Hence, by allowing manipulation of fluid aided by acoustics, our acousto-interfacial approach has potential to provide a versatile platform for studies in acousto-biology27 and development of acousto-mechanical characterization tools.

Methods

Preparation of microfluidic flows

The device used in the experiment is a microcapillary co-flow device used in previous studies17. A round capillary with tapered tip is coaxially inserted in a square capillary. The diameter of the tip ranges from 30 to 200 μm and the internal dimension of the square capillary is 1.05 mm. The aqueous two-phase system (ATPS) is prepared by dissolving a polymer (PEG, 8.5–10 wt%, MW = 4000, 8000) and a salt (sodium citrate, 12 wt% or tripotassium phosphate, 7.5 wt%) in deionized water and centrifuged to form a top polymer-rich layer and a bottom salt-rich layer. Such ATPS is in equilibrium to ensure the absence of any net osmotic effect28. The interfacial tension between inner and outer phase is estimated to be ~0.03–0.06 mN/m. The capillary length, which describes the balance between interfacial force and gravitational force exerted on the liquid-liquid interface, is 0.46 mm, which is significantly larger than the wavelengths of the ripples (typically ~50 μm) observed. The viscosity ratio μout/μin ranges from 2.8 to 23.1. The polymer-rich layer is used as the outer phase while the bottom salt-rich layer is taken as the inner phase. The outer phase flows in the outer square capillary, and the inner phase flows in the inner round capillary. The two phases meet at the tip of the nozzle and form an expanding jet. To avoid the fluctuations introduced by the syringe pumps, both the inner and outer phases are driven hydrostatically (Supplementary Fig. S1). The inlet fluids are continuously supplied from open syringes without the plungers; the syringes are held at known heights above the microfluidic device, which is connected to the syringes via plastic tubing. The device is placed horizontally on a microscope stage for imaging. The height differences between the fluid levels and the stage are fixed to ensure constant flow rates. By setting the reservoir level at a height that ranges from 0.2 m to 1.2 m above the device, the range of flow rates used for the inner and outer flows can be controlled to 0.5–5 ml/h and 5–10 ml/h respectively.

Imaging and analysis

We observe the ripples generated on the interface of the jet with an inverted optical microscope (DM 180, Motic Inc.; XD-101, Jiangnan, Inc.) equipped with a high-speed camera (Phantom, V9; MotionPro X4, Redlake, Inc.) typically taking 4000 frames per second.

A series of high-speed images is first processed to enhance the sharpness of the interface. To obtain the frequency of ripples, we trace the vertical displacement of the interface at a fixed distance from the nozzle. The vertical displacement over time can be converted to the frequency domain via Fast Fourier Transform (FFT), resulting in a frequency spectrum (Fig. 2c). For a single frequency input, the frequency spectrum always shows a peak at the input frequency. The frequency output from image analysis of the ripples can be used to reconstruct the music as demonstrated in Supplementary Movie S3.

Preparation of sound tracks

The sound waves are generated with a laptop and played by a loudspeaker (SPA2210V, Philips). Unless otherwise stated, all sound waves are made as simple sine waves by Matlab with a sample rate of 44.1 kHz. To facilitate image-processing without presenting any arbitrary distortion of the music piece, Für Elise, is played at a pace of 0.25 second per note. Vibration of the sound is induced to the flow directly by attaching the tubing on the membrane of the loudspeaker; therefore, the tubing vibrates with the membrane of the loudspeaker to introduce variations in the driving pressure of the fluids in the tubing. The vibration amplitude of the membrane of the loudspeaker is measured with a CCD Laser Displacement Sensor (LK-G150, G3000, Keyence).

Author Contributions

S.Y.M., Z.L. and H.C.S. designed the project. S.Y.M., Z.L., A.F. and T.C.C. performed the experiments. S.Y.M., Z.L. and T.C.C. constructed the program for analyzing the data. S.Y.M. prepared the schematic drawings using MS PowerPoint and SolidWorks. S.Y.M. and H.C. S. wrote the manuscript. H.C.S. supervised the study. All authors commented on the paper.

Supplementary Material

Supplementary Information

Supplementary Information

srep06675-s1.doc (76KB, doc)
Supplementary Information

Supplementary Movie S1: Cymatics of Beethoven's Fifth Symphony.

Download video file (14.9MB, mov)
Supplementary Information

Supplementary Movie S2: Cymatics of some monophonic and homophonic musical notes.

Download video file (2.1MB, mov)
Supplementary Information

Supplementary Movie S3: Reverse cymatics of a song Für Elise and the music output by frequency analysis of the interfacial ripples.

Download video file (2.6MB, mov)

Acknowledgments

We thank Professor Liqiu Wang and Professor Lixi Huang for providing the equipment for high-speed microscope imaging and vibration measurement. This research was supported by the Early Career Scheme (HKU 707712P), the General Research Fund (HKU 719813E) sponsored by the Research Grants Council of Hong Kong, the Basic Research Program-General Program (JC201105190878A) from the Science and Technology Innovation Commission of Shenzhen Municipality, the Young Scholar's Program (NSFC51206138/E0605) from the National Natural Science Foundation of China as well as the Seed Funding Program for Basic Research (201211159090) and Small Project Funding (201109176165) from the University of Hong Kong.

References

  1. Popper A. & Schilt C. in Fish Bioacoustics Vol. 32 Springer Handbook of Auditory Research (eds JacquelineF Webb, RichardR Fay, & ArthurN Popper) Ch. 2, 17–48 (Springer New York, 2008). [Google Scholar]
  2. Roederer J. in The Physics and Psychophysics of Music Ch. 3, 76–112 (Springer US, 2009).
  3. Smith S. T. & Chadwick R. S. Simulation of the Response of the Inner Hair Cell Stereocilia Bundle to an Acoustical Stimulus. PLoS ONE 6, e181611 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Plack C. J. Auditory Perception. Handbook of Cognition. SAGE Publications Ltd. (SAGE Publications Ltd, 2004).
  5. Robert F. & Carole M. H. The sensory and motor roles of auditory hair cells. Nat. Rev. Neurosci. 7, 19–29 (2006). [DOI] [PubMed] [Google Scholar]
  6. Powers R. et al. Stereocilia Membrane Deformation: Implications for the Gating Spring and Mechanotransduction Channel. Biophys. J. 102, 201–210 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Yaralioglu G. G., Wygant I. O., Marentis T. C. & Khuri-Yakub B. T. Ultrasonic Mixing in Microfluidic Channels Using Integrated Transducers. Anal. Chem. 76, 3694–3698 (2004). [DOI] [PubMed] [Google Scholar]
  8. Liu Y. & Lim K.-M. Particle separation in microfluidics using a switching ultrasonic field. Lab Chip 11, 3167–3173 (2011). [DOI] [PubMed] [Google Scholar]
  9. Ding X. et al. Surface acoustic wave microfluidics. Lab Chip 13, 3626–3649 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Yeo L. Y. & Friend J. R. Ultrafast microfluidics using surface acoustic waves. Biomicrofluidics 3, 012002 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Schmid L. & Franke T. SAW-controlled drop size for flow focusing. Lab Chip 13, 1691–1694 (2013). [DOI] [PubMed] [Google Scholar]
  12. Länge K., Rapp B. & Rapp M. Surface acoustic wave biosensors: a review. Anal Bioanal Chem 391, 1509–1519 (2008). [DOI] [PubMed] [Google Scholar]
  13. Daniel C. L. et al. Frequency-specific flow control in microfluidic circuits with passive elastomeric features. Nature Phys 5, 231–235 (2009). [Google Scholar]
  14. Begley M. R. et al. Periodic response of fluidic networks with passive deformable features. Appl.Phys. Lett. 95, 203501 (2009). [Google Scholar]
  15. Langelier S. M., Chang D. S., Zeitoun R. I. & Burns M. A. Acoustically driven programmable liquid motion using resonance cavities. PNAS 106, 12617–12622 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Tan S. H., Maes F., Semin B., Vrignon J. & Baret J.-C. The Microfluidic Jukebox. Sci. Rep. 4, 4787 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Li Z., Mak S. Y., Sauret A. & Shum H. C. Syringe-pump-induced fluctuation in all-aqueous microfluidic system implications for flow rate accuracy. Lab Chip 14, 744–749 (2014). [DOI] [PubMed] [Google Scholar]
  18. Ng K. S., Zhou Z. L. & Ngan A. H. W. Frequency-dependent cell death by optical tweezers manipulation. J. Cell. Physiol. 228, 2037–2041 (2013). [DOI] [PubMed] [Google Scholar]
  19. Sauret A., Spandagos C. & Shum H. C. Fluctuation-induced dynamics of multiphase liquid jets with ultra-low interfacial tension. Lab Chip 12, 3380–3386 (2012). [DOI] [PubMed] [Google Scholar]
  20. Garstecki P., Fuerstman M. J., Stone H. A. & Whitesides G. M. Formation of droplets and bubbles in a microfluidic T-junction-scaling and mechanism of break-up. Lab Chip 6, 437–446 (2006). [DOI] [PubMed] [Google Scholar]
  21. Ziemecka I., van Steijn V., Koper G. J. M., Kreutzer M. T. & van Esch J. H. All-aqueous core-shell droplets produced in a microfluidic device. Soft Matter 7, 9878–9880 (2011). [Google Scholar]
  22. Geschiere S. D. et al. Slow growth of the Rayleigh-Plateau instability in aqueous two phase systems. Biomicrofluidics 6, 022007–022011 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Utada A. S., Fernandez-Nieves A., Stone H. A. & Weitz D. A. Dripping to Jetting Transitions in Coflowing Liquid Streams. Phys. Rev. Lett. 99, 094502 (2007). [DOI] [PubMed] [Google Scholar]
  24. Nunes J. K., Tsai S. S. H., Wan J. & Stone H. A. Dripping and jetting in microfluidic multiphase flows applied to particle and fibre synthesis. J. Phys. D: Appl. Phys. 46, 114002 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Cho G. J. The Discovery of Musical Equal Temperament in China and Europe in the Sixteenth Century. (Edwin Mellen, Lewiston, N.Y., 2003).
  26. Salt A. N. & Hullar T. E. Responses of the ear to low frequency sounds, infrasound and wind turbines. Hear. Res. 268, 12–21 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Solmaz M. E. et al. Optical stretching as a tool to investigate the mechanical properties of lipid bilayers. RSC Adv 3, 16632–16638 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Song Y., Sauret A. & Shum H. All-aqueous multiphase microfluidics. Biomicrofluidics 7, 061301 (2013c). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep06675-s1.doc (76KB, doc)
Supplementary Information

Supplementary Movie S1: Cymatics of Beethoven's Fifth Symphony.

Download video file (14.9MB, mov)
Supplementary Information

Supplementary Movie S2: Cymatics of some monophonic and homophonic musical notes.

Download video file (2.1MB, mov)
Supplementary Information

Supplementary Movie S3: Reverse cymatics of a song Für Elise and the music output by frequency analysis of the interfacial ripples.

Download video file (2.6MB, mov)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES