Review of treatment assessment using DCE-MRI in breast cancer radiation therapy

Abstract

As a noninvasive functional imaging technique, dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is being used in oncology to measure properties of tumor microvascular structure and permeability. Studies have shown that parameters derived from certain pharmacokinetic models can be used as imaging biomarkers for tumor treatment response. The use of DCE-MRI for quantitative and objective assessment of radiation therapy has been explored in a variety of methods and tumor types. However, due to the complexity in imaging technology and divergent outcomes from different pharmacokinetic approaches, the method of using DCE-MRI in treatment assessment has yet to be standardized, especially for breast cancer. This article reviews the basic principles of breast DCE-MRI and recent studies using DCE-MRI in treatment assessment. Technical and clinical considerations are emphasized with specific attention to assessment of radiation treatment response.

Core tip: Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) has shown great potentials not only in diagnosis, but also in therapy. DCE-MRI is a promising technique for assessing breast cancer radiation treatment due to its inherent sensitivity to the microvascular environment changes. Correlative studies have demonstrated proof concepts of DCE-MRI parameters as potential biomarkers. This article reviews the basic principles of breast DCE-MRI and recent studies using DCE-MRI in breast treatment assessment. Future clinical trials and research works are needed to develop standardized DCE-MRI assessment methods, towards the goal of individualized radiation therapy.

INTRODUCTION

Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is an advanced MRI technique that can be used to acquire tissue functional information noninvasively. Following the administration of low molecular weight contrast agent (CA), DCE-MRI is sensitive to microvessel density and vascular permeability differences that can be associated with tumor angiogenesis. Because of this merit, DCE-MRI has been investigated in various oncologic tasks including early diagnosis[1-5], tumor staging[6,7], treatment planning[8,9], and treatment response assessment[10-14]. To assess treatment response, the acquisition of pre-treatment DCE-MRI and post-treatment DCE-MRI scans are required to measure treatment induced changes[14,15]. The change could be quantitatively characterized by a few parameters, which can be derived in the analysis of the DCE-MRI data. For intuitive comparison, simple semi-quantitative information can be obtained from the features of CA concentration evolution curve[16]. The quantitative functional information, such as micro-vascularity permeability, tissue perfusion and cellular density, must be obtained through the application of an appropriate pharmacokinetic model.

As a potential treatment assessment tool, DCE-MRI’s application in breast cancer radiation treatment is of our particular interest. Currently, breast cancer is one of leading incidences in women. Earlier statistics shows one out of eight (12.5%) women will eventually be affected by breast cancer during her lifetime[17]. Since 1990, the death rate of breast cancer have steadily decreased in the United States due to earlier detection and improved treatment[18], and radiation therapy (RT) has become an important technique in breast cancer treatment. Currently, conserving treatment consisting of lumpectomy followed by 6 wk of daily external beam RT has become one of the common treatment regimes in United States. At the same time, some advanced radiation treatment techniques have been proposed to neutralize complexities in breast cancer treatment[19-21]. With its intrinsic superiority in soft tissue contrast and added ability of vascularity measurement, DCE-MRI is a particularly attractive technique in early assessment of breast cancer radiation treatment. The value of using DCE-MRI as a tool for breast cancer radiation treatment assessment relies on the accuracy of quantitative DCE-MRI parameters derived by modeling injected CA pharmacokinetics. However, this is far from straightforward[15]. Some DCE-MRI technical factors will potentially affect the consistency of measured parameters accuracy. For example, differences in pharmacokinetic parameters were observed using different temporal resolution and spatial resolution during image acquisition, and the effect of this tradeoff has yet to be clarified[22]. For clinical consideration, different pharmacokinetic models as well as the interpretation may lead to biased results[23]. Thus, optimizing and standardizing DCE-MRI measurement methods in breast cancer radiation treatment assessment presents as a prerequisite for its clinical application.

In this article, we outline the basic principles in breast DCE-MRI methodology and highlight some relevant techniques and theories in DCE-MRI application. We then present the current findings to date and discuss future directions for DCE-MRI in breast cancer radiation treatment assessment.

DCE-MRI MEASUREMENT AND ANALYSIS METHOD

Basic principles

DCE-MRI involves a sequential acquisition of magnetic resonance images of tissue before and after the intravenous injection of CA. The CA is usually a small molecular weight compound such as gadopentetate dimeglumine. T₂^* weighted MRI can be used right after the administration of CA in a few seconds to observe CA first-pass effect which contains perfusion information. Since the first-pass T₂^* effect is transient, the rapid imaging method performed over a single slice through tissue-of-interest (TOI) is necessary. This is of limited value in breast study because of the necessary larger volume coverage for comprehensive disease morphology assessment[24]. In contrast, T₁-weighted DCE-MRI technique is more commonly used in breast cancer research.

The T₁-weighted DCE-MRI is usually used over a longer time course in several minutes to measure the accumulation of low molecular T₁-shortening paramagnetic CA in the tissue. When CA enters into the tissue-of-interest, the tissue T₁ value decreases to an extent which is determined by the CA concentration. A CA concentration evolution curve as a function of time can be acquired from sequentially sampled T₁-weighted magnetic resonance images signal intensity at the TOI[25]. The CA concentration at each time point after the administration, C(t), is calculated from longitudinal relaxation rate R₁(t) [i.e., the inverse of T₁(t)] and the longitudinal relaxation rate R₁₀ before the CA administration with assumed linear dependence[26]:

R₁(t) = rC(t) + R₁₀ (1)

r is the longitudinal relaxivity of the CA at certain magnetic field strength. The conventional T₁ measurement methods are usually based on inversion recovery spin echo technique. This theory follows a spin inversion and waits for an inversion time TI before the data acquisition. Sometimes, multiple TIs are necessary to accurately estimate a wide range of T₁ values[27,28], which is the major contribution of long scan time. To reduce the scan time with uncompromised image quality, many T₁ scanning methods have been proposed in brain research domain[29-32]. Another T₁ mapping approach is to use multiple flip angles scans. To reduce imaging time, T₁ value can be obtained by simple dual flip angles technique[33]. In this method, the ratio of signals of two T1-weighted MR scans with different flip angle φ and ψ is expressed as Ρ. With the general assumption about echo time TE < T₂^*, T₁ value can be calculated by equation (2):

Math 6

Math 6.

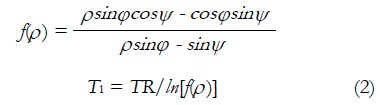
Math(A1).

TR is denoted as repetition time. equation (2) is used for both R₁(t) and R₁₀ calculation. To get R₁₀ information, two additional T1-weighted MR scans must be performed prior to DCE-MRI scan to get T₁ baseline information. These two scans with different flip angles are also called T1-calibrations. The following DCE-MRI scans are then acquired with flip angle φ (or ψ), and R₁(t) is derived using the DCE-MRI signal at time point t and the T1-calibration with flip angle ψ (or φ) in equation (2). After applying longitudinal relaxation information into equation (1), the CA concentration evolution curve then can be expressed in pixel-by-pixel pattern or volume-of-interest pattern.

For image acquisition, fast T1-weighted sequence is usually adopted for clinical studies. To cover the large breast imaging volume, the imaging time for each frame is relatively longer. Currently, the typical temporal resolution is about 1 min covering the whole breast with three-dimensional fast (3D) spoiled gradient echo (SPGR) dynamic sequence[34,35]. A recent feasibility study demonstrated that the temporal resolution could potentially be enhanced when compressed sensing theory was employed to reconstruct undersamped acquisitions[36].

Semi-quantitative analysis

Semi-quantitative analysis is usually performed on MR signal intensity-time curves or CA concentration evolution curves. In 1998, Daniel et al[37] proposed a patient classification scheme based on visually inspection on MR signal intensity-time curve shape. This scheme defines 5 types of curves. A change in the curve shape type to a higher number is considered as a transformation to a more aggressive type. For a more quantitative approach, the enhancement ratio (ER), which is the percent increase of MR signal intensity at the first acquirement after CA administration (also known as early contrast uptake ECU), is reported as a prediction of tissue physiological environment for routine clinical applications[38]. At the same time, some other quantities, such as initial wash-in rate, the wash-out rate, the maximum point, and extrapolation point were associated as important parameters for the description of curve shape. In the analysis of CA concentration evolution curve, the most frequently used parameter is the initial Area Under the Curve (iAUC_τ). iAUC_τ denotes the integration of CA concentration evolution curve from injection point (t = 0) to a certain time point (t = τ), and it parameterizes the initial rise of the evolution curve. The concept of onset time representing time lag between CA injection and the appearance of contrast in the tissue is also a commonly used biomarker. Similarly, the gradients of CA uptake and washout as well as the maximum concentration have been investigated in some studies[39,40]. Rigorous mathematic models were also introduced to describe the CA kinetic curve. For example, Fan et al[41] developed an empirical mathematical model (EMM) to parameterize the mathematical behavior of CA concentration evolution curve in transplanted rodent prostate tumors:

Math 7

Math 7.

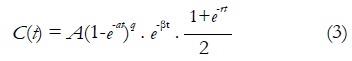
Math(A1).

A is the upper limit of CA concentration, α is the rate constant of CA uptake, β is the overall rate of CA washout, γ is the initial rate of CA washout, and q is the related to the radius of curvature of C(t) at the transition from first-pass to initial washout. Results showed fitted parameters from EMM demonstrated the significant difference between metastatic tumors and nonmetastatic tumors. The same model was also demonstrated to be effective in differentiation of benign lesions from malignant lesions in a human breast study[42].

Quantitative analysis

In quantitative analysis, biological parameters depicting vascular permeability, tissue perfusion and extracellular volume fraction can be derived from CA concentration evolution curves by fitting into an appropriate pharmacokinetic model. For breast tissue, the most widely used pharmacokinetic model is the one proposed by Tofts et al[43] in 1991. This two-compartment model describes the bidirectional transendothelial movement of CA between blood plasma and the extravascular-extracellular space (EES) through capillary walls (Figure 1). There are three functional parameters in this model: K^trans, the transport rate of CA from blood plasma to EES; k_ep, the transport rate describing the return of CA from EES to blood plasma, and v_e, the volume fraction of EES in tissue. The three parameters are related by the equation k_ep = K^trans/v_e; as a result, K^trans and v_e were reported in most breast DCE-MRI studies. The measured CA concentration C(t) consists of two components:

Figure 1.

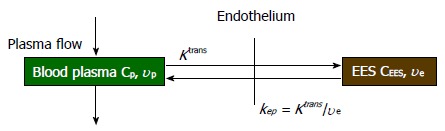
A sketch of two-compartment model. K^trans: Transport rate of CA from blood plasma to EES; k_ep: Transport rate of CA from EES to blood plasma; υ_e: Volume fraction of EES. The three quantities are related by k_ep = K^trans/υ_e. EES: Extravascular-extracellular space.

C(t) = C_EES(t) + v_pC_p(t) (4)

In equation (4), C_EES(t) is the CA concentration in EES, C_p(t) is the CA concentration in blood plasma, and v_p is the plasma volume fraction in the tissue[44]. The C_EES(t) term can also be expressed by the Kety Rate Law as the convolution of C_p(t) with an exponential term[45]:

Math 8

Math 8.

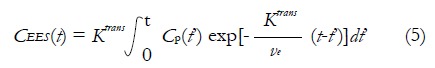
Math(A1).

K^trans is the CA extravasation rate, and v_e is the EES volume fraction. Tofts argued that plasma volume fraction v_p was very small for many TOIs including breast, so the contribution from C_p(t) in equation (4) is neglected. Then equation (5) can be rewritten as equation (6), which is referred as Standard Tofts Model:

Math 9

Math 9.

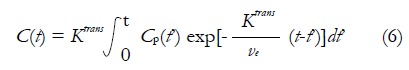
Math(A1).

The knowledge of C_p(t) is acquired separately from pharmacokinetic model and will be discussed later.

Though the Standard Tofts Model is acceptable in tumors with no large increase in blood volume, the assumption is likely to be invalid in some contexts as blood volume can increase markedly. As a result, some investigators incorporated the effects of possible significant vascular signals[46,47], and equation (6) is added by an additional vascular term:

Math 10

Math 10.

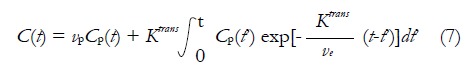
Math(A1).

The above equation is frequently called Extended Tofts Model. It was argued that Extended Tofts Model could be reliable in the region with higher vascular signal (abdomen, v_p up to 0.3) than the region with lower corresponding signal (brain, v_p up to 0.005)[48].

It has to be pointed out that both standard tofts model and extended tofts model are applied to the CA concentration evolution curve C(t), which is oftenly obtained by equation (1). However, the linear dependence of CA concentration and longitudinal relaxation change is not always the case, because this statement is equivalent to assuming that interstitium behaves as a homogeneous solution. To use equation (1), the water exchange from the extravascular intracellular space (EIS) to the EES must be sufficiently fast; but in practice, this is not always guaranteed[49-51]. equation (1) is then modified by taking Bloch equations into account[52]:

Math 11

Math 11.

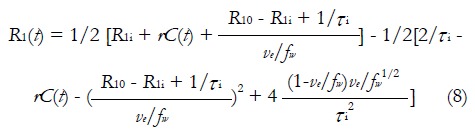
Math(A1).

R_1i is the intracellular longitudinal relaxivity, r is the CA longitudinal relaxivity, C_p(t) is the CA concentration in blood plasma, v_e is EES volume fraction, τ_i is the average intracellular water lifetime, and f_w is the fraction of water that is accessible to mobile CA. Since the Standard Tofts Model doesn’t rely on the fast water change assumption, the C(t) can be replaced by equation (6), leading to “Fast-Exchange Regime” FXR Model:

Math 12

Math 12.

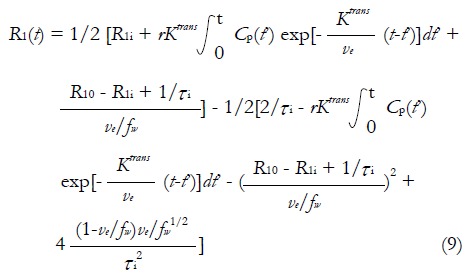
Math(A1).

In practice, R_1i is set to R₁₀, and f_w is assigned as a constant between 0 and 1. As seen in equation (9), a new variable τ_i is introduced in FXR Model. In theory, τ_i is the measurement of cell size. Presumably, as tumor cells apoptose in response to effective treatment, an decrease of τ_i would be observed. The utility of this parameter has yet to be fully studied[52].

Compared to the two-compartment models, the multi-compartment model has a potential capability of more precise description of pharmacokinetics inside human body. In a pilot study on mammary DCE-MRI, the tumor was modeled by 4 compartments and three of them were accessible to the CA from the central compartment (blood plasma). In addition, a peripheral compartment was introduced to distinguish normal tissues from the tumor[53]. Although the tumor heterogeneity was considered in this model, the in-tumor exchange pattern was still vague. As a nature of the multi-compartment model, the mathematic complexity limits the model’s capacity in breast DCE-MRI study.

Aside from the conventional compartmental models, distributed-parameter (DP) models are seen as another category of DCE-MRI pharmacokinetic model. While the conventional compartmental models have been widely used for more than two decades, they may not possess sufficient realism CA concentration gradients within compartments are assumed to be zero; consequently, CA is assumed to distribute the compartments on arrival instantaneously[54]. On the contrary, DP models describe concentration gradients in vascular compartment as a function of both space and time. Several DP models have been proposed[55,56], but the application in breast clinical study is far from prevalent.

In all pharmacokinetic models mentioned above, the information of CA concentration in blood plasma at each time point C_p(t), which is also known as Arterial Input Function (AIF), must be known prior to the model fitting. This knowledge can be achieved by imaging the major blood pool inside the field of view of images during DCE-MRI scan. For example, the study performed by Rijpkema et al[57] automatically extracted AIF data from DCE-MRI data in head-and-neck region tumor, prostate tumor and brain tumor cases. Unfortunately, such measurement is not feasible for clinical breast cancer studies because no large vasculature is qualified for MR sampling in breast tissue. Though Port et al[58] was able to acquire individual AIF through the visualization of aorta in the breast tumor study, the special procedure was not standardized in clinical protocols. Another approach is to use a population based AIF as an approximation of individual AIF[59,60]. A commonly used model is expressed by a bi-exponential decay [25]:

C_p(t) = D[a₁ exp(-m₁t) + a₂ exp(-m₂t)] (10)

D is the CA administration dose as per unit of bodyweight. The two terms in this curve correspond to the fast dynamic equilibrium of CA between blood plasma and EES (represented by a₁ and m₁) and the slow renal removal of CA (represented by a₂ and m₂). Several groups of parameter values were reported[44,61].

As can be observed, appropriate AIF is important for accurate quantitative DCE-MRI analysis. However, current approaches in AIF analysis are far from satisfactions. Some investigators have made a lot of efforts in quantitative DCE-MRI analysis in absence of AIF knowledge. Inspired by positron emission tomography, Yankeelov et al[62] proposed a reference region model in 2005. This compartmental model compares the TOI’s CA concentration evolution curve shape to that of a reference region; as a result, the need of AIF information is eliminated. Based on two-compartment model, CA diffuses from blood plasma into EES of the reference region and the TOI respectively, and no exchange of CA exists between the reference region and the TOI. Following equation (1), the longitudinal relaxation signal for TOI, R_1,TOI(t), can be derived from reference region’s longitudinal relaxation signal R_1,Ref.Region(t):

Math 13

Math 13.

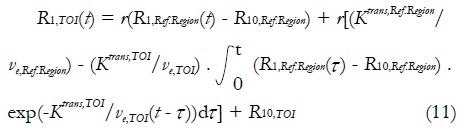
Math(A1).

As can be seen, the K^trans,TOI and v_e,TOI must be known in the reference region model. In the mouse tumor study, these values were assigned to the muscle values from publications. But evidently, individual variation of K^trans and v_e values of the selected reference region may result in errors in the values of TOI.

The aforementioned pharmacokinetic models are organized in a hierarchal scheme in Figure 2. To get the functional parameters, appropriate model fitting algorithm must be applied to the DCE-MRI data. For clinical application, the mathematical fitting method should to be fast and accurate. Currently, non-linear Levenberg-Marquart algorithm have been widely used in DCE-MRI studies[63]. Some other fitting methods also have been investigated[64,65]. In some cases, however, the convergence of the fitting algorithm is not guaranteed, thus the accuracy of model fitting may be compromised. Schmid et al[61] raised a semi-parametric approach with which the AIF is convolved with a set of B-splines to produce a design matrix from Bayesian penalized spline models (P-spline). The model parameter is then obtained from the deconvolved response function. At a cost of computation time, the semi-parametric technique was suggested to be more accurate when traditional fitting methods were poor during in vivo validation.

Figure 2.

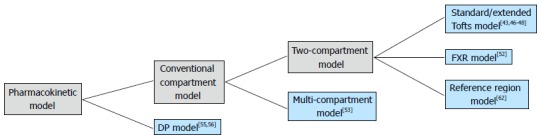
A hierarchical relationship diagram of the introduced pharmacokinetic models. DP: Distributed-parameter; FXR: Fast-exchange regime.

DISCUSSIONS ON DCE-MRI IMPLEMENTATION AND ANALYSIS IN RADIATION TREATMENT ASSESSMENT

Biologically optimized radiotherapy is a novel technique in which a treatment plan is tailored individually to emphasize variations of pathological context[66]. This approach is made possible by the assessment of treatment response, an indispensable tool in the evaluation of new treatment techniques. As a non-invasive approach, the conventional medical images, including X-ray, ultrasound, computed tomography (CT) and MRI, have been used to evaluate the radiation treatment through the tumor morphological assessment[67]. However, this approach may be of limited value in gauging the radiation treatment efficacy because the tumor may have already developed its radiation resistance when the observation of morphology change is available[68]. In addition, the population-based evaluation standard in patient’s follow-up care after the radiation treatment may not be optimal considering the pathological variations among individuals. The functional analysis of cancer treatment with the possible individualized standards may be a promising approach. The reliability and validity of the functional assessment has been proved in some pilot studies[69,70]. In the radiation treatment context, the non-invasive functional imaging during the early stage of the fractionated therapy would be promising in providing early evidences in treatment management. The unnecessary systemic toxicity and the treatment delays could be avoided as treatment plans could be optimized based on individualized pathological analysis during the treatment regime[71].

The non-invasive function imaging approach is also valuable in the development of advanced treatment techniques. The recent progress in breast cancer radiation treatment allows the accurate delivery of a high dose in one or several fractions. Due to the unconventional dose size and fraction scheme, the biological response of the new techniques should be fully investigated in view of safety and effectiveness. One of the factors of radiation response is tumor oxygenation. Radiobiology theory claims that hypoxia leads to decreased radiation damage induced cell death with an increased level of DNA repair enzymes and radial scavengers[68]. Hypoxia can also cause genome changes which favor the radiation resistant cell population, thus promoting the development of cells with more aggressive phenotypes[66,72-74]. The varying degree of hypoxia is characterized by microvasculature abnormalities, including abnormal microvessel architectures and an increased permeability[75]. Due to the natural sensitivity of the microvascular environment, DCE-MRI measurement parameters were studied in correlation with physiological variables at the breast site. Some of the results are listed in Table 1. Although histopathological studies have shown discrepancies in the outcome, the results suggest that DCE-MRI is suitable for RT assessment of perfusion, permeability and oxygenation[66].

Table 1.

Dynamic contrast-enhanced magnetic resonance imaging parameter correlations with physiological parameters at breast tissue

Ref.	Correlation		Direction of correlation	P
	Physiological parameter	DCE-MRI measurement
Buadu et al[76], 1996	MVD	Amplitude	+	< 0.01
		Slope maximum	+	< 0.01
		Enhancement Maximum time	-	< 0.01
		Tumor size	..	NS
Stomper et al[77], 1996	DNA S-phase percentage	Signal enhancement amplitude	..	NS
		Signal enhancement rate	..	NS
		Signal washout	..	NS
Hulka et al[78], 1997	Tumor grade	RSI	+	< 0.01
Matsubayashi et al[79], 2000	Peripheral-central MVD ratio	Early rim enhancement	+	0.048
	Peripheral-central fibrosis ratio	Early rim enhancement	-	< 0.01
	Central-peripheral fibrosis ratio	Delayed rim	+	0.013
Gianfelice et al[80], 2003	Residue tumor percentage after MRIgFUS	ISI	+	NR
		MDF	+	NR
		PEI	+	NR
Su et al[81], 2003	VEGF	Apparent Vb	..	NS
		In-flux rate and distribution volume in interstitial space (VeK1)	..	NS
		Out-flux rate (K2)	..	NS

NS: Not significant; NR: Not reported; RSI: Relative signal intensity; MVD: Microvessel density; ISI: Increase in signal intensity; MDF: Maximum difference function; PEI: Positive enhancement interal; Vb: Vascular volume; VEGF: Vascular endothelial growth factor.

Conventionally, the workflow of RT consists of CT simulation, radiotherapy planning and treatment delivery. Specifically, a breast cancer patient may be scanned with CT simulator to obtain the CT data for treatment planning, as shown in Figure 3A. Based on the CT data, a state-of-the-art RT plan can be developed with a conformal dose distribution, as shown in Figure 3B and 3C. The conventional workflow is summarized in Figure 4A for an easy appreciation. The conventional workflow may, however, miss one critical stage of treatment: treatment assessment. Effective treatment assessment would not only potentially help optimize the radiation treatment strategy, but also could provide valuable insights on the future development of RT. As shown in Figure 4B, the proposed workflow of RT consists of four critical components: CT simulation, radiotherapy planning, treatment delivery and treatment assessment. To assess treatment response using DCE-MRI, one DCE-MRI scan must be obtained before the treatment for baseline data. In addition to standard CT image, the pre-treatment DCE-MRI scan can also be used in target delineation during treatment planning. After radiation treatment, at least one post-treatment DCE-MRI scan must be acquired, and the DCE-MRI parameters derived by the semi-quantitative analysis and/or the quantitative analysis will be compared to the corresponding baseline values. Multiple post-treatment scans allow the longitudinal study of biological response through the parameter dynamic change. Figure 5 illustrates an example of pre-treatment and post-treatment DCE-MRI image comparison from a selected patient. Table 2 lists some studies of the DCE-MRI application in breast cancer radiation treatment assessment. Currently, limited studies have been done in this specific area; further study focusing on breast radiation response assessment is desirable and urgent. In addition to the radiation treatment assessment studies, some representative breast non-radiation treatment studies are also included to provide valuable references and insights on the DCE-MRI application in radiation treatment assessment.

Figure 3.

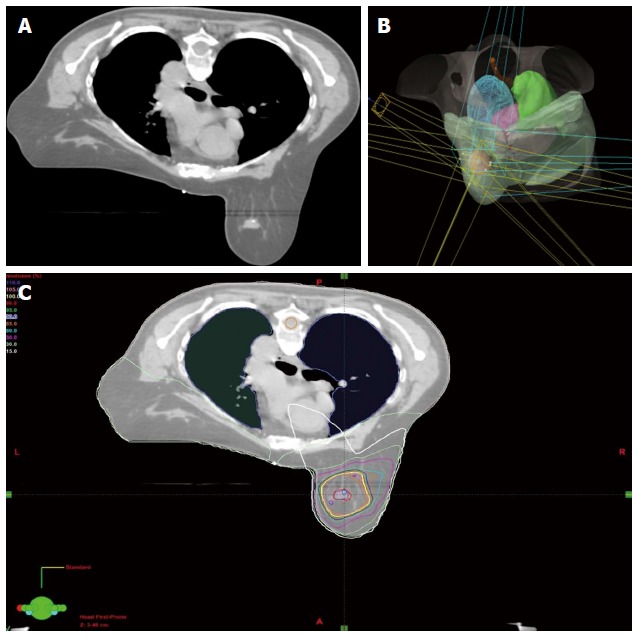
Radiation treatment planning. A: A computed tomography simulation image for a selected patient breast stereotactic body radiosurgery (SBRT) treatment plan; B: 3D planned beams view for the selected patient’s SBRT plan; C: Calculated conformal dose distribution of the selected patient’s SBRT plan.

Figure 4.

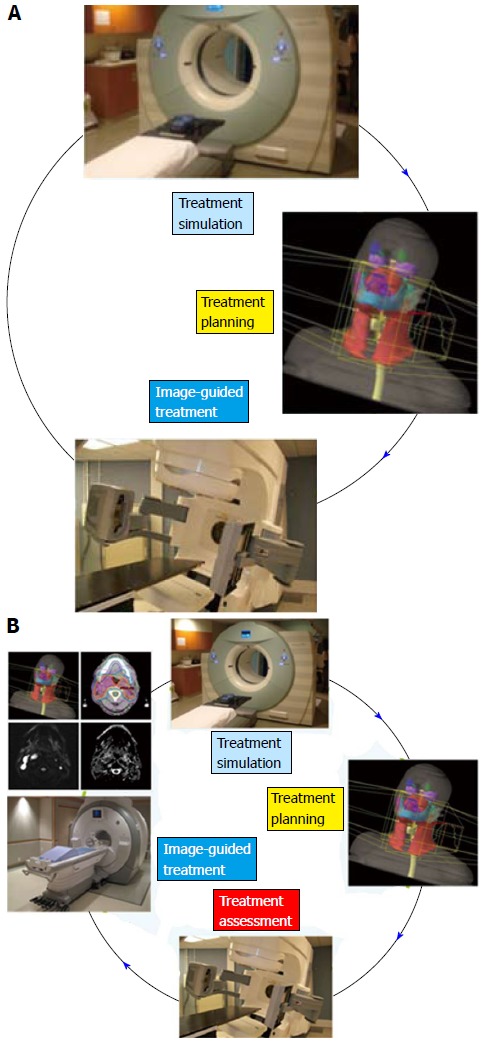
Conventional radiation treatment workflow. The proposed workflow (A) with treatment assessment component (B). Radiation treatment assessment can be used in plan optimization based on understanding towards biological response.

Figure 5.

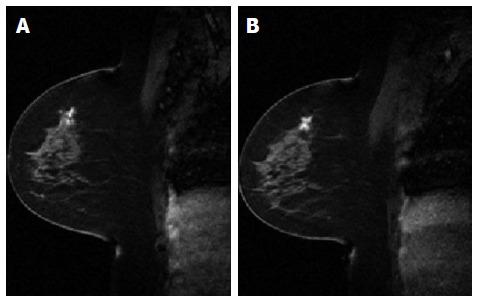
A comparison between pre-treatment dynamic contrast-enhanced magnetic resonance imaging image (A) and post-treatment dynamic contrast-enhanced magnetic resonance imaging image (B).

Table 2.

Dynamic contrast-enhanced magnetic resonance imaging studies in breast cancer treatment assessment

Ref.	Treatment method	DCE-MRI measurement	Major results
Dao et al[82] 1993	Conserving radiation therapy	Signal intensity	The signal intensity over time in localized fibrosis showed a different pattern from the one in tumor recurrence; early increased signal intensity of the lesion within 3 min after CA administration were observed in recurrent tumors
Drew et al[83] 2001	Neoadjuvant chemoradiotherapy	DCE-MRI image	DCE-MRI detected the presence of residual disease with 100% accuracy
Hayes et al[16] 2002	Neoadjuvant chemotherapy	Ktrans	The absolute change in the Ktrans values correlated negatively with the pretreatment values. The trend is more obvious for responding patients
Martincich et al[38] 2004	Primary chemotherapy	ECU	ECU reduction was associated with a MHR (OR = 2.50, 95%CI: 0.263-23.775); no statistical significance was observed (P = 0.42)
Overmoyer et al[84] 2004	Antiangiogenic drug	Kep	Correlative studies suggested a reduction of tumor Kep and tumor MVD
Wedam et al[85] 2006	Antiangiogenic drug	Ktrans and ve	Ktrans decreased by 34.4% (P = 0.003), and ve was decreased by 14.3% (P = 0.002) after the treatment using bevacizumab
Yankeelov et al[52] 2007	Neoadjuvant chemotherapy	Ktrans, ve, and τi (average intracellular water lifetime)	Significant (P < 0.05) changes were seen in Ktrans and ve; Ktrans in voxels with values in 0.2-0.5 min-1 before treatment were found decreased (P < 0.035)
Chang et al[86] 2013	SBRT	iAUC5min	The mean iAUC5min in GTV increased from 1.93 ± 0.20 mmol-min to 2.31 ± 0.16 mmol-min, about 16% (P = 0.012) after treatment

Highlighted studies were related to radiation treatment. DCE-MRI: Dynamic contrast-enhanced magnetic resonance imaging; ECU: Early contrast uptake; MHR: Major histopathological response; GTV: Gross tumor volume; SBRT: Stereotactic body radiotherapy.

Although DCE-MRI is a promising and a powerful tool for assessing treatment response, there are several technical factors to be considered during its clinical implementation, which are crucial to the precise meaning of the derived results. Some key points in DCE-MRI analysis will be briefly discussed below to provide some valuable references for the future work with specific interest on DCE-MRI radiation treatment assessment.

T₁ measurement uncertainty

Of all available fast T₁ measurement techniques, SPGR imaging with dual flip angles has the superiority in noise efficiency compared with others[30,87]. For high precision T₁ measurement which is often necessary in brain studies, multiple flip angle pairs can be adopted to minimize the statistical uncertainty of measured values. In the breast region, acceptable accuracy in T₁ value can be achieved if the optimized flip angle pair is found. These two optimal angles are obtained by minimizing T₁ variance which comes from the manipulation of the error propagation theory on equation (2) above[33]. In another pilot study of Deoni et al[30], it was argued that optimization of T₁ accuracy can be achieved when the product of normalized dynamic range and the fractional signal is maximized. Both methods yield similar optimal flip angle pairs for a certain TR and T₁ range. In a simulation study of breast pharmacokinetic parameter estimation[88], both K^trans and v_e were proved to be overestimated if tissue T₁ is underestimated; on the contrary, if the T₁ is overestimated, K^trans and v_e were less severely underestimated. Specifically, when the ductal native tissue T₁ value is underestimated by 65%, K^trans would be potentially overestimated by 531%. With the same T₁ underestimation, v_e hit its ceiling threshold with any combination of true K^trans and v_e. As can be seen, optimization of T₁ measurement in the DCE-MRI imaging protocol is crucial for accurate quantitative pharmacokinetic analysis.

B1 inhomogeneity effect

The error in the optimization of the nominal flip angle is a consequence of B1 inhomogeneity which becomes more prominent at higher magnetic field strength. Kuhl et al[89] proved that for the same breast lesion, the enhancement rate obtained at 3.0 T magnetic field was lower than the respective rate at 1.5 T magnetic field. In the further study[90], B1 field across the bilateral breast MRI field at 3.0 T showed substantial variation, and the variation was independent of coil type. The actual pulse angle varied between 22° and 12.5° over the field of view. Similarly, up to 55% error of nominal flip angle was observed from the healthy volunteer’s B1 maps at 3.0 T[91]. In a breast DCE-MRI study at 3.0 T[92], the median measured B1 field at the right side of breast (in prone position) was reduced by nearly 40% of the expected value. Experiment and simulation showed that a reduced B1 field decreased the ER of dynamic signal curve, and this trend became more prominent when CA uptake was higher. The pharmacokinetic parameters were also affected by B1 inhomogeneity through the varying flip angle[88]. Simulation results showed when the flip angle was underestimated by 55% of its nominal value, K^trans measurement dropped by 66%, and 55% overestimation of flip angle led to 61% increase of K^trans. As v_e increased, K^trans sensitivity to the varying flip angle was strengthened. On the other hand, v_e showed similar changing pattern except the sensitivity to varying flip angle was independent of K^trans value. In contrast to 3.0 T, the B1inhomogeneity is less prominent at 1.5 T and is less studied.

Temporal resolution

The temporal resolution in DCE-MRI is directly dependent on the imaging volume. In a clinically feasible scan which is a part of treatment planning imaging, the frame time covering the whole breast is about 1 min[52]. Theoretically, the reduced temporal resolution would affect the precision of pharmacokinetic analysis by changing the CA concentration evolution curve. In an animal study with 4.7 T magnetic field strength[93], DCE-MRI data was first acquired with 5 s temporal resolution. The data was then downsampled to temporal resolutions ranging from 15 to 85 s. The CA concentration curve showed large discrepancies during the earlier phase. Quantitatively, as temporal resolution decreased, K^trans was progressively underestimated from 4% to 25%, and v_e was overestimated from 1% to 10%. In another simulation study[88], as temporal resolution reduced, K^trans underestimation was more pronounced at higher nominal values, while v_e displayed a 2% minor variation.

One simple way to increase the temporal resolution is to image the lesion only. For radiation treatment assessment purpose, the planning target volume (PTV) is a good candidate, but the knowledge of the TOI must be known prior to scan. As an alternative strategy, undersampling the image with intensive mathematic operation can also increase the temporal resolution[36]. However, since there is no gold standard of true values for pharmacokinetic parameters, the benefit of high temporal resolution imaging is limited. Nevertheless, improvement of high temporal resolution in DCE-MRI will be a continuing interest for researchers.

Importance of AIF

Ideally, the AIF should be measured from DCE-MRI data for each case, as it varies between individuals in reflection of cardiac output, vascular tone and renal function[15]. Unfortunately, as discussed above, the measurement is not practical in clinical routine imaging because no larger vascularity is within field of view. Besides, the measurement demands high temporal resolution which is not achievable in whole breast imaging[22,59,94,95]. The idealized mathematical model functions are commonly used, though the used functions make no attempt to reflect the true blood supply to the volume of interest[22]. Some other quantitative methods require no AIF information[62,96], but further studies must be done focusing on human breast tissue. In conclusion, one should be aware that AIF methodology leads to potential inaccuracy of pharmacokinetic parameters.

Pharmacokinetic model

There is no uniform standard of choosing a pharmacokinetic model in quantitative DCE-MRI analysis. The current consensus is that simple models describing the CA transfer rate from the blood plasma to the EES (K^trans) and the EES volume fraction (v_e) should be used for the assessment of vascularity change[15]. The Standard Tofts model and the Extended Tofts model have been widely used due to their simplicity. Despite the limitation of describing the biological picture of CA transport, the two simple models have been proved to be very useful with limited temporal resolution and without accurate AIF information[94]. However, these two models are not identical: in a comparative study into the robustness of compartmental modeling on abdominal tumors and gliomas, the K^trans calculated by Extended Tofts Model was considerably lower than the value from Standard Tofts Model, while v_e maintained similar range in both methods[48].

In pursuit of a more realistic biological mechanism, other models have been evaluated the aspect of accurate parameter reproducibility. For example, initial application of the FXR Model suggested that K^trans and v_e were underestimated by values up to 300% in the assumption of a linear relationship between CA concentration and longitudinal relaxivity change[50,51]. The FXR model was also reported as with the most complete statistical description of DCE-MRI time courses for the patients selected in the study[97]. As a DP model, adiabatic approximation of the tissue homogeneity model (ATH) was proved to be more effective in CA dynamic curve fitting than Tofts models for Time-resolved angiography With Stochastic Trajectories data[98]. However, these comparisons cannot be seen as the evidence of superiority in biological reality. The pharmacokinetic parameter, for example, K^trans, does not absolutely measure capillary permeability in any model, though it is often assumed to do so; the exact meaning depends on the specific model used for analysis. For instance, the reduction of K^trans can be interpred as a reduction of blood permeability in ATH model, or a reduction of both blood flow and permeability in Tofts models. As a result, the choice of model reflects the tradeoff between parameters that are either simple in math but lack biological specificity or more physiologically congruent but less stable in math.

Region of interest and statistical analysis

Radiation treatment has certain regions of interest including Gross Tumor Volume, Clinical Target Volume and PTV. Data analysis performed over the TOI using the average CA concentration or average signal intensity generates the regional parameters. Though this method is faster, it ignores heterogeneity within the volume of interest. Alternatively, the parameters can be extracted in a pixel-by-pixel pattern within the TOI. The statistics summary such as the mean or median value and standard deviation can be used for assessment[52,90,100]; this method can describe the parameter distributions and limited information about microvessel heterogeneity[15]. In practice, the second method may be too slow for clinical application depending on voxel number and mathematic complexity of model fitting. The challenge can be neutralized by selecting meaningful voxels through certain simple metric[101], or using the advanced GPU acceleration to reduce analysis time[102-105].

CONCLUSION

DCE-MRI is a promising technique for assessing breast cancer radiation treatment due to its inherent sensitivity to change in the microvessel environment. Correlative studies have demonstrated proof concept of DCE-MRI parameters as potential biomarkers. Presently, an insufficient number of clinical studies have been done in breast cancer radiation treatment. Currently, progress has been achieved in pharmacokinetic model development in pursuit of precise physiology description; however, these methodologies have yet to be fully studied in correlation with clinical outcome in breast cancer radiation treatment. For future work, the study of new pharmacokinetic model with special interests on breast tumor pathology will help improve the interpretation of the DCE-MRI parameter. Advancement in DCE-MRI image acquisition with high spatial and temporal resolution will contribute to the utility of DCE-MRI application in radiation treatment assessment. On the perspective clinical trials are needed with primary aim designed to test standardized DCE-MRI assessment methods for both image acquisition and quantitative biomarker derivation. This is a crucial step towards the goal of individualized radiation treatment planning.