Carotid Artery Stenosis Near a Bifurcation Investigated by Fluid Dynamic Analyses

Summary

Haemodynamic physical parameters play a role in determining endothelial cell phenotype and influence vascular remodelling. Accurate measurement of total pressure, velocity magnitude, and wall shear stress is vital for studies on the pathogenesis of atherosclerosis. This paper investigated a lesion-based computational fluid dynamic (CFD-Fluent) pilot analysis to understand the complex haemodynamic changes prevailing in patients with high-grade carotid artery stenosis (CS) 90%. All subjects were examined with colour-flow Doppler, power Doppler, and digital subtraction angiography to enable visualization of carotid stenosis and plaque surface morphology, and used to generate computational meshes. Two models were devised: the first without any stenosis and the second with an 82% grade of stenosis localized in the external carotid artery. The distribution of the principal parameters can be obtained by computational fluid dynamics (CFD-Fluent) using patient-specific geometries and flow analytical measurements. The total pressure distribution ranged between 16,000 and 8,000 Pa in the case of normal carotid artery and 16,000 and 5,500 Pa in the case of the stenosed artery. The velocity registered a peak in the stenosis region of 5 m/s. The mean wall shear stress within the stenosis region was 360 Pa. In conclusion, patient-based CFD-Fluent analysis of CS predicts a complex haemodynamic environment with large spatial haemodynamic parameter variations that occur very rapidly over short distances. Our results improve estimates of the flow changes and forces at the vessel wall in CS and the link between haemodynamic changes and stenosis pathophysiology.

Introduction

Local modifications in the rate and pattern of blood flow are associated with transitions in artery wall configuration at bends and bifurcations. These regions are also predisposed to the development of intimal thickenings, including the formation of atherosclerotic plaques. Attempts have therefore been made to assess the role of haemodynamic factors in atherogenesis by correlating the distribution of intimal lesions, usually in excised collapsed arteries, with presumed changes in flow conditions or with flow patterns visualized in idealized glass or plastic models. On the basis of such studies, elevations or variations in flow velocity and shear stress ¹, decreased wall shear ², flow separation ³, and turbulence ^4-6 have each been proposed as haemodynamic catalysts of lesion formation. Quantitative studies in which precise locations of intimal deposits in specimens restored to normal dimensions are correlated with flow phenomena measured in anatomically accurate models could help identify which of the several possible haemodynamic variables is most consistently associated with the presence or absence of intimal disease. The human carotid bifurcation is particularly well-suited for such an investigation. It is a site of early lesion formation ⁷ and of clinically significant disease ⁸, and the division of the common carotid artery in this region into two channels of unequal size and flow distribution results in a wide range of haemodynamic changes. Specimens suitable for controlled pressure-fixation are obtainable at autopsy, and the dimensions of the carotid bifurcation determined from in vivo angiograms can be used to construct geometrically accurate scale models. Recent clinical trials have shown that the risk of stroke increases with carotid lesion severity, resulting in a considerable effort to develop techniques to characterize carotid stenoses. The North American (NASCET) and European (ECST) carotid surgery trials have shown a surgical benefit for symptomatic stenosis greater than 70%. However, carotid plaque is a common occurrence, so the presence of carotid lesions alone is not a good indicator of subsequent stroke risk. Although about 60% of individuals aged 65-74 exhibit carotid atherosclerosis ⁹, the absolute risk of stroke in the asymptomatic population is low (2.1% over three years). Among symptomatic individuals, the risk of major or fatal stroke ipsilateral to a severe carotid stenosis is 13% over two years ¹⁰. Although this risk is significant, it also indicates that the majority of individuals with carotid disease do not suffer stroke, and that grading of stenosis severity with respect to linear reduction of lumen diameter is only a surrogate measure of stroke risk with relatively poor specificity. Clearly other mechanisms must be at work to make a subgroup of individuals with carotid plaque more vulnerable to cerebral embolus production.

Patients and Methods

Five patients (two women, median age 73 years) with symptomatic CS of the cervical carotid bifurcation recalcitrant to medical therapy were evaluated, as detected by a continuous-wave Doppler (CWD) examination. The patients were recruited prospectively and consecutively for the study after neurovascular screening. All patients volunteered to participate in the study after being informed that they would be examined with the use of Colour Flow Doppler (CFD) and Power Doppler (PD) ultrasonography, and they gave their written consent. Bidirectional CWD ultrasound was used to determine the presence of carotid stenosis and all patients were examined with a 4.0-MHz Multi-Dop^® X digital probe, (Compumedics DWL, Germany GmbH). The differentiation in grade stenosis was estimated by analysis of the frequency spectrum. Low-grade stenosis was defined as <50%, middle-grade stenosis was defined as 50% to 69% stenosis, and high-grade stenosis was defined as equal to or greater than 70%. The carotid arteries were examined in all patients with the use of a Masters ultrasound device (Diasonics) with a 7.5-MHz linear array and pulsed-wave transducer that enabled superimposed, simultaneous colour-encoded (PD and CFD) blood flow information to be obtained. The CFD and PD examinations were performed with the patient's head in a sideways position, focusing on the longitudinal and transverse views of the common carotid artery (CCA), internal carotid artery (ICA), and external carotid artery (ECA), paying attention to the level of the narrowest part of the stenosis. The stenosis was first visualized with B mode, and measurements were immediately made with CFD and PD. In this way, the former ICA or ECA lumen, as well as the residual lumen, can be delineated. The amount of luminal reduction was determined as the percentage of both cross-sectional area and longitudinal diameter reductions, to yield two independent estimates of luminal reduction. Selective digital subtraction angiography (DSA) of the carotid arteries was performed in all patients with a minimum of two projections. ICA or ECA diameter reduction was measured by the linear-based method used in the European Carotid Surgery Trial ¹¹. The order in which carotid artery examinations were made was as follows: CWD, followed by either CFD or PD, and DSA. The CFD and PD duplex sonographic examinations were performed blindly with regard to the DSA and CWD findings. The CFD-assisted duplex imaging was performed by a different individual from the one who performed CWD sonography or DSA. The imaging data were evaluated by independent investigators, and in instances of disagreement the case was eliminated. Interobserver reliability was 95%. The issue is that atherosclerosis is a highly complex phenomenon. It involves the interaction of haemodynamics on the stenosis of the arterial wall deformation and the interaction of the deformation on the haemodynamics. Both the flow of blood affects the stenotic region and the stenotic region affects the flow. It is this interaction that first creates the stenosis and eventually causes the stroke. A combination of computational fluid dynamics and finite element analysis techniques allows the physics involved in atherosclerosis to be studied. Due to the aforementioned complexity of atherosclerosis, however, one simply cannot study all the different aspects in one study. Therefore the solution has been to study individual aspects of the problem and use the results of many different studies to create overall assumptions. In this study, a fluid dynamic code FLUENT was used to investigate Newtonian fluid flow in a straight tube with an occlusion. Two models were created in the end by using the data obtained by CFD and PD ultrasonography: the first without any stenosis (24,948 tetrahedral elements, and 6,453 nodes) and the second with an 82% grade of stenosis, reproducing the geometrical and haemodynamic characteristics of patient number 3, (28,425 tetrahedral elements, and 6,968 nodes), as shown in Figure 1. An alternative means for invasive flow measurements is presented by the calculation of models in which blood flow can be virtually simulated, a method that is called computational fluid dynamics (CFD-Fluent). Several in vitro studies have shown that CFD-Fluent allows reliable physiologic blood flow simulation and measurements of total pressure, velocity magnitude, and WSS. The surfaces of the carotid bifurcation were imported as a stereo lithography format file into the CFD-Fluent front-end software Gambit (v. 2.2.30; Fluent Inc., Lebanon, NH, USA) to add an unstructured mixed Tet/Hybrid mesh. The mesh file was then exported after the boundary conditions were specified. The unsteady three-dimensional incompressible Navier-Stokes equations were used for blood-flow simulations with the CFD software Fluent (v. 6.1.22; Fluent Inc., Lebanon, NH, USA), and blood was considered a Newtonian fluid. For simplicity, the vessel walls were assumed to be rigid and a no slip boundary condition was imposed. Physiologic flow conditions were obtained by three different measurements performed at two slice locations below and above the carotid occlusion carried out with a Seldinger catheter. The pressure inlet was defined at 16,000 Pa while the outlet ones were defined as outflow conditions for each ramification of the bifurcation. The simulations were performed with the following material constants: blood density 1041 kg/m³, blood dynamic viscosity 0.004 Pa. Turbulence intensity at the inlet boundary was set to 0.05 kg/ms, simulating a disturbance free inlet, and grid independence was established for all the cases reported here. The convective terms in the momentum and turbulence equations were discretised using second-order up winding and pressure-velocity coupling was achieved using the SIMPLEC solver. All computations were converged to residuals less than 10E-05. Before discussing the circulation of blood there are two principles that must be addressed. The first is the conservation of mass, which states that mass can neither be created nor destroyed. The implication of this is that the mass of the fluid flowing into a closed system must be equivalent to the mass of the fluid flowing out. In vivo, however, this is not strictly the case because the density of blood can vary (so that a greater mass occupies the same volume), or the volume of the system of blood vessels increases through the expansion of flexible blood vessel walls. The second principle is that blood is incompressible. Because of these two principles, it can be roughly assumed that the blood flowing into a tube (circulatory system) has the same properties (mass, volume, etc.) as the blood that flows out. Therefore, based on the principles of fluid dynamics, in a tube of cross-sectional area, A, and an average fluid velocity, v, the volume flow rate is given by the volumetric flow rate equation 1, see also Figure 2:

$${\displaystyle Q=Av=\mathit{cost};}$$

${\displaystyle \begin{array}{c}{Q}_1=Q_2;\phantom{+Q4}\phantom{\mathrm{spazio}}\pi r_1^2{v}_1=\pi r_2^2{v}_2\phantom{{\mathrm{ir}}_{3\mathit{mal}}^2{v}_{3\mathit{mal}}+\pi r_4^2{v}_4;\pi }\\ Q_2=Q_3+Q_4;\phantom{\mathrm{spazio}}\pi r_2^2{v}_2=\pi r_{3\mathit{normal}}^2{v}_{3\mathit{normal}}+\pi r_4^2{v}_4;\phantom{v_4}\\ \phantom{Q_2=Q_3+Q_{\mathrm{}};}\phantom{\mathrm{spazio}}\pi r_2^2{v}_2=\pi r_{3\mathit{stenosis}}^2{v}_{3\mathit{stenosis}}+\pi r_4^2{v}_4;\end{array}}$

Figure 1.

Numerical models of arteries.

Figure 2.

Schematic representation of arteries.

Results

The results of the examinations are reported in Table 1, which shows at different distances (from the beginning x = 0 [mm], to the end x = 60 [mm]), the values of CCA, ICA, and ECA lumen evaluated by CWD, PD, and DSA techniques, pertinent to each of the five patients. Moreover the results of the CFD-Fluent analysis are reported in Table 2, which shows at different distances (from the beginning x = 0 [mm], to the end x = 60 [mm]), the average values of pressure, velocity flow, and WSS calculated in each section. Both tables take into account the presence of ICA and ECA ramifications in order to describe the local haemodynamic parameters, see also Figure 2.

Table 1.

Comparison of the section diameters evaluated by CFD, PD, and DSA techniques measured at different distances.

		Distance [mm].
Middle grade stenosis 60%	Patient 1					ER	IR	ER	IR	ER	IR
	CFD	.3	.1	.5	.0	.6	.5	.5	.6	.5	.7
	PD	.3	.2	.7	.1	.6	.4	.7	.6	.4	.5
	DSA	.2	.0	.8	.3	.5	.5	.6	.8	.5	.5
Stenosis localized in external ramification of carotid artery. ICA lumen = 4.5 [mm], residual lumen = 1.8 [mm]
Low grade stenosis 14%	Patient 2					ER	IR	ER	IR	ER	IR
	CFD	.5	.3	.0	.8	.7	.1	.6	.8	.2	.0
	PD	.4	.3	.1	.7	.8	.0	.7	.8	.3	.0
	DSA	.2	.1	.1	.6	.8	.2	.8	.9	.1	.1
Stenosis localized in internal ramification of carotid artery. ICA lumen = 4.8 [mm], residual lumen = 4.1 [mm]
High grade stenosis 82%	Patient 3					ER	IR	ER	IR	ER	IR
	CFD	.0	.1	.2	.5	.0	.1	.4	.5	.0	.1
	PD	.0	.0	.3	.4	.1	.2	.5	.7	.9	.0
	DSA	.1	.9	.5	.3	.1	.5	.6	.6	.8	.1
Stenosis localized in external ramification of carotid artery. ICA lumen = 5.4 [mm], residual lumen = 1.0 [mm]
Middle grade stenosis 52%	Patient 4					ER	IR	ER	IR	ER	IR
	CFD	.0	.1	.9	.0	.6	.4	.6	.5	.6	.7
	PD	.3	.1	.7	.2	.6	.7	.8	.8	.8	.6
	DSA	.2	.2	.8	.1	.8	.8	.5	.1	.7	.6
Stenosis localized in internal ramification of carotid artery. ICA lumen = 4.6 [mm], residual lumen = 2.2 [mm]
High grade stenosis 72%	Patient 5					E.R.	I.R.	E.R.	I.R.	E.R.	I.R.
	CFD	.9	.9	.0	.5	.3	.5	.4	.4	.6	.5
	PD	.8	.0	.1	.5	.8	.7	.7	.3	.8	.6
	DSA	.8	.1	.5	.3	.6	.4	.6	.2	.8	.7
Stenosis localized in internal ramification of carotid artery. ICA lumen = 4.7 [mm], residual lumen = 1.3 [mm]

ER = External ramification of carotid artery; IR = Internal ramification of carotid artery.

Table 2.

Results of pressure, flow velocity, and wall shear stress (WSS), calculated by fluid dynamic analysis, evaluated at different distances.

Patient N° 3	Pressure [Pa]	Flow Velocity [m/s]	WSS [Pa]
Distance "0" [mm]	16,000	1.15	140
Distance "10" [mm]	15,800	1.55	90
Distance "20" [mm]	15,200	2.08	110
Distance "30" [mm]	14,300	4.54	180
Distance "35" [mm] external ramification	11,800	5.08	360
Distance "35" [mm] internal ramification	12,000	3.01	216
Distance "50" [mm] external ramification	4,000	2.54	90
Distance "50" [mm] internal ramification	1,000	2.33	164
Distance "60" [mm] external ramification	5,000	3.01	111
Distance "60" [mm] internal ramification	10,500	3.00	146

Pressure Distribution

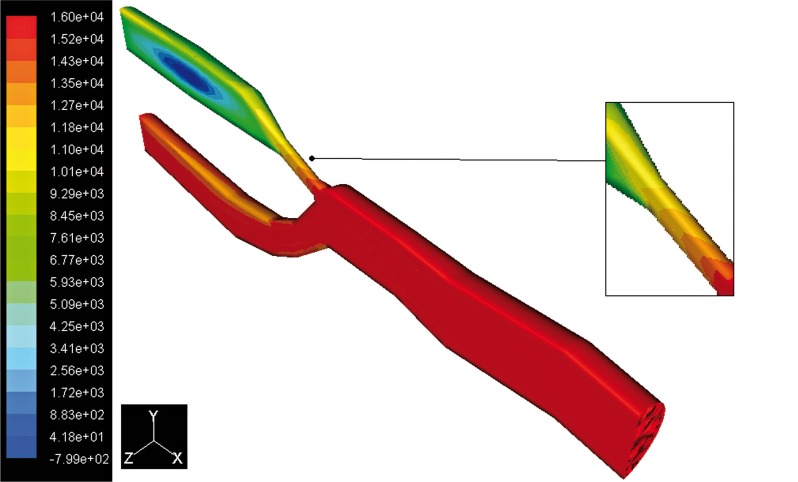
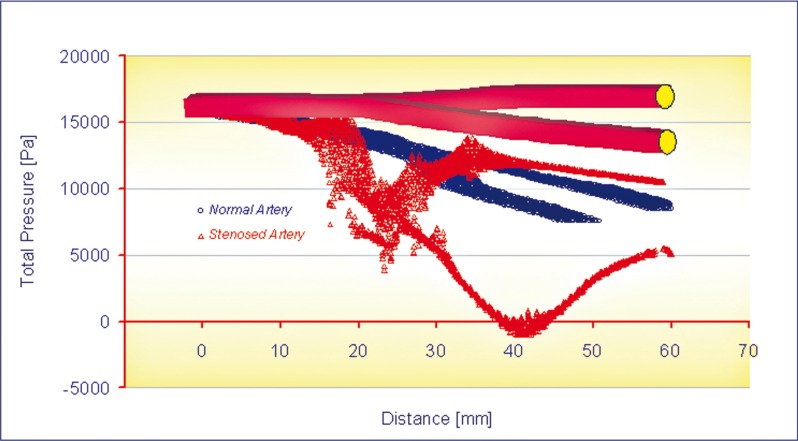
The pressure distributions at peak systole, along the axial direction are shown in Figures 3 and 4. Figure 5 shows the curves of total pressure [Pa] in both models versus the distance measured in mm. As can be seen, the pressure drop is significant close to the stenosed area, lying within 5,500 Pa and 12,000 Pa in this region, with respect to the 10,000 and 12,000 Pa recorded in the healthy artery of the same area. Here it is possible to notice a depression of about -700 Pa probably caused by the disturbed flow near the stenosis. In this study, the wall pressure decreased towards the periphery of the coronary artery tree with elevated pressure drops in stenotic segments. The increased pressure drop in stenosis reflects the elevated energy needed to drive the flow through these narrow regions. Energy loss associated with such flow expansion after each constriction will be large and consequently the pressure drop will be higher. The overall pressure drop increased from 2,000 [Pa] at the end diastole to 16,000 [Pa] at the peak systole.

Figure 3.

Contours of total pressure in the normal artery.

Figure 4.

Contours of total pressure in the stenosed artery.

Figure 5.

Curves of total pressure vs. distance.

Velocity Magnitude Distribution

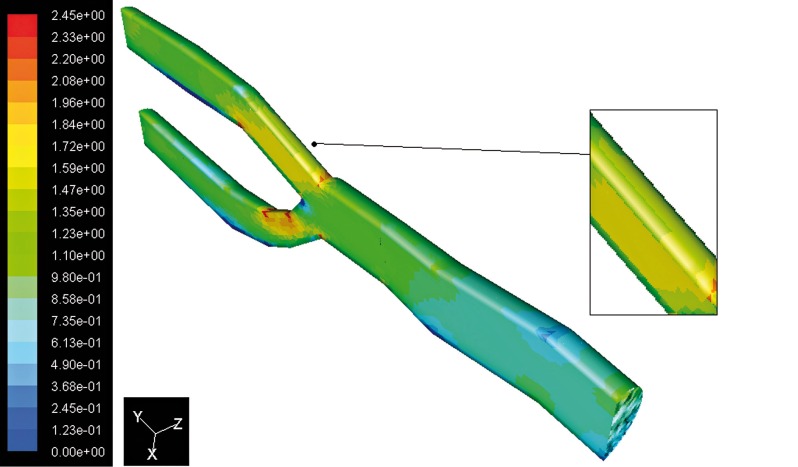
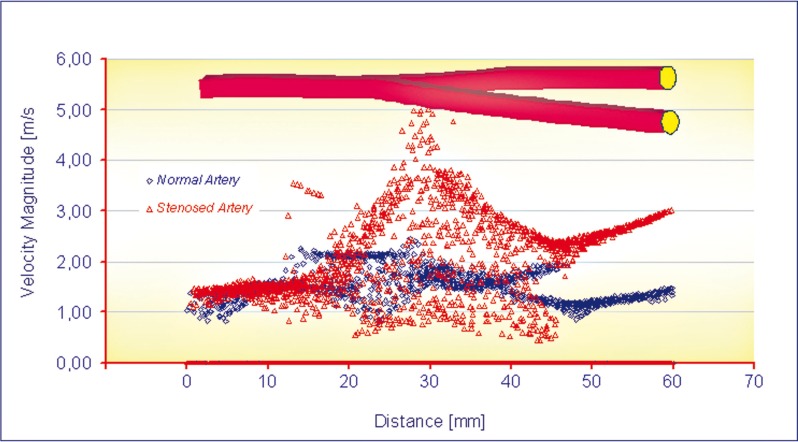
The flow separation regions can be seen clearly from the instantaneous velocity vector panels illustrated in Figures 6 and 7. By comparing the two images the pattern of velocity vector clearly shows the recirculation zones with the formation of the eddy at the downstream of stenosis present in Figure 7 but not in Figure 6. From these figures it can be observed that the recirculation eddies are formed downstream of the stenosis. There exists a separation streamline that divides the flow into two regimes one of which is the recirculating region distal to the stenosis, and the other is the main flow field carrying the bulk of the flow near the centre of the tube. Evidently, the development of the recirculation zone downstream to the constriction is restricted by the presence of the stenosis. The results of the simulation show that the peak velocity at the throat of the stenosis is about 5.06 m/s, against a value of 2.45 m/s in healthy arteries at peak systole, as shown in Figure 8. Downstream of stenosis, flow might become transitional because of the sudden expansion and strong non-symmetric recirculation. At the end of diastole the values of the peaks in velocity magnitude are 0.85 m/s and 0.36 m/s respectively.

Figure 6.

Contours of velocity magnitude in the normal artery.

Figure 7.

Contours of velocity magnitude in the stenosed artery.

Figure 8.

Curves of velocity magnitude vs. distance.

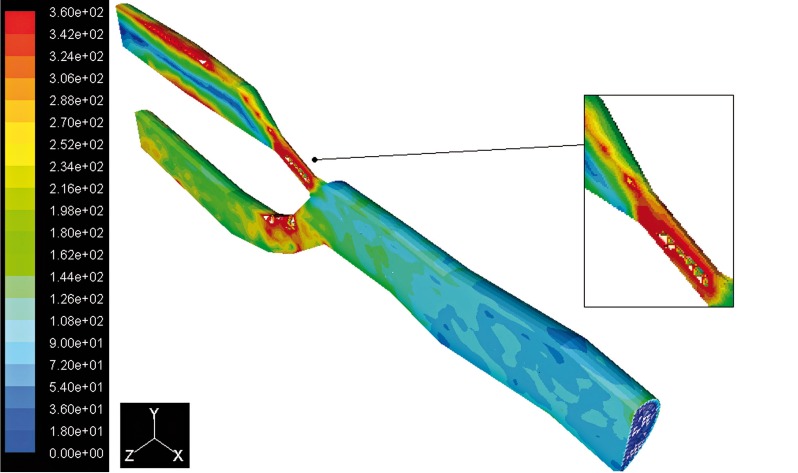
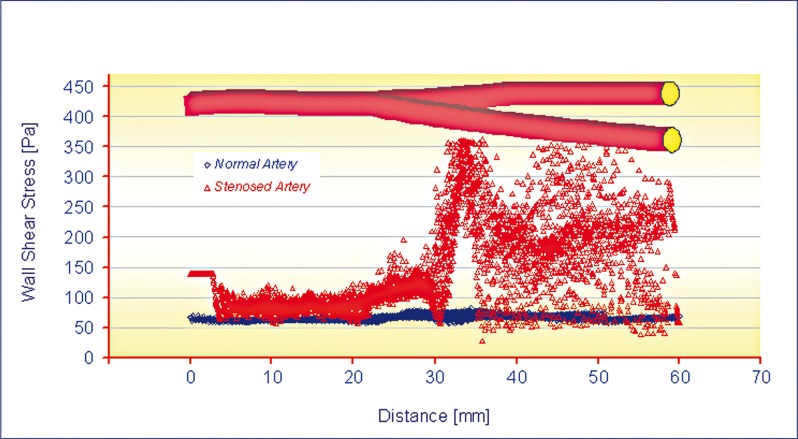
Wall Shear Stress and Intimal Thickening

With regard to fluid dynamics, especially in the case of post stenotic regions, the areas of low wall shear stress (WSS) are also associated with flow separation, that is, a reversal or disturbance of the flow, and a greater fluctuation of wall shear stress (see Figures 9 and 10). This may be important because it has been suggested that the fluctuation of WSS or disturbed flow leads to increased endothelial cell turnover and intimal thickening. Importantly, in vivo study has shown that the post stenotic region of subcritical stenoses, for example less than 60%, is associated with increased intimal thickening, and this intimal thickness also correlated inversely with shear stress ¹². If the blood flow is increased, that increases WSS, and an adaptive increase in arterial luminal size is observed. If the blood flow is decreased, usually by a proximal stenosis that decreases the WSS, and there is an adaptive decrease in arterial lumen size. This decrease in luminal size elevates the WSS, and the decrease in lumen continues until the WSS is returned to normal ¹³. The point where the maximum shear stress occurs lies at the narrowest cross-section of the stenosis. There is a rapid increase in WSS upstream of the stenosis, then after the critical height of stenosis, the WSS decreases until separation occurs, as seen in Figure 10. The results indicate (Figure 11) a peak of WSS almost of 360 Pa reached at the throat of the stenosis, high enough to damage the endothelial cells, versus a value of 83 Pa recorded in the healthy artery. This phenomenon suggests that there may be a stripping of endothelial cells at the start of the stenosis stage. In atherosclerotic coronary arteries, regions of flow acceleration were associated with high WSS varying from point to point along the irregular geometry of the stenosis. The sudden narrowing of the stenosed lumen leads to characteristic disturbances of the flow profile: high local WSS at the arterial stenosis, post-stenotic vortices, and stagnation point. Both wall high shear and stagnant flow have been identified as favourable conditions for platelet aggregation through inherently different pathways ¹⁴.

Figure 9.

Contours of WSS in the normal artery.

Figure 10.

Contours of WSS in the stenosed artery.

Figure 11.

Curves of WSS vs. distance.

Discussion

Carotid artery stenosis (CS) is diagnosed using a combination of history, clinical examination, and imaging. Rapid advancement of non-invasive imaging modalities notwithstanding, biplane and rotational digital subtraction angiography still provide unsurpassed anatomic resolution of the endoluminal aspect of CS. As the evaluation of angiographic images remains limited to measurement of the geometric degree of stenosis, the ultimate evaluation of a stenosis relies on the experience of the treating physician. Significant atherosclerotic stenosis produces epicardial conduit resistance. In response to the loss of perfusion pressure and flow to the distal (post-stenotic) vascular bed, the small resistance vessels dilate to maintain satisfactory basal flow appropriate for myocardial oxygen demand ¹⁵. Viscous friction, flow separation forces, and flow turbulence at the site of the stenosis produce energy loss at the stenosis. Energy is extracted reducing pressure distal to the stenosis, producing a pressure gradient between proximal and distal artery regions ^16,17. Multiple stenoses may occur in a diseased vascular bed because of the formation of the primary stenosis that can result in downstream circulation flow. As a result of the secondary stenosis, a circulation zone will form at its downstream, thus resulting in a third stenosis, etc. The effects of these stenoses result in a series of sequence constrictions. Talukder et al. ¹⁸, and Van Dreumel and Kuiken ¹⁹ carried out experimental studies related to flow dynamics in doubly constricted vessels. They suggested that the flow energy loss due to the presence of the stenoses, which is directly related to the pressure drops across them, increases with the number of stenoses and is not strongly dependent on the spacing between them. Lee ²⁰ and Damodaran ²¹ made a 2D steady flow computational analysis of flow in multiply constricted vessels. Kilpatrick et al. ²² presented an approximate assessment of the combined effect by summing the value of the resistance for each stenosis, but not by the degree of the stenoses. Gould and Lipscomb ²³, and Sabbah and Stein ²⁴ concluded that multiple stenoses produce more resistance to flow than a single stenosis of similar length. Johnston and Kilpatrick ²⁵ simulated the arterial blood flow in paired smooth stenoses and triple smooth stenoses respectively. They concluded that the more severe stenosis dominates the pair and the recirculation between stenoses is stronger with a severe proximal stenosis than a severe distal stenosis. Bertolotti et al. ²⁶ studied the influences of multiple stenoses numerically as well as experimentally to diagnose peripheral arterial diseases and evaluated the peak systolic velocity ratio and pressure drop to detect and grade multiple stenoses in lower limb mimicking arteries. There is considerable evidence that both early atherosclerotic changes in vessel walls and the deposition of platelet thrombi occur preferentially at the entrances of branching arteries where, from a fluid mechanical point of view, flow is likely to be disturbed, and separation of streamlines from the vessel wall and formation of eddies may occur. Hence, to elucidate the possible connection between blood flow and the localized genesis and development of atherosclerosis and thrombosis, a considerable amount of work, both theoretical and experimental, has been carried out by many investigators ^27,28. Among the theories and hypotheses proposed to account for the localization of atherosclerosis, the causative effects of WSS on atherogenesis have received much attention and are still being fervently debated. Based on his experimental findings in dogs, Fry ¹ suggested that atherosclerotic changes occur preferentially at the arterial wall experiencing high shear stress because of the resulting mechanical damage to the arterial endothelium and because of an enhanced transport of lipids, including cholesterol, from the blood to the endothelium. In contrast to this, Caro et al. ², in their post-mortem studies, found that early atherosclerotic lesions in human arteries develop more readily in regions where the wall shear rate is expected to be low, such as at the inner walls of curved vessels and at the hips of bifurcations. Therefore, they suggested that the local wall shear rate exercises a control on atheroma formation through flow-dependent diffusion of lipids (synthesized within the arterial wall) away from the vessel wall, leading to the accumulation of lipids in the vessel wall in areas of low wall shear rate. Because of these contradictory hypotheses on atherogenesis, it became important to obtain exact and precise flow patterns and distributions of shear rate (or shear stress) existing in various branching arteries and to correlate these results with the clinical findings of atherosclerosis and thrombosis. In the early stage of our investigation into this problem, we described the detailed flow patterns in various glass models of stenoses ²⁹ and T-junctions ^30,31. More recently, we developed a new technique to prepare isolated transparent natural blood vessels from animals and humans post mortem ³². This has, for the first time, enabled us to study the exact flow patterns and distributions of fluid velocity and shear rate existing in various regions of disturbed flow in the mammalian circulation by directly observing and photographing the behaviour of tracer particles and blood cells flowing through the isolated transparent blood vessels. The technique was first applied to venous valves to elucidate the mechanism of thrombus formation ³³. The study has since been extended to the major arteries of the cardio and cerebrovascular systems. The present paper describes the detailed flow characteristics in the human carotid artery bifurcation. The study was motivated by the fact that one of the most frequent sites for the occurrence of cerebrovascular disease is the area of the carotid artery bifurcation ^34-38 where, because of the unusual geometric structure, i.e., bulging of the internal carotid artery at the junction, flow is likely to be disturbed and eddies may form. In fact, formation of such eddies has been demonstrated in vitro using a glass model of the human carotid sinus ^39,40. Flow separation, stasis and transient flow reversals in the carotid sinus have also been detected in vivo in human subjects ⁴¹. A link between atherogenesis and WSS forces, defined as the internal friction forces between the flowing blood and the vessel wall, has been proposed, suggesting that high shear stress could lead to both mechanical damage to the endothelial cells (ECs) and potential denudation ⁴². Low and oscillatory shear stress promote monocyte adhesion to the EC through the increased expression of vascular adhesion molecules-1 (VCAM-1), which binds integrins expressed on leukocytes and directs their firm adhesion to and entry into EC ⁴³. CFD-Fluent methods can offer an additional important layer of functional information to enrich and complement the anatomical information. It has been proposed that transient cerebrovascular ischaemia (in the absence of arrested cardiac function or stroke) is associated with the development of cognitive impairment. The putative correlates of such transient ischaemic attacks are diverse and include heart failure, ⁴⁴ atrial fibrillation, ⁴⁵ and carotid artery stenosis ⁴⁶. The mechanism by which cerebral hypoperfusion is related to cognitive impairment in humans is largely speculative, since neuropathological studies have been confined to animal models of ischaemia. Such studies have demonstrated disruption of central cholinergic function after bilateral ICA occlusion ^47,48. It is known that watershed areas in the cerebral cortex and deep white matter are most sensitive to hypoxia, but, because the cortex has a lower threshold for ischaemia and a higher metabolic demand, severe transient ischaemia commonly results in infarction in cortical areas more readily than in deep white matter. The present paper describes the detailed flow characteristics in the human carotid artery bifurcation. The study was motivated by the fact that one of the most frequent sites for the occurrence of cerebrovascular disease is the area of the carotid artery bifurcation ^36,49 where, because of the unusual geometrical structure, i.e., bulging of the ICA at the junction, flow is likely to be disturbed and eddies may form. In fact, formation of such eddies have been demonstrated in vitro using a glass model of the human carotid sinus ⁵⁰. Flow separation, stasis and transient flow reversals in the carotid sinus have also been detected in vivo in human subjects ^51,52. The challenge of experimental and numerical investigations on the blood flow in stenotic arteries are the non-Newtonian rheology of blood, the compliant characteristic of arterial wall, the wall composition in layers, the pulsatile inlet flow determination, the mass transfer process, the geometry of the stenosis, and the transition to unsteady turbulent flow. The unsteady flow in a stenotic artery is characterized by high pressure and wall shear stress at the throat and a recirculation zone distal to the stenosis ^53,54.

Study limitations

Some limitations of our study should be pointed out. It could be interesting to define a methodology which may use only a DSA examination followed by a CFD-Fluent analysis. The initial information deriving from the DSA analysis can be investigated to optimize the construction of the CFD Fluent model. By comparing the results of both the techniques, a picture of the real situation can be obtained. The strongest limitation of this kind of approach derives from the fact that it needs a previous examination CWD, PD or DSA. Thus the results are deeply influenced by this (see Table 1). The influence of the ECA and the intracranial collateral circulation was not considered in our approach, as we sought to limit the analysis to the area of the carotid bifurcation. Another limitation is that only a trunk of the carotid artery was modelled by ignoring all its other branches. In this model, vessel walls are assumed rigid; results might differ in elastic models of the coronary artery wall. Finally this approach represents a snapshot in time, after carotid stenosis has already progressed to a symptomatic lesion, and does not account for the complex multicellular autocrine and paracrine interactions among the various vessel wall cells and components.

Conclusions

Highly accurate anatomy for the generation of geometric models is a principal requirement to perform reliable flow simulations and to make assumptions about pressure flow, velocity magnitude, and WSS. Results confirm that severe stenosis caused a considerably large pressure drop across the throat of almost 50% (5,500 to 12,000 Pa in stenosed region, versus 10,000 to 12,000 Pa in the healthy artery). The results of the simulation show that the peak velocity at the throat of the stenosis is about 5.06 m/s, against a value of 2.45 m/s in healthy arteries, at peak systole. Maximum WSS indicates a peak of almost of 360 Pa reached at the throat of the stenosis, high enough to damage the endothelial cells, versus a value of 83 Pa recorded in healthy artery. Thus a dangerous situation may occur at 30% stenosis by diameter, which is generally not regarded as being clinically significant. These results could provide data to guide further experimental studies and understand the haemodynamic component of the multifactorial driving forces behind the progression of carotid disease. Better results can be obtained through continuous practice which allows a correct interpretation of the data collected by different or singular analyses, thereby defining a useful non-invasive method to prevent stroke attacks. Moreover a predictive evolution of the damage can be calculated if the lesion's law of growth is known.