Effect of the Central Canal in the Spinal Cord on Fluid Movement within the Cord

Summary

Computational studies are used to demonstrate the effect of oscillating CSF flow on pressures within the spinal cord. We tested the hypothesis that the central canal in the spinal cord affects spinal cord pressure gradients resulting from oscillatory CSF flow. Two computational models of the spinal cord were created with the same dimensions. Model 1 had a homogeneous porous structure. Model 2 had the same structure with the addition of a central fluid filled space, representing the central canal of the cord. We simulated oscillatory flow in the fluid space using standard computational fluid dynamics tools. For all phases of the CSF flow cycle and for specific projections through the model we calculated pressure gradients and fluid movement in the cord models. Pressures in the models varied through the flow cycle. Model 1 had linearly varying pressure along its long axis that varied with the cycle and had no pressure gradients across the cord. Model 2 had nonlinear varying pressure along its long axis varying with the time in the cycle and had transient centrifugal and centripetal pressure gradients with a central fluid space. The radial pressures varied linearly with distance from the fluid space. Centrifugal and centripetal pressure gradients resulted in radially directed fluid flow in the cord. The central canal within the spinal cord alters the pressure fields occurring during oscillatory CSF flow and creates centrifugal and centripetal fluid flux in the cord.

Introduction

Abnormal CSF flow in theory causes the syringomyelia associated with the Chiari I malformation. Flow abnormalities in the Chiari I patient include flow jets and greater than normal CSF velocities in the foramen magnum and upper cervical spinal canal ^1-5. Flow resistance of the cervical spinal canal ⁶ and the relative amount of spinal canal obstruction ⁷ determine the CSF velocities in the spinal canal. The CSF velocities in the upper cervical spinal canal result from longitudinal pressure gradients during portions of the cardiac cycle. Although these CSF flow abnormalities are known, their role in the pathogenesis of syringomyelia has not yet been adequately explained.

Computational models are used to investigate the effects of pressures and fluid velocities on the cord. Models for the study of the spinal cord and subarachnoid space include co-axial tube models, where the outer tube represents the dura and the inner tube the spinal cord ^8-10, computational fluid-structure interaction models ^11-13, and physical models ^14-16. The models include the spinal cord with or without a syrinx, but do not consider the inhomogeneous porosity of spinal cord tissue. In some computational models, the perivascular spaces have been considered ^17,18. Poroelastic cord models, in which fluid movement can be simulated, have been described ^19-21. To our knowledge no studies simulating oscillatory CSF flow have included both a porous tissue and a central canal within the spinal cord, although the central canal may provide a channel of preferred flow, which alters fluid movement through porous materials. Therefore the status of the central canal may affect the volume of water in the spinal cord. Studying the effect of the canal on fluid movement in the cord may lead to new insights into the pathogenesis of syringomyelia. The purpose of this study was to test the hypothesis that the central canal alters pressure fields and fluid movement in the cord. To test the hypothesis we compared fluid movement in spinal cord models with and without the central canal.

Methods

We created two computational models of the spinal cord surrounded by fluid (Figure 1). Model 1 had a cord 1.00 cm diameter, with a porosity of 0.2 and a permeability of 1.4 ⋅ 10⁻¹⁵ m². The dimensions were chosen to match the typical dimensions of the normal human spinal cord and the tissue properties were chosen to match the human brain ^22-24, since porosity and permeability of the spinal cord have been less completely studied. Its length was 6 cm. Model 2 had identical dimensions and properties with the addition of a central fluid space 2 mm in diameter and 4 cm in length (Figure 1), leaving 1 cm of the model at each end without a central canal. The models were assumed to be immersed in fluid having the properties of water at 37 degrees C. We assumed a 1 Hz sinusoidally-varying pressure difference between the ends of the channel and iteratively modified the magnitude to achieve a peak velocity of about 4 cm/s.

The cord models were assumed to be saturated with fluid from the surrounding space. No-slip conditions were assumed for the boundaries of the fluid spaces. Pressures and velocities were computed simultaneously in the fluid and the cord models by means of programs in FEniCS ²⁵, with fluid movement outside the cord calculated from the Navier Stokes relationships and fluid movement in the spinal cord by Darcy's law. The viscous and the porous domains were assumed coupled by mass conservation, continuity of normal stress and the Beavers-Joseph-Saffman condition ^26,27. Pressures and velocities in the models during the cycle were displayed and plotted for specific times in the cycle and specific locations in the models.

Figure 1.

Graphic representation of the two models used in the study. The model with the solid cord (right) illustrates the simulated fluid space surrounding the cord in light gray and the simulated spinal cord in darker gray. The model on the left illustrates a central spinal canal in the cord in light gray. The canal has a width of 0.2 cm and extends to within a centimeter of each end of the model.

Results

CSF flow in the space around the cord varied through the 1 second cycle with null flow at 0 s and 0.5 s, maximal flow at 0.25 s and 0.75 s. Flow in the external fluid space did not differ noticeably between Models 1 and 2.

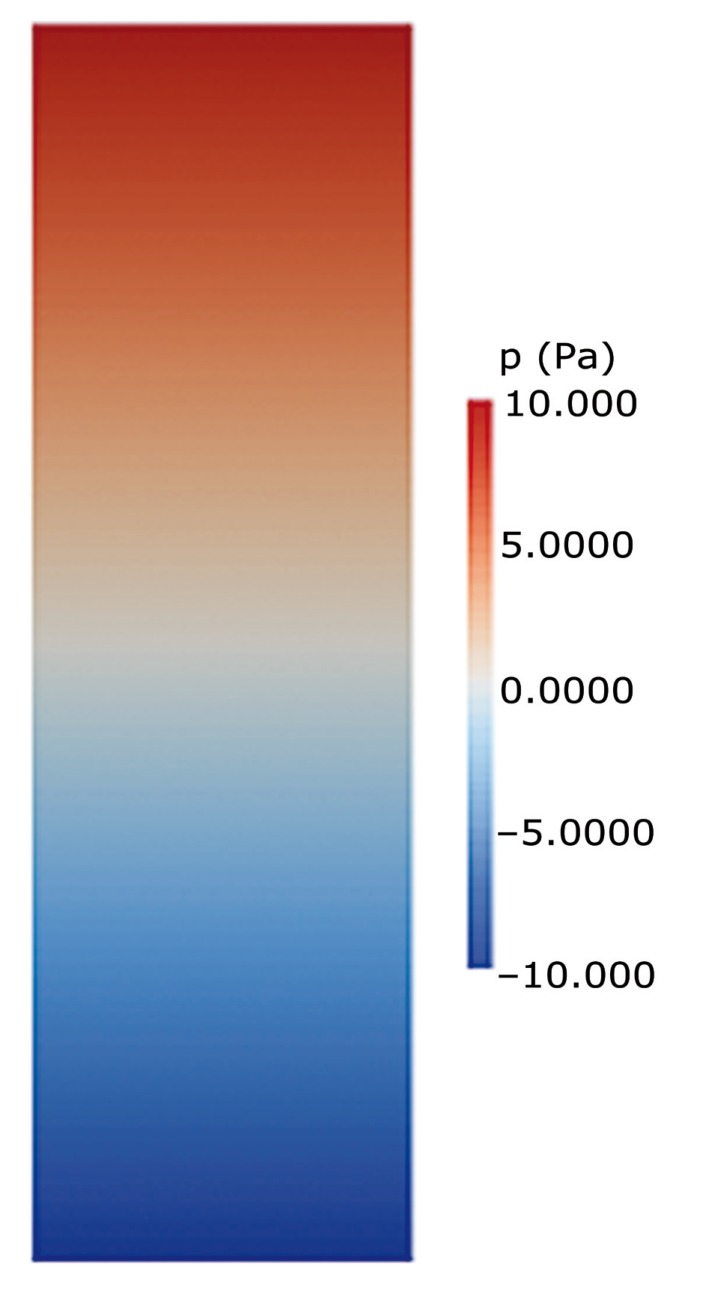
Fluid velocities in the models varied through the cycle approximately 90 degrees out of phase with the pressure. Longitudinal pressure gradients were maximal at 0 and 0.5 s and null at 0.25 and 0.75 s. In Model 1, pressure varied along the long axis of the cord, as it did in the fluid space, but not across the model (Figure 2). Pressures in the cord at any point equalled pressures in the fluid space at the same level along the entire length of the model.

Figure 2.

Graphic display of pressures in model 1 at t = 0.5 when the pressure gradient is maximal. In this model without a central spinal canal, pressures diminish from top to bottom along the model. Pressures do not vary transversely across the model. The pressure in the cord equals the pressure in the fluid space at each level.

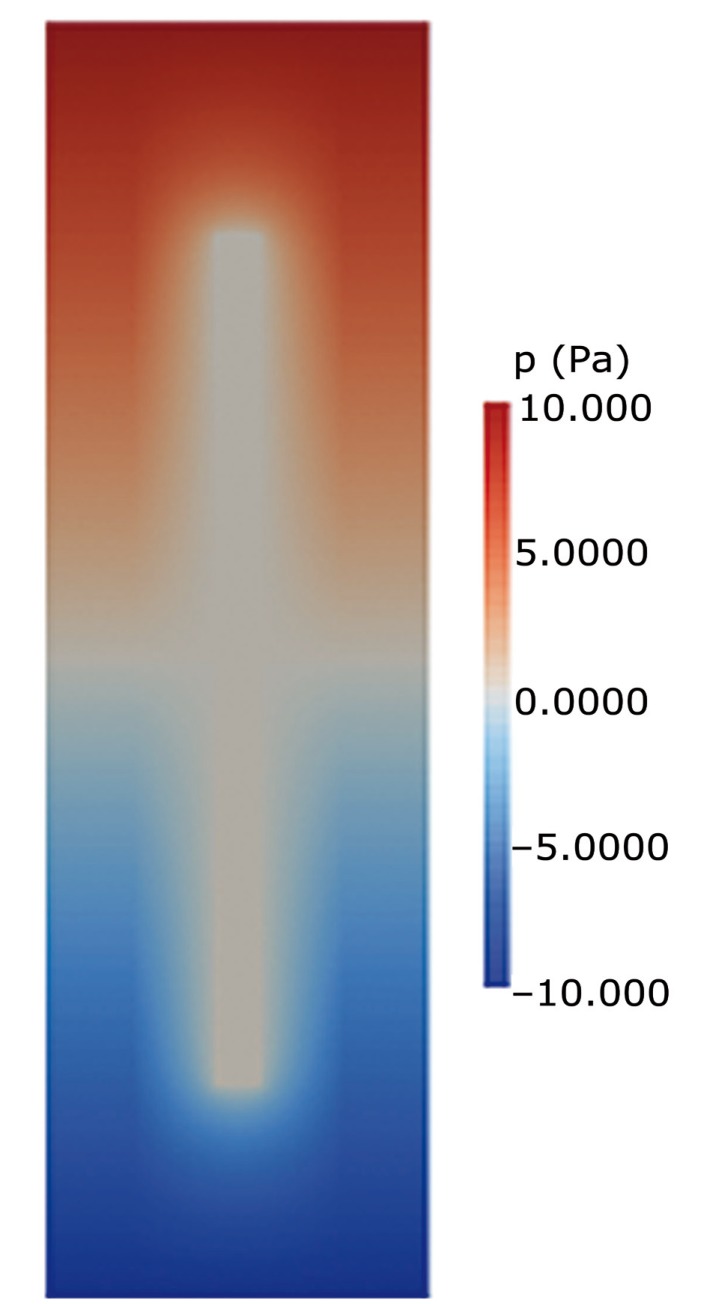
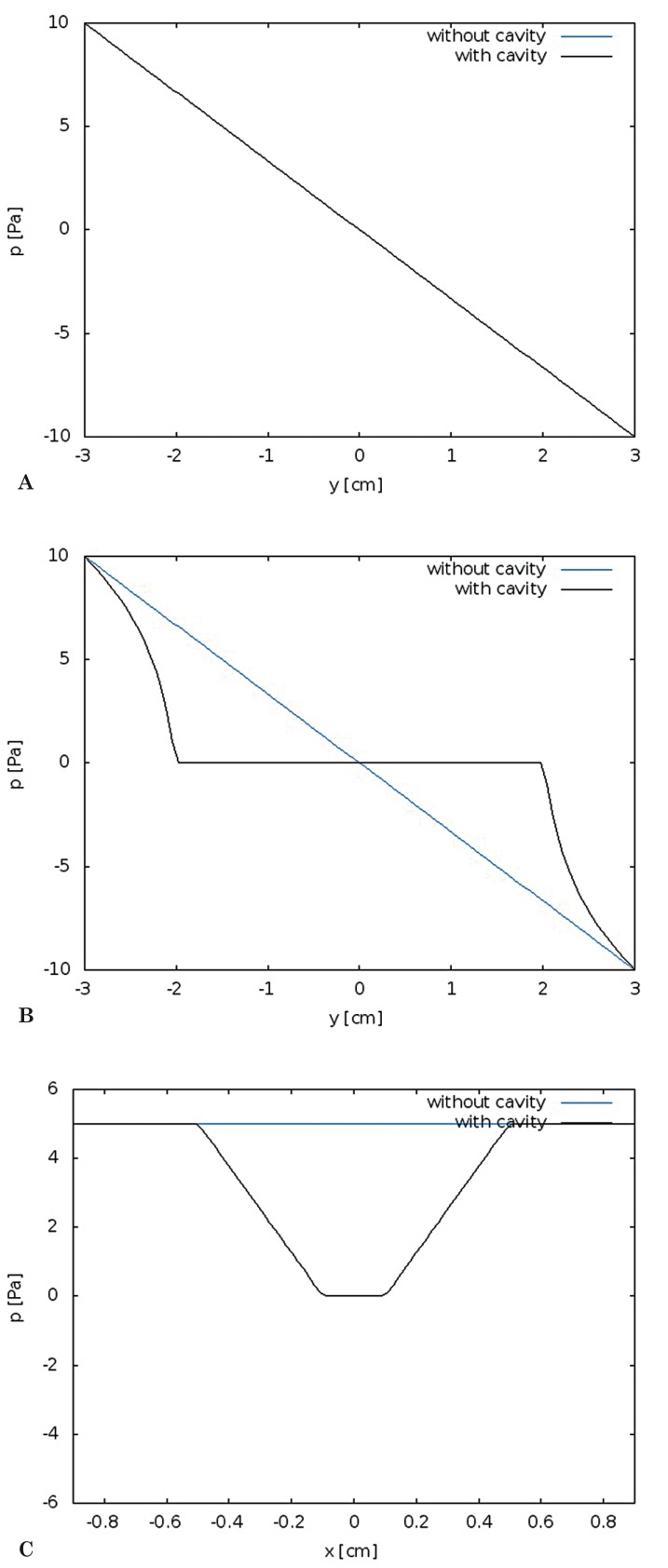
Pressure gradients in model 2 differed from those in model 1 (Figure 3). The central canal in the cord had no visible pressure difference between its ends. The cord in model 2 had longitudinal and radial pressure gradients (Figure 3). Radially-oriented pressure gradients occurred in the portion of the model containing the central canal. Pressure gradients were centripetal when the pressure in the external fluid space was higher than in the central canal, or centrifugal when the external pressure was lower. The centrifugal and centripetal pressures varied in magnitude through the cycle and along the length of the model. Longitudinal pressure gradients in the fluid external to the models were almost identical in the two models (Figure 4A). The longitudinal pressure gradients in the cord were not identical in the two models. In Model 1, pressure along the center of the cord varied linearly; in Model 2 it varied nonlinearly, with no pressure change along the portion of the cord containing the cavity and steeper changes near the ends of the model (Figure 4B). Centrifugal and centripetal pressure gradients occurred in Model 2, (Figure 4C), but not in Model 1. The transverse gradients were steepest near the ends of the central canal.

Figure 3.

Graphic display of pressures in Figure 2 at t = 0.5. In this model with a central spinal canal, pressures vary in a complex manner along the cord. They also vary across the model where the central spinal canal present.

Figure 4.

Pressure gradients plotted for the two models at t = 0.5. Pressures plotted longitudinally (A) for the fluid space external to the cord at t = 0.5 show pressure decreasing linearly in both models. Pressures plotted along the midline of the models (B) show a non-linear decrease in pressure in model 2. Where the central canal is present, pressures do not change with distance along the model and at either end of the central canal pressures change more rapidly than in model 1. Pressures plotted transversely across the models (C) show a constant pressure in model 1 and a pressure gradient varying with distance from the central canal in model 2.

Fluid moved radially in the cord model when centrifugal or centripetal pressure gradients were present. Velocities of fluid movement were greatest at the ends of the central canal at t = 0 and 0.5. The magnitude of centrifugal and the centripetal flow varied through the flow cycle. Fluid velocities in the cord reached 3e-7cm/s.

Discussion

Simulations showed that a central cavity in the spinal cord alters the pressure gradients and fluid flux in the cord resulting from oscillatory CSF flow. Radial pressure gradients develop in segments of the cord with a central canal. The radial gradients reach their greatest magnitude near the ends of the central canal. The radial pressure gradients cause small centrifugal or centripetal fluid fluxes.

To facilitate the computation, the models have a simpler structure than the spinal cord in vivo. The models have rigid boundaries, disregarding the effect of motion which may approach 150 micrometers ¹⁵. The cavity in the model is centered equidistant from the cord surface on either side, while in vivo the central canal has closer proximity to the anterior median fissure, which is part of the anterior subarachnoid space, than to the lateral and posterior subarachnoid spaces. Radial pressure gradients in vivo may vary in steepness depending on distance between the CSF and central cavity. Measurements of pressure gradients in more anatomically correct models of the spinal cord may be warranted.

We performed tests to evaluate the magnitude of potential errors in the computational solutions. We verified that the simulations produced solutions that converged towards a known solution ²⁸. To test accuracy, we measured changes in key values resulting from changes in time steps. We found decreasing temporal resolution from 0.001 s to 0.005 s changed pressures by less than 0.1%. For the effect of spatial resolution, we compared key values for meshes with 0.025 and 0.05 cm resolution and found differences in key values less than 6% in the case of 0.01 s time steps. For this study, boundary conditions were similar to those used in other CSF flow simulations ².

In our models, flow in the fluid space had characteristics of flow in the human subarachnoid space. Peak velocities were in a range for normal human subjects and some patients with the Chiari malformation ^1-4,29. To our knowledge studies measuring fluid flux in spinal cords with and without a central spinal canal have not been reported. Radial fluid flow in the spinal cord has previously been demonstrated in computational models with permeable cord tissue ¹⁷.

This study demonstrates the effect of a patent central spinal canal on pressures and fluid movement in the spinal cord. Where a central canal is present, radially directed pressure gradients and fluid movement occur. The effects of asymmetric caudad and craniad CSF flow and tapering of the spinal canal on a spinal cord model warrant additional study. The location of open segments of the central spinal canal varies with age and between subjects ³⁰, with the result that spinal cord fluid fluxes vary between individuals.

Conclusions

The study shows that a central canal in a spinal cord model affects the pressures in the spinal cord, causing radial pressure gradients and radial fluid flux. The effect of the central canal varies with its length. Since the human spinal cord has irregularly spaced patent segments of the central canal, radial pressure patterns may vary along the length of the adult human cord.