A Novel Structure-aware Sparse Learning Algorithm for Brain Imaging Genetics

Abstract

Brain imaging genetics is an emergent research field where the association between genetic variations such as single nucleotide polymorphisms (SNPs) and neuroimaging quantitative traits (QTs) is evaluated. Sparse canonical correlation analysis (SCCA) is a bi-multivariate analysis method that has the potential to reveal complex multi-SNP-multi-QT associations. Most existing SCCA algorithms are designed using the soft threshold strategy, which assumes that the features in the data are independent from each other. This independence assumption usually does not hold in imaging genetic data, and thus inevitably limits the capability of yielding optimal solutions. We propose a novel structure-aware SCCA (denoted as S2CCA) algorithm to not only eliminate the independence assumption for the input data, but also incorporate group-like structure in the model. Empirical comparison with a widely used SCCA implementation, on both simulated and real imaging genetic data, demonstrated that S2CCA could yield improved prediction performance and biologically meaningful findings.

1 Introduction

Brain imaging genetics is an emerging research field aiming to identify associations between genetic factors such as single nucleotide polymorphisms (SNPs) and quantitative traits (QTs) extracted from neuroimaging data. While univariate analyses [9] have been widely used to discover single-SNP-single-QT associations, recent studies have also started to perform regression analyses [5] to examine the joint effect of multiple SNPs on one or a few QTs, and bi-multivariate analyses [4, 6, 10, 12] to examine complex multi-SNP-multi-QT associations.

Sparse canonical correlation analysis (SCCA) [7, 14] is a bi-multivariate analysis method that has been applied to both real [6] and simulated [4] imaging genetics data, as well as other omics data sets [2, 3, 7, 14]. Most existing SCCA algorithms use the soft threshold strategy for solving the Lasso [7, 14] or group Lasso [4, 6] regularization terms. However, the soft threshold approach requires the input data X to have an orthonormal design X^TX = I (see Section 10 in [11]), meaning that the features in the data should be independent from each other. However, for neuroimaging and genetics data, correlation usually exists among regions of interest (ROIs) in the brain and among linkage disequilibirum (LD) blocks in the genome. Simply treating the covariance of the input data as an identity or diagonal matrix will inevitably limit the capability of identifying meaningful imaging genetic associations.

One possible solution to address this issue is to orthogonalize the input data by performing principal component analysis (PCA) before running SCCA. However, we aim to identify relevant imaging and genetic markers, and thus prefer a sparse model. The combined PCA and SCCA strategy cannot achieve this goal, since PCA loadings on the original imaging and genetic markers are non-sparse.

To overcome this limitation, in this paper, we propose a novel structure-aware SCCA (denoted as S2CCA) algorithm for brain imaging genetics applications to achieve the following two goals: (1) our algorithm is not based on the soft threshold framework and eliminates the independence assumption for the input data; (2) our model can incorporate group-like structure (e.g., voxels in an ROI, or SNPs in an LD block) to yield more stable and biologically more meaningful results than conventional SCCA model. We perform an empirical comparison between the proposed S2CCA algorithm and a widely used SCCA implementation in the PMD software package (http://cran.r-project.org/web/packages/PMA/) [14] using both simulated and real imaging genetic data. The empirical results demonstrate that the proposed S2CCA algorithm can yield improved prediction performance and biologically meaningful findings.

2 Structure-aware SCCA (S2CCA)

We denote vectors as boldface lowercase letters and matrices as boldface upper-case ones. For a given matrix M = (m_ij), we denote its i -th row and j -th column to mⁱ and m^j respectively. Let X = {x₁, …, x_n}^T ⊆ ℜ^p be the SNP data and Y = {y₁, …, y_n}^T ⊆ ℜ^q be the imaging QT data, where n is the number of participants, p and q are the numbers of SNPs and QTs, respectively. Canonical correlation analysis (CCA) seeks linear combinations of variables in X and Y which maximize the correlation between Xu and Yv:

$$\underset{\mathbf{u},\mathbf{v}}{max}{\mathbf{u}}^T{\mathbf{X}}^T\mathbf{Yv}s.t.{\mathbf{u}}^T{\mathbf{X}}^T\mathbf{Xu}=1,{\mathbf{v}}^T{\mathbf{Y}}^T\mathbf{Yv}=1$$ (1)

where u and v are canonical vectors or weights. Two major weaknesses of CCA are that it requires the number of observations n to exceed the combined dimension of X and Y and that it produces nonsparse u and v which are difficult to interpret. The sparse CCA (SCCA) method removes these weaknesses by maximizing the correlation between Xu and Yv subject to the weight vector constraints P₁(u) ≤ c₁ and P₂(v) ≤ c₂. The penalized matrix decomposition (PMD) toolkit [14] provided a widely used SCCA implementation, where the L₁ penalty $P(A)={\sum }_{k=1}^p\mid A(k)\mid$ was used for both P₁ and P₂. As mentioned earlier, similar to most SCCA methods, PMD employed the soft threshold strategy for solving the L1 penalty term, which required the input data to have an orthonormal design X^TX = I and Y^TY = I (see Section 10 in [11]). This independence assumption usually does not hold in imaging genetic data (e.g., correlated voxels in an ROI, correlated SNPs in an LD block), and thus inevitably limits the capability of identifying meaningful imaging genetic associations.

To overcome this limitation, we propose a novel structure-aware SCCA (denoted as S2CCA) algorithm to not only eliminate the independence assumption for the input data, but also incorporate group-like structure in the model. Instead of using L₁, we define a group L₁ constraint on P₁ and P₂ as follows:

$$\begin{array}{l}{P}_1={\Vert \mathbf{u}\Vert }_G={\gamma }_1\sum _{k_1=1}^{K_1}\sqrt{\sum _{i\in {\pi }_{k_1}}{u}_i^2}={\gamma }_1\sum _{k_1=1}^{K_1}{\Vert {\mathbf{u}}^{k_1}\Vert }_2,\\ P_2={\Vert \mathbf{v}\Vert }_G={\gamma }_2\sum _{k_2=1}^{K_2}\sqrt{\sum _{i\in {\pi }_{k_2}}{v}_i^2}={\gamma }_2\sum _{k_2=1}^{K_2}{\Vert {\mathbf{v}}^{k_2}\Vert }_2.\end{array}$$ (2)

In Eq. (2), SNPs are partitioned into K₁ groups ${\mathit{\Pi }}_1={\{{\pi }_{k_1}\}}_{k_1=1}^{K_1}$, such that ${\{u_i\}}_{i=1}^{m_{k_1}}\in {\pi }_{k_1}$, and m_k1 is the number of SNPs in π_k1; and imaging QTs are partitioned into K₂ groups ${\mathit{\Pi }}_2={\{{\pi }_{k_2}\}}_{k_2=1}^{K_2}$, such that ${\{v_i\}}_{i=1}^{m_{k_2}}\in {\pi }_{k_2}$, and m_k2 is the number of QTs in π_k2. || · ||_G is the constraint for the group structure. In this work, we partition voxels using AAL ROIs and SNPs using LD blocks.

Now the S2CCA objective function can be formally written as follows:

$$\begin{array}{c}\underset{\mathbf{u},\mathbf{v}}{max}{\mathbf{u}}^T{\mathbf{X}}^T\mathbf{Yv}-{\gamma }_1\sum _{k_1=1}^{K_1}{\Vert {\mathbf{u}}^{k_1}\Vert }_2-{\gamma }_2\sum _{k_2=1}^{K_2}{\Vert {\mathbf{v}}^{k_2}\Vert }_2\\ s.t.{\mathbf{u}}^T{\mathbf{X}}^T\mathbf{Xu}=1,{\mathbf{v}}^T{\mathbf{Y}}^T\mathbf{Yv}=1,\end{array}$$ (3)

Using Lagrange multipliers, Eq. (3) can be transformed as follows:

$$\underset{\mathbf{u},\mathbf{v}}{max}{\mathbf{u}}^T{\mathbf{X}}^T\mathbf{Yv}-{\gamma }_1{\Vert \mathbf{u}\Vert }_G-{\gamma }_2{\Vert \mathbf{v}\Vert }_G-{\beta }_1{\Vert \mathbf{Xu}\Vert }_2^2-{\beta }_2{\Vert \mathbf{Yv}\Vert }_2^2$$ (4)

Taking the derivative about u and v and setting them to zero, we have

$${\mathbf{X}}^T\mathbf{Yv}/2-{\gamma }_1{\mathbf{D}}_1\mathbf{u}-{\beta }_1{\mathbf{X}}^T\mathbf{Xu}=0,$$ (5)

$${\mathbf{Y}}^T\mathbf{Xu}/2-{\gamma }_2{\mathbf{D}}_2\mathbf{v}-{\beta }_2{\mathbf{Y}}^T\mathbf{Yv}=0,$$ (6)

where D₁ is the block diagonal matrix of the k₁-th diagonal block as $\frac{1}{2{\Vert {\mathbf{u}}^{k_1}\Vert }_2}$, and D₂ is the block diagonal matrix of the k₂-th diagonal block as $\frac{1}{2{\Vert {\mathbf{v}}^{k_2}\Vert }_2}$.

Algorithm 1.

Structure-aware SCCA (S2CCA)

Require.
X = {x1, …, xn}T, Y = {y1, …, yn}T
Ensure:
Canonical vectors u and v.
1:	t = 1, Initialize ut ∈ ℜp×1, vt ∈ ℜq×1;
2:	while not converged do
3:	Calculate the block diagonal matrix D1t, where the k1-th diagonal is $\frac{1}{2{\Vert {\mathbf{u}}_t^{k_1}\Vert }_2}$;
4:	ut+1 = (β1XTX + γ1D1t)−1XTYvt/2; Scale ut+1 so that ${\mathbf{u}}_{t+1}^T{\mathbf{X}}^T\mathbf{X}{\mathbf{u}}_{t+1}=1$;
5:	Calculate the block diagonal matrix D2t, where the k2-th diagonal is $\frac{1}{2{\Vert {\mathbf{v}}_t^{k_2}\Vert }_2}$;
6:	vt+1 = (β2YTY + γ2D2t)−1YTXut+1/2; Scale vt+1 so that ${\mathbf{v}}_{t+1}^T{\mathbf{Y}}^T\mathbf{Y}{\mathbf{v}}_{t+1}=1$;
7:	t = t + 1.
8:	end while

With v fixed, we can use an approach similar to G-SMuRFS [13] to solve for u. With u fixed, we can do the same to solve for v. We propose Algorithm 1 to alternatively compute u and v until the result converges. We use max{|δ| | δ ∈ (u_t+1 − u_t)} < 10⁻⁵ and max{|δ| | δ ∈ (v_t+1 − v_t)} < 10⁻⁵ as stopping criterion, and nested cross-validation to automatically tune parameters γ₁, γ₂, β₁ and β₂.

3 Experimental Results

3.1 Results on Simulation Data

We first performed a comparative study between S2CCA and PMD using simulated data. We used the following procedure to generate two sets of synthetic data X and Y, both with n = 1000 and p = q = 50: 1) We created a random positive definite non-overlapping group structured covariance matrix M. 2) Data set Y with covariance structure M was calculated through Cholesky decomposition. 3) We repeated the above two steps to generate another data set X. 4) Canonical loadings u and v were set based on the group structures of X and Y respectively, where all the variables within the group share the same weights. In this initial study, for simplicity, we selected only one group in Y to be associated with 4 groups in X. 5) The portion of the specified group in Y were replaced based on the u, v, X and the assigned correlation. We generated 7 pairs of X and Y with correlations ranging from 0.45 to 0.99. The canonical loadings and group structure remained the same across all the synthetic data sets.

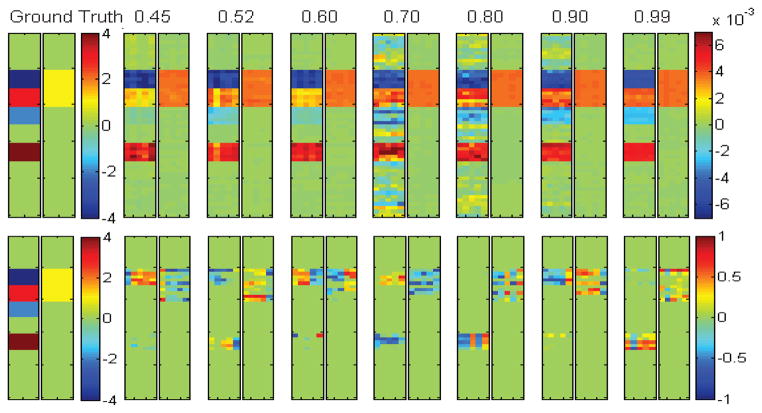
We applied S2CCA and PMD to all seven data sets. The regularization parameters were optimally tuned using a grid search from 10⁻⁵ to 10⁵ through nested 5-fold cross-validation. The true and estimated u and v values are shown in Fig. 1. Due to different normalization strategies, the weights yielded through S2CCA and PMD showed different scales. Yet the overall profile of the estimated u and v values from S2CCA remained consistent with the ground truth across the entire range of tested correlation strengths (from 0.45 to 0.99), while PMD only identified an incomplete portion of all the signals. Furthermore, we also examined the correlation in the test set computed using the learned CCA models from the training data for both methods. The left part of Table 1 demonstrates that S2CCA outperformed PMD consistently and significantly, and it could accurately reveal the embedded true correlation even in the test data. The right part of Table 1 demonstrates the sensitivity and specificity performance using area under ROC (AUC), where S2CCA also significantly outperformed PMD no matter whether the correlation was weak or strong. From the above results, it can also be observed that S2CCA could identify the correlations and signal locations not only more accurately but also more stably.

Fig. 1.

5-fold trained weights of u and v. Ground truth of u and v are shown in the most left two panels. S2CCA results (top row) and PMD results (bottom row) are shown in the remaining panels, corresponding to true correlation coefficients (CCs) ranging from 0.45 to 0.99. For each panel pair, the five estimated u values are shown on the left panel, and the five estimated v values are shown on the right panel.

Table 1.

Five-fold cross-validation performance on synthetic data: mean±std is shown for estimated correlation coefficients and AUC of the test data using the trained model. P-value of paired t-test between S2CCA and PMD results is also shown.

True CC	Correlation Coefficient (CC)			Area under ROC (AUC)
	S2CCA	PMD	p	S2CCA:u	PMD:u	p	S2CCA:v	PMD:v	p
0.445	0.42±0.05	0.27±0.08	7E-4	1.00±0	0.68±0.02	4E-6	1.00±0	0.84±0.02	4E-5
0.526	0.48±0.04	0.32±0.11	4E-3	1.00±0	0.66±0.01	3E-7	1.00±0	0.87±0.06	3E-3
0.594	0.56±0.07	0.39±0.12	2E-3	1.00±0	0.64±0.01	3E-7	1.00±0	0.81±0.05	7E-4
0.697	0.67±0.01	0.47±0.07	2E-3	0.94±0.02	0.66±0.03	6E-5	1.00±0	0.85±0.04	3E-4
0.814	0.80±0.04	0.49±0.06	7E-5	0.98±0.02	0.63±0.01	1E-6	1.00±0	0.83±0.04	5E-4
0.906	0.90±0.01	0.56±0.06	9E-5	1.00±0	0.66±0.01	4E-7	1.00±0	0.82±0.04	4E-4
1.000	0.99±0.00	0.65±0.04	2E-5	1.00±0	0.66±0.01	3E-7	1.00±0	0.86±0.07	4E-3

3.2 Results on Real Neuroimaging Genetics Data

S2CCA and PMD were also compared using real neuroimaging and SNP data. The magnetic resonance imaging (MRI) and SNP data were downloaded from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database. One goal of ADNI has been to test whether serial MRI, positron emission tomography, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early AD. For up-to-date information, see www.adni-info.org.

This ADNI study included 176 AD, 363 MCI and 304 healthy control (HC) non-Hispanic Caucasian participants (Table 2). Structural MRI scans were processed with voxel-based morphometry (VBM) in SPM8 [1, 8]. Briefly, scans were aligned to a T1-weighted template image, segmented into gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF) maps, normalized to MNI space, and smoothed with an 8mm FWHM kernel. Rather than using ROI summary statistics, in this study we subsampled the whole brain and examined correlations between the voxels (GM density measures) and SNPs. Totally 465 voxels spanning all brain ROIs were extracted. All SNPs within LD block of APOE e4 were extracted from an imputed genetic data set containing only SNPs in Illumina 610Q and/or OmniExpress arrays after basic quality control. As a result, four SNPs (rs429358, rs439401, rs445925, rs534007) from this LD block were included in this study. Using the regression weights derived from the healthy control participants, VBM and genetic measures were pre-adjusted for removing the effects of the baseline age, gender, education, and handedness.

Table 2.

Participant characteristics.

	HC	MCI	AD
Num	304	363	176
Gender(M/F)	111/193	235/128	95/81
Handedness(R/L)	190/14	329/34	166/10
Age (mean±std)	76.07±4.99	74.88±7.37	75.60±7.50
Education (mean±std)	16.15±2.73	15.72±2.30	14.84±3.12

Both S2CCA and PMD were performed on the normalized VBM and SNP measurements. Similar to the previous analysis, 5-fold nested cross-validation was applied to optimally tune the parameters. Table 3 shows 5-fold cross-validation canonical correlation results, indicating that S2CCA significantly and consistently outperformed PMD in terms of identifying high correlations from the training data and replicating those in the testing data. Shown in Fig. 2(a) are the canonical loadings trained from 5-fold cross-validation, suggesting relevant imaging and genetic markers. Although the S2CCA model did not explicitly impose sparsity on individual voxels, it was still able to discover a very small number of relevant ROIs for easy interpretation due to the imposed group sparsity. The strongest imaging signals came from the right hippocampus, which were inversely correlated with APOE e4 allele rs429358. In contrast, despite the flat sparsity design, PMD identified many more ROIs than S2CCA (Fig. 2(ab)), making results hard to interpret. In addition, comparing the results from 5 cross-validation trials, S2CCA yielded a more stable and consistent pattern than PMD. It is reassuring that S2CCA identified a well-known correlation between hippocampal morphometry and APOE in an AD cohort, which shows the promise of S2CCA to correctly identify biologically meaningful imaging genetic associations.

Table 3.

Five-fold cross validation canonical correlation results on real data: the CCA models learned from the training data were used to estimate the correlation coefficients between canonical components for both training and testing sets. P-values of paired t-tests were obtained for comparing S2CCA and PMD results.

Correlation coefficients	S2CCA					PMD					p-value
	F1	F2	F3	F4	F5	F1	F2	F3	F4	F5
Training	0.28	0.27	0.27	0.27	0.27	0.26	0.26	0.26	0.26	0.24	0.016
Testing	0.21	0.24	0.28	0.23	0.26	0.20	0.21	0.21	0.20	0.24	0.017

Fig. 2.

Comparison of S2CCA and PMD canonical vectors in cross-validation trials: (a) 5-fold canonical loadings of u and v on 4 APOE SNPs and 465 VBM measures; (b) mapping the average of imaging canonical loadings v of 5 cross-validation trials onto the brain.

4 Conclusions

Most existing SCCA algorithms (e.g., [4, 6, 7, 12, 14]) are designed using the soft threshold strategy, which assumes that the features in the data are independent from each other. This independence assumption usually does not hold in imaging genetic data, and thus limits the capability of yielding optimal results. We have proposed a novel structure-aware sparse canonical correlation analysis (S2CCA) algorithm, which not only removes the above independence assumption, but also takes into consideration group-like structure in the data. We have compared S2CCA with PMD (a widely used SCCA implementation) on both synthetic data and real imaging genetic data. The promising empirical results demonstrate that S2CCA significantly outperformed PMD in both cases. In addition, S2CCA accurately recovered the true signals from the synthetic data and yielded improved canonical correlation performance and biologically meaningful findings from real data. This study is an initial attempt to remove the feature independence assumption many existing SCCA methods have. Since joint multivariate modeling of imaging genetic data is computationally and statistically challenging, we downsampled our data via a targeted APOE analysis to reduce computational burden and overfitting risk. The S2CCA sparsity was designed to reduce model complexity and further overcome overfitting. Future directions include evaluating S2CCA using more realistic settings and expanding S2CCA to address efficiency and scalability.